Abstract
Key points
The standard method of magnetic nerve activation using pulses of high current in coils has drawbacks of high cost, high electrical power (of order 1 kW), and limited repetition rate without liquid cooling.
Here we report a new technique for nerve activation using high speed rotation of permanent magnet configurations, generating a sustained sinusoidal electric field using very low power (of order 10 W).
A high ratio of the electric field gradient divided by frequency is shown to be the key indicator for nerve activation at high frequencies.
Activation of the cane toad sciatic nerve and attached gastrocnemius muscle was observed at frequencies as low as 180 Hz for activation of the muscle directly and 230 Hz for curved nerves, but probably not in straight sections of nerve.
These results, employing the first prototype device, suggest the opportunity for a new class of small low‐cost magnetic nerve and/or muscle stimulators.
Abstract
Conventional pulsed current systems for magnetic neurostimulation are large and expensive and have limited repetition rate because of overheating. Here we report a new technique for nerve activation, namely high‐speed rotation of a configuration of permanent magnets. Analytical solutions of the cable equation are derived for the oscillating electric field generated, which has amplitude proportional to the rotation speed. The prototype device built comprised a configuration of two cylindrical magnets with antiparallel magnetisations, made to rotate by interaction between the magnets’ own magnetic field and three‐phase currents in coils mounted on one side of the device. The electric field in a rectangular bath placed on top of the device was both numerically evaluated and measured. The ratio of the electric field gradient on frequency was approximately 1 V m−2 Hz−1 near the device. An exploratory series of physiological tests was conducted on the sciatic nerve and attached gastrocnemius muscle of the cane toad (Bufo marinus). Activation was readily observed of the muscle directly, at frequencies as low as 180 Hz, and of nerves bent around insulators, at frequencies as low as 230 Hz. Nerve–muscles, with the muscle elevated to avoid its direct activation, were occasionally activated, possibly in the straight section of the nerve, but more likely in the nerve where it curved up to the muscle, at radius of curvature 10 mm or more, or at the nerve end. These positive first results suggest the opportunity for a new class of small, low‐cost devices for magnetic stimulation of nerves and/or muscles.
Key points
The standard method of magnetic nerve activation using pulses of high current in coils has drawbacks of high cost, high electrical power (of order 1 kW), and limited repetition rate without liquid cooling.
Here we report a new technique for nerve activation using high speed rotation of permanent magnet configurations, generating a sustained sinusoidal electric field using very low power (of order 10 W).
A high ratio of the electric field gradient divided by frequency is shown to be the key indicator for nerve activation at high frequencies.
Activation of the cane toad sciatic nerve and attached gastrocnemius muscle was observed at frequencies as low as 180 Hz for activation of the muscle directly and 230 Hz for curved nerves, but probably not in straight sections of nerve.
These results, employing the first prototype device, suggest the opportunity for a new class of small low‐cost magnetic nerve and/or muscle stimulators.
Abbreviations
- MQS
magnetoquasistatics
- NdFeB
neodymium iron boron
- TENS
transcutaneous electrical nerve stimulation
Introduction
The activation of nerves is being used, or trialled, for the treatment of many medical conditions including: pain (Johnson, 2014), epilepsy (Jobst, 2010), migraine (Schoenen et al. 2013), incontinence (Horrocks et al. 2014), muscle atrophy (Robinson & Snyder‐Mackler, 2007), depression and Parkinson's disease (Kobayashi & Pascual‐Leone, 2003). Presently, there are three classes of neurostimulators. Transcutaneous electrical nerve stimulation (TENS) devices are widely used for masking pain with a tingling sensation and to produce muscle contraction (Robinson & Snyder‐Mackler, 2007). They are low cost (ca US$100) but they use surface electrodes to pass current through the skin, which can activate nociceptive nerves causing pain and burning sensations, or indeed burning (Gondin et al. 2011). Implanted electrical neurostimulators avoid this drawback and can activate specific nerves, but they are expensive (ca US$10,000) and require surgery, with consequent infection risk. Devices of the third type activate nerves non‐invasively by employing a changing magnetic flux density B penetrating the body to generate an electric field E via Faraday's Law:
| (1) |
Existing magnetic neurostimulators repeatedly charge and discharge a capacitor bank to drive short pulses of high current in a coil placed outside the body (Barker, 1991). They are expensive (exceeding US$10,000), high power (of order 1 kW) and large (usually trolley‐mounted) devices. The high current generates high ohmic heating in the coil, and if a high pulse repetition rate is used, pumped liquid cooling is required through the coil, adding to complexity and cost. The MagPro X100 can provide 100 pulses s−1, but only at 30% of full amplitude (MagVenture, 2007).
In contrast, moving permanent magnets can provide a time‐varying magnetic field without any heating. The latest high‐strength neodymium iron boron (NdFeB) magnets have magnetic remanence of 1.45 T and are equivalent to a 1.1 kA surface current density loop for every millimetre of magnet thickness (Watterson, 2000). However, there are no reports in the product or academic literature of nerve or muscle activation solely from the motion of permanent magnets. Nikken Inc. markets the ‘Biaxial Powermag’ which spins a low‐strength barium ferrite spherical magnet about two axes (Nikken, 2014) at up to 1500 r.p.m., but there is no claim of nerve activation in the related patent (Ardizzone, 2003) and the device does not cause ‘any discernible sensory effects’ (Weintraub et al. 2009). A device which rotates three magnets positioned near a subject's head to produce electromagnetic fields of frequency at the subject's alpha‐wave, 8–13 Hz, is being trialled as a treatment for major depression (Jin & Phillips, 2014; Leuchter et al. 2015). Jin & Phillips (2014) assert that ‘the energy of the sinusoidal magnetic field is estimated at less than 1% of a standard rTMS [repetitive transcranial magnetic stimulation] device’ (without giving details of how they calculated that estimate) and infer that the stimulation is ‘sub‐threshold and does not cause neuronal depolarization, but instead uses low level alternating induced electric field to entrain neuronal firing’. Thus the authors assert that the imposed electric field modulates the endogenous alpha‐wave, but that the electric field if acting alone would not cause activation of any nerve cell.
A complementary range of medical applications might arise if, for frequencies and electric field amplitudes which were sub‐threshold for the activation of a particular nerve, the oscillating electric field was found to block an action potential travelling along the nerve. Such nerve conduction blocking by AC biphasic electrical stimulation generally requires frequencies greater than 1 kHz (Kilgore & Bhadra, 2014) but partial blocking has been observed at 600 Hz (Shaker et al. 1998). Applications could include the blocking of motor nerves to treat spasticity and the blocking of sensory nerves to treat peripheral nerve pain (Kilgore & Bhadra, 2014).
Here we report a new technique for direct magnetic activation of nerves and muscles, namely the high speed rotation of a configuration of permanent magnets in a device which resembles a motor, but one with no mechanical output and no ferromagnetic material. The electromagnetic field theory is first developed and a new analysis is made of previously published data on magnetic nerve activation. The Methods section gives mechanical and electrical details of the prototype device made, as well as details of the physiological testing. The Results section compares the measured and calculated electric fields generated by the device and reports results from a range of in vitro experiments undertaken on the sciatic nerve and attached gastrocnemius muscle from cane toads (Bufo marinus).
Electromagnetic field theory
Hereafter, we consider the electric field E generated inside the body by a rotating configuration of permanent magnets, which can be evaluated as the solution of eqn (1) of form:
| (2) |
where the magnetic vector potential A satisfies and the Coulomb gauge . In a conducting medium of isotropic electrical resistivity η, the electric field E drives a current density J obeying Ohm's Law:
| (3) |
For an oscillation of frequency f, the penetration skin depth δ of the magnetic field into the medium (assumed non‐magnetic) is
| (4) |
where μ0 is the vacuum magnetic permeability (Lorrain & Corson, 1970). Over the range 0.1–1 kHz, the resistivity of human tissue can be stated as generally in the range 1–10 Ω m (Gabriel et al. 1996). The smallest implied penetration depth, for 1 kHz and 1 Ω m, is δ = 16 m, which is very much larger than human anatomical dimensions. Thus the magnetic field generated by eddy currents is negligible relative to the applied magnetic field and A can be approximated as that from the magnets alone, in vacuum. The components of A can therefore be taken as constant when specified relative to a co‐ordinate frame rotating with the rotating magnet configuration. Suppose the rotating cylindrical co‐ordinate frame aligns with the fixed space frame at and that the rotation angular velocity is ωr so that , and . In terms of the initial magnetic vector potential = , the electric field component from the magnet configuration rotation alone, as if in vacuum, is
| (5) |
which is seen to be proportional to the rotational speed.
Away from the nerve fibre, the charge build‐up needed to generate the potential field is very small and the magnetoquasistatics (MQS) approximation (Larsson, 2007) can be made, entailing:
| (6) |
Substitution of J from eqns (2) and (3) into eqn (6) gives the equation to be solved for the potential external to a nerve fibre φe:
| (7) |
which simplifies to Laplace's equation if η is uniform. The boundary condition assumed on the skin surface is that the normal component of current is negligible, , hence by eqns (2) and (3):
| (8) |
The above approximations cannot be employed to determine the electric potential interior to the axon φi as the capacitive effect across the semi‐insulating myelin membrane cannot be ignored. Instead, the potential difference across the nerve fibre membrane can be modelled prior to activation by the one‐dimensional ‘cable equation’ (Hodgkin & Huxley, 1952; Basser & Roth, 1991; Nagarajan & Durand, 1996):
| (9) |
where s is distance along the nerve fibre, is the tangential component along the nerve of the electric field external to the nerve, λ is a length constant, τ is a time constant, and v r is a resting potential difference sustained by ion pumps in the membrane, typically ca −70 mV. By eqn (3), the boundary condition of zero interior current from a nerve fibre end requires zero tangential component of the interior electric field at the fibre end, i.e. . By eqn (2) and continuity of across the nerve fibre membrane, the boundary condition at the nerve fibre ends for any magnetic excitation is
| (10) |
(with b > a assumed).
This is a much simpler, though equivalent, condition to that used by Rotem & Moses (2008) who imposed at the nerve end but also applied a δ‐function at the end, which when eqn (9) is integrated infinitesimally in from the end results in eqn (10) as the effective boundary condition. Activation of a nerve action potential occurs when v rises (is depolarised) to a threshold value, usually ca −50 mV (Malmivuo & Plonsey, 1995). The term is called the ‘activating function’.
For any rotating magnet configuration (or any rotating current configuration with constant current amplitude), the amplitude of the electric field increases proportional to the rotation frequency, since by eqn (5) both the magnet in vacuum component E m and the implied boundary forcing terms (E m)n in eqn (8) are proportional to the rotation angular frequency ωr. If p magnet pole pairs are disposed around the configuration, then the electrical angular frequency is , related to the frequency f (in Hz) by . The ratio of the maximum amplitude of the activating function over a cycle at a point divided by frequency,
| (11) |
is thus independent of frequency for a rotating magnet configuration.
For an electric field which is purely sinusoidal in time, solutions of the cable equation are sought via separation of variables. Using bold face italic upper case letters to denote complex phasors, in particular:
| (12) |
where Re denotes the Real part and i is the imaginary unit, the cable eqn (9) becomes the following complex linear diffusion equation:
| (13) |
with boundary condition eqn (10) at the nerve fibre ends becoming:
| (14) |
For electric fields which are periodic in time but not purely sinusoidal, a Fourier series decomposition can be used and the solution can be obtained by summing over all harmonics.
Analytical solutions to eqn (13) can be obtained by a convolution with a Green's function obtained from the solution for delta function forcing, under given boundary conditions (Rotem & Moses, 2006; Cole et al. 2011). For example, if the nerve fibre is very long and the boundary conditions are taken as
| (15) |
then the solution to eqn (13) is
| (16) |
where σ involves a principal complex square root:
| (17) |
For certain limits, explicit results can be established for eqns (13) and (14) by considering the order of magnitudes of the terms of eqn (13):
| (18) |
where l is the length scale of variation of (hence also of V), and V m and F m are the maximum magnitudes of V and F.
In the limit of low frequency, the scaling analysis (18) shows that providing either or , the term of eqn (13) becomes negligible compared to the other terms on the left‐hand side. There is no other dependence on ω in eqns (13) and (14), other than dependence of E es (and ) on ω. Thus, in the low frequency limit, V m is governed by the activating function and the boundary E es with no other reference to ω. Because of the factor in eqn (11), for V m to reach a given activation threshold magnitude V th (e.g. 20 mV), the required maximum magnitude F th of F would have to increase inversely proportional to frequency as frequency approaches zero.
An approximate analytic solution can be given to eqns (13) and (14) when the scaling analysis (eqn (18)) suggests that the first term, the diffusion term, should be much smaller than the other terms on the left‐hand side of eqn (13), which is when the following condition applies:
| (19) |
Boundary layer theory (Bender & Orszag, 1978) shows that the diffusion term can be neglected away from the ends, but forms a ‘dominant‐balance’ with the V terms over boundary layers at the ends in order that the boundary conditions (eqn (14)) can be satisfied. The solution over each boundary layer is a steep exponentially decaying oscillation, and the global first‐order solution can be written
| (20) |
where σ is given by eqn (17). If the electric field at a nerve end is non‐trivial, then by eqn (19) the boundary layer terms dominate at the ends and the maximum potential amplitude will occur at the end with the higher electric field amplitude and have amplitude
| (21) |
In the low frequency limit , the limiting condition (eqn (19)) applies if , and by eqn (17), and eqn (21) simplifies to . This boundary layer solution with was noted by Miranda et al. (2007) for a semi‐infinite nerve fibre in a steady state uniform electric field. In the high frequency limit , the limiting condition (eqn (19)) always applies, and by eqn (17), and eqn (21) simplifies to . Both these limiting V m values for low and high frequency were observed by Rotem & Moses (2008, p. 5077) in numerical solutions for low and high τ. For a rotating magnet excitation, in which is proportional to ω, would increase as . Thus in the high frequency limit, if the electric field is significant at an end of the nerve, then activation will first occur at the end with the higher electric field and the threshold amplitude of the electric field and its related F th would fall with frequency, scaling as .
Assuming that eqn (19) holds and that the electric field is negligible at the nerve ends, then the boundary layer terms of eqn (20) vanish leaving
| (22) |
showing that V depends on the local . To reach threshold amplitude V th thus requires, in terms of the metric F defined by eqn (11):
| (23) |
where
| (24) |
If , then eqn (19) holds for all ω and so eqn (23) holds for all ω. In the limit , eqn (19) holds whatever the value of , and F th approaches a constant value:
| (25) |
If eqn (19) is not satisfied, i.e. if the diffusion term is not negligible in (13), then the diffusion term can be expected to reduce the peak in , hence the threshold F th should be greater than that given by eqn (23). Thus the high frequency limit value F b should be a base value for F th.
In the low frequency limit, eqn (19) holds if , and eqn (22) simplifies to
| (26) |
showing the explicit dependence of V on the activating function with no other dependence on ω.
In the high frequency limit, eqn (19) always holds, and eqn (22) simplifies to
| (27) |
showing that the amplitude of the membrane potential depends only on the local value of the metric F, defined by eqn (11). For real and negative, i.e. for a negative cosine wave, eqn (27) shows that is a positive sine wave. Thus activation should first occur near the end of a negative half cycle of . This can be understood in terms of the cable eqn (9), which becomes a balance between the time derivative term and the activating function in the high frequency limit. Since the change in v depends on times its duration, it is not alone which governs the change in v but the product of with its duration. Division of by the frequency is equivalent to multiplying by the period, and so the metric F quantifies the electric field gradient times its duration (alternatives would have been to multiply by half the period, being the duration of a lobe of the sine wave, or to divide by angular frequency, but using frequency and introducing Hz in the metric's unit ensures certainty in the metric's evaluation).
While the importance of the stimulus duration is well‐known for electrical stimulation, it is often neglected in magnetic stimulation, with emphasis placed on the electric field gradient alone. For example, Davey et al. (1994) examined the threshold activation of an African bullfrog sciatic nerve threaded through the hole in a ferromagnetic toroidal core, wound by a coil excited sinusoidally. Based on pulsed current experimental results by Maccabee et al. (1993), Davey et al. had sought a threshold electric field gradient of with no reference to frequency. However, the observed threshold electric field gradients for their large core (their Table II) ranged by factor 50 from to as the frequency varied from 102 Hz to 104 Hz, so no single threshold electric field gradient can be stated. Instead of using the electric field gradient as the metric, the observations can be much more clearly interpreted when plotted in terms of the metric F proposed above – see our Fig. 1. There is considerable experimental variation, but for each core, F th is seen to decrease with f before settling, by about 1 kHz, to limiting values of about for the large core (axial height 11 mm) and for the small core (height 6.35 mm). The approach of F th to a constant base value is consistent with the conclusion eqn (25) above, given that the nerve ends can be inferred from Fig. 10 of Davey et al. (1994) to be in a region where the electric field is negligible. According to eqn (24), the limiting values for the two cores should be equal, dependent only on nerve properties, and given the uncertainty in numerical differentiation from measurements and the variability in the plotted F, their equality can be considered within the tolerance on their values. The observed increase in F th at low frequency was never as fast as the dependency established analytically above for , equivalently the threshold electric field gradient never settled to a constant value with decreasing f. Lower f may have been needed but magnetic saturation of the core prevented such measurement (and may have also affected the lowest frequency reading since the cores were driven just up to saturation).
Figure 1. Analysis of experimental results in Davey et al. ( 1994 ) .
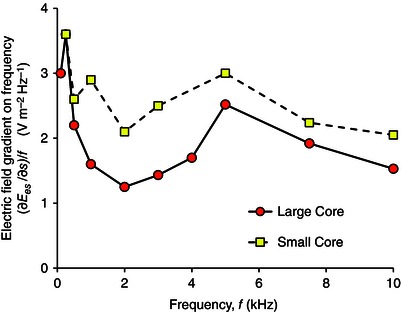
Electric field gradient amplitude on frequency versus frequency for activation threshold of an African bullfrog sciatic nerve.
For any rotating magnet configuration (or magnetic field driven by sinusoidal current if the current amplitude is independent of frequency), F given by eqn (11) is independent of frequency. The magnet configuration will either activate the nerve positioned along a certain path or not depending on whether F is above or below F b, if the rotation speed is taken sufficiently high. The simplicity of this criterion for activation makes F the most useful metric in assessing nerve activation by rotating magnets. A gradient of the parallel component of the electric field along the nerve can be achieved even for a uniform electric field if the nerve is curved, as has been examined for pulsed current magnetic induction (Maccabee et al. 1993; Rotem & Moses, 2006). But for straight nerves, a high straight‐line gradient is needed.
Methods
Ethical approval
The physiological testing reported here was approved by the University of Technology Sydney Animal Care and Ethics Committee and conformed to the Australian NHMRC Code of Practice for the use of animals in research. The authors understand the ethical principles under which The Journal of Physiology operates and confirm that this work complies with The Journal’s animal ethics checklist.
Prototype device magnetic configuration
A number of magnet configurations are proposed in the patent application (Watterson, 2012) for the creation of high electric field gradients. Here we report results on one of those configurations, called a ‘bipole’, comprising two diametrically magnetised cylindrical magnets placed adjacent to each other with opposite magnetisation directions (Fig. 2 A). The electric field component E m from the rotation of these cylindrical magnets is sinusoidal in time at any point. Large E m in opposite directions are created below the oppositely directed magnets (Fig. 2 A). Hence a high gradient is created on the mid‐plane () of the bipole, for z the axial co‐ordinate, axes shown in Fig. 2 A. The use of two adjacent magnets doubles the electric field gradient created on the mid‐plane, compared to one magnet cylinder acting alone. It also doubles the peak component of E m perpendicular to the axis, , on the mid‐plane line (, x = constant), which occurs 90 deg out of phase with the peaks in . The prototype bipole device used two NdFeB magnets, grade N52 from China Rare Earth Magnet Limited (2015), nominal remanence 1.43–1.48 T at 20°C, each with diameter and axial length 30 mm.
Figure 2. First prototype device .
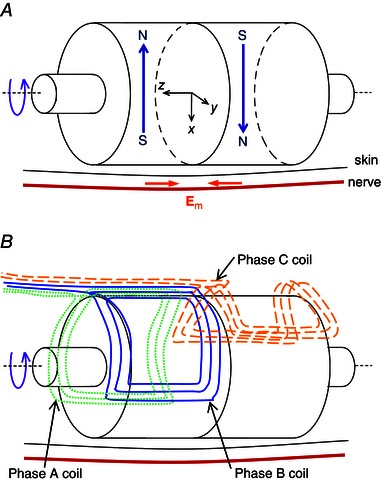
A, schematic diagram of the bipole magnet configuration; open arrows show magnetisation directions and filled arrows show directions of the magnet‐induced electric field E m along a nerve parallel to the axis of the bipole; co‐ordinate axes z along the device rotation axis, x towards the nerve, and y in a plane parallel to the skin. B, schematic diagram of the 3‐phase coil configuration used to drive the bipole magnet configuration.
Prototype device mechanical aspects
NdFeB magnets are brittle and the design of the device rotor must ensure its mechanical robustness. A 0.88 mm thick containment tube of Ti‐6Al‐4V (CEM International Pty Ltd, Coolaroo, VIC, Australia) was heat shrunk onto the magnets, interference fit in diameter approximately 0.06 mm. Calculations using formulae established by Pfister & Perriard (2008) show that this reduced the radial stress in the magnet on its axis for the rotor at 60,000 r.p.m. and 60°C to 17 MPa, less than one‐quarter of a typically quoted tensile strength for NdFeB of 75 MPa (Neorem Magnets Oy, 2015). The actual stress resistance of NdFeB is more complicated than a simple tensile strength, with another NdFeB manufacturer (Vacuumschmelze GmbH & Co., 2014) quoting a minimum stress crack resistance factor (Sih & Macdonald, 1974) of indicating that for stress , an internal crack of width would grow. Such a flaw in the magnet is extremely unlikely, especially assuming inspection of each magnet surface. However, in any case, the chosen tube material yield strength of 880 MPa was safety factor 2 times higher than the stress in the sleeve at 60,000 r.p.m. if the magnets were to split down the middle on a plane containing the axis. The rotor housing forms a primary physical safety barrier; however, as an additional safety precaution for this prototype, the tests reported here were conducted in an acrylic box. The prototype used end‐plates incorporating stub shafts at each end of the rotor, with full ceramic bearings made of zirconia oxide (part number 625 ZRO2 T9; Boca Bearing Company, Boynton Beach, FL, USA). Eddy currents would occur in the balls and stationary bearing races if they were metallic. The dynamic stability against bending modes is not discussed here but is assured for the prototype rotor up to the desired maximum rotation speed of 60,000 r.p.m. (even if the magnets and end‐plates were not glued together or if the magnets were completely shattered and provided no bending stiffness).
Prototype device motor drive
One method of rotating the magnet configuration would be to couple the shaft to a drive motor but that method would have various problems including mechanical loss in the coupling, leakage of magnetic flux across to the drive motor, and increases in the overall device size and cost. Instead, it has been realised that the magnet configuration can be driven to rotate by electromagnetic interaction between its own magnet field and alternating currents in coils suitably positioned nearby. The particular coil configuration chosen to rotate the bipole is that depicted in Fig. 2 B. The requirements sought were that the configuration be a balanced 3‐phase winding with one side of the device free of coils so that the magnets could be as close as possible to the nerve. Though not essential, another objective was to minimise radial build‐up by avoiding overlapping the coils. These objectives were met by using just one coil per phase, two coils at one end of the bipole and one at the other end, with each coil spanning approximately 120 deg. For the low voltage sought, just three turns per coil were required. A highly stranded copper Litz wire (60 strands of American Wire Gauge 38 wire, New England Wire Technologies Corp., Lisbon, NH, USA) was used to minimise the winding eddy loss. The coils were hand‐wound into pockets on the outer surface of an inner housing tube made of ABSPlus thermoplastic (Stratasys Inc., Eden Prairie, MN, USA) by 3‐D printing. That tube was inserted into a thicker outer polycarbonate (AllPlastics Engineering Pty Ltd, Chatswood, NSW, Australia) tube, which was screwed to polycarbonate end plates into which the outer bearing seats were machined. The housing was cut to a planar surface on one side making the magnet to surface separation nominally 2.9 mm. In Fig. 4 A, the width of the lighter strip (of ABSPlus) spanning the device axial centre‐line is 20 mm.
Figure 4. Experimental configurations using the cane toad sciatic–gastrocnemius nerve–muscle preparation .
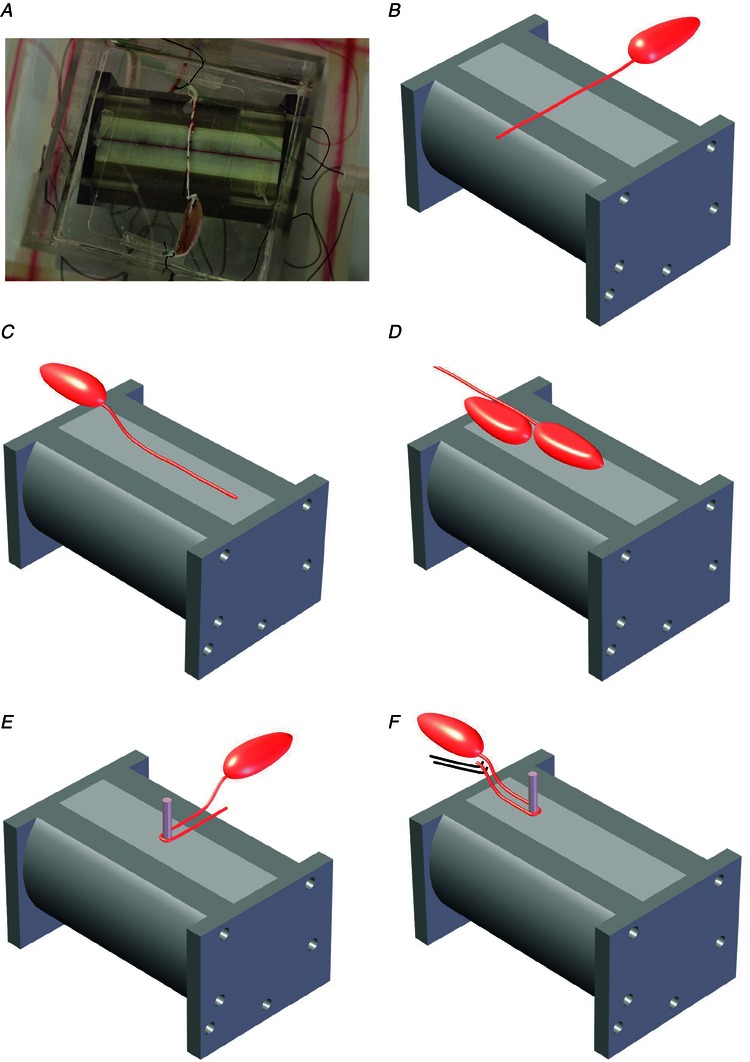
A, photograph of the bipole device underneath the bath housing the nerve–muscle preparation, aligned perpendicular to the bipole axis (Expt 1). B–F, schematic diagrams. B, nerve perpendicular to the bipole axis as in A (Expt 1). C, nerve parallel to the bipole axis, muscle raised onto a platform (Expt 5). D, nerve–muscle parallel to the bipole axis, muscle at its centre dorsal side down and nerve raised (Expt 8); a second muscle with nerve severed is centred on the point of highest parallel electric field. E, nerve wrapped one half‐turn around an insulating pillar positioned at the device centre, nerve approaching pillar perpendicular to the axis (Expt 12). F, test of blocking of action potential propagation created near the ligated end of the nerve by electrical stimulation (Expt 19).
A small commercial sensorless brushless DC motor electronic speed controller from the radio‐controlled toy market was used to drive the motor, namely a Losi ‘Excelorin 1/36 Brushless ESC' (Horizon Hobby LLC, Champaign, IL, USA), with speed varied by a Turnigy ‘CCPM’ (hexTronik Limited, Hong Kong) radio‐control signal generator. The controller's starting algorithm was not designed for a rotor inertia as high as this prototype, and an initial mechanical twist was needed via a rod pushed against the shaft end and rotated by hand or drill. In a custom‐made controller, a suitably long speed ramp can instead be introduced. Inductors (18 turns, core RM12, part number B65815E0160A041, Epcos AG, Munich, Germany) of 52 μH per phase were added to smooth the phase ripple current. Tests confirmed that a small battery is perfectly capable of powering the device, but for the results here a laboratory DC power supply with parallel 3.3 mF smoothing capacitor was used.
For this ‘bipole’ magnet configuration, the rotation frequency, the electromagnetic field frequency and the coil current frequency are all identical since the number of pole pairs is . The frequency was measured using a flux pick‐up coil positioned on the device housing surface, following the outline of the Phase C coil shown in Fig. 2 B. The frequency of the voltage induced by the coil's oscillating flux was inferred by an Agilent DSO6034A oscilloscope and/or an Agilent 34401A digital multimeter. The device was tested up to 60,900 r.p.m. corresponding to 1015 Hz, but was generally run up to 930 Hz requiring a 9.24 V DC supply.
The required total input power varied approximately as the frequency squared with coefficient 3 × 10−5 W Hz−2, for example 7.5 W at 500 Hz, primarily from windage loss and bearing loss (which was minimised by running the bearings unlubricated), but with contributions from inverter loss, copper loss and inductor loss. No balancing machine able to handle the device's high magnetic fields was available for the prototype manufacture; the bearing loss and noise were probably higher due to slight rotor imbalance. Optimisation such as balancing and increasing the winding copper area could reduce the power use, but it is already miniscule compared to pulsed current devices – for example, the 2.3 kW peak power used by the MagPro X100 (MagVenture, 2007).
Electric field measurement
The measured electric field was inferred from voltage measurements made in a rectangular Perspex bath of inner dimensions 85 mm × 85 mm, floor thickness 0.6 mm over a trough 75 mm × 50 mm and 1.9 mm thick elsewhere, filled to depth 20.5 mm over the trough with 0.116 m NaCl solution, resistivity 0.78 Ω m (measured by passage of DC current between aluminium plates in another rectangular container). The voltage probe comprised three twisted enamelled 0.67 mm copper diameter wires (overall diameter with enamel 0.78 mm), with the cut tips of two wires separated horizontally by 5.0 mm and the cut tip of the third wire positioned in the fluid approximately 30 mm away to act as a ground point (earth). The electric field was calculated as half the peak–peak difference between the front tip‐to‐ground tip voltage and the rear tip‐to‐ground tip voltage, divided by the front tip‐to‐rear tip 5 mm separation. The voltage difference measurement represents the integral of the electric field along the probe wires and so the wire to the front probe was made to pass as close as possible past the rear probe wire tip. The subtraction of the voltage difference for the front tip‐to‐ground tip from the voltage difference for the rear tip‐to‐ground tip was performed by a Tektronix ADA400A Differential Preamplifier using 10:1 gain, coupled with a Tektronix 1103 Tekprobe Power Supply to an Agilent DSO1024A oscilloscope. To eliminate noise from the motor controller pulse width modulation switching, the voltage waveform was saved at 301 Hz while the speed decayed from about 320 Hz with the motor controller unpowered. For the electric field parallel to the device axis, the voltage waveform had a considerable third harmonic component approximately half the fundamental component, with a sign such as to increase the peak amplitude. Accurate modelling would require solutions of eqn (13) for each harmonic component.
The measured electric field profiles given below are for the probe tips 2.4−2.5 mm above the trough floor, which has thickness 0.6 mm, when the bath was separated (by graph paper and tape) 0.23 mm above the device, which has a top plane nominally at x = 17.9 mm. The probe assembly was made to travel horizontally by attaching it to a rig with a sliding platform driven by a spring‐loaded screw thread. The metallic rig was kept distant from the device to avoid eddy currents and so some imprecision in the probe location was inevitable. The tolerance on the profile location can be stated as x = 21.2 ± 0.2 mm. Measurements on the same plane were made of the parallel electric field for fluid depths 10.5 mm and 28 mm, and the electric field was found to only very weakly increase with depth, and was about 5% lower for depth 10.5 mm compared to 20.5 mm.
Electric field calculation
The electric field was calculated by Finite Element Analysis using ANSYS APDL for a rectangular bath with fluid between 18.9 mm ≤ x ≤ 39.4 mm (ignoring the variable wall thickness in the actual bath base), −42.5 mm ≤ y ≤ 42.5 mm, and −42.5 mm ≤ z ≤ 42.5 mm. In brief, the electric field (eqn (2)) was calculated in two steps. First, the electric field in vacuum from the rotating magnet configuration was determined at a desired rotor angle by central‐differencing of the calculated A for the rotor at a small angle (5 deg) either side of the desired position. After the normal component of E m on the fluid boundaries was evaluated, the potential field was obtained as the solution of eqn (7) subject to eqn (8), i.e. with the normal component on the boundary necessary to cancel the normal component of E m. The total E was then obtained by the addition as per eqn (2).
In the magnetoquasistatics approximation (Larsson, 2007), since outside the conducting medium, the normal current at the boundary is assumed negligible, , but more precisely, a very small oscillating J n is required to supply the oscillating surface charge distribution to produce the boundary assigned in eqn (8). It was confirmed that for the frequencies and the resistivity of our solution, the actual E n needed to drive this small J n was indeed many orders of magnitude smaller than its components and , confirming the validity of eqn (8).
Physiological testing
An exploratory series of physiological tests was conducted using the prototype device on six sciatic–gastrocnemius nerve–muscle preparations, one from each of six unsexed large cane toads (Bufo marinus). For one toad, the gastrocnemius muscle from the other leg was also used, with sciatic nerve severed. The toads were supplied by a commercial supplier (Peter Douch, Mareeba, QLD, Australia). The toads were housed for up to 14 days in glass aquariums within an atmospherically controlled amphibian housing room. Water was provided in a large bowl and the toads were fed every 3–4 days with crickets. Each toad was killed by cooling at 4°C to a stupor and stunning, followed immediately by decapitation and rapid pithing. Anaesthetics were precluded as they would have degraded nerve function. The sciatic nerve and branches were dissected from the level of the posterior tibial and peroneal nerves at the ankle to their rootlets at the vertebral column. The nerve was typically of length 60 mm and diameter 1 mm and the attached muscle was typically of length 30 mm. Following dissection, the nerve–muscle preparation was ligated using cotton thread around the nerve cut end and around the Achilles’ tendon at the muscle end. The nerve–muscle preparation was then immersed in toad Ringer solution at ambient temperature and of the following composition (in mm): NaCl 79, NaHCO3 24, KCl 3.22, Na2HPO4 3.18, MgSO4 1, d‐glucose 5.55, Hepes 10, CaCl2 1, with the pH adjusted to 7.4 using 1 m NaOH. In the tests described here, the nerve–muscle preparation was positioned in the rectangular Perspex bath described above, with toad Ringer solution generally of depth 11 mm, except for those tests where it is stated that the muscle was raised off the bath floor, for which the depth was 21 mm. The first nerve–muscle preparation was tested in the rectangular bath prior to the trough being machined in its base and those trials do not feature in the results described here, though one trial in a shallow circular Petri dish, base thickness 1 mm, is mentioned. The solution resistivity was 0.74 Ω m, slightly lower than human tissue values. The change in power use with, and without, the bath present due to eddy currents generated in the solution was too low to be recorded within the measurement precision of approximately 1%. This was also the case for the Perspex dish containing a piece of rump steak. Similarly, when the device is placed against human tissue the heating of the tissue should be inconsequential. The nerve–muscle was usually positioned as low as possible in the bath but in some tests the muscle was raised by placing it on a platform (see Video S1 in the online Supporting information) made of perforated synthetic resin‐bonded paper (SRBP), height adjustable by plastic screws, with windows cut in the platform (allowing the nerve to be low and the muscle high at the perimeter, for example). The presence of this insulating platform will have distorted the local electric field. Muscle contraction was used as the indicator for nerve activation, though this could only indicate motor nerve activation, not sensory nerve activation. Electrical probes were deliberately not used in order to prevent the possibility of activation being caused by voltages induced on the probes from the oscillating electric fields. Without action potential voltage recordings it was not possible to determine the activation site. Experiments on a nerve–muscle preparation lasted up to 6 h, with a slight decline in responsiveness evident towards the end of the experiment. In all, 89 tests were undertaken, with recordings made using digital photos and video.
Testing the activation of curved nerves was undertaken by bending the nerve one half‐turn around an insulating pillar. The presence of the pillar distorts the local electric field due to the boundary condition eqn (8) applying at the perimeter of the pillar, an effect not included in the analysis by Rotem & Moses (2006). Suppose an otherwise uniform electric field in the y direction, , must go around a pillar of radius R with axis parallel to the axis, centred on and , then the irrotational and divergence‐free electric field with zero normal component on the pillar surface is given by
| (28) |
where
| (29) |
in cylindrical co‐ordinates , measuring θ from the axis around towards the axis (Batchelor, 1967). For a nerve fibre touching the pillar, the tangential electric field is doubled from its value if the nerve executed the bend with no pillar present, and the maximum activating function is:
| (30) |
Statistics
To minimise the number of animals killed, and because this was an initial exploratory study, each experiment was repeated on only a low number of nerve–muscle preparations. In each test, the electromagnetic frequency was slowly raised and the frequency at which contractions commenced was noted. When repeated by lowering and again raising the frequency, the standard deviation of the activation frequencies had a median value of 18 Hz and had almost no correlation with the mean frequency of the repeated values. Here, the lowest reading of the repeated readings is reported, rounded to the nearest 10 Hz. In some experiments on the same nerve–muscle preparation, activation did not occur in one test, but did occur in a repeated test, after a different intermediate experiment had caused activation.
Results
Calculated and measured electric fields
The electric field generated by the prototype device in the rectangular fluid bath placed on top of it was calculated and measured. The calculations showed that the effect of the conducting medium boundary condition was very significant for the electric field parallel to the axis, reducing the total field to about one‐third of the value obtained in a vacuum, E m, whereas the perpendicular electric field was only reduced by about 10%. Figure 3 A compares the measured results on the plane x = 21.2 mm (2.4–2.5 mm above the internal base of the dish) with the calculated results. Calculated curves have been slightly shifted to align with the measured curves because the measurement grid may not have aligned perfectly with the rotor centre. The curves are of similar shape but the measured curves are around 30% higher than the calculated curves. The discrepancy could be due to the probe wire configuration influencing the field. Figure 3 B of the electric field gradient inferred from the measured curves shows that the maximum parallel electric field gradient is about 1.0 V m−2 Hz−1 at the origin (after some smoothing of the central‐differencing noise), and the maximum perpendicular electric field gradient is about 0.7 V m−2 Hz−1 at around y = 20 mm. At x = 20.2 mm, 1 mm closer to the device, the measured parallel electric field was about 13% higher and the measured perpendicular electric field was about 6% higher. Figure 3 C and D shows the decay with height of the calculated electric field components parallel to, and perpendicular to, the bipole axis. By height 6.8 mm above the bath floor the fields dropped to just less than half their maximum values on the floor (assumed 1 mm from the device top).
Figure 3. Electric field in the test bath .
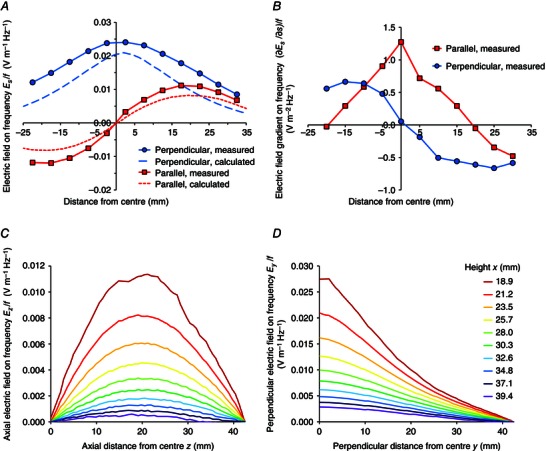
A, electric field amplitude divided by frequency, measured (full lines) and calculated on x = 21.2 mm (3.3 mm above the device top at x = 17.9 mm and 6.2 mm from the magnets of radius 15 mm), along lines parallel (on y = 0 mm, +ve z to the left) and perpendicular (on z = 0 mm, +ve y to the right) to the device axis. B, measured electric field gradient amplitude on frequency computed by central‐differencing. C and D, calculated electric field amplitude on frequency at different heights in bath: parallel to axis (C); perpendicular to axis (D).
Physiological results
The following results were obtained applying the prototype bipole device to the sciatic nerve and attached gastrocnemius muscle isolated from cane toads. Key experiments are summarised in Table 1, with the first column giving experiment numbers referred to below. A selection of the experiments is depicted in Fig. 4. In each experiment, the likely site of activation is suggested but this is highly uncertain because the nerve was of similar length to our device, making it impossible to eliminate any influence of nerve end effects in the experiments, which the limiting analytical solution (eqn (20)) has shown may be significant. Thus it is often not possible to know with certainty whether the activation site is: on a straight section of the nerve; at the nerve ligated end; due to curvature of the nerve in the vicinity of its entry to the muscle, especially when the muscle was raised; at the nerve end within the muscle; within small intramuscular nerves; or in the muscle tissue itself. The co‐ordinates referred to below are as defined by the axes shown in Fig. 2 A, though in this experiment the bath is above the device and so x, the direction toward the nerve, is upwards not downwards. The device ‘centre’ refers to , (at any x).
Table 1.
Summary of magnetic activation experiments on cane toad sciatic–gastrocnemius nerve–muscle preparations
| Proportion of | Number of | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Nerve vertical | Muscle vertical | nerve–muscle | nerve–muscle | ||||||
| Expt | Experiment | Align‐ment | separation from | separation from | Lowest activation | preparations | preparations | Likely | Figure or |
| No. | description | with device axis | device (mm) | device (mm) | frequency (Hz) | activated | tested (n) | activation site | videoa |
| 1 | Nerve spanning centre, muscle low | Perpendicular | 0.7 | 0.7 | 260 | 0.5 | 2 | Uncertain, either in muscle over y ≤ −20 mm or in nerve spanning 10 mm ≤ y ≤ 25 mm | 4A, 4B |
| 2 | Nerve spanning centre, muscle high | Perpendicular | 0.7 | ≥8 | 240 | 0.5 | 2 | Nerve, either at ligated end or where rising over y ≤ −25 mm or where straight over −25 mm ≤ y ≤ −10 mm | |
| 3 | Nerve ligated end at centre, muscle high | Perpendicular | 0.7 | ≥8 | 320 | 1 | 1 | Nerve, either at ligated end or where rising over y ≤ −29 mm or where straight over −25 mm ≤ y ≤ −10 mm | |
| 4 | Nerve spanning centre, muscle low | Parallel | 0.7 | 0.7 | None | 0 | 2 | None | |
| 5 | Nerve spanning centre, muscle high | Parallel | 0.7 | ≥8 | 790 | 0.33 | 3 | Nerve, either at ligated end or where rising over z ≤ −10 mm or at centre z = 0 | 4C |
| 6 | Nerve ligated end at centre, muscle high | Parallel | 0.7 | ≥8 | 770 | 1 | 1 | Nerve, either near centre z = 0 or where rising from z ≤ −32 mm | |
| 7 | Nerve spanning centre, muscle high | 45 deg to axis | 0.7 | 8 | 440 | 1 | 1 | Nerve | |
| 8 | Muscle at centre | Parallel | 6 | 0.7 | 180 | 1 | 2 | Muscle | 4D, S1 |
| 9 | Muscle at centre, bath raised | Parallel | ≥4.8 | 4.8 | 590 | 1 | 1 | Muscle | S2 |
| 10 | Muscle at centre | Perpendicular | 6 | 0.7 | 480 | 1 | 2 | Muscle | |
| 11 | Muscle at centre as in Expt 6, d‐tubocurarine blocking nerve‐evoked activation | Parallel | 9 | 0.7 | 460 | 1 | 1 | Muscle | |
| 12 | Nerve wrapped one half‐turn around 2.9 mm diameter pillar at device centre | Perpendicular | 1.5 | 8 | 230 | 1 | 1 | Nerve bend | 4E, S3 |
| 13 | Nerve wrapped one half‐turn around 2.9 mm diameter pillar at device centre | Parallel | 1.5 | ≥8 | 480 | 1 | 3 | Nerve bend | |
| 14 | Nerve wrapped one half‐turn around 2.9 mm diameter pillar at z = 18 mm | Parallel | 0.7 | 11 | 250 (though slight twitching at 190) | 0.67 | 3 (includes 1 in Expt 19) | Nerve bend | |
| 15 | Nerve wrapped one half‐turn around 5.0 mm diameter pillar at z = 18 mm | Parallel | 0.7–2 | 11 | 360 | 1 | 1 | Nerve bend | |
| 16 | Nerve wrapped one half‐turn around 8.5 mm diameter pillar at z = 18 mm. | Parallel | 2 | 11 | 350 | 1 | 2 | Nerve bend | |
| 17 | Nerve electrically activated at ligated end; nerve spanning centre, muscle raised | Parallel | ≥1 | ≥5.4 | Electrical activation not blocked to 940 Hz | 0 | 2 | None | |
| 18 | Nerve electrically activated at ligated end; nerve spanning centre, muscle raised | Perpendicular | ≥1 | 5.4 | Electrical activation not blocked to 930 Hz | 0 | 1 | None | |
| 19 | Nerve electrically activated at ligated end; nerve wrapped one half‐turn around 2.9 mm diameter pillar at z = 18 mm | Parallel | 1.5 | 5.4 | 730, with electrical activation not blocked | 1 | 1 | Nerve bend | 4F |
Videos (S1–S3) can be found in the online Supporting information.
Expt 1
Activation of straight nerve–muscle preparations on the bath floor and aligned perpendicular to the bipole axis was observed in 1 of 2 nerve–muscle preparations tested. In the trial photographed in Fig. 4 A and depicted schematically in Fig. 4 B, activation was seen at 260 Hz. The peak in the perpendicular electrical field gradient spans roughly 10–25 mm horizontally from the centre plane (i.e. ) (Fig. 3 B) and it is uncertain whether the activation site was in the muscle located on , or within one of the straight nerve sections or , or at the nerve ligated end at To rule out vibrations as the cause of the activation, the bath was then raised off the device by 0.9 mm at its closest using cotton thread (making the bath base 3.8 mm from the magnets). Activation still occurred, albeit at a higher frequency of 800 Hz.
Expt 2
In a variation on Expt 1, with the nerve perpendicular to the axis spanning the device centre, the muscle was raised to 8 mm from the device on a platform, sufficiently high to rule out the muscle as the activation site. Activation was seen in 1 of 2 nerve–muscle preparations tested. In one trial, activation was seen at 430 Hz, then the nerve was withdrawn from the bath floor and placed alongside the muscle on the platform. Activation did not occur, confirming that activation was previously in the nerve. In another trial with the nerve–muscle in its original position, a 2.9 mm diameter insulating pillar was positioned adjacent to the nerve (at ). The pillar would have produced a localised increase in the electric field by its side as per eqn (29), implying a short +ve pulse then, close by, a short –ve pulse in the electric field gradient in the nerve. This seemed to have no significant net effect as the activation frequency was 610 Hz, probably within random variation from the 430 Hz with no pillar present. The lowest activation frequency seen was 240 Hz for a nerve low from its ligated end at , passing a pillar at , then rising from , initially at a radius of curvature about 10 mm, to the muscle with tip on . It is uncertain whether the activation site was at the nerve ligated end, in the straight section of the nerve from , or in the curved section of the nerve over where it rose to the elevated muscle. In that curved section, the gradient of the parallel electric field component along the nerve has contributions from both the variation of the nerve angle to the electric field and from the reduction in electric field amplitude with increasing distance from the device. The activating function over both the straight and curved sections would have combined to contribute to the activation, if it occurred in either of these sections.
Expt 3
In this variation on Expt 2, featuring the nerve perpendicular to the axis and muscle raised, the ligated end of the nerve was placed on the centre, where the perpendicular electric field was maximum. The nerve passed a pillar at then curved up to the muscle over , initially at a radius of curvature about 15 mm. The lowest activation frequency was 320 Hz.
Expt 4
Activation of straight nerve–muscles on the rectangular bath floor spanning its centre and aligned parallel to the bipole axis did not occur in trials on two nerve–muscles. In a trial on another nerve–muscle in a shallow circular Petri dish, activation did occur, probably of the muscle spanning , but trials using that dish have been excluded from Table 1 since it is a different nerve environment.
Expt 5
In the experiment depicted in Fig. 4 C, wherein the nerve parallel to the device axis spans the centre and the muscle was raised onto a platform of height 8 mm above the device, activation did occur, at 790 Hz, in 1 of 3 nerve–muscles tested. When the nerve was withdrawn and placed alongside the muscle on the platform, activation did not occur, indicating that the site of activation was within the nerve, but it is likely to have been where the nerve rose over , initially at a radius of curvature about 15 mm. This activation was very marginal, as it did not occur in two earlier trials on the same nerve, including one taken to 950 Hz where the nerve rose over with an initial radius of curvature 10 mm and with the ligated end at .
Expt 6
In an attempt to minimise the end‐effect for the case of the nerve parallel to the device axis, the ligated end of the nerve was positioned at the device mid‐plane , where the parallel electric field component vanishes, . By symmetry, the behaviour might equate to a nerve of twice the length along the axis. In such a test, in which the muscle was elevated and axially very distant, with tip at , and the nerve rose to it over , initially at a radius of curvature about 20 mm, the lowest activation frequency was 770 Hz. However, in that test, the positioning cotton had raised the nerve ligated end slightly over its last 6 mm, which would have perturbed the parallel electric field gradient, and the bath wall had been shifted to , so that would have been perturbed from zero at the centre given the resulting change to the boundary condition eqn (8). Activation did not occur in an earlier test of this expt to 950 Hz on the same nerve though the bath wall was then at .
Expt 7
One test was conducted for the nerve spanning the centre at 45 deg to the axis, from the ligated end at to rising up to the elevated muscle from about , and activation was seen at 440 Hz. This was intermediate to the lowest activation frequencies seen for the perpendicular and parallel cases, Expt 2 and Expt 5, and shows that nerve activation does not require alignment either parallel or perpendicular with the device axis.
Expt 8
The lowest frequency at which muscle contraction was observed was 180 Hz. This occurred for a nerve–muscle preparation aligned parallel to the axis with muscle centred on the device with the dorsal side (the more curved side, furthest from the toad tibiofibula) on the bath floor 0.7 mm from the device (Fig. 4 D and Video S1). The nerve was elevated approximately 6 mm above the device, making it unlikely that the nerve was the cause of activation. With the muscle dorsal side up and the nerve insertion point into the muscle low, the lowest activation frequency was higher, 410 Hz (cf. 180 Hz when the dorsal side was facing down and the nerve was high), suggesting that the muscle was more sensitive with the dorsal side facing down and confirming that the nerve was not the cause of the activation. In the same bath was placed the gastrocnemius muscle from the other leg of the toad with the sciatic nerve severed near the muscle. For the muscle with the severed nerve at the device centre (as in Fig. 4 D but with the muscle positions swapped) the lowest activation frequency was 370 Hz, again showing that the sciatic nerve was not the activation site. Neither muscle, with or without the nerve, was activated when centred 18 mm axially from the mid‐plane (i.e. at ), approximately at the location of the highest parallel electric field (Fig. 3 A). The muscle with severed nerve, dorsal side up, did not activate when displaced laterally 16 mm from the plane.
Expt 9
For the nerve–muscle just described, with the muscle centred on the device and with dorsal side up, the bath was raised using spacers to make the muscle base 4.8 mm from the top of the device (hence 7.7 mm from the magnets), and activation occurred at 590 Hz (Video S2). This vertical separation from the device of 4.8 mm was the highest for which activation was noted (though activation may have occurred at a greater radius, for example at a radius exceeding 27 mm in Expt 1 if activation was in the muscle then). There was no activation at a separation of 6.8 mm. In a related experiment in which the muscle was also raised to 5 mm from the device, but by placing it across the bars of the platform with fluid underneath the platform, activation did not occur, but the platform may have affected the electric fields.
Expt 10
For the nerve–muscle preparation aligned perpendicular to the axis, muscle centred on the device, dorsal side down, activation occurred at 480 Hz, a higher frequency than for the 180 Hz when the muscle was aligned parallel to the axis of the device (Expt 8). This suggests the muscle is more efficiently activated by the large parallel electric field gradient spanning the centre.
Expt 11
This variation on Expt 8, with muscle centred on the device and dorsal side down, serves to further examine the location of the activation site. For the second of the two nerve–muscle preparations on which Expt 8 was trialled, activation occurred at 320 Hz, illustrating the variability cf. 180 Hz for the nerve–muscle preparation described above. The nicotinic acetylcholine receptor antagonist d‐tubocurarine (10 μm) was added to the toad Ringer solution to block nerve‐evoked muscle contractions. After incubation for 65 min, when probes of a Digitimer DS9A electrical stimulator applied to the nerve were no longer able to activate the muscle, the magnetic bipole was still able to activate the muscle, at 460 Hz. This indicates that the muscle itself was directly activated.
Expt 12
Activation was readily achieved for nerves wrapped one half‐turn around a 2.9 mm diameter insulating pillar located at the device centre. The lowest frequency of activation observed was 230 Hz which occurred for the nerve approaching perpendicular to the axis, and the muscle raised to 8 mm from the device (Fig. 4 E, Video S3). Given the measured peak perpendicular electric field on frequency of (Fig. 3 A), eqn (30) asserts that a nerve fibre which wraps around the pillar on its surface at radius , would experience maximum . A fibre on the outside limit of the nerve bundle of diameter 1 mm would experience maximum .
Expt 13
For the 2.9 mm diameter pillar at the centre, with the nerve approaching the pillar parallel to the axis, the lowest activation frequency was 480 Hz. These results are consistent with the highest electric field being the perpendicular field at the centre. When the nerve approaches the 180 deg bend axially, the nerve still experiences the same peak perpendicular electric field at the mid‐point of the bend. However, when the nerve approaches the bend perpendicularly (Expt 12), the induced gradient in the tangential component of the electric field is of the same sign over twice the span compared to when it approaches axially, leading to greater membrane potential change since the diffusion term in eqn (9) is less significant.
Expt 14
For nerves approaching parallel to the axis and wrapped one half‐turn around the 2.9 mm diameter pillar placed at the point of attraction of a steel spike hung above the device, which was at , where the parallel electric field was greatest, 2 of 3 nerves tested were activated (including the test of Expt 19). The peak may have varied slightly from that shown on Fig. 3 due to the bath wall being positioned at . The nerve which failed to activate also did not activate when approaching perpendicular to the pillar.
Expt 15
This expt was the same as Expt 14, a nerve wrapped around a pillar at the peak point, but for a pillar diameter of 5.0 mm. Activation was seen at 360 Hz for the one nerve tested, slightly higher than the lowest frequency seen for the smaller diameter 2.9 mm pillar placed there.
Expt 16
This expt was the same as Expts 14 and 15, a nerve wrapped around a pillar at the peak point, but for pillar diameter 8.5 mm. The lowest activation frequency was 350 Hz, surprisingly slightly lower than for the 5.0 mm pillar but in the second of the two nerves tested the lowest frequency was 900 Hz, when a very slight tail twitch commenced (which actually persisted for about 10 min after the test ceased). Given the measured peak parallel electric field on frequency of , eqn (30) asserts that a nerve fibre which wraps around the pillar on its surface at radius would experience a sinusoidal F profile with maximum , between zeros spaced 13.4 mm apart. A fibre on the outside limit of the nerve bundle of diameter 1 mm would experience maximum .
Initial tests were undertaken to investigate the possibility that magnetic excitation over an interval of the nerve below the threshold for nerve activation might block the passage of an action potential evoked by other means. An action potential was generated using electrical stimulation by draping the sciatic nerve near its ligated end over probes connected to a Digitimer DS9A electrical stimulator. Muscle contractions were evoked by electrical nerve stimulation at 1 pulse s−1 and a rising magnetic frequency was applied.
Expt 17
In this attempt to block action potentials, the nerve was aligned parallel to the axis, spanning the centre by about 12 mm on either side before rising to the Digitimer probes at the nerve ligated end or, at the other end, to the muscle, elevated on a platform to avoid it being directly activated magnetically. There was no blocking of electrically evoked contraction up to the maximum magnetic oscillation frequency tested, 940 Hz.
Expt 18
This expt was the same as Expt 17 but with the nerve perpendicular to the axis. There was no blocking of electrically evoked action potentials up to 930 Hz.
Expt 19
In this expt (Fig. 4 F), high magnetically induced electric field gradients were imposed by bending a parallel nerve one half‐turn around a 2.9 mm diameter pillar placed at , where the parallel electric field was greatest. Action potentials were not blocked by the magnetic field oscillations – and in this test magnetic stimulation of the nerve caused additional muscle contractions above 730 Hz. Electrical action potentials were also not blocked when the nerve was wrapped 1.5 turns around the pillar, and magnetic stimulation set in above 410–420 Hz, with or without the nerve over the Digitimer probes.
A number of other experiments undertaken of lesser importance have not been described here for brevity. These include: tests in a circular Petri dish, including one test on a whole cane toad leg (not activated); tests on nerve–muscles in some other alignments especially where the alignment was ill‐defined or the nerve–muscle drifted during the test.
A typical muscle contraction pattern, as seen in the Videos S1–S3, comprised between 1 and 3 partial contractions sustained over 0.3–1 s, followed by a resting interval of 1–1.7 s, during which there was no muscle contraction even though the sinusoidal excitation was sustained. This fatigue behaviour is of interest but is beyond the scope of this paper, which has focused on the activation threshold.
Discussion
It is believed that this is the first report of nerve or muscle activation being directly achieved using permanent magnets. The rotation of the magnet configuration produces an alternating electromagnetic field which is sustained, in contrast to conventional magnetic stimulation, in which the coil current is confined to pulses, with much longer zero intervals between the pulses. The magnetic field of the bipole prototype, Fig. 2 A, bears resemblance to that produced by a figure‐of‐eight coil, with opposite magnetic polarity on adjacent lobes, though the figure‐of‐eight coil produces a stationary magnetic field pattern with time‐varying amplitude, whereas the bipole configuration provides a rotating magnetic field pattern with constant amplitude.
Our analysis of the cable eqn (9) for sustained sinusoidal magnetic excitation showed that in the limit of low frequency, activation should be governed by the electric field gradient and that F th, the threshold ratio F of the activating function divided by frequency eqn (11), should increase inversely with frequency. In the limit of high frequency, F th should approach a constant, F b given by eqn (24), providing the electric field is negligible at the nerve fibre ends. These two limiting behaviours at low and high frequency are consistent with those found for electrical nerve stimulation. Weiss's law states that the threshold electric current I th and its pulse width PW satisfy
| (31) |
for I rh and τsd constants (Holsheimer, 2003). The analogous relationship for sinusoidal magnetic excitation would be
| (32) |
for I th corresponding to the activating function , PW corresponding to , corresponding to F b, and τsd corresponding to . For a given magnetic spatial configuration and nerve alignment, eqn (32) will not follow exactly from the solution of eqn (13). In particular, in the case when eqn (19) applies and diffusion is negligible, the dependence is instead given by eqn (23). Nevertheless, when diffusion is not negligible, eqn (32) might be found to be a useful approximation.
Our re‐analysis (Fig. 1) of the experimental results by Davey et al. (1994) showed that the predicted high frequency threshold behaviour was observed, with limiting threshold base value F b in the range 1.2–2.2 . F th was rising with falling frequency (Fig. 1), but it did not quite rise as steeply as , equivalently the threshold electric field gradient appeared to be still falling at 100 Hz for their large core and at 250 Hz for their small core.
The metric F can only be calculated for periodic excitation, when the frequency exists. While the metric cannot be applied to experiments using a monophasic or rapidly decaying biphasic current pulse, one can attempt to evaluate an effective frequency for such experiments to enable a rough comparison. For example, Maccabee et al. (1993, page 211) observed a threshold electric field gradient of for straight sheep nerves, near a figure‐of‐eight coil carrying a monophasic current pulse produced by damping a decaying polyphasic current wave of period 280 μs, or frequency (motivating Davey et al. 1994 to seek ). Though the electric fields do not establish a sinusoidal time dependence within the monophasic pulse, dividing the electric field gradient by that frequency would give , which is larger than, but of similar magnitude to, the threshold F th observed in Fig. 1.
Our prototype bipole device produced a measured F near the bath floor of about 0.9–1.1 V m−2 Hz−1 over a 10 mm straight line segment parallel to the axis spanning the centre and about 0.6–0.8 V m−2 Hz−1 over a 15 mm straight line segment perpendicular to the axis between 10 and 25 mm from the vertical plane that includes the axis (Fig. 3). These values are slightly below the limiting F b inferred from the Davey et al. (1994) measurements on African bullfrog sciatic nerves.
Direct activation of muscle was readily observed for the muscle at the maximum parallel electric field gradient at the centre, at the lowest frequency 180 Hz for muscle 0.7 mm from the device (Expt 8) and at 590 Hz for muscle separation of 4.8 mm from the device (Expt 9).
Activation of nerves curved by wrapping one half‐turn around an insulating pillar was also readily observed, with full muscle contraction at lowest frequency 230 Hz for a 2.9 mm diameter pillar placed at the point of the highest electric field, the centre for the perpendicular electric field (Expt 12). This could be expected given the peak electric field gradient on frequency there of on the pillar surface. For the 8.5 mm diameter pillar at the lower peak of the parallel electric field, the maximum F was only and activation was seen at 350 Hz in one nerve and 900 Hz in another (Expt 16).
Initially it was thought that the results of Expts 1–6 indicated occasional activation of straight cane toad sciatic nerves. For example, in Expt 1 on a straight perpendicular nerve–muscle with the muscle tip at lateral distance 20 mm from the mid‐plane y = 0, it was initially thought that the activation was in the nerve because the muscle was at such a high radius, namely beyond 27 mm. However, the greater ease at which the muscle was directly activated, shown by Expt 8, and the fact that the perpendicular electric field gradient was still significant beyond (Fig. 3 B) indicates that the activation may have been in the muscle. In Expts 2 and 6, the muscle was raised and placed even further from the device centre. This required shifting the bath and so the electric field is not known, but estimates can be made based on Fig. 3. In Expt 2, for the nerve perpendicular to the device axis, with lowest activation frequency 240 Hz, if the activation was not triggered at the nerve ligated end, then it is likely to have been triggered in the nerve where it curved up to the muscle, as the electric field gradient on frequency was probably about 1.1 V m−2 Hz−1 over the first 10 mm of that curved section, larger than the 0.7 V m−2 Hz−1 of the straight section even though the curved section did not commence until 25 mm laterally. In Expt 6, for the nerve parallel to the device axis and with ligated end at the device centre, the electric field gradient on frequency of about 1.1 V m−2 Hz−1 near the device centre was probably larger than in the rising curved section beyond z = –32 mm, but the ligated end was also slightly raised which may have assisted the activation via slight nerve curvature. Generally, nerves spanning the centre parallel to the axis were not activated (Expts 4 and 5). Although the electric fields generated appear to have been just below the threshold required for activation of straight cane toad sciatic nerves, nerves with a gradual radius of curvature, exceeding 10 mm, may have been marginally activated.
However, there is a possibility that some activations were triggered either at the ligated end or at the nerve end in the muscle. For example, in Expt 2, the activation may have occurred at the ligated end at , where the measured perpendicular electric field at 240 Hz was approximately 5.6 V m−1. This is of similar magnitude to the threshold value of 6.2 V m−1 obtained by Reilly (1989) from numerical modelling of long monophasic pulses for a 20 μm diameter nerve fibre. Nevertheless, other tests with a higher electric field at the nerve end did not activate. For example, in the Expt 5 test which had the nerve ligated end at and did not activate, the measured parallel electric field there at 950 Hz was approximately 12 V m−1.
The variability in test results between nerves and even for the one nerve makes it difficult to infer nerve parameters, which must have a distribution of values, both from the range of nerve fibres within the sciatic nerve and from statistical variation. Different nerve fibres may activate in different experiments making it impossible to infer a single set of parameters. Nevertheless, the following makes a first attempt at such an inference, based on the results of this initial study. Suppose the Expt 2 activation just mentioned was due to the end effect at the nerve ligated end. Given the low frequency, 240 Hz, assume that the in the denominator of eqn (21) can be neglected, then it can be inferred that . The threshold potential for the cane toad sciatic nerve is not known, but if it were , then eqn (21) would imply . This is less than the perpendicular electric field gradient length scale, of order , and so condition eqn (19) was met, justifying the use of eqn (21). The measurements of Davey et al. (1994) were for the sciatic nerve of an African bullfrog, not a cane toad, but suppose the cane toad sciatic nerve has a high frequency base threshold of , at the low end of the range apparent in our re‐analysis of the Davey et al. measurements (Fig. 1) and consistent with our observation that straight parallel nerves were mostly not activated by our device at its centre where . Then accepting the above values for V th and λ, eqn (24) would imply . For a nerve configuration in which diffusion could be neglected, then at the rated maximum frequency of this device, 1 kHz, eqn (23) with the above values of τ and F b would suggest a threshold which would explain why the device struggled to activate straight nerves.
The following suggests that the large diameter bent nerve Expt 16 result may be consistent with the above values of τ and F b. If diffusion could be neglected, i.e. if condition eqn (19) applied, then eqn (23), ignoring harmonic decomposition of the electric field, would suggest that for the peak , activation should be reached at ω = 1.62 × 103 rad s−1, i.e. at . However, the variation length scale l can be taken as equal to the pillar radius , and the condition eqn (19) is not satisfied for that ω and . Thus diffusion would not be negligible and a higher frequency would be needed, perhaps in the range of the frequencies at which activation was observed in the two tests, 350 Hz and 900 Hz. Examining this further requires modelling of the cable eqn (13), including decomposition into the harmonics of the electric field.
The value developed above is 3 times the value suggested by Basser & Roth (1991) and the value is 1.5 times the value 2.34 mm suggested by Basser & Roth (1991) for an axon of diameter 20 μm. These differences are not excessive but comparison with other assessments is needed, ideally for cane toad sciatic nerves.
While the above can be considered an indicative model, it does not predict all observations. For example, in the Expt 5 test with no activation at 950 Hz for nerve ligated end subject to 12 V m−1, assumed comprising 8 V m−1 at the fundamental frequency 950 Hz and 4 V m−1 at the third harmonic, eqn (20) for the above parameters would predict . This exceeds the assumed and so activation should have occurred from the end effect, but it did not. The activation in Expt 6 is also not explained since there should not have been any end effect activation at the ligated end, as the axial electric field there is in principle zero, and the curvature was very gradual up to the muscle. The most significant assumption made was that the base threshold F b was the same for cane toad sciatic nerves as that found by Davey et al. (1994) for African bullfrog sciatic nerves. If a lower value than actually applied, then activations could be explained as being in straight or gradually curved nerves. The estimation of parameters λ and τ has been based on the measured electric fields, which were approximately 30% higher than the calculated fields. If the calculated fields actually applied, the inferred value of λ would be approximately 30% higher and that of τ approximately 69% higher. Further experiments and numerical solutions of the cable equation are needed to resolve these uncertainties and infer more reliable estimates of the nerve parameters.
For the case of negligible diffusion occurring when , and if the electrical field at the nerve ends is sufficiently small that the end potential given by eqn (21) can be neglected, then the solution to eqns (13) and (14) for all ω is given by eqn (22). This solution simplifies to eqn (26) when or to eqn (27) when . Thus, the transition between low and high frequency regimes can be taken as occurring in the vicinity of , when the second and third terms of the scaling analysis (eqn (18)) are equal. If the diffusion is not negligible, then even if is not small compared to 1, it is still possible for the frequency‐dependent term to be much smaller than the diffusion term and hence negligible in eqn (13), namely if . However, solutions for that case have not been presented here.
For the cane toad sciatic nerve, assuming as inferred above, the transition from low to high frequency is thus where ω = 8.06 krad s−1, i.e. where . Thus the 1 kHz maximum design frequency of the prototype device is only in the transition region and not the high frequency limit. In consequence, eqn (23) shows an increase in the threshold F th at 1 kHz by 63% above the base value F b which would apply in the high frequency limit.
Initial attempts to block action potentials excited electrically were unsuccessful (Expts 17–19). It may be the case that frequencies higher than 1 kHz are required, as usually found for electrical stimulation (Kilgore & Bhadra, 2014).
Each rotating magnet employed by Leuchter et al. (2015) was a diametrically magnetised neodymium cylinder of diameter and length each 1 inch (25.4 mm). In our bipole magnet configuration, each of the two NdFeB magnets were of diameter and length 30 mm, 18% larger, and the bipole configuration, featuring reversed magnet directions, approximately doubles the peak electric field gradient (which is for a path parallel to the axis) and approximately doubles the peak electric field (which is for a path perpendicular to the axis). (In both cases the peak is not quite doubled because the peak for the single magnet case is close to but not exactly on the magnet endplane.) The lowest frequency of excitation we observed for cane toad sciatic nerves was 230 Hz. While the properties and curvatures of human cortical nerves will differ from those of the cane toad sciatic nerves used in our experiments, it seems most likely that at the order 10 Hz frequency used by Leuchter et al. (2015), the threshold F th needed for activation would be in the region required for activation (presuming the cable equation applies down to these frequencies) and that F th would be much higher than that provided by each of their magnets, so their device would not cause activation, consistent with their expectation that their system was subthreshold.
Our prototype device was designed and built to reach the very high rotation speed of 60,000 r.p.m., thus achieving 1000 Hz excitation. This brings the excitation closer to the high frequency limit (how close depending on τ) where the threshold F th for a nerve configuration away from its ends approaches the base value F b, giving the device the greatest chance of activating the nerve. The novel method of driving the rotation via coils positioned adjacent to the magnet configuration, as depicted in Fig. 2 B for the prototype, was a significant enabling technology to achieve such high rotation speed, overcoming dynamic issues of other rotation methods such as shaft or belt drive.
An exciting field of theoretical work and experimental testing is opened up by this initial study. Further detailed testing is needed, ideally on longer nerves in vitro, but also on animals and humans in vivo (after ethical approval). The activation threshold will be different for human nerves than for the cane toad nerve used so far, and will vary with human nerve type and structure. Equation (24) shows that in the limit of high frequency, the most critical nerve fibre property dictating its susceptibility to activation away from the nerve ends is its ratio . Modelling of each test configuration should be undertaken including solution of the cable eqn (9) for the precise nerve path and electric field gradient along it to see how well that equation can describe the activation thresholds observed. An analytic solution, eqn (20), has been given for cases when eqn (19) applies, which is when the diffusion term is negligible except near the nerve ends. If the electric field is non‐negligible at an end, the peak membrane potential will occur at the nerve end with higher electric field, and eqn (21) can be used to predict when activation will occur. If the electrical field is negligible at the ends, then eqn (23) should predict activation. Generally, however, numerical methods will be needed to solve eqn (9). The range of new assessments of the cable equation obtained for sinusoidal excitation, made possible by rotating magnet configurations, will increase our understanding of nerve physiology and, in particular, give more accurate estimates of nerve parameters. The interaction of the electromagnetic excitation with other nerve phenomena, especially a propagating action potential, remains to be studied, requiring modification of the pre‐threshold cable eqn (9) to include active membrane effects (Roth & Basser, 1990).
The results presented here were obtained with a first prototype of the bipole magnet configuration (Fig. 2). Other magnet configurations such as those described in the patent application (Watterson, 2012) should be designed, built and tested. In particular, some configurations, including the ‘quadrupole’, will suffer less from reduction in the electric field due to charge build‐up on the conducting region surface. The depth of penetration of the electromagnetic field into the body scales with the device dimension, but there is a tradeoff that the rotation speed and excitation frequency must be reduced inversely proportional to the length scale to maintain the same stresses in the containment sleeve and magnets (with the sleeve–magnet interference fit also having to be scaled proportional to the length scale). The metric F remains the same, however, along a curve at the larger depth in the body, and applies for a corresponding greater length, increasing the membrane potential produced.
After further fundamental studies on animal nerves using different devices, possible medical applications can be explored. Success appears most likely for activation of muscles or activation of nerves that lie close to the skin, especially at nerve ends and at nerve bends, particularly where the nerve turns inwards away from the skin or bends over non‐conducting tissue or bone. The high frequency at which the nerve can be activated by the sustained sinusoidal excitation may be advantageous for some applications but deleterious for others. High frequency excitation of motor nerves could be advantageous in enabling maximum muscle contraction. If the method is able to penetrate to sufficient depth to activate cortical nerves, the high frequency may be generally precluded if it induces seizures (Rossi et al. 2009), though conversely, there may be therapeutic applications from inducing seizures under anaesthesia (Luber et al. 2013). As well as applications entailing nerve activation, the alternative possibility of a travelling action potential being blocked by rotating magnet configurations should also be further investigated as this might have valuable applications, especially to pain relief. If successful, devices based on rotating magnets would be significantly smaller, cheaper and lower in electrical power use compared to existing pulsed current devices.
Additional information
Competing interests
P.A.W. declares a potential financial interest in being the inventor of the related patent application (Watterson, 2012), owned by his employer, the University of Technology Sydney.
Author contributions
P.A.W. conceived the concept described, designed the prototype, and undertook the electric field theory, calculations and measurements. P.A.W. and G.M.N. jointly undertook the physiological testing. G.M.N. performed the toad surgical procedures. The paper was principally written by P.A.W. with contributions on the physiological testing and editing by G.M.N. The work was performed at the University of Technology Sydney (Australia). Both authors have approved the final version of the manuscript and agree to be accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.
Funding
The work was funded solely by the University of Technology Sydney (Australia). This funding included grant UTS223 from the UTS Invention Commercialisation Seed Fund.
Supporting information
Video S1. Muscle activation (Expt. 8)
Video S2. Muscle activation in raised bath (Expt. 9)
Video S3. Bent nerve activation (Expt. 12)
Acknowledgements
The authors thank: Siegfried Holler for precision machining and assembly of the prototype device; Dr Francesca Marcon for technical assistance with the physiological testing; and Dr Greg Hunter for advice on electrical testing.
References
- Ardizzone V (2003). Biaxial rotating magnetic therapeutic device. US Patent No 6,648,812.
- Barker AT (1991). An introduction to the basic principles of magnetic nerve stimulation. J Clin Neurophysiol 8, 26–37. [DOI] [PubMed] [Google Scholar]
- Basser PJ & Roth BJ (1991). Stimulation of a myelinated nerve axon by electromagnetic induction. Med Biol Eng Comput 29, 261–268. [DOI] [PubMed] [Google Scholar]
- Batchelor GK (1967). An Introduction to Fluid Mechanics, p. 424 Cambridge University Press, Cambridge. [Google Scholar]
- Bender CM & Orszag SA (1978). Advanced Mathematical Methods for Scientists and Engineers, chap. 9. McGraw Hill, New York. [Google Scholar]
- China Rare Earth Magnet Limited (2015). NdFeB magnet properties. http://www.permanentmagnet.com/neodymium_sintered.html. (Accessed 11 January 2015). China Rare Earth Magnet Limited, Shenzhen, China.
- Cole KD, Haji‐Sheikh A, Beck JV & Litkouhi B (2011). Heat Conduction Using Green's Functions, 2nd edn, pp. 87–88. CRC Press, Boca Raton. [Google Scholar]
- Davey K, Luo L & Ross DA (1994). Toward functional magnetic stimulation (FMS) theory and experiment. IEEE Trans Biomed Eng 41, 1024–1030. [DOI] [PubMed] [Google Scholar]
- Gabriel S, Lau RW & Gabriel C (1996). The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys Med Biol 41, 2251–2269. [DOI] [PubMed] [Google Scholar]
- Gondin J, Cozzone PJ & Bendaham D (2011). Is high‐frequency neuromuscular electrical stimulation a suitable tool for muscle performance improvement in both healthy humans and athletes? Eur J Appl Physiol 111, 2473–2487. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL & Huxley AF (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 117, 500–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holsheimer J (2003). Principles of neurostimulation. In Electrical Stimulation and the Relief of Pain, Pain Research and Clinical Management, Vol. 15, ed. Simpson BA, pp. 17–36. Elsevier Science, Philadelphia. [Google Scholar]
- Horrocks EJ, Thin N, Thaha MA, Taylor SJC, Norton C & Knowles CH (2014). Systematic review of tibial nerve stimulation to treat faecal incontinence. Br J Surg 101, 457–468. [DOI] [PubMed] [Google Scholar]
- Jin Y & Phillips B (2014). A pilot study of the use of EEG‐based synchronized transcranial magnetic stimulation (sTMS) for treatment of major depression. BMC Psychiatry 14, 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jobst BC (2010). Electrical stimulation in epilepsy: vagus nerve and brain stimulation. Curr Treat Options Neurol 12, 443–453. [DOI] [PubMed] [Google Scholar]
- Johnson M (2014). Transcutaneous electrical nerve stimulation: review of effectiveness. Nurs Stand 28, 44–53. [DOI] [PubMed] [Google Scholar]
- Kilgore KL & Bhadra N (2014). Reversible nerve conduction block using kilohertz frequency alternating current. Neuromodulation 17, 242–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobayashi M & Pascual‐Leone A (2003). Transcranial magnetic stimulation in neurology. Lancet Neurol 2, 145–156. [DOI] [PubMed] [Google Scholar]
- Larsson J (2007). Electromagnetics from a quasistatic perspective. Am J Phys 75, 230–239. [Google Scholar]
- Leuchter AF, Cook IA, Feifel D, Goethe JW, Husain M, Carpenter LL, Thase ME, Krystal AD, Philip NS, Bhati MT, Burke WJ, Howland RH, Sheline YI, Aaronson ST, Iosifescu DV, O'Reardon JP, Gilmer WS, Jain R, Burgoyne KS, Phillips B, Manberg PJ, Massaro J, Hunter AM, Lisanby SH & George MS (2015). Efficacy and safety of low‐field synchronized transcranial magnetic stimulation (sTMS) for treatment of major depression. Brain Stimul 8, 787–794. [DOI] [PubMed] [Google Scholar]
- Lorrain P & Corson DR (1970). Electromagnetic Fields and Waves, 2nd edn, p. 476 W.H. Freeman and Co, San Francisco. [Google Scholar]
- Luber B, McClintock SM & Lisanby SH (2013). Applications of transcranial magnetic stimulation and magnetic seizure therapy in the study and treatment of disorders related to cerebral aging. Dialogues Clin Neurosci 15, 87–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maccabee PJ, Amassian VE, Eberle LP & Cracco RQ (1993). Magnetic coil stimulation of straight and bent amphibian and mammalian peripheral nerve in vitro: locus of excitation. J Physiol 460, 201–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MagVenture (2007). Product Information Sheet: MagPro X100, Technical Data October 2007. MagVenture A/S, Farum, Denmark.
- Malmivuo J & Plonsey R (1995). Bioelectromagnetism: Principles and Applications of Bioelectric and Biomagnetic Fields, chap. 2. Oxford University Press, New York: Updated edition http://www.bem.fi/book/index.htm. (Accessed 12 January 2009). [Google Scholar]
- Miranda PC, Correia L, Salvador R & Basser PJ (2007). The role of tissue heterogeneity in neural stimulation by applied electric fields. Conf Proc IEEE Eng Med Biol Soc 2007, 1715–1718. [DOI] [PubMed] [Google Scholar]
- Nagarajan SS & Durand MD (1996). A generalized cable equation for magnetic stimulation of axons. IEEE Trans Biomed Eng 43, 304–312. [DOI] [PubMed] [Google Scholar]
- Neorem Magnets Oy (2015). Characteristic physical properties of sintered NdFeB material at 20°C. http://www.neorem.fi/permanent‐magnets.html?file=files/neorem/product‐PDF/permanent%20magnets/NdFeB_PhysicalProperties_of_NdFeB_material.pdf. (Accessed 11 January 2015). Neorem Magnets Oy, Ulivila, Finland.
- Nikken (2014). Magnetic biaxial rotation. http://www.nikkentechnologies.com/magnetic‐biaxial.cfm. (Accessed 11 January 2015). Nikken Inc., Fukuoka, Japan.
- Pfister P‐D & Perriard Y (2008). A 200 000 rpm, 2 kW slotless permanent magnet motor. In Proceedings of the 11th International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2015, pp. 3054–3059. IEEE. [Google Scholar]
- Reilly JP (1989). Peripheral nerve stimulation by induced electric currents: exposure to time‐varying magnetic fields. Med Biol Eng Comput 27, 101–110. [DOI] [PubMed] [Google Scholar]
- Robinson AJ & Snyder‐Mackler L (2007). Clinical Electrophysiology: Electrotherapy and Testing Procedures, 3rd edn Lippincott Williams and Wilkins, Baltimore. [Google Scholar]
- Rossi S, Hallett M, Rossini PM & Pascual‐Leone A (2009). Safety, ethical considerations, and application guidelines for the use of transcranial magnetic stimulation in clinical practice and research. Clin Neurophysiol 120, 2008–2039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rotem A & Moses E (2006). Magnetic stimulation of curved nerves. IEEE Trans Biomed Eng 53, 414–420. [DOI] [PubMed] [Google Scholar]
- Rotem A & Moses E (2008). Magnetic stimulation of one‐dimensional neuronal cultures. Biophys J 94, 5065–5078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roth BJ & Basser PJ (1990). A model of the stimulation of a nerve fiber by electromagnetic induction. IEEE Trans Biomed Eng 37, 588–597. [DOI] [PubMed] [Google Scholar]
- Schoenen J, Vandersmissen B, Jeangette S, Herroelen L, Vandenheede M, Gérard P & Magis D (2013). Migraine prevention with a supraorbital transcutaneous stimulator: A randomized controlled trial. Neurology 80, 697–704. [DOI] [PubMed] [Google Scholar]
- Shaker HS, Tu LM, Robin S, Arabi K, Hassouna M, Sawan M & Elhilali MM (1998). Reduction of bladder outlet resistance by selective sacral root stimulation using high‐frequency blockade in dogs: an acute study. J Urology 160, 901–907. [DOI] [PubMed] [Google Scholar]
- Sih GC & Macdonald B (1974). Fracture mechanics applied to engineering problems–strain energy density fracture criterion. Eng Fract Mech 6, 361–386. [Google Scholar]
- Vacuumschmelze GmbH & Co. (2014). Rare earth permanent magnets VACODYM and VACOMAX. PD002 Edition 2014. Vacuumschmelze GmbH & Co., Hanau, Germany.
- Watterson PA (2000). Energy calculation of a permanent magnet system by surface and flux integrals (the flux‐MMF method). IEEE Trans Magn 3, 470–475. [Google Scholar]
- Watterson PA (2012). Device including moving magnet configurations. PCT Application No. WO/2012/126044.
- Weintraub MI, Herrmann DN, Smith AG, Backonja MM & Cole SP (2009). Pulsed electromagnetic fields to reduce diabetic neuropathic pain and stimulate neuronal repair: a randomized controlled trial. Arch Phys Med Rehabil 90, 1102–1108. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Video S1. Muscle activation (Expt. 8)
Video S2. Muscle activation in raised bath (Expt. 9)
Video S3. Bent nerve activation (Expt. 12)


