Movement: How the Brain Communicates with the World

Abstract

Voluntary movement is a result of signals transmitted through a communication channel that links the internal world in our minds to the physical world around us. Intention can be considered the desire to effect change on our environment, and this is contained in the signals from the brain, passed through the nervous system to converge on muscles that generate displacements and forces on our surroundings. The resulting changes in the world act to generate sensations that feed back to the nervous system, closing the control loop. This Perspective discusses the experimental and theoretical underpinnings of current models of movement generation and the way they are modulated by external information. Movement systems embody intentionality and prediction, two factors that are propelling a revolution in engineering. Development of movement models that include the complexities of the external world may allow a better understanding of the neuronal populations regulating these processes, as well as the development of solutions for autonomous vehicles and robots, and neural prostheses for those who are motor impaired.

Introduction

The way the nervous system generates movement has been studied formally for about 150 years. Earlier work was based on anatomical observations: the way the brain and spinal cord were shaped and how one place in the system appeared to be connected to another. This, combined with careful observation of motor deficits and corresponding lesions of system structures, was the foundation of motor neurology. The introduction of electrical stimulation in animal models added another dimension to motor systems experimentation. Along with targeted lesions of different system components, these were the underpinnings of the original theories of motor control. Although the complexities of relating anatomical structures to specific aspects of behavior were well recognized by motor control pioneers, results of lesion and electrical stimulation experiments were viewed primarily in terms of fairly discrete connectivity pathways that are now referred to as “circuits,” with the implication that they operate in a way that is similar to their engineered counterparts, such as computers. More recently, experimentalists have been using technology that enables the simultaneous recording of action potentials from many neurons while natural movements are performed. Conventional concepts of discrete circuits working with distinct functionality have been challenged by experimental results that show that many neurons are active together, with a large population throughout the neural axis generating similar signals used for movement generation. This evolution in the field of motor control offers new insights for understanding purposeful behavior, as well as suggestions for new design principles that could be implemented in engineered systems.

Movement—Reflex and Volition

Traditionally, movements have been divided into those subserving reflexes and those associated with purposeful action. Volitional movement is the result of cognitive processes, which lead to the exertion of some action on the world. These processes are not clearly defined or understood, making it difficult to develop concrete, rigorous models to describe the way they operate. Although the resulting physical movement can be measured well and task-related neural activity can be recorded and correlated to the movement, in the absence of well-identified drivers of neural activity, the meaning of an association between any given neural pattern and the task will be open to debate.

Reflexes

In contrast to volitional movement, reflexes seem especially amenable to the modeling approach used by engineers. Instead of a process that begins with intention, the generation of reflexive movement starts with sensation. A given stimulus (input) elicits a set motor action (output). As described by Sherrington at the turn of the 19^th century, these movements are stereotypical and generated by neuronal action that takes place in an orderly fashion beginning in the spinal cord, with elaboration by groups of neurons in progressively “higher” neural structures such as the hindbrain, midbrain, and cerebral cortex. Sherrington arrived at this hierarchical scheme by surgically separating these different structures and studying the remaining reflexive behavior. He found that each level could be characterized by inputs and outputs, allowing system identification procedures whereby mathematical transfer functions were used to predict outputs given an input and giving rise to the use of linear system approaches (a linear equation that describes how output results from input) in the 1960s and 70s to describe reflex inception. One of the first attempts in this regard was modeling the stretch reflex, based on the workings of the crayfish stretch receptor (Borsellino et al., 1965). The process of transforming a physical stretch into a train of impulses in the afferent fiber was considered to take place as a set of steps, each of which could be modeled with a transfer function (the input-output equation) (Loewenstein et al., 1963; Terzuolo and Washizu, 1962; Washizu and Terzuolo, 1966). The same principles were subsequently applied to the mammalian stretch receptor (Poppele and Terzuolo, 1968; Roberts et al., 1971). Stretching the muscle (by other muscles or external forces) activates the receptor which, in turn, excites the muscle that contains it, causing the muscle to shorten, effectively counteracting the stretch to maintain stability. Thus, reflexive movements act on the principle of feedback, where the output of the system is used to modify its input. In this case, the feedback is negative because the stimulus invoking the reflex is a lengthening of the muscle and the response, muscle contraction, shortens it.

The use of linear systems analysis was also fundamental to studies of the vestibular ocular reflex (Robinson, 1981), which functions to stabilize images on the retinas when the head accelerates. Based on the same principle as the stretch reflex, this system uses negative feedback to move the eyes in the direction opposite of the head movement. In this case, head acceleration from the semicircular canals of the vestibular system was considered the system input, which is transformed to velocity and position used to activate the extraocular muscles. We can see that these examples of negative feedback conform to basic engineering principles. However, even these basic reflexes are constantly modified by the context in which they occur. For instance, in mammals, the sensitivity of sensory muscle spindle receptors is regulated by gamma motorneurons, which change the stiffness of the receptor itself. The gamma motorneurons are controlled by supraspinal structures, which are influenced by the setting or context in which the subject is situated. Essentially, the gamma system adjusts the gain of stretch receptors to accommodate a predicted range of sensations that will be encountered. Similarly, the vestibular-ocular reflex is modified by output from the cerebellum, which can change the gain of the reflex. Donning a pair of bifocals is an everyday illustration of how feedback systems are readily modified. The glasses act as prisms that displace the world so that a given eye movement no longer results in the same shift of vision. After learning, the gain (ratio of output to input) of the vestibular-ocular reflex is adjusted rapidly to compensate for this change as soon as the viewer peers through alternate lenses.

Reflex Action and Volitional Movement

Reflexes are effective during volitional movement, and they contribute to the successful production of an intended action. In laboratory experiments using instructed tasks, movement intention is, at least partly, specified. The idea of “motor set” experiments in the mid-70s and early 80s was to separate a volitional component of the task (instruction) from that which was more related to the mechanics of the movement (reflex). This logic was followed in experiments (Evarts and Tanji, 1974) in which monkeys were trained to move to a target in response to a rapid displacement (“go” signal) of the handle they were holding. A target light served as the instruction and indicated which of two directions to move before the go signal. Although the handle displacement was the cue to move, its direction had no behavioral meaning. Two types of neuronal responses were found in motor cortical neurons. An early response (20 ms) after the handle perturbation was correlated with the direction of the rapid displacement. A later pattern of discharge corresponded to the direction of the instructed movement (40–50 ms) but was unrelated to the perturbation direction. The first response was deemed to be reflexive and due to afferent input elicited by the perturbation (since it carried directional information unrelated to the subsequent behavior), while the second was considered more volitional in that it was target related. The subject’s response, as registered by the onset of muscle activity, began 70 ms after the perturbation, and the movement began 20 ms later. The same paradigm was used to study responses in the cerebellum (Strick, 1983) with the idea that the early and late neuronal responses in the motor cortex may be mediated by the cerebellum. Recordings in the dentate nucleus showed that neurons changed their firing rates in a way that was dependent both on the cued target and the direction of the imposed perturbation. This dual dependency is interesting, since the mechanics needed to move the arm to the target depend on the initial position of the arm (which was altered by the perturbation) and the position of the target. Even though the perturbation direction had no behavioral meaning, the direction of the prior perturbed displacement had to be accounted for when generating the subsequent forces needed to make the volitional movement. These experiments defined components of the control signals that may contribute to the generation of volitional movement.

Reaching as Volitional Movement

Volitional movement is, by definition, the intended execution of an action. These movements are often considered to be singular events, even though, in real-world behavior, they take place in a continuous cycle of action-intention-action.… (Johansson and Flanagan, 2008). Nonetheless, because this chain is sequential, there are delays between intention and action and then between action and registration of that action via sensation. The first delay requires the intention to be predictive; the second means that sensory feedback cannot function in real time. This suggests that there are distinct phases of the task that may be controlled differently. During a reach for an object, the path of the hand is divided into two components; the first is a rapid displacement of the hand to the vicinity of the object, followed by a series of smaller “submovements” (acceleration-deceleration) of the hand until the target is reached (Meyer et al., 1982; Schmidt et al., 1978). The initial component, which covers about 80% of the distance, is on the order of 200 ms, whereas the second component takes slightly less time. Before and during the reach, the eyes are fixed on the target. Because the minimal time for a visually mediated movement to take place is estimated to be in the range of 190–200 ms (Beggs and Howarth, 1972; Cordo, 1987; Keele and Posner, 1968; Newell and Houk, 1983), it follows that the first phase of the movement is essentially over before a visual correction could be effective; this phase is often referred to as “ballistic” because it was thought to take place in the absence of feedback (Hollerbach, 1982). Even accounting for proprioceptive loop times, which, as ascertained by perturbations, are slightly shorter, at about 120–150 ms (Cordo and Flanders, 1989; Higgins and Angel, 1970), this would mean that only the very beginning of the movement could be regulated by this feedback. Based on these considerations, the general view by the late 1980s held that reaching was divided into two phases: an initial ballistic component that transported the hand to a location near the target, followed by a homing phase executed with visual feedback as a series of small, fine movements used to acquire the target.

Feedback Control

How could a movement take place in the absence of feedback? In 1979, Polit and Bizzi (1979) hypothesized that arm movement would automatically arrive at a pre-specified equilibrium point in the absence of feedback. Muscles were considered to be much like springs with adjustable stiffness. Stiffness is the ratio of force to length. A pair of antagonist muscles around a joint would have equal and opposite forces at a length (the equilibrium point) that was dictated by each of their stiffnesses. By presetting the stiffness of the arm muscles before a movement began, the arm would naturally come to rest at the end of the movement when the equilibrium point was reached (Feldman, 1986). In this scheme, no control would be needed during the movement. However, this form of the equilibrium point hypothesis was disproven in an elegant experiment (Bizzi et al., 1984). Monkeys were trained to make a single-joint elbow movement in an exoskeleton that could rapidly move the forearm. The task began at an initial position followed by a forearm movement to capture a visual target. After the task was learned, the monkeys’ arms were deafferented. The monkeys were still able to capture the target, even in a darkened room, suggesting that feedback was not needed. However, when the arm was quickly displaced to the target and released at the beginning of the movement, the arm returned to the initial position and then moved to the target along the normal path. If a single equilibrium point had been specified at the target, the arm should have remained at the target when released. Faced with this result, the original hypothesis was modified to a series of equilibrium points forming an “equilibrium trajectory” (Flash, 1987). Although this specification was hypothesized to take place before the movement began, other theories suggested that control was taking place continuously through the movement (Flanagan et al., 1993). Sudden displacements of a target in the middle of a reach could be compensated for quickly with a response that was proportional to the target shift (Georgopoulos et al., 1981; Massey et al., 1986), and motor cortical activity, normally modulated through these tasks, was interrupted with short latency when the target shift occurred (Georgopoulos et al., 1983a). Indeed, evidence from neuronal recording experiments suggested that trajectory specification (as sampled from the motor cortex) begins 150 ms before movement onset but then continues throughout the movement with the same predictive interval during reaching (Georgopoulos et al., 1988b) and drawing (Schwartz, 1993, 1994). Taken together, these results show that there is a continuous specification of trajectory that begins before movement onset and continues as the arm moves. The planning to produce an arm movement takes place, at least partially, as on-line control, and is controlled throughout its duration; strikingly, this control takes place even when continuous feedback is absent.

A sensory feedback-free control signal was originally invoked for eye movements. Like the “ballistic” phase of reaching, saccades, the rapid eye movements that allow us to scan the environment, seem to take place too rapidly for sensory feedback to be effective. An “efferent copy” of the motor command to move was suggested by von Holst and Mittelstaedt (1950). This hypothetical signal was thought to work in parallel to those used more directly to contract muscles. In this initial proposal, the efferent copy served to ascertain agency during eye movement, distinguishing the moving visual surround generated by self-motion from that produced by the world itself. The efferent copy concept was substantiated by gaze perturbations as the head was rapidly moved during saccades. Even in the absence of vision (Keller et al., 1996) and proprioception (Guthrie et al., 1983), subjects compensated for these perturbations, suggesting that feedback was not necessary. Evidence for a similar control operation can also be found for arm movements. For instance, in reaching tasks in which subjects had to choose a target to acquire, they sometimes chose incorrectly but could seemingly correct the error much more rapidly than feedback could accommodate (Cooke and Diggles, 1984; Higgins and Angel, 1970). This finding suggests that “internal” recognition of a target error, for instance by using efferent copy, can lead to corrections without real-time feedback of the movement. This concept can be expanded even further as there is evidence that visual feedback of the target can also modify the movement-generation process, albeit in an asynchronous manner. For instance, perturbations of the movement by shifting the target also elicit a very rapid response (van Sonderen et al., 1989), even in deafferented subjects with only a shifted target visible (Bard et al., 1999). When reaching to visual targets, the eyes saccade to foveate the target before the arm begins to move, even though the muscles of the eye and arm are activated almost simultaneously (Biguer et al., 1982; Prablanc and Martin, 1992). A number of experiments were performed in which the target was shifted during the saccade (Pélisson et al., 1986; Prablanc and Martin, 1992; Prablanc et al., 1986) and showed that the subjects corrected their trajectories quickly (110 ms after movement onset) and smoothly. These studies were conducted with the subjects’ hands out of their line of sight and show how extrinsic information can be incorporated into the ongoing movement generation process.

In opposition to the idea that the initial movement component in reaching is “ballistic”—that it reflects operations that are independent of feedback—a number of experiments have shown that visual information is incorporated into the control of this component. Specifically, the direction of motion can drive responses sensed in the peripheral (non-foveal) visual fields, and this can be contrasted with the position sensitivity of the foveal fields (Paillard, 1996). In a directional reaching task, seeing the hand as it starts to move (Bard et al., 1985), but not before (Blouin et al., 1993), improves the accuracy of the movement.

These results show that the signals used to control the arm’s trajectory are transmitted continuously throughout a reach. The efferent signal for the movement is modifiable by intrinsic errors and extrinsic cues at the beginning of the movement and by target modifications during the transport of the arm. Intrinsic sensation of the moving arm is used in the formulation of the ongoing commands to the arm. This type of scheme emphasizes the predictive nature of an efferent operation that can be modified by sensation of the body and its surroundings.

Feed-Forward Control

Feedback, in which the output of the system is used to regulate its input, contrasts with movement generated in the absence of sensation (MacKay, 1965) using feed-forward control. Motor control theorists and experimentalists have made either-or arguments about these two schemes for more than 100 years (Desmurget and Grafton, 2003). In practice, the two types of controls are merged. Modern feed-forward concepts invoke learning, in which the prediction of an intended action is modified by prior sensation. “The idea behind this concept is that the motor system can progressively learn to estimate its own behavior in response to a given command (efferent signal). During the movement, this prediction can be used to estimate the current state of the motor apparatus and to predict what the final state will be” (Desmurget and Grafton, 2003). Further refinement of the feed-forward idea shows that accurate prediction relies critically on accurate knowledge of the initial state of the system. At issue is how often the physical state of the system is assessed for accurate predictions (i.e., updated by feedback). For instance, subjects without somatosensation of their arms were unable to make accurate movements in the dark. However, when allowed prior visualization of their limbs, the resulting movements were near normal (Ghez et al., 1995; Sainburg et al., 1995), and as discussed above, knowledge of the initial position of the hand and its motion leads to more accurate reaching in typical individuals. The utility of prior information before movement supports the idea of feed-forward control systems since they are deterministic—their operation is determined by initial conditions.

Feed-Forward Control Is Learned

Learning is essential for making accurate predictions and, as such, is a major topic of investigation for systems neuroscientists. The term “internal model” is often used to describe the prior knowledge, gained by learning, used to make accurate predictions of how an intended action will result in the desired outcome. Internal models are an essential ingredient of forward-control theories of movement. A good example is a study by Shadmehr and Mussa-Ivaldi (1994), in which human subjects moved a planar manipulandum to eight different targets equally spaced around a circle from a center start position task. The subjects could easily make normal movements that were fairly straight and had characteristic bell-shaped speed profiles of the speed and time dependency. The manipulandum was then programmed to produce different types of force fields as the handle was moved. When the fields were first applied, the subjects’ movements were characteristically distorted, but after repetition, their trajectories straightened out and matched the normal movement trajectories that were produced in the control, unloaded condition. After the subjects learned to compensate for the imposed force fields, the forces were suddenly removed. Subjects again made trajectories that were distorted, but this time, the distortions mirrored those made when the fields were initially applied. Since the original trajectory was restored when compensating for the imposed force fields and the trials following the perturbation were indicative of learning, the authors took these results to support the idea that subjects were developing internal models of the forces generated to achieve an intended trajectory. More specifically, the subjects learned to predict not only the shape and dynamics of the force field on the handle but also the combinations and dynamics of the internal forces generated by their muscles needed to produce the proper endpoint forces. Referred to as solving the “inverse” problem (going backward from endpoint to internal coordinates), this process is often separated into kinematics (the combination of joint displacements needed to produce an endpoint trajectory) and dynamics (the combination of muscle activations needed to produce the proper joint torques that are summed to produce endpoint force). Both inverse problems are complex: there are many degrees of freedom that could be chosen for a given endpoint displacement (more degrees of freedom than dimensions of arm movement) and many muscle combinations that could produce the same joint torque. The torques needed to generate endpoint movements are dependent on the arm’s configuration and the external forces imposed on the arm. The internal model is thus the learned solution to this problem.

Prediction

The concept of a model trajectory implemented as a set of forces generated by muscles can be incorporated into a framework of motor planning. To achieve the desired action in the external world (e.g., a specific arm trajectory), a set of computations or “operations” (Mountcastle, 1998) need to take place. Theorists have formulated the idea of coordinate system transformation as a framework for performing these operations during volitional reaching. In this framework, a desired target is visualized as a pattern of light projected on the retina. This position and direction of the target in “retinocentric” coordinates need to be transformed to a frame that represents the direction of the hand relative to the target in the coordinate system in which the movement will take place. This process was hypothesized to take place as a series of steps from retina-, to head-, shoulder-, and finally hand-centered axes (Flanders et al., 1992; Gordon et al., 1994; McIntyre et al., 1997; Vindras and Viviani, 1998; Yardley, 1990). Evidence of planning is supported by findings that the hand’s trajectory is straight and smooth, “invariant” across a wide range of conditions. When force fields were applied and maintained (Shadmehr and Mussa-Ivaldi, 1994; Lackner and Dizio, 1994), compensation was found over repeated trials. In this situation, a learned adaptation took place to restore the original trajectory. In other experiments, subjects quickly compensated for added loads by making smooth, straight, reaching trajectories when holding a novel weight. These results suggest that planning occurs in stages. The plan begins with an intended hand trajectory consisting of a smooth, straight movement followed by a transformation to a set of forces generated by muscle contraction and joint torques to displace the limb. The forces needed to achieve this trajectory were found to take place as a secondary process that was fairly independent from the first. The transformations were considered to be informed by an internal model of the physical mechanics (the “plant”), which accounted for the configuration-dependent force production of muscles and bones, as well as by the external forces encountered during the movement. The internal model is a theoretical construct used to explain how predictions are made to account for the delays between a generated command, the action that is produced, and the registration of its consequences. In order to make an accurate prediction, the internal model has to account for the mechanics used to transform a kinematic plan to an endpoint trajectory.

Models of Control

Recent experiments with human subjects have reinstated the use of mechanical perturbations during arm movement but in a wider variety of behaviors such as obstacle avoidance (for a review, see Scott et al., 2015). Perturbations to ongoing arm movement again showed learning-dependent compensatory responses, and this class of experiment has been used to gain insight into the learning process used for internal models. “Optimal control theory” has been particularly influential in shaping this work (Scott, 2004). An early account of optimal control applied to movement generation (Pew and Baron, 1978) was motivated by the desire to add mathematical rigor and engineering modeling to descriptive theories put forth by psychologists. This work, carried out as part of the manned space program, used a corrupted display of simulated flight information to test a subject’s ability to compensate for noisy and delayed information, with the inference that the learned compensation was analogous to an internal model update. Learning was described by an equation that minimized error. Error was considered to be a “cost.” The smaller the cost, the more “optimal” the control. Subsequently, a number of cost functions were proposed to inform the internal models pertinent to the motor system. Jerk (Flash and Hogan, 1985), torque (Uno et al., 1989), energy (Alexander, 1997), effort (Hasan, 1986), and the magnitude of the control signal (Harris and Wolpert, 1998; Todorov, 2002) were considered as candidates. These functions could be grouped into three categories (Kistemaker et al., 2014): control “effort”—thought to be reflected as a magnitude-related quantity when the motor system’s output is considered to be net force; “dynamics” (energy output); and “kinematics” (jerk). In principle, once a cost function is identified and expressed as an equation, its minimum can be found with straightforward least-square methods, resulting in a combination of parameters that, when realized, result in the optimal condition. For arm movements the idea is to rank-order a set of possible behaviors (Flash and Hogan, 1995). However, defining the cost function is still problematic because often the optimal solution is context dependent and elusive (Nelson, 1983). In the motor control literature, this basic theme, incorporating cost functions and the resulting parameters, was extended to include feedback (Pew, 1974), and the scheme became known as “optimal feedback control” (Hoff and Arbib, 1993; Todorov and Jordan, 2002).

A recent review of this theory (Diedrichsen et al., 2010) is summarized in Figure 1. In this scheme, motor commands u_t, in the form of muscle activation signals, are sent not only to the muscles but to a forward model that estimates the physical system to predict the next state of the arm x^*, in terms of kinematics (position, velocity). This prediction is sent to a sensory integrator, which also receives a delayed and noisy sensory signal, y, from the action generated by a previous command. The plant (musculoskeletal system and the environment) generates the next movement increment x_t+1 with a corresponding measurement of y_t+1. However, when registered in the sensory integrator, this sensation has been delayed and degraded (y). At the current timestep, t, the plant has not yet generated the next step, so the measurement, y, is from the previous iteration of the loop. The sensory integrator functions to compensate for the delayed feedback. Here, a predicted sensation, Hx^*, based on the state predicted by the forward model, is subtracted from the physical sensation. This difference can be considered as a predicted distance between successive states. The Kalman gain, K, scales this prediction. If the physical sensation is considered accurate, the gain will be large, and confidence in the predicted distance is high. Conversely, with corrupted sensation, this distance should be discounted. The predicted distance is then added (or, perhaps, more conceptually, subtracted) from the predicted state, and this is used as the estimate of the next state, which, in the subsequent iteration of the loop, becomes the current state estimate.

Figure 1. Diagram of an Optimal Feedback Control Mode.

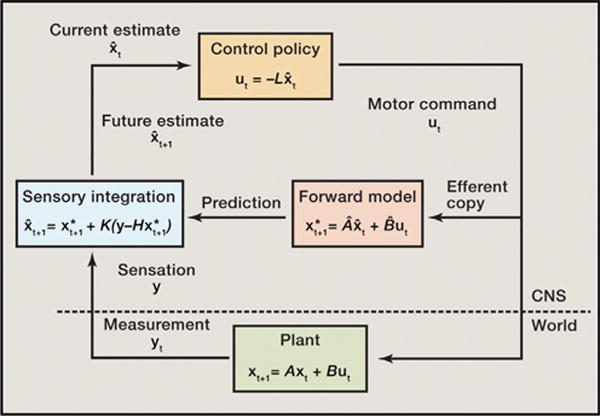
This diagram has been modified from Diedrichsen et al., 2010. See text for explanation.

This particular implementation of optimal control theory encompasses many of the features discussed in the current literature. The basic chain of operations can be considered as a sequence of commands (e.g., trajectory segments) sent both to the mechanical apparatus and simultaneously, as “efferent copy,” to an internal model of the mechanical system (skeletomotor plus the environment). This “forward” model of the physical plant, in which forces generate movement (not to be confused with “feed-forward control”), predicts future movement as current action takes place. Since it takes time for a command to be executed, the current movement was specified by a former command. This, in addition to the time needed to register and transmit the sensation of the movement, means that there will always be a delay between the predicted and actual movement. The delay between these signals complicates calculation of the error. As shown in Figure 1, a common solution to this problem is to employ a Kalman filter, an algorithm that compares current data to predictions of the future. In this scheme, the filter uses the delayed sensory input and the output of the forward model as a way of estimating the current state (position along a trajectory) of the arm. This estimate is used to produce the next command. The Kalman filter is one example of a broader class of theories encompassed by the idea of “Bayesian inference” (Vaziri et al., 2006) in which decisions are made on the statistical basis of prior beliefs (historical evidence) and hypotheses (prediction). An alternative approach to handling the delay between a current output signal and the delayed sensation of that output is to assume that the output signal occurs in steps and that past steps (of the efferent copy) can be stored and compared to the delayed sensory output (Miall et al., 1993). This would suggest that the control policy was operating on a delayed version of the state variables. As a final alternative to addressing sensory delay, it has been proposed that an internal model of sensation can be applied to the delayed sensory input to predict the current state of the movement (Crevecoeur and Scott, 2013). This could then be compared to the prediction of a forward model of the efferent copy.

Control Policy: Costs and Intention

The control policy in Figure 1 can be considered the volitional component of the model. It generates movement commands using an inverse model to transform kinematics to muscle activations. In the Diedrichsen et al. (2010) paper, this model is learned by optimizing a cost function, L. Interestingly, the authors divided this function in two parts. There is a regularization component, consisting of internal costs (e.g., effort, kinematics, and dynamics, as described above) that occur in generating the movement, and one that is task-based—the intention. The proposed medium of the regularization component was force magnitude, which would minimize motor noise and effort. However, as with any choice of a single optimized variable, there are problems with this cost function. Muscle co-contraction is a clear violation of this hypothesis. Force vectors of muscles that contract simultaneously often counteract each other so that the net force (vector sum) is much less than the magnitude of summed muscle contractile force. Co-contraction could be related, for instance, to regulating joint impedance (Hogan, 1984) or to preventing unwanted movement in skeletal segments sharing common tendons (Schieber and Santello, 2004). Despite problems with choosing a single cost function, the overall idea of optimizing control efficiency is attractive. From a control perspective, force resolution or the number of force “categories” that can be specified is especially relevant. These categories consist not only of different levels of force magnitude but may also be defined as force direction, timing, and distribution through the skeletomotor apparatus. This formulation is consistent with information theory, which, in addition to optimal control, is another major approach to motor control (Accot and Zhai, 1997; Fitts, 1954; Fitts and Peterson, 1964; Georgopoulos and Massey, 1988; Lai et al., 2005; Meyer et al., 1982, 1988; Zahedi et al., 2010). The basic concept here is that a certain number of decisions (bits) are needed to specify the value of the commands (e.g., force levels) sent to the muscles. These bits can only be transmitted at some maximum rate (bits/s), determined by the structure of the motor system. This structure or system constraint is referred to as the “channel capacity.” It is assumed that a movement requires a certain number of bits and that the speed of the movement (with continuous control) will be proportional to the length of time it takes to transmit the needed information through the channel. Thus, as shown by Fitts (1954), reaches of larger displacement to smaller targets require more bits and therefore take a longer time to complete (speed-accuracy tradeoff).

How might the control signal be optimized? Volitional movements are goal driven, and the ability to successfully reach a goal requires accurate prediction. A relevant example is the consistent psychophysical finding from reaching studies that reaching trajectories are optimally smooth (Flash and Hogan, 1985). It takes fewer bits of information to predict a smooth trajectory (Flash and Hogan, 1995). Maximizing smoothness minimizes the control burden.

The other component of the proposed control policy is related to intention, encapsulated in the question: what is the goal of the movement and how should it be achieved? As we have seen for movement execution, prediction of the outcome also features large in this domain. For instance, Friston (Adams et al., 2013), using arguments first put forth by Helmholtz, proposed an “active inference” scheme based on the idea that the brain, instead of representing “sensory images,” represents their causes. The generation of these causes from sensory input is carried out with an iterative generative model. The estimated state input to the control policy is replaced by these inferred causes—e.g., the action that produced the sensation. A larger difference between the optimal control theory and Friston’s scheme is in the nature of the command signal. In contrast to specified muscle contraction in optimal control, Friston proposes that the signal is composed of expected proprioception, with the idea that this will be compared to actual proprioceptive signals and, through local reflex circuits in the spinal cord, will be transformed to effective muscle contraction.

Whether or not the details of this particular theory are valid, the themes of prediction and causation fit into the evolving cognitive theories of behavior, which emphasize the incorporation of the body and its surroundings into the control scheme (Beer, 2008; Sanz et al., 2008) and where decisions, expressed as command signals, are based on predictions of actions that will take place in the physical world. This approach is particularly pertinent when considering the acts of grasping and manipulation of objects, which, differently from simple reaching that may not require a great deal of control, is information rich, requiring detailed positioning and application of force. Gibson (1979), for instance, proposed the idea of “affordance,” defined as the set of possible actions that could take place on an object, as a primary constraint of manipulation. Rather than describing objects by their physical qualities, Gibson emphasized that graspable, detachable objects were perceived in terms of the behavior they afforded. The theory was extended to visual perception, forming the basis of a school termed “Ecological Psychology” (Turvey, 1977).

The importance of the physical environment also has been championed in studies of human grasping and manipulation. For instance, proper placement of the fingers and subsequent application of force on the object require accurate prediction of how the object will react as the hand interacts with it. Anticipation of the sensation that will be encountered upon contact is evident as the object is visualized, early in reaching, well before grasping takes place (Gordon et al., 2013), and this was considered due to memory of previous encounters. Skilled hand use consists of a series of events in which the hand is making contact and exerting forces in different configurations with each event eliciting different sensations. The expectation and registration of this sensation is used to regulate the sequence of subtasks composing the movement (Flanagan et al., 2006). This scheme uses an inverse model to generate commands followed by a forward model to produce expected sensation (Flanagan et al., 2003). The expectation is dependent on knowledge of how the object will react to the commanded movement. Extending this logic to complex, skilled tool use, these theories merge with those supporting “embodied cognition,” which “distributes control and processing to all aspects of the agent (its central nervous system, the material properties of its musculoskeletal system, the sensor morphology, and the interaction with the environment” (Pfeifer et al., 2008). In addition to cognitive neuroscience, these theories are prominent in the fields of artificial intelligence and robotics (Brooks, 1991a, 1991b, 2002). The acquisition of internal models that can be used to predict the outcome of future actions requires learning of body mechanics and the physics of actions that take place in the environment. Those predictions become more complex with tool use because movements of the hand become less directly related to the action of the tool in the world, essentially dissociating command signals to move from the intention to act. Clearly, this type of problem falls within the purview of cognition.

Neural Substrate of Control

To summarize what I have discussed so far, motor control theory has evolved from concepts of simple reflexes consisting of obligatory muscle contraction in response to a specific stimulus to those that are approaching explanations of cognition. Some of these theories have led to behavioral experiments, the results of which have led to revisions of the motor control principles. Like almost all engineered control systems, there are very few, if any, biological systems that are not subject to feedback. In contrast, even the simplest reflexes cannot be clearly defined as feedback only, as they are almost always modified by the changing contexts in which they operate. Early volitional control schemes were described using the ideas of feed-forward control in which a movement was completely determined before it began, but these were rapidly modified to accommodate experimental findings showing that control signals were transmitted continuously through the movement. At the same time, these theories were improved to incorporate feedback and the delays associated with real-world functioning. While most motor psychology experiments use impoverished tasks in the laboratory, at least current theories recognize the importance of the physical world in determining the control characteristics of the motor system. Prediction is a major factor in behavior generation and is fundamental to motor control theory. Internal models are invoked to predict future sensory states and the outcome of motor commands. By extending these models to include the complexities of the external world, we can begin to build models that include more complex motor actions such as manipulation and tool use. Invoking motor control theories that encompass skilled manipulation of the external world may provide a concrete avenue for exploring cognitive processing.

Motor control theories have been assembled from observations of motor behavior, and they help define operational principles likely to be contained in a motor control system. However, there is a major distinction, often overlooked, that separates these principles from their mechanistic expression in the nervous system. This problem starts with very basic assumptions used in describing these theories. We diagram motor control models with boxes and arrows, where each box denotes some type of process and the arrows signify input and output to each of these. Inherent in this type of description is discreteness; the borders of each box separate processes, and the arrows suggest that the input and output are singular and synchronized; inputs arrive as distinct messages and outputs are generated as complete products. This follows neuroscience dogma, which surmises function from anatomical connectivity: physical structures in the CNS are assigned specific functional roles and are interconnected in putative circuits in an attempt to define causal sequences of interaction. Theorists adopt these conventions by warping their diagrams to conform with those produced by mainstream neuroscience. All too often, the motor control theorist attempts to follow through by placing a particular box within a particular structure of the nervous system. “… if the nervous system is treated as a black box, any model drawn to represent its operation must be regarded as describing the nervous system’s actual mode of operation. Some cognitive approaches fail to make this distinction explicit, and tend to regard such models as operational analogues…” (Young, 1988). While this may be the way electronic circuits and mechanical systems are designed, it is unlikely that biological systems, and in particular the nervous system, follow these rules. Indeed, it should be emphasized that motor control theories are constructs: models that attempt to elucidate control principles. A problem arises when components of these models are assigned to the nervous system. For instance, the cerebellum—with its access to both afferent sensory signaling and descending output containing efferent information, its learning-dependent activity patterns, and with cells that show clear responses to perturbations—has been hypothesized to contain various aspects of the internal model (Ebner and Pasalar, 2008; Miall et al., 1993; Pasalar et al., 2006; Shadmehr and Krakauer, 2008; Wolpert et al., 1998). Although there is some consistency between model-based theory and the way cerebellar neurons fire during movement, cells in many other neural structures fire in much the same way. For example, evidence for formulation of an internal model can be found in the observation-related activity of neurons throughout the cerebral cortex (Nelissen et al., 2005, 2011; Rizzolatti et al., 1996; Savaki, 2010) and not only the cerebellum.

Attempts to reconcile model control theories with brain circuitry can be seen in works dealing with the latency of a learned response to perturbation, which is often used to place some component of motor control within a particular biological control loop. The idea of motor control loops is very old. Long loops were found to span from spinal cord to motor cortex (Francois-Franck, 1887), whereas short loops were confined to the spinal cord and composed of as few as two neurons for the stretch reflex in muscles (Liddell and Sherrington, 1924). Sherrington (1906), in his monograph “The Integrative Action of the Nervous System,” separated “short reflexes,” limited to a single limb, from “long reflexes,” which comprised conjoint action across multiple body segments. Short reflexes were thought to be elicited from receptors in the same body part that moved in response to their activation. Long reflexes were considered to encompass movements across multiple body segments. Sherrington stated that these “long series of movements” were “initiated and guided by ‘distance receptors”’ such as vision, audition and smell that sampled the external world. He considered these long reactions to be mediated by the cerebrum as analogs of volitional movement. Importantly, Sherrington emphasized that there was no clear separation of short and long pathways, as they are combined through dense networks of interconnections: “…we find the neural arcs from these receptors particularly wide and far-reaching.” More recently, the distinctions between classic motor structures have been blurred by neuronal responses sensitive to somesthetic input, including skin indentation, muscle stretch, and joint displacement to the motor cortex. Passive sensory responses correspond to the way the same neurons fire during arm movement (Conrad et al., 1975; Evarts, 1973; Porter and Rack, 1976). Since this input from the portion of the moving limb matches the output of the motor cortical cell driving that segment during movement, this was taken as evidence for “long loop” feedback. Perturbations of the arm during a reach reliably elicit responses in motor cortex with a latency between 20 and 40 ms, which is consistent with long-loop timing. In comparison, muscle responses occur about 12 ms after a muscle stretch, and these are likely mediated by muscle spindles and mediated by a two-neuron, “short” feedback loop in the spinal cord. Muscle perturbations in monkey motor cortex were found with a latency of 30–40 ms, only after learning, and this was taken as evidence that the long loop pathway was readily modifiable (Evarts, 1973). Using response latency in isolation as an index to locate learning sites is hazardous. For example, later experiments with perturbations that followed a more random schedule showed that, although the motor cortical cells responded consistently, the 30–40 ms EMG response was more variable (Conrad et al., 1975; Porter and Rack, 1976), suggesting that, in conditions that preclude learning, there is still consistency in the motor cortical response and that this is dissociated from muscle contraction. Feedback and latency considerations cannot explain this type of result. It should be emphasized that any role of the motor cortex in a reflex loop has to be viewed in context of its operation during volitional aspects of movement. As discussed above, monkeys that were given prior cues of an impending arm perturbation generated expectation-dependent motor cortical responses when the disturbance was applied (Evarts and Tanji, 1974). Furthermore, motor cortical cells have a task-dependent change in firing rate, well before movement onset when no movement-related sensory cues are present (Evarts, 1966a).

Current perturbation studies aimed at elucidating control principles still use timing and learning criteria to place modeled components in specific loops (Crevecoeur and Scott, 2013; Kurtzer et al., 2008; Scott et al., 2015). However, it is important to note that learned compensatory responses occur at different levels of the neuroaxis. For instance, it was shown that decerebrate ferrets walking on a treadmill could learn to step over an obstacle after 10–15 steps (Lou and Bloedel, 1988). Similar plasticity was even found in walking cats with lesions that separated their spinal cords from the rest of the nervous system (Zhong et al., 2012).

The Utility of Modeling Neuronal Activity during Naturalistic Movement

How can theory be combined with empirical studies using behavioral and neurophysiological methods? In the 1960s and 70s, motor control investigations of neural activity transitioned away from electroanatomical, perturbation, and otherwise restricted paradigms toward those involving behaving animals. One example was the use of awake monkeys in which single-neuron cortical activity was recorded. Following recording advances made by Jasper and Bertrand (1966), Evarts (1966b) developed a skull-mounted microdrive that allowed a microelectrode to be introduced into the motor cortex for recording extracellular recordings of action potentials as monkeys made trained movements of their wrists (Evarts, 1966a). A variant of this recording method (Mountcastle et al., 1975) was used by Georgopoulos in the early 80s (Georgopoulos et al., 1982, 1983b, 1984) with monkeys that performed natural reaching movements. Up to that point, most motor control paradigms were designed to examine the mechanics of movement—for instance, by restricting movements to a single joint in such a way that emphasized agonist-antagonist muscle activation. Coordinated, multi-joint movements could be studied with the introduction of the center->out paradigm, in which monkeys reached from a central location on a plane to different peripheral targets located radially around the start position. Neurons recorded from the motor cortex were modulated in a way that was related to the direction of the target the monkeys were reaching toward. More specifically, the firing rates of these neurons, when averaged over the duration of the movement, could be modeled as a cosine tuning function that mapped movement direction to discharge rate. Data plotted as movement direction versus firing rate fell along a cosine-shaped curve or “tuning function.” The tuning had a single, maximum firing rate corresponding to a “preferred” movement direction. All directions of movement were spanned by the function, which had a minimum firing rate in the direction opposite from the preferred direction. The broad cosine tuning means that these neurons change their firing rates for every change of movement. Since these functions are maps of direction to firing rate, they are referred to as “encoding” because they function as movement direction codes. However, in practice, they cannot be used to directly “decode” movement direction by going from discharge rate to direction. Because the cosine function is symmetrical about its preferred direction, each discharge rate maps to two directions (except at the peak rate, which corresponds to a single preferred direction). Furthermore, if trial-by-trial noise is added to the function, only very crude estimates of direction can be made. The cosine tuning function, because it incorporates all movement directions, provided a way out of the decoding dilemma. Motor cortical neurons have different preferred directions, which, combined with broad tuning, means that many neurons change their firing rates simultaneously as directions change. For any movement direction, each neuron will fire at a different rate in a way that depends on its preferred direction. This was captured by the population vector algorithm that Georgopoulos developed. This method used vectors to represent each neuron’s tuning function. A vector for each cell pointed in its preferred direction with a magnitude proportional to its firing rate. The collection of weighted cell vectors added together resulted in the “population vector”—the decoded predicted direction of movement for a particular reach. This simple method used encoding (cosine fit of discharge rate to direction) and decoding (vector summation) to accurately predict movement direction.

Since this original observation, cosine tuning of movement direction has been found in many structures of the nervous system and can be considered a general principle of movement generation (van Hemmen and Schwartz, 2008). Since the directionfiring rate relation could also be well characterized by other statistical distributions (e.g., Gaussian, Poisson, or von Mise), why emphasize the cosine fit? Mechanistically, it may seem unlikely that there is a specific neural operation that “calculates” cosine functions. Computationally, one might view cosine tuning as a convenience that allows a vector approach to directional coding. However, there may be some theoretical utility to the cosine tuning and vector representation. Cosine tuning, from a vector perspective, can be thought of as a projection of movement direction on to a cell’s preferred direction (Schwartz, 2007) and expressed as an inner product between vectors. This is a geometric analog to cross-correlation. With a slight extension, this type of correlation could be considered a way to convey directional information through the nervous system. Correlation between elements generates statistical structure in systems. When the system is sampled with analytical tools, this structure can be recognized and used to gain insight into system states that, for instance, are related to learning (Sadtler et al., 2014) and attention (Velliste et al., 2014). The identification of “latent drivers,” as factors that induce correlational structure, can be used to describe task-dependent system organization (Chase and Schwartz, 2011; Chase et al., 2010; Churchland et al., 2012; Kaufman et al., 2014; So et al., 2012). An advantage of these correlation-based techniques is that they are based on neuron-neuron interactions without a priori assumption of neuron-behavior causation.

The population vector method has proven to be a robust decoding method for movement. When used on short timescales during movement, the method can predict details of the arm’s trajectory during reaching and drawing (Georgopoulos et al., 1988a; Moran and Schwartz, 1999a; Schwartz, 1993, 1994; Schwartz and Moran, 1999, 2000). This work also showed that the population vector is an analog of endpoint velocity, as it not only predicts instantaneous direction but speed as well (Moran and Schwartz, 1999b). Once again, it should be emphasized that the population vector is a construct. It does not exist physically as a network node that gathers directional information with an output of endpoint velocity.

The findings of broad directional tuning and the validity of the population vector approach can be used to help define preliminary principles of motor control. Widespread neural modulation takes place throughout the neural axis during volitional movement. Individual neurons encode consistent, but relatively weak, movement information. Yet consideration of population activity provides a detailed prediction of movement trajectory. Movement velocity is readily extracted from the population. This supports a major tenet of motor control theory: movement kinematics, represented in neuronal firing patterns, are predictive of the upcoming movement.

Toward Prosthetics for Movement

Results collected over the last 20 years from cortical recordings during reaching and characterization of the correspondence between movement kinematics and neuronal firing form the basis of the brain-controlled interfaces (BCI) used for neural prosthetic movement. The extent of our ability to extract detailed movement signals from motor cortex is demonstrated in the movements made by paralyzed individuals as they operate high-performance prosthetic arms and hands to recover near-normal functionality. In essence, this technology is restoring the communication channel disrupted by paralyzing pathology. Using the basic concepts of kinematic encoding and widespread population decoding, this work began with monkeys (Isaacs et al., 2000; Serruya et al., 2002; Taylor et al., 2002; Wessberg et al., 2000) and then progressed to a demonstration with paralyzed human subjects (Hochberg et al., 2006; Kennedy et al., 2000). In these initial tasks, subjects controlled a cursor on a computer screen. Subsequently, the number of parameters that could be decoded simultaneously increased from three dimensions of cursor control, to four (Velliste et al., 2008), seven (Collinger et al., 2012), and ten degrees of freedom using a robot (Wodlinger et al., 2015). The last two demonstrations were of a paralyzed woman operating a high-performance prosthetic arm and hand to carry out tasks of daily living. She could move the arm through 3D space, orient its wrist in three dimensions, and change the shape of its hand using four basic configurations as building blocks. By beginning with monkey experiments in which subjects progressed from movements of their arms in 3D space, to closing of the hand, orientation of the wrist and then to shaping of their hands, we were eventually able to build decoding algorithms that could extract ten movement parameters simultaneously. From the perspective of basic science, this means that individual neurons encode many aspects of movement in their firing patterns. At the same time, these findings, incorporated into the extraction algorithms used for neural prosthetics, are offering new therapies to those who are paralyzed.

Use of BCI also allowed the study of the role of learning in movement generation. When brain-controlled interfaces are used with virtual reality—for example, when moving cursors in a computer display—the internal model of the physical mechanics (the “plant”) can be either removed or altered in precise ways from the control loop. This is an ideal situation to study learning. Because operating the device is directly dependent on the way neurons in the recorded sample are modulated during the task, any change in task performance has to be related to the firing patterns of these neurons. Learning takes place as the decoded movement is displayed back to the subject, and undesired movement is modified by changing the way neurons in the sampled population fire during the task. The direct linkage between firing rate and movement (e.g., the computer cursor) is governed by the encoding model. In early demonstrations, for instance, it was shown that there was a direct correlation between the model’s fit to the data and performance of the task. Over successive days, both the fit and the performance increased (Carmena et al., 2003; Taylor et al., 2002), suggesting that the encoding model was being learned. In addition to the importance that learning has in improving BCIs (Koyama et al., 2010; Orsborn et al., 2014; Zhang et al., 2012), the BCI task can be used explicitly to study the learning process by purposefully distorting the encoding model. This makes it possible to visualize neuronal adaptation to the imposed perturbation (Chase et al., 2012; Ganguly et al., 2011; Jarosiewicz et al., 2008; Legenstein et al., 2009; Sadtler et al., 2014). Essentially, this methodology allows internal model theories to be examined directly (Golub et al., 2013, 2015).

A next frontier with neural prosthetics is dexterous interaction with objects. The ability of human subjects to grasp and manipulate objects is limited with current decoders (Wodlinger et al., 2015). Beyond the sheer amount of information required to carry out this type of behavior, this limitation may be due to fundamental inadequacies of the model itself. For instance, the current kinematic model assumes an endpoint-centered coordinate system. For object manipulation, behavioral considerations suggest that the coordinate system may be object centered (Jeannerod, 2003). An essential component of dexterous object manipulation is the correct application of forces between the contact surfaces of the hand and fingers and those of the object. Although some studies have looked at the way hand forces are encoded by neural activity during grasping (Georgopoulos et al., 1992; Kalaska et al., 1989; Sergio et al., 2005), details of this encoding with respect to hand-object force vectors are unknown. To achieve dexterity with neural prosthetics that approaches that of normal human behavior, it is likely that we will need to distinguish brain activity patterns corresponding to the intention to act from control signals of the hand itself. This subtle distinction is present with tool use (Umiltà et al., 2008). As we move toward this objective, considerations normally ascribed to cognitive function, such as learning, object identification, intended action using the object, and the prediction of future consequences, will be unavoidable.

Conclusions

Motor control theory and experimentation have progressed from descriptions of simple reflexes to the frontiers of cognitive processing. Models have become more sophisticated as theories begin to account for the differences between biological function and conventional engineered control approaches. An increasing appreciation of the complexity within the motor system suggests that the current view of separate processing steps, contained in discrete nervous system loci connected in fixed circuits, should be modified. Pertinent neural operations are widely distributed throughout the system with statistical interactions governing functional connectivity. Instead of assigning functional labels to pieces of the system, appropriate samples of neural activity can be used to better understand the underlying principles used to control movement. Despite the difficulty of studying such a system, large-scale recordings of neural activity, combined with rich behavioral paradigms, have already led to methods for extracting high-fidelity movement information that restore coordinated, useful movement to paralyzed individuals. Cognitive neuroscience and systems neurophysiology are converging on the idea of movement as communication of intention from the brain to the external world. A revolution is occurring as machines are being designed to infer and operate on intention and to predict future action (Levinson et al., 2011; Muelling et al., 2015; Stentz et al., 2015). In biological systems, these factors are evident as the incorporation of expectation in even the simplest neuronal operations. Theorists have converged on the concept of internal models to generate these predictions. BCI technology is being used to directly examine these previously covert constructs. Further advances promise not only increased functionality of neural prosthetic devices but also pathway to basic scientific investigation of cognitive processing.