Dual-pathway multi-echo sequence for simultaneous frequency and T₂ mapping

Abstract

Purpose

To present a dual-pathway multi-echo steady state sequence and reconstruction algorithm to capture T₂, T₂* and field map information.

Methods

Typically, pulse sequences based on spin echoes are needed for T₂ mapping while gradient echoes are needed for field mapping, making it difficult to jointly acquire both types of information. A dual-pathway multi-echo pulse sequence is employed here to generate T₂ and field maps from the same acquired data. The approach might be used, for example, to obtain both thermometry and tissue damage information during thermal therapies, or susceptibility and T₂ information from a same head scan, or to generate bonus T₂ maps during a knee scan.

Results

Quantitative T₂, T₂* and field maps were generated in gel phantoms, ex vivo bovine muscle, and twelve volunteers. T₂ results were validated against a spin-echo reference standard: A linear regression based on ROI analysis in phantoms provided close agreement (slope/R² = 0.99/0.998). A pixel-wise in vivo Bland-Altman analysis of R₂=1/T₂ showed a bias of 0.034 Hz (about 0.3%), as averaged over four volunteers. Ex vivo results, with and without motion, suggested that tissue damage detection based on T₂ rather than temperature-dose measurements might prove more robust to motion.

Conclusion

T₂, T₂* and field maps were obtained simultaneously, from the same datasets, in thermometry, susceptibility-weighted imaging and knee-imaging contexts.

Introduction

The goal of the present work is to develop a method to obtain T₂ and T₂* maps as well as field maps in a combined, simultaneous manner. Differences in T₂ value between tissues have arguably been the most significant driver of MRI developments since its inception and can be exploited to detect a wide array of pathologies. Field maps can also prove valuable, for example in quantitative susceptibility mapping and in susceptibility-weighted imaging (1-3), thermometry (4, 5), shimming and in Dixon-based fat-water separation methods (6, 7). However, T₂ and field information are not typically acquired jointly as they often involve different pulse sequences: a spin-echo based sequence for T₂ and a gradient-echo based sequence for field mapping.

Methods based on asymmetrical spin echoes and/or on a combination of ‘free-induction decay’ (FID) and spin echo signals can capture T₂ and field information together (8-12), but such sequences tend to be relatively slow. Alternately, phase-cycled versions of the ‘steady-state free precession’ (SSFP) sequence or the ‘dual echo in the steady state’ (DESS) sequence (13) can be employed for this purpose. The signal equation for these sequences involves T₂ along with several other parameters, making it possible to generate T₂ maps (14-17). More specifically, the DESS sequence samples two different magnetization pathways: the FISP (for ‘fast imaging with steady state precession’) and the PSIF (for inverted FISP). Differences between FISP and PSIF signal levels can be interpreted toward evaluating T₂ (17). Similarly, the present method also involves a DESS sequence toward generating T₂ maps, but two or more echo times are employed here. The main advantage of the dual-pathway multi-echo sequence proposed here and of its associated reconstruction algorithm is that they allow T₂ to be calculated without explicit knowledge of the flip angle. B₁ fields vary spatially and as such, flip angles often differ from their user-prescribed nominal value. Treating the flip angle as an unknown rather than a known quantity provides improved robustness in the presence of such variations.

Potential applications were investigated where the proposed imaging method might prove particularly useful: susceptibility-weighted imaging (SWI), thermometry and cartilage imaging. SWI is often utilized to detect iron accumulations in the brain associated with bleeding: Due to its very strong magnetic susceptibility, iron can very much alter the overall susceptibility of tissues when present in greater-than-usual concentrations (18). Unusual iron concentrations may also be associated with neurological diseases such as Parkinson's disease, Alzheimer's disease, and multiple sclerosis (19-23). Field maps are generated from the phase information of the acquired images and larger-scale phase variations that are not tissue-specific are removed, yielding images that provide susceptibility-induced contrast between tissues. In a neuroimaging application, the proposed method can provide simultaneous field maps and T₂ maps for susceptibility imaging and tissue characterization.

Thermometry represents a second MR application where the simultaneous acquisitions of field maps and T₂ maps might prove beneficial. Thermal therapies offer minimally-invasive alternatives to conventional surgeries and MRI can be used for image-guidance (24-26). More specifically, the proton resonance frequency (PRF) method allows measured field maps to be converted into temperature measurements (4, 5, 27, 28), which in turn can be converted into thermal dose (TD) to help detect tissue damage and guide thermal ablations (29). However, TD calculations involve the entire thermal history of each volume of tissue and prove difficult to obtain in a reliable fashion in the presence of motion. Interestingly, tissue damage is associated with changes in T₂ as well as with elevated TD exposures (30). Especially in abdominal organs where motion is problematic, detecting damage on a frame-by-frame basis in a temporally-resolved series of T₂ maps might provide a motion-robust alternative to the more traditional TD-based approach. In thermal-ablation applications the proposed method could enable the simultaneous use of two complementary damage-detection methods through joint TD and T₂ measurements (31).

Knee imaging might prove the most straightforward application of the proposed imaging method tested here, as DESS is already a widely-employed sequence for cartilage segmentation. The proposed method can provide information similar to that of a regular DESS sequence, with T₂ maps added as a bonus. This extra information may prove helpful as T₂ has been shown to be a useful bio-marker for early knee osteoarthritis (32).

The theory of the proposed method (33) is closely related to that of the ‘gradient-echo sampling of FID and echo’ (GESFIDE) method (8), as both de-phasing and re-phasing signals are measured and compared to allow T₂ and T₂* effects to be discriminated. As opposed to GESFIDE the present method does not involve any 180° refocusing pulse and does not require any explicit spin echoes to be generated. For this reason shorter TR values typical of gradient-echo rather than spin-echo sequences can be achieved, for faster imaging. Results were obtained in phantoms, in ex vivo tissues and in volunteers, as the proposed imaging method was tested for use in neuro, thermometry and musculoskeletal applications.

Methods

Generating quantitative R₂ and R₂′ maps

Steady-state signals from more than one magnetization pathway were sampled at more than one echo-time, as depicted in Fig. 1. More specifically, FID-like FISP ($S_j^{+}$) and spin echo-like PSIF ($S_j^{-}$) signals were sampled at echo times $T{E}_j^{+}$ and $T{E}_j^{-}$, respectively, where j represents the echo number. The irreversible and reversible decay parameters R₂ and R₂′, defined through T₂ ≡ 1/ R₂ and T₂* ≡ 1/ (R₂ + R₂′), are obtained as described below.

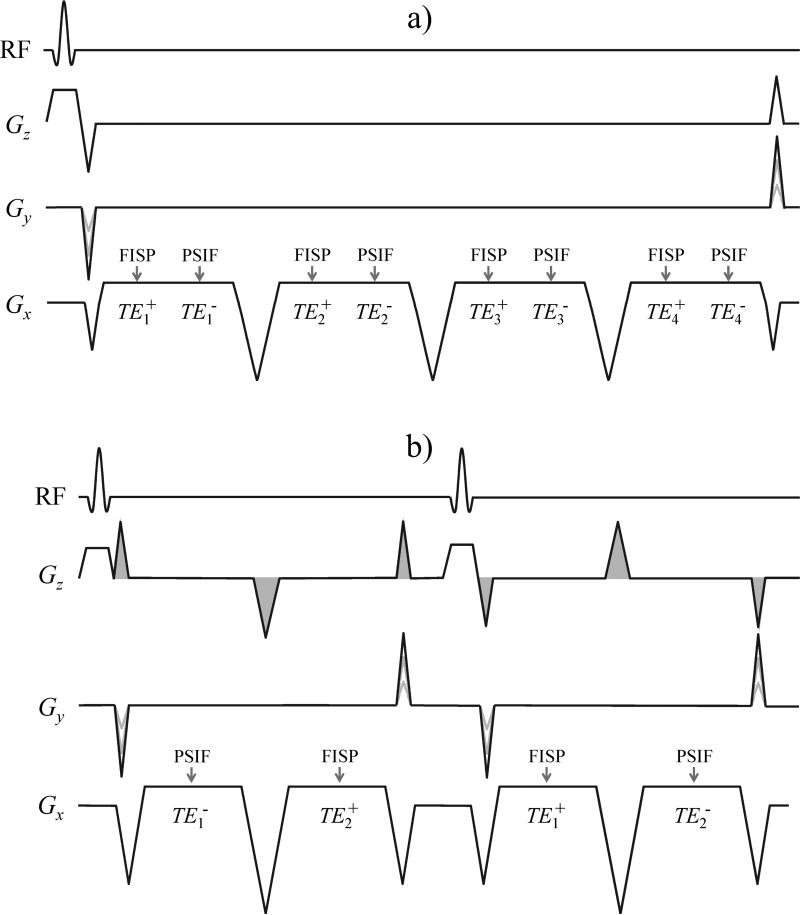
Fig. 1.

a) The dual-pathway multi-echo pulse sequence employed here is depicted for the case N_TE = 4. The 2D version is shown; the 3D version is nearly identical except for the addition of phase-encoding blips along G_z. b) A shorter-TR version of the sequence was also implemented whereby different echo times were obtained by switching the order of the FISP and PSIF echoes on alternate TR periods. The order of the echoes is determined by the size of the pre- and re-phaser pulses, shown shaded. The sequence in (b) was implemented on a GE system with moving table, for motion-related tests, while that in (a) was implemented on Siemens systems.

As usual for a gradient-echo sequence the signal magnitude $\mid S_j^{+}\mid$ evolves through TR under the combined influence of an irreversible T₂ decay, $\exp (-R_2\times T{E}_j^{+})$, and of a reversible decay, $\exp (-{R_2}^{\prime }\times T{E}_j^{+})$:

$$\mid S_j^{+}\mid =\mid S_0^{+}\mid \times e^{-\left(R_2+{R_2}^{\prime }\right)\times T{E}_j^{+}},$$ [1]

where S₀⁺ represents the signal at t = 0, just after the RF excitation. Unlike the $\mid S_j^{+}\mid$ of Eq. 1, the $\mid S_j^{-}\mid$ signal is similar to a spin-echo on its way to formation in the sense that reversible decay is progressively being cancelled. While both $\mid S_j^{+}\mid$ and $\mid S_j^{-}\mid$ signals decay under the influence of a similar irreversible decay term, $\exp (-R_2\times T{E}_j^{-})$, the reversible decay term for $\mid S_j^{-}\mid$ in Eq. 2 below differs from that in Eq. 1 above because the $\mid S_j^{-}\mid$ magnetization is being refocused at a time TR:

$$\mid S_j^{-}\mid =\mid S_{TR}^{-}\mid \times e^{-R_2\times T{E}_j^{-}-{R_2}^{\prime }\times \left(TR-T{E}_j^{-}\right)}=\mid S_{TR}^{-}\mid e^{-{R_2}^{\prime }\times TR}\times e^{-\left(R_2-{R_2}^{\prime }\right)\times T{E}_j^{-}}=\mid S_0^{-}\mid \times e^{-\left(R_2-{R_2}^{\prime }\right)\times T{E}_j^{-}}.$$ [2]

As can be seen from Eq. 1 and 2, the $\mid S_j^{+}\mid$ signal decays according to (R₂ + R₂′) while the $\mid S_j^{-}\mid$ signal decays according to (R₂ - R₂′). By sampling both types of signals at multiple TE values one can evaluate (R₂ + R₂′) as well as (R₂ - R₂′), thus allowing R₂, R₂′, T₂ and T₂* to be found.

One way to solve Eq. 1 and 2 involves applying a logarithm operator to both, leading to a linear system of equations:

$$\ln \left(\mid S_j^{+}\mid \right)=\ln \left(\mid S_0^{+}\mid \right)-\left(R_2+{R_2}^{\prime }\right)\times T{E}_j^{+},\ln \left(\mid S_j^{-}\mid \right)=\ln \left(\mid S_0^{-}\mid \right)-\left(R_2-{R_2}^{\prime }\right)\times T{E}_j^{-}.$$ [3]

Alternately, the Levenberg-Marquardt (LM) algorithm, known to have better noise properties than the log-linear method from Eq. 3, can be used instead to fit Eq. 1 and 2. Algorithms faster than LM (34) or a more general T₂* decay model (12) could also be considered. With N_TE the number of echoes per pathway and only two different pathways (FISP and PSIF), Eq. 3 gives 2× N_TE equations and four unknowns: $\mid {S_0}^{+}\mid$, $\mid {S_0}^{-}\mid$, R₂ and R₂′. While a minimum number of echoes N_TE = 2 is required to solve, a higher number of echoes may help improve the stability of the solution. Please note that $\mid {S_0}^{+}\mid$ and $\mid {S_0}^{-}\mid$ are treated here as fit parameters. While the $\mid {S_0}^{+}\mid ∕\mid {S_0}^{-}\mid$ ratio could be further exploited toward gaining information regarding T₁ and/or the flip angle (35) such further steps are considered beyond the scope of the present work.

Generating relative temperature maps

The potential advantages, and disadvantages, of using the proposed dual-pathway multi-echo sequence for thermometry purposes are developed and analyzed below. The phase of any given MR image may be difficult to predict and somewhat arbitrary; however, in PRF thermometry one is typically interested in phase differences rather than in the phase value itself. Taking the phase difference between pre- and post-heating images and assuming all phase changes are due to temperature only, any arbitrary phase component simply cancels out in the subtraction. In this PRF context, a TNR (temperature-to-noise-ratio)-optimum expression is derived below which is a generalization of that from (36), to handle multi-pathway multi-TE data. With TE_p,j the echo time for pathway p and echo j, the temperature sensitivity Λ_p,j is defined here in close analogy with Eq. 1 from (36):

$${\Lambda }_{p,j}=\left(\gamma \alpha B_0\right)\times \left(pTR+T{E}_{p,j}\right),$$ [4]

where p = 0 for FISP signal and −1 for PSIF signal, γ is the gyromagnetic ratio for hydrogen (2π × 42.58 MHz/T), α is the PRF change coefficient (−0.01 ppm/°C) and B₀ the main magnetic field. For each pathway and echo time a phase difference Δϕ_p,j is obtained, leading to a temperature change measurement ΔT_p,j:

$$\Delta T_{p,j}(\overrightarrow{r},t)=\frac{\Delta {\varphi }_{p,j}(\overrightarrow{r},t)}{{\Lambda }_{p,j}}.$$ [5]

The TNR-optimum combination of all temperature estimates ΔT_p,j requires a reliable estimate of signal levels, for example a simple root-sum-of-square combination of coil images, where I_p,j,c is the image acquired with coil-element c:

$$A_{p,j}(\overrightarrow{r},t)=\sqrt{\sum _c{\mid I_{p,j,c}(\overrightarrow{r},t)\mid }^2}.$$ [6]

A factor W_p,j is further employed to capture noise variations related to imaging parameters, such as voxel size or receive bandwidth. In most foreseeable applications W_p,j values will all be the same and will cancel out of Eq. 7 below. A temperature-change estimate ΔT is obtained:

$$\Delta T(\overrightarrow{r},t)=\frac{\sum _p\sum _j\left({\left({\Lambda }_{p,j}{A}_{p,j}(\overrightarrow{r},t)W_{p,j}\right)}^2\times \left(\frac{\Delta {\varphi }_{p,j}(\overrightarrow{r},t)}{{\Lambda }_{p,j}}\right)\right)}{\sum _p\sum _j{\left({\Lambda }_{p,j}{A}_{p,j}(\overrightarrow{r},t)W_{p,j}\right)}^2+\epsilon },$$ [7]

where ε is an arbitrarily-small positive number. In the limit where A_p,j is known with high SNR Eq. 7 provides a TNR-optimum estimate for ΔT. In the present work only two pathways were sampled, the FISP (p = 0) and the PSIF (p = −1); using the simplified notation from Eq. 1-3 with ‘+’ and ‘−’ subscripts one obtains $A_{0,j}=\mid S_j^{+}\mid$ and $A_{-1,j}=\mid S_j^{-}\mid$. Differences between Eq. 7 and Eq. 2 from (36) include: 1) A summation over j to handle multiple echoes, and 2) weights raised to the second power, as Λ_p,j×A_p,j×W_p,j is applied a first time to equalize the noise level among all terms and a second time to emphasize/de-emphasize the least/most noisy terms and optimize TNR.

TNR performance

If TNR were the only concern, a single echo time would be sampled for each pathway, as done in (36). However, to also map T₂ and T₂* as described above multiple TE values are needed. In other words, T₂ and T₂* knowledge comes at a price in TNR, as described below and in Fig. 2.

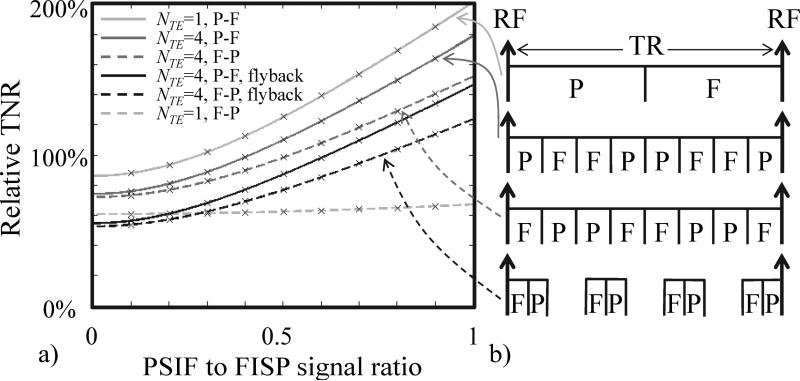
Fig. 2.

a) Relative temperature-to-noise-ratio as compared to a regular gradient-echo sequence is plotted as a function of the PSIF to FISP signal ratio, $\mid {S_0}^{-}\mid ∕\mid {S_0}^{+}\mid$, for a few different scenarios indicated in (b): A single echo per pathway (N_TE = 1), four echoes per pathway (N_TE = 4), using a FISP-PSIF ordering such that the FISP pathway is sampled first or alternately a reversed ordering such that the PSIF pathway is sampled first, with or without flyback. A few of these sampling schemes are depicted on the right-hand side of the figure, where the label ‘F’ represents readout windows when FISP signals are sampled while ‘P’ indicates when PSIF signals are acquired.

As compared to a thermometry sequence with a single gradient echo of amplitude A_ref, sensitivity Λ_ref and weight W_ref, the relative TNR expected from a multi-pathway multi-echo pulse sequence is given by:

$$\text{relative TNR}=\frac{\sqrt{\sum _p\sum _j{\left({\Lambda }_{p,j}{A}_{p,j}(\overrightarrow{r},t)W_{p,j}\right)}^2}}{{\Lambda }_{ref}{A}_{ref}(\overrightarrow{r},t)W_{ref}}.$$ [8]

The factor Λ_p,j×A_p,j×W_p,j determines how noise varies from one term to the next in the summation from Eq. 7; adding these terms in quadrature and dividing by the scaling factor from Eq. 7 gives the inverse of the numerator in Eq. 8. The inverse of the denominator in Eq. 8 is proportional to the noise level in the reference gradient-echo sequence. As a result Eq. 8 is a ratio of temperature noise, which for a same temperature also corresponds to a TNR ratio.

Inserting Eqs 1 and 2 into Eq. 8, and assuming a readout period of τ_ref for the reference and τ for the dual-pathway multi-TE sequence, the ratio W_ref / W_p,j is equal to $\sqrt{{\tau }_{ref}∕\tau }$ and one obtains an expression for relative TNR as a function of R₂, R₂′ and the ratio $\mid {S_0}^{-}\mid ∕\mid {S_0}^{+}\mid$:

$$\text{relative TNR}=\frac{\sqrt{\sum _j{\left(T{E}_j^{+}\times e^{-\left(R_2+{R_2}^{\prime }\right)\times T{E}_j^{+}}\right)}^2+\sum _j{\left(\left(TR-T{E}_j^{-}\right)\times \left(\mid S_0^{-}\mid ∕\mid S_0^{+}\mid \right)\times e^{-\left(R_2-{R_2}^{\prime }\right)\times T{E}_j^{-}}\right)}^2}}{\sqrt{{\tau }_{ref}∕\tau }\times T{E}_{ref}\times e^{-\left(R_2+{R_2}^{\prime }\right)\times T{E}_{ref}}}.$$ [9]

Figure 2a shows plots of relative TNR as a function of $\mid {S_0}^{-}\mid ∕\mid {S_0}^{+}\mid$ for a number of different scenarios, most of which are depicted in Fig. 2b. Neglecting all waveforms other than readout windows, and neglecting ramp durations, the timing of all readout windows in a dual-pathway multi-TE sequence is depicted in Fig. 2b. The various cases shown in Fig. 2b represent different settings for N_TE, different choices for FISP-PSIF vs. PSIF-FISP orderings, with and without fly-back.

Field mapping

An SNR-optimum equation is developed below to generate field maps from the multi-pathway multi-echo signal acquired here. As opposed to Eq. 7 above, MRI's arbitrary phase does not readily vanish in a phase difference operation and must be taken into account instead. The phase evolution model is given by:

$$\angle \left(S_j^{+}\right)=\angle \left(S_0^{+}\right)+\omega \times T{E}_j^{+},\angle \left(S_j^{-}\right)=\angle \left(S_{TR}^{-}\right)-\omega \times \left(TR-T{E}_j^{-}\right),$$ [10]

where the $\angle (\cdot )$ operator extracts the phase of a complex signal, and ω = γ × B. Using a matrix format for a weighted least-square solution, with M_TE the matrix that relates the unknowns (ω, $\angle \left(S_0^{+}\right)$ and $\angle \left(S_{TR}^{-}\right)$) to the phase measurements in Φ, and using a diagonal matrix $\mid \overline{W}\mid$ as a weight, Eq. 10 becomes:

$$\begin{array}{c}\hfill \mid \overline{W}\mid \Phi =\mid \overline{W}\mid M_{TE}\left[\begin{array}{c}\hfill \omega \hfill \\ \hfill \angle \left(S_0^{+}\right)\hfill \\ \hfill \angle \left(S_{TR}^{-}\right)\hfill \end{array}\right],\Phi ={\left[\angle \left(S_1^{-}\right)\cdots \angle \left(S_{N_{TE}}^{-}\right)\angle \left(S_1^{+}\right)\cdots \angle \left(S_{N_{TE}}^{+}\right)\right]}^{\mathrm{T}},\hfill \\ \hfill M_{TE}={\left[\begin{array}{cccccc}\hfill -\left(TR-T{E}_1^{-}\right)\hfill & \hfill \cdots \hfill & \hfill -\left(TR-T{E}_{N_{TE}}^{-}\right)\hfill & \hfill T{E}_1^{+}\hfill & \hfill \cdots \hfill & \hfill T{E}_{N_{TE}}^{+}\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \end{array}\right]}^{\mathrm{T}},\hfill \\ \hfill \mathrm{diag}\left(\mid \overline{W}\mid \right)={\left[\mid W_1^{-}\times S_1^{-}\mid \cdots \mid W_{N_{TE}}^{-}\times S_{N_{TE}}^{-}\mid \mid W_1^{+}\times S_1^{+}\mid \cdots \mid W_{N_{TE}}^{+}\times S_{N_{TE}}^{+}\mid \right]}^{\mathrm{T}}.\hfill \end{array}$$ [11]

A weighted least-square solution to Eq. 11 yields ω, from which B is obtained, along with $\angle \left(S_0^{+}\right)$ and $\angle \left(S_{TR}^{-}\right)$. An analytic relationship between $\angle \left(S_0^{+}\right)$ and $\angle \left(S_{TR}^{-}\right)$ would have allowed the number of unknowns in Eq. 11 to be reduced from 3 to 2, but many factors such as k-space offsets may make the phase of FISP and PSIF images to differ in ways that are difficult to predict. For this reason, $\angle \left(S_0^{+}\right)$ and $\angle \left(S_{TR}^{-}\right)$ were treated here as independent variables.

Note that Eq. 11 could be used for PRF thermometry, by applying it twice separately on pre- and post-heating data and calculating temperature changes based on measured frequency differences rather than phase differences. But as compared to Eq. 7, applying Eq. 11 twice would lead to lower TNR because of the additional degrees of freedom involved in evaluating arbitrary phase terms for both pre- and post-heating data separately. On the other hand, separately evaluating these phase terms would provide improved robustness whenever phase might vary unexpectedly, for example in the presence of field drifts, as phase changes unrelated to heating would introduce errors in Eq. 7. As confirmed through Monte Carlo simulation, Eq. 11 can be made numerically equivalent to Eq. 7 by replacing all phase terms by a phase difference instead, and by assuming both $\Delta \left(\angle \left(S_0^{+}\right)\right)$ and $\Delta \left(\angle \left(S_{TR}^{-}\right)\right)$ equal to 0.

Synthetic DESS images

In the cartilage-imaging application, FISP and PSIF signals were synthesized at the same echo time as in a standard DESS sequence, $T{E}_{ref}^{+}$ and $T{E}_{ref}^{-}$, respectively. These synthetic signals, $\mid S_{synth}^{+}\mid$ and $\mid S_{synth}^{-}\mid$, were calculated using Eqs 1 and 2 along with evaluated results for $\mid S_0^{+}\mid$, $\mid S_0^{-}\mid$, R₂ and R₂′:

$$\mid S_{synth}^{+}\mid =\mid S_0^{+}\mid \times e^{-\left(R_2+{R_2}^{\prime }\right)\times T{E}_{ref}^{+}},\mid S_{synth}^{-}\mid =\mid S_0^{-}\mid \times e^{-\left(R_2-{R_2}^{\prime }\right)\times T{E}_{ref}^{-}}.$$ [12]

Synthetic DESS images were then generated, as $\mid S_{synth}^{+}\mid +\mid S_{synth}^{-}\mid$.

Pulse sequence design

Two variations of the pulse sequence employed here are depicted in Fig. 1. Both are steady-state unbalanced sequences: They are steady-state sequences because RF spoiling is not employed and magnetization is allowed to endure from one TR interval to the next, and they are unbalanced because all gradients waveforms do not add up to zero area. The zeroth-moment of the gradient waveforms determines how far apart magnetization pathways are in k-space and where to find them. Individual pathways can be thought of as replicas of the k-space signal and these replicas differ from each other mostly due to differing T₁, T₂ and T₂* weightings. Such pathways/replicas always exist when unbalanced steady-state sequences are employed but only the 0^th (FISP) pathway typically gets sampled. By changing the sampling scheme and by traveling farther than usual in k-space extra pathways beyond the 0^th can be reached and sampled. The sequences from Fig. 1 were designed for G_x to be the only unbalanced gradient waveform, i.e., G_y and G_z are both balanced, so that different pathways are separated in the k_x direction only and can be reached/sampled through the use of extra-long readout windows.

The two implementations from Fig. 1 differ on whether different echo times get sampled during a same TR (Fig. 1a) or consecutive TRs (Fig. 1b). The dual-pathway 4-echo sequence in Fig. 1a samples a FISP and a PSIF pathway at 4 different echo times each, i.e., N_TE = 4. The dual-pathway 2-echo sequence in Fig. 1b samples a PSIF and a FISP signal in a given order for one TR and then switches the order for the following TR, i.e., N_TE = 2. Due to its shorter TR and smaller number of gradient pulses, the sequence from Fig. 1b is believed to be more motion robust than that from Fig. 1a. A 3D version of the sequence in Fig. 1a was also implemented, which further included phase-encoding gradient pulses on the G_z waveform.

Scanning and reconstruction

Two 3 T Siemens systems (Skyra and Trio) and a 3 T General Electric system (Signa HDxt Twin Speed) were used as part of this project. Fig. 1a represents the sequence as implemented on the Siemens systems while Fig. 1b represents that implemented on the GE system. The patient table of the GE scanner could be programmed to move while the imager is actually acquiring data, and for this reason the GE implementation from Fig. 1b was employed for motion-related experiments.

All data processing was performed in the Matlab programming environment (The MathWorks, Natick, MA) on an off-the-shelf personal computer (HP Z600 workstation, 8 core 2.8GHz CPU, 28 GB of RAM). Raw data was exported and Fourier transformed, and separate coil images were combined using coil sensitivity profiles estimated from the 1^st FISP images. As a consequence the phase information of all images was biased by a constant amount. Magnitude and phase information of the combined images then underwent different numerical processes, as mentioned above, for the estimation of relaxation rates and thermometry/field mapping, respectively. The LM algorithm was used here to fit the imaging results according to Eq. 1, on a pixel-by-pixel basis. Physically-impossible cases as indicated by R₂′ < 0 values were corrected by assigning a fairly small number (10⁻⁸) to R₂′ while keeping the summation of R₂ and R₂′ unchanged, because the FISP signal has been found empirically to have stronger signal strength and higher relaxation rates, which makes the estimation of R₂* less susceptible to noise.

T₂ and T₂* maps, gel phantoms

T₂ and T₂* results calculated using the present method were validated against reference results obtained using a product spin-echo and gradient-echo sequence, respectively. The sequence from Fig. 1a was used to image a multi-tube gel phantom with different concentrations of manganese sulfate for different tubes: MnSO₄ varied from 170 to 1000 ppm, T₁ from about 1460 to 395 ms and T₂ from about 55 to 30 ms. The imaging was performed with TR = 25 ms, flip angle = 25°, N_TE = 4, $T{E}_j^{+}∕T{E}_j^{-}$ = 5.5 / 6.8, 9.8 / 11.0, 14.0 / 15.2, and 18.3 / 19.5 ms, bandwidth = 399 Hz/px, axial orientation, FOV = 18.0×18.0 cm², matrix size = 64×128, voxel size = 2.8×1.4×5.0 mm³, 12-channel head coil, total scan time = 3.2 s. T₂ results from the proposed method were compared with those from a regular spin-echo sequence with 6 different TE values acquired in separate spin-echo scans: TR = 3000 ms, TEs = 12.0 / 20.0 / 30.0 / 40.0 / 60.0 / 120.0 ms, bandwidth = ±31.25 kHz, axial orientation, FOV = 12.0×12.0 cm², matrix size = 128×128, voxel size = 0.9×0.9×5.0 mm³, 8-channel head coil, total scan time = 38 min. T₂* results were compared with those from a gradient-echo sequence with 7 different TE values per TR interval: TR = 500 ms, TEs = 4.0 / 10.0 / 15.0 / 20.0 / 50.0 / 70.0 / 90.0 ms, flip angle = 60°, bandwidth = ±31.25 kHz, axial orientation, FOV = 12.0×12.0 cm², matrix size = 128×128, voxel size = 0.9×0.9×5.0 mm³, 8-channel head coil, scan time = 7.5 min.

A circularly-shaped region-of-interest (ROI) with a radius of about 9.6 mm was placed at the center of each tube, and average T₂ and T₂* values were obtained for all tubes and all methods. Linear regression was performed to compare the T₂ and T₂* values obtained from the present method and the product sequences. The standard deviation of T₂ and T₂* values was obtained for each one of the tubes independently, and then averaged over all 5 tubes.

T₂ maps to detect heat-induced damage, ex vivo tissues

Detecting and directing tissue damage is the primary purpose of MR guidance during thermal ablations. With PRF thermometry, field maps are converted into relative temperature maps and then into TD maps. A TD of 240 CEM₄₃ (cumulative equivalent minutes at 43°C) is often used as the threshold for indicating tissue damage (37). Using Eq. 3 to generate field maps, the combination of both PSIF and FISP information can enable improvements in TNR as compared with using FISP signals alone (36).

Unlike more typical PRF thermometry methods the present approach generates time-resolved T₂ maps in addition to field maps. Tissue damage is generally believed to be associated with changes in T₂ value, and time-resolved T₂ maps might prove useful toward detecting thermal damage as it develops. The ability to detect damage from these T₂ maps was tested through comparisons with TD measurements; heat-damaged regions were identified based on T₂-based thresholding as well as TD calculations.

A focused ultrasound (FUS) heating experiment was performed on ex vivo bovine muscle: A meat sample (never frozen), degassed for 3 hours in saline, was sonicated at 41 W for 30 s using a single-element spherically curved piezoelectric transducer (frequency = 1.5 MHz, diameter = 10 cm, radius of curvature = 10 cm). The imaging was performed with the sequence from Fig. 1a and parameters: TR = 20.6 ms, flip angle = 35°, N_TE = 4, $T{E}_j^{+}∕T{E}_j^{-}$ = 3.4 / 4.7, 7.6 / 8.8, 11.8 / 13.0, and 15.9 / 17.2 ms, bandwidth = 399 Hz/pixel, sagittal orientation, FOV = 20×20 cm², matrix size = 64×128, voxel size = 3.1×1.6×3.0 mm³, 12-channel head coil and 2.6 s per frame. Field maps were obtained from Eq. 3 and R₂ maps from Eq. 1. The size of damaged regions as measured through T₂-based thresholding (R₂ change ≥ 100%) and TD-based thresholding (TD ≥ 240 CEM₄₃) were compared.

T₂ maps with motion, ex vivo tissues

In the presence of motion, the fact that the proposed T₂-mapping approach functions on a frame-by-frame basis while the TD-based approach involves an integral over the time history of any given parcel of (moving) tissue may provide a marked advantage for the former over the latter. T₂-change calculations, just like relative-temperature ones, require only two reliable measurements: One with and one without heating. In contrast TD calculations involve essentially all time points, a difficult task in the presence of motion. Heating experiments were performed on a moving ex vivo tissues to help test motion robustness.

The pulse sequence from Fig. 1b was employed with and without table motion: Ex vivo degassed bovine muscle, 69 W for coronal acquisitions, 60 s sonication, TR = 14.5 ms, flip angle = 30°, N_TE = 2, $T{E}_j^{+}∕T{E}_j^{-}$ = 2.2 / 9.5 and 9.5 / 2.2 ms, bandwidth = ±61.3 kHz, FOV = 19.2×19.2 cm², matrix size = 64×128, voxel size = 3.0×1.5×5.0 mm³, 8-channel head coil. Because all echoes were acquired over a 2×TR period, scan time was equal to 2×128×TR = 3.7 s per time frame. The table was programmed to move 30 mm away from the landmarked location, stop for 6 s, move back to the landmarked location, wait for 6 s, and so on with a period of about 24 s. Both transducer and ex vivo tissues moved together, meaning that the presence or absence of motion should not affect the size or position of the resulting heat-induced lesion within the sample. A wait period of at least 30 min separated consecutive heating experiments to ensure that temperature returned to baseline and that heating would be reproducible from one experiment to the next. Results from TD-based and T₂-based damage detection with and without motion were compared.

B₀ and T₂ map, in vivo neuroimaging

Nine healthy volunteers were imaged following informed consent with an IRB-approved protocol, using the 3D version of the imaging sequence from Fig. 1a (Subjects A-E and F-I on Skyra and Trio systems, respectively). Numerical simulations based on the Bloch equations were performed to predict the signal behavior, in order to help identify TR and flip angle values that might maximize SNR efficiency in the calculated field maps, where the SNR efficiency is defined as the averaged frequency divided by the standard deviation of all estimates. The target tissue property was selected with expected relaxation values of roughly T₁/T₂/T₂* = 1500/100/60 ms. These simulations showed a broad maximum, in the sense that SNR efficiency did not depend in any sharp manner on a precise set of imaging parameters being employed. Recommendations for the neuroimaging application were developed: TR = 40 to 50 ms, flip angle = 25 to 30°, a reasonably-high bandwidth setting, and as many automatically-set TE values as possible for the given TR and bandwidth. As seen in Table 1, parameters for Subjects A-E spanned these intervals to help confirm that small variations in parameter settings should have little to no impact on results, which is not an unusual behavior for a steady-state sequence. One fixed protocol was then employed for the last four Subjects, F-I (Table 1). Further parameters common to all scans included: 1.0×1.0×2.0 mm³ resolution, axial orientation, 32-channel head coil. For the last four Subjects, F-I, spin-echo scans with varying TE were performed to evaluate T2 and provide a reference standard for the R₂ values obtained with the proposed method (12 slices, TR= 1500 ms, TE = 10, 45, 100 ms, 1.0×1.0×2.0 mm³ resolution, acquisition time = 14.4 min).

Table 1.

Scan parameters for all nine neuroimaging volunteers, A-I.

Volunteer	A	B	C	D	E	F-I
flip angle (°)	25	25	30	30	25	25
TE+ (ms)	3.8, 13.1, 22.6, 32.3	4.3, 15.8, 27.8, 40.1	3.9, 13.5, 23.2, 32.9, 42.7	6.3, 15.0, 23.7, 32.4, 41.0	6.5, 17.5, 28.6, 39.7	4.5, 15.0, 25.5, 36.0
TE- (ms)	6.6, 15.8, 25.3, 35.1	8.2, 19.7, 31.6, 45.0	7.0. 16.5, 26.2, 35.9, 45.7	8.9, 17.6, 26.3, 35.0, 43.7	10.3, 21.4, 32.5, 43.5	8.7, 19.2, 29.7, 40.2
TR (ms)	40	50	50	50	50	45
pxBW (Hz/px)	362	260	330	382	260	237
matrix size	192×192×32	192×192×40	192×192×40	192×192×36	192×192×40	192×192×40
Slice over-sampling (%)	20	30	30	33	30	30
Scan Time (min)	5:07	8:19	8:19	7:41	8:19	7:29

For field mapping, BET and PRELUDE (FSL, Oxford, UK) (38) were used for brain extraction and phase unwrapping. Unlike the regular procedure of susceptibility-weighted imaging, which utilized a high-pass filter to remove background phase, a spherical mean value method (39) was adopted to filter out external field perturbations, based on the harmonic property of the external field perturbations which satisfies Laplace's equation (40). R₂ values from the proposed method and from the spin-echo reference standard were compared through Bland-Altman analysis.

Anatomical imaging and T₂ mapping, in vivo musculoskeletal imaging

Three healthy volunteers were imaged following informed consent (sequence from Fig. 1a, Trio system). The protocol was identical to that recommended by the Osteoarthritis Initiative (41, 42): water-only excitation, sagittal orientation, flip angle 25°, resolution = 0.37×0.46×0.7 mm³, TR = 16.3 ms, TE⁺ / TE⁻ = 5.3 / 10.8 ms (referenced DESS). For our multi-TE approach, TE⁺ = 3.35 / 9.03 / 10.73 ms and $T{E}_j^{-}$ = 5.34 / 7.04 / 12.72 ms. Cartilage segmentation was performed for both datasets as in (43).

Results

T₂ and T₂* maps, gel phantoms

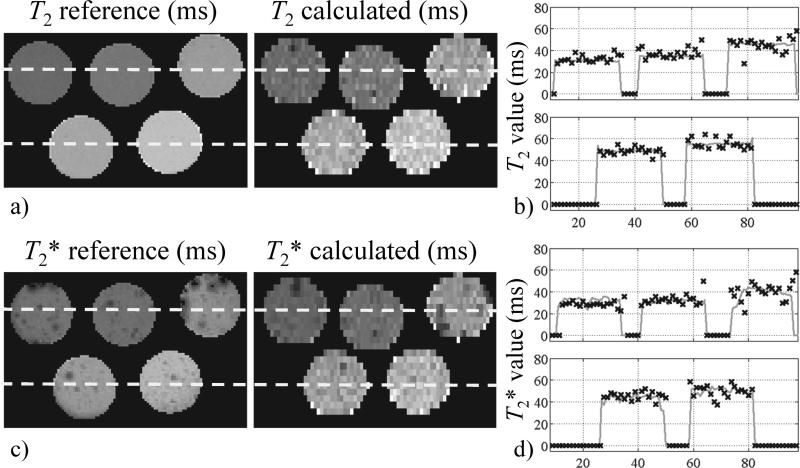
Calculated T₂ and T₂* maps are shown in Fig. 3 along with independently obtained reference T₂ and T₂* maps. Please note that the reference maps took much longer to acquire: 38 min for the reference T₂ map, 7.5 min for the reference T₂* map, as compared to only about 3 s for the proposed method to generate both types of maps jointly. Scan time was 140-time longer for the reference T₂* mapping than for our scan because of the difference in TR and the 7 repeats to sample different TE values (7 repeats × 500 ms / 25 ms = 140), and 720-time longer for the reference T₂ mapping (6 repeats × 3000 ms / 25 ms = 720). In this context, considerably-higher image quality may be expected for the reference maps. Line plots for the locations indicated by dashed lines in Fig. 4a and 4c are provided in Fig. 4b and 4d, respectively. Reconstruction time from raw data to T₂ and T₂* maps was 14.1 s. The images in Fig. 3 are rectangular ROIs (6.4 × 12.0 cm) cropped from a larger FOV.

Fig. 3.

a) T₂ results obtained from a multi-tube gel phantom are compared to a reference. The vast difference in SNR comes mainly from very different scan times: 51 min for the reference T₂ map and only 3 seconds or so for the present joint T₂ and T₂* acquisition. b) Line plots are provided for the locations indicated by dashed lines in a), solid lines represent the reference while ‘×’ symbols are for the present method. c) T₂* maps are compared; as in (a) differences in SNR come in part from very different scan times (64 s vs. 3 s). d) Line plots are provided for locations indicated by dashed lines in (c).

Fig. 4.

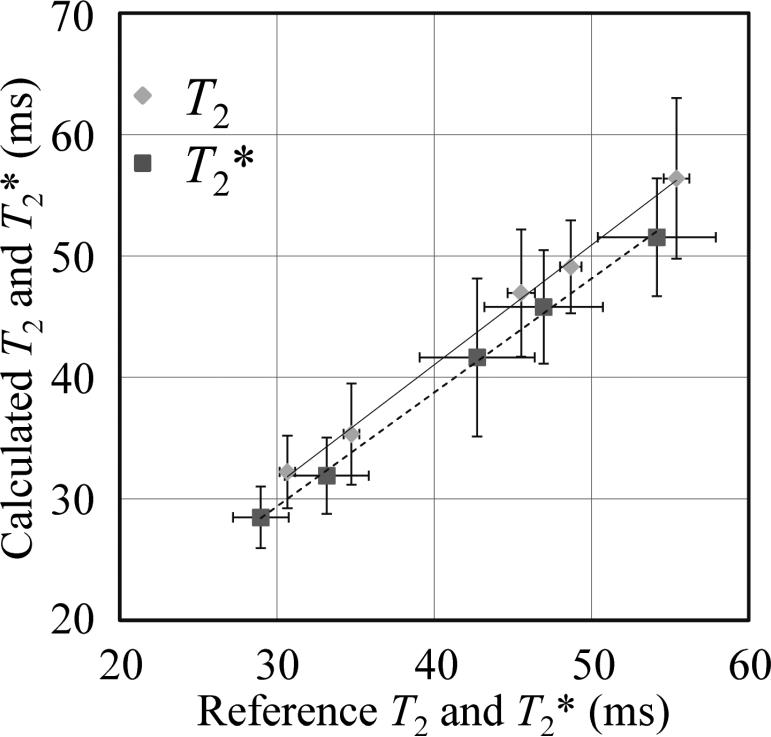
Average T₂ and T₂* values were obtained from ROIs at the center of the tubes shown in Fig. 2, and a linear regression was performed to test the accuracy of the proposed T₂ and T₂* mapping scheme against reference results. The fit results indicated good accuracy: Slope of 0.99/0.94, intersect of 1.61 /1.24 ms and R² = 0.998/0.998 for T₂ and T₂*, respectively.

In Fig. 4, T₂ and T₂* values from the double-pathway sequence are compared to those from the reference scans. Linear regression provided a slope of 0.99 / 0.94, intersect of 1.61 / 1.24 ms and R² = 0.998 / 0.998 for T₂ and T₂*, respectively. In other words, as can be visually judged from Fig. 4, the difference between our proposed method and the reference was fairly small (the largest differences were 1.5 and −2.6 ms for T₂ and T₂*, respectively). In terms of precision, the standard deviation was found to be 4.56 and 4.34 ms for T₂ and T₂* values, respectively.

T₂ maps to help detect heat-induced damage, ex vivo tissues

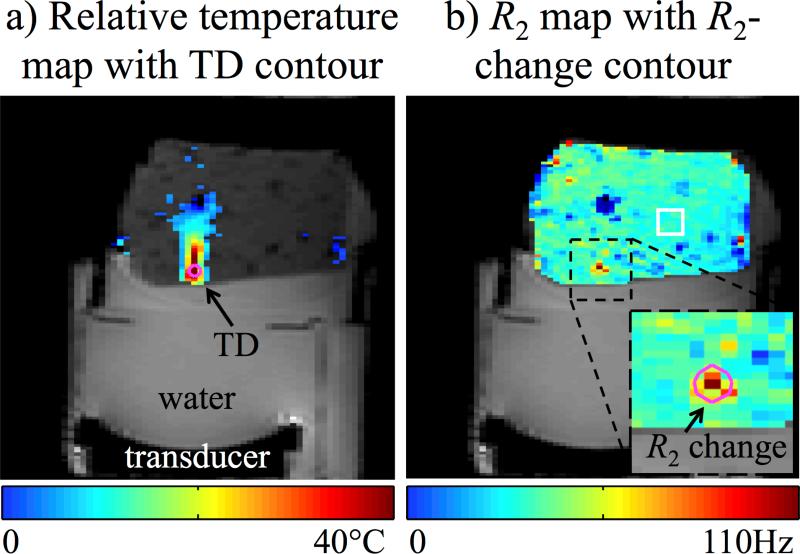
A temperature map and an R₂ map at the time of maximum heating were overlaid on magnitude images and shown in Fig. 5a and 5b, respectively. The pink contour shown in Fig. 5a marks the region where TD exceeded the 240 CEM₄₃ threshold, while the pink contour in Fig. 5b marks the region where R₂ exceeded the 100% change threshold. The mean T₂ value in the 12.5×12.5 mm² ROI indicated by a white square in Fig. 5b was 46±3 ms, which is consistent with the 50±4 ms or so expected for skeletal muscle (44). The area of the damage zones from T₂- and TD-based methods differed by 18% (28.5 compared to 24.2 mm²), and their geometric centroids coincided (i.e., same pixel). With an in-plane resolution of about 5 mm², the area of damage covers here about 5 pixels. The reconstruction time from raw data to R₂ maps was 10.7 s per time frame, on average.

Fig. 5.

In the absence of motion a tissue damage criterion based on R₂ changes (b) proved roughly equivalent to a thermal-dose criterion (a), as regions of similar size and location were identified in both cases: 28.5 vs. 24.2 mm² in size (18% difference), and geometric centroids within the same pixel. While significant heating can be seen outside of the contoured region in (a), such heating was not sufficient to cause damage according to the 240 CEM₄₃ criterion, pink contour in (a), or to the 100% R₂-change criterion, pink contour in (b). A T₂ value of 46±3 ms was measured over the white square ROI shown in (b).

T₂ maps with motion, ex vivo tissues

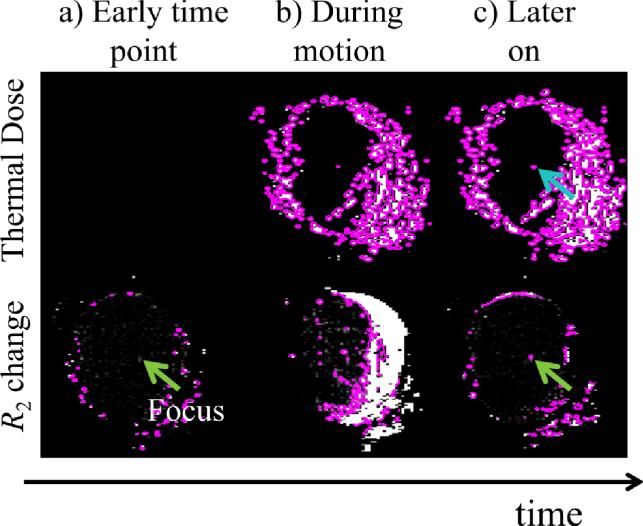
The presence of motion very much affected the phase-based temperature measurements but not nearly as much the magnitude-based R₂ measurements. In Fig. 6a, in an early time frame, both TD-based and R₂-based damage assessments were in agreement: No meaningful damage had yet occurred to the central part of the meat phantom. In Fig. 6b, at a subsequent time point and during rapid motion, both TD-based and R₂-based assessments suffered much degradation. Figure 6c illustrates the main advantage of the R₂-based approach: At a later time point, during a period of relative quiet in terms of motion, the R₂-based assessment recovered and credibly captured the location and size of the damaged region at that instant (green arrow). While TD contours also captured the damaged region (blue arrow in Fig. 6c), other regions corrupted in past time frames (e.g., see Fig. 6b) could not recover and remained corrupted in later time frames as well. While R₂-based damage assessments can recover from one or more bad time frames, the time integral involved in TD calculations prevents TD-based assessments from similarly recovering. Once TD-based damage assessments become erratic at one time point they remain in error for all subsequent time points.

Fig. 6.

R₂ changes and temperature dose before (a), during (b), and after motion (c). In moving objects R₂ changes may prove more reliable than thermal dose toward detecting tissue damage because the former are made on a frame-by-frame basis while the latter involve a time integral. For this reason, R₂ measurements can recover from one or more bad frames while errors in temperature dose will propagate to all future time frames.

In vivo tests – B₀ and T₂ mapping in the brain

Neuroimaging results for R₂, R₂* and the internal field B_int are shown in Fig. 7 for the last four Subjects acquired with identical parameters, Subjects F-I, for two different slices per Subject. Results from Subjects A-E are not shown here; except for Subject D, they appeared of equivalent quality to the results in Fig. 7, which tends to confirm that small changes in parameter settings are not expected to have discernable effects on reconstructed results. The parameters employed for Subject D were at one extremity of the tested parameter range, with highest tested values for TR, flip angle and bandwidth. The fact that this setting did not appear as beneficial as other tested ones helped in fixing the protocol employed for the last four Subjects, F-I. B_int in Fig. 7 could be further used either for quantitative susceptibility mapping (39) or, in combination with the magnitude image from a heavily T₂*-weighted echo, for SWI (1). Reconstruction time from raw data to 3D R₂, R₂* and B_int maps was 91 min per volunteer, on average.

Fig. 7.

R₂, R₂* and B_int maps are shown for two different axial slices in the 3D volume, for our last 4 volunteers (F-I). Green arrows indicate regions that suffered from strong susceptibility effects, which led to higher R₂* values and possibly less reliable R₂ results than in other locations.

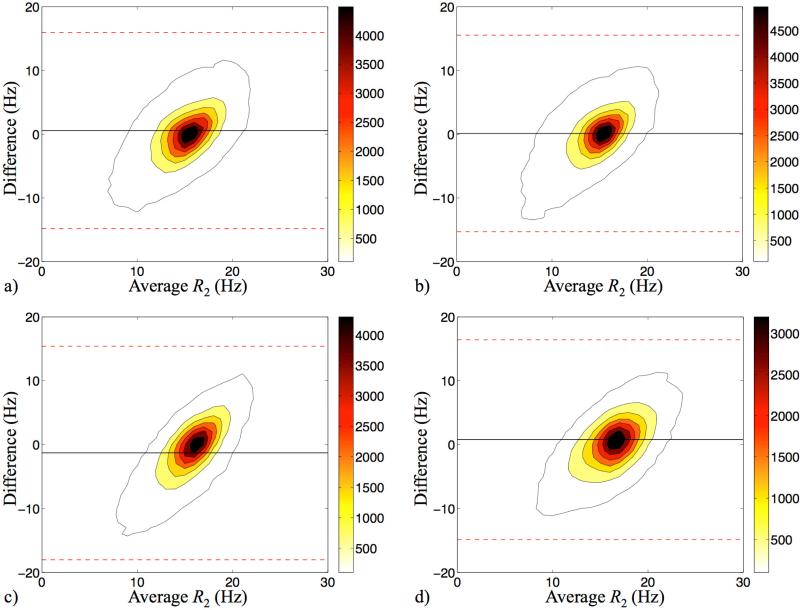
A Bland-Altman comparison of R₂ values from our method and from the spin echo reference standard is shown in Fig. 8, for volunteers F-I. The comparison involves 12 slices per Subject, excluding pixels outside the head and CSF. The density of points, in number of points per Hz², is plotted in Fig. 8 using contour lines and a Bland-Altman format. The average R₂ bias, averaged over the four Subjects, was 0.034 Hz and 95% intervals are shown using dashed lines.

Fig. 8.

Contoured Bland-Altman plots compared the R₂ results from spin-echo experiments and our DESS approach, for Subjects F-I (a-d). The outmost contours represent the sample density of 100 counts/Hz². Black solid lines show the mean difference of the two measurements, and the red dashed lines represent the 95% limits of agreement. The averaged R₂ difference was 0.034 Hz.

In vivo tests – Anatomical imaging and T₂ mapping in the knee

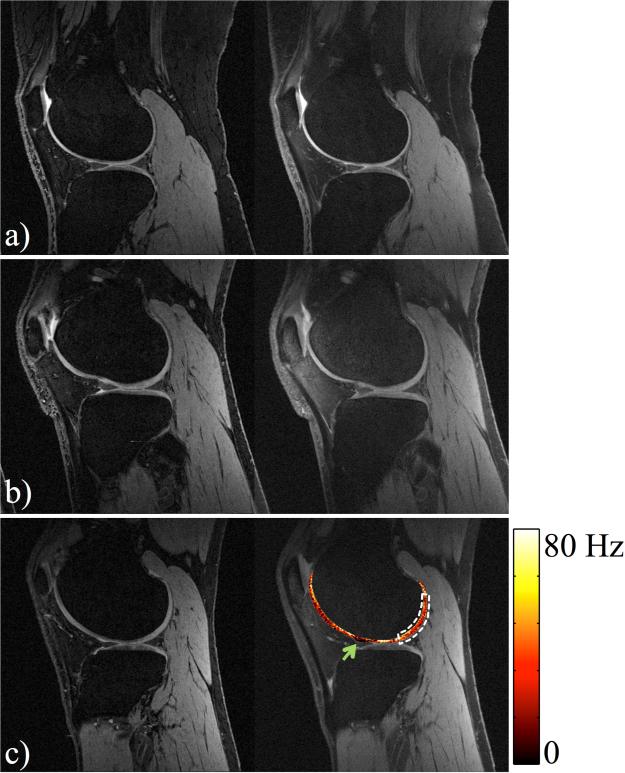
Fig. 9 shows a comparison between reference DESS and synthetic DESS images generated from our acquisitions, for volunteer J-L. A similar image contrast was achieved with slightly larger background noise. Cartilage volumes were computed over the joint: 359.0, 746.4, and 783.3 mm³ for the reference, and 327.8, 706.1, and 778.0 mm³ for synthetic results, for Subjects J-L, respectively, for an average difference of −4.93%. R₂ maps were obtained as a bonus (fig.9 c).

Fig. 9.

Reference DESS (left) and synthetic DESS images (right) for Subjects J-L. Similar image contrast was achieved in both cases, and led to similar measurements of cartilage volume (average difference: −4.93%). R₂ information was displayed as an overlay in (c). The dark red region as marked with the green arrow, where R₂ values were very small, may indicate the presence of joint fluid. An average T₂ of 33.8 ms was calculated over the indicated ROI (white dashed region).

Discussion

Field maps as well as R₂ and R₂* maps were generated from the same acquired data, in thermometry, neuroimaging and knee imaging contexts. As compared to other methods for simultaneous mapping of MR parameters, a main strength of the present approach is its insensitivity to T₁ and flip angle. In contrast, methods that actually evaluate T₁ and flip angle might be too slow for the present applications, and methods that assume these parameters known a priori would be prone to errors.

Potential further improvements might include accelerating the image acquisition through combinations of partial-sampling methods (45). For example, the large amount of artifact seen in Fig. 6b indicates that higher temporal resolution might be needed to resolve motion. Further limitations include having scanned only a small number of healthy volunteers. Recruiting patients rather than healthy volunteers would have allowed more varied conditions, tissue types and R₂ values to be encountered, as R₂ estimation is expected to become noisier for very long and/or very short R₂ values.

In the knee imaging application, good agreement was obtained between synthetic DESS images and standard DESS images, both in terms of general appearance and measured cartilage volume; differences were however observed, especially within bone regions (see Fig. 9), as possibly caused by inconsistencies in the performance of the water-only excitation pulse and by associated residual fat signals.

In the thermometry application, only ex vivo tissues were imaged, and their motion may not have been entirely representative of that associated with breathing. Furthermore, ex vivo tissues do not exhibit the biological responses normally expected from living tissues, such as edema and changes in blood perfusion. How well R₂ changes may correlate with lesion formation and tissue damage remains a question that cannot be addressed from ex vivo experiments. More specifically, the relative timing of R₂ changes vs. irreversible damage might determine whether R₂ monitoring will prove most helpful toward preventing damage (to healthy tissues) or on the contrary toward confirming damage (to targeted tissues). While a 100% threshold on R₂ change leads to ‘damaged’ areas that correlated well with a 240 CEM₄₃ TD threshold, there is no guarantee that such R₂-based criterion might hold as part of in vivo tests. However, based on the fact that tissue damage is known to induce T₂ changes (30), it is hoped that such criterion may indeed exist, and that it should prove more motion-robust than a TD threshold, as demonstrated here in Fig. 6.

Motion robust damage detection was obtained here because R₂ changes, just like relative temperature, can be calculated from as little as two reliable measurements: A non-heated reference and a measurement after heating. In contrast, TD calculations require knowledge of essentially all time points, a much more challenging task especially in the presence of motion. The main message from Fig. 6 was that R₂-change contour maps can significantly recover from a given motion-corrupted time point (Fig. 6b) to a later time point (Fig. 6c), while TD contour maps could not. However, the fact that R₂-change maps greatly recover is of course not a guarantee of ultimate utility. Also, more involved acquisition and/or processing methods might always be devised to help improve the TD maps in the presence of motion, thus reducing the need for a more motion-robust alternative approach. But it is tempting to think that even in cases where sufficient processing and complexity might be brought to bear toward achieving motion-robust TD measurements, a complementary R₂-change measurement might still have value as a simple and complementary alternative.

Conclusion

A dual-pathway multi-echo steady-state sequence was proposed to simultaneously perform R₂, R₂* and field mapping. Imaging speed was typical of a gradient-echo sequence: For example, non-accelerated parameter maps were obtained with 1.0×1.0×2.0 mm³ resolution over a 3D FOV roughly 20×20×8 cm³ in size in about 8 min scan time, in a neuroimaging application. In a thermometry application, T₂ maps were obtained with temporal resolution equal to that of the temperature maps, to better detect tissue damage. For knee imaging, T₂ maps were obtained as a bonus, at no increase in scan time compared to regular DESS.

Highlights.

• . T₂, T₂*, and field maps were simultaneously obtained with a new pulse sequence design.

• . The pulse sequence acquired multiple echoes in a dual-pathway steady state sequence.

• . A reconstruction algorithm was developed to extract T₂, T₂*, and field information.

• . T₂ and field maps were used in thermometry, neuroimaging, and knee imaging.