Abstract
Phase diagram investigation of the Cu–Sn system was carried out on twenty Cu-rich samples by thermal analysis (DTA), metallographic methods (EPMA/SEM-EDX) and crystallographic analysis (powder XRD, high temperature powder XRD). One main issue in this work was to investigate the high temperature phases beta (W-type) and gamma (BiF3-type) and to check the phase relations between them. In the high temperature powder XRD experiments the presence of the two-phase-field between the beta- and the gamma-phase could not be confirmed. Detailed study of primary literature together with our experimental results leads to a new phase diagram version with a higher order transformation between these two high temperature phases. The present work is designated as part I of our joint publication. The new findings described here have been included into a completely new thermodynamic assessment of the Cu–Sn phase diagram which is presented in part II.
Keywords: A. Intermetallics miscellaneous, B. Phase diagrams, B. Phase identification, B. Order/disorder transformations
Highlights
► Extended literature review from 1897 up today. ► Extended HT-XRD in the Cu-rich part. ► New phase diagram version of Cu–Sn.
1. Introduction
In the European Union by 2006 the RoHS regulation (Restriction of the use of certain hazardous substances in electric and electronic equipment) was updated in order to ban lead and lead containing substances in electronic devices. This means that formerly used lead containing soft solder materials have to be substituted by less harmful materials. High temperature soft solders (Fp > 230 °C) often possess a lead content of more than 85 wt%. Despite the fact that the high temperature soft solders are excluded from this regulation, the trend to substitute hazardous substances from solders will continue and the pressure to find new alloys which contain less harmful metals and offer similar properties at the same time will increase. High temperature soft solders, such as the Pb95–Sn5 solder (Fp = 308–312 °C [1]), are mainly used for advanced packing technologies, e.g. the die-attach and Ball Grid Array solder spheres, the chipscale packaging and the multi-chip modelling [2]. The binary system Cu–Sn is the key system for lead-free soldering, because tin is the main component of most of such solder materials and Cu is the most frequently used contact material. Furthermore, Cu–Sn alloys could be interesting materials for substituting the graphite anodes of Lithium ion batteries. Intermetallic compounds like Cu6Sn5 are considered as promising candidates to enhance the storage capacity of such cells and to improve their cycling stability. Due to its high importance for other applications, e.g. bronze alloys, the Cu–Sn system has been investigated first more than 100 years ago. To understand its development in the historic context, an extensive literature research back to the end of the 19th century was done.
A first complete freezing point curve, as the liquidus was designated that time, was published by Heycock and Neville in 1897 [3]. Some years later the same authors [4] published the first complete phase diagram based on cooling curves and metallographic studies, which were notably detailed and extended. Although the theoretical knowledge of phase relations in multi component systems was very scarce that time, they could establish nearly all phase equilibria as they are presented till today. One could say this work is not only essential for Cu–Sn, but also for the basic understanding of phase relations and development of phase diagrams. In Ref. [4] all phases in the Cu–Sn system, except the later found ζ-phase [5], are present. The two high temperature phases β and γ were distinguished. However, neither crystal structure nor the mechanism of phase transformation within this large phase field was described thitherto. In 1906 Shepherd and Blough [6] assumed a rather large two-phase field separating the β- and γ-phases. Based on thermal analysis and microscopic methods in 1913 Hoyt [7] published a phase diagram, where those two high temperature phases were separated by a significantly smaller two-phase field. After the invention of X-ray diffraction techniques at the beginning of the 20th century the crystal structure of the Cu–Sn phases could be determined. In this context one of the most important publications is that of Westgren and Phragmen [8], who correctly described the structure of all phases, except γ and the later found ζ. The eutectoid decomposition of the δ-phase into (Cu) and ɛ at ∼350 °C was the first time reported by Haase in 1936 [9]. In 1938 Hamasumi and Morikawa [10] published the first HT-XRD study on Cu–Sn. They could determine the crystal structure of the ζ-phase, confirmed the structure of the β-phase and assumed the γ-phase to be bcc with lattice parameters similar to the β-phase. In 1944 the available data were very assiduously assessed by Raynor [11]. This work was fundamental for all later assessments. Knoedler [12], [13] made further HT-XRD studies and described the γ-phase as an fcc cell with the double lattice parameter compared to the β-phase. The assessment of Hansen et al. [14], [15] shows a phase diagram version which has been widely accepted until today. Later, up to the early 1990s a wide range of X-ray studies was performed, investigating different sections and phases of the phase diagram [16], [17], [18], [19], [20]. A comprehensive assessment of experimental data was done by Saunders and Miodownik [21], which describes as well various metastable phases, which mainly occur in the Cu-rich part of the system. The equilibrium diagram, however, does not differ significantly to that given by Hansen [14], [15]. HT-XRD, HT-ED and DSC were performed on a few samples by Liu et al. in 2004 [22]. Thermochemical data have been reported by several authors. The corresponding literature review on thermochemical data will be given in part II together with various thermodynamic assessments and CALPHAD calculations.
2. Experimental procedure
2.1. Sample preparation
20 samples from 11 to 48 at% Sn (see Table 1) were produced from 99.98% Cu (Goodfellow, Cambridge, UK; treated under H2 flow at 200 °C for 5 h to remove oxide layers) and 99.95% Sn (Advent, Oxford, UK). Weighed amounts of the metals were melted together in an arc furnace under Ar-atmosphere, the obtained reguli were inverted several times and the arc melting process was repeated to ensure a complete homogenization of the alloys. The samples were encapsulated in quartz glass tubes under vacuum (∼10−3 mbar) and annealed for 14 days at selected temperatures (400, 600 & 700 °C) and for 6 months at 170 °C. Finally, the alloys were removed from the furnace and quenched in cold water.
Table 1.
Cu–Sn samples, their heat treatment and applied analytical methods.
| sample | Annealing temperature (°C) | Analytical methods |
||||
|---|---|---|---|---|---|---|
| DTA | Micrographs | XRD | High temperature XRD | EPMA/ESEM | ||
| Cu89Sn11 | 400, 700 | X | X | X | Xv | X |
| Cu87Sn13 | 400 | X | ||||
| Cu86Sn14 | 400 | X | ||||
| Cu85Sn15 | 400 | X | Xi | |||
| Cu84.5Sn15.5 | 400, 700 | X | X | X | Xv | X |
| Cu84Sn16 | 400 | X | Xi | |||
| Cu83Sn17 | 400 | X | Xi, 650 | |||
| Cu82Sn18 | 400 | X | Xi | |||
| Cu81.5Sn18.5 | 400, 700 | X | X | X | Xv | X |
| Cu81Sn19 | 400 | X | ||||
| Cu80Sn20 | 400 | X | Xi | |||
| Cu79Sn21 | 400, 700 | X | X | X | Xv | X |
| Cu78Sn22 | 700 | Xi | ||||
| Cu77Sn23 | 400, 600 | X | X | |||
| Cu76Sn24 | 400, 600, 700 | X | X | X | Xv | X |
| Cu75Sn25 | 400, 600 | X | X | |||
| Cu72.5Sn27.5 | 400, 700 | X | X | X | Xv | X |
| Cu58Sn42 | 170 | X | X | |||
| Cu55Sn45 | 170 | X | X | |||
| Cu52Sn48 | 170 | X | X | |||
i: isotherm (700 °C) for several hours, 6 measurements with 150 min per measurement.
v: variable temperature steps (2 cycles 400–700 °C in 25 °C-steps, 150 min per step).
650: isotherm measurement at 650 °C.
2.2. Analytical methods
The thermal analysis was performed in open alumina crucibles in Argon atmosphere (99.999%) using sample amounts of approximately 100 mg. A comparably high sensitivity was ensured by the 3-point thermocouple technique of the instrument. Reference material was sliced Ti-sheet in a second crucible, which served at the same time as a getter material for remaining traces of oxygen. The applied heating rates were 5 and 10 K/min, respectively. The temperature measurement was calibrated with pure metals, as tin, silver and gold.
The powder XRD was performed with a Bragg-Brentano diffractometer (Θ/2Θ-geometry) at room temperature. For the investigation at high temperature, a diffractometer with fixed sample holder (Θ/Θ-geometry) was used. X-rays in both cases were produced by a copper-radiation source at an accelerating voltage of 40 kV and an electron current of 40 mA. A Ni-filter was used for removing the Kβ emission. For the measurements which were done at room temperature, the powder was fixed with petroleum jelly on a silicon monocrystal, which was rotated during the measurement. For HT-XRD the powder was fixed on a moulded ceramic specimen holder, which was equipped with a thermocouple. The measurements at higher temperatures were accomplished in an inert gas atmosphere of 99.999% pure nitrogen with a Ti-foil as an oxygen getter. Two different setups for the XRD at higher temperatures were found to be reasonable. In the first one, the sample temperature was increased from 400 °C up to the estimated liquidus temperatures in temperature intervals of 25 K. At each isothermal step a diffractogram was recorded. In the other setup, the samples were heated rapidly to a certain temperature (650 or 700 °C) and kept constant until equilibration for several hours. In each case the measurement time was 150 min. The first setup provided a survey of temperature dependent phase transformations, whereas the second setup should show the phase equilibria at a certain temperature. Both diffractometers have been equipped with line detectors. Diffractograms have been evaluated and refined using the Topas3® software, provided by Bruker AXS.
For metallographic investigations an optical microscope (reflected light microscope Zeiss Axiotech 100) as well as WDX (wavelength dispersive spectroscopy; EPMA CAMECA SX 100) and EDX techniques (energy dispersive spectroscopy; ESEM Zeiss Supra 55 VP) were used. For scanning electron microscopy the excitation energy of the electron beam was about 15–20 kV. Backscattered electrons were used for the visualisation of the polished samples and have been detected by the BSE (backscattered electrons detector). For quantitative chemical analysis (EDX, WDX) the instruments have been calibrated using the K-line (Cu) and the L-line (Sn).
3. Results and discussion
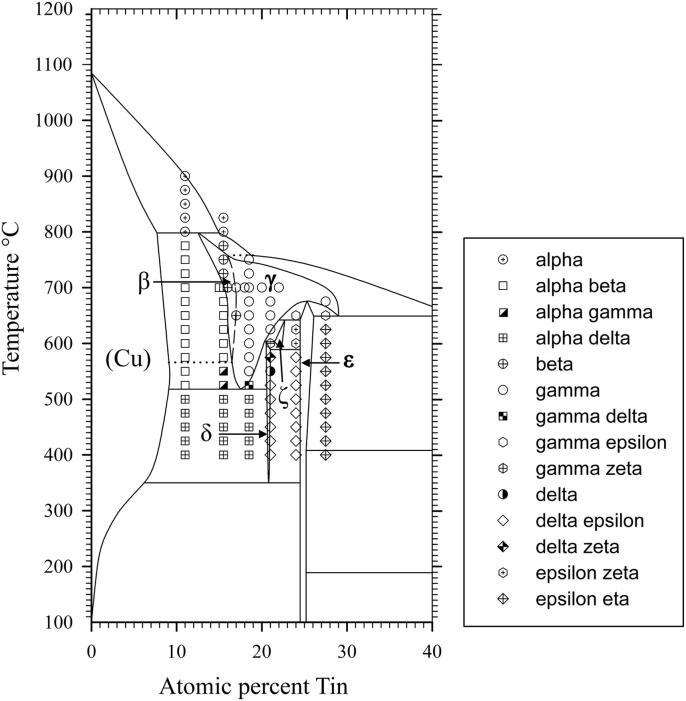
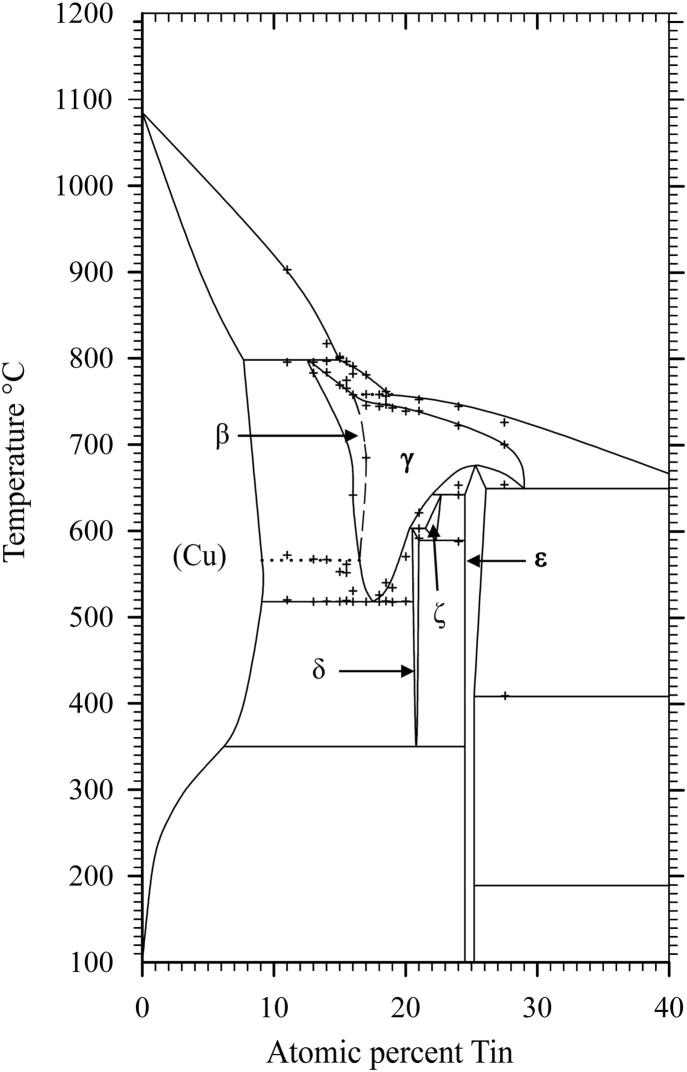
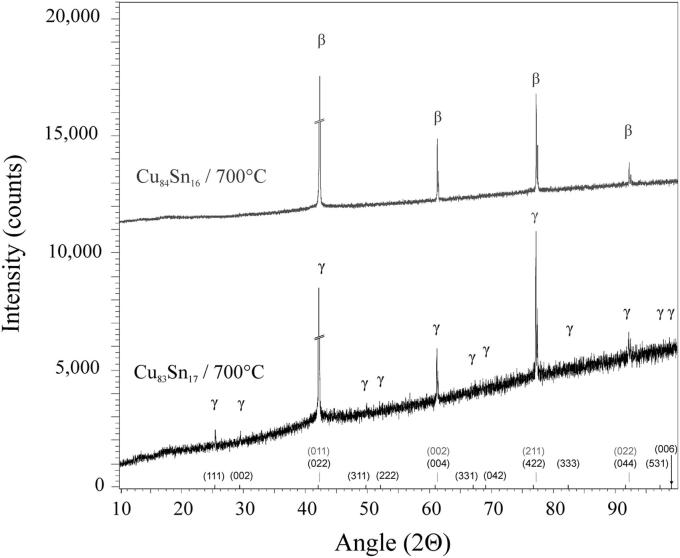
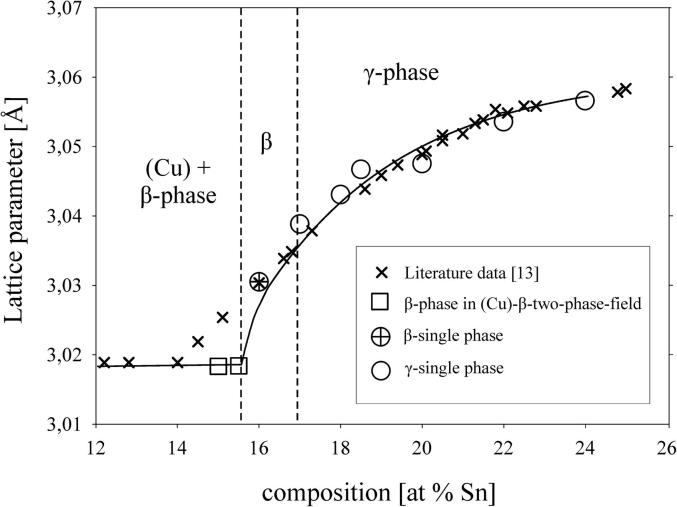
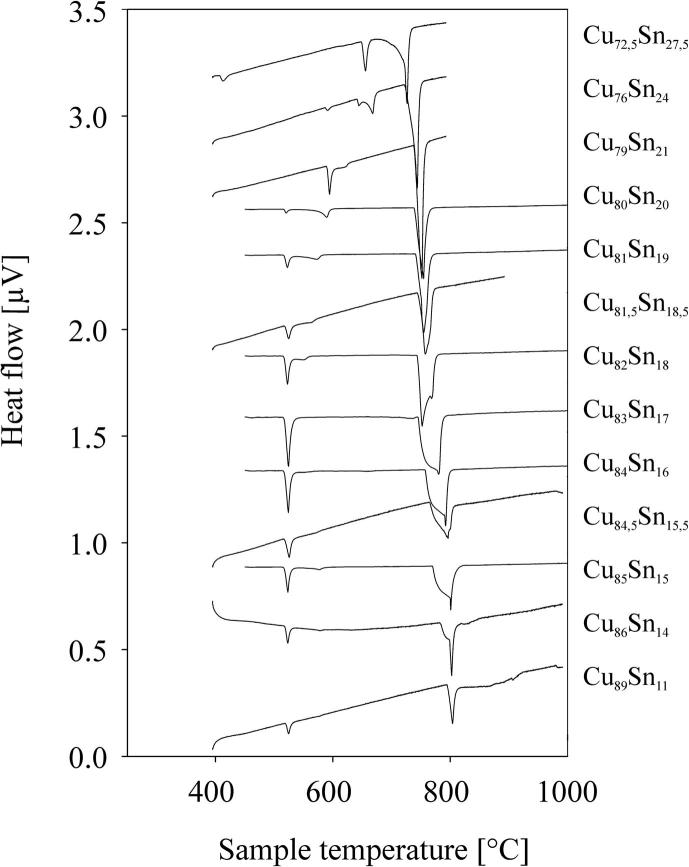
Several samples with compositions from 11 to 48 at% Sn were annealed at 170, 400, 600 and 700 °C, respectively, quenched in cold water, powdered and analysed by XRD at room temperature. All phases (Table 2), except the β- and the γ-phase, were found in the quenched samples as described in literature (see Introduction and Table 3). These two phases are high temperature phases, which cannot be quenched, but undergo bulk transformation to the respective low temperature phases or transform to metastable phases [12], [13]. Thus, in some samples we could find more than two phases, contrary to the Gibbs' phase rule in binary systems. In order to clarify structure and phase transformations we decided to perform high temperature powder X-ray diffraction measurements. Measurements at constant temperature (700 °C) in very narrow concentration steps (1 at%) have been applied, as well as measurements at certain concentrations in narrow temperature steps (25 K). The combination of these two procedures allowed us a rather detailed presentation of phase relations in the Cu-rich part of the phase diagram; this was within 10–30 at% Sn and from 400 °C up to the liquidus. All results of HT-XRD on samples equilibrated at 700 °C are listed in Table 4. The results of phase analysis of samples measured at varying temperatures are shown graphically in Fig. 1. Generally speaking, the results of our HT-XRD measurements (Fig. 1) and thermal analyses (see Table 5 and Fig. 2) agree to each other and also confirm the phase relations as reported in the most recent experimental assessment of Saunders and Miodownik [21]. Our results for the characteristic temperatures of invariant reactions agree in most of the cases within a few Kelvin (see Table 5). Also our results for SEM-EDX and EPMA-measurements support the data of the assessment mentioned above. The deviations do not exceed 1 at% and thus are only slightly beyond the accuracy of the methods (see Table 6). A detailed comparison of invariant reaction temperatures, compositions and homogeneity ranges between this work and the literature [21] is given in Table 3 in Part II. The crucial point is, however, that we cannot confirm the two-phase region between β- and γ-phase as it was reported in almost all works after Shepherd and Blough [6] (also see Introduction). We did a critical evaluation of original experimental results [6], [7] which have supported the establishment of that two-phase field. The two-phase region between the β- and γ-phase was based on the occurrence of two weak effects in thermal analysis at 586 °C and 755 °C and on the micrographic image of quenched samples which show two-phase equilibria. In contrast to up-to-date knowledge these observations should be differently interpreted. It was proved by many authors, e.g [12], [13], [25], that both the β- and γ-phase cannot be quenched but show bulk transformation to low-temperature phases or martensitic transformation. Thus we assume that the two phases present in micrographs of quenched samples cannot be β- or γ-phase. Knoedler [13] performed HT-XRD at 605 and 710 °C for many samples from 12 to 25 at% Sn. Both his and our results do not exhibit the coexistence of the β- and the γ-phase in any sample (Fig. 3). Furthermore, a plot of the reduced lattice parameters versus concentration for a given temperature shows a continuous course (see Fig. 4 and Table 4). In Fig. 4 one can see that the values for the lattice parameters at the Cu-rich side, respectively in the (Cu)-β-two-phase region, differ between Knoedler's and our results. This could be explained by the fact that we found in samples up to 15.5 at% Sn mixed crystals of (Cu) and β, in which the β-phase shows necessarily a constant lattice parameter. At higher concentrations of Sn only β-single-crystals occurred, which leads to increasing lattice parameters due to the solid solution of Sn in β. Knoedler reported this phase field boundary to be at 14 at% Sn, therefore he found lattice parameters which start to increase from that concentration. This all together strongly indicates a higher order transformation between β and γ, which is also found from the crystallographic point of view (group–subgroup relationship between Im-3m and Fm-3m). We could reproduce the both mentioned effects at 566 and 758 °C by our thermal analysis (see Fig. 5 and Table 5). According to our measurements, these two effects are associated with the second order phase transformation between the β- and γ-phase. This is supported by the fact that the eutectoid-like decomposition of the β-phase (566 °C) causes a much weaker effect that the eutectoid decomposition of the γ-phase (518 °C); see e.g. sample Cu85Sn15 in Fig. 5. It should be mentioned at this point, that Liu et al. in 2004 [22] published a phase diagram version showing higher-order phase transformation within the β–γ-region. They did HT-XRD and could only find the A2 and D03 structures separately. However, performing high temperature electron diffraction on diffusion samples, they could only find A2 and B2-phases (CsCl structure).
Table 2.
Crystallographic data of Cu–Sn phases.
| Phase | Stoichiometry | Type | Pearson symbol | Space group | No. | a (Å) | b (Å) | c (Å) | β (°) | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|
| (Cu) | (Cu) | Cu | cF4 | Fm-3m | 225 | 3.61443 | – | – | 90 | [23] |
| β | Cu17Sn3 | W | cI2 | Im-3m | 229 | 3.0261 | – | – | 90 | [13] |
| γ | Cu3Sn | BiF3 | cF16 | Fm-3m | 225 | 6.1176 | – | – | 90 | [13] |
| B2-bcc | No data av. | CsCl | cP2 | Pm-3m | 221 | No data available | 90 | [22] | ||
| δ | Cu41Sn11 | Cu41Sn11 | cF416 | F-43m | 216 | 17.98 | – | – | 90 | [18] |
| ɛ | Cu3Sn | Cu3Ti | oC80 | Cmcm | 63 | 5.529 | 47.75 | 4.323 | 90 | [17] |
| ζ | Cu10Sn3 | ζ-AgZn | hP26 | P63 | 173 | 7.330 | – | 7.864 | 90 | [19] |
| η | Cu6Sn5 | AsNi | hP4 | P63/mmc | 194 | 4.192 | – | 5.037 | 90 | [20] |
| η′ | Cu6Sn5 | η′-Cu6Sn5 | mC44 | C2/c | 15 | 11.022 | 7.282 | 9.827 | 98.84 | [16] |
| (Sn) | Sn | Sn | tI4 | I41/amd | 141 | 0.5832 | – | 0.3181 | 90 | [24] |
Table 3.
XRD analysis of quenched sample.
| Nominal composition (at%) | Heat treatment (°C) | Phase analysis |
||
|---|---|---|---|---|
| Phase | Space group | Lattice param. (Å) | ||
| Cu89Sn11 | 400 °C, 14d | (Cu) = Cu | Fm-3m | a = 3.68902(1) |
| δ = Cu41Sn11 | F-43m | a = 17.9516(3) | ||
| ζ = Cu10Sn3 | P63 | a = 7.3304(2) c = 7.8539(3) | ||
| Cu84.5Sn15.5 | 400 °C, 14d | (Cu) = Cu | Fm-3m | a = 3.68981(2) |
| δ = Cu41Sn11 | F-43m | a = 17.9580(2) | ||
| ζ = Cu10Sn3 | P63 | a = 7.3307(1) c = 7.8632(1) | ||
| Cu81.5Sn18.5 | 400 °C, 14d | (Cu) = Cu | Fm-3m | a = 3.6847(2) |
| δ = Cu41Sn11 | F-43m | a = 17.9577(2) | ||
| Cu79Sn21 | 400 °C, 14d | δ = Cu41Sn11 | F-43m | a = 17.9579(1) |
| ɛ = Cu3Sn | Cmcm | a = 5.497(1) b = 47.82(1) c = 4.3288(5) | ||
| Cu76Sn24 | 400 °C, 14d | δ = Cu41Sn11 | F-43m | a = 17.9569(8) |
| ɛ = Cu3Sn | Cmcm | a = 5.5192(2) b = 47.573(2) c = 4.3294(1) | ||
| Cu72.5Sn27.5 | 400 °C, 14d | ɛ = Cu3Sn | Cmcm | a = 5.5277(7) b = 47.681(2) c = 4.3291(1) |
| η = Cu6Sn5 | P63/mmc | a = 4.2199(3) c = 5.1009(7) | ||
| Cu89Sn11 | 700 °C, 14d | (Cu) = Cu | Fm-3m | a = 3.7179(9) |
| δ = Cu41Sn11 | F-43m | a = 17.9526(6) | ||
| Cu84.5Sn15.5 | 700 °C, 14d | (Cu) = Cu | Fm-3m | a = 3.7020(9) |
| δ = Cu41Sn11 | F-43m | a = 17.9447(6) | ||
| Cu81.5Sn18.5 | 700 °C, 14d | δ = Cu41Sn11 | F-43m | a = 17.9469(2) |
| Cu79Sn21 | 700 °C, 14d | δ = Cu41Sn11 | F-43m | a = 17.97531(9) |
| Cu76Sn24 | 700 °C, 14d | ζ = Cu10Sn3 | P63 | a = 7.3306(1) c = 7.8650(2) |
| Cu72.5Sn27.5 | 700 °C, 14d | ɛ = Cu3Sn | Cmcm | a = 5.5124(4) b = 47.453(4) c 4.3384(2) |
| ζ = Cu10Sn3 | P63 | a = 7.3258(1) c = 7.8662(2) | ||
| Cu77Sn23 | 600 °C, 14d | ɛ = Cu3Sn | Cmcm | a = 5.4913(2) b = 47.772(2) c = 4.3326(1) |
| ζ = Cu10Sn3 | P63 | a = 7.3280(2) c = 7.8680(3) | ||
| Cu76Sn24 | 600 °C, 14d | ɛ = Cu3Sn | Cmcm | a = 5.5126(2) b = 47.576(1) c = 4.33164(9) |
| Cu75Sn25 | 600 °C, 14d | ɛ = Cu3Sn | Cmcm | a = 5.5135(2) b = 47.603(1) c = 4.3308(1) |
| Cu58Sn42 | 170 °C, 6m | ɛ = Cu3Sn | Cmcm | a = 5.515(2) b = 47.74(2) c = 4.3293(2) |
| η′ = Cu6Sn5 | C2/c | a = 11.0344(9) b = 7.2919(3) c = 9.844(1) β = 98.768(8) | ||
| Cu55Sn45 | 170 °C, 6m | ɛ = Cu3Sn | Cmcm | a = 5.515(4) b = 47.74(4) c = 4.3262(5) |
| η′ = Cu6Sn5 | C2/c | a = 11.0117(2) b = 7.2950(1) c = 9.8328(2) β = 98.925(1) | ||
| Cu52Sn48 | 170 °C, 6m | η′ = Cu6Sn5 | C2/c | a = 11.008(1) b = 7.2751(6) c = 9.820(2) β = 98.77(1) |
| (Sn) = Sn | I41/amd | a = 5.8285(3) c = 3.1792(2) | ||
Table 4.
HT-XRD at 700 °C, table of lattice parameters.
| Composition | Lattice parameter of β or γ (Å) | Phases identified |
|---|---|---|
| Cu85Sn15 | a = 3.0184(1) | (Cu) + β |
| Cu84.5Sn15.5 | a = 3.0185(1) | (Cu) + β |
| Cu84Sn16 | a = 3.0307(1) | β |
| Cu83Sn17 | a = 3.0390(2) | γ |
| Cu82Sn18 | a = 3.0432(2) | γ |
| Cu81.5Sn18.5 | a = 3.0469(4) | γ |
| Cu80Sn20 | a = 3.0477(1) | γ |
| Cu78Sn22 | a = 3.0537(2) | γ |
| Cu76Sn24 | a = 3.0567(1) | γ |
Fig. 1.
Experimental results obtained by high temperature x-ray diffraction. Dotted line: second order transition.
Table 5.
Invariant reactions from DTA results.
| Invariant reactions | Temperature (°C) [21] | Temperature (°C), this work |
|---|---|---|
| (Cu) + L → β | 798 | 798 |
| β + L → γ | 755 | 758 |
| ɛ → γ | 676 | Not investigated |
| γ + ɛ → ζ | 640 | 641 |
| γ → ɛ + L | 640 | 649 |
| γ + ζ → δ | 590 | 603 |
| β → (Cu) + γ | 586 | 566 |
| ζ → δ + ɛ | 582 | 589 |
| γ → (Cu) + δ | 520 | 518 |
| ɛ + L → η | 415 | 408 |
| δ → (Cu) + ɛ | 350 | Not investigated |
| L → η + (Sn) | 227 | Not investigated |
Fig. 2.
Experimental results obtained by DTA measurements. Dotted line: second order transition.
Table 6.
Summary of SEM/EPMA results.
| Phase | 170 °C → quenched |
400 °C → quenched |
600 °C → quenched |
700 °C → quenched |
|---|---|---|---|---|
| at% Sn | at% Sn | at% Sn | at% Sn | |
| (Cu) | 7.7 (8.0) | |||
| δCu | 20.8 (20.2) | 20.7 (ne) | ||
| δSn | 21.0 (20.8) | 21.7 (ne) | ||
| ζCu | 22.2 (ne) | |||
| ζSn | 21.3 (22.5) | 22.7 (ne) | ||
| ɛCu | 25.3 (24.5) | 24.4 (24.5) | 25.5 (ne) | |
| ɛSn | 24.4 (25.3) | 25.8 (25.3) | ||
| ηCu | 44.5 (43.5) | |||
| η′Cu | 43.4 (44.8) | |||
| η′Sn | 44.3 (45.5) |
XCu…concentration limit of phase X at Cu-rich side.
XSn…concentration limit of phase X at Sn-rich side.
Values in brackets: Literature [21].
(ne)…phase formed during quenching, not in equilibrium.
Fig. 3.
Diffraction patterns of Cu84Sn16 and Cu83Sn17 at 700 °C, showing the additional superlattice reflections of Cu83Sn17.
Fig. 4.
Lattice parameters at different compositions, HT-XRD at 700 °C.
Fig. 5.
Measured DTA curves for various alloy compositions in the Cu–Sn system.
4. Conclusions
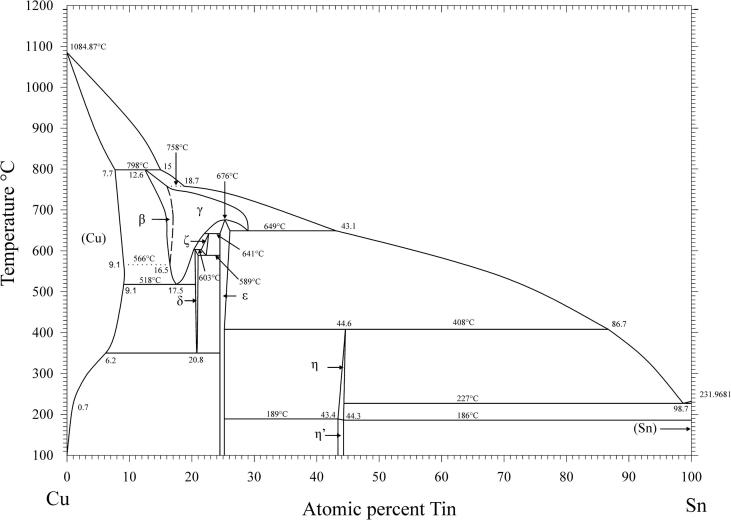
A very detailed study of the primary literature which finally led to the well-known phase diagram version of Cu–Sn, published e.g in Massalski's compilation [26], was the starting point of the present work. It became clear that the β–γ-two phase field was basically established by Shepherd and Blough [6], and adopted by nearly all other authors. Considering these very early experimental results against the background of nowadays knowledge and experimental techniques their conclusions could not be sustained any more. Supported by our comprehensive and thoroughly evaluated HT-XRD experiments and regarding corresponding literature data from Knoedler [13] and Liu [22] we concluded, that the β-phase transforms to the γ-phase by a higher order reaction. Depending on temperature and concentration, the randomly distributed tin atoms order according to the BiF3 structure type. The results of this work have been implemented in a new version of the Cu–Sn phase diagram (Fig. 6).
Fig. 6.
New Cu–Sn phase diagram.
Acknowledgements
We thank the FWF for funding this work under the project P21507-N19 within the COST Action MP0602 and the project I559-N19, which is part of the DFG Priority Program SPP 1473 “WeNDeLIB”. We also thank Christian Lengauer for his technical support to perform the HT-XRD measurements.
References
- 1.Wuich W. Vogel; Würzburg: 1972. Löten. Lötverfahren, Lote, Flußmittel, Anwendungstechniken. [Google Scholar]
- 2.COST_Action_MP0602. 2010. http://cost602.ipm.cz/mp0602-mou.pdf [Google Scholar]
- 3.Heycock C.T., Neville F.H. vols. 47–51. 1897. Complete freezing-point curves of binary alloys. (Philosophical Transactions of the Royal Society of London Series A-containing papers of a mathematical or physical character, A189). p. 62–66. [Google Scholar]
- 4.Heycock C.T., Neville F.H. vol. 202. 1904. On the constitution of the copper-tin series of alloys. (Philosophical Transactions of the Royal Society of London Series A-containing papers of a mathematical or physical character). p. 1–70. [Google Scholar]
- 5.Verö J. The composition of tin bronzes. Zeitschrift Für Anorganische Und Allgemeine Chemie. 1934;218:402–424. [Google Scholar]
- 6.Shepherd E.S., Blough E. The constitution of the copper-tin alloys. Journal of Physical Chemistry. 1906;10:630–653. [Google Scholar]
- 7.Hoyt S.L. On the copper-rich kalchoids (copper-tin-zinc alloys) Journal of the Institute of Metals. 1913;10:235–274. [Google Scholar]
- 8.Westgren A., Phragmen G. X-ray analysis of copper-tin alloys. Zeitschrift Für Anorganische Und Allgemeine Chemie. 1928;175:80–89. [Google Scholar]
- 9.Haase C., Pawlek F. Zur Kenntnis der Kupfer-Zinnlegierungen. Zeitschrift für Metallkunde. 1936;28:73–80. [Google Scholar]
- 10.Hamasumi M., Morikawa K. Copper-tin equilibrium diagram. Nippon Kinzoku Gakkaishi. 1938;2:39–44. [Google Scholar]
- 11.Raynor G.V. vol. 2. The Institute of Metals; 1944. (The equilibrium diagram of the system copper-tin). [Google Scholar]
- 12.Knödler H. Die Überstruktur der gamma-Hochtemperaturphase im System Kupfer-Zinn. Acta Crystallographica. 1956;9:1036. [Google Scholar]
- 13.Knödler H. Über Kristallstruktur und strukturellen Zusammenhang der Phasen gamma und epsilon im System Kupfer-Zinn. Metall. 1966;20:823–829. [Google Scholar]
- 14.Hansen M., Anderko K. Constitution of binary alloys. In: Mehl R.F., editor. Mc Graw-Hill Book Company, Inc.; 1958. (Metallurgy and metallurgical engineering series). [Google Scholar]
- 15.Hansen M., Anderko K. 2 ed. Genum Publishing Corporation; New York: 1985. Cu–Sn copper–tin. [Google Scholar]
- 16.Larsson A.K., Stenberg L., Lidin S. The superstructure of domain-twinned Eta'-Cu6Sn5. Acta Crystallographica Section B-Structural Science. 1994;50:636–643. [Google Scholar]
- 17.Watanabe Y., Fujinaga Y., Iwasaki H. Lattice modulation in the long-period superstructure of Cu3Sn. Acta Crystallographica Section B-Structural Science. 1983;39:306–311. [Google Scholar]
- 18.Booth M.H., Brandon J.K., Brizard R.Y., Chieh C., Pearson W.B. Gamma-brasses with F cells. Acta Crystallographica Section B-Structural Science. 1977;33:30–36. [Google Scholar]
- 19.Brandon J.K., Pearson W.B., Tozer D.J.N. A single-crystal x-ray diffraction study of the zeta bronze structure, Cu20Sn6. Acta Crystallographica. 1975;B31:774–779. [Google Scholar]
- 20.Gangulee A., Das G.C., Bever M.B. X-ray-diffraction and calorimetric investigation of compound Cu6Sn5. Metallurgical Transactions. 1973;4:2063–2066. [Google Scholar]
- 21.Saunders N., Miodownik A.P. The Cu–Sn (copper–tin) system. Bulletin of Alloy Phase Diagrams. 1990;11:278–287. [Google Scholar]
- 22.Liu X.J., Wang C.P., Ohnuma I., Kainuma R., Ishida K. Experimental investigation and thermodynamic calculation of the phase equilibria in the Cu–Sn and Cu–Sn–Mn systems. Metallurgical and Materials Transactions A-Physical Metallurgy and Materials Science. 2004;35A:1641–1654. [Google Scholar]
- 23.Kantola M., Tokola E. X-ray studies on the thermal expansion of copper–nickel alloys. Annales Academiæ Scientiarum Fennicæ. 1967;223:1–10. [Google Scholar]
- 24.Lee J.A., Raynor G.V. The lattice spacings of binary tin-rich alloys. Proceedings of the Physical Society. 1954;67B:737–747. [Google Scholar]
- 25.Kennon N.F., Miller T.M. Martensitic transformations in beta-1 Cu–Sn alloys. Transactions of the Japan Institute of Metals. 1972;13:322. [Google Scholar]
- 26.Massalski T.B., Okamoto H. ASM International; Materials Park, Ohio: 2001. Binary alloy phase diagrams. [Google Scholar]