Phase equilibria and structural investigations in the system Al–Fe–Si

Abstract

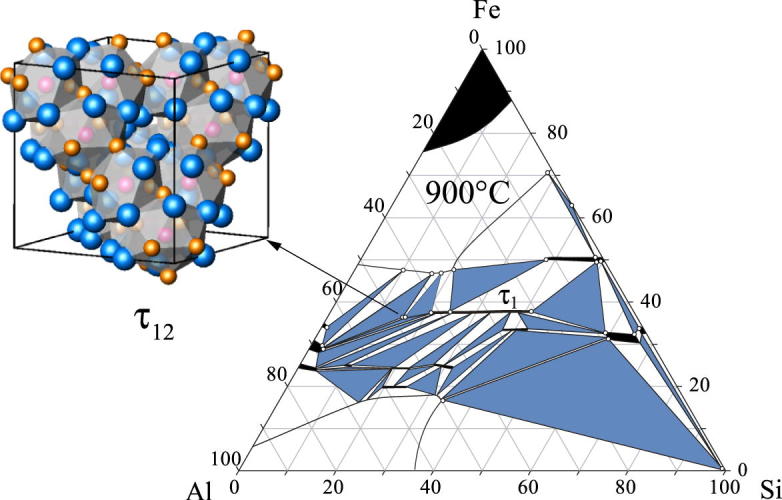
The Al–Fe–Si system was studied for an isothermal section at 800 °C in the Al-rich part and at 900 °C in the Fe-rich part, and for half a dozen vertical sections at 27, 35, 40, 50 and 60 at.% Fe and 5 at.% Al. Optical microscopy and powder X-ray diffraction (XRD) was used for initial sample characterization, and Electron Probe Microanalysis (EPMA) and Scanning Electron Microscopy (SEM) of the annealed samples was used to determine the exact phase compositions. Thermal reactions were studied by Differential Thermal Analysis (DTA). Our experimental results are generally in good agreement with the most recent phase diagram versions of the system Al–Fe–Si. A new ternary high-temperature phase τ₁₂ (cF96, NiTi₂-type) with the composition Al₄₈Fe₃₆Si₁₆ was discovered and was structurally characterized by means of single-crystal and powder XRD. The variation of the lattice parameters of the triclinic phase τ₁ with the composition Al_2+xFe₃Si_3−x (−0.3 < x < 1.3) was studied in detail. For the binary phase FeSi₂ only small solubility of Al was found in the low-temperature modification LT-FeSi₂ (ζ_β) but significant solubility in the high-temperature modification HT-FeSi₂ (ζ_α) (8.5 at.% Al). It was found that the high-temperature modification of FeSi₂ is stabilized down to much lower temperature in the ternary, confirming earlier literature suggestions on this issue. DTA results in four selected vertical sections were compared with calculated sections based on a recent CALPHAD assessment. The deviations of liquidus values are significant suggesting the need for improvement of the thermodynamic models.

Graphical abstract

1. Introduction

The ternary system Al–Fe–Si was studied extensively in the past, especially in the aluminium rich corner. This system is of high interest because iron and silicon are two of the most common impurities in aluminium alloys. Within aluminium alloys, these two elements form hard and brittle ternary phases which exert an influence on the chemical and mechanical properties, like corrosion resistance and the surfaces quality. At the same time, a large variety of aluminium materials are known, in which iron is a necessary and basic component. Among such materials are alloys produced by rapid solidification and by mechanical alloying; composite materials, and some wrought and casting heat-resistant conducting and corrosion-resistant alloys. The system was also studied in the context of iron aluminide-based materials.

The binary limiting systems Al–Fe, Al–Si and Fe–Si are given in Massalski’s Handbook of Binary Alloy Phase Diagrams [1]. Phase equilibria of the binary systems are generally well known. In the binary Al–Fe system the following phases have been found to exist: Al₂Fe (with recently corrected crystal structure) [2], Al₅Fe₂ [3] and Al₁₃Fe₄ [4], (labelled as Al₃Fe by some authors). The crystal structure of the high-temperature phase ε (Al₈Fe₅) was recently determined by Stein et al. [5]. Phase boundaries in the Al-rich part in the Al–Fe system are not well specified. The iron-rich part of the system is dominated by extended solid solutions of Al in αFe, AlFe (B2) and AlFe₃ (D0₃) ordered phases [6], [7]. The binary Fe–Si system in Ref. [1] is already accepted from [8]. Similar to the Al–Fe system, the iron-rich bcc alloys exist in both ordered, B2 and D0₃, and disordered A2 modifications. The following compounds are stable: Fe₂Si (β) [9], Fe₅Si₃ [10], FeSi [11] and FeSi₂ in a high- and low-temperature modifications, ζ_α [12] and ζ_β [13]. The binary Al–Si system [1] is a simple eutectic system with a eutectic reaction temperature of 577 °C at the composition Al_87.8Si_12.2. A summary of all relevant binary phases is given in Table 1.

Table 1.

Binary and ternary phases reported in the systems Al–Fe, Al–Si and Fe–Si and Al–Fe–Si.

Phase	Sructure type	Pearson symbol	Space group	Reference
AlFe (α2)	CsCl/B2	cP2	Pm$\overline{3}$m	[7]
AlFe3 (α1)	BiF3/D03	cF16	Fm$\overline{3}$m	[7]
Al2Fe	Al2Fe	aP18	P$\overline{1}$	[2]
Al5Fe2	Al5Fe2	oC16	Cmcm	[3]
Al13Fe4	Al13Fe4	mC102	C2/m	[4]
Al8Fe5 (ε)	Cu5Zn8/D82	cI52	I$\overline{4}$3m	[5]
HT-FeSi2 (Fe2Si5)	FeSi2	tP3	P4/mmm	[12]
LT-FeSi2	FeSi2	oC48	Cmca	[13]
Fe2Si	Fe2Si	hP6	P63/mmc	[9]
Fe5Si3	Mn5Si3	hP16	P63/mcm	[10]
FeSi	FeSi	oP8	P213	[11]
Al2Fe3Si3 (τ1) Al21.5−45Fe36.5−37.5Si8.5−41.5a	Al2Fe3Si3	aP16	P$\overline{1}$	[22]
Al3FeSi (τ2) Al53.9−65.3Fe19.5−20.5Si15.2−25.6a	Al3FeSi	m∗∗	mC∗	[23]
Al2FeSi (τ3) Al53−56Fe23.5−24.5Si20.5−22.5a	Al2FeSi	oC128	Cmma	[24]
Al3FeSi2 (τ4) Al45.5−54Fe15.5−16.5Si30.5−38a	GaPd5	tI24	I4/mcm	[25]
Al7.4Fe2Si (τ5) Al68−72Fe18−19.5Si10−12.5a	Al7.4Fe2Si	hP244	P63/mmc	[26]
Al4.5FeSi (τ6) Al64.5−67.5Fe15.5−16.5Si17−19a	Al9Fe2Si2	mC52	C2/m	[27]
Al3Fe2Si3 (τ7) Al39.2−48.7Fe23.5−24.5Si27.8−36.3a	Al3Fe2Si3	mP64	P21/n	[28]
Al2Fe3Si4 (τ8) Al24.1−28.6Fe31.9−32.9Si39.5−43a	Al2Fe3Si4	oC48	Cmcm	[22]
τ10 Al57−59Fe24−25Si17−18a	–	hexagonal?	–	[19]
Al4Fe1.7Si (τ11) Al64–66.5Fe24−25Si9.5−11a	Co2Al5	hP28	P63/mmc	[29]

^aComposition ranges of ternary phases according to Ref. [19].

A critical review of the ternary Al–Fe–Si system was given by Ghosh [14], [15]. The author assessed the work of more than 150 research papers up to the year 1989. Updates of evaluated constitutional data were later given in Refs. [16], [17], [18], including also more recent information.

The system is characterized by a large number of ternary phases, both stable and metastable. Nineteen invariant reactions and ten ternary phases were listed in Refs. [14], [16], but only the Al-rich corner of the phase diagram was well understood and some of the phases were not sufficiently characterized in terms of their crystal structures and composition ranges. Krendelsberger et al. [19] reinvestigated the complete ternary system Al–Fe–Si within several isothermal sections and by thermal analysis. These authors constructed a complete liquidus surface projection and a consistent reaction scheme (Scheil diagram). Du et al. [20] subsequently published a thermodynamic assessment of the ternary system which basically relies on the data of Krendelsberger et al. [19], but differences are found in the liquidus projection as well as in parts of the reaction scheme. Maitra and Gupta [21] investigated the Al–Fe–Si system in the temperature range between 600 and 900 °C concerning the microstructure of binary and ternary phases using ternary diffusion couples. Isothermal sections in this work are inconsistent in some details with literature given by [16]. The 10 stable ternary phases are listed together with the respective Refs. [22], [23], [24], [25], [26], [27], [28], [29] in Table 1. Note that τ₉ is missing in this table, as it was found to be identical with τ₁ [19].

Our investigation of the Al–Fe–Si system is part of an ongoing research project with the aim to systematically investigate phase equilibria of transition metals with Al and Si. The current work was concentrated on the description of vertical sections in order to compare these with predictions based on the existing reaction scheme and liquidus surfaces [19], [20]. In addition, two isothermal sections at 800 and 900 °C are presented, detailed crystallographic information on triclinic τ₁ is given, and a new high-temperature phase τ₁₂ is introduced.

2. Experimental

All samples were prepared from pure elements using an iron foil/sheet (99.95%, melted and cast in vacuum), aluminium slug (3.175 mm, 99.999% Alfa Aesar, Karlsruhe, Germany) and silicon lump (0.1–2.5 cm, 99.9999% Alfa Aesar, Karlsruhe, Germany). Calculated amounts of the elements were weighed to an accuracy of better than 0.06% and then arc melted on a water-cooled copper plate under an argon atmosphere of 0.5 bar, using zirconium as a getter material. The samples were remelted 2–4 times for homogenization. After this procedure the samples were weighed back in order to check the mass losses. The mass loss was between 0.2 and 0.8%. For equilibration, the reguli were annealed in alumina crucibles at 800 °C and 900 °C for 336–870 h in sealed and evacuated quartz glass tubes. After quenching in water samples were characterized by X-ray diffraction (XRD), optical microscopy, scanning electron microscope (SEM), electron microprobe analysis (EPMA) and differential thermal analysis (DTA).

For metallographic investigations, pieces of the quenched samples were incorporated into a mixture of resin and carbon powder. The embedded samples were ground and polished in order to perform optical microscopy as well as electron probe microanalysis (EPMA) and scanning electron microscopy (SEM). For the investigation by optical microscopy a Zeiss Axiotech 100 microscope equipped for operation under polarized light was used.

Selected samples were analyzed by EPMA and SEM in order to determine reliable compositions of the various phases. Measurements were carried out on a Cameca SX 100 electron probe and a Zeiss Supra 55 VP scanning electron microscope, using wavelength dispersive X-ray spectroscopy (WDS) for quantitative analysis and employing elemental aluminium, iron and silicon as standard materials. The measurements were carried out at 15–20 kV and 4–8 nA (SEM) and 10–20 nA (EPMA). Conventional ZAF matrix correction was used to calculate the final composition. At least three measurements were taken in each phase and the measured compositions were averaged. Overall sample compositions were not determined by EPMA.

DTA measurements were performed on a DTA 404 S and 404 PC (NETZSCH, Germany) using open alumina crucibles and employing a slow permanent argon flow of 50 ml min⁻¹. A sample mass between 25 and 60 mg was used for the experiments and the samples were checked routinely for possible mass changes during the DTA investigations. No relevant mass changes were observed. Two heating- and cooling-curves were recorded for each sample using a heating rate of 5 K min⁻¹. The Pt/Pt10%Rh thermocouples of the DTA instrument were calibrated using the melting points of pure Al, Au and Ni.

X-ray powder diffraction was performed with Cu Kα-radiation on a Bruker D8 Advance diffractometer with Bragg–Brentano geometry using a one-dimensional silicon-strip detector (Lynxeye) or an energy-dispersive detector (Sol-X, Lithium drifted Silicon detector), respectively. The X-ray powder diffractograms were refined with the program TOPAS^® 3 [30].

Single crystals for the structure determination were separated from the bulk sample under an optical microscope. Diffraction data were collected on a NONIUS four-circle diffractometer equipped with a CCD detector and a 300 μm capillary-optics collimator (Mo tube, graphite monochromator). Unit-cell parameters were obtained by least-squares refinements of 2ϑ values. Corrections for Lorentz, polarization and absorption effects were done by application of the multi-scan method, complex scattering functions [31]. The structure solution by direct methods and subsequent structure refinement was performed using SHELXL-97 [32], [33].

Calculated vertical sections based on the thermodynamic model published by Du et al. [20] were provided by the author [34] for a comparison with experimental data.

3. Results and discussion

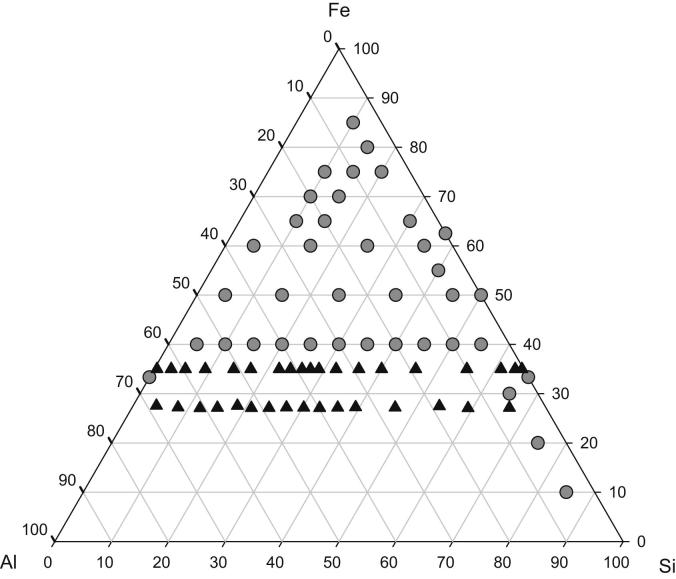
A total number of 73 samples were studied for isothermal phase equilibria and for thermal reactions. These samples were situated in 6 different sections at 27, 35, 40, 50 and 60 at.% Fe and at 5 at.% Al, respectively. The sample compositions are shown in Fig. 1 with different symbols indicating annealing at 800 and 900 °C, respectively.

Fig. 1.

Sample composition of binary and ternary samples investigated in the system Al–Fe–Si annealed at 800 °C (black triangles) and at 900 °C (grey circles).

Additional samples were prepared in different areas of the system for primary crystallization tests (as cast), and for various annealing experiments to clarify details of solid-state equilibria at different temperatures.

3.1. Isothermal sections at 800 and 900 °C

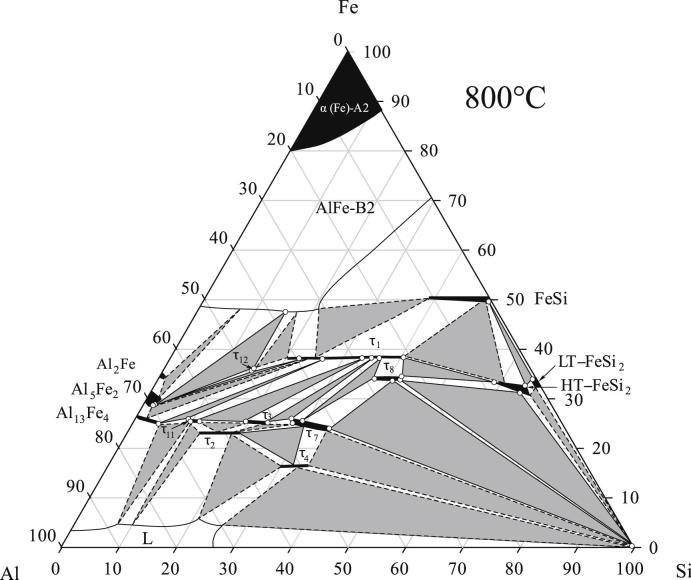
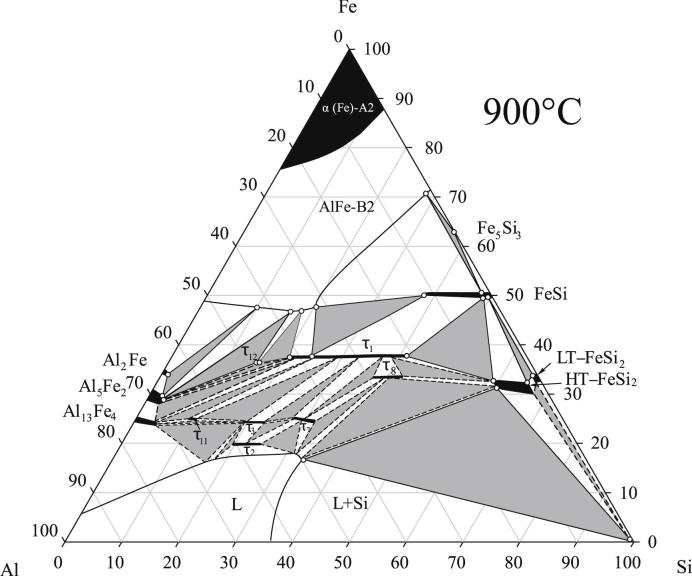
The isothermal sections as proposed from our experimental investigations are shown in Fig. 2, Fig. 3. These figures combine our results from XRD with exact phase compositions measured by EPMA, shown as open circles. The iron-poor part of the system, i.e. the equilibria with the liquid and τ₄ were not directly measured by EPMA. Instead the phase fields were extrapolated on basis of the work from Krendelsberger et al. [19]. Experimental data for selected samples situated in relevant three-phase fields are listed in Table 2. One sample in each three-phase field is listed in Table 2. Two-phase samples and redundant three-phase samples are not given in the table, but are well in line with these results and were also used for the construction of the isothermal sections.

Fig. 2.

Isothermal section of Al–Fe–Si at 800 °C. Phase equilibria are drawn according to experimental results listed in Table 2. The composition of the phase boundaries measured with EPMA, are plotted with open circles.

Fig. 3.

Isothermal section of Al–Fe–Si at 900 °C. Phase equilibria are drawn according to experimental results listed in Table 2. The composition of the phase boundaries measured with EPMA, are plotted with open circles.

Table 2.

Experimental phase compositions and cell parameters of selected samples (situated in three-phase fields) in the partial isothermal sections at 800 °C and 900 °C.

Sample #	Nominal sample composition (at.%)	Annealing (°C)	Phases (XRD)	Cell parameter (Å)			Phase composition determined by EPMA
							Al (at.%)	Fe (at.%)	Si (at%)
1	Al62Fe27Si11	800	Al13Fe4	a = 15.4980(2)	b = 7.9627(2)	c = 12.5567(1)	70.7(1)	24.9(2)	4.4(2)
					β = 107.96
			τ1	a = 4.6335(1)	b = 6.3467(2)	c = 7.5355(2)	36.4(2)	37.5(1)	26.1(2)
				α = 102.14	β = 106.04	γ = 101.30
			τ11	a = 7.5355(1)		c = 7.5805(2)	64.7(2)	26.1(2)	9.2(1)
2	Al55Fe27Si18	800	τ1	a = 4.6483(1)	b = 6.3225(3)	c = 7.5063(3)	28.6(3)	38.0(2)	33.4(4)
				α = 101.35	β = 105.92	γ = 101.21
			τ3	a = 7.9755(1)	b = 15.2067(1)	c = 15.2378(1)	54.5(1)	26.6(1)	18.9(2)
			τ11	a = 7.5253(1)		c = 7.5605(2)	62.3(2)	25.9(1)	11.8(3)
3	Al46Fe27Si27	800	τ1	a = 4.6840(2)	b = 6.3370(2)	c = 7.4952(3)	27.1(2)	37.8(1)	35.1(3)
				α = 101.40	β = 105.75	γ = 101.60
			τ3	a = 7.9557(1)	b = 15.1789(5)	c = 15.2259(6)	51.8(2)	25.2(1)	23.0
			τ7	a = 7.3257(1)	b = 8.2792(1)	c = 14.6096(3)	46.6(3)	26.1(2)	27.3(2)
					β = 93.71
4	Al27Fe27Si46	800	Si	a = 5.4229(2)			0.3(3)	0.5(1)	99.2(3)
			τ7	a = 7.1829(3)	b = 8.3569(3)	c = 14.4564(6)	41.3(2)	23.8(1)	34.9(1)
					β = 93.81
			τ8	a = 3.6665(5)	b = 12.3419(1)	c = 10.1365(1)	25.5(1)	33.5(1)	41.0(3)
5	Al14Fe27Si59	800	HT-FeSi2	a = 2.7067(1)		c = 5.1797(2)	4.5(5)	31.0(2)	64.5(5)
			τ1	a = 5.4293(1)			0.0(1)	0.6(1)	99.4(1)
			τ8	a = 3.6679(5)	b = 12.3430(2)	c = 10.1413(2)	24.0(1)	33.7(1)	42.3(1)
6	Al51Fe35Si14	800	AlFe	a = 2.8508(6)			37.0(1)	47.5(1)	15.5(1)
			Al5Fe2	a = 7.6381(5)	b = 6.3876(4)	c = 4.2302(3)	68.8(1)	29.0(5)	2.2(4)
			τ12	a = 10.8011(2)			48.3(2)	36.3(2)	15.4(1)
7	Al48Fe35Si17	800	Al5Fe2	a = 7.6461(2)	b = 6.3879(2)	c = 4.2427(1)	70.1(2)	27.4(2)	2.5(2)
			τ1	a = 4.7385(2)	b = 6.3217(3)	c = 7.4828(3)	40.0(1)	37.7(2)	22.3(3)
				α = 100.17	β = 104.97	γ = 102.39
			τ12	a = 10.8141(2)			49.5(3)	34.9(2)	15.6(2)
8	Al29Fe35Si36	800	τ1	a = 4.6134(3)	b = 6.3304(4)	c = 7.5082(4)	25.4(2)	38.0(2)	36.6(1)
				α = 101.76	β = 106.29	γ = 100.75
			τ7	a = 7.2656(3)	b = 8.3165(3)	c = 14.5216(7)	44.9(2)	25.8(1)	29.3(2)
					β = 93.83
			τ8	a = 3.6599(4)	b = 12.4729(5)	c = 10.1568(2)	28.6(1)	34.1(1)	37.3(1)
9	Al19Fe35Si46	800	HT-FeSi2	a = 2.7171(1)		c = 5.2131(1)	7.8(2)	33.5(2)	58.4(2)
			τ1	a = 4.5889(1)	b = 6.3373(2)	c = 7.5251(2)	21.1(1)	38.3(2)	40.6(2)
				α = 101.93	β = 106.45	γ = 100.70
			τ8	a = 3.6689(1)	b = 12.3245(2)	c = 10.1407(1)	23.2(1)	34.5(2)	42.3(2)
10	Al1Fe35Si64	800	FeSi	a = 4.4909(1)			0.9(1)	50.6(1)	48.5(1)
			HT-FeSi2	a = 2.6792(5)		c = 5.1676(6)	2.7(3)	32.4(1)	64.9(3)
			LT-FeSi2	a = 9.8886(1)	b = 7.8073(1)	c = 7.8487(1)	0.7(1)	34.3(1)	65.0(1)
11	Al55Fe40Si5	900	AlFe	a = 2.8790(1)			44.3(1)	47.5(1)	8.2(1)
			Al5Fe2	a = 7.6464(4)	b = 6.4002(3)	c = 4.2223(2)	68.7(1)	30.2(1)	1.1(1)
			Al2Fe	a = 4.8811(6)	b = 6.4472(7)	c = 8.7706(1)	64.5(1)	34.0(1)	1.5(1)
				α = 91.65	β = 73.21	γ = 96.61
12	Al48Fe37Si15	900	AlFe	a = 2.8544(2)			36.5(1)	46.7(1)	16.8(0)
			Al5Fe2	a = 7.6446(1)	b = 6.3938(1)	c = 4.2340(1)	69.6(1)	28.6(1)	1.8(2)
			τ12	a = 10.8039(1)			47.6(1)	36.4(2)	16.0(1)
13	Al40Fe40Si20	900	AlFe	a = 2.8471(1)			35.0(2)	46.8(2)	18.2(1)
			τ1	a = 4.7553(1)	b = 6.3208(2)	c = 7.4757(2)	41.7(1)	37.5(1)	20.8(1)
				α = 99.92	β = 104.72	γ = 102.55
			τ12	a = 10.8008(5)			47.7(1)	36.4(0)	15.9(2)
14	Al35Fe40Si25	900	AlFe	a = 2.8400(1)			32.0(0)	47.3(1)	20.7(1)
			FeSi	a = 4.5329(2)			11.5(1)	49.9(0)	38.6(1)
			τ1	a = 4.7238(1)	b = 6.3224(2)	c = 7.4866(2)	37.7(3)	37.8(1)	24.5(2)
				α = 100.45	β = 105.10	γ = 102.21
15	Al15Fe40Si45	900	FeSi	a = 4.4925(1)			1.8(0)	49.4(0)	48.8(1)
			HT-FeSi2	a = 2.7174(1)		c = 5.2150(4)	8.5(0)	32.9(0)	58.6(0)
			τ1	a = 4.5855(1)	b = 6.3357(1)	c = 7.5259(2)	21.2(0)	37.6(0)	41.2(1)
				α = 101.96	β = 106.45	γ = 100.70
16	Al1.5Fe33Si65.5	900	FeSi	a = 4.4892(3)			0.7(0)	49.6(2)	49.7(2)
			LT-FeSi2	a = 9.8867(3)	b = 7.8056(2)	c = 7.8482(2)	0.6(0)	33.7(0)	65.8(0)
			HT-FeSi2	a = 2.7037(1)		c = 5.1639(4)	2.4(0)	31.8(0)	65.8(0)
17	Al5Fe10Si85	900	HT-FeSi2	a = 2.7107(1)		c = 5.4303(1)	8.4(1)	31.3(0)	60.3(0)
			Si	a = 5.1990(3)			0.3(4)	0.2(0)	99.5(4)
			L	–			49.6(2)	16.7(1)	33.7(1)
18	Al1.4Fe63Si35.6	900	AlFe	a = 2.8193(1)			1.4(0)	71.2(3)	27.5(3)
			FeSi	a = 4.4936(2)			1.5(0)	50.9(1)	47.5(1)
			Fe5Si3	a = 6.7142(2)	b = 4.7260(1)		0.1(0)	62.7(3)	37.2(3)

The isothermal sections at 800 °C and 900 °C are, in their basic outline consistent, with the section at 550 °C given by Krendelsberger et al. [19]. They contain, however, two additional features. The first point concerns the observation of a new ternary phase τ₁₂ with the measured composition Al₄₈Fe₃₆Si₁₆ occurring in both sections. Details on this new compound are given is Section 3.4. The second point concerns the binary phase FeSi₂. In both sections, the high-temperature phase as well as the low-temperature phase was found to be present, although the high-temperature form is not stable at temperatures below 937 °C in the binary. While the low-temperature modification does not dissolve significant amounts of Al, the high-temperature form is only present as ternary phase field and was found to dissolve up to 8.5 at.% Al. Details on the ternary stabilization and decomposition of the high-temperature phase are discussed in Section 3.3.

The two points mentioned above are not in contradiction to the work of Krendelsberger et al. [19], as they concern phase equilibria at higher temperatures and are not found at 550 °C. In fact, it was already suggested in Ref. [19], that the high-temperature form of FeSi₂ is stabilized by Al additions down to temperatures of approx. 700 °C. However, isothermal sections at 800 °C and 900 °C given in Refs. [16], [20], [21] do not show these features and are therefore partly incorrect.

The solubility ranges of τ₁, τ₃, τ₇, τ₈ and τ₁₁ were re-determined in the present study and noticeable differences to the values given by other authors were observed. Table 2 contains full information on lattice parameters and phase compositions in various three-phase fields. The corresponding homogeneity ranges observed at 800 °C are listed in Table 3. The details for the change of structural parameters in the extended homogeneity range of the triclinic phase τ₁ are discussed in Section 3.2.

Table 3.

Homogeneity ranges of various ternary phases in the Al–Fe–Si system at 800 °C determined by EPMA.

Phase	Homogeneity range/at.%
τ1	Al21.0–41.5Fe37.5−38.5Si41.5–21.0
τ3	Al52.0−54.5Fe25.0−26.5Si23.0−19.0
τ7	Al41.0−46.5Fe24.0−26.0Si35.0−27.5
τ8	Al23.0−28.5Fe33.5−34.5Si42.5−37.5
τ11	Al62.5−65.0Fe26.0Si11.5−9.0

3.2. The homogeneity range of Al₂Fe₃Si₃ (τ₁)

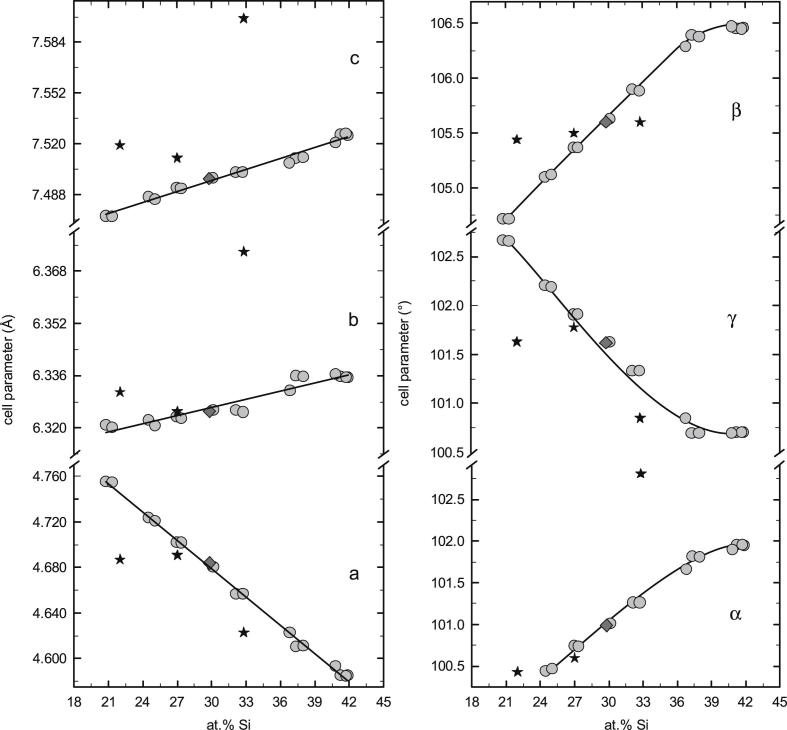
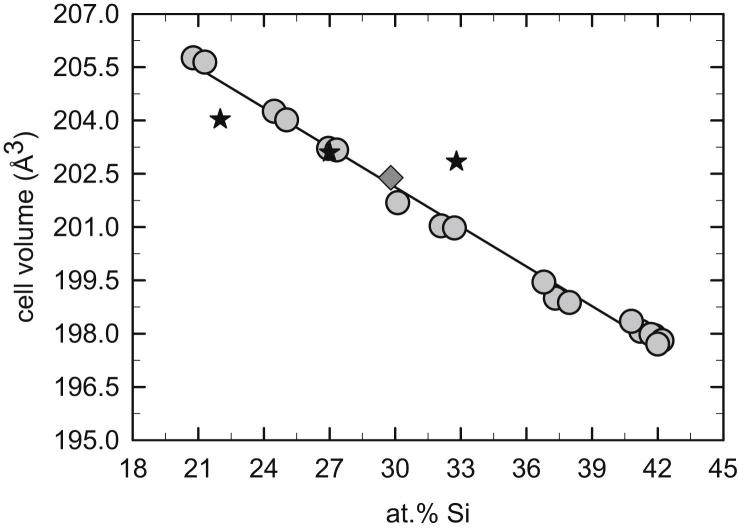
In 2001 Krendelsberger [35] established that the previously reported phases τ₁ (Al_21.5−45Fe_36.5−37.5Si_8.5−41.5) and τ₉ (Al₃₆Fe₃₆Si₂₈) are actually the same phase and she also confirmed a triclinic structure for τ₁/τ₉ (aP16, P$\overline{1}$, Al₂Fe₃Si₃-type). Bosselet et al. [36] came to the same conclusion. The identification of τ₁ by X-ray powder diffraction is especially demanding, because this phase combines a large homogeneity range with a low symmetry structure (space group P$\overline{1}$), so the XRD powder pattern changes drastically over the composition range. In fact, our initial attempts to index the observed patterns based on existing literature structure data [17], [19], [35] failed. Therefore a detailed study of lattice-parameter variation with the composition was performed. More than 15 samples prepared within the entire composition range of the phase were characterized by Rietveld refinement and combined with data from single-crystal lattice-parameter determination at a composition at 33 at.% Al and literature data from [35]. The single-crystal data for τ₁ determined in this study agree well with structural data published earlier [22], and were deposited in the Inorganic Crystal database of the FIZ Karlsruhe¹ under the depository number CSD 422342. In this way it was possible to accurately determine the course of lattice parameters with the composition for τ₁. A graphical representation of the lattice parameters of the triclinic unit cell a, b, c, α, β and γ as a function of composition is shown in Fig. 4. The parameters a and γ decrease with increasing Si-content while b, c, α and β increase. Fig. 5 shows the variation of the cell volume with the composition which is practically linear. The cell volume decreases with increasing Si-content, which is consistent with the substitution of the larger Al- by smaller Si-atoms. The respective covalent radii are 125 pm for Al and 117 pm for Si [37].

Fig. 4.

Unit-cell parameters of τ₁ phase (Al_2+xFe₃Si_3−x, aP16, P$\overline{1}$) shown as a function of the composition. Grey circles show results from powder XRD; dark grey diamond show data from single-crystal XRD; black stars representing literature data given in Ref. [35].

Fig. 5.

Cell volume τ₁ (Al_2+xFe₃Si_3−x) (aP16, P$\overline{1}$, Al₂Fe₃Si₃-type) shown as a function of the composition. Grey circles show results from powder XRD; dark grey diamond show data from single-crystal XRD; black stars representing literature data given in Ref. [35].

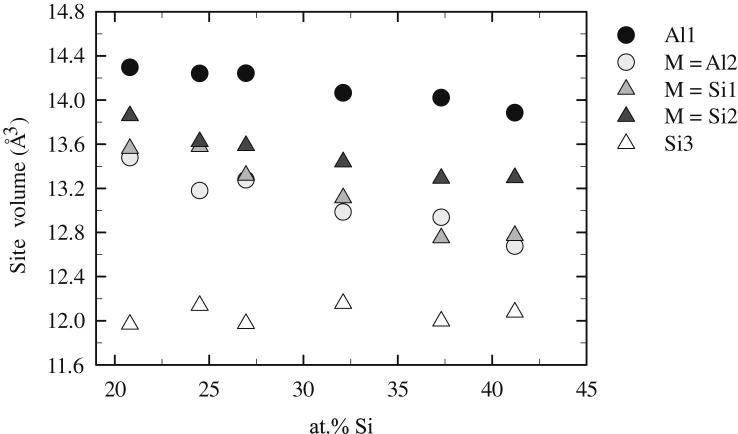
The phase τ₁ represents an unusual combination of broad homogeneity range with a very low symmetry crystal structure. The original structure determination describes the phase as Al₂Fe₃Si₃ [22] with two positions occupied by Al and three by Si-atoms, respectively. Given the homogeneity range from Al_21.0Fe_37.5Si_41.5 to Al_41.5Fe_37.5Si_21.0 the phase has to be described rather as Al_2+xFe₃Si_3−x with −0.3 < x < 1.3. It is clear, that Al and Si are sharing at least some of the positions by mixed occupation, but these mixed occupations cannot be determined directly by XRD due to the very similar scattering factors of Al and Si. In order to address this problem, the site volumes (volumes of the Wigner–Seitz cell) were calculated from our structural data as function of the composition using the program DIDO95 [38]. The graphical representation of the site volume change shown in Fig. 6 may be interpreted as follows: Position Al 1 (the largest) and Si 3 (the smallest) do not significantly change their size with composition, and are therefore regarded to be fully occupied by Al and Si. The other three positions (Al2, Si1, Si2) have intermediate site volume which changes with the composition. Therefore it can be concluded that mixing at Al and Si takes place mainly at these 3 positions and that the Al/Si ratio at these positions is varying with the composition.

Fig. 6.

Volume of the Wigner–Seitz cell (site volume) for the five Al/Si positions of the τ₁ phase (Al_2+xFe₃Si_3−x, aP16, P$\overline{1}$) shown as a function of the composition.

3.3. Solid state reactions involving HT-FeSi₂ (ζ_α, Fe₂Si₅) and LT-FeSi₂ (ζ_β)

In the binary Fe–Si system, two modifications of FeSi₂ are established. In the literature the terms α-FeSi₂, β-FeSi₂, ζ_α and ζ_β are not used systematically for these compounds, yielding some confusion. So HT and LT were used to designate the high- and low-temperature form in this work. The binary high-temperature phase is stable between 1220 °C (congruent melting) and 937 °C (eutectoid decomposition). The low-temperature form is stable up to 982 °C and decomposes in a peritectoid reaction. The high-temperature phase deviates from the stoichiometric composition, and has a tetragonal structure (tP3, P4/mmm) with about 13% Fe vacancies. The low-temperature phase has stoichiometric composition and crystallized in an orthorhombic structure type (oC48, Cmca). In their thermodynamic assessment of Al–Fe–Si, Anglézio et al. [39] allowed Al/Si substitution in HT-FeSi₂ and found this phase to be stable down to room temperature with a maximum solubility of about 6 at.% Al. According to the assessment of Guéneau et al. [40] the compound (Al,Si)_2.4Fe dissolves up to 10 at.% Al at room temperature. On the other hand, Krendelsberger et al. [19] did not find the high-temperature modification in the sample with composition Al₁₀Fe₄₀Si₅₀ at 550, 700 as well as at 800 °C. In contrast they found the three-phase field [(Si) + Fe₂Si₅ + τ₇] in a sample with the composition Al₂₀Fe₂₀Si₆₀ at 700 °C. At 800 °C they found the three-phase field [(Si) + Fe₂Si₅ + τ₈] at the composition Al₁₂Fe₂₃Si₆₅. Their conclusion is that the HT-modification is stabilized by Al in the ternary down to 700 °C.

In the present work a small solubility of 0.7 at.% Al was found in the orthorhombic LT-modification, whereas a solubility of up to 8.5 at.% Al was observed in the tetragonal HT-modification. Both modifications are found in equilibrium with each other in our ternary isothermal sections at 800 °C (Fig. 2) and 900 °C (Fig. 3). Thus, the tetragonal high temperature form of FeSi₂ is definitely stabilized to lower temperatures by the addition of Al. By systematic annealing experiments the stability of ternary HT-FeSi₂ was confirmed down to a temperature of 750 °C where the phase field [LT-FeSi₂ + HT-FeSi₂ + T8] was observed. Samples annealed below this (i.e. at 720 °C and 700 °C) did not show HT-FeSi₂ any more. At 720 °C the three-phase fields [LT-FeSi₂ + τ₁ + FeSi], [LT-FeSi₂ + τ₈ + τ₇] and [LT-FeSi₂ + τ₇ + (Si)] were found; at 700 °C [LT-FeSi₂ + τ₈ + τ₇] and [LT-FeSi₂ + τ₈ + FeSi] were found. These findings are not in agreement with the isothermal section at 727 °C given by Bosselet et al. [36], who proposed different phase equilibria at this temperature, but also confirmed that the high-temperature form is not longer present at this temperature.

Based on the current experimental results, a eutectoidic decomposition reaction E: HT-FeSi₂ = LT-FeSi₂ + (Si) + τ₈ at 720°C < T < 750 °C is proposed. This reaction and the reaction temperature are different to the eutectoid of HT-FeSi₂ = LT-FeSi₂ + (Si) + τ₇ between 600 °C and 700 °C which is suggested in Ref. [19]. A hypothetical but conclusive schematically representation of the reaction path based on our results is given in Fig. 7.

Fig. 7.

Reaction scheme of solid-state reactions involving the ternary solid solution of HT-FeSi₂.

3.4. Crystal structure of Al₃Fe₂Si (τ₁₂)

During the investigations of the exact homogeneity range and the lattice parameters of τ₁, a new, previously unknown powder pattern was observed at the Al-rich side of τ₁. In order to determine the exact composition of this phase, a couple of samples were prepared in the corresponding composition area. EPMA measurements and the X-ray powder diffraction refinement are consistent, as results of selected samples given in Table 2 show.

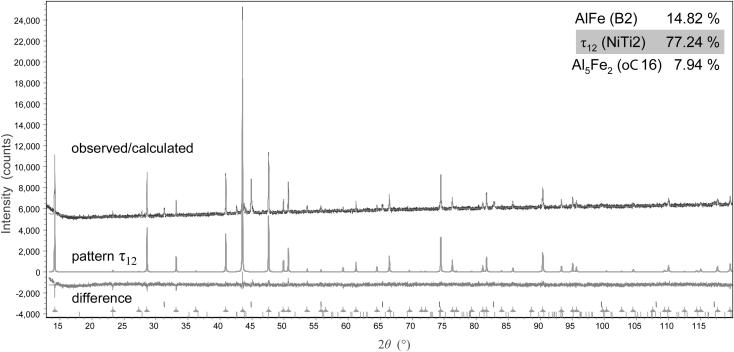
The diffractogram of sample #12 (Al₄₈Fe₃₇Si₁₅) annealed at 900 °C showing the three-phase field of [AlFe + Al₅Fe₂ + τ₁₂] and with τ₁₂ as the main phase is given in Fig. 8. The percentage of phases given in Fig. 8, correspond to the refined area of the powder pattern and are in good agreement with expectations from the lever rule. The microstructure of a sample Al₄₅Fe₄₀Si₁₅ representing the same phase field is given in a BSE image in Fig. 9. According to EPMA measurements, the phase τ₁₂ does not show a significant homogeneity range and the composition is approximately given by Al₄₈Fe₃₆Si₁₆.

Fig. 8.

X-ray diffractogram of sample #0.12 with the nominal composition Al₄₈Fe₃₇Si₁₅, showing the three phases AlFe, τ₁₂ and Al₅Fe₂. The calculated pattern of τ₁₂ and the difference curve are shown in the bottom of the graph.

Fig. 9.

BSE image of a sample with the nominal composition Al₄₅Fe₄₀Si₁₅, representing the three-phase field [AlFe + Al₅Fe₂ + τ₁₂].

For characterizing the thermal behaviour of the phase, a couple of samples were annealed at different temperature between 700 °C for more than 28 days and 1200 °C for 7 days. According to these annealing experiments τ₁₂ was found to be stable from about 720 to 1005 °C. At 1010 °C and above the pattern of this phase could not be observed anymore. Instead the three phases, AlFe, Al₅Fe₂ and τ₁ were found to be present in these samples. There is no indication for the formation of the liquid phase during the decomposition of τ₁₂. Additional experiments on primary crystallization confirmed these findings. A series of as cast samples in the composition area was investigated to find a possible primary crystallization field of τ₁₂. However, τ₁₂ was not found in any of the as cast samples, confirming its formation in a solid-state reaction. The reversibility of the formation/decomposition reaction of τ₁₂ was checked and confirmed by annealing experiments. Therefore our proposal for the formation of τ₁₂ is a peritectoid-type reaction at around 1005 °C [AlFe + Al₅Fe₂ + τ₁ → τ₁₂] and a eutectoid-type reaction at around 720 °C [τ₁₂ → AlFe + Al₅Fe₂ + τ₁].

As τ₁₂ does not crystallize directly from the melt, but is formed in a solid-state reaction, a long procedure was necessary to get a single crystal of suitable quality. Some crystals from a sample with the composition Al₄₈Fe₃₆Si₁₆ could be obtained after an annealing time of more than eight weeks. The crystal structure of τ₁₂ was determined from a small crystal chip. Data collection was performed based on trigonal symmetry. The crystal structure was solved by direct methods [32]. During refinement successively it turned out that the actual symmetry is cubic, space group Fd$\overline{3}$m (Pearson symbol cF96), and belongs to the NiTi₂-type structure. The crystal was twinned; the twin plane is (112). During final refinement based on cubic symmetry, the twin components were obtained as 0.232:0.767(2). Details on data collection and structure refinement are given in Table 4, Table 5, and that of final interatomic bond distances in Table 6. Further details of the crystal structure investigation can be obtained from the Fachinformationszentrum Karlsruhe on quoting the depository number CSD 422341.

Table 4.

Single crystal data collection and structure refinements of τ₁₂.

Empirical formula	Al3Fe2Si
Z	16
Crystal system, Space group	Fd$\overline{3}$m
Structure type	NiTi2
Cell parameter (Å)	10.806(2)
Cell volume (Å3)	1261.8(6)
Crystal dimensions (μm)	20 × 40 × 50
2 θ range for data collection (°)	3–70
Reflections collected/unique	1790/1201
Extinction coefficient	0.0002(2)
R1 = Σ(||Fo| − |Fc||)/ΣFo (164 merged reflections)	0.042
wR2 = ${\left[\sum w{\left(F_o^2-F_c^2\right)}^2/\sum |w\left(F_o^4\right)\right]}^{1/2}$	0.061
Final difference Fourier map/eÅ−3	−0.92 to +1.09

Table 5.

Fractional atomic coordinates and displacement parameters of Al₃Fe₂Si (τ₁₂)

Position	Wykoff symbol	Fractional coordination			Displacement parameters
		x	y	z	U11	U22	U33	U23	U13	U12	Uequiv.
Fe	32	0.21402(3)	= x	= x	0.0092(2)	= U11	= U11	0.0005(1)	= U23	= U23	0.0092(2)
Al	48	0.42756(9)	1/8	1/8	0.0075(5)	0.0070(3)	= U22	0.0011(3)	0	0	0.0072(2)
Si	16	0	0	0	0.0089(3)	= U11	= U11	0.0015(3)	= U23	= U23	0.0089(3)

The anisotropic displacement parameters are defined as: $\exp \left[-2{\pi }^2{\sum }_{i=1}^3{\sum }_{j=1}^3{U}_{ij}{a}_i^{\ast }{a}_j^{\ast }{h}_i{h}_j\right]$.

Table 6.

Interatomic bond lengths (Å) of Al₃Fe₂Si (τ₁₂).

Al–Fe	2.4915(8), 2×	Fe–Si	2.3771(9), 3×	Si–Fe	2.3771(9), 6×
Al–Fe	2.6787(11), 2×	Fe–Al	2.4915(8), 3×	Si–Al	2.7075(10), 6×
Al–Si	2.7075(10), 2×	Fe–Al	2.6787(11), 3×
Al–Al	2.8184(11), 4×	Fe–Fe	2.7207(9), 3×
Al–Al	3.0172(16), 4×

The NiTi₂-type was found to exist in several binary systems and also in some ternary systems like e.g. Mn₃Ni₂Si, Ni₂SiV₃, Nb₃Ni₂Si, Ni₂SiTa₃, Ni₂SiZn₃, GeNi₂Zn₃ or Co₂Nb₃Si [41]. The basic structure contains 96 atoms per unit cell; the three independent positions Ti1, Ni and Ti2 exhibit multiplicities of 16, 32 and 48; i.e. in the ratio 1:2:3. Ni and Ti1 sites are icosahedrally coordinated, while the site Ti2 has fourteen neighbours. In τ₁₂, Si occupies the Ti1 site, Al the Ti2 and Fe the Ni site.

The ideal composition of τ₁₂ based on the crystal structure is therefore Al₃Fe₂Si; i.e. 50 at.% Al, 33.3 at.% Fe and 16.7 at.% Si. This deviates slightly from the real composition of the phase as determined by EPMA which is 48 at.% Al, 36 at.% Fe and 16 at.% Si. It is not completely clear what mechanism is responsible for this shift towards the Fe-rich side. The most significant mechanism of nonstoichiometry of the different phases in the system Al–Fe–Si is the Al/Si substitution. This is reflected in the usual extension of ternary phases which show fixed Fe composition but often variable Al/Si ratio (compare Fig. 2, Fig. 3). This mechanism is obviously not responsible for the composition shift in this case. It is not possible to constitute conclusive evidence on this issue with the information from Rietveld refinement, and the single-crystal structure refinement using different models of substitution mechanism and vacancies mechanism are not unambiguous.

Some authors report on the possible stabilization of the NiTi₂-type structure by heteroatoms like oxygen [42]. There are strong indications that this is not the case for τ₁₂. Firstly the phase can be completely decomposed and formed again by annealing in the proper temperature range, and secondly, not any significant residual electron density could be found in the single-crystal refinement (compare Table 4). Therefore it can be concluded that τ₁₂ is not stabilized by oxygen, but is a true ternary compound.

3.5. Vertical sections

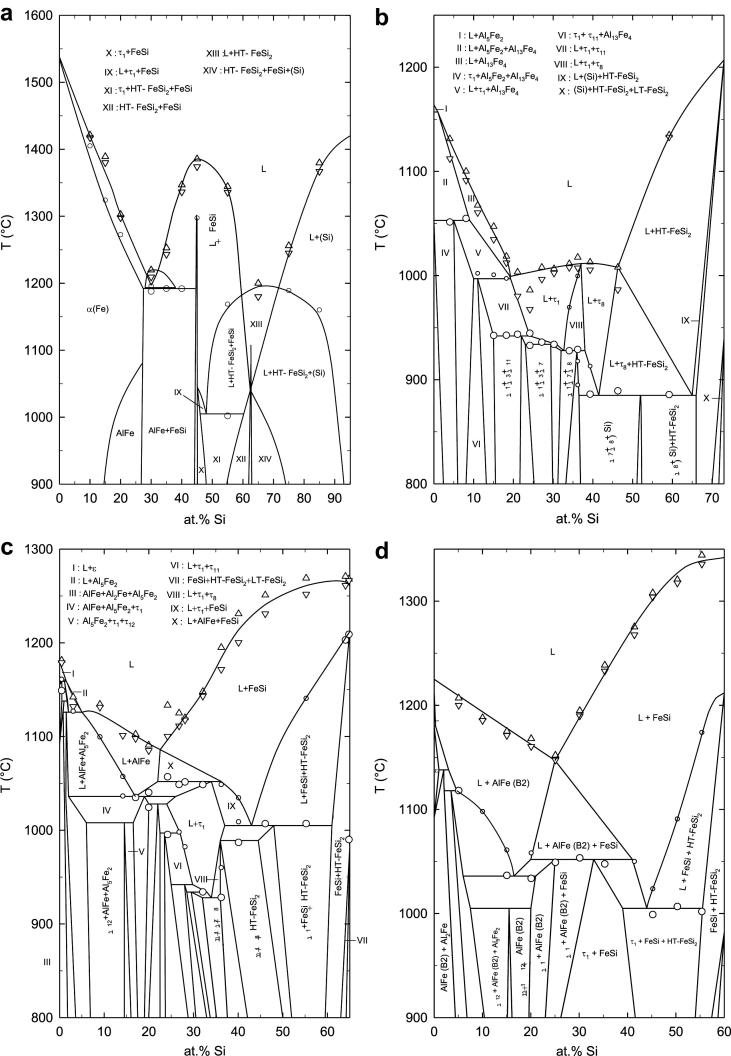
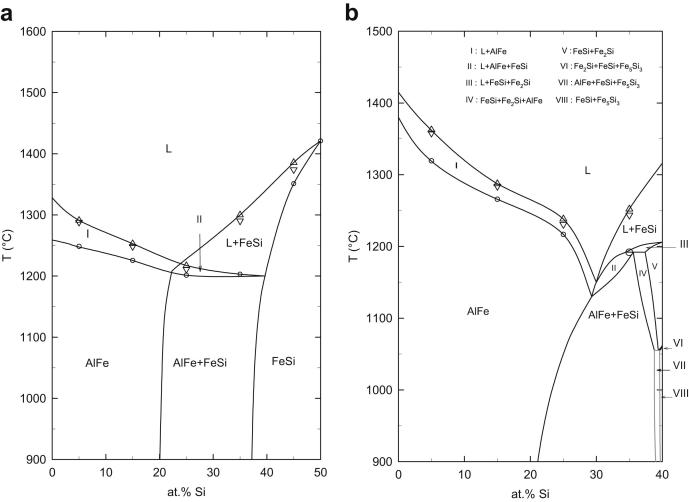
The ternary phase reactions in the system Al–Fe–Si were studied by DTA analysis of samples situated in six different vertical sections at 5 at.% Al and at constant Fe contents of 27, 35, 40, 50 and 60 at.%. Two heating- and cooling-cycles were performed in each measurement. The starting temperature was 800 and 900 °C i.e. the respective annealing temperature of the samples. The maximum temperature reached in these experiments was 1450 °C. The results of thermal analyses are shown in Fig. 10, Fig. 11. The experimental data points for thermal effects shown in Fig. 10, Fig. 11 (large and small circles) represent mainly DTA results obtained on first heating of the annealed samples. The liquidus values (triangles) were evaluated from heating- and cooling-curves, respectively. These figures contain our experimental data points and the evaluated phase equilibria. The reaction scheme from Krendelsberger et al. [19] was used as input for interpretation. The phase boundaries were adapted according to our own experimental data (phase compositions) determined in the two isothermal sections at 800 °C and 900 °C. Generally, the phase reactions observed in this study are in good agreement with the reaction scheme and the liquidus surface given in Ref. [19], although some changes of phase boundaries were necessary to fit our experimental results.

Fig. 10.

Vertical sections of Al–Fe–Si at (a) 5 at.% Al, (b) 27 at.% Fe, (c) 35 at.% Fe and (d) 40 at.% Fe. Experimental data from DTA experiments are shown as circles (invariant thermal effects), small circles (non-invariant thermal effects), triangles up (liquidus on heating) and triangles down (liquidus on cooling).

Fig. 11.

Vertical sections of Al–Fe–Si at (a) 50 and (b) 60 at.% Fe. Experimental data from DTA experiments are shown as circles (invariant thermal effects), small circles (non-invariant thermal effects), triangles up (liquidus on heating) and triangles down (liquidus on cooling).

As already discussed in the previous sections, the presence of LT-FeSi₂ and HT-FeSi₂ was observed, while [16], [20] reported only about the existence of LT-FeSi₂ at 800 °C. In the area of τ₁ and the additional ternary phase τ₁₂, the new three-phase fields [AlFe + τ₁ + τ₁₂] and [AlFe + Al₅Fe₂ + τ₁₂] were detected. These facts are included in the corresponding vertical sections shown in Fig. 10, Fig. 11.

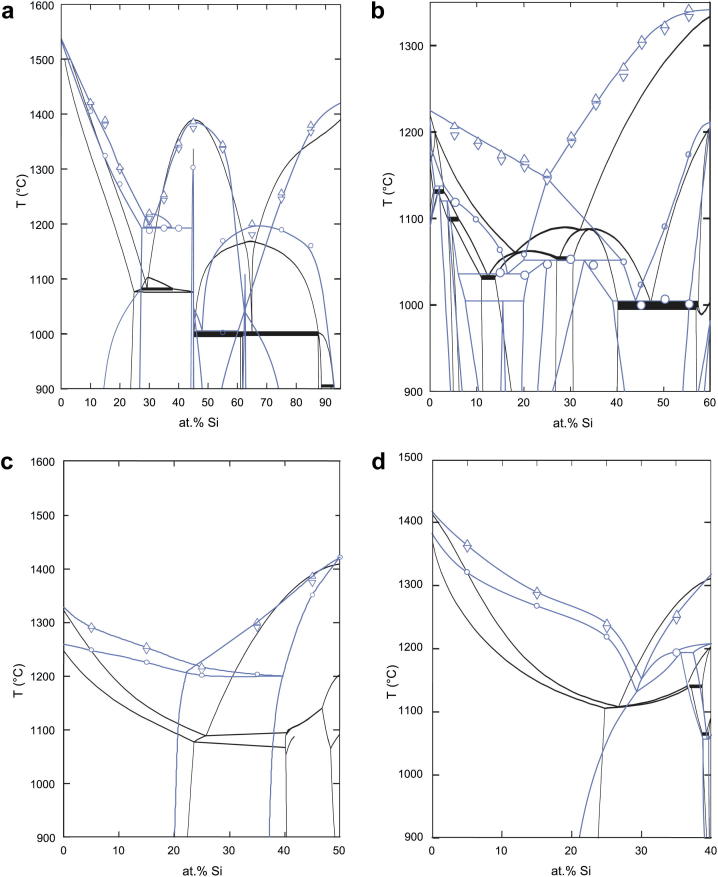
The situation of the liquidus valleys found in the various sections in Fig. 10, Fig. 11 match reasonably well with the liquidus projection given in Ref. [19]. For the liquidus curves and liquidus valleys a trend to significantly higher temperature could be observed in the isopleths at 40, 50 and 60 at.% Fe in this work compared to the vertical sections calculated by Du et al. [20]. Due to our results in the FeSi₂ area, the vertical section at 5 at.% Al deviates in terms of some additional phase fields. A comparison of our experimental results with the sections at 5 at.% Al and at 40, 50, 60 at.% Fe calculated with the thermodynamic model of Du et al. [20] is shown in Fig. 12. Given the significant differences of the liquidus lines, a re-assessment of this phase diagram appears to be necessary. A full list of thermal effects observed by DTA in our study is provided as supplementary material.

Fig. 12.

Comparison of vertical sections in Al–Fe–Si at (a) 5 at.% Al, (b) 40 at.% Fe, (c) 50 at.% Fe and (d) 60 at.% Fe. Black lines: calculated isopleths according to Du et al. [20], [34]; blue: isopleths and experimental data according to the current study. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

During the current investigation, also some binary Fe–Si samples were prepared in order to check consistency with the literature phase diagram given by Ref. [8]. These data are included in Fig. 10 (b) and 10 (c). In case of the congruent melting point of FeSi a slight difference to the literature value is found: according to our DTA results this value is 1421 °C while the assessed phase diagram [1] gives 1410 °C.

4. Summary

The system Al–Fe–Si was reinvestigated for two isothermal sections and six vertical sections. In the course of the work, lattice parameters of triclinic τ₁ were described as a function of composition and a new high-temperature phase τ₁₂ (NiTi₂-type) was observed. The new phase was found to be stable between 720 °C and 1005 °C. Solid-state reactions involving the ternary solid solution of HT-FeSi₂ were studied and a corresponding reaction scheme was developed. Liquidus values observed in the iron-rich part of the phase diagram deviate considerably from a recent thermodynamic assessment of the system.

Appendix. Supplementary data

The following are the supplementary data related to this article: