Abstract
“Language is a form and not a substance”
— Ferdinand de Saussure Objective: Analyses of speech processes in schizophrenia are invariably focused on words as vocal signals. The results of such analyses are, however, strongly related to content, and may be language- and culture-dependent. Little attention has been paid to a pure measure of the form of speech, unrelated to its content: inter-words time intervals. Method: 15 patients with schizophrenia and 15 healthy volunteers are recorded spontaneously speaking for 10–15 min. Recordings are analyzed for inter-words time intervals using the following non-linear dynamical methods: unstable periodic orbits, correlation dimension, bi-spectral analysis, and symbolic dynamics. Results: The series of inter-word time intervals in normal speech have the characteristics of a low-dimensional chaotic attractor with a correlation dimension of 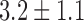 . Deconstruction of the attractor appears in psychosis with re-establishment after anti-psychotic treatment. Shannon entropy, a measure of the complexity in the time series, calculated from symbolic dynamics, is higher for psychotic speech, which is also characterized by higher levels of phase coupling: higher bicoherence, obtained using bi-spectral analysis. Conclusion: Non-linear dynamical methods applied to ITIs thus enable a content-independent, pure measure of the form of normal thought, its distortion in psychosis, and its restoration under treatment.
. Deconstruction of the attractor appears in psychosis with re-establishment after anti-psychotic treatment. Shannon entropy, a measure of the complexity in the time series, calculated from symbolic dynamics, is higher for psychotic speech, which is also characterized by higher levels of phase coupling: higher bicoherence, obtained using bi-spectral analysis. Conclusion: Non-linear dynamical methods applied to ITIs thus enable a content-independent, pure measure of the form of normal thought, its distortion in psychosis, and its restoration under treatment.
Keywords: Schizophrenia, speech form, psychotic speech, inter-words time intervals (ITIs), nonlinear dynamics, cognitive neuroscience
I. Introduction
In 1911 bleuler gave pre-eminence to formal thought disorder: Bleuler's ‘four As’, as primary symptoms of schizophrenia. Critical to the theoretical complexity of Bleuler's approach, Schneider introduced the concept of ‘first-rank’ symptoms that are related to thoughts' content. The popularity of easy recognizable, ‘content-related’ symptoms as a diagnostic tool may represent a drawback, since these symptoms can be feigned or concealed by patients as easily as they can be recognized by clinicians.
Clinical evaluations and diagnoses that are related to “content” may be language and culture dependent. Thus, African Americans were diagnosed to have a schizophrenic spectrum disorder more frequently than did Latinos and European Americans and present more commonly with first-rank symptoms [1] even when a semi-structured instruments and defined DSM criteria were used. The findings underscore the importance of clinical judgment within the context of cross-race and cross-ethnic diagnosis [2].
Formal thought disorders are difficult to assess and quantify. To overcome some of the limitations of Bleuler's approach, various instruments for assessing formal thought disorder were developed: Thought, Language, and Communication Scale [3]; Thought Disorder Index; Thought and Language Index [4]. These procedures are time-consuming for routine clinical use and require extensive training.
One of Bleuler's primary symptoms of schizophrenia related to formal thought disorder is altered affect. Non-verbal aspects of language such as rate and rhythm, which are regarded as a distinct neuropsychological function, called “prosody” , are commonly divided into affective and non-affective prosody. While affective prosody, which is necessary for establishing emotional “rapport” , is highly lateralized to the right hemisphere, non-affective prosody, which mainly serves a function in removing syntactic ambiguities and in clarifying the general interactive character of a sentence, is not lateralized [5]. Spontaneous prosody assessment by the Prosody Abnormality Score [5], as well as prosodic comprehension and prosodic repetition, is highly dependent on subjective evaluation by the rater.
Inter-words time intervals (ITIs) are a feature of speech prosody, a ‘formal’ characteristic of speech. ITIs can be measured objectively. Analyses of speech processes in schizophrenia have invariably focused on words as vocal signals. Only few studies have examined speech ITIs in schizophrenia. Pauses duration in patients with schizophrenia of predominantly negative symptoms was correlated with flat affect and alogia [6]. Context dependency of pauses was found in healthy subjects and schizophrenic patients without thought disorder, but not in thought-disordered patients with schizophrenia [7]. These linear methods used to quantify pauses in schizophrenia can give only limited information concerning the dynamical system underlying the phenomenon of pausing. As speech is generated by a complex time-varying physical dynamical system, even at the level of the vocal folds [8]–[10], the analysis of speech ITIs using non-linear dynamical methods can give more information and better understanding of the phenomenon of speech pausing in schizophrenia.
Linear dynamical systems are characterized by changes in input that result in proportional changes to the output. In contrast, in nonlinear dynamics, due to the phenomena of bifurcations, changes in input can result in seemingly unpredictable but rule-based large or small changes to the output. A unique character of nonlinear dynamics is its sensitivity to initial conditions: two initial observations that differ by a small amount lead to strikingly different sequences of observations in space and time (trajectories) and different final states [11], [12]. Through an universally ordered transition [13] successive bifurcations lead from order to an irregular and unpredictable time evolution of deterministic nonlinear systems designated chaos [11], [12]. A chaotic system is characterized by a trajectory that, while predictable and lawful, may appear random often with extreme sensitivity to initial conditions [11], [12]. The coherent sequence of observations to which a system evolves over time is called an attractor [12]. Dynamical systems, that exhibit chaotic behavior, are often characterized by strange attractors [14]. A quantitative method that has been proposed to characterize the geometry of attractors is the dimension: simple attractors are associated with integral dimension. In contrast, strange attractors are characterized by fractal dimensions.
Advances in nonlinear dynamics have provided techniques that enable researchers to quantify dysregulated dynamical patterns in psychiatry [15]–[17]. The application of nonlinear methods suggest that schizophrenia is characterized by altered sequential or temporal architecture, in which complex nonlinear phenomena alternate with random events in molecular to molar levels [17]. In “choice task” studies undertaken in order to understand the sequential structure of self-generated behavioral patterns, patients with schizophrenia showed an intermittency pattern of fixed and random choice sequences [18], [19]. Similar changes were described in sequential and temporal architecture of the clinical course of symptoms in schizophrenia and bipolar disorder [20]. Though nonlinear dynamic methods were applied in research work on various behavioral phenomena in schizophrenia, such methods have not yet been applied for the analysis of thought/speech in schizophrenia.
In the present study we show that the neglected time series of ITIs in human communication is not random, but contains inherent information. Non-linear dynamical methods applied to ITIs enable a content-independent, pure measure of the form of normal thought, its distortion in psychosis, and its restoration under treatment.
II. Methods
Patients: All patients were diagnosed according to DSM-IV criteria using SCID (DSM-IV). Inclusion criteria were normal results of physical examination, electrocardiogram, and laboratory tests for renal, hepatic, hematological, and thyroid function. The study was approved by the Institutional Review Board and has therefore been performed in accordance with the ethical standards laid down in the 1964 Declaration of Helsinki. After complete description of the study to the subjects, all persons gave their informed consent prior to their inclusion in the study.
The group of 15 (11 males) physically healthy hospitalized psychotic patients, age 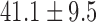 (25–55), were diagnosed as suffering from schizophrenia or schizoaffective disorder. Patients were symptomatic as assessed by PANSS (
(25–55), were diagnosed as suffering from schizophrenia or schizoaffective disorder. Patients were symptomatic as assessed by PANSS (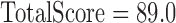 ,
, 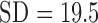 ;
; 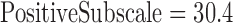 ,
, 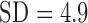 ;
; 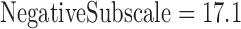 ,
, 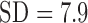 ). Patients were examined upon admission before initiation of psychopharmacological treatment. It was verified that no treatment was given during one month (two months in case of depot antipsychotics) prior to referral. None of the patients were prevented medication for a period longer than several hours needed to complete structured interview and recordings. The patients were not necessarily symptomatic for a whole month before being admitted to treatment. Same patients were then examined after at least 4 weeks of antipsychotic treatment (equivalents of haloperidol 5–10 mg/day). The group of 15 (11 males) healthy volunteers, age
). Patients were examined upon admission before initiation of psychopharmacological treatment. It was verified that no treatment was given during one month (two months in case of depot antipsychotics) prior to referral. None of the patients were prevented medication for a period longer than several hours needed to complete structured interview and recordings. The patients were not necessarily symptomatic for a whole month before being admitted to treatment. Same patients were then examined after at least 4 weeks of antipsychotic treatment (equivalents of haloperidol 5–10 mg/day). The group of 15 (11 males) healthy volunteers, age 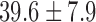 (26–56) years were recruited from the staff and students of Ben-Gurion University.
(26–56) years were recruited from the staff and students of Ben-Gurion University.
Subjects were recorded while freely speaking for 10–15 minutes. Recorded speech was analyzed for the series of ITIs. The non-linear dynamical methods used to analyze ITIs included the followings:
Unstable Periodic Orbits (UPOs): UPO is an orbit that repeats itself after a period, and is unstable [21]. In this method encounters with UPOs are searched for and compared to the number of events found in a surrogate [22]. ITIs of normal and psychotic subjects were searched for the number of UPOs, 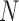 , within 100 successive ITIs. The process was repeated in 100 surrogate records, constructed using 100 different realizations of the randomization process.
, within 100 successive ITIs. The process was repeated in 100 surrogate records, constructed using 100 different realizations of the randomization process. 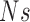 is the average number of UPOs within 100 ITIs in the surrogate records. A measure of significance is defined by:
is the average number of UPOs within 100 ITIs in the surrogate records. A measure of significance is defined by:
-
(1)
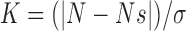
where 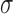 is the standard deviation of the surrogate values.
is the standard deviation of the surrogate values.
Assuming Gaussian statistics the p value is given by:
-
(1)
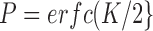 .
.
Correlation Dimension: A strange attractor in m-dimensional space can be constructed from a single component time series by forming an n-dimensional vector [23]
-
(1)
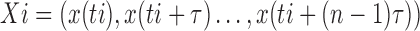
where 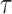 is the delay constant.
is the delay constant.
Grassberger and Procaccia [24] proposed a simple method to obtain the correlation dimension. They defined the correlation integral, C(r, n), as
-
(1)
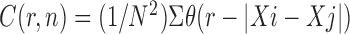 ,
, 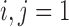
where N is the total number of data points, 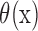 is the Heaviside step function, which is defined as
is the Heaviside step function, which is defined as
-
(1)
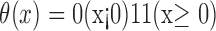
and Xi and Xj are reconstructed vectors as shown in Equation 3.
The main finding of Grassberger and Procaccia is that C(r, n) behaves as a power of r for small r:
-
(1)
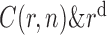
d is the correlation dimension of the attractor for that n.
Thus for an n-dimensional phase space, a ‘cloud’ of points is generated in which the number of pairs, C(r, n), with distances 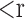 are found. If for significantly small r C(r, n) is proportional to
are found. If for significantly small r C(r, n) is proportional to 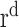 , equation 6 can be tested for increasing n, the embedding dimension of the phase space. If the value of d reaches a saturation value, ds, the system represented by the time series should possess an attractor with a dimension ds; otherwise the time series is random or of higher dimensions.
, equation 6 can be tested for increasing n, the embedding dimension of the phase space. If the value of d reaches a saturation value, ds, the system represented by the time series should possess an attractor with a dimension ds; otherwise the time series is random or of higher dimensions.
Bi-Spectral Analysis: in order to characterize the degree of phase coupling in the signal, it is necessary to use a signal processing technique called bi-spectral analysis [25]. The bi-spectrum, 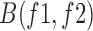 , is computed as the triple product:
, is computed as the triple product:
-
(1)
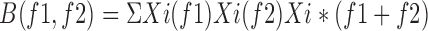
for each pair 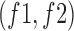 of Fourier frequency components, where
of Fourier frequency components, where 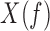 represents the Fourier transform of the sampled input signal and
represents the Fourier transform of the sampled input signal and 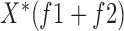 indicates the conjugate of
indicates the conjugate of 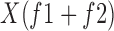 . The resulting bi-spectrum, which is sensitive to the phase coupling, is normalized to the real triple product,
. The resulting bi-spectrum, which is sensitive to the phase coupling, is normalized to the real triple product, 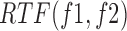 , the triple product with perfect phase coupling to yield the Bicoherence function
, the triple product with perfect phase coupling to yield the Bicoherence function  .
.
-
(1)
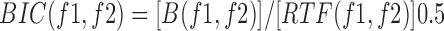
The BIC function' values move within the interval 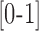 . When BIC values are near 1 there is a high level of phase coupling [25].
. When BIC values are near 1 there is a high level of phase coupling [25].
Symbolic Dynamics: The concept of symbolic dynamics (Hao 1991) is based on coarse-graining of the dynamics. ITIs are transformed into symbol sequences. A set of predetermined ranges of measured values is defined and identified with a set of corresponding symbols. Any measured value that falls in a predetermined range is transformed to a symbol. The data is analyzed by seeking different symbol patterns. By comparing different kinds of such transformations, we found that the use of four symbols was appropriate for our purpose, and investigated the probability distribution of length 3 words. The Shannon entropy: 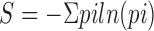 , where
, where 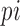 is the probability of the
is the probability of the 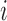 -th state, calculated from the distribution of selective words is a suitable measure of the complexity in the time series [26].
-th state, calculated from the distribution of selective words is a suitable measure of the complexity in the time series [26].
Statistical Analysis: The Chi-Square Test was used to compare rates of saturation of the Correlation Integral as well as Proportions of Double Circulatory Forms between the two groups of healthy and psychotic subjects.
The Mann-Whitney U-test was used to compare values for Shannon Entropy and BIC between the two groups of subjects.
III. Results
Fig. 1(a) and (b) depicts representative plots of ITIs recorded from a healthy subject and a psychotic patient. Linear methods of analysis: average ITIs length, power spectrum, Auto Regressive Integration Moving Average (ARYMA) models, could not detect significant differences in the ITIs vector between the two groups of subjects (not shown).
Fig. 1.
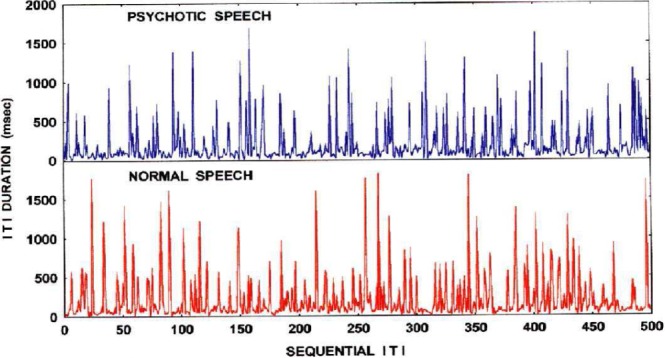
Representative series of ITIs in a normal subject and a psychotic patient.
70% of ITIs, in normal as well as psychotic subjects showed statistically significant more encounters with UPOs in the original data than their surrogates (Table I). These findings characterize low-dimensional dynamics in ITIs of normal and psychotic speech.
Table I. Non-Linear Dynamics of Inter-Words Time Intervals in Normal and Psychotic Speech.
| Normal Subjects | Untreated Psychotic Patients | Patients treated with Antipsychotics | |
|---|---|---|---|
| Significant UPOs over surrogate files | 67% | 67% | 60% |
| K values | 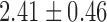 |
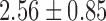 |
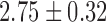 |
| Saturation of the correlation integral | 87% | 7%a | 100% |
| Correlation dimension | 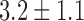 |
No saturation | 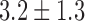 |
| Shannon entropy | 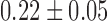 |
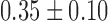 b b
|
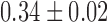 |
| Bi-spectral analysis Double Circulatory Forms | 6.7% | 80.0%c | 25.0% |
| Bi-spectral analysis BIC-values | 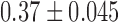 |
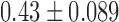 d d
|
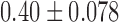 |
Significantly different from normal group, 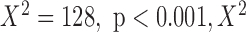 test.
test.
Significantly different from normal group, 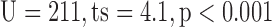 Mann-Whitney U-test.
Mann-Whitney U-test.
Significantly different from normal group, 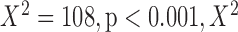 test.
test.
Significantly different from normal group, 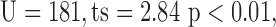 Mann-Whitney U-test.
Mann-Whitney U-test.
Fig. 2(a) is a representative plot of the correlation integral as function of the embedding dimension for ITIs of a normal subject. As 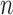 was increased
was increased  approached a saturation value,
approached a saturation value, 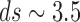 . A surrogate record resulted in a non-saturable curve of
. A surrogate record resulted in a non-saturable curve of 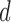 , fitting a random set (Fig. 2(a)). A representative ITIs record of a psychotic patient showed a continuously increasing non-saturable plot of the correlation integral as function of the embedding dimension (Fig. 2(b)). A surrogate record was similar to the original plot (Fig. 2(b)).
, fitting a random set (Fig. 2(a)). A representative ITIs record of a psychotic patient showed a continuously increasing non-saturable plot of the correlation integral as function of the embedding dimension (Fig. 2(b)). A surrogate record was similar to the original plot (Fig. 2(b)).
Fig. 2.
The correlation integral for the series of inter-words time intervals as function of the embedding dimension. A representative plot of the correlation integral 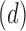 as function of the embedding dimension
as function of the embedding dimension 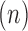 for ITIs of a normal (A) and a psychotic (B) subject. Closed circles represent original files. Open circles represent surrogate files.
for ITIs of a normal (A) and a psychotic (B) subject. Closed circles represent original files. Open circles represent surrogate files.
A group of normal subjects analyzed for the dynamics of their ITIs showed characteristics of a low-dimensional chaotic attractor with 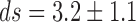 (Table I). Their surrogate files resulted in non-saturable plots (Table I). In contrast, in the group of psychotic patients, both the original and the surrogate ITIs records yielded non-saturable plots for the correlation integral as function of the embedding dimension (Table I). ITIs of psychotic patients under anti-psychotic treatment regained the low dimensional attractor with a normal-like correlation dimension (Table I). Unlike the dynamic behavior of the ITIs, the time vector of the words themselves both in normal and in psychotic subjects was characterized by non-saturable plots of the correlation integral as function of the embedding dimension.
(Table I). Their surrogate files resulted in non-saturable plots (Table I). In contrast, in the group of psychotic patients, both the original and the surrogate ITIs records yielded non-saturable plots for the correlation integral as function of the embedding dimension (Table I). ITIs of psychotic patients under anti-psychotic treatment regained the low dimensional attractor with a normal-like correlation dimension (Table I). Unlike the dynamic behavior of the ITIs, the time vector of the words themselves both in normal and in psychotic subjects was characterized by non-saturable plots of the correlation integral as function of the embedding dimension.
Significantly higher values were observed for Shannon entropy in psychotic in comparison with normal speech (0.35, 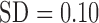 and 0.22,
and 0.22, 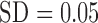 , respectively;
, respectively; 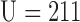 ,
, 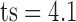 ,
, 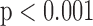 , Mann-Whitney U-test) (Table I). Shannon entropy values of the patients group significantly correlated with PANSS positive subscale (Spearman's
, Mann-Whitney U-test) (Table I). Shannon entropy values of the patients group significantly correlated with PANSS positive subscale (Spearman's 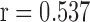 ,
, 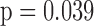 ), with no correlation with total PANSS
), with no correlation with total PANSS 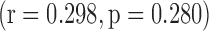 , or PANSS negative subscale
, or PANSS negative subscale 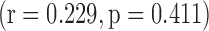 .
.
Bi-spectral analysis resulted in elevated BIC values for the speech of the psychotic patients (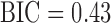 ,
, 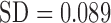 ,
, 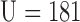 ,
, 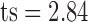 ,
, 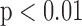 , Mann-Whitney U-test) in comparison with healthy volunteers
, Mann-Whitney U-test) in comparison with healthy volunteers 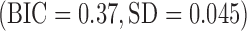 (Table I). The elevated BIC values were significantly correlated with the severity of the psychotic symptoms, assessed by total PANSS (Spearman's
(Table I). The elevated BIC values were significantly correlated with the severity of the psychotic symptoms, assessed by total PANSS (Spearman's 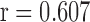 ,
, 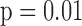 ), by PANSS negative sub-scale
), by PANSS negative sub-scale 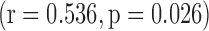 , but not by PANSS positive sub-scale
, but not by PANSS positive sub-scale 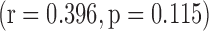 .
.
Fig. 3(a) and (b) depicts three-dimensional contour graphs, showing the normalized bi-spectral product of ITIs of normal and psychotic subjects, respectively, as function of  and
and  . The contours are different in structure with double circulatory forms in the psychotic patient (Fig. 3(b)) but no such circles in the normal subject (Fig. 3(a)). While ITIs series of psychotic patients presented double circulatory, “mountain-like”
forms in 80% of the cases, ITIs series of normal subjects and of anti-psychotic-treated patients presented “plain-like”
forms in more than 90% of the cases (Table I).
. The contours are different in structure with double circulatory forms in the psychotic patient (Fig. 3(b)) but no such circles in the normal subject (Fig. 3(a)). While ITIs series of psychotic patients presented double circulatory, “mountain-like”
forms in 80% of the cases, ITIs series of normal subjects and of anti-psychotic-treated patients presented “plain-like”
forms in more than 90% of the cases (Table I).
Fig. 3.
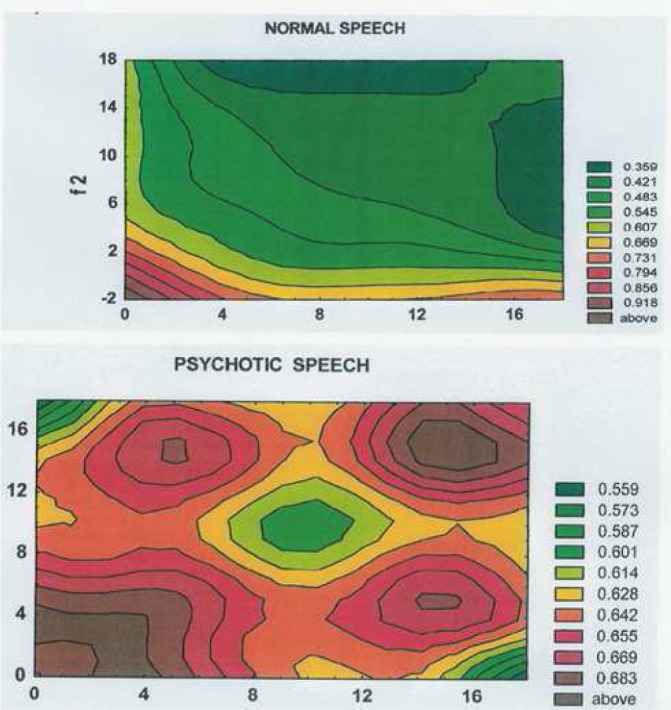
Representative contour plots of normalized bi-spectral triple product of normal and psychotic ITIs as function of two frequency variables. The contours are totally different in structure with double circulatory forms in the psychotic patient (B) with no such circles in the normal subject (A). The values that appear to the side of the figure reflect ranges of BIC values. A special color is adapted to each range of BIC values. The BIC function's values are pure numbers that move within the interval 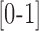 . When the value is near 0 there is no phase coupling. When BIC values are near 1 there is a high level of phase coupling. The BIC function is three dimensional. It is represented as a contour map. A special color is adapted to each range of BIC values. The contour graph connects similar colors, similar BIC values, by lines to form a topographical-like map.
. When the value is near 0 there is no phase coupling. When BIC values are near 1 there is a high level of phase coupling. The BIC function is three dimensional. It is represented as a contour map. A special color is adapted to each range of BIC values. The contour graph connects similar colors, similar BIC values, by lines to form a topographical-like map.
IV. Discussion
A major finding of the present study is the characterization of a low dimensional chaotic attractor in the form of speech of normal subjects. The calculated correlation dimension of 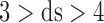 suggests that the mental dynamic system underlying the formation of speech is characterized by a minimum of four degrees of freedom in healthy subjects. ITIs measurement is important since it describes a pure content-independent measure of the form of speech.
suggests that the mental dynamic system underlying the formation of speech is characterized by a minimum of four degrees of freedom in healthy subjects. ITIs measurement is important since it describes a pure content-independent measure of the form of speech.
In order to calculate the correlation dimension it is usually supposed that a large number of vector points are needed [24]. However, in several cases, the dimension was calculated from a relatively small number of vector points [27]–[29]. Estimations of the minimal number of vector points needed for dimension calculations [30], [31] suggest that in vectors of around 500 points a reliable result for the correlation dimension requires 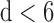 . Our determination of the correlation dimension, based on sequences of about 600 vector points, thus seems acceptable due to the following facts: (I) Saturation of the correlation integral was reached at
. Our determination of the correlation dimension, based on sequences of about 600 vector points, thus seems acceptable due to the following facts: (I) Saturation of the correlation integral was reached at 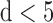 (600 vector points), and was demolished in surrogate files; (II) Smaller number of data points resulted in similar outcome for the correlation dimension.
(600 vector points), and was demolished in surrogate files; (II) Smaller number of data points resulted in similar outcome for the correlation dimension.
Another major finding of the present study is the deconstruction of the attractor in psychotic speech. ITIs test proves a pure measure of the disruption of psychotic form of thought that is independent of speech content, thus being language and culture independent. Though the correlation integral of ITIs in psychotic speech did not reach a saturation value, it should not be considered random as low-dimensional dynamics was proven through the UPOs assay. The non-saturability of the correlation integral in psychotic speech may be related to the existence of a correlation dimension of a higher order, 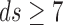 , which is beyond our accurate detection abilities of the present study.
, which is beyond our accurate detection abilities of the present study.
The fact that several altered non-linear parameters in untreated patients with schizophrenia were normalized by antipsychotic treatment (Table I) suggests that these methods might potentially serve to objectively monitor therapeutic effects of antipsychotic treatments. Future studies addressing the dynamics of normalization of these non-linear parameters in comparison with the dynamics of clinical improvement may reveal whether these methods can also predict clinical response.
The manifestations of formal thought disorder depend on the form and content of the clinical interview [4]. Substantial evidence indicates that formal thought disorder reflects abnormalities in the executive control of language [32]. The degree to which executive control is required depends on the extent to which the speaker is responsible for determining the content of the spoken output. An assessment of formal thought disorder should, therefore, be performed while the patient has substantial autonomy in determining output's content [4]. Indeed our ITIs test was conducted on subject's free speaking. It is the essence of non-linear dynamic analysis that the time series of ITI will be long enough and not interrupted by interventions or questions by the interviewer.
Although a large body of work examined biological and linguistic abnormalities in schizophrenia only few studies evaluated the utility of various indices for diagnosing schizophrenia. Utility is defined in terms of sensitivity and specificity. Receiver operator characteristic (POC) analyses characterize sensitivity and specificity across the full range of index values. Fig. 4 describes ROC analysis of our combined test of four non-linear ITI measures in patients with schizophrenia versus healthy subjects. The calculated area under the curve (AUC), 0.89, gives an index of the performance of the combined test. Potential AUC values range from 0.0 to 1.0. An index that perfectly distinguishes between two groups has AUC value of 1.0. An index in which the two groups overlap completely has an AUC value of 0.5.
Fig. 4.
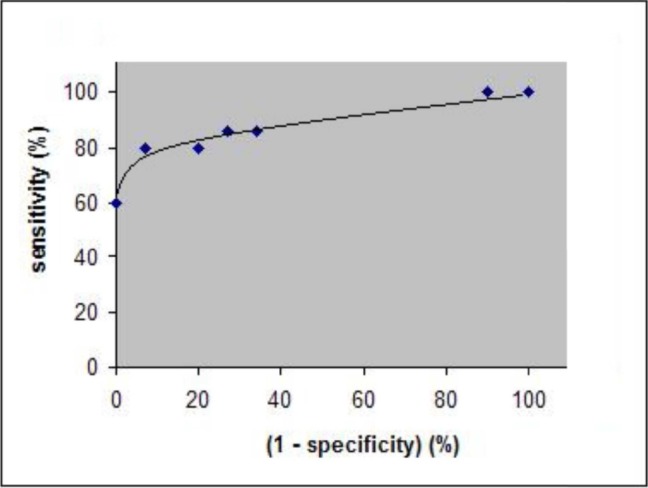
ROC analysis of a combined test including indexes of the four non-linear tests applied to the ITI series of patients with schizophrenia in comparison with a healthy volunteer group. The calculated area under the curve (AUC) of the ROC gives an index of the performance of the given measures. In our case the value is 0.89 (AUC is significantly above 0.5).
It is of interest to compare the performance of our non-linear test with other linguistic as well as biological tests. Patients with schizophrenia were evaluated for formal thought disorder by Clinical Language Disorder Rating scale (CLANG). ROC analysis yielded AUC values of 0.47–0.8 for the CLANG factors differentiating between the schizophrenia and the other diagnostic groups, and values of 0.54–0.79 for the CLANG factors differentiating between non-affective psychosis and affective disorders [33]. Linguistic variables used in a discriminant function analysis could predict diagnosis of schizophrenia in 79% of cases [34]. Thus, the performance of the non-linear ITI test proves better than the linear linguistic measures of formal thought disorder. The performance of biological tests for possible diagnosis of schizophrenia is definitely lower in comparison with the non-linear ITI assay. Thus, when comparing patients with schizophrenia with healthy volunteers, AUC values in the range of only 0.55–0.66 were obtained for the biological indices such as smooth-pursuit ocular motor function, low frequency and alpha band EEG power, etc [35].
Our findings on alterations in non-linear ITIs measures, which represent altered prosody, are in accord with previous findings of disturbances in affective prosody in patients with schizophrenia [5], [36], [37] that are highly lateralized to the right hemisphere. These findings are supported by fMRI studies correlating between the signal changes in right hemispherical areas and the severity of formal thought disorder [38], [39]. In addition, fMRI studies have shown that language processing is less lateralized in patients with schizophrenia due to increased activation and failure to inhibit the right hemisphere [40], [41], that may constitute a genetic predisposition for schizophrenia [42].
The research was conducted on a relatively modest number of 15 patients and 15 healthy volunteer subjects. However, it should be noted that the differences between the two groups of subjects were found to be highly statistically significant. Also, significant differences were detected between the findings observed for untreated patients and patients under antipsychotic treatment. The present study should be considered a pilot study forming the basis for by a larger multi-modality study which should be correlated with other measures such as fMRI and neuropsychological testing in subsequent experiments.
V. Conclusion
Non-linear dynamical methods applied to ITIs enable a content-independent, pure measure of the form of normal thought, its distortion in psychosis, and its restoration under treatment. ROC analysis of our combined test of four non-linear ITI measures in patients with schizophrenia versus healthy subjects shows that the performance of t non-linear ITI test proves better than the linear linguistic measures of formal thought disorder. The performance of biological tests for possible diagnosis of schizophrenia is definitely lower in comparison with the non-linear ITI assay. Our non-linear tests should be extended to measurements in other psychiatric disorders, to the analysis of the development communicative signals in children and for the comparison of human and animal communicative signals.
Biographies

Doron Todder was born in Beer-Sheva, Israel, in 1964. He received the Undergraduate degree in mathematics and physics and the M.Sc. degree in physics from the Hebrew University of Jerusalem, Jerusalem, Israel. He is a Lecturer of psychiatry with Ben Gurion University of the Negev, Beer-Sheva. He is the Head of the Brain Neuromodulation and Telepsychiatry Units and the Coordinator of the Anxiety Clinic, Beer-Sheva Mental Health Center, Beer-Sheva. He was with the School of Medicine, Ben Gurion University of the Negev. His Ph.D. thesis entitled the analysis of time series lingual characteristics a measure of normal development and psychosis, through linear, nonlinear, and chaotic dynamical mathematical methods.

Sofia Avissar was born in Tel Aviv, Israel. She is a Professor of psychopharmacology with the Faculty of Health Sciences, Ben-Gurion University of the Negev, Beer Sheva, Israel. She received the Undergraduate degree in biology from the Hebrew University, Jerusalem, Israel, and the M.Sc. and Ph.D. degrees in neurobiochemistry from Tel-Aviv University, Tel-Aviv. She was a Visiting Associate with the Laboratory of Clinical Science, National Institute of Mental Health, Bethesda, MD, USA.

Gabriel Schreiber was born in Tel Aviv, Israel, in 1953. He is a Professor of psychiatry and the Dean of the Faculty of Health Sciences, Ben-Gurion University of the Negev, Beer Sheva, Israel. He is the Head of the Department of Psychiatry, Barzilai University Medical Center, Ashkelon, Israel. He received the B.Sc. degree in biology, the M.Sc. degree in biochemistry, and the Ph.D. degree in neurochemistry from Tel Aviv University, Tel Aviv. He was supported by a Rothschild Fellowship Award for Post-Graduate Studies, NIMH, Bethesda, MD, USA
He received the Bennett and the Ziskind–Somerfeld Awards of the American Society of Biological Psychiatry and the European Anna Monika Award for Research in Depression.
References
- [1].Arnold L. M., Keck P. E., Collins J., Wilson R., Fleck D. E., Corey K. B., and Amicone J., “Ethnicity and first-rank symptoms in patients with psychosis,” in Schizophrenia Res., vol. 67, no. 2–3, pp. 207–212, 2004. [DOI] [PubMed] [Google Scholar]
- [2].Neighbors H. W., Trierweiler S. J., Ford B. S., and Muroff J. R., “Racial differences in DSM diagnosis using a semi-structured instrument: The importance of clinical judgment in the diagnosis of African Americans,” in J. Health Soc. Behavior, vol. 44, no. 3, pp. 237–256, 2003. [PubMed] [Google Scholar]
- [3].Andreasen N. C., “Thought, language, and communication disorders,” in Arch. General Psychiatry, vol. 36, no. 12, pp. 1315–1330, 1979. [DOI] [PubMed] [Google Scholar]
- [4].Liddle P. F., Ngan E. T. C., Caissie S. L., Anderson C. M., Bates A. T., Quested D. J., White R., and Weg R., “Thought and language index: An instrument for assessing thought and language in schizophrenia,” in Brit. J. Psychiatry, vol. 181, no. 4, pp. 326–330, 2002. [DOI] [PubMed] [Google Scholar]
- [5].Leentjens A. F. G., Wielaert S. M., van Harskamp F., and Wilmink F. W., “Disturbances of affective prosody in patients with schizophrenia: A cross sectional study,” in J. Neurol. Neurosurg Psychiatry, vol. 64, no. 3, pp. 375–378, 1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Alpert M., Kotsaftis A., and Pouget E. R., “At issue: Speech fluency and schizophrenic negative signs,” in Schizophrenia Bull., vol. 23, no. 2, pp. 171–177, 1997. [DOI] [PubMed] [Google Scholar]
- [7].Spitzer M., Beuckers J., Beyer S., Maier S., and Hermle L., “Contextual insensitivity in thought-disordered schizophrenic patients: Evidence from pauses in spontaneous speech,” in Lang. Speech, vol. 37, no. 2, pp. 171–185, 1994. [DOI] [PubMed] [Google Scholar]
- [8].Vaziri G., Almasganj F., and Behroozmand R., “Pathological assessment of patients' speech signals using nonlinear dynamic analysis,” in Comput. Biol. Med., vol. 40, no. 1, pp. 54–63, 2010. [DOI] [PubMed] [Google Scholar]
- [9].Little M. A., Costello D. A. E., and Harries M. L., “Objective dysphonia quantification in vocal fold paralysis: Comparing nonlinear with classical measures,” in J. Voice, vol. 25, no. 1, pp. 21–31, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Choi S. H., Zhang Y., Jiang J. J., and Welham N. V., “Nonlinear dynamic based analysis of severe dysphonia in patients with vocal fold scar and sulcus vocalis,” in J. Voice, vol. 26, no. 5, pp. 566–576, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Li T. Y. and Yorke J. A., “Period 3 implies chaos,” in Amer. Math. Monthly, vol. 82, no. 10, pp. 985–992, 1975. [Google Scholar]
- [12].Eckmann J. P. and Ruelle D., “Ergodic theory of chaos and strange attractors,” in Rev. Modern Phys., vol. 57, no. 3, pp. 617–656, 1985. [Google Scholar]
- [13].Feigenbaum M. J., “Quantitative universality for a class of nonlinear transformations,” in J. Stat. Phys., vol. 19, no. 1, pp. 25–32, 1978. [Google Scholar]
- [14].Ruelle D. and Takens F., “On the nature of turbulence,” in Commun. Math. Phys., vol. 20, no. 3, pp. 167–192, 1971. [Google Scholar]
- [15].Freeman W. J., “Chaos in psychiatry,” in Biol. Psychiatry, vol. 31, pp. 1079–1081, May 1992. [DOI] [PubMed] [Google Scholar]
- [16].Globus G. G. and Arpai J. P., “Psychiatry and the new dynamics,” in Biol. Psychiatry, vol. 35, no. 5, pp. 352–364, 1994. [DOI] [PubMed] [Google Scholar]
- [17].Paulus M. P. and Braff D. L., “Chaos and schizophrenia: Does the method fit the madness?,” in Biol. Psychiatry, vol. 53, no. 1, pp. 3–11, 2003. [DOI] [PubMed] [Google Scholar]
- [18].Paulus M. P., Geyer M. A., and Braff D. L., “Use of methods from chaos theory to quantify a fundamental dysfunction in the behavioral organization of schizophrenic patients,” in Amer. J. Psychiatry, vol. 153, no. 5, pp. 714–717, 1996. [DOI] [PubMed] [Google Scholar]
- [19].Paulus M. P., Perry W., and Braff D. L., “The nonlinear, complex sequential organization of behavior in schizophrenic patients: Neurocognitive strategies and clinical correlations,” in Biol. Psychiatry, vol. 46, no. 5, pp. 662–670, 1999. [DOI] [PubMed] [Google Scholar]
- [20].Tschacher W., Scheier C., and Hashimoto Y., “Dynamical analysis of schizophrenia courses,” in Biol. Psychiatry, vol. 41, no. 4, pp. 428–437, 1997. [DOI] [PubMed] [Google Scholar]
- [21].Pierson D. and Moss F., “Detecting periodic unstable points in noisy chaotic and limit cycle attractors with application to biology,” in Phys. Rev. Lett., vol. 75, no. 11, pp. 2124–2127, 1995. [DOI] [PubMed] [Google Scholar]
- [22].Theiler J., Eubank S., Longtin A., Galdrikian B., and Farmer D., “Testing for nonlinearity in time series: The method of surrogate data,” in Phys. D, vol. 58, no. 1–4, pp. 77–94, 1992. [Google Scholar]
- [23].Takens F., “Detecting strange attractors in turbulence,” in Dynamical Systems and Turbulence, Rand D. A. and Young L. S., Eds., Berlin, Germany: Springer-Verlag, 1981, pp. 366–381. [Google Scholar]
- [24].Grassberger P. and Procaccia I., “Characterization of strange attractors,” in Phys. Rev. Lett., vol. 50, no. 5, pp. 346–349, 1983. [Google Scholar]
- [25].Sigl J. C. and Chamoun N. G., “An introduction to bispectral analysis for the electroencephalogram,” in J. Clin. Monit., vol. 10, no. 6, pp. 392–404, 1994. [DOI] [PubMed] [Google Scholar]
- [26].Hao B. L., “Symbolic dynamics and characterization of complexity,” in Phys. D, Nonlinear Phenomena, vol. 51, no. 1–3, pp. 611–617, 1991. [Google Scholar]
- [27].Abraham N. B., Albano A. M., Das B., DeGuzman G., Yong S., Gioggia R. S., Puccioni G. P., and Tredicce J. R., “Calculating the dimension of attractors from small data sets,” in Phys. Lett. A, vol. 114, no. 5, pp. 217–221, 1986. [Google Scholar]
- [28].Ellner S., “Estimating attractors dimension from limited data: A new method with error estimates,” in Phys. Lett. A, vol. 133, no. 3, pp. 128–133, 1998. [Google Scholar]
- [29].Judd K., “Estimating dimension from small samples,” in Phys. D, vol. 71, no. 4, pp. 421–429, 1994. [Google Scholar]
- [30].Eckmann J. P., “Fundamental limitations for estimating dimensions and Lyapunov exponent in dynamical systems,” in Phys. D, vol. 56, no. 2–3, pp. 185–187, 1992. [Google Scholar]
- [31].Pisarenko D. V. and Pisarenko V. F., “Statistical estimation of the correlation dimension,” in Phys. Lett. A, vol. 197, no. 1, pp. 31–39, 1995. [Google Scholar]
- [32].Grath J. M., “Ordering thoughts on thought disorder,” in Brit. J. Psychiatry, vol. 158, pp. 307–316, Mar. 1991. [DOI] [PubMed] [Google Scholar]
- [33].Ceccherini-Nelli A. and Crow T. J., “Disintegration of the components of language as the path to a revision of Bleuler's and Schneider's concepts of schizophrenia,” in Brit. J. Psychiatry, vol. 182, no. 3, pp. 233–240, 2003. [DOI] [PubMed] [Google Scholar]
- [34].Fraser W. I., King K. M., Thomas P., and Kendell R. E., “The diagnosis of schizophrenia by language analysis,” in Brit. J. Psychiatry, vol. 148, no. 3, pp. 275–278, 1986. [DOI] [PubMed] [Google Scholar]
- [35].Sponheim S. R., Iacono W. G., Thuras P. D., Nugent S. M., and Beiser M., “Sensitivity and specificity of select biological indices in characterizing psychotic patients and their relatives,” in Schizophrenia Res., vol. 63, no. 1–2, pp. 27–38, 2002. [DOI] [PubMed] [Google Scholar]
- [36].Ross E. D., Orbeto D. M., Cartwright J., Hansel S., Burgard M., Testa J. A., and Buck R., “Affective-prosodic deficits in schizophrenia: Profiles of patients with brain damage and comparison with relation to schizophrenic symptoms,” in J. Neurol. Neurosurgery Psychiatry, vol. 70, no. 5, pp. 597–604, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Mitchell R. L., Elliott R., Barry M., Cruttenden A., and Woodruff P. W., “Neural response to emotional prosody in schizophrenia and bipolar affective disorder,” in Brit. J. Psychiatry, vol. 184, no. 3, pp. 223–230, 2004. [DOI] [PubMed] [Google Scholar]
- [38].Kircher T. T., Liddle P. E., Brammer M. J., Williams S. C., Murray R. M., and McGuire P. K., “Neural correlates of formal thought disorder in schizophrenia: Preliminary findings from a functional resonance imaging study,” in Arch. General Psychiatry, vol. 58, no. 8, pp. 769–774, 2001. [DOI] [PubMed] [Google Scholar]
- [39].Kircher T. T., Liddle P. E., Brammer M. J., Murray R. M., and McGuire P. K., “Neural correlates of ‘negative’ formal thought disorder,” in Nerenarzt, vol. 74, no. 9, pp. 748–754, 2003. [DOI] [PubMed] [Google Scholar]
- [40].Sommer I. E., Ramsey N. F., and Kahn R. S., “Language lateralization in schizophrenia, an fMRI study,” in Schizophrenia Res., vol. 52, no. 1–2, pp. 57–67, 2001. [DOI] [PubMed] [Google Scholar]
- [41].Sommer I. E., Ramsey N. F., Mandl R. C., and Kahn R. S., “Language lateralization in female patients with schizophrenia, an fMRI study,” in Schizophrenia Res., vol. 60, no. 2, pp. 183–190, 2003. [DOI] [PubMed] [Google Scholar]
- [42].Sommer I. E., Ramsey N. F., Mandl R. C., van Oel C. J., and Kahn R. S., “Language activation in monozygotic twins discordant for schizophrenia,” in Brit. J. Psychiatry, vol. 184, no. 2, pp. 128–135, 2004. [DOI] [PubMed] [Google Scholar]


