Automatic Deformable Diffusion Tensor Registration for Fiber Population Analysis

Abstract

In this work, we propose a novel method for deformable tensor–to–tensor registration of Diffusion Tensor Images. Our registration method models the distances in between the tensors with Geode-sic–Loxodromes and employs a version of Multi-Dimensional Scaling (MDS) algorithm to unfold the manifold described with this metric. Defining the same shape properties as tensors, the vector images obtained through MDS are fed into a multi–step vector–image registration scheme and the resulting deformation fields are used to reorient the tensor fields. Results on brain DTI indicate that the proposed method is very suitable for deformable fiber–to–fiber correspondence and DTI–atlas construction.

1 Introduction

Diffusion Tensor Imaging (DTI) [1] is a relatively new Magnetic Resonance Imaging (MRI) technique for observing the macro–level anisotropic diffusion of water molecules. DTI makes use of directional signal attenuation information to model the water diffusion with symmetric positive–definite tensors. In addition to clinical applications, DTI can be used to understand the variations of WM fiber organization to better analyze brain functionality and disorders. A key functionality in many clinical applications of DTI is the need to establish the correspondence between the fibers on any two scanned volumes. However, the lack of mathematical tools limits the use of DTI in full potential. A vexing problem pertaining to population and longitudinal studies is that the tensors extracted from DTI scans of different subjects do not lie in the same coordinate frame given different head orientations and motion artifacts that occur during patient scans. Additionally, different subjects’ brains variability and Echo Planar Imaging (EPI) artifacts, renders the problem of automatic fiber–to–fiber correspondence, a challenging one. This requires more advanced techniques than simple registration of diffusion weighted images followed by tensor reconstruction.

The early approaches to DTI registration used derived scalar fields such as Apparent Diffusion Coefficients (ADC), Fractional Anisotropy (FA) or tensor components. In spite of their simplicity, these approaches disregard important information such as orientation and other shape related features. Next generation of methods operated on the tensor manifolds and employed a metric to compute tensor distances such as Riemannian [2] or Log-Euclidean [3]. Zhang et al. proposed an affine registration algorithm based on diffusion profiles, the rate of diffusion at a point, as a function of spatial direction [4]. These methods suffer from the disadvantage that the employed metric does not have a physical implication such as anisotropy or diffusitivity [5]. To compensate for these problems, several multi–channel registration algorithms have been proposed. Park et al. [6] introduced a multi-channel demons algorithm using the sum of squared differences calculated from the independent tensor components along with FA, ADC and a T2–weighted channel. Similarly, Leemans et al. [7] proposed an affine registration method using K-channel mutual information calculated from diffusion weighted and T2-weighted images. Other tensor registration approaches include but the works of Guimond et al. [8] and Ruiz et al. [9].

In this paper, we propose a method that exploits the salient statistics of tensors. Our method uses a dissimilarity metric between tensors, namely the geodesic–loxodrome distance [5], so it does not neglect any tensor information. It then vectorizes the tensors using a version of Multi Dimensional Scaling (MDS) algorithm to yield multi–channel vector images. The channels used in the registration process come from the eigen–modes of the MDS algorithm so the entire tensor information is encoded in these channels without the need for extraneous dimensions for tensor shape or orientation. In essence, it identifies the most salient tensors and describes a lower–dimensional vector subspace wherein meaningful measurements are conducted. This vector space allows for faster and more intuitive computations than what a typical tensor manifold can. The registration process for vector images starts with a coarse, rigid registration, continues with affine and is concluded with a fine B–Spline deformable registration. The deformation fields from each step are used to reorient the original tensor field.

2 Methodology

2.1 Distance Metric

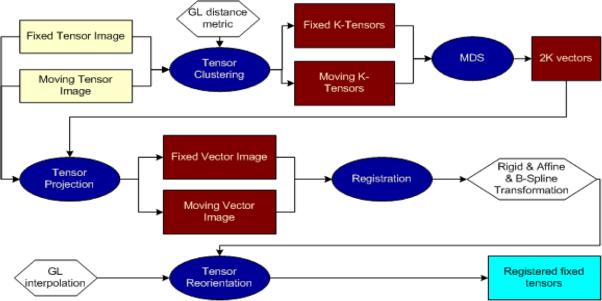
Our registration algorithm's flow is described in Figure 1. The most important operators in this flow are the metrics and interpolators. The biggest challenge in tensor field registration is the need to operate on a manifold, which fully characterizes clinically significant shape and orientation information. Multi–channel registration approaches heuristically try to achieve this by padding extra channels for diffusion norm and anisotropy. Riemannian geodesics get one step closer by implicitly (monotonically) interpolating tensor determinants but anisotropy strength and type of anisotropy are not considered. Geodesic–loxodromes proposed by Kindlmann et al. introduce an intuitive way to compute the distance in between two tensors, which monotonically interpolates all basis shape parameters and orientation [5]. The shape of the tensor $\mathcal{D}$ is modelled with three orthonormal invariant bases R_i chosen as:

$$R_1\left(\mathcal{D}\right)=\Vert \mathcal{D}\Vert R_2\left(\mathcal{D}\right)=FA\left(\mathcal{D}\right)R_3\left(\mathcal{D}\right)=mode\left(\mathcal{D}\right)$$

Geodesic–loxodrome γ(t), the curve connecting tensor $\mathcal{A}$ and $\mathcal{B}$ is defined as:

$$\begin{array}{cc}\hfill & \gamma \left(0\right)=\mathcal{A},\gamma \left(l\right)=\mathcal{B},\Vert {\gamma }^{\prime }\left(t\right)\Vert =1\hfill \\ \hfill & {\gamma }^{\prime }\left(t\right):\widehat{\nabla }{R}_i\left(\gamma \left(t\right)\right)={\alpha }_i\text{for all}t\in [0,1],\mathrm{i}\in 1,2,3\hfill \end{array}$$

where the operator : signifies tensor contraction, l and α_i are constants that characterize the path of the curve, $\widehat{\nabla }{R}_i\left(\gamma \left(t\right)\right)$ is the gradient of the invariant i on the tensor space. The curve γ(t) connects the tensors $\mathcal{A}$ and $\mathcal{B}$ while monotonically interpolating, in a controlled manner, the invariants R_i. The distance in between tensors $\mathcal{A}$ and $\mathcal{B}$ is defined as : $d\left(\mathcal{A}\right),\left(\mathcal{B}\right)={\int }_0^l\parallel {\gamma }^{\prime }\left(t\right)\parallel$. This way of computing dissimilarity accords ample importance to clinically significant shape parameters as well as orientation.

Fig. 1.

Illustration of the algorithm. Rectangular boxes represent input, generated and output data and elliptic boxes represent algorithm operators.

2.2 Tensor Vectorization

Geodesic–Loxodromes (GL) provide a clinically intuitive way to do tensor interpolation and distance measurement but can not directly be used to compute tensor population statistics. An ideal way to achieve this would be to unfold the GL manifold (if any) onto a planar one, in such a way that the statistics and distances are preserved on the new plane. Then it would be possible to just consider the vector coordinates of the points on the projected space.

The main goal of pre–processing is to convert the tensor images into vector images, with independent channels, with GL pairwise dissimilarities in between the voxels of all DT images. Multi Dimensional Scaling [10] is a statistical dimensionality reduction tool used to extract the coordinates of data points on a lower dimensional manifold, when only pairwise dissimilarities among the data points are available. In our case, the goal is to compute the dissimilarity matrix in between the voxels of two diffusion tensor images, from the tensor data and unfold this symmetric matrix onto vectorial coordinates using MDS.

Tensor Sampling

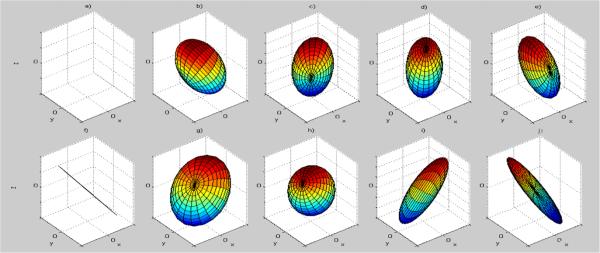
Theoretically, it is possible to use the tensors from every voxel of the DT image, build the dissimilarity matrix to be used in MDS, and extract the coordinates of each voxel in the lower dimensional space. However, the dissimilarity matrix for two regular size DT images would require about 10000GB of memory. Instead, we sample both DT images in such a way that the sampled tensors are the best representatives for the entire tensor sets in the images. We employ the K–means clustering algorithm on the tensors of both images with the GL distance metric, to select the best tensor representatives. K was empirically chosen to be 100 based on experiments with a validation set with values ranging from 10 to 1000. The mean tensors obtained with clustering are fed into the MDS algorithm. Figure 2 displays the mean tensors when K=10 based on the data described in 3. In this figure, the tensor a) is the zero–tensor that represents background. Please note that only one tensor, tensor h, is completely isotropic and eight tensors are needed to describe the anisotropic behavior. Please also note that three tensors (tensors e) , f) and j)) have similar directions but different determinants and modes, which is due to special importance assigned to these invariants by GL metric.

Fig. 2.

Mean tensors obtained with clustering displayed with ellipsoids

Multi Dimensional Scaling

Let the mean tensor from K–means be M_i for the first image and L_i for the second image where i ∈ [1,K]. We concatenate the mean tensors and compute the pairwise distances to obtain the symmetric dissimilarity matrix A, where A_ij = d(M_i, M_j) when i, j < K, A_ij = d(M_i, L_j) when i < K, K ≤ j < 2K and A_ij = d(L_i, L_j) when K ≤ i, j < 2K.

In classical metric MDS, the Euclidean distances are tried to be preserved. Let I_2K×2K be an identity matrix and 1_2K×2K be a matrix full of ones, define:

$$\begin{array}{cc}\hfill P=& I_{2K\times 2K}-1_{2K\times 2K}\hfill \\ \hfill B=& P(-\frac{1}{2}\mathbf{A}\odot \mathbf{A})P\hfill \end{array}$$

where $\odot$ signifies component by component multiplication. The matrix B is equal to B = XX^T where the matrix X contains the coordinates of the data.

We used this classical MDS approach just to understand the intrinsic dimensionality of the data by examining the eigenvalues. The first six eigenvalues after spectral decomposition were on the order of +1E¹⁰ where the remaining eigenvalues were on the order of 1E⁻² except the last six ones which were negative with order −1E³. This fact suggested that the intrinsic dimensionality of the data is six. With this in consideration, we applied the non–classical, non–metric version of MDS [10] to extract the final coordinates of the data points.

DTI projection onto MDS space

MDS vectorizes only the mean tensors computed with the clustering algorithm. However, for registration purposes, every tensor in both DTI images has to be projected on to this vector space. Here we explain our protocol to project the distances for unobserved tensor points to the MDS space. Let $X_i^t$ be the i^th coordinate of the t^th data point in the salient MDS space, Y_i be the corresponding coordinate of the unobserved point, where i ∈ [1,6] and t ∈ [1,2K]. Let d^t be the distance of Y to mean point X^t. Then Y lies on the sphere defined as ${\sum }_{i=1}^6{(Y_i-X_i^t)}^2={\left(d^t\right)}^2$. We need to use at least six different points X^t in order to have a non–infinite number of solutions for Y_i. Because of the imperfections in distance computations and in MDS, this system of equations might not have a solution. Therefore, we introduce slack variables ξ^t for distances d^t and setup up a minimization problem over the slack variables:

$$\begin{array}{c}\hfill \min {\sum }_{t=1}^6{\left({\xi }^t\right)}^2\hfill \\ \hfill s.t.{\sum }_{i=1}^6{(Y_i-X_i^t)}^2-{(d^t-{\xi }^t)}^2=0\text{for all}t\in [1,6]\hfill \end{array}$$

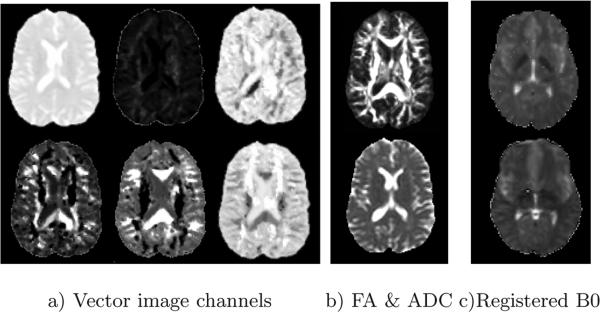
We solve this non–linear optimization problem for each voxel in each image with a sequential quadratic programming (SQP) method. The mean points, X^t, used in the constraints are chosen to be the closest six points to Y and the optimization is initialized with the closest point's coordinates. This optimization procedure is inexpensive and requires a few seconds to project both images onto the MDS space with a modern computer. To test its accuracy, we also implemented the Log–Euclidean metric [3], which has a closed–form expression, and were able to recover the exact point coordinates after our projection operator. Figure 3 displays the corresponding slices for each of six dimensions from the vector images produced with this method.

Fig. 3.

a) The 6 channels of vector images. Top–left corresponds to largest eigenvalue, bottom–right corresponds to the lowest one. b) FA and ADC maps. c)B0 map of fixed image (top) and registered moving image (bottom).

2.3 Registration Framework

Vector Image Registration

Once the diffusion tensors in all images are converted to vector images as described in Section 2.2, the images are registered with well–known registration algorithms, using the following steps:

1. The moving image is translated so that its center of mass matches that of the fixed image.

2. The moving image is registered to the fixed image with rigid transformation, vector mean squares metric, linear interpolation, and evolutionary optimization. The parameters are set to perform the search in a coarse manner.

3. The moving image is registered to the fixed image with an affine transformation initialized with a rigid transformation of step 2. The vector mean squares metric and linear interpolation are used in conjunction with a regular step gradient descent optimizer. After this fine-scale registration, the moving image is resampled and transformed to match the fixed image.

4. The output image of step 3 is registered to the fixed image with a B–Spline transformation with 15 × 15 × 15 B–Spline grid resolution.

Figure 3 c) displays the output of the registration on the B = 0 image along with the fixed image.

Tensor Reorientation

The tensors are reoriented based on the transformation matrix from affine registration and the deformation field from B–Spline registration, with Preservation of Principal Direction (PPD) method [11]. Let $\mathcal{D}$ be the tensor to be transformed and ${\mathcal{D}}^{\prime }$ be the resulting tensor.

1. When the transformation is rigid, the new coordinates and the resulting tensors can be found as T (x) = Rx + t, ${\mathcal{D}}^{\prime }=\mathbf{R}\mathcal{D}{\mathbf{R}}^T$, where x is the coordinate vector, R is the rotation matrix, t the translation vector.

2. When the transformation is affine the coordinates can be found with T (x) = Fx + t where F is the affine transformation matrix. F can be decomposed as F = UR, where R = (FF^T)^−1/2F is the rotation matrix and U is the strain matrix. The simple approach for tensor reorientation would be to rotate the tensor with R but U also affects the orientation of the tensors so it needs to be included in a detailed reorientation strategy.

3. When B–Spline registration is employed, there is no closed linear form for the transformation. Since every transformation is locally affine if the underlying deformation field u(x) is continuous and smooth, the affine transformation matrix can be locally estimated for each point. Let the local coordinate transformation be T (x) = x + u(x) and T (x) = Fx + t. Equating the two equations and differentiating w.r.t. x yields F = I + J_u, where J_u is the Jacobian of the deformation field.

3 Experiments and Results

We acquired data from five healthy subjects with an 8–channel head coil in a 3T MR system (Achieva, Philips Medical Systems, Cleveland, OH, USA). Diffusion tensor imaging (DTI) was performed using a single shot EPI sequence (SENSE factor = 3, b = 1000s/mm2, 6 diffusion gradient directions). Image sizes for all images were 153 × 153 × 80. One of the images was chosen to be the fixed image and the other four were used as moving images. The diffusion tensors were extracted by imposing the constraint of positive-definiteness on the tensors. For comparison, we implemented a reference multi–channel registration algorithm with six channels for tensor components, including one channel for FA and one channel for ADC. The reference method had the same vector image registration steps. Figure 4 the principal eigenvectors of the moving tensors generated with the proposed method and the reference method on the FA map of the fixed image to signify the conformance. Please also note that the Euclidean Frobenius difference norm in between the fixed tensor field and registered moving tensor field was on the average 1.259 × 10⁹ with the proposed method, whereas that quantity was 1.751 × 10⁹ with the reference method. Additionally, the proposed method take about two hours on a modern PC, whereas the reference method took 3 hours on the average because of the extra channels. About 90% of computations for both methods were for B–Spline registration.

Fig. 4.

Moving images’ eigenvectors plotted on fixed image's FA map. a) Full FA slice with ROI in rectangle. b) Proposed method. c) Reference method. Reference method's vectors are correct on sides but there is a mismatch on regions indicated by the arrow.

Figure 5 a) shows the corresponding fiber set from the fixed image (blue colored fibers) and registered moving image (skin colored fibers). The fiber differences are mostly due to anatomy and imperfections in the fiber tracking algorithm. Please note the fully corresponding fibers on the right picture.

Fig. 5.

a) Corresponding fibers from fixed and registered moving images. b) Zoomed in version of a. Arrows indicate the fully corresponding fibers.

For statistical purpose, we chose an ROI and computed statistics of the tensors and the projected vectors. We automatically segmented the Corpus Callosum (CC) within the algorithm by selecting K = 2 and compared the mean values of the variables from our method with mean tensors from Log-Euclidean.

The mean vector computed from CC with the proposed method was: [6.91, 0.15, –0.21, 5.62, 0.035, 5.7]^T where the matrix produced with Log–Euclidean was [6.8694, 0.1464, – 0.2083; 0.1464, 5.6471, 0.0338; – 0.2083, 0.0338, 5.6081]. These results indicate that the proposed method yield similar outputs for tensor statistics to Log-Euclidean approach.

4 Discussion and Future Work

In this work, we proposed a novel, robust and fast approach for tensor–to–tensor registration for Diffusion Tensor Images, which is very suitable for fiber correspondence matching problem. Our method was based on vectorization of tensors in such a way to conserve all shape and orientation properties. The registration was done on vector image space and the resulting deformation fields were used to reorient the tensors. Our next step will be to use this approach to compute the mean tensor images and variation mode images and establish a protocol for DTI–atlas construction and shape change analysis.