Abstract
Circulating tumor cells (CTCs) are known to be a harbinger of cancer metastasis. The CTCs are known to circulate as individual cells or as a group of interconnected cells called CTC clusters. Since both single CTCs and CTC clusters have been detected in venous blood samples of cancer patients, they needed to traverse at least one capillary bed when crossing from arterial to venous circulation. The diameter of a typical capillary is about 7 μm, whereas the size of an individual CTC or CTC clusters can be greater than 20 μm and thus size exclusion is believed to be an important factor in the capillary arrest of CTCs – a key early event in metastasis. To examine the biophysical conditions needed for capillary arrest, we have developed a custom-built viscoelastic solid–fluid 3D computational model that enables us to calculate, under physiological conditions, the maximal CTC diameter that will pass through the capillary. We show that large CTCs and CTC clusters can successfully cross capillaries if their stiffness is relatively small. Specifically, under physiological conditions, a 13 μm diameter CTC passes through a 7 μm capillary only if its stiffness is less than 500 Pa and conversely, for a stiffness of 10 Pa the maximal passing diameter can be as high as 140 μm, such as for a cluster of CTCs. By exploring the parameter space, a relationship between the capillary blood pressure gradient and the CTC mechanical properties (size and stiffness) was determined. The presented computational platform and the resulting pressure–size–stiffness relationship can be employed as a tool to help study the biomechanical conditions needed for capillary arrest of CTCs and CTC clusters, provide predictive capabilities in disease progression based on biophysical CTC parameters, and aid in the rational design of size-based CTC isolation technologies where CTCs can experience large deformations due to high pressure gradients.
Keywords: Circulating tumor cell, Finite element, Computational model, Capillary, Microvessel
1. Introduction
The presence of circulating tumor cells (CTCs) indicates that the process of blood-borne cancer metastasis has already been initiated [1,2]. Numerous technologies [3] (e.g. microfluidic devices [4,5]) have been employed to isolate the rare CTCs from blood samples of cancer patients, usually obtained from venous blood draws. Several studies have also shown that the presence of CTC clusters in the circulation potentially plays an important role in metastasis [6–9]. CTCs or larger CTC clusters generally need to traverse: (1) venous drainage of the tumor leading to the right side of the heart followed by passage through the pulmonary capillaries leading back to the heart; (2) then from the left heart to the distal small arteries in the hand followed by passage through the distal hand capillary bed leading to venous side of the arm. This implies that not one, but two capillary beds may need to be crossed by the CTCs and CTC clusters. The typical diameter of a capillary is around 7 microns (although the range can be from 5–10 microns) [10,11], whereas an individual CTCs can be as large as ~20 μm and the CTC clusters can be much larger, on the order of 100 μm [4,5,12]. Based on this considerable size difference, it has been postulated that the larger size of CTCs prevents them from passing through capillaries [13], implying that size restriction plays an important role in cancer metastasis [13,14]. The arrest of CTCs in capillaries is believed to be a key part of the metastatic process, as the step prior to their extravasation and subsequent growth in the surrounding tissues [14,15]. Additionally, in certain blood cancers, such as acute leukemia, a very large number of cancer blood cells can exist in blood due to uncontrolled proliferation of myeloid or lymphoid lineage cells. This situation can then precipitate the onset of leukostasis – a poorly understood condition where cancer cells aggregate within the vasculature and cause grave clinical symptoms [16–18]. In the above cases, the arrest of the CTCs or CTC clusters as well as large leukemic cells in capillaries is mainly dictated by two mechanisms: (1) the interaction of the cells with the vasculature, which we term as the biochemical component and (2) the size and mechanical properties of the cells coupled to the local fluid conditions, termed the biophysical component. Although there has been considerable focus on the former [14,15], the effect of the latter, biophysical component, is not well understood.
We here present a custom-built computational platform that allows us to determine how a large visco-elastic solid (CTC) deforms and passes through a smaller-sized narrowing (microvessel). The platform is finite-element based, and we introduce a strong-coupling method that enables direct coupling of the solid properties (e.g. stiffness) to the fluid conditions (e.g. pressure) in order to solve for the resulting deformations. With this customized approach we examine the biophysical conditions needed to allow large-diameter CTCs to pass through a typical 7 μm capillary. The computational model reveals a simple relationship between the three key biophysical parameters: (1) CTC diameter, (2) CTC stiffness, and (3) fluid (blood) pressure gradient across the capillary. Our analysis spans several orders of magnitude for cell diameter and stiffness, and offers predictive capability about what kind of CTC (e.g. size) may be arrested in the microvasculature under physiological conditions. The pressure–size–stiffness relationship reveals that, for a given pressure, cell stiffness strongly affects the maximal cell size that can pass into the capillary. We have found that, under physiological conditions, even a very large cell or a cluster of cells (~100 μm diameter) can pass only if its stiffness is very small (~10Pa), and conversely a CTC whose stiffness is 1000 Pa will be arrested in the capillary if its diameter is greater than 12 μm. Taken together, the computational results and derived biophysical relationship provide a tool to better understand how large CTCs go through smaller-sized capillaries; this is central not only for cancer metastasis but also for size-based CTC isolation technologies where CTCs can experience large pressure gradients [19].
2. Methods
In order to develop a computational model of an incompressible solid (cell) going through a smaller-sized narrowing (capillary) we had to address the following two challenging issues: (1) to model solid–fluid interaction with motion of the deformable solid within the fluid, and (2) to model solid–solid interaction with large relative displacements of the interacting surfaces as well as to model large deformations of the incompressible solid. We here summarize the basic relations and steps involved in addressing these issues.
2.1. Fundamental relations
For the fluid, we have the basic equations of balance of linear momentum, known as the Navier–Stokes equations:
| (1) |
where ρf and pf are density and pressure of the fluid, respectively, μ is the viscosity, are the volumetric forces, and vi are fluid velocities. We consider an incompressible fluid (water), hence, the continuity equation is expressed as
| (2) |
Using a standard Galerkin procedure [20], Eqs.(1) and (2) can be transformed into the finite element (FE) incremental-iterative algebraic equations (corresponding to one FE):
| (3) |
where Vf are velocities of FE nodes ( is the velocity at the start of the time step), Pf is the pressure of the element (we use a constant pressure assμmption for the element), and are external nodal forces, which include actions of other elements; Δt is the time step size, and ‘i’ is the equilibrium iteration counter. The explicit expressions for the element matrices Mf, Kvv and Kvp can be found elsewhere [20].
For the solid, treated as incompressible, we adopt the approach analogous to the one generally used for modeling incompressible elastic or inelastic material deformation [21,22]. The stress tensor σij can be decomposed into the deviatoric stress σ′ij and the mean stress p,
| (4) |
| (5) |
Then, differential equations of balance of linear momentum can be written in the form:
| (6) |
where ρs is the solid density, ui are displacements, and are volumetric forces. Further, we use deviatoric strains ,
| (7) |
where ev = e11+e22+e33 is the volumetric strain, and δij is the Kronecker delta symbol. Elastic constitutive relations can be written as
| (8) |
where are elastic deviatoric stresses, and G is the shear modulus. In order to treat the solid as viscoelastic, we employ linear viscoelastic relations,
| (9) |
where are viscoelastic stresses, and D is the damping coefficient. The incompressibility condition has the same form as for the fluid (Eq. (2)).
Using the principle of virtual work, the above fundamental equations for the solid can be transformed into equations of balance for a solid finite element:
| (10) |
where are nodal velocities, Ps is the mean stress of the element (assumed constant over the element, as for the fluid), and Fint are the internal element forces, corresponding to stresses. Details about element matrices and derivations of this equation can be found in [20,23].
2.2. Solid–fluid interaction
Modeling of solid–fluid interaction has been a challenging problem in computational mechanics, particularly in case of motion of deformable solids within fluid. A number of approaches have been proposed, such as fictitious domain method [24,25], arbitrary Lagrangian–Eulerian (ALE) formulation [26], Lattice Boltzmann method [27], Lagrange multiplier method [25,28], immerse boundary finite element method [29], and finite element method with remeshing using an explicit–implicit procedure, called direct simulation [30]. We employ a strong coupling approach where the FE equations for the solid and fluid domain are assembled into one system of equations and solved simultaneously. Also, we implement a remeshing procedure during the solution process.
In our methodology, the FE model for solid and fluid is generated in a way that, at the current position of the solid, the FE meshes for the two domains have common nodes at the solid surface. The basic assumption is that common nodes have the same velocities over the time step, as shown in Fig. 1A; and we are solving for increments of velocities (Eqs. (3) and (10)) using the same velocities at the start of the time step for the common nodes. Displacements of solid nodes are calculated during equilibrium iterations, as follows:
| (11) |
where U(i) and U(t) are nodal displacements at iteration ‘i and at the start of the time step, respectively. When convergence is reached, the solid is displaced as schematically shown in Fig. Fig. 1B [31]. Then, a new mesh for the fluid domain is generated, using the displaced common nodes at the solid surface. Also, it is necessary to map the solutions for fluid velocity and pressure from the old to the new mesh. Although this remeshing procedure requires additional computational time, we have used this approach since we determined that this procedure is advantageous in accuracy and robustness when compared to other methods.
Fig. 1.
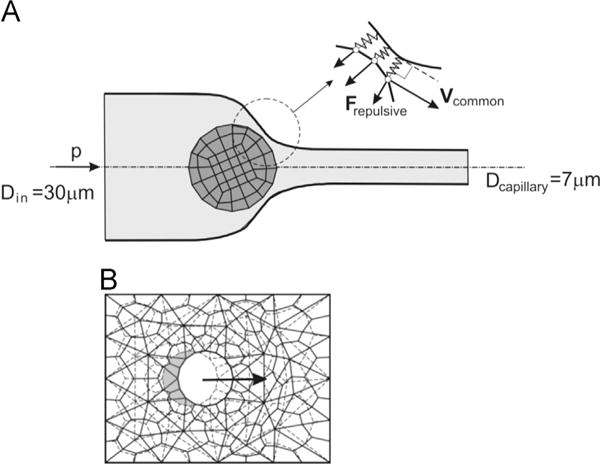
(A) Model geometry of the axisymmetric channel with the cell approaching the capillary narrowing. Inlet and capillary diameters were 30 μm and 7 μm, respectively. Pressure gradient P causes fluid (and cell) movement from left to right. Inset depicts interaction between cell and the wall, where within 0.75 μm of the wall, repulsive spring-like forces act on the cell. (B) Remeshing procedure concept. When convergence at time step is reached (using the finite element (FE) mesh shown by dashed lines), the solid is displaced and a new mesh (solid lines) for the fluid domain is generated, with common nodes at the displaced solid surface [31]. The new mesh is then employed for the next time step.
Interaction between the moving deformable solid and the wall has been resolved using a simple, yet very robust concept. Namely, we introduce a repulsive stress field, or repulsive forces, acting on the solid nodes which are within a selected range of influence from the wall, as schematically shown in Fig. 1A (inset). A repulsive force at a node within the interaction domain is Fn = k(ℓ0−ℓ), where Fn is the force normal to the cell surface, k is the stiffness, ℓ0 and ℓ are the interaction domain and the current distance between cell surface and the wall, respectively. For all of the simulations presented in the paper, the region where repulsive forces begin to act was ℓ0 = 0.75 μm from the wall. Hence, the forces are proportional to the deformation of the fictitious springs (ℓ0−ℓ), with zero-forces when the distance is greater or equal to the domain of influence, i.e. when the distance is greater than ℓ0. We found that this concept is reliable and can be applied to 2D, axisymmetric and 3D conditions. The described methodology is implemented within our custom-built FE program PAK [32].
3. Results
3.1. Solid and fluid velocity field
The 3D model of the CTC and capillary was constructed by assuming symmetry along the axial axis, i.e. by taking a 2D cross section and rotating it around the axial axis for each time point. Thus, for a given pressure and the appropriate boundary conditions (see Methods section) we solved for the resulting fluid and solid velocity field. Fig. 2 depicts the transit of a spherical CTC with diameter D=18 μm through a d=7 μm capillary. The entrance region into the capillary tapers from a diameter of 30 μm to 7 μm over a length 50 μm (see Fig. 1A). The wire frame corresponding to the finite element mesh is visible for both the cell (black lines) and the capillary contour (red lines). For clarity, the fluid is omitted, and the colors represent the velocity of the surface of the CTC (the scalebar is the same for all panels of Fig. 2). The viewpoint is chosen askew to demonstrate the 3D nature of the model, and for Fig. 2A–C the field-of-view is set the same, whereas Fig. 2D is zoomed out in order to show the moment when the cell is just about to completely enter the d=7 μm capillary (the 7 μm diameter of capillary appears smaller for Fig. 2D, when compared to Fig. 2A–C). For Fig.2 the cell stiffness was E=100 Pa.
Fig. 2.
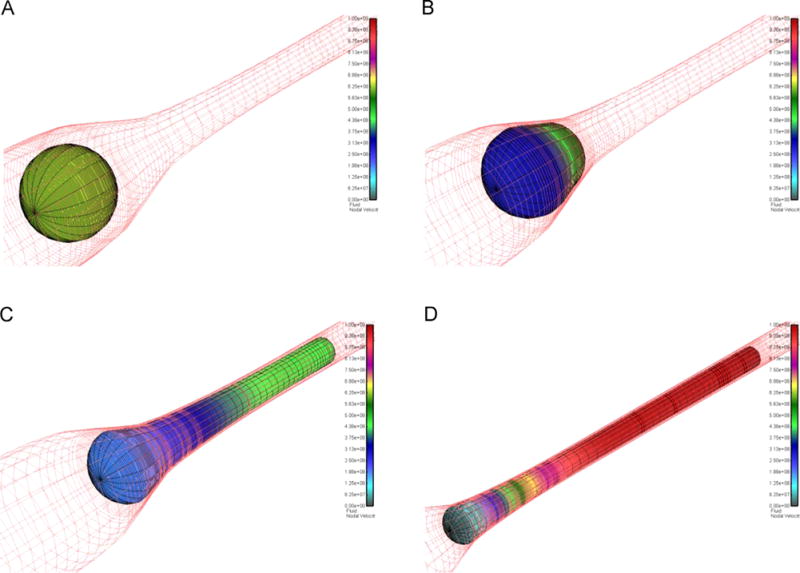
Passage of an 18 μm CTC into the 7 μm capillary. (A) The CTC in the initial, undeformed state. Black lines indicate the FE mesh of the solid, red lines represent the wall geometry. Colors: CTC velocity. (B) CTC begins to enter the capillary. (C) About half of the CTC is inside the capillary. (D) The CTC is just about to be completely inside the capillary. Scalebars are the same for all panels. Fluid omitted for clarity; CTC stiffness 100 Pa. Same view for (A)–(C), zoomed out for (D). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
In Fig. 3, we show the cross section of Fig. 2, but this time we include the fluid velocity by displaying the resulting fluid velocity vectors (vector color/length indicates intensity). The CTC velocities are also shown in Fig. 3A, B (same scalebar for velocity) and are omitted for clarity in Fig. 3C. Since the applied repulsive interaction between the wall and cell (see Methods section) provides a small fluid gap between the cell and capillary wall, there is an increase in the fluid velocity in these gaps as is evident in Fig. 3C. In order to best display the velocity vectors prior to the CTC entering the d=7 μm region and in the early stages of deformation (Fig. 3A, B) we show a zoomed-in region around the cell (the same view for Fig. 3A, B) and zoom out for Fig. 3C (the 7 μm diameter of the capillary appears smaller on Fig. 3C compared to Fig. 3A, B).
Fig. 3.
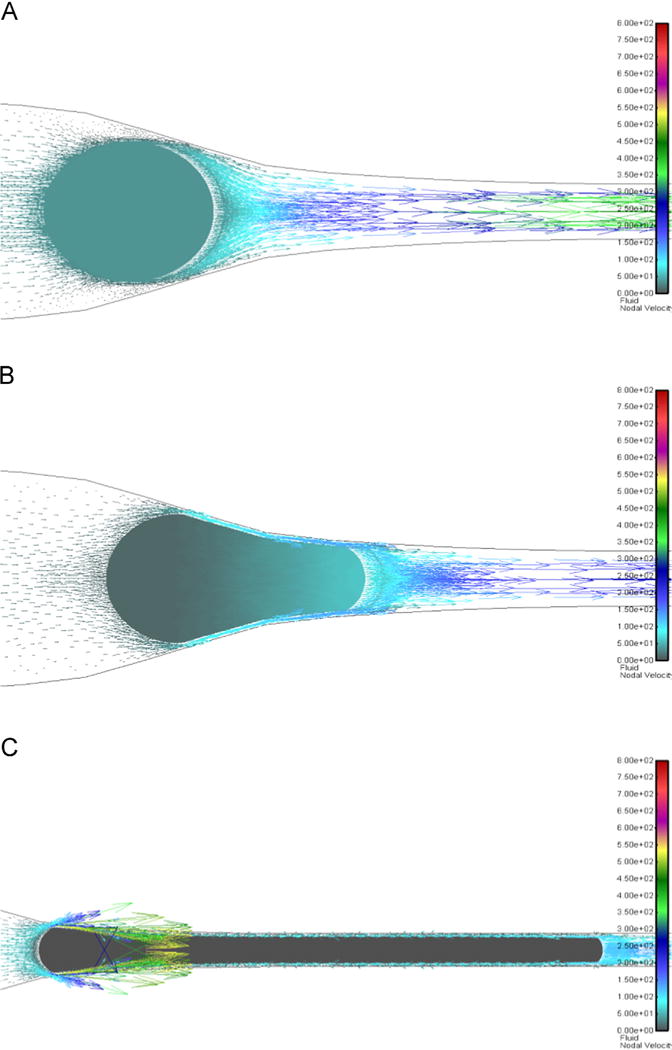
Solid and fluid vectors: 2D cross-sectional representation of Fig. 2. (A) 18μm CTC (stiffness 10 Pa) about to enter capillary. Fluid: colors/lengths indicate intensity of velocity vectors. Solid colors: velocity. (B) CTC partially inside the capillary. (C) CTC is just about to be completely inside capillary (solid velocity here omitted for clarity). Scalebars are the same for all panels. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.2. Pressure required for CTC to fully enter the capillary
In order to determine the minimum pressure required for the CTC from Fig. 2 to deform and pass through the 7 μm capillary, we employed the following approach. A small pressure of 3 cmH2O was first applied as shown in Fig. 4A. This resulted in the CTC beginning to enter the 7 μm capillary; however, the pressure was insufficient to deform the cell further to make it fully enter the capillary and a steady-state was reached, with no further cell deformation, as shown in Fig. 4B. From this steady-state position, a step increase in pressure from 3 to 5 cmH2O resulted in the CTC further entering the capillary until a new steady-state was reached (see Fig. 4C). Then, another step increase in pressure was introduced from 5 to 6 cmH2O, which was sufficient to drive the CTC completely into the capillary (see Fig. 4D). It should be noted that once the CTC fully enters the capillary, it continuously moves through the capillary at a constant speed, with no additional deformation. To ensure that the minimum pressure is the one displayed, we have performed even finer resolution pressure increases of 0.1 cmH2O, but omit these cases for clarity. Therefore, by employing incremental increases in the transcapillary pressure we are able to determine, for a CTC of given size and mechanical properties, the minimum pressure needed for capillary traversal.
Fig. 4.
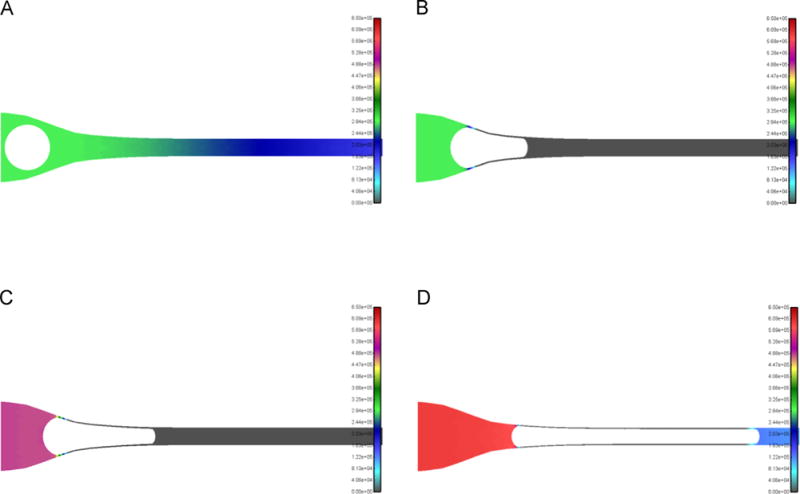
Fluid pressure field during 18 μm CTC passing through 7 μm capillary. Step-increase in pressure approach employed to determine minimum pressure required for CTC to be completely inside capillary. Colors indicate value of pressure. (A) A relatively small pressure of 3 cmH2O applied (CTC about to enter capillary). (B) For the conditions of (A), CTC partially enters capillary and reaches the steady-state position shown (where no further deformation occurs). (C) A step increase in pressure to 5 cmH2O results in the CTC entering deeper into the capillary and reaching a new steady-state position shown. (D) An additional step increase in pressure to 6 cmH2O results in the CTC completely entering into the capillary. View and scalebars are the same for all panels, CTC stiffness E=100 Pa (same as Fig. 2). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.3. Pressure required for a chain-like CTC cluster to fully enter capillary
In our previous work, we have detected clusters of CTCs from clinical blood samples of cancer patients [5,9,12]; thus, prompting us to examine the conditions needed for a chain-like cluster to fully enter and transit through the capillary. First, we analyzed two-cell cluster geometry (see Fig. 5A) by treating the cluster as a homogeneous deformable solid (same properties as in Fig. 2). Here, it was assumed that the CTC cluster behaves as a single CTC of equivalent size. Going through the step-wise pressure increase procedure explained above, we determined that the pressure gradient required for a two-cell cluster to pass through the capillary is the same as in the single cell case (see Fig. 5B). The scalebars for Figs. 3 and 4 are the same and Figs. 4D and 5B display the same pressure value of 6 cmH2O. The cases of larger chain-like cluster geometries (3, 4, 5 cell clusters) were also modeled and resulted in only small increases in pressure (<5%) from the single CTC case.
Fig. 5.
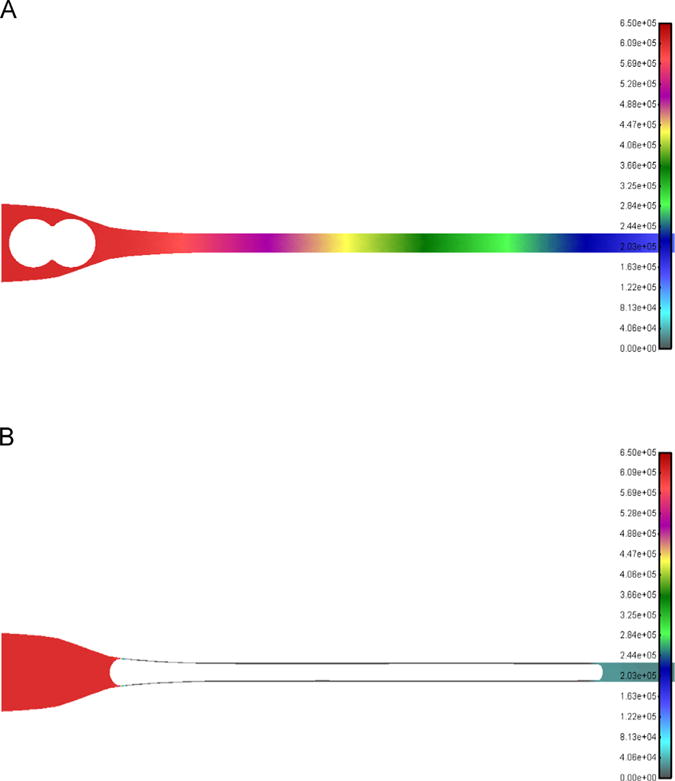
Pressure field during the passage of a 2-cell CTC cluster into the 7 μm capillary. (A) An additional identical D=18 μm CTC forms the 2-cell cluster (stiffness 100 Pa), shown prior to entering the capillary. Applied pressure is 6 cmH2O, same as that required for a single CTC (see Fig. 4D). Colors represent pressure values. (B) 2-cell CTC cluster is completely inside the capillary. Scalebars are the same for both panels and also identical to Fig. 4D. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.4. Pressure–diameter–stiffness relationship
In Fig. 4 we have shown the minimum pressure required to have a CTC with a diameter of 18 μm and stiffness of 100 Pa pass through a 7 μm capillary. The same computational procedure was repeated by varying first the CTC size and then the stiffness. For each combination of CTC properties, a single minimum pressure was obtained and the cases spanned the range of cell diameter from 12 to 20 μm and stiffness from 10 to 1000 Pa. Fig. 6 displays 15 of the run cases, where each data point represents a single simulation. For the data points of same CTC stiffness values, a line was fit through the data (with R2=0.99 for each fit). Based on the linear nature of the system, the following relationship between the fluid pressure and CTC diameter and stiffness was obtained:
| (12) |
Here, the CTC diameter (D) is in microns, stiffness (E) is in Pa, and the pressure (P) is in cmH2O. To compare to the typical physiological pressure gradient of 10 cmH2O across a capillary [33–35], the P=10 cmH2O line was included in Fig. 6. The shaded area below the P=10 cmH2O line indicates the conditions for which CTCs will pass through the 7 μm capillary.
Fig. 6.
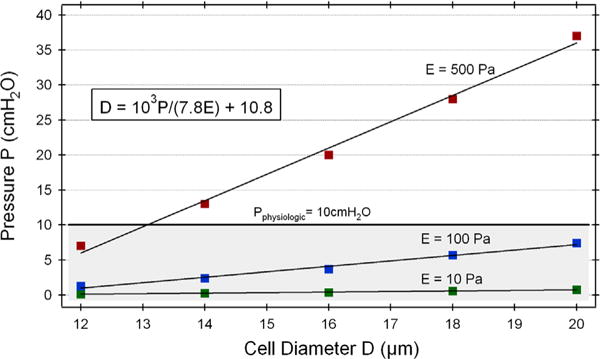
Fluid pressure needed for CTC passage into the 7 μm capillary as a function of cell size and stiffness. Each point represents a single simulation; same colors indicate same cell stiffness values (green: 10 Pa, blue: 100 Pa, red: 500 Pa). Lines through points: linear fit for the same-stiffness data points. Shaded area below the typical physiologic pressure line (P=10 cmH2O) represents the region for capillary passage – data points within this region indicate conditions for which CTCs will pass into capillary. Based on the overall linear behavior of the system, a relationship between fluid pressure–cell diameter–cell stiffness was derived (Eq. (12)); equation shown in boxed inset (units same as those displayed on graph). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Another way of examining the data is to employ the pressure–diameter–stiffness relation and to calculate, for a given pressure, the maximum diameter of a CTC that will go through the capillary as a function of stiffness. Fig. 7 displays the results on a log–log scale for three different pressures: Physiologic=10 cmH2O (thick line), P=20 cmH2O, and P=5 cmH2O. The dashed lines indicate the experimentally measured stiffness values for various cell types: Jurkat (lymphoid cell line) [18], HL60 (myeloid cell line) [18], neutrophil [18], chondrocyte [36,37], and leukemia patient cells (asymptomatic and symptomatic patients) [16,35]. The inset shows the same data, but now on a linear scale and in the stiffness range of 100–1000 Pa, and for clarity the inset only displays the leukemia stiffness values from the log–log plot. The leukemia cells were obtained from clinical blood samples of pediatric acute lymphoblastic leukemia (ALL) patients with and without observable symptoms [16,35].
Fig. 7.
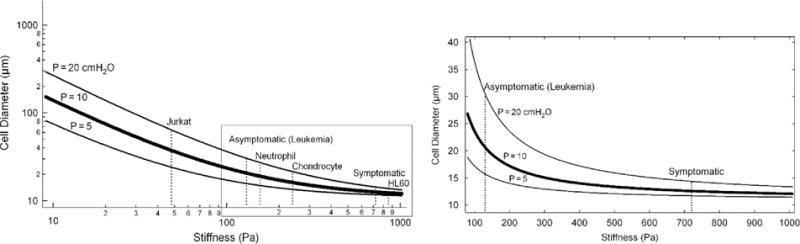
Pressure curves based on the pressure–diameter–stiffness relationship. Left: Log–log plot of CTC diameter as a function of CTC stiffness for three pressure curves: Pphysiologic=10 cmH2O (thick solid line), P=20 cmH2O, and P=5 cmH2O. Vertical dashed lines indicate experimentally measured stiffness values for various cell types (see Results for details) [16,18,35–37]. The intersection of the dashed lines with the 3 solid pressure curves indicate the maximal cell size that can pass for the given pressure curve (e.g. for P=10 cmH2O the maximum size of Neutrophil that will pass through is 20 μm). Asymptomatic and symptomatic: cell stiffness measured from clinical blood samples of pediatric acute lymphoblastic leukemia (ALL) patients [16,35]. Right inset: Boxed region on left is re-plotted on a linear scale to better demonstrate the hyperbolic character of the pressure curves. For clarity only the leukemia stiffness values are shown on the linear plot.
4. Discussion
We have developed a 3D computational model of how large CTCs deform and pass through smaller-sized capillaries. The model utilizes axial symmetry in order to convert a 2D cross-section into a 3D solution and is based on the finite element method, building on our previous modeling methodology [38–41]. Several important additions were incorporated, including (1) the fluid and solid were strongly coupled, which enabled us to model motion of the deformable cell within the fluid, (2) the remeshing algorithm ensured robustness of the solution under a variety of conditions, (3) a robust solid–solid interaction model, and (4) an algorithm for large deformation of an incompressible solid. The model was then employed to explore the parameter space of three interconnected parameters: fluid pressure, CTC size, and stiffness.
The primary motivation of this study was to examine the biophysical conditions (cell and fluid properties) needed for a large CTC to go through a small capillary. In Fig. 2, the 3D solutions for an 18 μm CTC indicate large deformations that the CTC experiences in order to be completely inside the 7 μm capillary. Furthermore, the non-uniform velocity field of the solid (see Fig. 2) indicates the dynamic nature of the deformation process occurring as the CTC transitions into the capillary. The CTC has a uniform velocity field in the undeformed state (see Fig. 2A) and also in maximally deformed state when it is completely inside the capillary (see Fig. 2D, showing the moment just prior to full entrance – after which the velocity becomes uniform). When the CTC begins to occlude the capillary entrance, a significant change in the fluid field occurs (see Fig. 3). By plotting the velocity vectors alongside the solid velocities, it becomes apparent that in the separation region between the cell and wall, where repulsive forces are acting (see Methods section), there is a transient increase in local velocity. Whether a similar separation region occurs physiologically remains an open question, but experiments with blood cells passing through capillaries suggest a cell free region between the cells and the wall [42].
The key issue we aimed to address in this work was what is minimal fluid pressure required to squeeze a CTC of a given size and stiffness into the capillary? To achieve this goal, we incrementally increased the pressure until the CTC was fully in the capillary (see Fig. 4 and Results section). As the CTC deforms and occludes the capillary, the fluid pressure changes from an initial, linearly decreasing profile (see Figs. 4A and 5A) to a step-like decrease across the cell. The linearly decreasing profile is restored once the CTC is completely inside and moves through the capillary. Furthermore, when the minimal pressure needed for full entry is applied initially (e.g. when the pressure of Fig. 4D is applied to Fig. 4A), the pressure gradient across the cell remains constant during the deformation process (data not shown).
Clusters of CTCs have been detected from blood samples of cancer patients and may play an important role in cancer progression [5,9]. We thus expanded our model to evaluate how chain-like clusters differ in the pressure needed for capillary transit when compared to single CTCs. Initially, we added one additional (and identical) CTC (see Fig. 5A) and treated the two-cell cluster as a homogeneous solid. The same procedure as in Fig. 4 was performed to obtain the minimal pressure for full entry of the two-cell cluster, and it was determined that the pressure was identical to the pressure needed for the single CTC (see Fig. 5B). Furthermore, extending the chain by incorporating additional cells (e.g. 4-cell cluster) did not considerably change the needed pressure (change <5%). This indicates that our analysis and results for a single CTC applies also to chain-like CTC clusters. Furthermore, the assumption that the CTC cluster is a homogeneous solid can be amended when the actual forces connecting individual cells in a CTC cluster are determined. This may result in the ability of larger, non chain-like clusters, such as those seen clinically [9], to traverse capillaries under physiological conditions. Specifically, since we demonstrate that a single 100 μm CTC (with stiffness of 10 Pa) can pass through a 7 μm capillary this suggests that a CTC cluster consisting of 15 individual 20 μm CTCs could also traverse the capillary.
To explore the parameter space of the CTC properties, the CTC size was varied between 12 and 20 μm, whereas the CTC stiffness ranged from 10 to 1000 Pa, and for each combination of CTC size and stiffness a minimum pressure for capillary transit was determined. Each obtained pressure represented an individual data point, and these data were then plotted on a graph of pressure as a function of CTC size (see Fig. 6). A closer inspection of the data revealed that for a given stiffness the pressure vs. cell size data points could be fit with a straight line (see Fig. 6). Furthermore, for a given CTC size, the increase in pressure corresponded exactly to the increase in stiffness (e.g. for an 18 μm CTC, a 10-fold increase in stiffness from 10 to 100 Pa resulted in a 10-fold increase in pressure from 0.6 to 6 cmH2O). The linear nature of the entire system enabled us to derive the relationship between the fluid pressure, CTC size, and CTC stiffness (see Eq. (12)). For comparison, the typical physiological pressure across capillary beds of 10 cmH2O [33–35] was displayed on the same graph (see Fig. 6). The area below this pressure line (shaded area in Fig. 6) indicates the range of physical properties of a CTC that can pass through the capillary. It should be noted that Eq. (12) relationship needs further experimental validation in order to be fully applicable in a clinical setting.
An alternative way to examine the fluid pressure–CTC size–stiffness relationship is to use Eq. (12) to plot, for a given pressure, the CTC size as a function of stiffness. Fig. 7 displays three different cell size–stiffness curves corresponding to the following pressure values: (1) physiologic P=10 cmH2O (thick line), (2) twice physiologic (P=20 cmH2O), and (3) half physiologic (5 cmH2O). The two additional pressures, besides physiologic, were chosen to represent the variations that could be encountered for various organs and conditions within the body. The pressure curves were plotted on a log–log scale, spanning three orders of magnitude. A closer inspection of the P=10 cmH2O (typical physiologic) curve reveals that for a stiffness of 10 Pa the maximum diameter that can pass through the capillary is 140 μm, implying that a large 140 μm CTC cluster consisting of a number of individually interconnected CTCs can traverse the capillary. Alternatively, the largest CTC with stiffness of 1000 Pa that could traverse the 7 μm capillary under typical physiological pressure would be only 12 μm in diameter. This indicates that cell stiffness dictates how large a CTC can pass through capillaries. In Fig. 7, the dashed lines indicate experimentally measured stiffness values for various cell types, suggesting that a cell-type specific stiffness could influence passage through capillaries. To further explore this hypothesis, we wanted to test if our model predictions could be used in a clinically relevant scenario where cell stiffness is believed to play an important role.
In leukemia, a cancer of the blood that is fueled by uncontrolled multiplying of certain blood cells, the plugging of capillaries by leukemia cells causes a condition termed leukostasis that has important implications in the pathophysiology of the disease and leads to manifestation of clinical symptoms [16,17,35]. The inset in Fig. 7 shows the same data as the main graph, but only now plotted on a linear scale (more clearly showing the hyperbolic character of the pressure curves); and along with two dashed lines corresponding to experimentally measured stiffness of blood cancer cells obtained from asymptomatic or symptomatic leukemia patients [16,35]. The intersection of the asymptomatic dashed line (stiffness=130 Pa) with the P=10 cm H2O curve reveals that the maximum cell size that could pass through capillaries is 20.6 μm; for P=5 cmH2O the maximum diameter is 15.7 μm, whereas Dmax=30.5 μm for P=20 cmH2O. In other words, the model predicts that under typical physiologic pressure even large cancer cells of D=20 μm should be able to traverse capillaries, and thus leukostasis would be unlikely – in agreement with the absence of clinical symptoms. On the other hand, the model suggests that for a stiffness of 400 Pa, the maximum size under physiologic pressure would be 14 μm. Therefore, above this value leukostasis, and accompanying clinical symptoms, may start to occur as there can be a population of CTCs whose diameter is larger than 14 μm. This prediction is confirmed by the actual measurement of stiffness for symptomatic patients: stiffness=720 Pa corresponding to Dmax=12.5 μm (within the size range of even normal neutrophils [43]). The good agreement between our model and clinically observed symptoms for leukemia patients represents an example of how the pressure–size–stiffness relationship (see Figs. 6 and 7) can be employed as a starting point for a more thorough examination of underlying pathophysiology. At present, the model provides a fundamental basis; however, the model needs rigorous testing and validation, first in in vitro setups followed by in vivo studies. Ultimately, we envision that, after considerable experimental validation, the appropriately modified model could be used as an aid in improving the predictive capabilities of various disease states, as well as to monitor the effectiveness of treatment. This could be especially important in patients where onset of symptoms occurs after the biophysical properties of CTCs change, potentially extending the therapeutic window for clinicians to intervene and improve patient outcomes.
The presented modeling approach highlights the importance of CTC physical characteristics, e.g. stiffness, in the context of not only the ability to traverse small capillaries under physiological conditions, but also to drive clinical symptoms. Especially interesting is the possibility to use the model in order to gain a deeper understanding of the basic biological mechanisms involved in altering the mechanical state from pre-malignant tumor cells to CTCs. Our surprising result that large CTCs and CTC clusters can effectively traverse micro-capillaries under physiologic conditions indicates that capillary arrest is not solely based on size-restriction, but rather is a multifaceted event. The ability to establish a relationship between the microvessel blood pressure and CTC mechanical properties (i.e. size and stiffness) provides a tool to help study the fundamentals of early metastasis and the biomechanical conditions required for capillary arrest.
Future work will focus on addressing additional aspects of CTC and CTC cluster transit through capillaries from a cellular and a capillary biomechanics perspective. For the former, examining how various cellular parts (e.g. the nucleus) contribute to the overall ability of the individual/cluster CTC to deform through capillaries could be performed by incorporating nuclear viscoelastic properties into the present homogeneous cellular model. Regarding capillaries, the assumption that they remain rigid during CTC transit may not be valid for all scenarios. For example, pulmonary capillaries may be more deformable than capillaries in the hand, leading to different transit dynamics – these situations can be simulated by including a capillary model with deformable walls. Yet another intriguing possibility is that there is considerable shunting between the arterial and venous circulation, such that a large number of CTCs and CTC clusters avoid the capillary bed altogether by going through relatively large microvessels that directly connect small veins and arteries. Taken together, the computational study of how large CTCs and CTC clusters traverse microvessels may yield critical insight into how cancer cells get arrested in capillaries and provide an additional tool in elucidating the multi-faceted nature of early cancer metastasis.
5. Conclusions
We have developed a custom-built viscoelastic solid–fluid 3D computational model that enables us to examine how large circulating tumor cells (CTCs) and CTC clusters traverse capillaries, whose diameter is considerably smaller than typical cell diameter. The models demonstrate that large CTCs and CTC clusters can successfully cross capillaries provided that their stiffness is sufficiently small. Through an exploration of the relevant parameter space, a relationship between the pressure gradient across a capillary and the CTC mechanical properties (size and stiffness) was determined. The established pressure–size–stiffness relationship can be employed as a tool for various biomedical applications, such as rational design of size-based CTC isolation technologies where CTCs can experience large deformations due to high pressure gradients, as well as providing predictive capabilities in disease progression based on biophysical CTC parameters.
References
- 1.Lianidou ES, Markou A. Circulating tumor cells in breast cancer: detection systems, molecular characterization, and future challenges. Clin Chem. 2011;57:1242–1255. doi: 10.1373/clinchem.2011.165068. [DOI] [PubMed] [Google Scholar]
- 2.Maheswaran S, Haber DA. Circulating tumor cells: a window into cancer biology and metastasis. Curr Opin Genet Dev. 2010;20:96–99. doi: 10.1016/j.gde.2009.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pantel K, Brakenhoff RH, Brandt B. Detection, clinical relevance and specific biological properties of disseminating tumour cells. Nat Rev Cancer. 2008;8:329–340. doi: 10.1038/nrc2375. [DOI] [PubMed] [Google Scholar]
- 4.Karabacak NM, Spuhler PS, Fachin F, Lim EJ, Pai V, Ozkumur E, Martel JM, Kojic N, Smith K, Chen P-i, Yang J, Hwang H, Morgan B, Trautwein J, Barber TA, Stott SL, Maheswaran S, Kapur R, Haber DA, Toner M. Microfluidic, marker-free isolation of circulating tumor cells from blood samples. Nat Protoc. 2014;9:694–710. doi: 10.1038/nprot.2014.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ozkumur E, Shah AM, Ciciliano JC, Emmink BL, Miyamoto DT, Brachtel E, Yu M, Chen PI, Morgan B, Trautwein J, Kimura A, Sengupta S, Stott SL, Karabacak NM, Barber TA, Walsh JR, Smith K, Spuhler PS, Sullivan JP, Lee RJ, Ting DT, Luo X, Shaw AT, Bardia A, Sequist LV, Louis DN, Maheswaran S, Kapur R, Haber DA, Toner M. Inertial focusing for tumor antigen-dependent and -independent sorting of rare circulating tumor cells. Sci Transl Med. 2013;5 doi: 10.1126/scitranslmed.3005616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Aceto N, Bardia A, Miyamoto David T, Donaldson Maria C, Wittner Ben S, Spencer Joel A, Yu M, Pely A, Engstrom A, Zhu H, Brannigan Brian W, Kapur R, Stott Shannon L, Shioda T, Ramaswamy S, Ting David T, Lin Charles P, Toner M, Haber Daniel A, Maheswaran S. Circulating tumor cell clusters are oligoclonal precursors of breast cancer metastasis. Cell. 2014;158:1110–1122. doi: 10.1016/j.cell.2014.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cho EH, Wendel M, Luttgen M, Yoshioka C, Marrinucci D, Lazar D, Schram E, Nieva J, Bazhenova L, Morgan A, Ko AH, Korn WM, Kolatkar A, Bethel K, Kuhn P. Characterization of circulating tumor cell aggregates identified in patients with epithelial tumors. Phys Biol. 2012;9 doi: 10.1088/1478-3975/9/1/016001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Stott SL, Lee RJ, Nagrath S, Yu M, Miyamoto DT, Ulkus L, Inserra EJ, Ulman M, Springer S, Nakamura Z, Moore AL, Tsukrov DI, Kempner ME, Dahl DM, Wu CL, Iafrate AJ, Smith MR, Tompkins RG, Sequist LV, Toner M, Haber DA, Maheswaran S. Isolation and characterization of circulating tumor cells from patients with localized and metastatic prostate cancer. Sci Transl Med. 2010;2 doi: 10.1126/scitranslmed.3000403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yu M, Bardia A, Wittner B, Stott SL, Smas ME, Ting DT, Isakoff SJ, Ciciliano JC, Wells MN, Shah AM, Concannon KF, Donaldson MC, Sequist LV, Brachtel E, Sgroi D, Baselga J, Ramaswamy S, Toner M, Haber DA, Maheswaran S. Circulating breast tumor cells exhibit dynamic changes in epithelial and mesenchymal composition. Science. 2013;339:580–584. doi: 10.1126/science.1228522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Berne RM, Koeppen BM, Stanton BA. Berne and Levy Physiology. Mosby/Elsevier; 2010. [Google Scholar]
- 11.Maton A. Human Biology and Health. Pearson Prentice Hall; 1993. [Google Scholar]
- 12.Stott SL, Hsu CH, Tsukrov DI, Yu M, Miyamoto DT, Waltman BA, Rothenberg SM, Shah AM, Smas ME, Korir GK, Floyd FP, Gilman AJ, Lord JB, Winokur D, Springer S, Irimia D, Nagrath S, Sequist LV, Lee RJ, Isselbacher KJ, Maheswaran S, Haber DA, Toner M. Isolation of circulating tumor cells using a microvortex-generating herringbone-chip. Proc Natl Acad Sci USA. 2010;107:18392–18397. doi: 10.1073/pnas.1012539107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Weinberg R. The Biology of Cancer. second. Garland Science; 2013. [Google Scholar]
- 14.Shibue T, Weinberg RA. Metastatic colonization: settlement, adaptation and propagation of tumor cells in a foreign tissue environment. Semin Cancer Biol. 2011;21:99–106. doi: 10.1016/j.semcancer.2010.12.003. [DOI] [PubMed] [Google Scholar]
- 15.Balzer EM, Konstantopoulos K. Intercellular adhesion: mechanisms for growth and metastasis of epithelial cancers. Wiley Interdiscip Rev—Syst Biol. 2012;4:171–181. doi: 10.1002/wsbm.160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lam WA, Fletcher DA. Cellular mechanics of acute leukemia and chemotherapy. In: Gefen A, editor. Cellular and Biomolecular Mechancis and Mechanobiology. Springer; New York: 2011. pp. 523–558. [Google Scholar]
- 17.Lichtman MA. Rheology of leukocytes, leukocyte suspensions, and blood in leukemia – possible relationship to clinical manifestations. J Clin Invest. 1973;52:350–358. doi: 10.1172/JCI107191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rosenbluth MJ, Lam WA, Fletcher DA. Force microscopy of nonadherent cells: a comparison of leukemia cell deformability. Biophys J. 2006;90:2994–3003. doi: 10.1529/biophysj.105.067496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhang Z, Xu J, Hong B, Chen X. The effects of 3D channel geometry on CTC passing pressure – towards deformability-based cancer cell separation. Lab Chip. 2014;14:2576–2584. doi: 10.1039/c4lc00301b. [DOI] [PubMed] [Google Scholar]
- 20.Kojic M, Filipovic N, Stojanovic B, Kojic N. Computer Modeling in Bioengineering: Theoretical Background, Examples and Software. John Wiley & Sons; Chichester, England; Hoboken, NJ: 2008. [Google Scholar]
- 21.Kojic M, Bathe KJ. Inelastic Analysis of Solids and Structures. Springer; Verlag, Berlin: 2005. [Google Scholar]
- 22.Weiss JA, Maker BN, Govindjee S. Finite element implementation of incompressible, transversely isotropic hyperelasticity. Comput Methods Appl Mech Eng. 1996;135:107–128. [Google Scholar]
- 23.Kojic M. Simple concepts in computational mechanics – do they really work? J Serb Soc Comput Mech. 2013;7:1–15. [Google Scholar]
- 24.Diaz-Goano C, Minev PD, Nandakumar K. Fictitious domain/finite element method for particulate flows. J Comput Phys. 2003;192:105–123. [Google Scholar]
- 25.Glowinski R, Pan TW, Hesla TI, Joseph DD, Periaux J. A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: application to particulate flow. J Comput Phys. 2001;169:363–426. [Google Scholar]
- 26.Hu HH, Patankar NA, Zhu MY. Direct numerical simulations of fluid–solid systems using the arbitrary Lagrangian–Eulerian technique. J Comput Phys. 2001;169:427–462. [Google Scholar]
- 27.Feng ZG, Michaelides EE. Equilibrium position for a particle in a horizontal shear flow, Int. J Multiphase Flow. 2003;29:943–957. [Google Scholar]
- 28.Singh P, Hesla TI, Joseph DD. Distributed Lagrange multiplier method for particulate flows with collisions. Int J Multiphase Flow. 2003;29:495–509. [Google Scholar]
- 29.Zhang L, Gerstenberger A, Wang XD, Liu WK. Immersed finite element method. Comput Methods Appl Mech Eng. 2004;193:2051–2067. [Google Scholar]
- 30.Hu HH, Joseph DD, Crochet MJ. Direct simulation of fluid particle motions. Theor Comput Fluid Dyn. 1992;3:285–306. [Google Scholar]
- 31.Isailovic V. Ph.D. thesis. Metropolitan University; Belgrade: 2012. Numerical Modeling of Motion of Cells, Micro- and Nano- Particles in Blood Vessels. [Google Scholar]
- 32.Kojic M, Filipovic N, Slavkovic R, Zivkovic M, Grujovic N. PAK-FS: Finite Element Program for Fluid Flow and Fluid–Solid Interaction. University of Kragujevac and R&D Center for Bioengineering; Kragujevac, Serbia: 2009. [Google Scholar]
- 33.Davis MJ, Ferrer PN, Gore RW. Vascular anatomy and hydrostatic-pressure profile in the hamster-cheek pouch. Am J Physiol. 1986;250:H291–H303. doi: 10.1152/ajpheart.1986.250.2.H291. [DOI] [PubMed] [Google Scholar]
- 34.Fung YC, Zweifach BW. Microcirculation – mechanics of blood flow in capillaries. Annu Rev Fluid Mech. 1971;3:189. [Google Scholar]
- 35.Lam WA, Rosenbluth MJ, Fletcher DA. Chemotherapy exposure increases leukemia cell stiffness. Blood. 2007;109:3505–3508. doi: 10.1182/blood-2006-08-043570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sanchez-Adams J, Athanasiou KA. Biomechanical characterization of single chondrocytes. In: Gefen A, editor. Cellular and Biomolecular Mechancis and Mechanobiology. Springer; New York: 2011. pp. 247–266. [Google Scholar]
- 37.Trickey WR, Lee GM, Guilak F. Viscoelastic properties of chondrocytes from normal and osteoarthritic human cartilage. J Orthop Res. 2000;18:891–898. doi: 10.1002/jor.1100180607. [DOI] [PubMed] [Google Scholar]
- 38.Kojic N, Huang A, Chung E, Ivanovic M, Filipovic N, Kojic M, Tschumperlin DJ. A 3-D model of ligand transport in a deforming extracellular space. Biophys J. 2010;99:3517–3525. doi: 10.1016/j.bpj.2010.09.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kojic N, Kojic A, Kojic M. Numerical determination of the solvent diffusion coefficient in a concentrated polymer solution. Commun Numer Methods Eng. 2006;22:1003–1013. [Google Scholar]
- 40.Kojic N, Kojic M, Tschumperlin DJ. Computational modeling of extracellular mechanotransduction. Biophys J. 2006;90:4261–4270. doi: 10.1529/biophysj.105.078345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kojic N, Panzer MJ, Leisk GG, Raja WK, Kojic M, Kaplan DL. Ion electrodiffusion governs silk electrogelation. Soft Matter. 2012;8:6897–6905. doi: 10.1039/C2SM25783A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Secomb TW. Mechanics and computational simulation of blood flow in microvessels. Med Eng Phys. 2011;33:800–804. doi: 10.1016/j.medengphy.2010.09.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Young B, Woodford P, O’Dowd G. Wheater’s Functional Histology: A Text and Colour Atlas. Elsevier Health Sciences; UK: 2013. [Google Scholar]


