Coupling of Replica Exchange Simulations to a non-Boltzmann structure reservoir

Abstract

Computing converged ensemble properties remains challenging for large biomolecules. Replica exchange molecular dynamics (REMD) can significantly increase the efficiency of conformational sampling by using high temperatures to escape kinetic traps. Several groups, including ours, introduced the idea of coupling replica exchange to a pre-converged, Boltzmann-populated reservoir, usually at a temperature higher than that of the highest temperature replica. This procedure reduces computational cost since the long simulation times needed for extensive sampling are only carried out for a single temperature. However, a weakness of the approach is that the Boltzmann-weighted reservoir can still be difficult to generate. We now present the idea of employing a non-Boltzmann reservoir, whose structures can be generated through more efficient conformational sampling methods. We demonstrate that the approach is rigorous and derive a correct statistical mechanical exchange criterion between the reservoir and the replicas that drives Boltzmann-weighted probabilities for the replicas. We test this approach on the trpzip2 peptide and demonstrate that the resulting thermal stability profile is essentially indistinguishable from that obtained using very long (>100ns) standard REMD simulations. The convergence of this reservoir-aided REMD is significantly faster than for regular REMD. Furthermore, we demonstrate that modification of the exchange criterion is essential; REMD simulations using a standard exchange function with the non-Boltzmann reservoir produced incorrect results.

Conformational sampling is crucial to simulating biologically relevant events in atomic detail, particularly when correct Boltzmann-weighted populations are required. Trapping in local energy minima often impairs complete exploration of conformational space. The challenges and improvements in conformational sampling have been discussed in several reviews ^1,2.

One popular approach to overcoming poor sampling in biomolecular simulation is the replica exchange method (also known as parallel tempering) ^3-5. In replica exchange molecular dynamics (REMD) ⁶, a series of molecular dynamics simulations (replicas) are performed for the system of interest. In the original form of REMD, each replica is an independent realization of the system, coupled to a thermostat at a different temperature. The temperatures of the replicas span a range from low values of interest up to high values at which the system is expected to rapidly overcome potential energy barriers. At intervals during the simulations, exchanges are attempted between conformations of the system being sampled by different replicas. These exchanges are based on a Metropolis-type criterion ⁷ that considers the probability of sampling each conformation at the alternate temperature. In this manner, REMD allows the conformations sampled at low temperatures to escape kinetic traps by “jumping” directly to alternate minima being sampled at higher temperatures. Importantly, the transition probability is constructed such that the canonical ensemble properties are maintained for each replica, providing useful information about conformational probabilities as a function of temperature. Thus REMD employs high temperature simulations for improved sampling and a series of coupled simulations over a range of temperatures to reweight the ensembles to the lower temperatures of interest. REMD has been widely applied to studies of peptide and small protein folding ^3,6,8-17.

For large systems, REMD becomes intractable since the number of replicas needed to span a given temperature range increases with the square root of the number of degrees of freedom in the system^18-21. Several promising techniques have been proposed to deal with this apparent disadvantage of REMD ^18,22-27 When starting from non-native conformations, high temperature replicas give limited advantage for finding native states since more minima on the free energy landscape become accessible, further complicating the search. When a high temperature REMD replica locates a favorable low-energy basin (such as the native structure), this conformation is exchanged to a lower temperature with very high probability, and the high temperature replica needs to repeat the search process. This search process happens in a time scale related to the folding time (which is often not strongly temperature dependent). As a result, the entire set of replicas is simulated for timescales on the order of the folding time even though the conformational search improvement of REMD is generally due only to the highest temperatures.

Recognizing this weakness, we and others^26-28 have introduced a method that separates the conformational sampling and reweighting aspects of the REMD replicas by using extensive simulations at a single high temperature to generate an ensemble of structures. Since the probabilities of alternate conformations at this high temperature are not the same as at the low temperature of interest, the ensemble is reweighted by subsequent coupling to REMD. Periodic exchanges are made between randomly chosen conformations from the reservoir set and the highest temperature replica, in a manner analogous to J-walking ²⁹. This process formally provides correct ensembles at lower temperature with free energies that reflect the proper relative populations of minima. We called this method Reservoir REMD (R-REMD) since REMD is coupled to a high temperature reservoir. ²⁸

One major advantage of the reservoir approach with REMD is that a converged ensemble of conformations has to be generated for only one temperature, as compared to standard time-correlated REMD where all replicas are simulated during the entire time that the highest temperatures perform efficient searches. In R-REMD, after extensive conformational search at one temperature, the remaining temperatures feed from this ensemble and anneal these structures to rapidly construct equilibrium distributions consistent with their own temperatures. As a result of coupling to a pre-converged ensemble, the R-REMD simulation converges much more rapidly than standard temperature REMD.

Although existing reservoir REMD schemes provide substantial improvement over the original REMD, the problem of generating a converged, Boltzmann-populated reservoir is by no means trivial, especially when an explicit water model is employed. This is an important point since the cost of reservoir generation must be included in the total effort required for the simulation. We recognize that it is very likely to be much less challenging to generate a set of low energy structures than to obtain an ensemble in which they are all present in correct relative populations. It is in this spirit that we demonstrate that a reservoir with a non-Boltzmann population can nonetheless be used to rapidly and efficiently converge REMD simulations. We start by re-deriving the REMD exchange probability equation, with emphasis on the steps that involve reservoir driven REMD. We demonstrate that any complete reservoir can be employed as long as the probability distribution is known, and correct Boltzmann-weighted ensembles can be obtained for the replicas.

We consider N replicas (R₁ to R_N), associated with N temperatures (T₁ to T_N). At time t, each replica is found with coordinate X_i, and temperature T_m, which we will write as $X_i^m$. We denote the set of coordinates for all replicas at time t as the vector $\mathbf{Q}=\{{\mathrm{X}}_{\mathrm{i}}^{\mathrm{m}}\}$ with both i and m indices bounded between 1 and N. The existence of a well defined limiting probability distribution of structures at each temperature is assumed, written as $P(X_i^m)$. Importantly, the distributions for each temperature need not obey the same rules³⁰. Since the replicas are non-interacting, the probability of finding coordinate set Q at the current distribution of temperatures can be written as a direct product.

We now consider the exchange of a pair of replicas, between coordinates X_j at temperature $s(X_j^s)$ and coordinate X_k at temperature $t(X_k^t)$. The rest of the replicas are not exchanged and hence stay at their previous temperatures. Ensuring microscopic reversibility, we require that the forward and backward transition rates are equal to each other.

$$W(X_1^1,\cdots ,X_j^s,X_k^t,\cdots ,X_N^N\to X_1^1,\cdots ,X_j^t,X_k^s\cdots ,X_N^N)P(X_1^1,\cdots ,X_j^s,X_k^t,\cdots ,X_N^N)=W(X_1^1,\cdots ,X_k^s,X_j^t,\cdots ,X_N^N\to X_1^1,\cdots ,X_j^s,X_k^t\cdots ,X_N^N)P(X_1^1,\cdots ,X_k^s,X_j^t,\cdots ,X_N^N)$$ (1)

Which, by renaming the transition probabilities and exploiting the ability to express the populations as products, yields:

$$\frac{W(X_j^s,X_k^t\to X_j^t,X_k^s)}{W(X_k^s,X_j^t\to X_j^s,X_k^t)}=\frac{P(X_k^s)P(X_j^t)}{P(X_j^s)P(X_k^t)}$$ (2)

The next step, which is key to the present algorithm, is the insertion of the limiting probability distributions for each temperature. In the particular case of Boltzmann populations in the canonical ensemble, with $P(X_k^s)\propto e^{-{\beta }_{s}E(X_k)}$ and β_s = (k_bT_s)⁻¹, the exchange criteria equation becomes the well known form of standard temperature REMD:

$$\frac{W(X_j^s,X_k^t\to X_j^t,X_k^s)}{W(X_k^s,X_j^t\to X_j^s,X_k^t)}=e^{({\beta }_t-{\beta }_s)(E_k-E_j)}$$ (3)

In the case of reservoir REMD, the equations for exchange resemble those of regular REMD, with the only difference being that the highest replica as been pre-obtained and it is not time-correlated with the others. This means that at every exchange point, the (N-1)th replica (or others also if desired) attempts to exchange with one of the members of the reservoir. Our present focus is to permit a different probability distribution for the reservoir.

Suppose that for replicas 1 to N-1, we desire a Boltzmann population of structures. Let's assume also that the reservoir has the limiting distribution P_R(X). It is clear that the derivation above would produce exchange probabilities exactly like those in REMD if none of the two replicas involved is the reservoir, but it would create a different condition when attempting to exchange between the reservoir and any regular replica.

Let's assume that one has a reservoir with M members, where each structure is present exactly one time, as would be obtained using a method such as a grid-based search. In this case, using the nomenclature above, the probability of finding structure i in the reservoir of size M is: $P(X_i^R)=\frac{1}{M}$. Under these conditions, the exchange probability between replicas NOT involving the reservoir obeys the standard e^{(β_t−β_s)(E_k−E_j)} expression, while exchanges between any real replica and the reservoir must obey:

$$\frac{W(X_j^R,X_k^t\to X_j^t,X_k^R)}{W(X_k^R,X_j^t\to X_k^t,X_j^R)}=\frac{P(X_k^R)P(X_j^t)}{P(X_j^R)P(X_k^t)}=\frac{(1/M)e^{-{\beta }_i{E}_j}}{(1/M)e^{-{\beta }_i{E}_k}}{e}^{-{\beta }_t(E_j-E_k)}$$ (4)

This is essentially the same as standard REMD except for the weighting factor for ΔE. The exchange between the reservoir and any temperature replica looks like a regular Metropolis MC step. In REMD terms this is also equivalent to having the highest replica being at an infinite temperature (β_R=0), consistent with a flat probability distribution. In practical terms, reservoir structures generated at very high temperatures would likely have a significant thermal component to the potential energy and thus the acceptance probability would be negligible.

Although the exchange probability equations can formally be derived for any reservoir of known probability distribution, we focus in this report on the straightforward case described above in which structures are present in the reservoir in equal probabilities (eq. 4). We implemented the resulting algorithm into the widely-used Amber program ³¹, and we describe below the results obtained for a non-trivial model peptide that we have previously studied using standard and reservoir REMD²⁸.

System and Results

In order to test the results of the modified exchange criterion (eq. 4), we studied the tryptophan zipper peptide that we have previously sampled using extensive standard REMD simulations²⁸ as well as REMD with a Boltzmann-weighted reservoir ²⁸. Developed by Starovasnik and coworkers ³² trpzip2 (PDB code 1LE1), has a high propensity to form a β-hairpin in solution at room temperature (Figure 1). We employed the same force field and simulation methodology as we used for those studies. (see supplemental information). We showed that this combination is able to reproduce not only the experimentally observed structure of trpzip2, but also the temperature-dependent stability. Thus the peptide provides an excellent model for testing sampling algorithms under conditions that are directly relevant to experimental data.

Figure 1.

The trpzip2 model peptide, in the native β-hairpin conformation. Backbone atoms are shown colored by element; for clarity, side chain heavy atoms are only shown for Trp residues (orange).

Our previous work using a Boltzmann-weighted reservoir for trpzip2 REMD employed a reservoir of 10,000 structures that were extracted from standard MD simulations at 400K. This was shown to be sufficient to properly seed the REMD exchange simulations at lower temperatures when the standard exchange criterion (eq. 3) was employed. We demonstrated that coupling to this reservoir provided significantly more rapid convergence, with the same thermal stability profile as standard REMD. To test whether similar results could be obtained with the non-Boltzmann reservoir, we performed a cluster analysis on the Boltzmann-weighted reservoir. We generated a new, non-Boltzmann weighted ensemble by extracting only the representative structures from each of the 700 clusters. This new “flat” reservoir has by definition a probability of 1/700 for each of the members, since the additional population of each cluster was discarded. While the original Boltzmann-weighted reservoir had approximately 3% native structures, the native hairpin is adopted by only 1 of the 700 structures in the non-Boltzmann reservoir. We note that clustering only approximates the flat distribution implied in eq. 4, since individual conformational basins are represented by single structures rather than a continuous probability density.

The main result of this letter is presented in Figure 2. Melting curves were generated for several simulations by calculating the average population of native structures at each temperature. The values are computed over the entire (post-equilibration) REMD ensemble. The simulations include standard REMD (black line, from our previously published data²⁸) along with two simulations in which the REMD replicas were coupled to the non-Boltzmann ensemble. In one simulation, the standard exchange criterion (eq. 3) was used (red line) to couple the reservoir and the replicas, while the other (blue line) employed an exchange criterion that accounted for the non-Boltzmann probability distribution in the reservoir (eq. 4). We observe that the thermal stability profile obtained using the modified exchange criterion is essentially indistinguishable from that obtained using standard REMD simulations without a reservoir.

Figure 2.

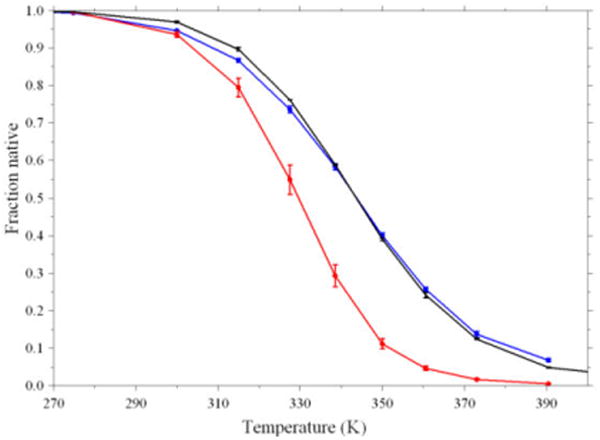
Thermal stability profiles for trpzip2 obtained from REMD simulations. Black: standard REMD (150ns); red: REMD with non-Boltzmann reservoir and standard (eq. 3) exchange probability (20ns); blue: REMD with non-Boltzmann reservoir and modified (eq. 4) exchange probability (25ns). Error bars indicate lower bounds to uncertainty, obtained from the difference between data calculated from first and last half of the ensemble.

Our main point is to demonstrate that the REMD exchange criterion can be successfully modified to rigorously incorporate non-Boltzmann weighted reservoirs without any detrimental effect on the equilibrium populations sampled by the temperature replicas. The reservoir that we generated has the same structure types as our Boltzmann-weighted reservoir (only the relative populations changed from the original values to the 1/M “flat” reservoir). One might therefore ask if the change in exchange acceptance criterion is truly needed. To address this point, we repeated the reservoir REMD calculation with the 700 member non-Boltzmann weighted reservoir, but used the standard REMD exchange acceptance criterion (eq. 3 instead of the modified version (eq. 4)). As shown in Figure 2, this procedure resulted in significant errors in the thermal profile over the entire range simulated due to the different scaling factor applied to the potential energy difference in the calculation of exchange probability. The Δβ scaling factor in standard REMD (eq. 3) is smaller than the β term in the criterion modified for the “flat” ensemble (eq 4); thus the low-energy native conformation is accepted too infrequently with the standard criterion. It is interesting to note that this strongly affects not only the ensemble sampled at 390 K where exchanges with the reservoir occur, but the ensembles at all other temperatures also show a depression of native stability when the incorrect exchange criterion is used. As shown in Figure 2, the use of an exchange criterion that directly accounts for the probability distribution in the reservoir essentially eliminates this error (despite the approximate nature of the clustering approach to “flat” reservoir generation, as noted above).

While standard REMD converges to the proper native population, the new method also does so but at a much faster rate. Figure 3 shows the population of the native state at the melting temperature versus simulation time. The colors are the same as the same as those in figure 2. It is clear that a speedup of the of the order of 10× is obtained for this particular system by using the reservoir. A similar speedup is obtained with the unmodified exchange criterion (eq. 3), but the final population has significant error. The speedup from using Boltzmann-weighted or non-Boltzmann weighted reservoirs is comparable (Figure 3).

Figure 3.

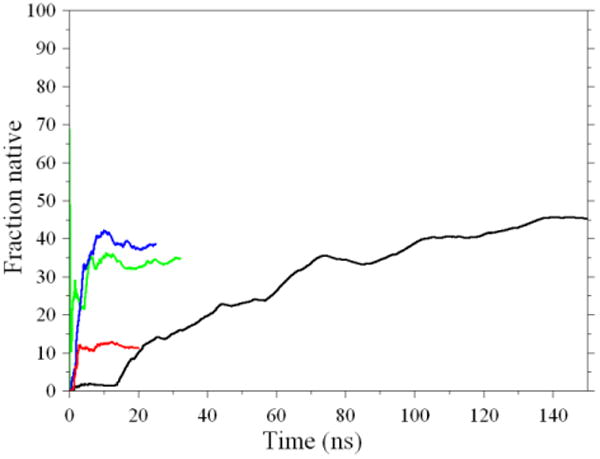
Fraction of native hairpin conformation as a function of time at 350K for four REMD simulations. Black: standard REMD; red: REMD with non-Boltzmann reservoir and standard exchange probability (eq. 3); blue: REMD with non-Boltzmann reservoir and modified exchange probability (eq. 4); green: REMD with Boltzmann reservoir and standard exchange probability (eq. 3). It is apparent that the simulations employing the reservoir reach a plateau value much more rapidly than standard REMD and that the non-Boltzmann reservoir requires modified exchange probability.

In summary, we have demonstrated that REMD simulations can be rigorously coupled to a reservoir with an arbitrary, known probability distribution, while still efficiently driving the REMD replicas toward Boltzmann-weighted ensembles. We employed a cluster-based approach to reservoir generation, but point out that the procedure we used to derive eq. 4 will also enable the use of more general methods for generation of structure reservoirs, at significantly reduced cost than previously reported Boltzmann-weighted reservoirs. We expect that this procedure will dramatically extend the range of problems that are amenable to study through REMD simulation.