Predicting Functional Independence Measure Scores During Rehabilitation with Wearable Inertial Sensors

Abstract

Evaluating patient progress and making discharge decisions regarding inpatient medical rehabilitation rely upon standard clinical assessments administered by trained clinicians. Wearable inertial sensors can offer more objective measures of patient movement and progress. We undertook a study to investigate the contribution of wearable sensor data to predict discharge functional independence measure (FIM) scores for 20 patients at an inpatient rehabilitation facility. The FIM utilizes a 7-point ordinal scale to measure patient independence while performing several activities of daily living, such as walking, grooming, and bathing. Wearable inertial sensor data were collected from ecological ambulatory tasks at two time points mid-stay during inpatient rehabilitation. Machine learning algorithms were trained with sensor-derived features and clinical information obtained from medical records at admission to the inpatient facility. While models trained only with clinical features predicted discharge scores well, we were able to achieve an even higher level of prediction accuracy when also including the wearable sensor-derived features. Correlations as high as 0.97 for leave-one-out cross validation predicting discharge FIM motor scores are reported.

I. Introduction

Often when an individual suffers from an injury or illness, such as stroke, they undergo intense inpatient rehabilitation in order to regain everyday functioning. Monitoring of motor recovery is typically accomplished by human observation using standard clinical rating scales, such as the functional independence measure (FIM), to determine independence in activities of daily living (ADLs) [1]. The FIM is administered at admission and discharge from inpatient rehabilitation by clinical staff who are credentialed to administer the instrument. The FIM is a well-validated assessment measuring functional status on a 0–7 rating scale for 18 items representing 6 domains: self-care, sphincter control, transfers, locomotion, communication, and social cognition. In addition to a total FIM score, separate scores are developed from the motor function items and cognitive function items.

Between the admission and discharge FIM assessments, clinical observations by therapists are typically used to characterize progress and make treatment decisions, including determining discharge dates. Because this approach relies on subjective judgment, it lacks detailed quantifiable information to characterize patient movement patterns. During this period, more precise quantitative measurement of patient performance can be collected via pervasive technology such as inertial measurement units (IMUs). IMUs are an ideal technology for tracking movement because they can easily be attached to the body. Computations based on data collected from wearable IMU sensors can provide therapists with measures that are not subject to the inter-observer bias that is possible with subjective clinical judgments. These supplementary measurements can identify subtle performance changes during rehabilitation that are difficult to directly observe, using metrics such as whole body or individual limb linear acceleration and angular velocity.

Sensor-based data, such as gait cycle parameters, can offer clinicians with insights on patient function and rehabilitation progress. We hypothesize that this data also provides power for predicting future patient performance on clinical rating scales. While data mining techniques have been applied to medical records to predict clinical performance, augmenting medical records with sensor data (such as IMU data) represents a new direction of research. To validate our hypothesis, we utilized patient medical record information, sensor data measured at mid-stay during inpatient rehabilitation, and a combination of the two data sources to predict FIM motor scores at discharge. Such a mapping of therapy-collected inertial sensor data into a standardized clinical assessment domain offers several benefits in comparison to human observation alone:

• More accurate tracking of the time course of recovery.

• Reduction in the subjectivity of therapist observations between admission and discharge.

• More ecologically valid assessment of patient ability by avoiding the “test” situation which is often not representative of everyday functioning [2].

In this paper, we propose a machine learning methodology to predict discharge FIM scores for patients at an inpatient rehabilitation hospital. Initially, we predict discharge scores using only patient medical record information available upon admission. We then improve prediction accuracy by utilizing wearable inertial sensor data collected during ambulatory tasks performed mid-stay during inpatient rehabilitation. Our approach provides insight into individual patient progress between admission and discharge by using movement data collected during therapy tasks, without the need to re-administer the entire FIM assessment.

II. Related Work

Several studies have built models to predict clinical outcomes, such as assessments and hospital length of stay (LOS), from patients at inpatient rehabilitation facilities. These studies can be grouped into two categories based on the features that are used as predictors: non-technology-based clinical metrics and technology-based metrics.

A. Clinical Predictors

Sonoda et al. [3] used linear regression to predict discharge FIM motor scores for 131 first-stroke patients at an inpatient rehabilitation hospital. Features used for prediction included admission data included age, days since onset of the stroke to admission, admission FIM cognitive and motor scores, and the reciprocal of the admission FIM motor score. The regression models yielded correlations of r = 0.89 for a training group and r = 0.93 for a validation group. Similar studies predicting FIM scores using only clinical predictors include Matsugi et al. [4], Jeremic et al. [5], Fujiwara et al. [6], Tsuji et al. [7], and Jeong et al. [8]. Jeong and colleagues predicted discharge FIM to investigate the differences between two stroke groups: 4,311 patients admitted to acute hospitals (R² = 0.78) and 1,941 patients admitted to convalescent hospitals (R² = 0.66).

Sakurai et al. [9] investigated the predictive ability of admission FIM scores of patients with stroke (N = 286) to determine functional independence. Independence was classified as either completely dependent/requiring maximal assistance, moderately dependent/requiring minimal assistance, or completely independent/requiring supervision. The study concluded the motor and cognitive scores of the FIM are valid predictors of functional independence, whereas the individual FIM tasks alone are not useful predictors.

In addition to predicting clinical assessments scores such as the FIM, a fair amount of research has been performed to predict individual patient length of stay [10]–[13]. Tan et al. [10] considered motor function on admission and the effects of patients’ socioeconomic status and family structure on LOS for patients with stroke. Franchignoni et al. [11] found individual FIM task scores on admission to be strong predictors of patients’ LOS, with the tasks related to transfers having the highest predictive ability. Brosseau et al. [12] discovered that age, functional status at one week after admission, perceptual status, and balance status accounted for 43.6% of the total variance in the rehabilitation LOS for stroke patients. Furthermore, functional status at admission, rehabilitation program, motor status, communication problems, and medical complications were indirect predictors of LOS.

B. Technology-based Predictors

In addition to utilizing clinical metrics, several studies have investigated mapping technology-based measurements onto clinical assessment scores. Zariffa et al. [14] considered the relationship between robot-collected kinematic data and the graded redefined assessment of strength, stability, and prehension, action research arm test (ARAT), and spinal cord independence measure. Olesh et al. [15] collected data from a Kinect sensor and mapped it to the Fugl-Meyer assessment (FMA) and ARAT. Similarly, Wang et al. [16] mapped accelerometer data from upper arm movements to the FMA for shoulder-elbow. Finally, Simila et al. [17] analyzed lower-back accelerometer data to estimate Berg balance scale scores for identifying subjects with high or low risk of falling.

The aforementioned studies have primarily examined the relationships between technology-based metrics and associated clinical rating scales. These studies do not utilize collected data to project into the future and predict discharge assessment scores. On the other hand, Mostafavi et al. [18] predicted several clinical scores using metrics collected from the kinensiological instrument for normal and altered reaching movements (KINARM) rehabilitation robotic device. Data were collected from two tasks: an upper limb reaching task and a positioning task. Using linear regression, robot-based measurements from these tasks for 126 stroke patients were mapped to predictions of FIM total score, FIM motor score, LOS, the Purdue pegboard test, and the modified Ashworth score with statistically significant accuracy (see [18], Table 1). This work differs from our study in the choice of technology (robotic device vs. wearable inertial sensors), the involved parts of the body (upper limb vs. whole body), and the timeline of participant data collection.

TABLE I.

Functional independence measure (FIM) tasks and associated categories

Category	Task Type	#	Task
Motor	Self-care	1	Eating
		2	Grooming
		3	Bathing
		4	Upper body dressing
		5	Lower body dressing
		6	Toileting
	Sphincter control	7	Bladder management
		8	Bowel management
	Transfers	9	Bed to chair transfer
		10	Toilet transfer
		11	Tub/shower transfer
	Locomotion	12	Walk/wheelchair
		13	Stairs
Cognitive	Communication	14	Comprehension
		15	Expression
	Social cognition	16	Social interaction
		17	Problem solving
		18	Memory

The study presented in this paper aims to further move the field forward in several aspects. First, we combine clinical metrics with movement data collected using IMU technology that is relatively inexpensive and unobtrusive. Furthermore, while wearing the inertial sensors, participants in our study perform a sequence of ambulatory tasks that are representative of the patient’s ecological environment. Potentially, our sensor platform will be able to collect movement profiles from various therapy tasks and map this information into clinical assessments. Finally, previous studies have focused on single, homogeneous populations, often only considering patients who do not have other medical complications [3], [9] or have a LOS greater than a certain duration [9]. While these restrictions are useful to narrow the scope of findings, we are investigating several rehabilitation populations with varying LOS and comorbidities. We do not distinguish between medical conditions because our proposed wearable sensor platform, algorithms, and machine learning methodologies are applicable to all individuals undergoing inpatient rehabilitation. In summary, we aim to lay the foundation for a monitoring system that uses movement data collected during therapy to predict discharge clinical scores at any point during rehabilitation for inpatient rehabilitation populations.

III. Methods

We undertook a study of subjects undergoing rehabilitation at an inpatient rehabilitation hospital following injuries and illnesses such as stroke, traumatic brain injury, and spinal cord injury. This study was approved by the Institutional Review Board of Spokane, WA. Our approach consists of three steps:

1. Collect patient data from two sources:

   1. Patient wearable inertial sensor data as they ambulated throughout an ecological environment (see Section III-A2).

   2. Medical records both from patients who participated in the wearable sensor study and from patients who were not involved in the wearable sensor study. The latter was collected to provide additional training instances for comparison to a baseline FIM prediction model using only clinical features available upon admission (see Section III-A4).

2. Compute sensor-based metrics and analyze each metric’s predictive utility (see Sections III-C and IV-A).

3. Train and test machine learning models to predict discharge FIM scores (see Section IV-B).

The following sections provide details on each of these steps.

A. Data Collection

1) Functional Independence Measure

The FIM is a clinical assessment used to measure patient functioning at inpatient rehabilitation hospitals [1]. The FIM is measured at two distinct points in time: admission (FIM_A) and discharge (FIM_D). The FIM measures the level of assistance required to perform 18 ADL tasks (see Table I) [19]. The tasks are categorized as either motor (13 tasks) or cognitive (5 tasks). Each task is scored on a 7-point ordinal scale to measure independence as determined by the amount of assistance required to perform each ADL task. A score of 7 denotes a helper is not required for the patient to perform the task and a score of 1 denotes total assistance from a helper is required for the patient to perform the task [19].

The FIM motor aggregate score (FIM_motor) is the sum of all 13 individual motor task scores. The cognitive aggregate score (FIM_cog) is the sum of all five individual cognitive task scores. Finally, the total FIM score is the sum of all individual task scores. The change in FIM from admission to discharge is important in the clinical setting, representing the improvement or regression exhibited by the patient during their stay at the rehabilitation hospital. The change in FIM is represented by:

$$\mathrm{\Delta }\mathit{FIM}={\mathit{FIM}}_D-{\mathit{FIM}}_A$$ (1)

Furthermore, the rehabilitation efficiency ratio (RER), also known as FIM efficiency, determines the average rate of FIM change per day:

$$\mathit{RER}=\frac{\mathrm{\Delta }\mathit{FIM}}{\mathit{LOS}}$$ (2)

where LOS is the length of stay at the rehabilitation facility, measured in number of days.

2) Ambulatory Circuit Sensor Data

Participants in a wearable sensor study were recruited as part of a single-arm prospective cohort study with repeated measures of participant performance on standardized gait tasks. Data were collected at two different testing sessions separated by seven days. The first test session (S1) occurred shortly after the participant became physically able to walk the distance required of the gait task. The second test session (S2) occurred one week later, a date that was typically close to their discharge. During each test session, participant performance was recorded two times, producing two separate trials (T1, T2) at S1 and two trials (T3, T4) at S2.

A standardized ambulatory circuit (AC) [20] was designed to assess the mobility and physical ability of the participants during the test sessions. The AC is a continuous sequence of activities performed in a simulated community environment at the rehabilitation facility. This circuit represents a more complex version of the traditional timed up and go (TUG) test that is frequently used for gait assessment [21]. The circuit includes rising from a seated position, moving with both linear and curvilinear gait, surface transitions, a transfer into and out of a sport utility vehicle (SUV), and sitting down in the chair from which the participant began. Fig. 1 outlines the AC components. The AC also includes a stops walking when talking test [22] (in Fig. 1 the vertical gray dashed line between linear and curvilinear walking sections), which determines if an individual who is walking slows down or stops when asked a simple question like “when is your birthday?” AC researchers manually record whether the participant slowed down or stopped to answer a question, but this feature was not included in the current study because it is not yet automatically computed from the sensor data.

Fig. 1.

The ambulatory circuit. The solid line represents the circuit path and the dashed line represents the mirrored return portion. Key circuit tasks are labeled with distances in meters.

Three Shimmer3 wireless IMUs were used to record participant motion as they ambulated through the AC. The Shimmer3 platform contains a tri-axial accelerometer and a tri-axial gyroscope. One IMU was placed centrally on the lumbar spine at the level of the third vertebrae, near the individual’s center of mass (COM) [23]. Additionally, one sensor was placed on each shank, above the ankle and in line with the tibia. The accelerometer range was set to ± 2g for the COM sensor and ± 4g for the shanks. The gyroscope ranges for the shank and COM sensors were set at 500 °/s and 250 °/s, respectively. The data were collected at a sampling frequency of 51.2 Hz for all sensor platforms. Processing of the sensor data consisted of several steps (see Fig. 2). First, the timestamps were aligned from the three different sensor platforms. Next, to correct for the orientation of the shank sensors along the tibia, the sensor local coordinate system was transformed to the body coordinate system. Acceleration data were filtered with a 4^th order band pass Butterworth filter using cutoff frequencies of 0.1 Hz and 3 Hz for the COM accelerometer [24] and 0.1 Hz and 10 Hz for the shanks [25]. The gyroscope signals for all sensors were low passed filtered at 4 Hz [26].

Fig. 2.

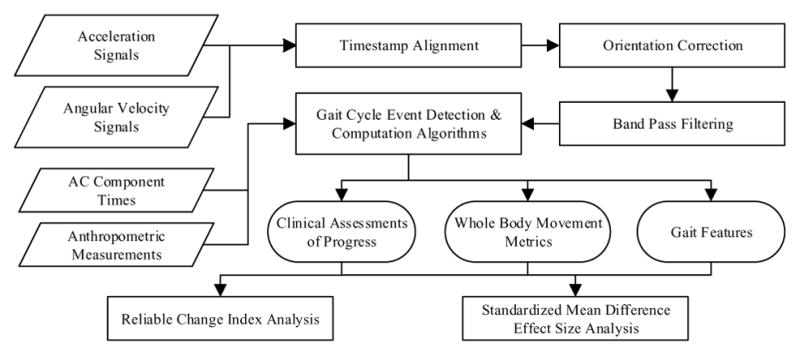
Sensor data processing. Wearable inertial sensor data were timestamp aligned, oriented, and filtered before metrics were computed and statistical analyses were performed.

3) Participant Characteristics

AC data collection is ongoing, with 20 participants completing both testing sessions to date. Participants were in various rehabilitation impairment categories (RICs), such as stroke and non-traumatic brain injury. Table II describes the AC participant demographics and FIM scores. As can be seen, the mean age of the group is 71.55 ± 10.62 years. Of the AC participants, 70% (N = 14) were receiving therapy services to recover from a stroke and the average LOS was 20.75 ± 5.35 days. S2 testing was near discharge, on average 2.65 ± 2.25 days from discharge.

TABLE II.

Characteristics and functional independence measure (FIM) scores for participants in the wearable sensor study

PID	RIC	Involved Side	Gender	Age	Comorbidities	LOS	#Days A→S1	#Days S2→D	FIMA-cog	FIMD-cog	FIMA-motor	FIMD-motor	Total RER
001	Stroke	L	M	73	N	31	16	8	23	34	25	70	1.81
002	Cardiac	N/A	M	84	Y	14	4	3	26	30	33	62	2.36
003	Misc	N/A	M	68	Y	19	8	4	32	33	37	65	1.53
004	Stroke	L	M	75	Y	21	14	0	15	26	24	52	1.86
005	Stroke	No paresis	M	63	Y	23	15	1	25	33	44	74	1.65
006	Stroke	L	F	82	Y	29	18	5	21	27	25	59	1.38
007	NTBI	N/A	M	52	Y	22	8	7	21	31	43	62	1.32
009	Stroke	No paresis	F	85	Y	20	8	5	22	30	46	58	1.00
010	NTBI	N/A	F	67	N	24	17	0	16	28	25	40	1.13
011	Stroke	L	M	74	N	20	11	2	16	23	28	49	1.40
013	NTSCI	N/A	M	76	N	15	7	1	25	30	26	58	2.47
014	Stroke	No paresis	M	55	Y	17	9	1	16	25	45	78	2.47
015	Stroke	L	M	85	N	13	4	2	32	33	55	80	2.00
016	Stroke	L	M	54	N	21	13	1	23	29	37	69	1.81
018	Stroke	L	M	88	N	29	19	3	26	32	27	60	1.34
019	Stroke	R	M	65	N	14	5	2	30	31	49	72	1.71
020	Misc	N/A	M	74	Y	28	17	4	21	30	31	61	1.39
021	Stroke	R	F	74	N	16	9	0	24	33	40	80	3.06
024	Stroke	L	F	63	N	18	9	2	29	31	38	73	2.06
025	Stroke	R	F	74	N	21	12	2	19	22	37	61	1.29
Mean	-	-	-	71.55	-	20.75	11.15	2.65	23.10	29.55	35.75	64.15	1.752
SD	-	-	-	10.62	-	5.35	4.75	2.25	5.20	3.43	9.27	10.51	0.53

A = admission, cog = cognitive, D = discharge, F = female, FIM = functional independence measure, L = left, LOS = length of stay, M = male, N = no, N/A = not applicable, NTBI = non-traumatic brain injury, NTSCI = non-traumatic spinal cord injury, PID = patient identification, R = right, RER = rehabilitation efficiency ratio, RIC = rehabilitation impairment category, SD = standard deviation, Y = yes.

4) Additional Medical Record Data

For training baseline admission models, additional data were collected from the in-patient rehabilitation hospital during October 2010–December 2013. The dataset contains data for 4,936 patients of various RICs. These patients did not participate in the AC wearable sensor study. Consequently, this dataset is henceforth referred to as the non-AC (NAC) dataset. Table III provides patient demographics and FIM performance summaries for the NAC patient data. As can be seen in Table III, NAC patients are primarily in the RICs of stroke and lower extremity joint replacement.

TABLE III.

Summary characteristics and functional independence measure (FIM) scores for patients with admission data only (non-ambulatory circuit dataset)

RIC	N (%)	Males (SD)	Age (%)	No comorbidities (SD)	LOS (SD)	FIMA-cog (SD)	FIMD-cog (SD)	FIMA-motor (SD)	FIMD-motor (SD)	Total RER (SD)
Amputation of lower extremity	96 (1.94%)	61 (63.54%)	69.91 (11.74)	32 (33.33%)	12.69 (6.18)	25.56 (6.22)	30.19 (4.78)	37.95 (11.93)	56.62 (14.60)	2.23 (1.39)
Cardiac disorders	344 (6.97%)	202 (58.72%)	78.12 (10.00)	179 (52.03%)	11.04 (5.28)	23.74 (6.05)	29.67 (4.68)	42.29 (9.67)	61.24 (13.07)	2.61 (1.41)
Fracture of lower extremity	338 (6.85%)	117 (34.62%)	80.27 (11.49)	240 (71.01%)	12.37 (4.49)	23.64 (6.79)	29.29 (5.48)	35.60 (9.63)	56.35 (13.71)	2.37 (1.33)
Guillain Barré syndrome	30 (0.61%)	17 (56.67%)	48.43 (18.07)	15 (50.00%)	14.80 (10.48)	26.30 (6.39)	32.10 (4.39)	35.67 (16.39)	61.73 (21.21)	2.63 (1.56)
MMT-BSCI	86 (1.74%)	51 (59.30%)	45.84 (17.88)	54 (62.79%)	18.91 (15.83)	21.40 (7.53)	29.91 (5.25)	33.48 (15.12)	56.09 (19.17)	2.60 (1.81)
MMT-NBSCI	155 (3.14%)	79 (50.97%)	64.36 (19.81)	110 (70.97%)	11.20 (5.34)	25.88 (6.38)	31.77 (4.13)	37.92 (10.77)	61.70 (13.25)	3.02 (1.66)
Miscellaneous	386 (7.82%)	203 (52.59%)	71.80 (17.19)	166 (43.01%)	11.44 (6.14)	24.36 (5.97)	29.92 (4.77)	40.74 (11.43)	60.41 (15.16)	2.72 (2.26)
Non-traumatic brain injury	295 (5.98%)	161 (54.58%)	62.82 (17.59)	129 (43.73%)	13.16 (7.00)	17.17 (6.75)	24.50 (6.75)	41.86 (13.72)	62.74 (17.27)	2.68 (2.00)
Non-traumatic spinal cord injury	176 (3.57%)	94 (53.41%)	66.16 (15.29)	129 (73.30%)	15.49 (9.62)	26.38 (6.09)	31.23 (4.47)	35.32 (12.92)	56.43 (18.06)	2.30 (1.85)
Neurological conditions	279 (5.65%)	128 (45.88%)	68.93 (14.78)	194 (69.53)	11.37 (5.92)	25.32 (6.62)	30.37 (5.24)	38.36 (11.18)	59.37 (16.58)	2.83 (1.77)
Other orthopaedic	281 (5.69%)	100 (35.59%)	75.34 (12.31)	209 (74.38%)	10.79 (4.73)	24.21 (6.54)	29.71 (4.99)	37.98 (10.35)	58.49 (14.58)	2.88 (2.07)
Osteoarthritis	1 (0.02%)	0 (0.00%)	88 (N/A)	1 (100.00%)	15 (N/A)	19 (N/A)	25 (N/A)	30 (N/A)	47 (N/A)	1.53 (N/A)
Pain syndromes	10 (0.20%)	2 (20.00%)	73.60 (16.30)	8 (80.00%)	10 (6.99)	23.40 (7.74)	30.50 (5.19)	40.20 (16.61)	55.20 (15.35)	2.72 (3.12)
Pulmonary disorders	59 (1.20%)	31 (52.54%)	74.32 (8.71)	34 (57.63%)	10.68 (4.85)	23.80 (6.81)	29.71 (4.30)	41.56 (12.16)	59.76 (17.37)	2.82 (2.14)
Replacement of lower extremity joint	744 (15.07%)	259 (34.81%)	73.56 (10.60)	541 (72.72%)	9.49 (3.80)	27.20 (5.29)	32.23 (3.17)	43.42 (9.19)	67.37 (10.10)	3.38 (1.49)
Rheumatoid arthritis	1 (0.02%)	1 (100.00%)	17 (N/A)	0 (0.00%)	7 (N/A)	28 (N/A)	35 (N/A)	50 (N/A)	43 (N/A)	0 (N/A)
Stroke	1270 (25.73%)	659 (51.89%)	71.55 (14.25)	943 (74.25%)	16.71 (9.17)	17.40 (6.56)	25.24 (6.54)	36.25 (14.47)	55.84 (19.31)	2.14 (1.70)
Traumatic brain injury	272 (5.51%)	188 (69.12%)	57.95 (23.38)	140 (51.47%)	17.52 (14.06)	13.65 (6.70)	22.28 (7.79)	38.71 (18.17)	61.19 (20.75)	2.55 (1.98)
Traumatic spinal cord injury	113 (2.29%)	91 (80.53%)	50.71 (19.00)	64 (56.64%)	28.61 (20.79)	27.64 (6.37)	32.60 (3.42)	25.81 (13.47)	48.12 (21.60)	1.59 (1.52)
Total	4936	2444 (49.51%)	70.24 (16.40)	3188 (64.59%)	13.63 (8.99)	22.12 (7.67)	28.46 (6.27)	38.58 (12.98)	59.53 (16.91)	2.60 (1.80)

A = admission, BSCI = brain injury or spinal cord injury, cog = cognitive, D = discharge, FIM = functional independence measure, LOS = length of stay, MMT = major multiple trauma, N = count, NBSCI = no brain injury or spinal cord injury, RER = rehabilitation efficiency ratio, RIC = rehabilitation impairment category, SD = standard deviation.

The information in this dataset represents traditional medical record data. Other projects have focused on mining medical records and predicting patient health from this information alone. In this paper, our goal is to show that prediction of rehabilitation outcomes can be enhanced by including sensor data in the predictive model alongside medical record data. As we will see, including both sources of information can present a challenge because the medical record is data rich (in number of patient records) while the sensor data is fairly sparse.

B. Clinical Outcome Prediction

Useful clinical outcomes to predict include discharge FIM motor and cognitive scores, which represent patient functioning at the end of inpatient rehabilitation. To see the distribution and changes of these scores between admission and discharge, Fig. 3 shows box-and-whisker plots for AC and NAC participant motor and cognitive FIM scores. Since AC performance metrics primarily measured motor functioning, our models focused on predicting the FIM motor score. To further explore the predictive abilities of the AC, we also trained models to predict FIM cognitive and individual FIM item scores.

Fig. 3.

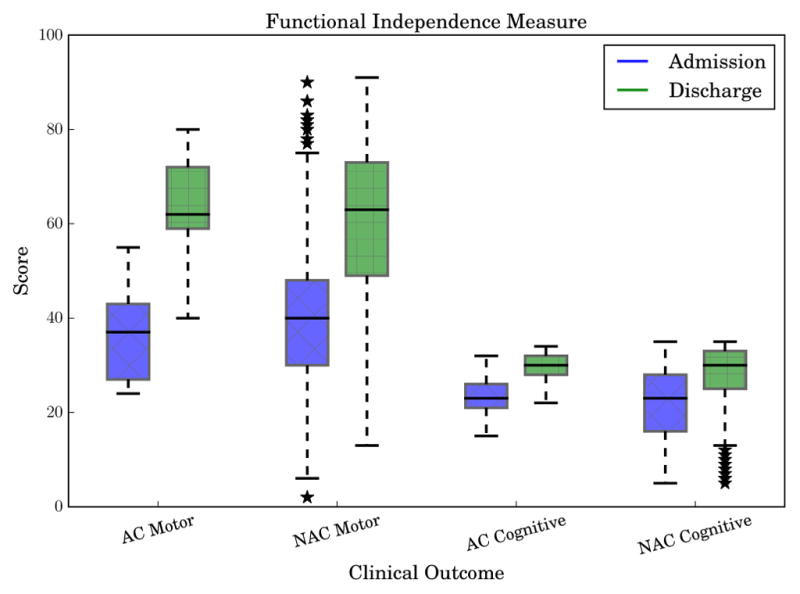
Admission and discharge functional independence measure (FIM) scores for motor and cognitive FIM. AC represents the participants in the ambulatory circuit study and NAC represents the non-AC patients used for training baseline admission models.

C. Predictor Variables

As AC participants underwent rehabilitation, data became available at four points displaced in time: admission, AC S1, AC S2, and discharge. Metrics computed from data collected from admission, AC S1, and AC S2 served as features to machine learning models, which were trained to predict FIM scores at discharge.

1) Admission Predictors

Data available at admission for both AC and NAC patients included patient characteristics such as age, gender, and RIC, as well as FIM task scores (see Table IV for all admission features). In addition, we included the reciprocal of the FIM motor score as suggested by Sonoda and colleagues [3]. Although additional data from medical records were available, we only included features that applied to all populations. For example, the number of days since stroke onset is only applicable to stroke populations and was not included as a predictor.

TABLE IV.

Features extracted from medical records available at admission

Category	Feature	Description
Patient characteristics	Age	Age in years
	Gender	Male or female
	RIC	Risk impairment category. Table III lists RICs in the NAC dataset
	Comorbidity tier	No relevant comorbidities, tier 1 (most severe/expensive), tier 2 (medium severe/expensive), tier 3 (least severe/expensive)
	Case mix group (CMG) relative weight	LOS modifier determined by presence of comorbidities and complications
Aggregated FIM	FIMA motor score	Sum of the 13 FIM motor task scores
	FIMA cognitive score	Sum of the 5 FIM cognitive task scores
	Reciprocal FIMA motor score	Reciprocal of admission FIM score [4]
Individual FIM tasks	17 FIMA task scores	17 total scores, one score for each FIM task

A = admission, D = discharge, FIM = functional independence measure, NAC = non-ambulatory circuit, RIC = rehabilitation impairment category, SD = standard deviation.

2) AC Predictors

Sensor-based metrics of AC performance were grouped into three categories: clinical assessments of progress (CAP), whole body movements (WBM), and gait features (GF). CAP metrics refer to commonly-used approaches for assessing mobility in a clinical setting, such as the duration of a task. WBM metrics are computed from the sensor placed on the COM. Finally, gait features refer to quantifications of steps and strides while walking. GFs are primarily computed from gait cycles derived from gait cycle event detection algorithms applied to the shank sensor angular velocity signals [27]. Table V summarizes the CAP, WBM, and GF metrics.

TABLE V.

Features computed from wearable inertial sensor data

Category	Feature	Units	Description	Reference
CAP	Duration	s	Total time to complete the ambulatory circuit or an individual task of the ambulatory circuit.
	Floor surface speed ratio		Measures the effect of walking speed on two different floor surfaces.
	Walking speed	m/s	Walking speed as determined by distance divided by time (normalized by leg length).
WBM	COM peak angular velocity		Maximum rotational velocity of the COM around the Z-axis.
	Root mean square (RMS)	m/s2/s	Square root of the mean of the squares of each COM acceleration signal (normalized by time). Represents acceleration magnitude. Synonymous with movement intensity (MI).	[28]
	Smoothness index (harmonic ratio)		Ratio of even to odd harmonics of the vertical Y-axis COM acceleration signal. A higher harmonic ratio represents a smoother walking pattern.	[29]
	Smoothness of RMS	m/s3/s	Square root of the mean of the squares of each COM acceleration signal derivative (normalized by time). Synonymous with RMS of jerk and smoothness of MI.	[28]
GF	Cadence	steps/min	The average number of steps taken per minute.
	Double support percent	%	Percentage of the gait cycle that both feet are on the ground. Computed as the sum of the initial double support time and the terminal double support time.	[30]
	Gait cycle time	s	Duration to complete one stride (time between two consecutive initial contacts of the same foot).	[30]
	Number of gait cycles		Total number of complete gait cycles (strides) that occurred.
	Shank peak angular velocity	°/s	Maximum rotational velocity of the shank around the Z-axis during the gait cycle. This occurs during the swing phase.
	Shank range of motion (ROM)	°	Range of integrated Z-axis angular velocity for each gait cycle. Provides an estimate of the degrees of shank movement.	[30]
	Step length	m	Distance between initial contacts of opposite feet (normalized by leg length).	[31]
	Step regularity	%	Regularity of the acceleration of sequential steps. Computed using the autocorrelation of the vertical Y-axis of the COM acceleration.	[23]
	Stride regularity	%	Regularity of the acceleration of sequential strides (see step regularity).	[23]
	Step symmetry	%	Ratio of step regularity to stride regularity.	[23]

CAP = clinical assessments of progress, COM = center of mass, GF = gait features, m = meters, MI = movement intensity, min = minute, RMS = root mean square, ROM = range of motion, s = seconds, WBM = whole body movement, ° = degrees.

Often, motor skills on only one side of the body are affected, called the involved or paretic side. Since several metrics computed in Table V are based on the left or right shank (e.g., shank peak angular velocity), we recast the left and right metrics as greater or lesser in value. For example, participant 001 exhibited average left shank peak angular velocity of 208.61 °/s, while right shank was 222.07 °/s at S1 testing. For 001, the left side would be cast as the lesser peak angular velocity limb, and the right side as the greater. This classification aligns with the medical record data, which reports participant 001 experienced a stroke with the left side of the body as the involved side (see Table II).

3) AC Change Predictors

At AC S2, we computed additional metrics to quantify the changes exhibited over one week of therapy from S1 to S2. For example, the percentage change for any given metric x was computed as the difference between the S1 and S2 metric scores for x and was normalized by the S1 metric score:

$$\mathrm{\Delta }\%=\frac{x_{S2}-x_{S1}}{x_{S1}}$$ (3)

Another metric used to quantify the changes between S1 and S2 was the standardized mean difference (SMD) effect size (ES) for repeated measures (RM) [32]:

$$d_{RM}=\frac{{\overline{X}}_{S2}-{\overline{X}}_{S1}}{S_D}$$ (4)

where S_D is the standard deviation of change [33]. The SMD ES was applied to gait cycle metrics. For example, gait cycle duration is the amount of time for the completion of one gait cycle (stride). For this study, a gait cycle corresponded to the time interval between one initial contact (heel strike) and the next initial contact of the same leg. If an individual took 15 strides at S1, then we derived 15 gait cycle durations, from which we computed the average gait cycle duration at S1 (X̄_S1). Fig. 2 depicts the AC data processing pipeline from sensor signals to statistical scores.

D. Supervised Scoring Models

We expressed discharge FIM score prediction as a supervised learning task that mapped the admission and AC features to predicted discharge FIM scores. The machine learning algorithm we used was an epsilon support vector machine (ε-SVM). SVMs utilize a subset of the training data, called support vectors, to identify boundaries of maximal distance from the support vectors. In the case of regression, the SVM learns a function F (x) → w · x – b to approximate a target variable y_i under ε precision for each feature vector x_i. The vector w is the learned weights, or coefficients, representing the relative importance of each feature for the SVM. We compared the prediction results of the SVM with linear regression and random forest with 100 regression trees. The 100 trees criterion was chosen because of its success in a previous inertial sensor and clinical assessment study [34]. These three machine learning algorithms were chosen because of demonstrated accuracy found in previous technology-based clinical assessment studies [18], [34], [35].

1) Model Construction

For AC participants, data from three different points in time were collected and the corresponding models were built. M₁ is a model trained with data available upon admission, M₂ is a model trained with data available at AC S1, and M₃ is a model trained with data available at AC S2. Fig. 4 depicts this timeline and its associated models. For NAC participants, only admission data were available for training M₁. Each model M₁, M₂, and M₃ produced a prediction (P₁, P₂, and P₃) for the same clinical outcome. These predictions represented the change in model prediction accuracy over time as new data were collected. Next, an ensemble learner (M_E) took P₁, P₂, and P₃ as inputs and produced a fourth prediction (P_E). An ensemble learner combines the predictions of multiple learning algorithms to produce a final prediction. Ensemble learners are usually applied as an effort to achieve higher performance than the individual algorithms achieve alone. For comparison with the ensemble result, predictions P₁, P₂, and P₃ were also averaged to produce a fifth prediction (P_avg).

Fig. 4.

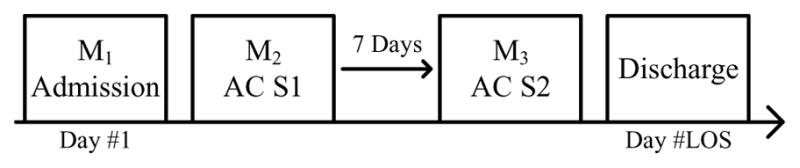
The wearable sensor study timeline.

Predictive models were constructed from two different approaches, separate and cumulative, in order to explore the performance of M₂ and M₃ with different training features. Each approach builds three models (M₁, M₂, M₃) representing the three different points during rehabilitation (admission, AC S1, AC S2); however, depending on the approach, different input features were utilized at M₂ and M₃. In the cumulative model construction approach, M₂ and M₃ were trained on all previous and current data available up to and including the corresponding point in time (see Fig. 5). In the separate model approach, M₂ and M₃ were not trained with previously collected data, only with the data collected at that point in time (see Fig. 6). The results of M₁, M₂, and M₃ were then combined by an ensemble learner to produce the final prediction. We included the separate model construction approach to examine the predictive power of M₂ and M₃ without utilizing any admission features (or in the case of M₃, without utilizing admission features or AC S1 features).

Fig. 5.

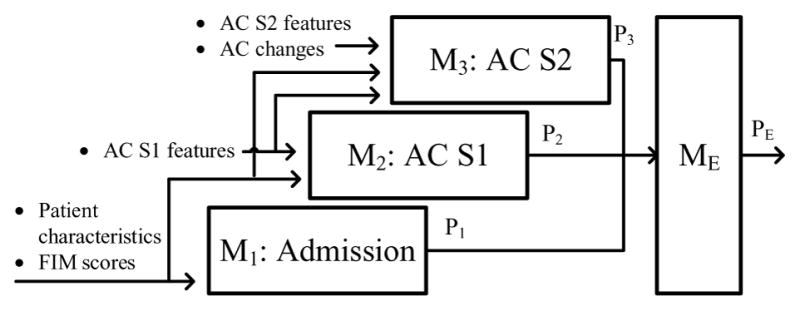
Cumulative model construction approach.

Fig. 6.

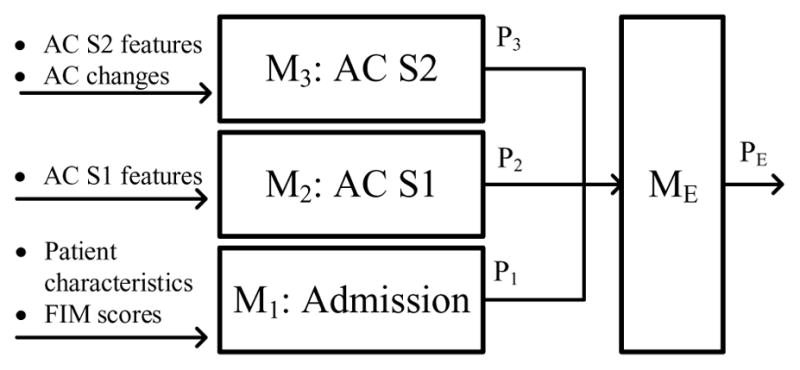
Separate model construction approach.

2) SMOTE Oversampling

As mentioned earlier, the relatively few AC values posed a challenge, particularly in comparison with the large number of NAC records that were available. With such a small AC population, the prediction algorithm was at risk of overfitting the training data. One method to compensate for a small number of samples is to oversample the data by replicating data points or adding synthetic data [36]. Resampled or synthetic data are only used during the training process and are designed to more thoroughly represent the space of possible data points.

To accommodate our low sample size, the oversampling technique of synthetic minority oversampling technique (SMOTE) was applied to the AC dataset [37]. SMOTE is an alternative to oversampling with replacement that creates synthetic data examples from the available training data. Synthetic examples are created by randomly interpolating features along the line segments joining any or all of the k nearest neighbors for each existing data point. The algorithm is typically applied to correct a class imbalance problem. Since our clinical outcomes are continuous target variables, we employed a version of SMOTE for regression (SMOTE-R) [38]. In SMOTE-R, the minority class is considered to be rare, extreme values in the target variable. By applying SMOTE to these instances, the distribution of the target variable becomes more uniform. SMOTE has shown success in a variety of applications that share characteristics with this data and was therefore used to boost the size and diversity of the training data for this prediction problem.

To apply SMOTE-R, a function ϕ(y_k) maps each value of the target variable y_k (discharge FIM scores in our study) to a notion of relevance (in this case, rarity and extremeness) in the range [0,1]. For example, if the target variable is assumed normal, the relevance function can be approximated by the complement of the variable’s probability density function. In this case, highly relevant values will be near the tails of the distributions.

To build a relevance function for rare extreme values, three control points were used to fit a cubic interpolating piecewise polynomial representing target variable relevance. The three control points (CP) were estimated using quartiles (Q): CP_H = Q₃ + C × IQR with relevance 1.0, CP_L = Q₁ – C × IQR with relevance 1.0, and the median, CP_Ỹ with relevance 0.0, where IQR = Q₃ – Q₁ (the interquartile range). C is a parameter reflecting the extent to which a sample is considered an outlier, where lower values of C imply more samples will be considered outliers. We set C = 1.2 due to our small sample size. All data points above CP_H or below CP_L were tagged as outliers and comprised the rare high extreme outliers and the rare low extreme outliers, respectively. An example relevance function ϕ for discharge total motor score is shown in Fig. 7. The three points in the Fig. 7 correspond to the control points CP_L = 41.7, CP_Ỹ = 62.0, and CP_H = 89.3. In this example, values less than 41.7 or greater than 89.3 are considered to be outliers with relevance 1.0. Finally, samples with relevance greater than a threshold t_E are considered relevant sample points and used to generate new synthetic samples. For our dataset we used t_E = 0.5 to obtain more relevant sample points on either tail of the discharge FIM score distributions. As the method suggests, the motivation behind this approach was to sample points around the outliers in order to give those points more representation in the training data.

Fig. 7.

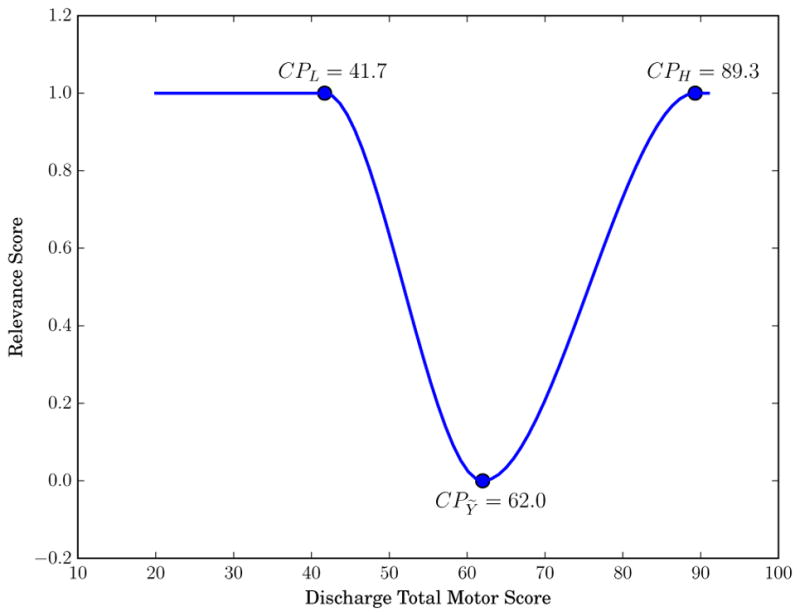
Example relevance function ϕ for discharge functional independence measure (FIM) motor score. The three scatter points denote the control points used to fit a cubic polynomial.

We introduced a sampling variation that is a combination of existing methods. For nominal variables, we used a majority vote of k nearest neighbors [37]. Discharge FIM scores were assigned using the SMOTE-R approach. For this method, a weighted average of the two seed samples’ (x and its nearest neighbor nn) discharge FIM score was computed [38]:

$${\mathit{FIM}}_{D,\mathit{synthetic}}\leftarrow \frac{d_2\times {\mathit{FIM}}_{D,x}+d_1\times {\mathit{FIM}}_{D,nn}}{d_1+d_2}$$ (5)

where d₁ and d₂ are the distances of the generated point to each of the two seed examples. This weighted the sample with the smaller distance to the new synthetic data point higher. Usually SMOTE-based oversampling is coupled with under-sampling of the majority class, or in the case of regression problems, undersampling of the more frequent samples. Since we wanted to retain all of our real AC data points, we did not undersample our dataset. Instead we applied SMOTE-R to the entire training set and performed additional sampling of the relevant samples. On each LOOCV fold, N − 1 training points were sampled to create N − 1 new synthetic data points that were added to the training set. SMOTE-R was applied in two configurations. The first configuration, extremes, only applied SMOTE to the outliers on the high and low tails of the training distribution [38]. The second configuration, all data, applied SMOTE to the entire training set.

3) Feature Selection

In order to understand the predictive utility of each feature and remove noisy or redundant features, feature selection techniques were applied [39]. First, individual features were correlated with the target variable to investigate their individual predictive ability. Features with a Pearson correlation coefficient r < 0.1 were determined to be noisy and not considered useful. Next, a wrapper-based recursive feature elimination algorithm with cross validation (RFECV) was applied to identify the optimal set of features [40]. The model used in RFECV was a linear SVM trained with 10-fold cross validation with mean squared error scoring. Starting with all features, an SVM learned a vector of weights, or coefficients, representing the relative importance of the feature in learning the separating hyper plane. The feature with the smallest SVM weight was then removed from the feature set and the model was re-trained on the remaining features. This process was repeated until the set with the lowest mean squared error was identified. Additionally, the size of this set denoted the optimal number of features. The top ranked features were then selected as the inputs to the prediction models.

4) Evaluation Methods

To evaluate the quality of the predicted clinical outcomes, several evaluation metrics were used. The regression models were evaluated using the mean absolute error (MAE), root mean squared error (RMSE) and normalized RMSE (NRMSE). RMSE and NRMSE are defined in Equations (6) and (7):

$$\mathit{RMSE}=\sqrt{\frac{{\displaystyle \sum _{i=1}^n}{(Y_{\mathit{actual},i}-Y_{\mathit{predicted},i})}^2}{n}}$$ (6)

$$\mathit{NRMSE}=\frac{\mathit{RMSE}}{Y_{\mathit{actual},\mathit{max}}-Y_{\mathit{actual},\mathit{min}}}$$ (7)

where Y is the predicted clinical outcome and n is the number of predicted samples. Pearson correlation coefficients, r, and associated p-values are also reported, as defined in Equation (8):

$$r=\frac{{\displaystyle \sum _{i=1}^n}(Y_{\mathit{actual},i}-{\overline{Y}}_{\mathit{actual}})·(Y_{\mathit{predicted},i}-{\overline{Y}}_{\mathit{predicted}})}{\sqrt{{\displaystyle \sum _{i=1}^n}{(Y_{\mathit{actual},i}-{\overline{Y}}_{\mathit{actual}})}^2·{\displaystyle \sum _{i=1}^n}{(Y_{\mathit{predicted},i}-{\overline{Y}}_{\mathit{predicted}})}^2}}$$ (8)

IV. Results

All data were processed with the Python programming language and the Sci-kit Learn machine learning library. Prior to training, admission and AC data were standardized by subtracting the mean and scaling to unit variance. Unless otherwise stated, an SVM with a linear kernel was trained and evaluated using leave-one-out cross validation (LOOCV).

A. Feature Selection: FIM Motor Score

Features were correlated with the FIM motor score at discharge and noisy features were removed. Table VI lists the 10 most highly correlated predictors and their correlation coefficients, grouped by the time points of admission, AC S1, and AC S2. Wrapper-based feature elimination results for discharge FIM motor score are shown in Table VII. This table contains the top 10 ranked features for each model, where M₁ is trained with AC participant admission data only (not including NAC patient admission data).

TABLE VI.

Correlations (r) between individual predictors and discharge functional independence measure (FIM) motor score

Admission	r	AC S1	r	AC S2	r
Reciprocal admission total motor score	−0.68**	COM acceleration stand to sit Z peak angular velocity	0.62**	S2 peak angular velocity average (lesser side)	0.65**
Admission bladder	0.62**	Shank range of motion average (greater side)	0.62**	S2 vehicle challenge duration	−0.60**
Admission upper body dressing	0.61**	Step length average	0.59**	S2 range of motion average (lesser side)	0.59**
CMG relative weight	−0.60**	Vehicle challenge duration	−0.56**	S2 number of gait cycles	−0.56**
Admission grooming	0.60**	Shank range of motion average (lesser side)	0.55*	Cadence percent change	0.51*
Admission problem solving	0.59**	Number of gait cycles	−0.51*	S2 swing percent CV	−0.50*
Admission memory	0.56*	Shank peak angular velocity average (greater side)	0.48*	Peak angular velocity SMD (greater side)	0.50*
Admission bed to chair transfer	0.53*	COM acceleration vehicle unload RMS	0.47*	S2 duration	−0.49*
Admission toilet transfer	0.50*	COM acceleration stand to sit RMS	0.46*	S2 COM acceleration RMS	0.48*
Admission comprehension	0.46*	Walking speed	0.44	S2 COM acceleration RMS jerk	0.46*

AC = ambulatory circuit, CMG = case mix group, COM = center of mass, CV = coefficient of variation, r = Pearson correlation coefficient, RMS = root mean square, S1 = session 1, S2 = session 2, SMD = standardized mean difference,

^*p < 0.05,

^**p < 0.01.

TABLE VII.

Cumulative recursive feature elimination with cross validation (RFECV) top ranked features for discharge functional independence measure (FIM) motor score

M1	Rank	M2	Rank	M3	Rank
Admission upper body dressing*	1	COM acceleration stand to sit Z peak angular velocity*	1	COM acceleration stand to sit Z peak angular velocity*	1
Admission memory*	1	Admission memory*	1	Admission memory*	1
RIC	1	COM acceleration stand to sit RMS*	1	Range of motion SMD (lesser side)	1
Admission bladder*	1	Shank range of motion average (greater side)*	1	Step length average*	1
Admission grooming*	1	Admission grooming*	1	Admission grooming*	1
Admission problem solving*	1	Double support percent CV	1	COM vehicle unload Z peak angular velocity percent change	1
Admission tub/shower transfer	1	Admission upper body dressing*	1	Admission upper body dressing*	1
Admission lower body dressing	1	Admission bed to chair transfer*	2	S2 peak angular velocity average (lesser side)*	1
Reciprocal admission total motor score*	2	Swing percent CV	3	Cycle duration CV percent change	1
CMG relative weight*	3	Limp average	4	S2 double support percent CV	1

CMG = case mix group, COM = center of mass, CV = coefficient of variation, M = model, RIC = rehabilitation impairment category, RMS = root mean square, S2 = session 2, SMD = standardized mean difference,

^*listed in Table VI.

B. Prediction Results

1) FIM Motor Score

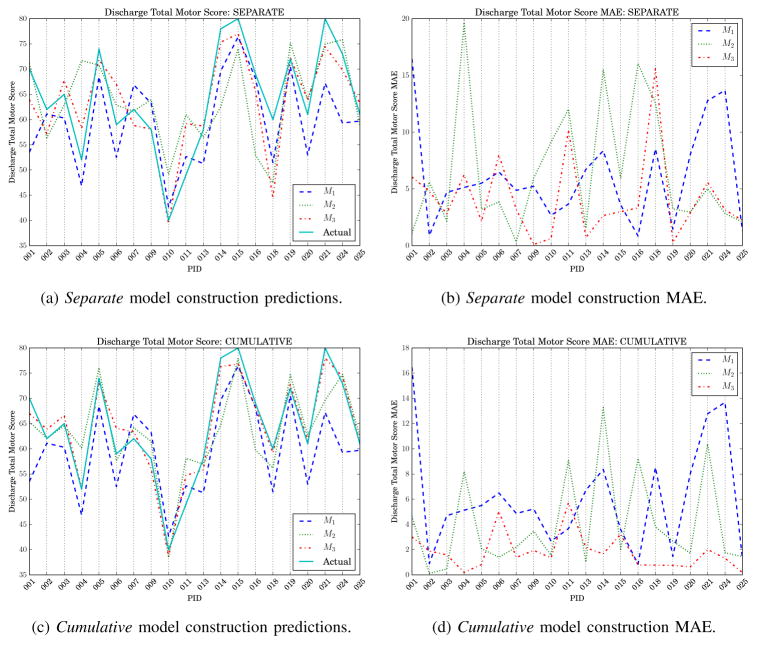
Table VIII shows results for predicting discharge total motor score with LOOCV. Two admission models (M₁) were trained, one with AC participant data only and a second model including NAC patient admission data. To visualize the FIM motor score predictions, each participant’s actual discharge score was plotted together with the predictions generated by M₁, M₂, and M₃ (see Fig. 8).

TABLE VIII.

Discharge functional independence measure (FIM) motor score prediction results

	Model	Linear SVM			Linear Regression			Random Forest
		RMSE	NRMSE	r	RMSE	NRMSE	r	RMSE	NRMSE	r
M1	M1 (w/o NAC)	4.66	11.65%	0.89**	6.07	15.19%	0.87**	8.14	20.36%	0.61**
	M1	7.36	18.41%	0.82**	7.95	19.87%	0.80**	10.86	27.14%	0.73**
Separate	M2	8.55	21.38%	0.60*	9.82	24.55%	0.55*	10.18	25.45%	0.25
	M3	5.54	13.86%	0.85**	5.43	13.57%	0.86**	10.70	26.76%	0.07
	Mavg	5.54	13.86%	0.87**	5.27	13.18%	0.89**	8.04	20.09%	0.69**
	ME	5.50	13.74%	0.84**	5.69	14.22%	0.84**	9.38	23.46%	0.44
Cumulative	M2	5.49	13.71%	0.85**	5.88	14.69%	0.85**	8.51	21.27%	0.59*
	M3	2.32	5.80%	0.97**†	2.60	6.50%	0.97**†	9.78	24.46%	0.31
	Mavg	4.00	10.01%	0.94**†	4.05	10.12%	0.94**†	7.38	18.46%	0.77**†
	ME	3.41	8.53%	0.95**†	2.90	7.26%	0.96**†	9.30	23.24%	0.45*

avg = average, E = ensemble, M = model, NAC = non-ambulatory circuit, NRMSE = normalized root mean square error, r = Pearson correlation coefficient, RMSE = root mean square error, SVM = support vector machine,

^*p < 0.05,

^**p < 0.01,

^†significantly (p < 0.05) improved results from M₁.

Fig. 8.

Discharge functional independence measure (FIM) motor score prediction results. For all figures, M₁ is trained with non-ambulatory circuit admission data.

2) FIM Motor with SMOTE

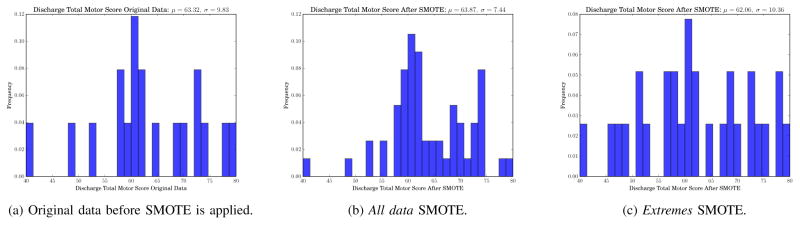
SMOTE-R (see Section III-D2) was applied to the discharge FIM motor distribution to generate additional training data. Table IX shows the results of training a linear SVM with synthetic data in both configurations. To illustrate the resulting synthetic data, Fig. 9 shows an example of how SMOTE-R in both configurations affected the distribution of the discharge FIM motor score in an example fold of LOOCV. Fig. 9a shows the histogram of the original training discharge FIM motor score, while Figs. 9b and 9c show the target variable distribution of the all data and extremes approach, respectively. For the example fold, the original data had a discharge FIM motor score of 63.32 ± 9.83. SMOTE-R for all data generated 19 new sample points which changed the values to 63.87 ± 7.44. SMOTE-R for extreme data points yielded a mean and standard deviation of 62.06 ± 10.36.

TABLE IX.

Discharge functional independence measure (FIM) motor score with synthetic training data prediction results

	Model	Extremes SMOTE-R			All data SMOTE-R
		RMSE	NRMSE	r	RMSE	NRMSE	r
M1	M1 (w/o NAC)	4.86	12.14%	0.89**	6.69	16.73%	0.83**
	M1	7.34	18.36%	0.82**	7.27	18.17%	0.82**
Separate	M2	8.39	20.97%	0.64**	9.40	23.50%	0.56*
	M3	5.40	13.49%	0.86**	5.35	13.39%	0.86**
	Mavg	5.44	13.61%	0.87**	5.11	12.77%	0.89**
	ME	5.35	13.38%	0.85**	5.75	14.38%	0.83**
Cumulative	M2	6.22	15.55%	0.82**	6.14	15.35%	0.84**
	M3	2.88	7.19%	0.96**	3.13	7.82%	0.95**
	Mavg	4.21	10.54%	0.93**	4.07	10.19%	0.94**
	ME	4.39	10.97%	0.91**	3.60	8.99%	0.94**

avg = average, E = ensemble, M = model, NAC = non-ambulatory circuit, NRMSE = normalized root mean square error, r = Pearson correlation coefficient, RMSE = root mean square error,

^*p < 0.05,

^**p < 0.01.

Fig. 9.

Histograms for discharge functional independence measure (FIM) motor score for an example fold of cross validation before and after applying SMOTE.

3) FIM Cognitive Score

To explore the possible relationship between cognitive functioning and performance on the AC, additional models were trained to predict the FIM cognitive score at discharge. Table X shows discharge FIM cognitive prediction results for a SVM with a linear kernel, linear regression, and a random forest with 100 regression trees.

TABLE X.

Discharge functional independence measure (FIM) cognitive score prediction results

	Model	Linear SVM			Linear Regression			Random Forest
		RMSE	NRMSE	r	RMSE	NRMSE	r	RMSE	NRMSE	r
M1	M1 (w/o NAC)	2.42	20.19%	0.70**	2.50	20.86%	0.67**	2.61	21.72%	0.64**
	M1	2.34	19.49%	0.73**	2.56	21.30%	0.73**	2.36	19.69%	0.73**
Separate	M2	3.10	25.82%	0.51*	5.50	45.81%	0.17	3.80	31.7%	−0.09
	M3	3.74	31.17%	−0.34	3.61	30.11%	−0.23	4.15	34.57%	−0.12
	Mavg	2.56	21.36%	0.68**	3.06	25.52%	0.45*	2.93	24.40%	0.52*
	ME	2.66	22.14%	0.64**	3.09	25.77%	0.56*	2.87	23.92%	0.53*
Cumulative	M2	3.44	28.69%	0.19	3.13	26.08%	0.37*	3.77	31.45%	0.15
	M3	2.42	20.19%	0.70**	2.50	20.86%	0.67**	2.61	21.72%	0.64**
	Mavg	2.40	20.01%	0.73**	2.32	19.34%	0.74**	2.47	20.56%	0.68**
	ME	2.71	22.59%	0.59*	1.48	12.36%	0.90**†	2.46	20.52%	0.68**

avg = average, E = ensemble, M = model, NAC = non-ambulatory circuit, NRMSE = normalized root mean square error, r = Pearson correlation coefficient, RMSE = root mean square error, SVM = support vector machine,

^*p < 0.05,

^**p < 0.01,

^†significantly (p < 0.05) improved results from M₁.

4) Individual FIM Tasks

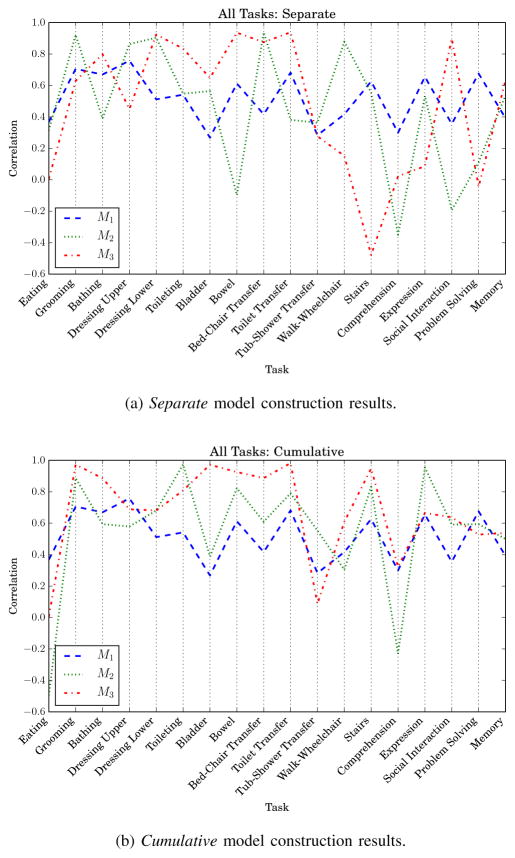
Each discharge FIM task, in turn, was predicted for M₁, M₂, and M₃. The correlation results for each task prediction are plotted in Fig. 10. The plot shows which tasks were more closely represented by the admission, AC S1, and AC S2 metrics and corresponding models M₁, M₂, and M₃.

Fig. 10.

Correlations for all functional independence measure (FIM) tasks. M₁ is trained with non-ambulatory data.

V. Discussion

We investigated the prediction of discharge FIM scores using data collected from wearable inertial sensors. Participants in the study were receiving inpatient therapy services for a variety of medical conditions. Regression models were trained to predict the discharge FIM motor score, cognitive score, and individual FIM task scores for participants who performed two testing sessions of the ambulatory circuit.

A. Predictor Strength

Of the predictors available at admission, the reciprocal of admission FIM motor score was the most highly correlated with discharge FIM motor score (r = −0.68). Sonoda et al. [3] found this feature was also highly correlated (r = −0.896) with discharge FIM motor score for first stroke survivors without the presence of other diseases. Other strong predictors at admission included admission bladder item scores, admission upper body dressing scores, and case mix group (CMG) relative weight. Highly uncorrelated predictors included admission walk/wheelchair scores and admission eating scores. Admission eating in particular was not an informative feature as it exhibited zero variance for our AC participants. For the AC metrics, vehicle challenge duration, shank peak angular velocity, shank range of motion, number of gait cycles, and COM RMS were all highly correlated with discharge FIM motor scores, whereas sit to stand duration, step symmetry, and walking speed percentage change were not strong predictors on their own. This finding is particularly interesting for walking speed percent change because walking speed is a common clinical measurement of gait functioning [41].

Often when considered on their own, strong individual predictors are outperformed by a linear combination of weaker predictors [39]. The prediction results using RFECV is such an example. For M₁, admission tub/shower transfer and admission lower body dressing were highly ranked; however, these features were not as highly correlated with FIM motor scores when considered alone. Furthermore, reciprocal admission motor FIM and CMG relative weight were not top ranked by RFECV and therefore not used to train M₁. Similar trends were seen in M₂ and M₃, which had 7 and 10 top ranked features, respectively.

B. Predictions

1) FIM Motor Score

When considering M₁ with AC data only, M₁ with NAC data, and M₂ and M₃ independently (the separate model construction approach), the correlations associated with discharge FIM motor score prediction were r = 0.89, 0.82, 0.60, and 0.85 respectively (see Table VIII). Much higher accuracy was achieved when utilizing all features from previous points in time as well, as is the case with the cumulative approach, with M₂ and M₃ correlations r = 0.85 and 0.97. As we expected, the correlations increased as additional AC features representing participants’ performance were included. Consequently, the strongest correlations were achieved with the cumulative M₃ model (RMSE = 2.32 and r= 0.97). Even though M₁ alone was already a high performing model, cumulative M₃ predictions produced a significantly higher correlation (p < 0.01) than M₁ with NAC data (RMSE = 7.36, r = 0.82). These results indicated that wearable sensors enhanced prediction of clinical rehabilitation outcomes over medical records alone.

Our results for M₁ are consistent with earlier literature for discharge FIM motor score prediction. Using only clinical information (no technology-based predictors) for stroke patients, Jeong et al. [8] reported a prediction correlation of r = 0.88 (R² = 0.77), Fujiwara et al. [6] reported R² between 0.66 and 0.75, and Tsuji et al. [7] reported R² = 0.68. These studies utilized additional clinical rating scale scores as predictors that were unavailable in our study. Despite this difference, our results for predictions based only upon admission features were consistent with previously reported results. Using technology-based predictors, Mostafavi et al. [18] utilized metrics from robot-assistive KINARM devices during upper limb reaching and positioning tasks to predict FIM at discharge with accuracy of RMSE = 11.8 (NRMSE = 17.3%). There are differences between this study and ours, including the technology (robot device vs. wearable sensors) and monitored body parts (upper limb vs. whole body). These differences make comparisons between the results of Mostafavi and colleagues and our results difficult; however, our lower error (RMSE = 2.32, NRMSE = 5.80%) does suggest the viability of wearable inertial sensors for work involving clinical outcome prediction of ambulatory tasks.

It is also worth noting that M₁ with AC participant data only outperforms M₁ with NAC participant data used for training (r = 0.89, 0.82 and RMSE = 4.66, 7.34 respectively). This difference suggests that our small sample size of 20 AC participants might result in overfit models. As this may be the case, there are also several differences between the two datasets to discuss. AC participants are patients who are able to physically perform the AC and have higher cognitive awareness on average than NAC patients (FIM_A-cog = 23.10, 22.12 and FIM_D-cog = 29.55, 28.46, respectively). This difference in cognition can be attributed to the requirement of passing the Mini-Cog exam in order to be a participant in the AC study. Furthermore, the variance in the NAC training data is higher, as there are additional RICs not represented by the AC participants. Several NAC patients also showed FIM regression, which is not evident in the AC participant dataset. The inclusion of the NAC patients suggests our results might be an overestimate of the accuracy that could be obtained for M₂ and M₃ when considering AC data from any patient, ignoring the study recruitment strategies.

When comparing the linear SVM results to other machine learning techniques, linear regression performs similarly to the SVM, whereas the random forest does not perform as well (see Table VIII for results). The random forest still yields statistically significant correlations with r = 0.73 and 0.59 (p < 0.05) for M₁ and cumulative M₂ respectively. The regression trees would most likely perform better with additional training examples, as is the case for M₁ AC only compared with M₁ with NAC (r = 0.61, 0.73 respectively). Additional synthetic data were generated using SMOTE for regression and used for training a linear SVM (see Table IX for results). Cumulative M₃ performance was not as high as without the synthetic data (original RMSE = 2.32, r = 0.97; extremes SMOTE RMSE = 2.88, r = 0.96; all data SMOTE RMSE = 3.13, r = 0.95), suggesting additional AC participant data might attenuate the prediction accuracy.

2) FIM Cognitive Score

Models based only on admission data were able to predict discharge FIM cognitive score fairly accurately (see Table X). M₁ with AC data only achieved RMSE = 2.42, r = 0.70 and M₁ with NAC data demonstrated slightly stronger results (RMSE = 2.34, r = 0.73). Highly ranked predictors by RFECV included admission memory task score, walk/wheelchair task score, and tub/shower transfer score. When adding features from AC data, the results were not as strong as M₁ for separate M₂, separate M₃, and cumulative M₂. Cumulative M₃ performed as well as M₁ without NAC data, while averaging cumulative M₁, M₂, and M₃ predictions barely outperformed M₁ without NAC data (RMSE = 2.40, r = 0.73). Considering the AC is primarily a motor task of physical functioning, it is not surprising that it was difficult to improve an initial prediction at M₁ with NAC data. On a related note, future work includes programmatically determining if the participant slowed down or stopped for the stops walking when talking test performed during the AC. This feature and others like it could provide cognitive information for the machine learning algorithms and improve discharge FIM cognitive score predictions.

3) Individual FIM Tasks

Analyzing the relevance of the AC features for predicting individual FIM task scores at discharge provided interesting insight about what tasks the AC most closely represents. Fig. 10 shows correlations for predictions of all 18 tasks for separate and cumulative construction approaches. As reported for FIM motor score predictions, cumulative features together (see Fig. 10b) offered more predictive power than considering each time point separately (see Fig. 10a). M₃ outperformed the other models on several tasks, most notably bathing, bladder management, all the transfers, and stairs. M₂ did particularly well on grooming, toileting, and expression, but particularly poorly on comprehension. M₁ performed consistently near r = 0.50 for all tasks, and better than M₂ and M₃ for most cognitive tasks. This confirmed the cognitive score results for predicting total discharge FIM cognitive scores (see Table X). Finally, the improvement of M₃ over M₁ for bladder and bowel control is especially interesting. Perhaps motor functioning on the AC exhibits a relationship between underlying mechanisms of sphincter control.

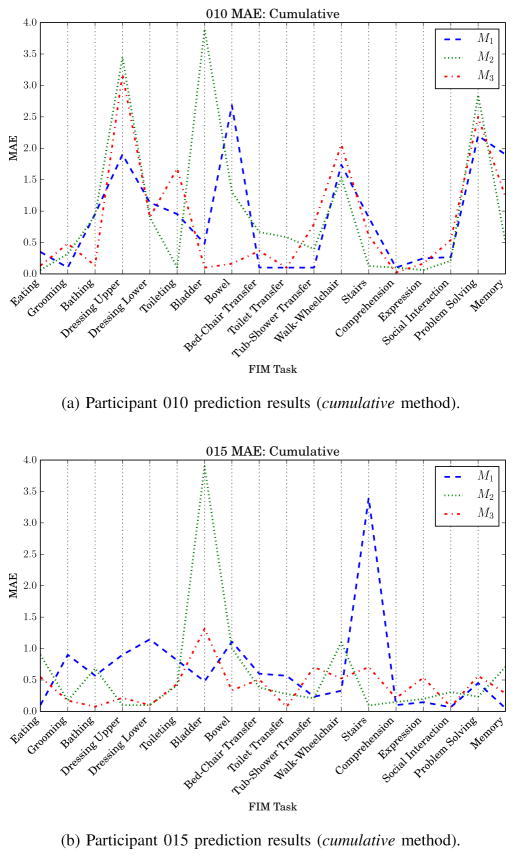
The FIM motor, cognitive, and individual task prediction results offer insight into the recovery process at the group level. The data can also be used to examine predictors and predictions made for individual patients. For example, participant 010 has the lowest FIM motor score at discharge (FIM_D-motor = 40, see Table II). Predicting individual FIM tasks for participant 010 revealed the models did not generalize well to the profile of participant 010 (see Fig. 11a). The models perform particularly poorly for the FIM tasks of upper body dressing, bladder sphincter control, and problem solving. On the contrary, participant 015 has the highest FIM score of the group (FIM_D-motor = 80, tied with participant 021). With the exception of the bladder control task (M₂) and stairs (M₁), scores for participant 015 were well predicted by the models (see Fig. 11b). The juxtaposition between these two participants is interesting from a research perspective, but its usefulness for clinicians remains to be seen. Future work will include measuring the clinical utility of such fine-grained predictions as individual patient scores on individual FIM tasks.

Fig. 11.

AC participant mean absolute error (MAE) for each functional independence measure (FIM) task. M₁ is trained with non-ambulatory circuit data.

C. Limitations

The low number of available AC data points is an important limitation of this study. The study is ongoing and additional participants are being recruited; however, for the current investigation we applied SMOTE-R to increase the sample size with synthetic data to overcome this drawback. Another limitation is all data were collected from the same inpatient hospital. A wide variety of patients attending other rehabilitation facilities would be more representative of the population and potential clinical utility of the models. Finally, the AC participant population was primarily recovering from a stroke (70%). A wider variety of patient impairments would be more representative of all types of patients admitted to inpatient rehabilitation.

VI. Conclusion

We investigated the predictive abilities of features derived from wearable inertial sensor data to predict discharge clinical outcomes of the functional independence measure without re-administering the FIM assessment battery. Participant data were collected from an ecological ambulation task at two time points during mid-stay for 20 patients at an inpatient rehabilitation hospital. While models trained only on admission data performed well, we were able to achieve an even higher level of prediction accuracy when incorporating inertial sensor-based features. Correlations as high as r = 0.97 (RMSE = 2.32, NRMSE = 5.80%) for LOOCV predicting discharge FIM motor score were obtained.

This research adds unique findings over previous studies by mapping longitudinal sensor data collected during physical therapy into the prediction of clinical outcomes. Often, technology-based features do not correspond to what standard clinical assessments are evaluating [14], thus it is reassuring that the results presented in Section IV demonstrated strong correspondence and can be leveraged to improve upon the predictive power of standard clinical assessments at admission. There are several opportunities and directions for future work:

• Recruiting additional participants of various impairments. A large enough sample size could allow for training RIC-specific models that take into account the differences and similarities exhibited amongst RIC populations.

• Deepening the understanding of the processes underlying recovery. For example, investigating the effects of comorbidities and complications at the group and individual patient levels.

• Designing and implementing a mobile application to automate data collection, processing, and prediction to generate reports mid-stay of inpatient rehabilitation.

• Exploring other machine learning techniques and optimization methods to improve performance.

• Computing features from the AC sensor data that are more representative of cognitive functioning.

In summary, this research lays the foundation for a sensor-based system that collects data from ambulatory tasks of physical rehabilitation. Models similar to those presented in this research can map the sensor data into an appropriate clinical assessment to provide updates about patient progress in a more universal domain; however, it is not the intention of such a system to replace the expertise of a trained clinician, but instead to provide the therapist with additional, meaningful information. Viewed in this regard, a wearable sensor system and its associated algorithms are potentially a tool to inform therapists and help them better provide services to their patients during recovery.

Biographies

Gina Sprint received a B.S. degree in computer science from Eastern Washington University, Cheney, WA, in 2012.

Currently she is working toward the Ph.D. degree in computer science at Washington State University, Pullman, WA. She is a National Science Foundation Fellow in the IGERT Integrative Training Program in Health-Assistive Smart Environments at Washington State University. Her research interests include wearable computing, machine learning, technology applications for healthcare, and computer science education.

Ms. Sprint is a student member of IEEE, IEEE Education Society, and the Association for Computing Machinery.

Diane J. Cook received a B.A. in math/computer science from Wheaton College, Wheaton, Illinois in 1985, a M.S. in computer science from the University of Illinois, Urbana-Champaign, Illinois in 1987, and a Ph.D. in computer science from the University of Illinois in is 1990. She became a Fellow of IEEE in 2007.

Since 2006, she has been a Huie-Rogers Chair Professor at Washington State University in Pullman, Washington. Prior to that, she was a faculty member at the University of South Florida from 1991 to 1992 and a faculty member at the University of Texas at Arlington from 1992 to 2006. She is the author of five books and more than 380 papers.

Dr. Cook is a member of AAAI an FTRA Fellow. She received the IEEE Systems, Man, and Cybernetics Society Outstanding Contribution Award in 2007. She is an associate editor for the IEEE Transactions on Knowledge and Data Engineering and the IEEE Transactions on Systems, Man, and Cybernetics.

Douglas L. Weeks received a B.S. degree in 1980 in biological sciences and kinesiology, and a M.S. degree in 1981 in human motor control from Texas A&M University. He obtained a Ph.D. in 1989 in Statistical Analysis, Research, and Evaluation Methodology from the University of Colorado, and completed post-doctoral research at the Rehabilitation Institute of Montreal in 1994.

Since 2004, he has directed the research program at St. Luke’s Rehabilitation Institute in Spokane, WA. In the 10 years prior to that, he was a professor in the Department of Physical Therapy at Regis University in Denver, CO. He has authored more than 60 publications in peer-reviewed basic science and clinical research journals. Dr. Weeks has received research funding through federal agencies, such as the National Institute on Disability and Rehabilitation Research and the Health Resources and Services Administration, as well as private agencies, such as the American Heart Association and the Craig H. Neilsen Foundation.

Dr. Weeks is a member of American Congress of Rehabilitation Medicine, and the American Society for Neurorehabilitation.

Vladimir Borisov received a B.S. degree in bioengineering from Washington State University, Pullman, WA, in 2009.

Currently he is pursuing his Ph.D. degree in engineering sciences through the Gene and Linda Voiland School of Chemical and Bioengineering at Washington State University. He is a National Science Foundation Fellow in the IGERT Integrative Training Program in Health-Assistive Smart Environments at Washington State University. His research interests include wearable monitoring systems, using simulations for studying complex biomechanical systems, and practical commercialization of technologies with healthcare applications.