ASSESSING PHENOTYPIC CORRELATION THROUGH THE MULTIVARIATE PHYLOGENETIC LATENT LIABILITY MODEL

Abstract

Understanding which phenotypic traits are consistently correlated throughout evolution is a highly pertinent problem in modern evolutionary biology. Here, we propose a multivariate phylogenetic latent liability model for assessing the correlation between multiple types of data, while simultaneously controlling for their unknown shared evolutionary history informed through molecular sequences. The latent formulation enables us to consider in a single model combinations of continuous traits, discrete binary traits, and discrete traits with multiple ordered and unordered states. Previous approaches have entertained a single data type generally along a fixed history, precluding estimation of correlation between traits and ignoring uncertainty in the history. We implement our model in a Bayesian phylogenetic framework, and discuss inference techniques for hypothesis testing. Finally, we showcase the method through applications to columbine flower morphology, antibiotic resistance in Salmonella, and epitope evolution in influenza.

1. Introduction

Biologists are often interested in assessing phenotypic correlation among sets of traits, since it can help elucidate many biological processes. For example, correlation across the presence or absence of resistance to different antibiotics characterizes the recent evolutionary history of important pathogenic bacteria such as Salmonella. Phenotypic correlation may be a result of genetic constraints, in which traits are partially determined by the same or linked loci. Alternatively, the correlation may be evidence of selective effects, in which the same environmental pressure acts on two seemingly unrelated traits or the outcome of one trait affects selective pressure on the other. Studying these processes is one of the aims of comparative biology.

The purpose of this paper is to present a statistical framework for estimating phenotypic correlation among many traits simultaneously for combinations of different types of data. We consider combinations of continuous data, discrete data with binary outcomes, and discrete data with multiple ordered and unordered outcomes. We also provide inference tools to address specific hypotheses regarding the correlation structure.

Several comparative methods have been proposed to assess the phenotypic correlation between groups of traits (Felsenstein, 1985; Pagel, 1994; Grafen, 1989; Ives and Garland, 2010). These methods estimate correlations in trait data across multiple species while controlling for shared evolutionary history through phylogenetic trees. Yet their use is generally limited to fixed phylogenetic trees, specific types of data or small datasets.

Markov chains are a natural choice to model the evolution of discrete traits, allowing for correlation between them (Pagel, 1994; Lewis, 2001). In this case, the state space of the Markov chain includes all combinations of possible values for all the traits, and correlation is assessed through the transition probabilities between states. Thus, when the number of traits and possible outcomes for each trait increase, the number of parameters to be estimated in the rate matrix scales up rapidly.

For continuous data, a common approach for assessing phenotypic correlation is the independent contrasts method that models the evolution of multiple traits as a multivariate Brownian diffusion process along the tree (Felsenstein, 1985). Correlation between traits is assessed through the precision matrix of the diffusion process. This method has been extended to account for phylogenetic uncertainty by integrating over the space of trees in a Bayesian context (Huelsenbeck and Rannala, 2003). Recent developments increase the method’s flexibility by allowing for different diffusion rates along the branches of the tree (Lemey et al., 2010), more efficient likelihood computation, and thus, larger datasets (Pybus et al., 2012).

Phylogenetic linear models and related methods naturally consider combinations of different types of data (Grafen, 1989; Ives and Garland, 2010). Developments in this area have led to flexible and efficient methods (Faria et al., 2013; Ho and Ané, 2014). These models assess the effects of independent variables on a dependent trait that evolves along a tree. Although it is possible that the independent variables are phylogenetically correlated, the evolution of these variables is not explicitly modeled. Thus, these models are not tailored to assess correlation between sets of traits evolving along the same phylogenetic tree.

An approach for assessing correlated evolution that can combine both binary and continuous data is the phylogenetic threshold model (Felsenstein, 2005, 2012). The threshold model is used in statistical genetics for traits with a discrete outcome determined by an underlying unobserved continuous variable (Wright, 1934; Falconer, 1965). Felsenstein (2005) proposed the use of this model in phylogenetics. In his model, the underlying continuous variable (or latent liability) undergoes Brownian diffusion along the phylogenetic tree. At the tips, a binary trait is defined depending on the position of the latent liability relative to a specified threshold. This non-Markovian model has the desirable property that the probability of transition from the current state to another can depend on time spent in that current state.

A possible interpretation for this model is that the binary outcome represents the presence or absence of some phenotypic trait, and the underlying continuous process represents the combined effect of a large number of genetic factors that affect this trait. During evolution, these factors undergo genetic drift, which is usually modeled as Brownian diffusion.

In its multivariate version, the threshold model allows for inference on the phenotypic correlation structure between a few continuous and binary traits. As with the independent contrasts method, this correlation can be assessed through the covariance matrix of the multivariate Brownian diffusion for the continuous latent liability.

In this paper we build upon the flexibility of the threshold model to create a Bayesian phylogenetic model for the evolution of binary data, discrete data with multiple ordered or unordered states and continuous data. We explore recent developments in models for continuous trait evolution that improve computational efficiency, and make the joint analysis of multiple traits feasible in the presence of possible phylogenetic uncertainty (Lemey et al., 2010; Pybus et al., 2012).

Importantly, our approach estimates the between trait correlation while simultaneously controlling for the correlation induced through the traits being shared by descent. As shown in one of our examples, failing to control for the evolutionary history can confound inference of correlation between traits, in analogy to false inference in association analysis when failing to control for population substructure or relatedness among individuals.

2. Methods

Consider a dataset of N aligned molecular sequences S from related organisms and an N × P matrix Y =(Y₁,…, Y_N)^t of P-dimensional trait observations from each of the N organisms, such that Y_i =(y_i1,…,y_iP) for i =1,…,N. We model the sequence data S using standard Bayesian phylogenetics models (Drummond et al., 2012) that include, among other parameters ϕ less germaine to our development here, an unobserved phylogenetic tree F. This phylogenetic tree is a bifurcating, directed graph with N terminal nodes (ν₁,…,ν_N) of degree 1 that correspond to the tips of the tree, N − 2 internal nodes (ν_N+1,…,ν_2N−2) of degree 3, a root node ν_2N−1 of degree 2 and edge weights (t₁,…,t_2N−2) between nodes that track elasped evolutionary time. Conditional on F, we assume independence between S and Y, and refer interested readers to, for example, Suchard, Weiss and Sinsheimer (2001) and Drummond et al. (2012) for detailed development of p(S, ϕ,F).

The dimensions of Y_i contain trait observations that may be binary, discrete with multiple states, continuous or a mixture thereof. Importantly, to handle the myriad of different data types, we assume that the observation of Y is governed by an underlying unobserved continuous random variable X =(X₁,…, X_N)^t, called a latent liability, where each row X_i = (x_i1,…,x_iD) ∈ ℝ^D with D ≥ P depending on the mixture of data types. We assume that X arise from a multivariate Brownian diffusion along the tree F (Lemey et al., 2010) for which we provide a more indepth description shortly. At the tips of F, the realized values of Y emerge deterministically from the latent liabilities X through the mapping function g(X).

2.1. Latent Liability Mappings

When column j of Y is composed of binary data, these values map from a single dimension j′ in X following a probit-like formulation in which the outcome is one if the underlying continuous value is larger than a threshold and zero otherwise. Without loss of generality, we take the threshold to be zero, such that

$$y_{ij}=g(x_{i{j}^{\prime }})=\{\begin{array}{ll}0\hfill & \text{if}{x}_{i{j}^{\prime }}\le 0\hfill \\ 1\hfill & \text{if}{x}_{i{j}^{\prime }}>0.\hfill \end{array}$$ (1)

Alternatively, if column j of Y assumes K possible discrete states (s₁,…,s_K), and they are ordered so that transitions from state s_k to s_k+2 must necessarily pass through s_k+1, we use a multiple threshold mapping (Wright, 1934). Again, column j of Y maps from a single dimension j′ in the latent liabilities X; however, the position of x_ij′ relative to the multiple thresholds (a₁,…,a_K−1) determines the value of y_ij through the function

$$y_{ij}=g(x_{i{j}^{\prime }})=\{\begin{array}{ll}{s}_1\hfill & \text{if}{x}_{i{j}^{\prime }}<a_1\hfill \\ s_k\hfill & \text{if}{a}_{k-1}\le x_{i{j}^{\prime }}<a_k\text{for}k=2,\dots ,K-1\hfill \\ s_K\hfill & \text{if}{x}_{i{j}^{\prime }}\ge a_{K-1},\hfill \end{array}$$ (2)

where a₂,…,a_K−1 in increasing values are generally estimable from the data if we set a₁ = 0 for identifiability. Let A = {a_k} track all of the non-fixed threshold parameters for all ordered traits.

When column j of Y realizes values in K multiple states, but there is no ordering between them, we adopt a multinomial probit model. Here the observed trait maps from K−1 dimensions in the latent liabilities X, and the value of y_ij is determined by the largest component of these latent variables,

$$y_{ij}=g(x_{i{j}^{\prime }},\dots ,x_{i,j^{\prime }+K-2})=\{\begin{array}{lll}{s}_1\hfill & \text{if}\hfill & \hfill 0=sup(0,x_{ij},\dots ,x_{i,j+\mathrm{K}-2})\\ s_{k+1}\hfill & \text{if}\hfill & \hfill x_{ik}=sup(0,x_{ij},\dots ,x_{i,j+\mathrm{K}-2}),\end{array}$$ (3)

where, without loss of generality, the first state s₁ is the reference state.

Finally, if column j of Y contains continuous values, a simple monotonic transform from ℝ suffices. For example, for normally distributed outcomes, y_ij = g(x_ij′)= x_ij′.

2.2. Trait Evolution

A multivariate Brownian diffusion process along the tree F (Lemey et al., 2010) gives rise to the elements of X. This process posits that the latent trait value of a child node ν_k in F is multivariate normally distributed about the unobserved trait value of its parent node ν_pa(k) with variance t_k × Σ. In this manner, the unknown D × D matrix Σ characterizes the between-trait correlation and the tree F controls for trait values being shared by descent.

Assuming that the latent trait value at the root node ν_2N−1 draws a priori from a multivariate normal distribution with mean μ₀ and variance τ₀ × Σ and integrating out the internal and root node trait values (Pybus et al., 2012), we recall that the latent liabilities X at the tips of F are matrix normally distributed, with probability density function

$$p(\mathbf{X}\mid \mathbf{V}(F),\mathbf{\sum },{\mathit{\mu }}_0,{\tau }_0)=\frac{exp\left\{-\frac{1}{2}\text{tr}\left[{\mathbf{\sum }}^{-1}{(\mathbf{X}-{\mathit{\mu }}_0)}^t{(\mathbf{V}(F)+{\tau }_0\mathbf{J})}^{-1}(\mathbf{X}-{\mathit{\mu }}_0)\right]\right\}}{{(2\pi )}^{NP/2}{\mid \mathbf{\sum }\mid }^{N/2}{\mid \mathbf{V}(F)+{\tau }_0\mathbf{J}\mid }^{P/2}},$$ (4)

where J is an N × N matrix of all ones and V(F)= {v_ii′} is an N × N matrix that is a deterministic function of F. Let d_F (u, w) equal the sum of edge weights along the shortest path between node u and node w in F. Then diagonal elements v_ii = d_F (ν_2N−1,ν_i), the time-distance between the root node and tip node i, and off-diagonal elements v_ii′ = [d_F (ν_2N−1,ν_i)+ d_F (ν_2N−1,ν_i′) − d_F (ν_i,ν_i′)]/2, the time-distance between the root and the most recent common ancestor of tip nodes i and i′.

We consider the augmented likelihood for the trait data Y and latent liabilities X and highlight a convenient factorization

$$p(\mathbf{Y},\mathbf{X}\mid \mathbf{V}(F),\mathbf{\sum },\mathbf{A},{\mathit{\mu }}_0,{\tau }_0)=p(\mathbf{Y}\mid \mathbf{X},\mathbf{A})\times p(\mathbf{X}\mid \mathbf{V}(F),\mathbf{\sum },{\mathit{\mu }}_0,{\tau }_0).$$ (5)

The conditional likelihood p(Y | X, A)= 1_(Y=g(X)) in factorization (5) is simply the indicator function that X are consistent with the observations Y. Consequentially, the augmented likelihood is a truncated, matrix normal distribution.

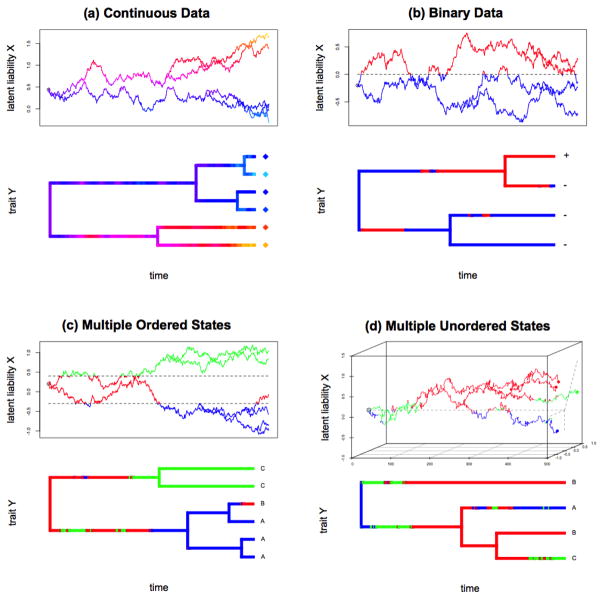
Figure 1 illustrates schematic representations of the latent liability model for all four types of data. In the figure, we include trees with N = 4 to 6 taxa, annotated with their observed traits Y at the tree tips and plot potential realizations of the latent liabilities X values along these trees that give rise to Y.

Fig 1.

Realizations of the evolution of latent liabilities X and observed trait Y for different types of data. Both tree and Brownian motion plots are color coded according to the trait Y. Realization (a) represents a continuous trait, (b) represents discrete binary data, (c) represents discrete data with multiple ordered states, and (d) represents discrete data with multiple unordered states, for which the latent liabilities X is multivariate. ** This figure was created using code modified from R package phylotools (Revell, 2012).

We complete our model specification by assuming a priori

$${\mathbf{\sum }}^{-1}~\text{Wishart}(d_0,\mathbf{T}),$$ (6)

with degrees of freedom d₀ and rate matrix T. For the non-fixed threshold parameters A, we assume differences a_k − a_k−1 for each trait are a priori independent and Exponential(α) distributed, where α is a rate constant. Finally, we specify fixed hyperparameters (μ₀, τ₀, d₀, T, α) in each of our examples.

2.3. Inference

We aim to learn about the posterior distribution

$$\begin{array}{l}p(\mathbf{\sum },F,\mathit{\varphi },\mathbf{A}\mid \mathbf{Y},\mathbf{S})\propto p(\mathbf{Y}\mid \mathbf{\sum },F,\mathbf{A})\times p(\mathbf{\sum })\times p(\mathbf{A})\times p(\mathbf{S},\mathit{\varphi },F)\\ =\left(\int p(\mathbf{Y},\mathbf{X}\mid \mathbf{\sum },F,\mathbf{A})\mathrm{d}\mathbf{X}\right)\times p(\mathbf{\sum })\times p(\mathbf{A})\times p(\mathbf{S},\mathit{\varphi },F).\end{array}$$ (7)

We accomplish this task through Markov chain Monte Carlo (MCMC) and the development of computationally efficient transitions kernels to faciliate sampling of the latent liabilities X. We exploit a random-scan Metropolis-with-Gibbs scheme. For the tree F and other phylogenetic parameters ϕ involving the sequence evolution, we employ standard Bayesian phylogenetic algorithms (Drummond et al., 2012) based on Metropolis-Hastings parameter proposals. Further, the full conditional distribution of Σ⁻¹ remains Wishart (Lemey et al., 2010), enabling Gibbs sampling.

MCMC transition kernels for sampling X are more problematic; tied into this difficulty also lies computationlly efficient evaluation of Equation (4). Strikingly, the solution to the latter problem points to new directions in which to attack the sampling problem. As written, computing p(X | V(F), Σ, μ₀,τ₀) to evaluate a Metropolis-Hasting acceptance ratio appears to require the high computational cost of 𝒪(N³) involved in forming (V(F)+ τ₀J)⁻¹. Such a cost would be prohibitive for large N when F is random, necessiating repeated inversion. This is one reason why previous work has limited itself to fixed, known F. However, we follow Pybus et al. (2012), who develop a dynamic programming algorithm to evaluate density (4) in 𝒪(N) that avoids matrix inversion. Critically, we extend these algorithmic ideas in this paper to construct computationally efficient sampling procedures for X.

Pybus et al. (2012) propose a post-order tree traversal that visits each node u in F, starting at the tips and ending at the root. For the example tree in Figure 2, one possible post-order traversal proceeds through nodes {1 → 2 → 4 → 3 → 5}. Let X_u for u = N +1,…, 2N − 1 imply now hypothesized latent liabilities at the internal and root nodes of F. Then, at each visit, one computes the conditional density of the tip latent liabilities ${\{\mathbf{X}\}}_u^{\text{post}}$ that are descendent to node u given X_pa(u) at the parent node of u by integrating out the hypothesized value X_u at node u. For example, when visiting node u = 4 in Figure 2, one considers the conditional density of (X₁, X₂) | X₅. Each of these conditional densities are proportional to a multivariate normal density, so during the traversal it suffices to keep track of the partial mean vector ${\mathbf{m}}_u^{\text{post}}$, partial precision scalar $p_u^{\text{post}}$ and remainder term ρ_u that characterize the conditional density. We refer interested readers to the Supplementary Material in Pybus et al. (2012) for further details.

Fig 2.

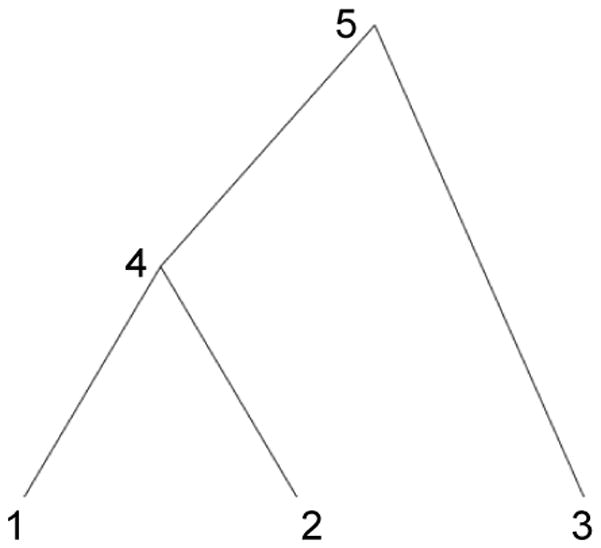
Example N =3 tree to illustrate pre-and post-order traversals for efficient sampling of latent liabilities X =(X₁, X₂, X₃)^t.

Building upon this algorithm, we identify that it is possible and practical to generate samples from p(X_i | X_(−i), V(F), Σ, μ₀, τ₀) for tip ν_i without having to manipulate V(F) via one additional pre-order traversal of F. This approach enables us to exploit p(X_i | X_(−i), V(F), Σ, μ₀,τ₀) as a proposal distribution in an efficient Metropolis-Hastings scheme to sample X_i, since the distribution often closely approximates the full conditional distribution of X_i.

To ease notation in the remainder of this section, we drop explicit dependence on V(F), Σ, μ₀, τ₀ in our distributional arguments. Further, let ${\{\mathbf{X}\}}_u^{\text{pre}}$ collect the latent liabilities at the tree tips that are not descendent to node u for u =1,…, 2N − 1, such that ${\{\mathbf{X}\}}_u^{\text{pre}}\cup {\{\mathbf{X}\}}_u^{\text{post}}=\mathbf{X}$ and ${\{\mathbf{X}\}}_u^{\text{pre}}\cap {\{\mathbf{X}\}}_u^{\text{post}}=\varnothing$. Notably, ${\{\mathbf{X}\}}_i^{\text{pre}}={\mathbf{X}}_{(-i)}$ and ${\{\mathbf{X}\}}_{2N-1}^{\text{pre}}=\varnothing$. With these goals and definitions in hand, we find p(X_i | X_(−i)) recursively.

Consider a triplet of nodes in F such that node u has parent pa(u)= w that it shares with sibling sib(u)= v. For example, in Figure 2, u = 1, v =2 and w = 4 is one of two choices. Because of the conditional independence structure of the multivariate Brownian diffusion process on F, we can write

$$p({\mathbf{X}}_u\mid {\{\mathbf{X}\}}_u^{\text{pre}})=\int p({\mathbf{X}}_u\mid {\mathbf{X}}_{\text{pa}(u)})p({\mathbf{X}}_{\text{pa}(u)}\mid {\{\mathbf{X}\}}_{\text{pa}(u)}^{\text{pre}},{\{\mathbf{X}\}}_{\text{sib}(u)}^{\text{post}})\mathrm{d}{\mathbf{X}}_{\text{pa}(u)},$$ (8)

where Equation (8) returns the desired quantity when i = u and the first term of the integrand is a multivariate normal density MVN (X_u; X_pa(u), (t_uΣ)⁻¹) centered at X_pa(u) with precision (t_uΣ)⁻¹. The second term requires more exploration

$$\begin{array}{l}p({\mathbf{X}}_{\text{pa}(u)}\mid {\{\mathbf{X}\}}_{\text{pa}(u)}^{\text{pre}},{\{\mathbf{X}\}}_{\text{sib}(u)}^{\text{post}})=\frac{p({\mathbf{X}}_{\text{pa}(u)},{\{\mathbf{X}\}}_{\text{sib}(u)}^{\text{post}}\mid {\{\mathbf{X}\}}_{\text{pa}(u)}^{\text{pre}})}{p({\{\mathbf{X}\}}_{\text{sib}(u)}^{\text{post}}\mid {\{\mathbf{X}\}}_{\text{pa}(u)}^{\text{pre}})}\\ \propto p({\{\mathbf{X}\}}_{\text{sib}(u)}^{\text{post}}\mid {\mathbf{X}}_{\text{pa}(u)})p({\mathbf{X}}_{\text{pa}(u)}\mid {\{\mathbf{X}\}}_{\text{pa}(u)}^{\text{pre}}),\end{array}$$ (9)

where the normalization constant does not depend on X_pa(u) and we fortuitously have determined that the probability $p({\{\mathbf{X}\}}_{\text{sib}(u)}^{\text{post}}\mid {\mathbf{X}}_{\text{pa}(u)})$ is proportional to $\text{MVN}\left({\mathbf{X}}_{\text{pa}(u)};{\mathbf{m}}_{\text{sib}(u)}^{\text{post}},p_{\text{sib}(u)}^{\text{post}}{\mathbf{\sum }}^{-1}\right)$ during the post-order traversal.

Substituting Equation (9) in Equation (8) furnishes a set of recursive integrals down the tree

$$p({\mathbf{X}}_u\mid {\{\mathbf{X}\}}_u^{\text{pre}})\propto \int p({\mathbf{X}}_u\mid {\mathbf{X}}_{\text{pa}(u)})p({\{\mathbf{X}\}}_{\text{sib}(u)}^{\text{post}}\mid {\mathbf{X}}_{\text{pa}(u)})p({\mathbf{X}}_{\text{pa}(u)}\mid {\{\mathbf{X}\}}_{\text{pa}(u)}^{\text{pre}})\mathrm{d}{\mathbf{X}}_{\text{pa}(u)}.$$ (10)

To solve the set of integrals in (10), we recall that $p({\mathbf{X}}_{2N-1}\mid {\{\mathbf{X}\}}_{2N-1}^{\text{pre}})=p({\mathbf{X}}_{2N-1})$ is MVN (X_2N−1 ; μ₀, (τ₀Σ)⁻¹) and so define pre-order, partial mean vector ${\mathbf{m}}_{2N-1}^{\text{pre}}={\mathit{\mu }}_0$ and partial precision scalar $p_{2N-1}^{\text{pre}}=1/{\tau }_0$. Since the convolution of multivariate normal random variables remains multivariate normal, we identify that $p({\mathbf{X}}_u\mid {\{\mathbf{X}\}}_u^{\text{pre}})$ is $\text{MVN}({\mathbf{X}}_u;{\mathbf{m}}_u^{\text{pre}},p_u^{\text{pre}}{\mathbf{\sum }}^{-1})$ where pre-order, partial mean vectors and precision scalars unwind through

$$\begin{array}{ll}{\mathbf{m}}_u^{\text{pre}}\hfill & =\frac{p_{\text{sib}(u)}^{\text{post}}{\mathbf{m}}_{\text{sib}(u)}^{\text{post}}+p_{\text{pa}(u)}^{\text{pre}}{\mathbf{m}}_{\text{pa}(u)}^{\text{pre}}}{{\mathbf{m}}_{\text{sib}(u)}^{\text{post}}+{\mathbf{m}}_{\text{pa}(u)}^{\text{pre}}},\text{and}\hfill \\ \frac{1}{p_u^{\text{pre}}}\hfill & =t_u+\frac{1}{p_{\text{sib}(u)}^{\text{post}}+p_{\text{pa}(u)}^{\text{pre}}},\hfill \end{array}$$ (11)

until we hit tip node i.

With a simple algorithm to compute the mean and precision of the full conditional p(X_i | X_(−i), V(F), Σ, μ₀,τ₀) at our disposal, we finally turn our attention toward a Metropolis-Hastings scheme to sample X_i. The algorithm needs to generate samples only for the latent liabilities X_i(−c) corresponding to the discrete traits, since the map function g(·) fixes the latent liabilities X_ic for all the continuous traits. Thus we consider the proposal distribution p(X_i(−c) | X_ic, X_(−i), V(F), Σ, μ₀, τ₀), which is obtained from p(X_i | X_(−i), V(F), Σ, μ₀, τ₀) by further conditioning on the fixed liabilities X_ic. This conditional distribution is $\text{MVN}({\mathbf{X}}_{ic};{\mathbf{m}}_i^{\text{cond}},p_i^{\text{pre}}{\mathbf{W}}_{cc})$, where

$${\mathbf{m}}_i^{\text{cond}}={\mathbf{m}}_{i(-c)}^{\text{pre}}-{\mathbf{W}}_{cc}^{-1}{\mathbf{W}}_{c(-c)}\left({\mathbf{X}}_{i(-c)}-{\mathbf{m}}_{i(-c)}^{\text{pre}}\right).$$ (12)

Here the vector ${\mathbf{m}}_{i(-c)}^{\text{pre}}=({\mathbf{m}}_{i(-c)}^{\text{pre}},{\mathbf{m}}_{ic}^{\text{pre}})$ is partitioned according to correspondence to continuous traits, as is the precision matrix for the diffusion process

$${\mathbf{\sum }}^{-1}=\left(\begin{array}{cc}{\mathbf{W}}_{(-c)(-c)}& {\mathbf{W}}_{(-c)c}\\ {\mathbf{W}}_{c(-c)}& {\mathbf{W}}_{cc}\end{array}\right).$$ (13)

Several approaches compete for generating truncated multivariate normal random variables, including rejection sampling (Breslaw, 1994; Robert, 1995) and Gibbs sampling (Gelfand, Smith and Lee, 1992; Robert, 1995) possibly with data augmentation (Damien and Walker, 2001). For the examples we explore in this manuscript, the dimension D of X_i can be large, ranging up to 54 with N = 360 tips, with occasionally high correlation in Σ. Gibbs sampling can suffer from slow convergence in the presence of high correlation between dimensions. Consequentially, we explore an extension of rejection sampling that involves a multiple-try Metropolis (Liu, Liang and Wong, 2000) construction. We simulate up to R draws ${\mathbf{X}}_i^{(r)}~p(·\mid {\mathbf{X}}_{(-i)},\mathbf{V}(F),\mathbf{\sum },{\mathit{\mu }}_0,{\tau }_0)$. For draw ${\mathbf{X}}_i^{(r)}$, if $p({\mathbf{X}}_i^{(r)}\mid {\mathbf{Y}}_i,\mathbf{A})\ne 0$, then we accept this value as our next realization of X_i. The Metropolis-Hastings acceptance probability of this action is 1. If all R proposals return 0 density, the MCMC chain remains at its current location.

In our largest example, we evaluate one approach to select R. We start with a very large R = 10000 and observe that most proposals that lead to state changes occur in the first 20 attempts; after 100 attempts, the residual probability of generating a valid sample becomes negligible. Thus, we set R = 100 for future MCMC simulations. As MCMC chains converge towards the posterior distribution, the probably of generating a valid sample approaches the 75 – 85% range in our examples. Finally, we employ a Metropolis-Hastings scheme to sample A in which the proposal distribution is a uniform window centered at the parameter’s current value with a tunable length.

2.4. Correlation Testing and Model Selection

To assess the phenotypic relationship between two specific components of the trait vector Y, we look at the correlation of the corresponding elements in the latent variable X. One straightforward approach entertains the use of the marginal posterior distribution of pair-wise correlation coefficients ρ_jj′ determined from Σ. As a simple rule-of-thumb, we designate ρ_jj′ significantly non-zero if > 99% of its posterior mass falls strictly greater than or strictly less than 0.

When scientific interest lies in formal comparison of models that involve more than pair-wise effects, we employ Bayes factors. Possible examples include identifying block-diagonal structures in Σ, comparing the latent liability model to other trait evolution models and, as demonstrated in our examples, state-ordering of multiple discrete traits.

The Bayes factor that compares models M₀ and M₁ can be obtained as

$$B_{01}=\frac{p(\mathbf{Y},\mathbf{S}\mid M_0)}{p(\mathbf{Y},\mathbf{S}\mid M_1)},$$ (14)

in which p(Y, S|M) is the marginal likelihood of the data under model M (Jeffreys, 1935). Computing these marginal likelihoods is not straightforward, involving high dimensional integration. We adopt a path sampling approach which estimates these integrals through numerical integration.

To estimate the marginal likelihoods in (14), we follow Baele et al. (2012) in considering a geometric path q_β(Y, S; X, θ) that goes from a normalized source distribution q₀(Y, S; X, θ) to the unnormalized posterior distribution p(Y, S|X, θ)p(X, θ). Here both distributions are defined on the same parameter space, and θ = {Σ, F, ϕ, A} collects all model parameters. The path sampling algorithm employs MCMC to numerically compute the path integral

$$log(p(\mathbf{Y},\mathbf{S}\mid M))={\int }_0^1{E}_{q_{\beta }}[log(q_1(\mathbf{Y},\mathbf{S};\mathbf{X},\mathit{\theta }))-log(q_0(\mathbf{Y},\mathbf{S};\mathbf{X},\mathit{\theta }))]\mathrm{d}\beta .$$ (15)

A natural choice for the source distribution is the prior p(X, θ). However, due to truncations in the distribution of X induced by the map function g(·), the path from the prior to the unnormalized posterior is not continuous. Since continuity along the whole path is required for (15) to hold, we propose here a different destination distribution that leads to a continuous path. Let

$$q_0(\mathbf{Y},\mathbf{S};\mathbf{X},\mathit{\theta })=p(\mathbf{X}\mid \mathbf{Y},\mathbf{A})\psi (\mathbf{X})p(\mathit{\theta }),$$ (16)

where p(θ) is the prior, p(X | Y, A)= 1_(Y=g(X)), and ψ(X) is a function proportional to a conveniently chosen matrix normal distribution. The proportionality constant of ψ(X) is selected to guarantee

$$\int p(\mathbf{X}\mid \mathbf{Y},\mathbf{A})\psi (\mathbf{X})\mathrm{d}\mathbf{X}=1,$$ (17)

and thus a normalized source distribution q₀(Y, S; X, θ).

The choice of function ψ(X)= ψ^*(X)/Q(Y, A) is central to the success of this path sampling approach. We select the matrix normal distribution ψ^*(X) so that all entries in X are independent, and consequently the proportionality constant is

$$Q(\mathbf{Y},\mathbf{A})=\prod _{i=1}^N\prod _{j=0}^{P}Q(y_{ij},\mathbf{A})=\prod _{i=1}^N\prod _{j=0}^P\int p({\mathbf{X}}_{i{j}^{\ast }}\mid y_{ij},\mathbf{A}){\psi }^{\ast }({\mathbf{X}}_{i{j}^{\ast }})\mathrm{d}{\mathbf{X}}_{i{j}^{\ast }},$$ (18)

where X_ij^* are all the entries of the latent liability corresponding to y_ij.

For binary traits, X_ij^* is univariate, and ψ(X_ij^*) is proportional to a normal distribution whose mean X̄_ij^* and variance ${\overline{\sigma }}_{i{j}^{\ast }}^2$ match those of the posterior distribution of X_ij^*. Considering that the map function g(·) restricts X_ij^* to be larger (or smaller) than 0, and that X̄_ij^* always belongs to this valid region, the proportionality constant for a binary trait is

$$Q({\mathbf{Y}}_{ij},\mathbf{A})=\mathrm{\Phi }\left(\frac{\mid {\overline{X}}_{i{j}^{\ast }}\mid }{{\overline{\sigma }}_{i{j}^{\ast }}}\right),$$ (19)

where Φ(·) is the cumulative distribution function (CDF) of the standard normal distribution.

For traits with K ≥ 3 ordered states, X_ij^* is also univariate, and we make the same choice for mean and variance parameters of ψ^*(X_ij^*). The map function depends on the threshold parameters A, that must be fixed for this analysis. If a_l(y_ij) and a_u(y_ij) denote respectively the lower and upper threshold for the valid region mapped from y_ij, then the proportionality constant becomes

$$Q(y_{ij},\mathbf{A})=\mathrm{\Phi }\left(\frac{a_u(y_{ij})-{\overline{X}}_{i{j}^{\ast }}}{{\overline{\sigma }}_{i{j}^{\ast }}}\right)-\mathrm{\Phi }\left(\frac{a_l(y_{ij})-{\overline{X}}_{i{j}^{\ast }}}{{\overline{\sigma }}_{i{j}^{\ast }}}\right).$$ (20)

When y_ij assumes one of the extreme states s₁ and s_K, then the normalizing constant considers the appropriate open interval.

For discrete data with K ≥ 3 unordered states, y_ij maps from K − 1 dimensions in Y. For simplicity, ψ^*(X_ij^*) is a standard multivariate normal distribution, and the proportionality constant is

$$Q(y_{ij},\mathbf{A})=\{\begin{array}{lll}{2}^{-(K-1)}\hfill & \text{if}\hfill & y_{ij}=s_1\hfill \\ \frac{1-2^{-(K-1)}}{K-1}\hfill & \text{if}\hfill & y_{ij}=s_2,\cdots ,s_K.\hfill \end{array}$$ (21)

Finally, for continuous y_ij we simply have ψ(X_ij^*) = y_ij.

Implementation

The methods described in this paper have been implemented in the software package BEAST (Drummond et al., 2012).

3. Applications

We present applications of our model to three problems in which researchers wish to assess correlation between different types of traits while controlling for their shared evolutionary history.

3.1. Antimicrobial resistance in Salmonella

Development of multidrug resistance in pathogenic bacteria is a serious public health burden. Understanding the relationships between resistance to different drugs throughout bacterial evolution can help shed light on the fundamentals of multidrug resistance on the epidemiological scale.

We use the phylogenetic latent liability model to assess phenotypic correlation between resistance traits to 13 different antibiotics in Salmonella. We analyse 248 isolates of Salmonella Typhimurium DT104, obtained from animals and humans in Scotland between 1990 and 2011 (Mather et al., 2013). For each isolate, we have sequence data and binary phenotypic data indicating the strains resistance status to each of the 13 antibiotics.

To assess which resistance traits are associated we examine the correlation matrix of the latent liabilities X. Because the trait data are binary, the underlying latent variables X_i for this problem are D = 13-dimensional, with each entry corresponding to resistance to one antibiotic. To highlight the main correlation structure of Σ, Figure 3 presents a heatmap of the significantly non-zero pair-wise correlation coefficients. This matrix contains only positive correlations, consistent with genetic linkage between resistance traits. Additionally, the significant correlations form a block-like structure. Table S1 presents posterior mean and 95% Bayesian credible interval (BCI) estimates for all correlations between resistance traits. Estimates of non-significant correlations tend to be slightly positive, with the exception of correlations involving resistance to ciprofloxacin.

Fig 3.

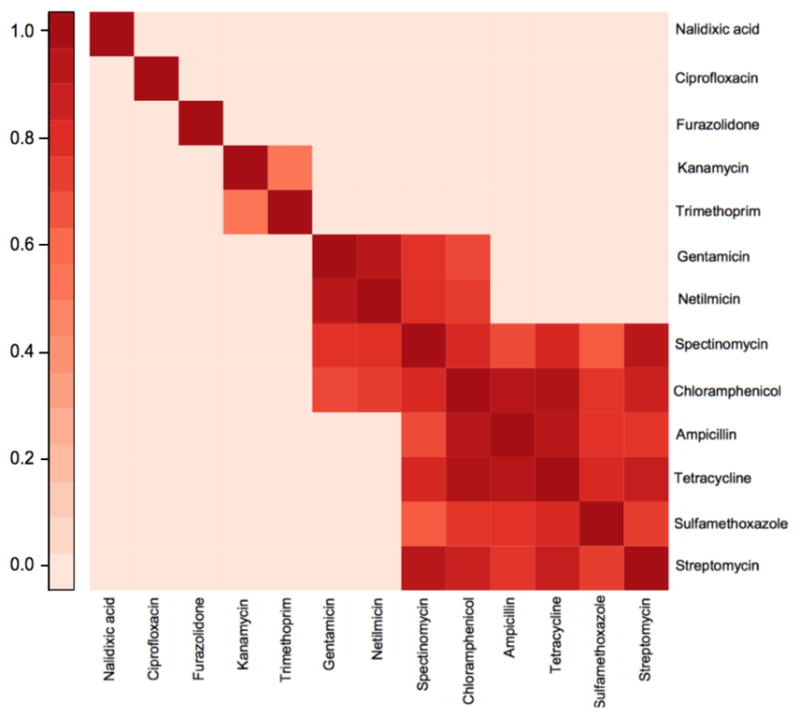
Heatmap of posterior means for significantly non-zero correlations between antibiotic resistance traits for the latent liability model. Darker colors indicate stronger positive correlation.

Our analysis reveals a block of strong positive correlations between resistance traits to the antibiotics tetracycline, ampicillin, chloramphenicol, spectinomycin, streptomycin and sulfamethoxazole (sulfonamide), similar to those found using a simpler model (Mather et al., 2012). We estimate a posterior probability > 0.9999 for positive correlation between all these resistance traits simultaneously. This block is consistent with the Salmonella genomic island 1 (SGI-1), a 43-kb genomic island conferring multidrug resistance. Among the drugs considered here, SGI-1 confers resistance to these 6 antibiotics (Boyd et al., 2001).

Another pair of antibiotic resistance traits that we infer to be strongly correlated are gentamicin and netilmicin, with a 95% BCI of [0.80, 0.98]. These drugs are both aminoglycoside antibiotics, and the same genes may confer resistance to both antibiotics. These drugs also appear correlated with some of the resistance traits connected to SGI-1.

Although previous analysis of this dataset has revealed that most of the evolutionary history that these data capture was spent in human hosts, human-to-animal or animal-to-human transitions do occur across the tree (Mather et al., 2013). We investigate whether these interspecies transitions also correlate with antibiotic resistance. To do so, we include host species (animal/human) as a 14th binary trait under in latent liability model. None of the pair-wise correlations are significantly non-zero given our rule-of-thumb definition. Table S2 contains estimated correlations to the host trait.

3.2. Columbine flower evolution

The flowers of columbine genus Aquilegia have attracted several different pollinators throughout their evolutionary history. One question that remains is the exact role the pollinators play in the tempo of columbine flower evolution (Whittall and Hodges, 2007). Since different pollinator species demonstrate distinct preferences for flower morphology and color, we investigate here how these traits correlate over the evolutionary history of Aquilegia.

We analyse P = 12 different floral traits for N = 30 monophyletic populations from the genus Aquilegia. Of these traits, 10 are continuous and represent color, length and orientation of different anatomical features of the flowers. Additionally, we consider a binary trait that indicates presence or absence of anthocyanin pigment, and another discrete trait that indicates the primary pollinator for that population. As the prevailing hypothesis is that evolutionary transitions from bumblebee-pollinated flowers (Bb) to those primarily pollinated by hawkmoths (Hm) are obligated to pass through an intermediate stage of hummingbird-pollination (Hb) (Whittall and Hodges, 2007), we treat pollinators as ordered states, but we formally test alternative orderings. Taken together, this results in a latent liability model with D = 12 dimensions. As sequence data are not readily available for all the taxa included in this analysis, we consider for our analysis the same fixed phylogenetic tree used in Whittall and Hodges (2007). The ability to either condition on a fixed phylogeny F or integrate over a random F in a single framework presents a strength in a field that has traditionally focused on either genetic or phenotypic data alone and joint datasets are an emerging addition. Whittall et al. (2006) and Whittall and Hodges (2007) have published the original data, that are available at (http://bodegaphylo.wikispot.org).

To draw inference on the phenotypic correlation structure of these traits, we focus on the 12 × 12 variance matrix Σ of the Brownian motion process that governs the evolution of X on the tree. We report posterior mean and BCI estimates for all pair-wise correlations in Σ in Table S3. Figure 4 presents a heatmap of the posterior means of the correlations. Our analysis reveals a strong block correlation structure between the floral traits. We find one block of positive correlation between chroma of both spur and blade and the presence of anthocyanins. All other color and morphological traits in the analysis form a second block of positive correlation. Additionally, phenotypic correlation between the first and second trait blocks are all negative.

Fig 4.

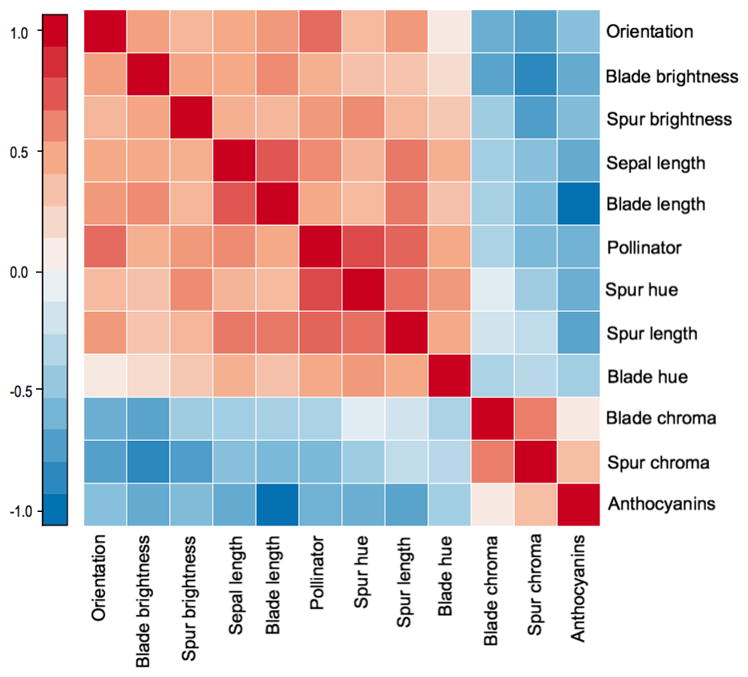
Heatmap of the posterior mean for the phenotypic correlation of columbine floral traits in the latent liability model. Darker colors indicate stronger correlations; shades of red for positive correlation and blue for negative correlation.

Whittall and Hodges (2007) highlight the relationship between changes in pollinators and increases in floral spur length. They argue that flowers with long spurs are only pollinated by animals with the long tongues required to access and feed on the nectar contained at the end of the spur. We estimate a positive correlation between pollinators and spur length, with a posterior mean of 0.76, and a 95% BCI of [0.60; 0.88], consistent with their findings.

The pollinator trait has K = 3 ordered states and, under the latent liability model, its outcome is determined by the relative position of one dimension in X to threshold parameters a₁ = 0 and a₂. Consequently, our estimate of a₂ is instrumental in determining the relative probabilities of the states in our model and the inferred trait state at the root of the tree. We estimate a₂ to have a posterior mean of 3.00 with a 95% BCI of [1.14; 5.34].

The bumblebee ↔ hummingbird ↔ hawkmoth (Bb-Hb-Hm) ordering is only one of several, and alternative hypotheses regarding pollinator adaptation have been proposed (van der Niet and Johnson, 2012). We examine whether the data support this ordering, or if there is another model with a better fit. We use Bayes factors to compare four different models for the pollinator trait: the Bb-Hb-Hm, Hb-Hm-Bb, Hm-Bb-Hb, and an unordered formulation. Note that there are only three possible orderings for a K =3 state ordered latent liability model since, for symmetric models such as Bb-Hb-Hm and Hm-Hb-Bb, inverting the order leads to equivalent models with inverted signs for the latent traits. The unordered model leads to a bivariate contribution to latent liability X. Table 1 presents the path sampling estimates for the marginal likelihood of each model and the corresponding Bayes factors. These comparisons indicate that, in agreement with Whittall and Hodges (2007), the data strongly support the Bb-Hb-Hm model.

Table 1.

Model selection for the ordering of bumblebee (Bb), hummingbird (Hb) and hawkmoth (Hm) pollinators in Columbine flowers.

Order	log Marginal Likelihood	log Bayes Factor
		Hm-Bb-Hb	Hb-Hm-Bb	unordered
Bb-Hb-Hm	−11.2	9.4	14.2	24.8
Hm-Bb-Hb	−20.6	-	4.8	15.3
Hb-Hm-Bb	−25.4	-	-	10.5
unordered	−36.0	-	-	-

Our latent liability model estimates correlation between traits while accounting for shared evolutionary history. To evaluate the effect that phylogenetic relatedness has on our estimates, we estimated the same correlation under a latent liability model with no phylogenetic structure. In this analysis, a star tree with identical distance between all taxa was used. Table S4 presents these correlation estimates and the corresponding 95% BCI. Comparing these results to the original latent liability analysis that accounts for shared evolutionary history, we noticed that most estimates were consistent between both analyses, with a mean absolute difference for posterior means of correlation of 0.11. However, for three of the pairwise correlations (anthocianins × orientation, orientation × blade length, spur length × spur hue) the BIC’s for the model that does not account for shared evolution did not contain the posterior mean for the evolutionary model. In particular, the evolutionary model estimates a significantly weaker correlation between orientation and anthocianins (posterior mean of −0.45) than does the model that does not account for shared history, with a 95% BCI of [−0.78; −0.46].

3.3. Correlation within and across influenza epitopes

In influenza, the viral surface proteins hemagglutinin (HA) and neuraminidase provide the antigenic epitopes to which the host immune system responds. Rapid mutation of these proteins to evade immune response, known as antigenic drift, severely challenges the design of annual influenza vaccines. The epitope regions in these genes are particularly important to the drift process (Fitch et al., 1991; Plotkin and Dushoff, 2003). In this context, we are interested in studying the phenotypic correlation among the amino acid sites of these epitopes, because the identification of correlated amino acids grants insight into the dynamics of antigenic drift in influenza.

The HA protein has five identified epitopes A–E, each containing around 20 amino acids. We focus on epitopes A and B, because these are the most immunologically stimulating for most influenza strains (Bush et al., 1999; Cox and Bender, 1995). We analyse sequence data for 180 strains of human H3N2 influenza dating from 1995 to 2012, obtained from the Influenza Research Database (http://www.fludb.org) and selected to promote geographic diversity. We use the amino acid information in epitope A and B for the latent liability part of the model, and the remaining sequence data in a standard phylogenetic approach to inform the tree structure.

Of the 40 amino acid sites in epitopes A and B of the HA protein, we find 17 to be variable in our sample. The number of unique amino acids in these sites varies between K = 2 and K = 5. Through a preliminary survey of a larger sample of influenza strains (900 samples) from the same period we find that all polymorphic sites for which the major allele frequency is < 99% are also variable in our 180 sequence sample, strongly suggesting that our limited dataset contains information about all the common variant sites in epitopes A and B during this period.

We model these data with the latent liability model for multiple unordered states. For each amino acid site, we have K − 1 corresponding latent traits, yielding a total of D = 32 latent dimensions in X. Without loss of generality, we take the amino acid observed in the oldest sequence of the sample as the reference state, and each entry of the latent liability column corresponds to one of the other amino acid variants for that site.

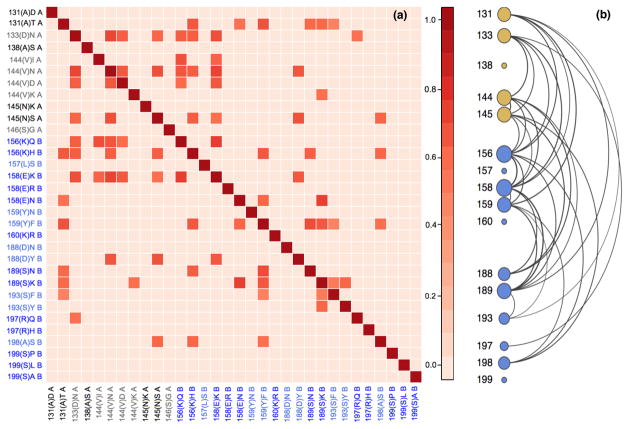
To assess the phenotypic correlation structure between sites in epitopes A and B, we estimate the correlation matrix associated with Σ of the latent liability X. Figure 5 presents pairwise correlations for the significantly non-zero estimates. The arrangement of states follows the order of sites in the primary amino acid sequence, even though the sites are not necessarily contiguous in folded protein-space.

Fig 5.

(a) Heatmap of the posterior mean for the non-zero phenotypic correlation of amino acids in H3N2 epitopes A and B in the latent liability model. Darker colors indicate stronger correlation. We list the sites as follows: the number of the amino acid site in the aligned sequence; the one letter code for the reference amino acid for the site, in parentheses; the code for the amino acid corresponding to the latent trait; and the epitope to which the site belongs.(b) Network representation of the correlation structure of antigenic sites. Yellow nodes represent sites from epitope A, and blue ones from epitope B. Edges represent significant correlations, edge thickness represent correlation coefficient, and node sizes are proportional to network centrality.

Our analysis suggests a group of 11 sites that are strongly correlated with each other. These sites have significant positive correlations to at least three other sites in the group. The group includes all the sites identified by Koel et al. (2013) as being the major determinants of antigenic drift that are polymorphic in our sample. We do not find preferential correlations within epitopes.

Table S5 presents a list with point estimates and 95% BCI of correlations whose credible intervals do not include zero. All correlations in this list are positive and point estimates range from 0.6 to 0.74. Since, for all sites the oldest variant was taken as the reference state, a positive correlation between two latent traits could be seen as association between novel amino acids in both sites. The strongest evidence for correlation was found between sites 158(E)K and 156(K)Q, with an estimated correlation coefficient of 0.74 (95% BIC of [0.40, 0.93]). Koel et al. (2013) identified these specific mutations in both sites as being the main drivers of major antigenic change taking place between 1995 and 1997. Mutations in sites 159 and 189 are another example of a pair of substitutions identified as driving major antigenic change taking place in the late 1980’s. Even though the oldest sequence in our sample only dates back to 1995, correlation between these two sites remains strongly supported by our analysis, with an estimated correlation coefficient between 159(Y)F and 189(S)N of 0.69 (95% BIC of [0.27, 0.92]).

4. Discussion

We present the phylogenetic latent liability model as a framework for assessing phenotypic correlation between different types of data. Through our three applications, we illustrate the use of our methodology for binary data, discrete data with multiple ordered and unordered states, continuous data and combinations thereof. The applications exemplify current biological problems which our method can naturally address. Additionally, we show how the model can be used to reveal the overall phenotypic correlation structure of the data, and we provide tools to test hypotheses about individual correlations and for general model testing.

The threshold structure of the phylogenetic latent liability model renders it non-Markovian for the discrete traits. Both Felsenstein (2005, 2012) and Revell (2013) argue that this is actually a valuable property for many phenotypic traits for which the probability of transitioning between states should vary depending on the time spent at that state. Based on this argument, Revell (2013) investigates ancestral state reconstruction for univariate ordered traits under the threshold model, and finds consistent reconstructions for simulated data. For our model, it would be straightforward to perform ancestral state estimation for multivariate traits of all types considered, because the inference machinery is already implemented in BEAST.

A problem with many comparative biology methods for phenotypic correlation is the requirement for a fixed tree. Through sequence data, our model can account for the uncertainty of tree estimation by integrating over the space of phylogenetic trees, as we do for the influenza epitope and antibiotic resistance examples.

As a caveat for this type of model, Felsenstein (2012) points out a general lack of power, arguing that for realistically sized datasets confidence intervals would be too large. This issue could be magnified on discrete traits, since the correlations are an extra step removed from the data. In our applications, the size of our posterior credible intervals are relatively large for intervals constrained between −1 and 1. However, this did not prevent us from recovering general correlation patterns and identifying important correlations. Moreover, for the columbine flower example, we find no difference in average size of credible intervals for correlations including latent traits and those between two continuous traits.

Analytically integrating out continuous trait values at root and internal nodes to compute the likelihood of Brownian motion on a tree leads to significant improvement in efficiency of inference methods (Pybus et al., 2012). This strategy computes successive conditional likelihoods by a post-order tree traversal in a procedure akin to Felsenstein’s peeling algorithm (Felsenstein, 1981). Its effectiveness has been explored in similar contexts in univariate (Novembre and Slatkin, 2009; Blum et al., 2004) and multivariate Brownian motion (Freckleton, 2012) and to estimate the Gaussian component of Lévy processes (Landis, Schraiber and Liang, 2013). A related post-order traversal approach improves computation in the context of phylogenetic regressions for some Gaussian and non-Gaussian models (Ho and Ané, 2014). Unfortunately, a similar solution is not available to marginalize the latent liability X at the tips of the tree in our model. Consequently this integration must be performed by MCMC. Integration for X is a critical part of our method, and for large datasets, mixing becomes a problem. To address this issue, we present an efficient sampler that, at each iteration, updates all components of the multivariate latent variable X at one tip of the tree. This algorithm builds upon the dynamic programming strategy of Pybus et al. (2012) to obtain a truncated multivariate normal as the full conditional distribution of X_i. Even though sampling from this truncated distribution requires an accept/reject step that could be highly inefficient, we find that as the chain approaches equilibrium, rejection rates become small.

Computational time for our method varies depending on the size and type of the dataset and on additional model specifications of phylogenetic inference. Our example with the shortest computational time is the columbine flower analysis, in which we used a fixed phylogenetic tree and only 2 of the traits required latent variables. This application ran at 0.02 hours per million states on a regular desktop computer, and the analysis was completed with parallel chains of 200 million states. On the other extreme, the influenza epitope analysis required the longest computational time, at 1.03 hours per million states and taking a couple of weeks to complete the analysis on independent chains. Computationally, the bottle neck in this analysis is the numerical integration over the latent traits; the analysis required a total 32 latent traits for 180 viral strains. Additionally, in this analysis, we jointly estimated the tree from sequence data.

In our analysis of influenza epitopes, we set the oldest amino acid observed for each site as the reference state, and for each of the remaining variants we assigned an entry in X. For the multiple unordered states model, this choice results in a reduction of dimensionality in the problem, but is done mainly to improve identifiability. However, this procedure breaks the symmetry of the model and complicates interpretability of correlations. In fact, a correlation between two entries of the latent trait X cannot be directly translated as a correlation between the states they represent, because variations in an entry of X are linked to all other states for that trait through the reference state. Despite this caveat, general statements about the correlation structure of the data can still be made based on the latent liability X, as we show in the influenza epitopes application.

In this context, different model choices could be used to change the interpretational links between correlations in X and in the data. Hadfield and Nakagawa (2010) briefly discuss a multinomial phylogenetic mixture model where a latent variable determines the probability of the multinomial outcome. They consider the common choice of constraining the latent variable to a simplex by setting the sum of its components to one. This makes the value of the latent trait immediately interpretable as probabilities, however it further complicates interpretability of the correlations. A possible alternative to address this issue is to model the evolution of X in the latent liability model with a central tendency such as the Ornstein-Uhlenbeck process. It remains to be investigated whether this change would improve identifiability, eliminating the need to impose constraints on the model.

Lartillot and Poujol (2011) have studied the correlation between continuous traits and parameters of the molecular evolution model, such as dS/dN ratio and mutation rate, by modelling the evolution of these parameters as a diffusion process along the tree. One possible extension to our method would be to incorporate the evolution of these parameters in our model, allowing for the estimation of correlations between our continuous and discrete traits and these evolutionary parameters.

The Bayesian phylogenetic framework in which we integrate our model easily lends itself to combination of different models. These could be phylogenetic models for demographic inference (Minin, Bloomquist and Suchard, 2008), methods for calibrating trees or relaxed clock models (Drummond et al., 2006). Additionally, we can explore the relaxed random walk (Lemey et al., 2010) to get varying rates of trait evolution along different branches of the tree. The latent liability model can easily be associated with these existing models to provide comprehensive analyses.