Identifying Neuroimaging and Proteomic Biomarkers for MCI and AD via the Elastic Net

Abstract

Multi-modal neuroimaging and biomarker data provide exciting opportunities to enhance our understanding of phenotypic characteristics associated with complex disorders. This study focuses on integrative analysis of structural MRI data and proteomic data from an RBM panel to examine their predictive power and identify relevant biomarkers in a large MCI/AD cohort. MRI data included volume and thickness measures of 98 regions estimated by FreeSurfer. RBM data included 146 proteomic analytes extracted from plasma and serum. A sparse learning model, elastic net logistic regression, was proposed to classify AD and MCI, and select disease-relevant biomarkers. A linear support vector machine coupled with feature selection was employed for comparison. Combining RBM and MRI data yielded improved prediction rates: HC vs AD (91.9%), HC vs MCI (90.5%) and MCI vs AD (86.5%). Elastic net identified a small set of meaningful imaging and proteomic biomarkers. The elastic net has great power to optimize the sparsity of feature selection while maintaining high predictive power. Its application to multi-modal imaging and biomarker data has considerable potential for discovering biomarkers and enhancing mechanistic understanding of AD and MCI.

1 Introduction

Multi-modal neuroimaging data, such as magnetic resonance imaging (MRI) and positron emission tomography (PET), studied independently or coupled with other biomarker data (e.g., cerebrospinal fluid (CSF) and neuropsychological assessments), have been shown to be sensitive to Alzheimer’s Disease (AD) and mild cognitive impairment (MCI, thought to be the prodromal stage of AD). Although recent studies reported promising prediction rates by integrating these multi-modal data [7,10,16], few were focused on identifying a small set of disease relevant biomarkers [13] to enhance our understanding of phenotypic characteristics and underlying mechanisms associated with complex disorders.

With these observations, this paper has the following aims: (1) investigate the predictive power of a new set of proteomic analytes from an RBM panel, (2) study whether or not combining structural MRI and proteomic data can enhance prediction rates, and (3) employ a principled sparse learning method, elastic net logistic regression [5], in the study to maximize prediction accuracy while optimizing the selection of disease sensitive biomarkers. Our overarching goal is to construct from multimodal data sparse models which combine ease of interpretation with high predictive power. The results may provide important information about potential surrogate biomarkers for therapeutic trials.

2 Materials and Methods

Data used in this study were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.ucla.edu). ADNI is a landmark investigation sponsored by the NIH and industrial partners designed to collect longitudinal neuroimaging, biological and clinical information from over 800 participants that will track the neural correlates of memory loss from an early stage. The following data from 819 ADNI participants were downloaded from the ADNI database: all baseline 1.5 T MRI scans, the RBM (Rules-Based Medicine) multiplex proteomic analytes extracted from plasma and serum, and demographic and baseline diagnosis information. Further information can be found in [15] and at www.adni-info.org. For one baseline scan of each participant, FreeSurfer V4 was employed to automatically label cortical and subcortical tissue classes [3,4] and to extract target region volume and cortical thickness, as well as to extract total intracranial volume (ICV). For each hemisphere, thickness measures of 34 cortical regions of interest (ROIs) and volume measures of 15 cortical and subcortical ROIs (Fig. 1) were included in this study. Using the regression weights derived from the healthy participants, all the FreeSurfer measures were adjusted for the baseline age, gender, education, handedness, and ICV, and all the RBM proteomic measures were adjusted for the baseline age, gender, education and handedness. 551 out of 819 participants (57 healthy control (HC), 388 MCI, 106 AD participants) had both FreeSurfer and RBM data available. To have a balanced data set among di3erent diagnostic groups, we included all HC and AD participants and a randomly selected set of 110 (out of 388) MCI participants in this study. Their characteristics are summarized in Table 1.

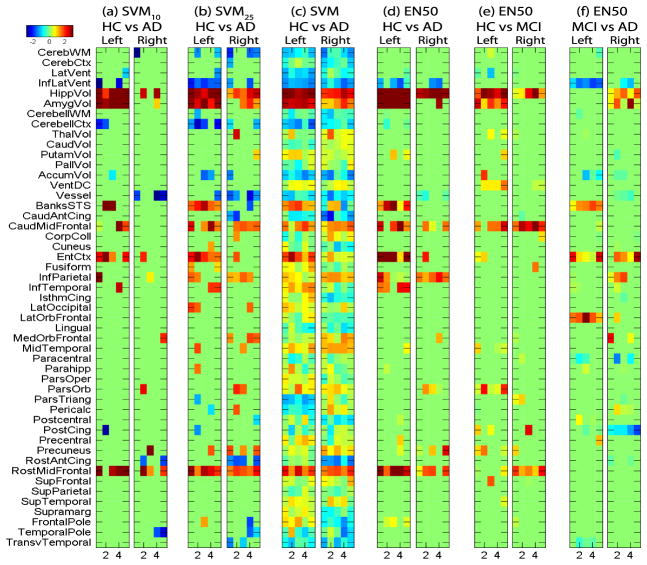
Fig. 1.

Heat maps of classifier weights −w for FreeSurfer measures, where weights were plotted against 5 di3erent trials in cross validation tests. Positive values (red) indicate lower measurement levels in cases.

Table 1.

Participant characteristics

Category	HC	MCI	AD	p-value
Gender (M/F)	30/27	60/50	60/46	0.88
Handedness (R/L)	53/4	104/6	99/7	0.91
Baseline Age (years, mean±SD)	75.2±5.8	75.0±7.4	74.8±8.1	0.95
Education (years, mean±SD)	15.7±2.7	15.5±3.0	15.1±3.3	0.37
ICV (cm3, mean±SD)	1506±143	1559±169	1558±195	0.13

Elastic Net

Elastic net logistic regression is a regularized version of logistic regression designed to provide good classification performance while employing a minimal number of predictor variables. Let y_i ∈ {0, 1} denote the class membership of the ith observation and let X_i denote the corresponding vector of p classification variables. Elastic net logistic regression uses the standard logistic regression model for the dependence of Y on X:

$$Pr(Y=1\mid X)=\frac{1}{1+e^{-({\beta }_0+X^T\mathit{\beta })}},Pr(Y=0\mid X)=\frac{1}{1+e^{+({\beta }_0+X^T\mathit{\beta })}}.$$

However, in order to produce sparse classification weight vectors, it estimates β by the maximizer of the penalized logistic regression log likelihood function

$$\mathcal{L}({\beta }_0,\mathit{\beta })=\frac{1}{n}\sum _{i=1}^n\{y_i({\beta }_0+X_i^T\mathit{\beta })-log(1+e^{({\beta }_0+X_i^T\mathit{\beta })})\}-\lambda P_{\alpha }(\mathit{\beta })$$

in which $P_{\alpha }(\mathit{\beta })=\alpha {\sum }_{j=1}^p\mid \mathit{\beta }(j)\mid +(1-\alpha ){\sum }_{j=1}^p{\{\mathit{\beta }(j)\}}^2$ is the elastic net penalty. Note that this penalty function is a convex combination of the L₁ lasso penalty and the L₂ ridge regression penalty. By providing a smooth trade-off between these two penalties, elastic net penalization capitalizes on the strengths of both while minimizing their weaknesses; see Friedman et al [5] for additional details. The imaging and proteomic biomarker data was analyzed using the implementation of elastic net logistic regression provided in the Matlab package glmnet.

Experimental Setting

The elastic net is in essence a linear classifier, where logistic regression is just a procedural step. For a fair comparison, a linear support vector machine (SVM) [14] coupled with a widely used feature selection scheme (SVM-based Recursive Feature Elimination, or SVM-RFE [6]) was applied in this study. The LIBSVM toolbox was employed to implement SVM and SVM-RFE using a linear kernel with default setting. We ran SVM-RFE using the training data only to select the top n% features and then trained a SVM classifier using these features only. We tested n = 10, 25 and 100, and denoted the corresponding procedures as SVM₁₀, SVM₂₅ and SVM (i.e., SVM₁₀₀, equivalent to no feature selection), respectively. For the elastic net, we did three experiments with α = 0.25, 0.5 and 0.75 (to adjust the amount of ridge and lasso), respectively, and the parameter λ was tuned by a 10-fold cross-validation procedure using the training data only. These experiments were applied to three data sets: (1) FreeSurfer data (98 variables), (2) RBM data (146 variables), and (3) combined FreeSurfer and RBM data (244 variables, a simple concatenation of the two modalities). Prediction accuracy was estimated using 5-fold cross-validation.

3 Results

We use EN25, EN50 and EN75 to indicate the elastic net classifiers with α = 0.25, 0.5, and 0.75, respectively. Table 2 summarizes the 5-fold cross-validation results for classifying HC vs AD, HC vs MCI, and MCI vs AD for each combination of six methods (SVM₁₀, SVM₂₅, SVM, EN25, EN50 and EN75) and three data sets (FreeSurfer, RBM, combined FreeSurfer and RBM). These results are very encouraging in the following sense: (1) Elastic net classifiers outperformed SVMs in terms of overall accuracy and area under ROC (AUROC) in almost all the cases, while the performances of EN25, EN50 and EN75 did not di3er significantly (paired samples test on AUROC p > 0.06 in all cases). (2) The best prediction rates using FreeSurfer were 86.6% for HC vs AD and 74.3% for HC vs MCI, comparable with the most recent studies using MRI as predictors [7,13,16]. (3) While FreeSurfer data performed slightly better in classifying HC vs AD than RBM data, the latter had surprisingly greater power to distinguish MCI from HC (87.4%) and AD (83.7%). (4) The combined set consistently outperformed either of FreeSurfer and RBM. While the resulting best prediction rate for HC vs AD (91.9%) was competitive with prior multi-modal studies [7,16], the prediction rates for HC vs MCI (90.5%) and MCI vs AD (86.5%) significantly exceeded results from prior studies that did not use RBM data (e.g., [16]).

Table 2.

Cross validation results (%): mean±SD is shown for accuracy and AUROC

		FreeSurfer (FS)		RBM		Combined FS and RBM
		Accuracy	AUROC	Accuracy	AUROC	Accuracy	AUROC
HC vs AD	SVM10	82.3 ± 4.1	88.9 ± 4.6	76.4 ± 5.6	84.0 ± 5.9	91.6 ± 4.6	97.0 ± 3.0
	SVM25	83.4 ± 7.4	89.8 ± 5.3	80.6 ± 3.3	87.2 ± 2.6	91.6 ± 5.1	97.1 ± 2.1
	SVM	84.5 ± 9.7	91.9 ± 6.2	80.0 ± 8.4	89.5 ± 4.4	91.9 ± 3.1	96.3 ± 2.4
	EN25	84.7 ± 5.3	94.2 ± 4.8	81.2 ± 3.3	91.8 ± 3.5	91.5 ± 4.2	97.6 ± 2.0
	EN50	85.9 ± 6.0	94.8 ± 4.7	83.5 ± 4.9	90.6 ± 3.7	91.5 ± 4.2	97.1 ± 3.3
	EN75	86.6 ± 6.2	94.6 ± 5.6	83.7 ± 5.1	89.9 ± 3.8	90.9 ± 5.3	97.1 ± 3.6
HC vs MCI	SVM10	70.7 ± 4.7	73.2 ± 8.1	74.9 ± 7.2	84.5 ± 5.0	85.0 ± 4.5	90.9 ± 6.3
	SVM25	65.9 ± 7.4	68.5 ± 10.5	81.5 ± 8.6	91.2 ± 4.2	89.2 ± 3.5	94.9 ± 4.5
	SVM	63.5 ± 10.1	63.7 ± 6.7	87.4 ± 4.4	92.8 ± 4.3	89.1 ± 6.3	93.7 ± 3.7
	EN25	74.3 ± 5.6	79.3 ± 8.3	87.4 ± 3.2	95.3 ± 2.6	89.2 ± 5.3	96.1 ± 3.3
	EN50	73.7 ± 6.2	79.8 ± 8.3	86.8 ± 6.7	94.8 ± 2.9	90.5 ± 7.6	96.0 ± 3.5
	EN75	74.3 ± 6.0	80.8 ± 7.5	84.5 ± 5.1	94.3 ± 3.2	89.9 ± 5.6	95.6 ± 4.0
MCI vs AD	SVM10	62.2 ± 10.3	70.6 ± 12.4	80.9 ± 8.2	86.1 ± 8.1	81.4 ± 5.1	88.7 ± 4.9
	SVM25	61.9 ± 8.3	70.0 ± 8.8	82.3 ± 3.3	89.4 ± 3.1	79.1 ± 8.7	90.1 ± 4.0
	SVM	53.5 ± 7.4	62.2 ± 8.9	80.4 ± 5.3	88.2 ± 5.4	82.8 ± 5.7	91.4 ± 5.5
	EN25	65.5 ± 12.4	72.7 ± 10.6	83.6 ± 6.8	93.0 ± 3.3	84.1 ± 5.7	92.9 ± 4.1
	EN50	66.4 ± 11.9	72.4 ± 11.4	82.7 ± 6.0	93.1 ± 2.7	86.0 ± 3.9	93.3 ± 3.7
	EN75	66.4 ± 13.3	72.4 ± 12.0	83.7 ± 4.0	93.1 ± 2.2	86.5 ± 5.2	94.0 ± 3.1

Either the SVM or the elastic net classifier can be characterized by a weight vector w, which projects each individual data point (i.e., a feature vector) into a 1-D space to produce a discriminative value. Each weight measures the strength of the contribution of the corresponding feature to the final discriminative value. Elastic net seeks to reduce the number of nonzero weights so that only relevant features contribute to the discriminative value. For consistency, we always visualize negative weights −w so that larger values (red) correspond to lower measurement levels in cases. We show the weight maps (Fig. 1–3) only for the combined set analysis, since single modality analyses yielded similar maps.

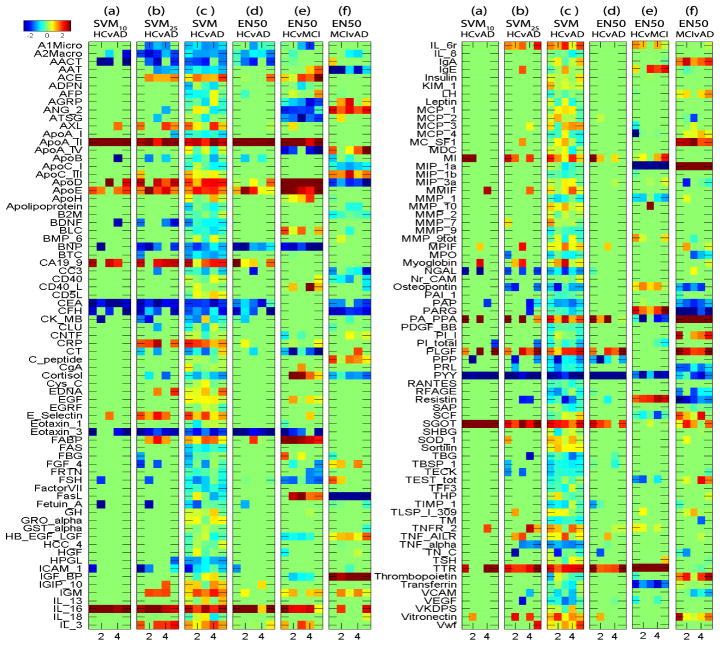
Fig. 3.

Heat maps of classifier weights −w for RBM measures, where weights were plotted against 5 di3erent trials in cross validation tests. Positive values (red) indicate lower measurement levels in cases.

Shown in Fig. 1 are the weights for the FreeSurfer data. Weights for classifying HC vs AD are shown in (a–d) for SVM₁₀, SVM₂₅, SVM and EN50 respectively. While most weights were close to zero, EN50 identified a small number of imaging markers known to be AD-relevant, including hippocampal volume, entorhinal cortex thickness, amygdala volume, and so on. Given many blue blocks (i.e., gray matter increase in AD, which is counter-intuitive), the SVM map was much less sparse and harder to interpret. While SVM₁₀ and SVM₂₅ identified a few relevant markers similar to EN50, they also yielded some questionable blue blocks and the selected features varied a lot among di3erent cross-validation trials.

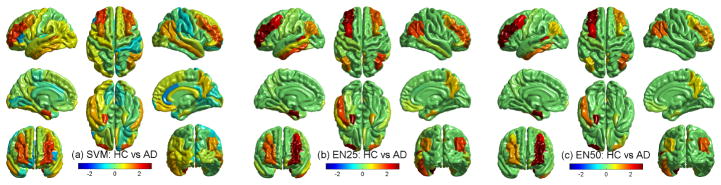
Fig. 1(d–f) compare selected features in di3erent classification tasks using EN50. Note that Panels (e,f) selected a smaller number of FreeSurfer features even though the overall prediction accuracies of all three analyses were comparably high. This might imply that the overall prediction accuracies of the latter two tasks (HC vs MCI and MCI vs AD) were more dependent on RBM features than FreeSurfer features. These weights can also be back-projected to the original image space for an intuitive visualization. Fig. 2 shows such a visualization for SVM, EN25 and EN50. EN25 and EN50 yield similar maps that are much more sparse than the SVM map.

Fig. 2.

Back-projection of negative weights (−w) onto cortical surface, where positive values (red) indicate lower measurement levels in cases

Shown in Fig. 3 are the weight maps for RBM features. Again, EN50 yielded fewer relevant features than SVM (see (c–d)). Although SVM₁₀ and SVM₂₅ (see (a–b)) were able to identify a few interesting features, the selected features varied a lot among di3erent cross-validation trials. Using Elastic Net, a number of RBM analytes were found to have altered concentrations in AD participants compared to HCs. This is consistent with previous studies showing reduced or elevated concentrations of specific analytes in plasma or serum samples of AD participants. The trends for some of the identified analytes follow those in the published literature and are summarized below. Using a similar RBM panel and methodology as done by the ADNI study, O’Bryant et al. identified the analytes alpha-2-macroglobulin (A2Macro), eotaxin 3 (Eotaxin 3) and pancreatic polypeptide (PPP) to be over expressed in the serum of AD participants relative to controls [11] similar to the current findings. Elevated plasma concentrations of complement factor H (CFH) and alpha-2-macroglobulin (A2Macro) [8], reduced plasma concentrations of apolipoprotein AII (ApoA II) [9] and elevated serum concentration of apolipoprotein B (ApoB) [2] have been observed in AD participants relative to controls, and these were also found in the present study. Apolipoprotein E (ApoE) is a major genetic risk factor for AD [1]. The ApoE concentration in the present study was observed to be reduced in AD participants relative to controls. There are conflicting reports regarding the serum or plasma concentrations of ApoE protein levels in AD, with some studies finding elevated levels, some finding reduced levels and others finding no di3erence in levels in AD participants relative to controls [12]. Thus its role as a potential AD biomarker is unclear at the present time and needs to be further investigated. A number of novel analytes have also been identified to have altered expression in AD such as carcinoembryonic antigen (CEA) and pregnancy-associated plasma protein A (PA PPA). These analytes may play a role in disease pathology and warrant further investigation in independent samples. Thus the identification of novel analytes in addition to known analytes demonstrates the power and utility of this approach in identifying potential candidate AD biomarkers.

4 Discussion

We have done an integrative analysis of structural MRI data and proteomic data to examine their predictive power and identify relevant biomarkers in a large MCI/AD cohort. RBM data showed high predictive power to separate MCI from HC and AD. Combining RBM and MRI data yielded further improved prediction rates: HC vs AD (91.9%), HC vs MCI (90.5%) and MCI vs AD (86.5%), which were competitive to or better than similar prior studies. The sparse models generated by elastic net identified a small set of meaningful imaging and proteomic biomarkers and were much easier to interpret than SVM-based models. The elastic net has great power to optimize the sparsity of feature selection while maintaining high predictive power. Its application to multi-modal imaging and biomarker data has considerable potential for discovering biomarkers and enhancing mechanistic understanding of AD and MCI.

Many identified RBM markers warrant further investigation. Replication in independent large samples will be important to confirm these findings. Pathway analysis could be performed as a future direction to identify underlying biological pathways of relevant genes and proteins. This work was focused on sparse linear classifiers applied to the simple concatenation of multi-modal data, since our major goal was to yield easily interpretable models while maintaining high predictive power. An initial analysis of applying SVM with a radial basis function kernel to the same data yielded comparable or less accurate results, and these nonlinear models were much harder to interpret. An interesting future topic is to investigate whether these nonlinear models can help improve the prediction rates as well as derive biologically meaningful results. Another future direction is to apply multi-kernel learning methods (e.g., [7,16]) and see if better predictive models can be achieved and relevant biomarkers can be identified.