Lower Bounds on Paraclique Density

Abstract

The scientific literature teems with clique-centric clustering strategies. In this paper we analyze one such method, the paraclique algorithm. Paraclique has found practical utility in a variety of application domains, and has been successfully employed to reduce the effects of noise. Nevertheless, its formal analysis and worst-case guarantees have remained elusive. We address this issue by deriving a series of lower bounds on paraclique densities.

1. Introduction

Clique-centric methods have long played an important role in data science and engineering. Classic techniques include algorithms for 𝒩𝒫-hard problems such as maximal clique [1] and maximum clique [2]. The availability of high-throughput data has prompted interest in noise-abatement relaxations, most notably k-clique communities [3] (more recently also called clique percolation) and paraclique [4]. These algorithms have been used for biological data clustering, and been found superior to traditional methods [5]. Although similar in objective, k-clique communities is hampered in practice by its bottom up approach relying on an exhaustive enumeration of maximal cliques. Paraclique, in contrast, applies top down design principles and employs maximum clique, for which there are highly efficient and reasonably scalable algorithms [6], plus viable alternatives based on duality and parameterized complexity [7].

Paraclique can be formulated in a variety of ways. The general idea is to expand a maximum clique by augmenting it with non-clique vertices adjacent to most, but not all, members of the clique. The motivation for deriving dense subgraphs in this fashion is based on the fact that so-called “missing” edges, while relevant, are often lost due to noise, improper thresholding, weak experimental design, and numerous other causes. A classic example of this phenomenon can be found in the use of DNA microarrays for transcriptomic data analysis. In this setting, vertices represent genes, edges signify co-expression, and paracliques denote molecular response networks differentially (in)activated by stimulus [4]. Depending on a variety of factors, most but not all network elements may be highly intercorrelated at any particular time.

Previous paraclique studies have focused mainly on practical results. Representative examples include [8, 9, 10]. Instead, our primary goal in this paper is to investigate paraclique’s theoretical basis. In so doing, we seek to derive bounds on its worst-case behavior, applying density as the classic clustering metric (we compute a subgraph’s density in the traditional way, as the number of edges present divided by the maximum number possible). In the original paraclique formulation, the total number of missing edges was left unchecked. Density could, therefore, in principle be driven to zero. By limiting paraclique size to at most twice the maximum clique size, however, and by requiring that a new non-clique vertex be adjacent to all but one vertex in the growing paraclique, it is known that density is maintained at no less than 50% [4]. Here, we greatly expand upon such density results.

In the next section, we formalize definitions, describe relevant background, and establish several helpful preliminary results. In Sections 3 and 4, we derive bounds on general and special cases, respectively. In a final section we draw conclusions and discuss directions for future research.

2. Preliminaries

Let G denote a finite, simple, undirected graph. A clique is a subgraph of G in which every pair of vertices is connected by an edge. A paraclique, P, is constructed by first finding a clique C of maximum size, then glomming onto non-clique vertices in a controlled fashion. An integer glom term, g, is used to accomplish this. In the original algorithmic formulation [4], a non-clique vertex was chosen if and only if it was adjacent to g or more vertices in P. The number of required adjacencies does not scale with the size of P using this approach, however, so we generally invert this comparison. Thus, we glom onto a non-clique vertex if and only if it is adjacent to all but at most g vertices in P. In applications, g is usually some small value. In any case we insist that 0 < g < k, where k denotes the number of vertices in C.

Pseudocode for the paraclique procedure is displayed in Algorithm 1. A sample paraclique construction is illustrated in Figure 1. For the reader’s convenience, definitions employed in the sequel are summarized in Table 1.

Algorithm 1.

The Paraclique Algorithm

input : graph G, glom term g

output: paraclique P, a subgraph of G

C ← maximum clique of G

V ← vertex set of C

while V̅ contains a vertex v adjacent to all but at most g vertices

in V do

| V ← V ∪ {v}

end

P ← subgraph induced by V

return P

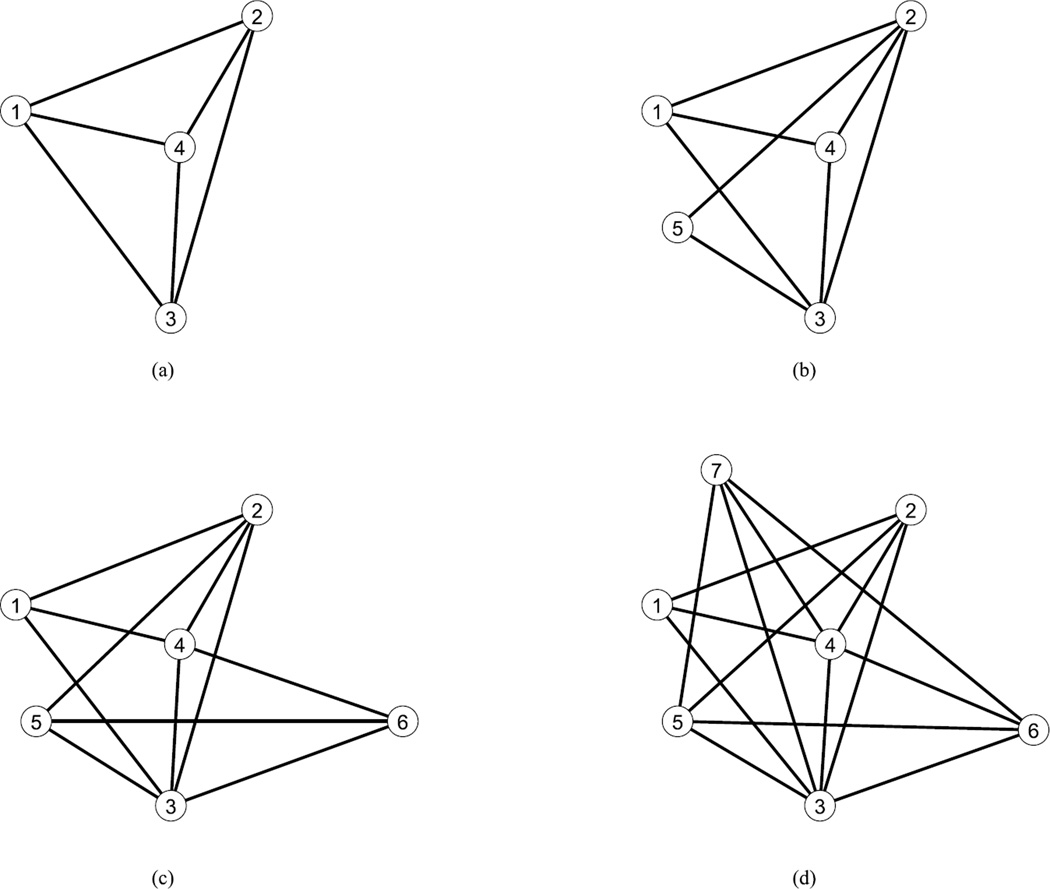
Figure 1.

An example paraclique grown with glom term g = 2 from an initial maximum clique of size four {1,2,3,4} (a) and successively adding vertices 5 (b), 6 (c) and 7 (d).

Table 1.

Definitions used in this paper

term	meaning
G	a finite, simple, undirected graph
C	a maximum clique in G
k	the number of vertices in C
P	a paraclique as produced by Algorithm 1
p	the number of vertices in P
g	the glom term used in Algorithm 1
d(P)	the density of P

We start by establishing lower and upper bounds on maximum paraclique size.

Lemma 1

A paraclique may contain as many as (g + 1)k vertices.

Proof

To construct a paraclique P that satisfies this bound, we begin with g+1 disjoint cliques of size k, denoting them C₀, C₁, …, C_g, and labeling the vertices of each C_i as υ_ik, υ_ik+1, …, υ_(i+1)k−1. To this we add edges connecting vertices υ_r and υ_s provided they are in different cliques and r ≢ s modulo k. The maximum clique size has not changed, since any set of k+1 vertices will contain at least two whose indices are in the same equivalance class modulo k (and are thus non-adjacent). Given a graph containing this structure, the paraclique algorithm may return P because υ_i is adjacent to all but at most g lower-indexed vertices for any 0 < i ≤ (g + 1)k − 1.

Lemma 2

A paraclique cannot contain more than 2gk vertices.

Proof

Let P denote a paraclique of size p > k. By construction, the number of edges in P is at least

$$\frac{k(k-1)}{2}+(k-g)+(k+1-g)+\cdots +(k+(p-k-1)-g)=\frac{k(k-1)}{2}+(p-k)(k-g)+(1+2+\cdots +(p-k-1))=\frac{k(k-1)}{2}+(p-k)(k-g)+\frac{(p-k-1)(p-k)}{2}=\frac{(p^2-p-2pg+2kg)}{2}.$$

Since P has no clique of size k +1, we know by Turán’s Theorem [11] that it contains at most ${(1-\frac{1}{k})}^{\frac{p^2}{2}}$ edges. Combining the two edge counts produces

$$\frac{p^2-p-2pg+2kg}{2}\le \frac{k{p}^2-p^2}{2k}$$

$$k{p}^2-kp-2kpg+2k^{2}g\le k{p}^2-p^2$$

$$p^2-(2g+1)kp+2g{k}^2\le 0$$

$$(p-2gk)(p-k)\le 0$$

Because p > k, we conclude that p ≤ 2gk.

3. General Case

Let us suppose that C has been isolated, and that g has been chosen. By comparing g and p, we will now prove that as P grows its density approaches 1.0. On the other hand, by comparing g and k, we will also prove that no matter how P changes its density never falls below 0.5.

Theorem 3

A paraclique’s density is at least $1-\frac{2g-1}{p-1}$.

Proof

As we have previously shown, the number of edges in P is at least

$$\frac{p^2-p-2pg+2kg}{2}.$$

Combining that with Lemma 2 ensures

$$d(P)\ge \frac{\frac{p^2-p-2pg+2kg}{2}}{\frac{p(p-1)}{2}}=\frac{p^2-p-2pg+2kg}{p(p-1)}\ge \frac{p^2-p-2pg+p}{p(p-1)}=\frac{p-2g}{p-1}=1-\frac{2g-1}{p-1}.$$

Theorem 4

A paraclique’s density is at least $1-\frac{g}{2k-1}$.

Proof

P is missing at most g(p−k) edges. From this it follows that d(P) is bounded below by

$$\frac{\frac{p(p-1)}{2}-g(p-k)}{\frac{p(p-1)}{2}}=1-\frac{2g(p-k)}{p(p-1)}.$$

Using basic calculus plus the fact that p ≥ k, we see that this function takes its minimum on the interval [k, 2gk] at $k+\sqrt{k^2-k}$. Because $2k-1<k+\sqrt{k^2-k}<2k$ for all k ≥ 2, d(P) is minimized when p is either 2k − 1 or 2k. We know from Lemma 1 that both values are possible, and in either case we find that d(P) is at least

$$1-\frac{2gk}{2k(2k-1)}=1-\frac{g}{2k-1}.$$

Sometimes Theorem 3 provides the better guarantee. This happens, for example, when k = 6, g = 2 and p = 20. At other times, say when k = 5, g = 4 and p = 10, Theorem 4 provides the tighter result. In any event, the following overall lower bound on density is obtained from Theorem 4 coupled with the fact that 1 ≤ g < k.

Corollary 5

A paraclique’s density always exceeds 1/2.

4. Special Case

The glom term setting g = 1 is frequently used in practice. Paraclique structure is considerably more scrutable in this special case. See Figure 2. In what follows, we say that P is nontrivial if it does not equal C.

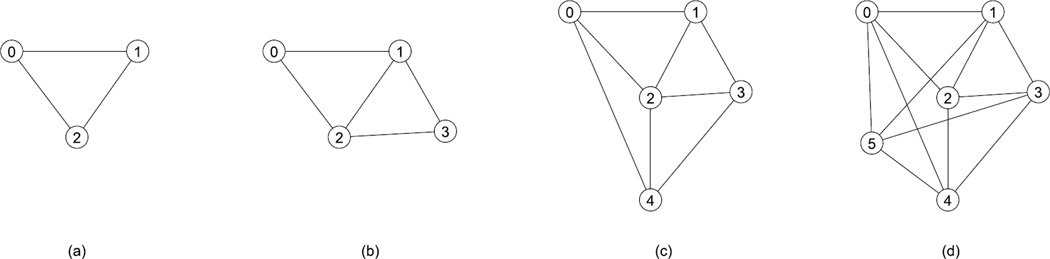
Figure 2.

An example of a paraclique with g=1, starting from maximum clique {0,1,2} (a), and successively adding vertices 3 (b), 4 (c), 5 (d).

Theorem 6

When g = 1, a nontrivial paraclique’s density lies between $1-\frac{2\lfloor \frac{p}{2}\rfloor }{p(p-1)}$ and $1-\frac{2}{p(p-1)}$, inclusive.

Proof

Suppose P is such a paraclique. From Lemma 2 and the nontriviality of P we know $\lceil \frac{p}{2}\rceil \le k\le p-1$. P must be missing exactly (p − k) edges, else G would have a clique of size k + 1. The number of edges in P is thus $\frac{p(p-1)}{2}-(p-k)$, and so

$$d(p)=1-\frac{2(p-k)}{p(p-1)}=\frac{2}{p(p-1)}k+\frac{p-3}{p-1}.$$

Given p, this is just a linear function of k with a positive slope. It’s minimum therefore occurs when $k=\lceil \frac{p}{2}\rceil$, ensuring

$$d(P)\ge 1-\frac{2(p-\lceil \frac{p}{2}\rceil )}{p(p-1)}=1-\frac{2\lfloor \frac{p}{2}\rfloor }{p(p-1)},$$

and its maximum occurs when k = p − 1, ensuring

$$d(P)\le 1-\frac{2}{p(p-1)}.$$

Theorem 7

When g = 1, a nontrivial paraclique’s density lies between $1-\frac{1}{2k-1}$ and $1-\frac{2}{k(k+1)}$, inclusive.

Proof

From Lemma 2 and the nontriviality of P we know k + 1 ≤ p ≤ 2k. Again we note that P must be missing exactly (p − k) edges, and so $d(P)=1-\frac{2(p-k)}{p(p-1)}$. As in the proof of Theorem 4, we find from basic calculus that this function is minimized at $1-\frac{1}{2k-1}$, which occurs at both p = 2k − 1 and p = 2k. It is maximized at $1-\frac{2}{k(k+1)}$ when p = k + 1.

Theorem 6 tends to provide a better lower bound when p is at the lower end of its range relative to k, while Theorem 7 tends to produce a better upper bound when p is at the upper end of its range. In any event, the following overall lower bound on density is obtained from Theorem 7 coupled with the fact that C must contain at least one edge.

Corollary 8

When g = 1, a paraclique’s density is always at least 2/3.

5. Conclusions and Directions for Further Research

We have derived density bounds for the paraclique algorithm, a noise-resilient clique-centric technique designed for dense subgraph extraction. To the best of our knowledge, other than the elementary result from [4], these are the first formal density limits for what have come to be popularly known as network community methods. This gives paraclique another potential practical endorsement, in addition to those due to biological enrichment as discussed in [5].

Although we remain primarily concerned with lower bounds, we were able to prove asymptotically tight lower and upper bounds for the special case g = 1. Proving better bounds for the general case remains an elusive open problem. Our lower bounds are not tight for arbitrary g > 1; our only upper bounds are weak because they are inherited from the special case. If formal analysis proves too difficult, and it may well might, then an alternate approach could center on empirical testing. Both real and synthetic data might be employed to estimate average densities and their expected deviations from our worst-case guarantees.