Low-dimensional dynamics of structured random networks

Abstract

Using a generalized random recurrent neural network model, and by extending our recently developed mean-field approach, we study the relationship between the network connectivity structure and its low dimensional dynamics. Each connection in the network is a random number with mean 0 and variance that depends on pre- and post-synaptic neurons through a sufficiently smooth function g of their identities. We find that these networks undergo a phase transition from a silent to a chaotic state at a critical point we derive as a function of g. Above the critical point, although unit activation levels are chaotic, their autocorrelation functions are restricted to a low-dimensional subspace. This provides a direct link between the network's structure and some of its functional characteristics. We discuss example applications of the general results to neuroscience where we derive the support of the spectrum of connectivity matrices with heterogeneous and possibly correlated degree distributions, and to ecology where we study the stability of the cascade model for food web structure.

I. INTRODUCTION

Advances in measurement techniques and statistical inference methods allow us to characterize the connectivity properties of large biological systems such as neural and gene regulatory networks [1–4]. In many cases connectivity is shown to be well modeled by a combination of random and deterministic components. For example, in neural networks, the location of neurons in anatomical or functional space, as well as their cell-type identity influences the likelihood that two neurons are connected [2, 5, 6].

For these reasons it has become increasingly popular to study the spectral properties of structured but random connectivity matrices using a range of techniques from mathematics and physics [7–14]. In most cases, the spectrum of the random matrix of interest is studied independently of the dynamics of the biological network it implies. Therefore, these results can be used only to make statements about the dynamics of a linear system where knowing the eigenvalues and eigenvectors is sufficient to characterize the dynamics.

Here we study the dynamics of nonlinear random recurrent networks with a continuous synapse-specific gain function that can depend on the pre- and post-synaptic neurons’ locations in an anatomical or functional space. These networks become spontaneously active at a critical point that is derived here, directly related to the boundary of the spectrum of a new random matrix model. Given the gain function we predict analytically the network's leading principal components in the space of individual neurons’ autocorrelation functions.

In the context of analysis of single and multi-unit recordings our results offer a mechanism for relating structured recurrent connectivity to functional properties of individual neurons in the network; and suggest a natural reduced space where the system's trajectories can be fit by a simple state-space model. This approach has been used to explain the dynamics of neurons in motor cortex by comparing the results of training recurrent artificial neural networks (“reservoir computing”) to neural data [15, 16]. These applications have thus far assumed the initial condition (i.e. the network before training) is a completely unstructured neural substrate.

Recently we showed how a certain type of mesoscopic structure can be introduced into the class of random recurrent network models by drawing synaptic weights from a finite number of cell-type-dependent probability distributions [13]. In contrast to networks with a single cell-type [17], these networks can sustain multiple “modes,” characterized in terms of the individual neuron autocorrelation functions.

Here these results are further generalized to networks where the synaptic weight between neurons i, j is drawn from a distribution with mean 0 and variance $N^{-1}{g}_{ij}^2$, where N is the size of the network. The smoothness conditions satisfied by the gain function g are stated below. This allows us to treat, for example, networks with continuous spatial modulation of the synaptic gain. The solution to the network's system of mean-field equations that we derive offers a new viewpoint on how functional properties of single neurons can in fact be a network phenomenon.

A. Model and main results

Consider a general synapse-specific gain function g(z_i, z_j) that depends on normalized neuron indices z_i = i/N, where i = 1, . . . , N. We assume that there is some length scale s₀ > 0 below which g has no discontinuities. That is, we let $g:{(0,1]}^2\to {\mathbb{R}}_{+}$ be a uniformly bounded, continuous function everywhere on the unit square except possibly on a measure zero set S₀. The function g may depend on N in such a way that its Lipschitz constant $C_L\left(N\right)=C_L^0{N}^{\beta }$, with $C_L^0<\infty$ and 1 > β ≥ 0. Every point where g does not satisfy the above smoothness conditions must be on the boundary between squares of side s₀ where it does.

The network connectivity matrix is then $J\in {\mathbb{R}}^{N\times N}$ with elements 2

$$J_{ij}=g(z_i,z_j)J_{ij}^0$$ (1)

where $J_{ij}^0$ is a random matrix with elements drawn at random from a distribution with mean 0, variance 1/N and finite fourth moment. In the simulations we use a Gaussian distribution unless noted otherwise.

In this paper we analyze the eigenvalue spectrum of the connectivity matrix J and the corresponding dynamics of the neural network. Note that by requiring that g is bounded and differentiable on the unit square outside of S₀ we allow the synaptic gain function to be a combination of discrete modulation (e.g., cell-type dependent connectivity for distinct cell types, as in [13]) and of continuous modulation (e.g., networks with heterogeneous and possibly correlated in- and out-degree distributions, as in [18, 19]).

When g can be written as an outer product of two vectors [i.e. g(z_i, z_j) = g₁(z_i)g₂(z_j)], the model discussed here overlaps with that studied by Wei and by Ahmadian et al. [9, 12], but those works also consider matrix models that are not studied here.

The connectivity matrix J must not represent an all-to-all connected network, as the distribution of elements of J⁰ can have a finite mass at 0 (see Sec. V). However, in the current work we do not consider sparse models where the number of non-zero elements is finite or scales sublinearly with N. Studies of such matrices exist in the literature (for example, [20, 21]), but are limited to models with no structure.

In Sec. II we show that the spectral density of J is circularly symmetric in the complex plane, and is supported by a disk centered at the origin with radius $r=\sqrt{{\Lambda }_1}$ with

$${\Lambda }_1=\max \left\{\lambda \left[G_N^{\left(2\right)}\right]\right\},$$ (2)

where $G_N^{\left(2\right)}\in {\mathbb{R}}_{+}^{N\times N}$ is a deterministic matrix with elements ${\left[G_N^{\left(2\right)}\right]}_{ij}=\frac{1}{N}{g}^2(z_i,z_j)$. Note that Λ₁ is the Perron-Frobenious eigenvalue of a non-negative matrix, so indeed ${\Lambda }_1,r\in {\mathbb{R}}_{+}$. For general synapse-specific gain function g it has not been possible so far to obtain an explicit formula for Λ₁. However, we have been able to derive explicit analytic formulas in three cases of biological significance. First, in Sec. IV we discuss the case where $G_N^{\left(2\right)}$ is a circulant matrix such that g(z_i, z_j) = g(z_ij) with

$$z_{ij}=\min \{\mid z_i-z_j\mid ,1-\mid z_i-z_j\mid \}$$ (3)

and show that ${\Lambda }_1=2{\int }_0^{\frac{1}{2}}{g}^2\left(z\right)dz$. This special case is important for large neural networks where connectivity often varies smoothly as a function of neuron's index. Moreover, for this parametrization all the eigenvalues and corresponding eigenvectors can be computed analytically, which will make it possible to make stronger statements about the dynamics as is explained in Secs. III and IV.

For two additional parametrizations of g, the current mean-field approach is insufficient to fully characterize the dynamics, but we can use the general result [Eq. (2)] to analytically characterize the spectrum of the connectivity matrix. In Sec. V we derive the support of the bulk spectrum and the outliers of a random connectivity matrix with heterogeneous joint in- and out-degree distribution. Finally, in Sec. VI we discuss a third example pertinent to large scale models of ecosystems. These systems are often modeled using g that has a triangular structure and in this case we also derive an analytic formula for Λ₁.

Given the connectivity matrix J defined in Eq. (1), the dynamics of neural network model with N neurons is described by

$${\stackrel{.}{x}}_i\left(t\right)=-x_i\left(t\right)+\sum _{j=1}^N{J}_{ij}{\varphi }_j\left(t\right),$$ (4)

where ϕ_j(t) = tanh[x_j(t)]. The x variables can be thought of as the membrane potential of each neuron, and the ϕ variables as the deviation of the firing rates from their average values.

Using a modified version of dynamic mean field theory we show that in the limit N → ∞ this system undergoes a phase transition, where r is the coordinate that describes this transition and r = 1 is the critical point. Below the critical point (r < 1), the neural network has a single stable fixed point at x = 0. Above the critical point the system is chaotic.

We analyze the dynamics above the critical point in more detail and find a direct link between the network structure (g) and its functional properties. To that end we define N dimensional autocorrelation vectors

$${\Delta }_i\left(\tau \right)=\langle x_i\left(t\right)x_i(t+\tau )\rangle ,C_i\left(\tau \right)=\langle {\varphi }_i\left(t\right){\varphi }_i(t+\tau )\rangle$$ (5)

where 〈·〉 denotes average over the ensemble of matrices J and time. Note that because the average of each element of J is zero and the nonlinearity is an odd function, autocorrelations are computed about the fixed point x_i = ϕ_i = 0. These vectors are restricted to the potentially low-dimensional subspace spanned by the right eigenvectors of $G_N^{\left(2\right)}$ with corresponding eigenvalues that have a real part greater than 1. Thus, although the network dynamics are chaotic, they are confined to a low-dimensional space, which has been suggested as a mechanism that could make computation in the network more robust [22].

B. Separate excitation and inhibition

There are some limitations to the interpretation of the dynamics in Eq. (4) with connectivity described by Eq. (1) as a neuronal network. Most importantly, every column of J has both positive and negative elements corresponding to the unrealistic assumption that every neuron is both excitatory and inhibitory, and the hyperbolic tangent nonlinearity implies that firing rates can be both positive and negative. The usual justification of these assumptions is that every degree of freedom x_i is in fact an average over a small number of neurons some of which are inhibitory and some are excitatory, and that ϕ_i represents the deviation of the firing rate from the steady state.

A more satisfying treatment to this problem is the recent work of Kadmon and Sompolinsky [23] extending our previous work [13]. They studied a network with block structure, where the distribution of elements in each block has a non-zero mean such that, if appropriately defined, the elements in each column can have the same sign. They also considered non-negative transfer functions in addition to the hyperbolic tangent. Their analysis showed that in addition to the stable fixed point and chaotic regimes, there is an additional regime of saturated firing rates. For the general case it was not possible to determine whether the transition to chaotic or saturated regime is seen first upon variation of the connectivity parameters, or what the dynamics look like if conditions for both instabilities hold (i.e., what the saturated and chaotic dynamics look like). We anticipate that for cases where the first transition is to the chaotic regime, the analysis presented here for synaptic weight distributions with mean 0 will apply (with the appropriate modifications similar to those in [23]) when the mean is nonzero.

Here we also treat networks with separate excitatory and inhibitory populations (Sec. V), by deriving the support of the bulk spectrum and outliers of connectivity matrices with heterogeneous degree distributions.

II. DERIVATION OF THE CRITICAL POINT

A. Finite number of partitions

We begin by recalling our recent results for a function g that has block structure. We defined a D × D matrix with elements g_cd and partitioned the indices 1, . . . , N into D groups, where the cth partition has a fraction α_c neurons. The synaptic gain function was then defined by g(z_i, z_j) = g_cicj, where c_i is the partition index of the ith neuron (c = 1, . . . , D).

Defining $n_d=N{\sum }_{c=1}^d{\alpha }_c$ allows us to write formally $c_i=\{c\mid \frac{i}{N}\in (\frac{n_{c-1}}{N},\frac{n_c}{N}]\}$. With these definitions, we rewrite Eq. (4):

$${\stackrel{.}{x}}_i=-x_i+\sum _{d=1}^D{g}_{c_{i}d}\sum _{j=n_{d-1}+1}^{n_d}{J}_{ij}^0{\varphi }_j\left(t\right).$$ (6)

In [13] we used the dynamic mean field approach [17, 24, 25] to study the network behavior in the N → ∞ limit. Averaging Eq. (6) over the ensemble from which J is drawn implies that neurons that belong to the same group are statistically identical. Thus, the behavior of the full network can be summarized by D representative neurons ξ_d(t) and their inputs η_d(t), provided that (a) they satisfy

$${\stackrel{.}{\xi }}_d\left(t\right)=-{\xi }_d\left(t\right)+{\eta }_d\left(t\right),$$ (7)

and (b) that η_d(t) is drawn from a Gaussian distribution with moments satisfying

$$\langle {\eta }_d\left(t\right)\rangle =0,$$ (8)

$$\langle {\eta }_c\left(t\right){\eta }_d(t+\tau )\rangle ={\delta }_{cd}\sum _{b=1}^D{\alpha }_b{g}_{cd}^2{C}_b\left(\tau \right).$$ (9)

Here 〈·〉 denotes averages over i = n_c–1 + 1, . . . , n_c and k = n_d–1 + 1, . . . , n_d in addition to average over realizations of J. The average firing rate correlation vector is denoted by C (τ). Its components using the mean field variables are

$$C_d\left(\tau \right)=\langle \varphi \left[{\xi }_d\left(t\right)\right]\varphi \left[{\xi }_d(t+\tau )\right]\rangle .$$ (10)

The cross-covariance matrix 〈η_c (t) η_d (t + τ)〉 is diagonal so we define the vector H(τ) to be the diagonal. Now we can rewrite Eq. (9) as

$$H\left(\tau \right)=MC\left(\tau \right),$$ (11)

where $M\in {\mathbb{R}}_{+}^{D\times D}$ is a constant matrix reflecting the network connectivity structure: $M_{cd}={\alpha }_d{g}_{cd}^2$.

A trivial solution to this equation is H(τ) = C(τ) = 0 which corresponds to the silent network state: x_i(t) = 0. Recall that in the network with a Girko matrix as its connectivity matrix (D = 1), the matrix M = g² is a scalar and Eq. (11) reduces to H(τ) = g²C(τ). In this case the silent solution is stable only when g < 1. For g > 1 the autocorrelations of η are non-zero which leads to chaotic dynamics in the N dimensional system [17].

When D > 1, Eq. (11) can be projected on the eigenvectors of M leading to D consistency conditions, each equivalent to the single group case. Each projection has an effective scalar given by the eigenvalue in place of g² in the D = 1 case. Hence, the trivial solution will be stable if all eigenvalues of M have real part < 1. This is guaranteed if Λ₁, the largest eigenvalue of M, is < 1. If Λ₁ > 1 the projection of Eq. (11) on the leading eigenvector of M gives a scalar self-consistency equation analogous to the D = 1 case for which the trivial solution is unstable. As we know from the analysis of the D = 1 case, this leads to chaotic dynamics in the full network. Therefore Λ₁ = 1 is the critical point of the D > 1 network. Furthermore, the fact that in the D = 1 case the presence of the destabilized fixed point at x = 0 corresponds to a finite mass of the spectral density of J with real part > 1 [17, 26] allowed us to read the radius of the support of the connectivity matrix with D > 1 and identify it as $r=\sqrt{{\Lambda }_1}$ [13].

B. Continuous case

The vector dynamic mean field theory we developed in [13] relies on having an infinite number of neurons in each partition with the same statistics. The natural choice is therefore to have the size of each group of neurons be linear in the system size: N_c = α_cN.

This scaling imposes two limitations for comparing the results to the dynamics of more realistic networks. First, it requires knowledge of the cell-type identity of each neuron in the recording, which often is not available. Second, it limits the analysis of the dynamics to quantities that are averaged over neurons that belong to the same cell type.

To lift the requirement of block structured variances [i.e., now g = g(z_i, z_j)], we can do the following. Let $K\left(N\right)\in \mathbb{N}$ be a weakly monotonic function of N such that

$$\underset{N\to \infty }{\lim }\frac{K\left(N\right)}{N}=0,\underset{N\to \infty }{\lim }\frac{N^{\beta }}{K\left(N\right)}=0.$$ (12)

Recall that we allow the Lipschitz constant of g to grow as N^β with 1 > β ≥ 0, implying that lim_N→∞ K(N) = ∞. A natural choice is $K\left(N\right)=N^{\tilde{\beta }}$ with $\tilde{\beta }=1-\beta$, but as long as $1>\tilde{\beta }>\beta$ the specific scaling behavior will not matter in our analysis. For convenience we will suppress the N dependence when possible.

Let μ = 1, . . . , K and let

$${\mu }_i=\left\{\mu \mid \frac{i}{N}\phantom{\mid }\in \left(\frac{\mu -1}{K},\frac{\mu }{K}\right]\right\}.$$ (13)

Furthermore, define $\tilde{g}\in {\mathbb{R}}_{+}^{N\times N}$ with elements

$${\tilde{g}}_{ij}=g\left(\frac{{\mu }_i-\frac{1}{2}}{K},\frac{{\mu }_j-\frac{1}{2}}{K}\right).$$ (14)

In other words, g̃ is an N × N matrix with K² equally sized square blocks. The value of elements in each block is the value of the function g in the middle of that block. These definitions allow us to bridge the gap between the block and the continuous cases. Indeed, consider the random connectivity matrix with elements ${\tilde{J}}_{ij}={\tilde{g}}_{ij}{J}_{ij}^0$ and the network that has J̃ as its connectivity.

First, since N/K → ∞ as N → ∞, the number of neurons in each group goes to infinity, and we may use the vector dynamic mean field theory as before, but in a K dimensional space [rather than D which was O(1)]. The critical point is now given in terms of the largest eigenvalue of an N × N matrix M̃ with elements

$${\tilde{M}}_{ij}=\frac{1}{N}{g}^2\left(\frac{{\mu }_i-\frac{1}{2}}{K},\frac{{\mu }_j-\frac{1}{2}}{K}\right),$$ (15)

where rank $\left\{\tilde{M}\right\}\le K$.

Second, recall that the function g is assumed to be smooth outside of a set with measure zero S₀. These properties will allow us to show (see Appendix A) that as N → ∞ we have

$${\tilde{g}}_{ij}\to g(z_i,z_j),{\tilde{M}}_{ij}\to {\left[G_N^{\left(2\right)}\right]}_{ij},$$ (16)

meaning that by studying the system with connectivity structure g̃ in the limit N → ∞ we are in fact obtaining results for the generalized connectivity matrix with a smooth synaptic gain function g.

C. Circular symmetry of spectrum

In [11] we used random matrix theory techniques to derive, for the case of block-structured J, an implicit equation that the full spectral density of J satisfies. The circular symmetry of the spectrum for that case is obvious because the equations [see Eq. (3.6) in [11]] depend on the complex variable z only through |z|². Similar implicit equations, with integrals instead of sums, can be written for the continuous case. Rigorous mathematical analysis of the spectral density implied by such equations is beyond the scope of this paper and will be presented elsewhere. Nevertheless, the integral equations still depend on |z|², supporting the circular symmetry of the spectrum.

III. DYNAMICS ABOVE THE CRITICAL POINT

A. Finite number of partitions

To study the spontaneous dynamics above the critical point we recall again the analogous result for a matrix with block structure. The D dimensional average autocorrelation vectors C(τ), Δ(τ) (see definition below) are restricted to a D^★ dimensional subspace, where D^★ is the number of eigenvalues of M with real part > 1 (i.e., the algebraic multiplicity of these eigenvalues). This result is obtained by projecting Eq. (11) on the right eigenvectors of M [13].

The definitions of the d = 1, . . . , D component of these vectors are

$${\Delta }_d\left(\tau \right)=\frac{1}{N{\alpha }_d}\sum _{i=n_{d-1}+1}^{n_d}\langle x_i\left(t\right)x_i(t+\tau )\rangle ,$$ (17)

$$C_d\left(\tau \right)=\frac{1}{N{\alpha }_d}\sum _{i=n_{d-1}+1}^{n_d}\langle {\varphi }_i\left(t\right){\varphi }_i(t+\tau )\rangle ,$$ (18)

and the D^★ dimensional subspace is

$$U_M=\mathrm{span}\{u_1^R,\dots ,u_{D^{\star }}^R\},$$ (19)

where $u_d^R$ are the right eigenvectors of M in descending order of the real part of their corresponding eigenvalue (see examples in Fig. 1). An equivalent statement is that, independent of the lag τ, projections of the vectors C(τ), Δ(τ) on any vector in the orthogonal complement subspace $U_M^{\perp }$ are approximately 0. Note that for asymmetric (but diagonalizable) M, Δ(τ) on any vector in the orthogonal complement subspace $U_M^{\perp }$ are approximately 0. Note that for asymmetric (but diagonalizable) M, $U_M^{\perp }$ is spanned by the left rather than the right eigenvectors of M:

$$U_M^{\perp }=\mathrm{span}\{u_{D^{\star }+1}^L,\dots ,u_D^L\}.$$ (20)

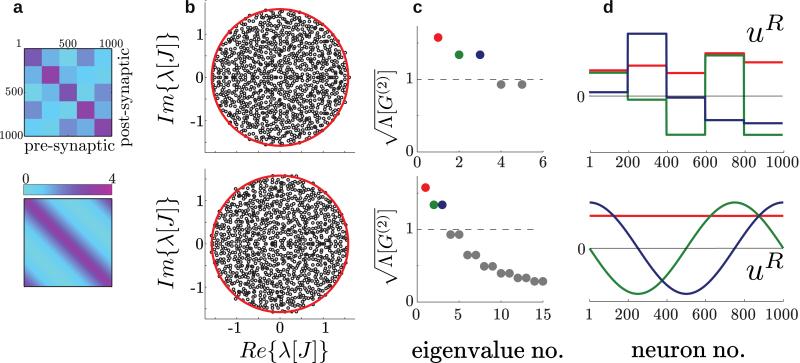
FIG. 1.

Eigenspaces of two example networks – one with block structured connectivity (top) and another with continuous gain modulation (bottom). (a) The synaptic gain matrix g_ij. (b) The spectrum of the random connectivity matrix J in the complex plane. The spectrum is supported by a disk with radius $r=\sqrt{{\Lambda }_1}$ indicated in red. (c) The square root of the largest eigenvalues of $G_N^{\left(2\right)}$. When these are greater than 1, the corresponding eigenvectors [shown in (d)] are active autocorrelation modes. For the continuous function we chose the circulant parametrization (see Sec. IV A) with g₀ = 0.3, g₁ = 3.0 and γ = 2.0. For the block structured connectivity, g was chosen such that the first five eigenvalues match exactly to those of the continuous network.

B. Autocorrelation modes in the generalized model

We can repeat the analysis of [13] for a network with connectivity $\tilde{J}={\tilde{g}}_{ij}{J}_{ij}^0$ that has K² blocks, and for each N, K(N) obtain the subspace U_M̃ that the K dimensional autocorrelation vectors C̃(τ), $\tilde{\Delta }\left(\tau \right)$ are restricted to. These vectors have components

$${\tilde{\Delta }}_{\mu }\left(\tau \right)=\frac{1}{K}\sum _{i=(N∕K)(\mu -1)+1}^{N∕K\mu }\langle x_i\left(t\right)x_i(t+\tau )\rangle ,$$ (21)

$${\tilde{C}}_{\mu }\left(\tau \right)=\frac{1}{K}\sum _{i=N∕K(\mu -1)+1}^{N∕K\mu }\langle {\varphi }_i\left(t\right){\varphi }_i(t+\tau )\rangle .$$ (22)

Now when we take the limit N → ∞ the dimensionality of the autocorrelation vectors C̃(τ), $\tilde{\Delta }\left(\tau \right)$ becomes infinite as well, but the subspace U_M̃ may be of finite dimension K★, where K★ is the algebraic multiplicity of eigenvalues of M̃with real part greater than 1 (see Sec. IV for an example).

We have shown that for g that satisfies the smoothness conditions, studying the network with connectivity $J_{ij}=g(z_i,z_j)J_{ij}^0$ is equivalent to studying the network with connectivity J̃ in the limit N → ∞. Therefore, in that limit, the individual neuron autocorrelation functions C_i(τ), Δ_i(τ) [Eq. 5] are restricted to the subspace spanned by the right eigenvectors of $\tilde{M}\to G_N^{\left(2\right)}$ corresponding to eigenvalues with real part > 1.

This in fact is equivalent to, given the network structure g, predicting analytically the leading principal components in the N dimensional space of individual neuron autocorrelation functions (see Fig. 2). Note that traditionally principal component analysis is performed in the N dimensional space of neuron firing rates rather than autocorrelation functions. Numerical analysis performed in [27] suggests that the system's trajectories, when considered in the space spanned by the vectors x or ϕ(x) (individual neuron activations or firing rates), occupy a space of dimension that is extensive in the system size N. However, when considered in the space of individual neuron autocorrelation functions, the dimension of trajectories is intensive in N and usually finite. In the subspace we derive here the information about the relative phases between neurons is lost, but the amplitude and frequency information is preserved. Section VII includes further discussion of the consequences of our predictions and how they may be applied.

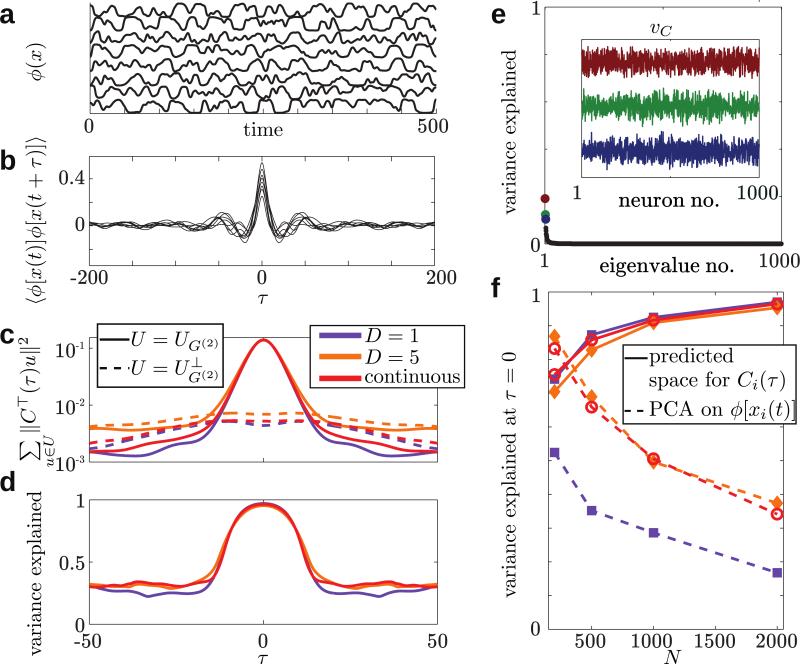
FIG. 2.

Low-dimensional structure of network dynamics. Traces of the firing rates ϕ[x_i(t)] (a) and autocorrelations C_i(τ) (b) of eight example neurons chosen at random from the network with continuous gain modulation (shown in the bottom row of Fig. 1). (c) The sum of squared projections of the vector C_i(τ) on the vectors spanning U_G⁽²⁾ (the active modes, solid lines) or $U_{G^{\left(2\right)}}^{\perp }$ (the inactive modes, dashed lines). The dimension of the subspace U_G⁽²⁾ is K★ = 1 for the network with g = const and K★ = 3 for the block and continuous cases (orange and red, respectively), much smaller than N – K★ ≈ N, orthogonal the dimension of the complement space $U_{G^{\left(2\right)}}^{\perp }$. (d) Our analytically derived subspace accounts for almost 100 percent of the variance in the autocorrelation vector for $\mid \tau \mid \lesssim 10$ (in units of the synaptic time constant). (e) Reducing the dimensionality of the dynamics via principal component analysis on ϕ(x) leads to vectors (inset) that account for a much smaller portion of the variance (when using same dimension K★ for the subspace), and lack structure that could be related to the connectivity. (f) Summary data from 50 simulated networks per parameter set (N, structure type) at τ = 0. As N grows the leak into $U_{G^{\left(2\right)}}^{\perp }$ diminishes if one reduces the space of the C_i(τ) data while the fraction of variance explained becomes smaller when using PCA on the ϕ[x_i(t)] data, a signature of the extensiveness of the dimension of the chaotic attractor.

C. Finite N behavior

For a finite system it is evident from numerical simulations that the N dimensional vector of autocorrelation functions has nonzero projections on inactive modes – eigenvectors of $G_N^{\left(2\right)}$ with corresponding eigenvalue which is < 1 (see Fig. 2). Here we study the magnitude of this effect, and specifically its dependence on N and on the model's structure function g. For simplicity, we will study the projections of the autocorrelation vector C(τ) at lag τ = 0. Let

$${\sigma }_C^2(g,N)=\frac{\langle {\Vert C^{\top }\left(0\right)U^{\perp }\left(G_N^{\left(2\right)}\right)\Vert }^2\rangle }{\langle {\Vert C\left(0\right)\Vert }^2\rangle },$$ (23)

where $U^{\perp }\left(G_N^{\left(2\right)}\right)$ matrix with columns equal to orthogonalized eigenvectors of $G_N^{\left(2\right)}$ with corresponding eigenvalue less than 1 [see Eqs. (19) and (20)]. Here 〈·〉 denotes averaging over an ensemble of connectivity matrices (with the same structure g and same size N).

Consider the homogeneous network [i.e., constant g(z_i, z_j) = g₀ > 1]. Now $U^{\perp }\left(G_N^{\left(2\right)}\right)$ contains all the vectors in ${\mathbb{R}}^N$ perpendicular to the dc mode $\frac{1}{\sqrt{N}}[1,\dots ,1]$ and the squared norm ∥C(0)∥² = O(N) because on average all neurons have the same autocorrelation function [Eq. (10)]. Thus, ${\sigma }_C^2(g_0,N)$ is simply the variance over the neural population of the individual neuron autocorrelation functions at lag τ = 0.

We can now use the mean-field approximation to determine the N dependence of ${\sigma }_C^2(g_0,N)$. For N >> 1, the elements of the vector C(0) follow a scaled χ² distribution

$$C_i\left(0\right)=N^{-1}q\left(g_0^2\right)y_i^N,y_i^N\sim {\chi }^2\left(N\right),$$ (24)

where $q\left(g_0\right)\sim \mathcal{O}\left(g_0\right)\sim \mathcal{O}\left(1\right)$ and χ²(N) is the standard χ² distribution N degrees of freedom. Thus, in this limit,

$$\begin{array}{cc}\hfill \langle C_i\left(0\right)\rangle =& q\left(g_0^2\right),\hfill \\ \hfill \langle C_i\left(0\right)C_j\left(0\right)\rangle -\langle C_i\left(0\right)\rangle \langle C_j\left(0\right)\rangle =& 2{\delta }_{ij}{N}^{-1}{q}^2\left(g_0^2\right)\approx {\delta }_{ij}∕N.\hfill \end{array}$$ (25)

The autocorrelation function is in general a single neuron property. Therefore, their variation about the mean is uncorrelated across neurons independent of the network's structure: 〈C_i(0)C_j(0)〉 – 〈C_i(0)〉〈C_j(0)〉 ∝ δ_ij. Thus, we can use the notation 〈(δC_i(0))²〉 = 〈C_i(0)C_i(0)〉 – 〈C_i(0)〉〈C_i(0)〉.

In the case with D partitions the vectors that span U_G⁽²⁾ are no longer parallel to the dc mode. We assume that the projections on $U_{G^{\left(2\right)}}^{\perp }$ can still be estimated using the χ² distribution, but here with α_cN degrees of freedom for the c partition [instead of N, see Eq. (24)]. Thus, for a network with D partitions,

$$\begin{array}{cc}\hfill \langle C_i\left(0\right)\rangle =& q_{c_i}\left(M\right),\hfill \\ \hfill \langle {\left(\delta C_i\left(0\right)\right)}^2\rangle =& 2q_{c_i}^2\left(M\right){\left({\alpha }_{c_i}N\right)}^{-1}\approx D∕N.\hfill \end{array}$$ (26)

Finally, for K(N) partitions,

$$\begin{array}{cc}\hfill \langle C_i\left(0\right)\rangle =& q_i\left(g_N^{\left(2\right)}\right),\hfill \\ \hfill \langle {\left(\delta C_i\left(0\right)\right)}^2\rangle =& 2q_i^2\left(G_N^{\left(2\right)}\right)(K∕N)\approx K\left[g\right]∕N.\hfill \end{array}$$ (27)

At this stage, Eq. (27) remains ambiguous because the function K(N) is not a property of the neural network model. Rather, it is a construction we use to show that in the limit N → ∞ we are able to characterize the dynamics using the vector dynamic mean field approach. Therefore, for finite N we now wish to estimate an appropriate value of K = K[g].

This can be done by noting that the network with block structured connectivity is a special case of the one with a continuous structure function. For that special case we know that K[g] = D. Since g is smooth, for sufficiently large N, we can assume that in each block g is linear in both variables z_i and z_j:

$$g(z_i,z_j)\approx {\tilde{g}}_{ij}+{\tilde{g}}_N^{(1,0)}({\mu }_i,{\mu }_j)\left(z_i-\frac{{\mu }_i-\frac{1}{2}}{K}\right)+{\tilde{g}}_N^{(0,1)}({\mu }_i,{\mu }_j)\left(z_j-\frac{{\mu }_j-\frac{1}{2}}{K}\right).$$ (28)

Here ${\tilde{g}}_N^{(1,0)}({\mu }_i,{\mu }_j)$ is the first derivative of g with respect to the first variable, evaluated in the middle of the μ_i, μ_j block.

The only expression for K[g] that depends on first derivatives of g and agrees with the homogeneous and block cases is

$$\begin{array}{cc}\hfill K\left[g\right]\approx & 1+\int \int \left[\mid g^{(1,0)}(x,y)\mid +\mid g^{(0,1)}(x,y)\mid \right]dxdy\hfill \\ \hfill \approx & 1+\int \int \Vert \nabla g\Vert dxdy.\hfill \end{array}$$ (29)

We are unable to test this prediction quantitatively, because we do not know the dependence of the function q on the structure g. We are able to show however that the dependence on N is the same as for the block models, which is confirmed by numerical simulations [compare solid purple, orange and red lines in Fig. 2(f)]. In the cases where g depends on N, the value of K[g] will also depend on N, such that the scaling of the “leak” may no longer be ∝ N⁻¹.

IV. AN EXAMPLE WHERE g IS CIRCULANT

When the matrix g(z_i, z_j) is circulant such that g(z_i, z_j) = g(z_ij) with

$$z_{ij}=\min \{\mid z_i-z_j\mid ,1-\mid z_i-z_j\mid \},$$ (30)

the eigenvalues and eigenvectors of $G_N^{\left(2\right)}$ are given in closed form by integrals of the function g²(z_ij) and the Fourier modes with increasing frequency. In particular, the largest eigenvalue of ${\Lambda }_1=2{\int }_0^{\frac{1}{2}}{g}^2\left(z\right)dz$ corresponds to the zero frequency eigenvector ∝[1, . . . ,1]. To show this, consider the k+1 eigenvalue of the circulant matrix $G_N^{\left(2\right)}$:

$${\Lambda }_{k+1}=\frac{1}{N}\sum _{j=1}^N\exp \left(\frac{2\pi ijk}{N}\right)g^2(z_1,z_j).$$ (31)

So in the limit N → ∞,

$$\begin{array}{cc}\hfill {\Lambda }_{k+1}=& \underset{N\to \infty }{\lim }\frac{2}{N}\sum _{j=1}^{N∕2}\exp \left(2\pi ik{z}_{1j}\right)g^2\left(z_{1j}\right)\hfill \\ \hfill =& 2{\int }_0^{\frac{1}{2}}\exp \left(2\pi ikz\right)g^2\left(z\right)dz,\hfill \end{array}$$ (32)

as desired.

A. A ring network

As an example we study a network with ring structure that will be defined by g(z_i, z_j) = g₀ + g₁(1–2z_ij), such that neurons that are closer are more strongly connected.

This definition leads to the following form for the critical coordinate along which the network undergoes a transition to chaotic behavior

$${\Lambda }_1=g_0^2+\frac{2g_0{g}_1}{\gamma +1}+\frac{g_1^2}{2\gamma +1}$$ (33)

Interestingly, as g₁ increases continuously, additional discrete modes with increasing frequency over the network's spatial coordinate become active by crossing the critical point Λ_k = 1. When modes with sufficiently high spatial frequency have been introduced, nearby neurons may have distinct firing properties.

B. A toroidal network

In contrast to the ring network discussed above, the connectivity in real networks often depends on multiple factors. These could be the spatial coordinates of the cell body or the location in a functional space (e.g., the frequency that each particular neuron is sensitive to). Therefore we would like to consider a network where the function g depends on the distance between neurons embedded in a multidimensional space.

This problem was recently addressed by Muir and Mrsic-Flogel [14] by studying the spectrum of a specific type of Euclidean random matrix. In their model, neurons were randomly and uniformly distributed in a space of arbitrary dimension, and the connectivity was a deterministic function of their distance. While their approach resolves the issue of the spectral properties of the random matrix when connectivity depends on distance in more than one dimension, the dynamics these matrices imply remain unknown.

To study the spectrum and the dynamics jointly, we define a network where neurons’ positions form a square K × K grid (with $K=\sqrt{N}$) on the [0, 1] × [0, 1] torus [see Fig. 3(a)]:

$${\theta }_i^1=\frac{\lfloor i∕K\rfloor }{K},{\theta }_i^2=\frac{i\mathrm{mod}K}{K}.$$ (34)

The positions of the neurons on the torus are schematized in Fig. 3(a).

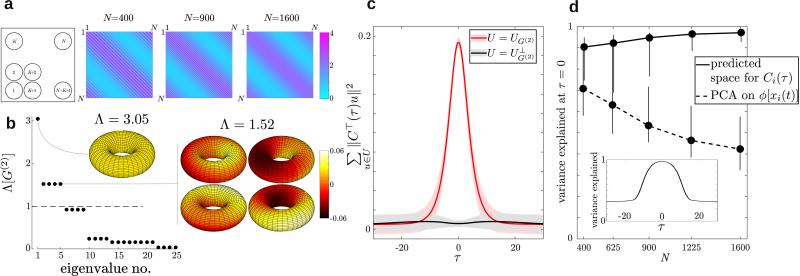
FIG. 3.

Results for a toroidal network. (a) A grid strategy with $K=\sqrt{N}$ for tiling the [0, 1] × [0, 1] torus with N neurons (left) and the resulting deterministic gain matrix with elements g_ij for three values of N as defined in Eq. (35) (right). Unlike the ring network, here g depends on N, and its derivative is unbounded so as N increases the gain function “folds.” The parameters of the connectivity matrix are g₀ = 0.7, g₁ = 0.8. (b) The 25 nonzero eigenvalues of $G_N^{\left(2\right)}$ for N = 1600 and the eigenvectors corresponding to eigenvalues that are greater than 1 plotted on a torus with coordinates $({\theta }_i^1,{\theta }_i^2)$. (c) The sum of squared projections of the vector C_i(τ) on the vectors spanning U_G(2) (the active modes, red line) or $U_{G^{\left(2\right)}}^{\perp }$ (the inactive modes, black line). Shades indicate the standard deviation computed from 50 realizations. (d) Comparison of the variance explained at τ = 0 by our predicted subspace (solid line) and by performing PCA on ϕ(x) (dashed line). Error bars represent 95% confidence intervals. Inset: the subspace we derived accounts for a large portion of the variance for time lags $\mid \tau \mid \lesssim 10$ (in units of the synaptic time constant).

An analogous parametrization for g to the one we used in the ring example which respects the toroidal geometry reads

$$g_{ij}=g_0+g_1\left[\cos \left(2\pi z_{ij}\right)+1\right]\left[\cos \left(2\pi \sqrt{N}{z}_{ij}\right)+1\right].$$ (35)

Note that now g depends on N, but it is bounded and its Lipschitz constant scales as $\sqrt{N}$, so it satisfies the smoothness conditions.

Figure 3(b) shows the spectrum of G⁽²⁾ and the corresponding eigenvectors, plotted on a torus. Because there are non-uniform modes that are active (2 through 5), then each neuron has a different participation in the vector of autocorrelation functions. In Figs. 3(c) and 3(d) we show for a network with a range of N values that indeed the vector of autocorrelation functions is restricted to the predicted subspace in contrast to the firing rate vector.

The gain function analyzed here depends on a Euclidean distance on the torus. Other metrics, for example a city-block norm, can be treated similarly.

Overall these results provide a mechanism whereby continuous and non-fine -tuned connectivity that depends on a single or multiple factors can lead to a few active dynamic modes in the network. Importantly, the modes maintained by the network inherit their structure from the deterministic part of the connectivity.

V. MATRICES WITH HETEROGENEOUS DEGREE DISTRIBUTIONS

Here we will use our general result to compute the spectrum of a random connectivity matrix with specified in- and out-degree distributions. Realistic connectivity matrices found in many biological systems have degree distributions which are far from the binomial distribution that would be expected for standard Erdős-Rényi networks [28]. Specifically, they often exhibit correlation between the in- and out-degrees, clustering, community structures and possibly heavy-tailed degree distributions [5, 29]. Some results exist for symmetric adjacency matrices with broad degree distributions [30, 31] that are useful to studying systems beyond neuroscience.

We consider a connectivity matrix appropriate for a neural network model. Since each element of this matrix will have a nonzero mean, our current theory cannot make statements about the dynamics. Nevertheless the spectrum of the connectivity matrix is important on its own as a step towards understanding the behavior of random networks with general and possibly correlated degree distributions.

Consider a network with N_E excitatory and N_I inhibitory neurons (N = N_E + N_I). The connectivity is defined through the in- and out-degree sequences, N dimensional vectors where the ith element represents the number of incoming or outgoing connections to or from neuron i. Each inhibitory neuron has incoming or outgoing connections with probability p₀ to or from every other neuron in the network. Within the excitatory subnetwork, degree distributions are heterogeneous. Specifically, kⁱⁿ, k^out are the average excitatory in- and out-degree sequences that are drawn from a joint degree distribution that could be correlated. We assume that ${\sum }_{i=1}^{N_E}{k}_i^{\mathrm{in}}={\sum }_{i=1}^{N_E}{k}_i^{\mathrm{out}}=N_E\stackrel{‒}{k}$, where k̄ is the mean connectivity, and that the marginals of the degree distribution are equal. Define x, y to be the N_E dimensional vectors $x=k^{\mathrm{in}}∕\sqrt{N_E\stackrel{‒}{k}}$ and $y=k^{\mathrm{out}}∕\sqrt{N_E\stackrel{‒}{k}}$.

The matrix P defines the probability of connections given the fixed normalized degree sequences and p₀:

$$P_{ij}=\{\begin{array}{cc}{x}_i{y}_i,\hfill & 1\le i,j\le N_E\hfill \\ p_0,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$ (36)

The random adjacency matrix is then A_ij ~ Bernoulli (P_ij). Note that because the adjacency matrix is random, kⁱⁿ and k^out are the average in- and out-degree sequences.

The connectivity matrix is then

$$J_{ij}=A_{ij}{W}_{ij}$$ (37)

with

$$W_{ij}=\{\begin{array}{cc}-W_0,\hfill & j>N_E\hfill \\ 1,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}},$$ (38)

where W₀ is the ratio of the synaptic weight of inhibitory to excitatory synapses. It should be noted that the connections to and from inhibitory neurons are much less well characterized empirically, and the evidence for specific structure in these connections is weaker than for excitatory neurons. For this reason, outside of the excitatory subnetwork connectivity is assumed to be homogeneous.

To leading order, the distribution of eigenvalues of J will depend only on the mean and variance of its elements, which are summarized in the deterministic matrices Q (means) and $G_N^{\left(2\right)}$ (variances) with elements

$$Q_{ij}=P_{ij}{W}_{ij},$$ (39)

$${\left[G_N^{\left(2\right)}\right]}_{ij}=P_{ij}(1-P_{ij})W_{ij}^2.$$ (40)

We will show that the rank of the deterministic matrix Q is ≤ 3 (generically for large N and non-fine-tuned parameters rank {Q} = 3). In [10], Tao considered a case similar to ours, studying the spectrum of the sum of a random matrix with independent and identically distributed elements and a low-rank perturbation. In Sec. 2 of that paper, it is shown that because the resolvent, (J⁰–z)⁻¹ (where z is a complex number), is close to $-\frac{1}{z}I$ outside the support of the spectrum, outlying eigenvalues fluctuate around the nonzero eigenvalues of the low-rank perturbation. Adapting the arguments of [32] in Sec. 5, as done in [11], it can be shown the resolvent of random matrices with independent and non identically distributed entries is also close to $-\frac{1}{z}I$ outside the support of the bulk spectrum. Hence, outlying eigenvalues will fluctuate around the deterministic low-rank eigenvalues.

Combining these, we expect that if the nonzero eigenvalues of Q are outside of the bulk that originates from the random part of the matrix, the spectrum of the matrix J (with nonzero means) will be approximately a composition of the bulk and outliers that can be computed separately and that the approximation will become exact as N → ∞. This is verified through numerical calculations (Fig. 4).

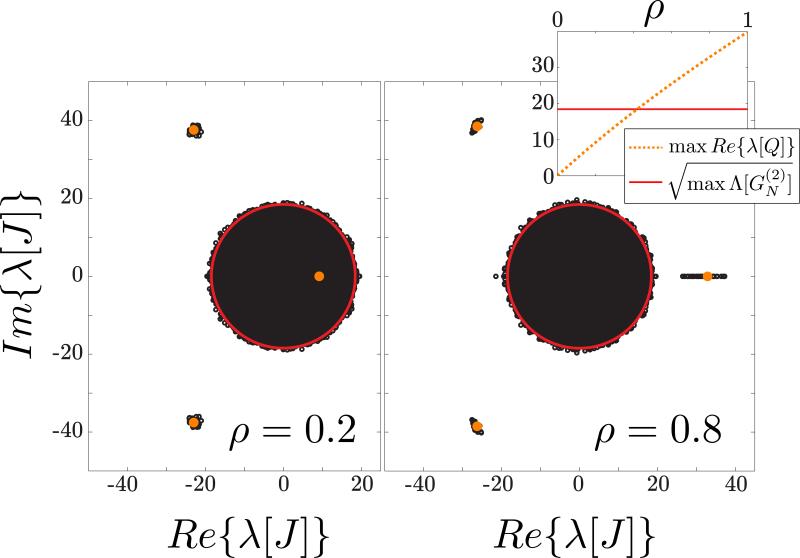
FIG. 4.

Spectrum of connectivity matrices with heterogeneous, correlated joint degree distribution. The network parameters were chosen to be κ = 0.7, θ = 28.57, N_E = 1000, N_I = 250, p₀ = 0.05, W₀ = 5, where κ and θ are the form and scale parameters respectively of the distribution from which the in- and out-degree sequences are randomly drawn. The average correlation ρ between the in- and out-degree sequences was varied between 0 and 1. For the values ρ = 0.2 (left) and ρ = 0.8 (right) we drew 25 degree sequences and based on them drew the connectivity matrix according to the prescription outlined in Sec. V. The eigenvalues of each matrix were computed numerically and are shown in black. For each value of ρ we computed the average functions $\langle \mathcal{T}\rangle$, $\langle \mathcal{S}\rangle$ etc., and the roots of the characteristic polynomials $\mathcal{A}\left(\Lambda \right)$ and $\mathcal{B}\left(\lambda \right)$ (see Appendixes B and C for derivation). The predictions for the support of the bulk (solid red line) and the outliers (orange points and dotted line) are in agreement with the numerical calculation. Inset: as a function of ρ, there is a positive outlier that exits the disk to the right.

Viewing the normalized degree sequences x, y as deterministic ministic variables we define

$$\begin{array}{cc}\hfill \mathcal{U}& =\sum _{i=1}^{N_E}{x}_i^2=\sum _{i=1}^{N_E}{y}_i^2,\hfill \\ \hfill \mathcal{S}& =\sum _{i=1}^{N_E}{x}_i=\sum _{i=1}^{N_E}{y}_i,\hfill \\ \hfill \mathcal{T}& =\sum _{i=1}^{N_E}{x}_i{y}_i,\hfill \\ \hfill \mathcal{V}& =\sum _{i=1}^{N_E}(x_i{y}_i^2+x_i^2{y}_i),\hfill \\ \hfill \mathcal{Z}& =\sum _{i=1}^{N_E}{x}_i^2{y}_i^2,\hfill \\ \hfill \mathcal{R}& =\left(\sum _{i=1}^{N_E}{x}_i{y}_i^2\right)\left(\sum _{i=1}^{N_E}{x}_i^2{y}_i\right).\hfill \end{array}$$ (41)

Given the parameters W₀,p₀, N_E, N_I, we show in Appendix B that $\mathrm{rank}\left\{G_N^{\left(2\right)}\right\}\le 4$ (generically for large N and non-fine-tuned parameters $\mathrm{rank}\left\{G_N^{\left(2\right)}\right\}=4$) and its characteristic polynomial is $\mathcal{A}\left(\Lambda \right)={\sum }_{k=0}^N{(-1)}^k{a}_k{\Lambda }^{N-k}$ with

$$\begin{array}{cc}\hfill a_0=& 1,\hfill \\ \hfill a_1=& \mathcal{T}-\mathcal{Z}+N_1{W}_0^2{p}_0(1-p_0),\hfill \\ \hfill a_2=& \mathcal{R}-\mathcal{Z}\mathcal{T}+N_I{W}_0^2{p}_0(1-p_0)[\mathcal{T}-\mathcal{Z}-p_0(1-p_0)N_E],\hfill \\ \hfill a_3=& N_I{W}_0^2{p}_0(1-p_0)\times \{\mathcal{R}-\mathcal{Z}\mathcal{T}+p_0(1-p_0)\times [{\mathcal{S}}^2-{\mathcal{U}}^2-N_E(\mathcal{T}-\mathcal{Z})]\},\hfill \\ \hfill a_4=& N_I{W}_0^2{p}_0^2{(1-p_0)}^2[N_E(\mathcal{Z}\mathcal{T}-\mathcal{R})-\mathcal{Z}{\mathcal{S}}^2-{\mathcal{U}}^2\mathcal{T}+\mathcal{S}\mathcal{U}\mathcal{V}],\hfill \end{array}$$ (42) †

and a_k = 0 for k > 4. Therefore, using our results, the radius of the bulk spectrum of J is equal to the square root of the largest solution to $\mathcal{A}\left(\Lambda \right)=0$.

Furthermore we show that the nonzero eigenvalues of Q are equal to the roots of the polynomial $\mathcal{B}\left(\lambda \right)={\sum }_{k=0}^N{(-1)}^k{b}_k{\lambda }^{N-k}$, with

$$\begin{array}{cc}\hfill b_0=& 1,\hfill \\ \hfill b_1=& \mathcal{T}-N_I{W}_0{p}_0,\hfill \\ \hfill b_2=& N_i{W}_0{p}_0[N_E{p}_0-\mathcal{T}],\hfill \\ \hfill b_3=& N_I{W}_0{p}_0^2[N_E\mathcal{T}-{\mathcal{S}}^2],\hfill \end{array}$$ (43)

and b_k = 0 for k > 3, such that the outlying eigenvalues of J are approximated by the roots of $\mathcal{B}\left(\lambda \right)$ that lie outside of the bulk.

If the degree sequences are not specified, but only the joint in- and out-degree distribution they are drawn from, the random matrix J will be constructed in two steps: first kⁱⁿ and k^out are drawn from their joint in- and out-degree distribution, and then the elements of J are drawn using the prescription outlined above. In such cases, one can in principle compute the averages $\langle \mathcal{T}\rangle$, $\langle \mathcal{S}\rangle$, etc., in terms of the moments of the joint degree distribution, and substitute these averages into the formulas we give assuming the degree sequences are fixed.

We have carried out that calculation (Appendix C) for Γ degree distributions with form parameter κ, scale parameter θ and arbitrary correlation ρ of the in- and out-degree sequences (see Fig. 4). We find that, for fixed marginals, the radius of the bulk spectrum depends extremely weakly on the correlation of the in- and out-degree sequences (see solid red line in inset to Fig. 4). The matrix Q however has a real, positive eigenvalue that for typical examples increases monotonically with the correlation, such that for some value it exits the bulk to the right (see Fig. 4). Work by Roxin [18], Schmeltzer et al. [19], and unpublished work by Landau and Sompolinsky [33] has shown that the broadness and correlation of the joint degree distribution can lead to qualitative changes in the behavior of a spiking network. Further work is required to investigate whether and why these changes can be explained by the spectrum of the connectivity matrix derived here. We anticipate that the outlier exiting the spectrum may be related to the transition to a saturated state observed in networks with block structure in [23].

VI. AN EXAMPLE FROM ECOLOGY

Random matrices have been used to study a wide variety of complex systems outside of neuroscience. Examples include metabolic networks, gene-regulatory networks, and communication networks. Here we analyze matrices with triangular structure that arise in ecology of food webs. The past few years have seen a resurgence of interest in the use of methods from random matrix theory to study the stability of ecosystems [34–36]. While the original work by R. May assumed a random unstructured connectivity pattern between species [37], experimental data shows marked departures from random connectivity [38]. This includes hierarchical organization within ecosystems where larger species have asymmetric effect on smaller species, larger variance in the number of partners for a given species [39], and fewer cycles involving three or more interacting species than would be expected from an Erdős-Rényi graph [40]. A popular model for food web structure is the cascade model [41], where species are rank ordered, and each species can exclusively prey upon lower-ranked species. The differential effects between predators and prey in the cascade model can be described using connectivity matrices with different statistics for entries above and below the diagonal [42]:

$$J_{ij}=\mu (z_i,z_j)∕\sqrt{N}+g(z_i,z_j)J_{ij}^0$$ (44)

with

$$\mu (z_i,z_j)={\mu }_aϴ(z_i-z_j)-{\mu }_bϴ(z_j-z_i)$$ (45)

$$g(z_i,z_j)=g_aϴ(z_i-z_j)+g_bϴ(z_j-z_i)$$ (46)

where Θ is the Heaviside step function. We use the convention Θ(0) = 0. Here, J describes the interactions between different species in the ecosystem. For μ_a, μ_b > 0 and sufficiently larger than g_a, g_b, the entries above (below) the diagonal are positive (negative), so the matrix describes a perfectly hierarchical food web, where the top-ranked species consumes all the other species, the second species consumes all the species but the first, and so on.

We will focus on the random part of the matrix (i.e., we set μ_a = μ_b = 0). The spectrum of the sum of the deterministic and random parts remains a problem for future study. Note that since the deterministic part has full rank, one cannot apply simple perturbation methods.

According to our analysis, the support of the spectrum of J is a disk with radius $\sqrt{{\Lambda }_1}$, ${\Lambda }_1={\lim }_{N\to \infty }\max \lambda \left[G_N^{\left(2\right)}\right]$, and

$$G_N^{\left(2\right)}(z_i,z_j)=N^{-1}(g_a^2ϴ(z_i-z_j)+g_b^2ϴ(z_j-z_i))$$ (47)

Following the derivation in [42] we will show that ${\Lambda }_1=\frac{g_a^2-g_b^2}{2\ln (g_a∕g_b)}$.

The characteristic polynomial ${\mathcal{D}}_N\left(\lambda \right)=\det \mid I\lambda -G_N^{\left(2\right)}\mid$ is simplified by subtracting the i+1 column from the ith column for i = 1,..., N – 1 giving

$${\mathcal{D}}_N\left(\lambda \right)=\det \mid \begin{array}{cccc}\hfill \lambda +a\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -a\hfill \\ \hfill -(\lambda +b)\hfill & \hfill \ddots \hfill & \hfill 0\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \ddots \hfill & \hfill \lambda +a\hfill & \hfill -a\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -(\lambda +b)\hfill & \hfill \lambda \hfill \end{array}\mid ,$$ (48)

where we have defined $a=g_a^2∕N$ and $b=g_b^2∕N$. This simplifies to the recursion relation ${\mathcal{D}}_N\left(\lambda \right)=(\lambda +a){\mathcal{D}}_{N-1}\left(\lambda \right)-a{(\lambda +b)}^{N-1}$. Taking into account that ${\mathcal{D}}_2\left(\lambda \right)={\lambda }^2-ab$, this recursion relation can be solved, giving:

$${\mathcal{D}}_N\left(\lambda \right)=\frac{1}{a-b}\left[a{(\lambda +b)}^N-b{(\lambda +a)}^N\right].$$ (49)

Setting the characteristic polynomial ${\mathcal{D}}_N\left(\lambda \right)$ to 0 leads to the equation,

$$b=a{\left(\frac{b+\lambda }{a+\lambda }\right)}^N,$$ (50)

which has multiple roots

$${\lambda }_k=a\frac{{\left(\frac{b}{a}\right)}^{1∕N}{e}^{2\pi ik∕N}-\frac{b}{a}}{1-{\left(\frac{b}{a}\right)}^{1∕N}{e}^{2\pi ik∕N}},k=1,\dots ,N.$$ (51)

We are interested in the largest among the N roots, which is real and positive. Taking into account the dependence of a and b on N, we find that:

$${\Lambda }_1=\underset{N\to \infty }{\lim }\underset{k}{\max }\left[a\frac{{\left(\frac{b}{a}\right)}^{1∕N}{e}^{2\pi ik∕N}-\frac{b}{a}}{1-{\left(\frac{b}{a}\right)}^{1∕N}{e}^{2\pi ik∕N}}\right]=\frac{g_a^2-g_b^2}{\ln \left(\frac{g_a^2}{g_b^2}\right)},$$ (52)

as desired.

Interestingly, for all values of g_a, g_b the spectral radius of J is smaller than the radius of the network if the predator-prey structure did not exist. The latter is equal to $\sqrt{(g_a^2+g_b^2)∕2}$. This suggests that the hierarchical structure of the interaction network serves to stabilize the ecosystem regardless of how dominant the predators are over the prey.

Note however that in this model there are no correlations. In [42], it was shown numerically that correlations (i.e., the expectation value of $J_{ij}^0{J}_{ji}^0$) can dramatically change the stability of the network, compared with one that has no correlations.

VII. DISCUSSION AND CONCLUSIONS

We studied jointly the spectrum of a random matrix model and the dynamics of the neural network model it implies. We found that, as a function of the deterministic structure of the network (given by g), the network becomes spontaneously active at a critical point.

Identifying a space where the dynamics of a neural network can be described efficiently and robustly is one of the challenges of modern neuroscience [43]. In our model, above the critical point, the deterministic dynamics of the entire network are well approximated by a potentially low-dimensional probability distribution, with dimension equal to the number of eigenvalues of a deterministic matrix that have real part greater than 1.

The two limitations of our previous studies [11, 13] for interpreting multi-unit recordings are (1) that the cell-type identity of each neuron in the network has to be known and (2) that predictions are averaged over all neurons of a specific type.

Here both limitations are remedied. First, while some information about the connectivity structure is still required, this could be in the form of global spatial symmetries (“rules”) present in the network, such as the connectivity rule we used in the ring model. Second, our analysis provides a prediction for single neuron quantities, namely the participation of every neuron in the network in the global active dynamic modes.

Existence of discrete network modules with no apparent fine-tuned connectivity has been shown to exist in networks of grid cells in mammalian medial entorhinal cortex [44]. These cells fire when the animal's position is on the vertices of a hexagonal lattice, and are thought to be important for spatial navigation. Interestingly, when characterizing the firing properties of many such cells in a single animal one finds that the the lattice spacing of all cells belongs (approximately) to a discrete set that forms a geometric series [44]. Much work has been devoted to trying to understand how such a code could be used efficiently to represent the animal's location (see for example [45, 46]) and how such a code could be generated [47].

However, we are not aware of a model that explains how multiple modules (subnetworks with distinct grid spacing) could be generated without fine-tuned connectivity that is not observed experimentally. In our model, continuous changes to a connectivity parameter can introduce additional discrete and spatially periodic modes into the network represented by finer and finer lattices. We are not arguing that the random network we are studying here could serve as a model of grid-cell networks, as there are many missing details that cannot be accounted for by our model. Nevertheless our analysis uncovers a mechanism by which a low-dimensional, spatially structured dynamics could arise as a result of random connectivity.

More broadly, our results offer insight into the question of what is the appropriate random matrix model for studying networks with structured connectivity. We focus our discussion on networks with increased probability of bidirectional connections (see for example [5]). Most empirical datasets consist of connectivity measurements within a subnetwork of a few neurons, and thus cannot distinguish between the following two processes giving rise to the observed over-representation of bidirectional connections [48]. One possibility is that microscopic (e.g., molecular) signaling is responsible for an increased probability that neuron i is connected to j, given that j is connected to i. An alternative possibility is that the in and out degree sequences are correlated macroscopically, so that if neuron j is connected to i the in- and out-degrees of i will be large with increased probability, so the chance that i is connected to j is larger than the average connectivity in the network. These two possibilities are related to different random matrix models that imply markedly different network dynamics: the first to an elliptic model where the elements J_ij and J_ji are correlated [7], and the second to a model with heterogeneous and correlated degree distributions, such as the one studied here that has a circularly symmetric spectrum.

Appendix A: The limit K, N → ∞

Here we will show that the difference between the piecewise estimate g̃ and the continuous synaptic gain function g goes to 0 as N → ∞. We assumed that the unit square can be tiled by square subsets of area $s_0^2>0$ where g is bounded, differentiable, and its first derivative is bounded in each subset. Note that the Lipschitz constant of g can depend on N, but s₀ cannot.

For $N,K\left(N\right)\in \mathbb{N}$, recall our definitions for g̃ and μ_i [Eqs. (13) and (14)] and define k_ij = (K⁻¹(μ_i – 1), K⁻¹μ_i × (K⁻¹(μ_j – 1), K⁻¹μ_j. Also recall our assumption that each point is either inside a square with side s₀ within which there are no discontinuities or on the border of such a subset. Thus, for $L>s_0^{-1}$ we can assume that every constant region of g̃ is contained within a single square subset.

We would like to show that for all i, j

$$\underset{N\to \infty }{\lim }\mid {\tilde{g}}_N(z_i,z_j)-g(z_i,z_j)\mid =0.$$ (A1)

Since s₀ is independent of N, we only have to show that Eq. (A1) is true within a subset where g satisfies the smoothness conditions.

Using our definitions and the fact that g has Lipschitz constant $C_L\left(N\right)=C_L^0{N}^{\beta }$,

$$\begin{array}{cc}\hfill \mid {\tilde{g}}_N(z_i,z_j)-g(z_i,z_j)\mid & =\mid g\left(\frac{{\mu }_i-\frac{1}{2}}{K},\frac{{\mu }_j-\frac{1}{2}}{K}\right)-g(z_i,z_j)\mid \le \underset{(z_i^{\prime },z_j^{\prime })\in k_{ij}}{\sup }\mid g\left(\frac{{\mu }_i-\frac{1}{2}}{K},\frac{{\mu }_j-\frac{1}{2}}{K}\right)-g(z_i^{\prime },z_j^{\prime })\mid \hfill \\ \hfill & \le C_L\underset{(z_i^{\prime },z_j^{\prime })\in k_{ij}}{\sup }{\left[{\left(\frac{{\mu }_i-\frac{1}{2}}{K}-z_i^{\prime }\right)}^2+{\left(\frac{{\mu }_j-\frac{1}{2}}{K}-z_j^{\prime }\right)}^2\right]}^{1∕2}=C_L^0\frac{N^{\beta }}{2K}.\hfill \end{array}$$ (A2)

So finally,

$$\underset{N\to \infty }{\lim }\mid {\tilde{g}}_N(z_i,z_j)-g(z_i,z_j)\mid \le \frac{C_L^0}{2}\underset{N\to \infty }{\lim }\frac{N^{\beta }}{K\left(N\right)}=0.$$ (A3)

Appendix B: The characteristic polynomials of $G_N^{\left(2\right)}$ and Q

Here we compute directly the characteristic polynomials of $G_N^{\left(2\right)}$ and Q (Eqs. 42, 43) using the minor expansion formula.

1. Calculation of spectrum of G⁽²⁾

Recall that N = N_E + N_I, and let ${\mathcal{G}}_k^{\left(2\right)}$ be the k × k matrix with elements taken from the intersection of k specific rows and columns of $G_N^{\left(2\right)}$. The notation ${\mathcal{G}}_{k_E,k_I}^{\left(2\right)}$ will indicate that exactly k_E and k_I of these rows and columns correspond to excitatory and inhibitory neurons, respectively.

For convenience we will use ν = p₀ (1 – p₀) and $w=W_0^2{p}_0(1-p_0)$. We would like to write an expression for the characteristic polynomial of $G_{N_E+N_I}^{\left(2\right)}$ using the sums over its diagonal minors

$${\mathcal{A}}_{N_E,N_I}\left(\Lambda \right)=\sum _{k=0}^N{(-1)}^k{a}_k{\Lambda }^{N-k},$$ (B1)

where $a_k=\sum \det {\mathcal{G}}_k^{\left(2\right)}$ for k ≥ 1 and a₀ = 1. The notation $\sum \det {\mathcal{G}}_k^{\left(2\right)}$ means a sum over all combinations of N_E, N_I such that N_E + N_I = k (i.e. the so-called k-row diagonal minors of $G_N^{\left(2\right)}$). We will compute a₀, . . . , a₄ explicitly and show that a_k = 0 for k > 4.

We begin by noting that the determinant of the 3 × 3 matrix

$${\mathcal{G}}_{3,0}^{\left(2\right)}=\mathrm{diag}(x_1,x_2,x_3)\left(\begin{array}{ccc}\hfill 1-x_1{y}_1\hfill & \hfill 1-x_1{y}_2\hfill & \hfill 1-x_1{y}_3\hfill \\ \hfill 1-x_2{y}_1\hfill & \hfill 1-x_2{y}_2\hfill & \hfill 1-x_2{y}_3\hfill \\ \hfill 1-x_3{y}_1\hfill & \hfill 1-x_3{y}_2\hfill & \hfill 1-x_3{y}_3\hfill \end{array}\right)\times \mathrm{diag}(y_1,y_2,y_3)$$

is 0 because the middle matrix is the sum of two rank 1 matrices.

The coefficient a₀

By definition, a₀ = 1.

The coefficient a₁

The second coefficient, a₁ is simply the trace

$$\begin{array}{cc}\hfill \mathrm{Tr}\left\{G_{N_E,N_I}^{\left(2\right)}\right\}=& \sum _{i=1}^{N_E}{x}_i{y}_i(1-x_i{y}_i)+N_{I}w,\hfill \\ \hfill a_1=& \mathcal{T}-\mathcal{Z}+N_{I}w,\hfill \end{array}$$ (B2)

where in the second row we used the functions of the degree sequences [Eq. (41)].

The coefficient a₂

The third coefficient a₂ is the sum of two row diagonal minors. There are three types of diagonal minors, only two of which are nonzero:

$$\begin{array}{cc}\hfill \det {\mathcal{G}}_{2,0}^{\left(2\right)}=& \det \left(\begin{array}{cc}\hfill x_i\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill x_j\hfill \end{array}\right)\det \left(\begin{array}{cc}\hfill (1-x_i{y}_i)\hfill & \hfill (1-x_i{y}_i)\hfill \\ \hfill (1-x_j{y}_i)\hfill & \hfill (1-x_j{y}_j)\hfill \end{array}\right)\det \left(\begin{array}{cc}\hfill y_i\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill y_j\hfill \end{array}\right)=x_i{x}_j{y}_i{y}_j(x_i{y}_j+x_j{y}_i-x_i{y}_i-x_j{y}_j)\hfill \\ \hfill \det {\mathcal{G}}_{1,1}^{\left(2\right)}=& \det \left(\begin{array}{cc}\hfill x_1{y}_1(1-x_i{y}_i)\hfill & \hfill w\hfill \\ \hfill v\hfill & \hfill w\hfill \end{array}\right)=w[x_1{y}_1(1-x_i{y}_i)-v],\hfill \\ \hfill \det {\mathcal{G}}_{0,2}^{\left(2\right)}=& \det \left(\begin{array}{cc}\hfill w\hfill & \hfill w\hfill \\ \hfill w\hfill & \hfill w\hfill \end{array}\right)=0.\hfill \end{array}$$ (B3)

Carrying out the summation over possible combinations

$$\begin{array}{cc}\hfill \sum \det {\mathcal{G}}_{2,0}^{\left(2\right)}=& \sum _{i\le j}{x}_i{x}_j{y}_i{y}_j(x_i{y}_j+x_j{y}_i-x_i{y}_i-x_j{y}_j)=\frac{1}{2}\sum _{i=1}^{N_E}\sum _{j=1}^{N_E}{x}_i{x}_j{y}_i{y}_j(x_i{y}_j+x_j{y}_i-x_i{y}_i-x_j{y}_j)\hfill \\ \hfill =& \mathcal{R}-\mathcal{Z}\mathcal{T},\hfill \\ \hfill \sum \det {\mathcal{G}}_{1,1}^{\left(2\right)}=& N_{I}w\sum _{i=1}^{N_E}[x_i{y}_i(1-x_i{y}_i)-v]=N_{I}w[\mathcal{T}-\mathcal{Z}-v{N}_E].\hfill \end{array}$$ (B4)

Putting these together we get

$$a_2=\mathcal{R}-\mathcal{Z}\mathcal{T}+N_{I}w[\mathcal{T}-\mathcal{Z}-v{N}_E].$$ (B5)

The coefficient a₃

The fourth coefficient a₃ is the sum of all three row diagonal minors. Now there are four types of minors, only one of which is nonzero:

$$\begin{array}{cc}\hfill \det {\mathcal{G}}_{3,0}^{\left(2\right)}=& 0\left(\text{shown above}\right),\hfill \\ \hfill \det {\mathcal{G}}_{2,1}^{\left(2\right)}=& \det \left(\begin{array}{ccc}\hfill x_i{y}_i(1-x_i{y}_i)\hfill & \hfill x_i{y}_j(1-x_i{y}_j)\hfill & \hfill w\hfill \\ \hfill x_j{y}_i(1-x_j{y}_i)\hfill & \hfill x_j{y}_j(1-x_j{y}_j)\hfill & \hfill w\hfill \\ \hfill v\hfill & \hfill v\hfill & \hfill w\hfill \end{array}\right)\hfill \\ \hfill =& w\det {\mathcal{G}}_{2,0}^{\left(2\right)}+vw[x_j{y}_i(1-x_j{y}_i)+x_i{y}_j(1-x_i{y}_j)-x_i{y}_i(1-x_i{y}_i)-x_j{y}_j(1-x_j{y}_j)],\hfill \\ \hfill \det {\mathcal{G}}_{1,2}^{\left(2\right)}=& \det {\mathcal{G}}_{0,3}^{\left(2\right)}=0\left(\text{repeated columns of inhibitory neurons}\right).\hfill \end{array}$$ (B6)

Carrying out the sum,

$$\begin{array}{cc}\hfill a_3=& \sum \det {\mathcal{G}}_{2,1}^{\left(2\right)}\hfill \\ \hfill =& w{N}_I[\mathcal{R}-ZT]+vw{N}_I\frac{1}{2}\sum _{i=1}^{N_E}\sum _{j=1}^{N_E}[x_j{y}_i(1-x_j{y}_i)+x_i{y}_j(1-x_i{y}_j)-x_i{y}_i(1-x_i{y}_i)-x_j{y}_j(1-x_j{y}_j)]\hfill \\ \hfill =& w{N}_I\{\mathcal{R}-\mathcal{ZT}+v[{\mathcal{S}}^2-{\mathcal{U}}^2-N_E(\mathcal{T}-\mathcal{Z})]\}.\hfill \end{array}$$ (B7)

The coefficient a₄

The last nonzero coefficient is a₄, the sum of all four row diagonal minors. Here there are five types, only one of which is nonzero:

$$\begin{array}{cc}\hfill \det {\mathcal{G}}_{4,0}^{\left(2\right)}=& 0(\text{because det}{\mathcal{G}}_{3,0}^{\left(2\right)}=0),\hfill \\ \hfill \det {\mathcal{G}}_{3,1}^{\left(2\right)}=& \det \left(\begin{array}{cccc}\hfill x_i{y}_i(1-x_i{y}_i)\hfill & \hfill x_i{y}_j(1-x_i{y}_j)\hfill & \hfill x_i{y}_k(1-x_i{y}_k)\hfill & \hfill w\hfill \\ \hfill x_j{y}_i(1-x_j{y}_i)\hfill & \hfill x_j{y}_j(1-x_j{y}_j)\hfill & \hfill x_j{y}_k(1-x_j{y}_k)\hfill & \hfill w\hfill \\ \hfill x_k{y}_i(1-x_k{y}_i)\hfill & \hfill x_k{y}_j(1-x_k{y}_j)\hfill & \hfill x_k{y}_k(1-x_k{y}_k)\hfill & \hfill w\hfill \\ \hfill v\hfill & \hfill v\hfill & \hfill v\hfill & \hfill w\hfill \end{array}\right)\hfill \\ \hfill =& vw(x_i-x_j)(x_i-x_k)(x_j-x_k)(y_i-y_j)(y_i-y_k)(y_j-y_k),\hfill \\ \hfill \det {\mathcal{G}}_{2,2}^{\left(2\right)}=& \det {\mathcal{G}}_{1,3}^{\left(2\right)}=\det {\mathcal{G}}_{0,4}^{\left(2\right)}=0\left(\text{repeated columns of inhibitory neurons}\right).\hfill \end{array}$$ (B8)

Carrying out the sum we get

$$\begin{array}{cc}\hfill a_4=& \frac{1}{6}vw{N}_I\sum _{i=1}^{N_E}\sum _{j=1}^{N_E}\sum _{k=1}^{N_E}(x_i^2{x}_j-x_i^2{x}_k+x_j^2{x}_k-x_j^2{x}_i+x_k^2{x}_i-x_k^2{x}_j)(y_i^2{y}_j-y_i^2{y}_k+y_j^2{y}_k-y_j^2{y}_i+y_k^2{y}_i-y_k^2{y}_j)\hfill \\ \hfill =& N_{I}vw[N_E(\mathcal{ZT}-\mathcal{R})-{\mathcal{ZS}}^2-{\mathcal{U}}^2\mathcal{T}+\mathcal{SUV}].\hfill \end{array}$$ (B9)

The coefficients a_k with k > 4

Now we show that a_k = 0 for k > 4. A diagonal minor representing a subnetwork of five neurons or more can have N_I = 0, N_I = 1, or N_I ≥ 2. If N_I ≥ 2 the diagonal minor is zero because of repeated columns. If N_I = 1, then N_E ≥ 4. Here, the determinant is a weighted sum of k = N_E −1 = N −2 row diagonal minors of the form $\det {\mathcal{G}}_{N_E-1,0}^{\left(2\right)}$ which is zero for N_E ≥ 4. Last, if N_I = 0 then again we have a sum of terms of the form ${\mathcal{G}}_{N_E,0}^{\left(2\right)}$ which are zero as discussed above.

2. Calculation of spectrum of Q

Using a similar approach we will compute the characteristic polynomial of Q and show that generically rank {Q} = 3. Using the sums over diagonal minors of Q_NE+NI,

$${\mathcal{B}}_{N_E,N_I}\left(\lambda \right)=\sum _{k=0}^N{(-1)}^k{b}_k{\lambda }^{N-k},$$ (B10)

where $b_k=\sum \det {\mathcal{Q}}_k$ for k ≥ 1 and where ${\mathcal{Q}}_k$ is a k × k matrix with elements taken from the intersection of k rows and columns of Q. Again, ${\mathcal{Q}}_{k_E,k_I}$ will indicate that k_E and k_I rows and columns correspond to excitatory and inhibitory neurons, respectively.

The coefficient b₀

By definition we have b₀ = 1.

The coefficient b₁

The second term is the trace

$$\begin{array}{cc}\hfill b_1=& \mathrm{Tr}\left\{Q_{N_E+N_I}\right\}=\sum _{i=1}^{N_E}{x}_i{y}_i-N_I{W}_0{p}_0.\hfill \\ \hfill =& \mathcal{T}-N_I{W}_0{p}_0\hfill \end{array}$$ (B11)

The coefficient b₂

The third coefficient is the sum over two row diagonal minors:

$$\begin{array}{cc}\hfill \det {\mathcal{Q}}_{2,0}=& \det \left(\begin{array}{cc}\hfill x_i{y}_i\hfill & \hfill x_i{y}_j\hfill \\ \hfill x_j{y}_i\hfill & \hfill x_j{y}_j\hfill \end{array}\right)=0,\hfill \\ \hfill \det {\mathcal{Q}}_{1,1}=& \det \left(\begin{array}{cc}\hfill x_i{y}_i\hfill & \hfill -p_0{W}_0\hfill \\ \hfill p_0\hfill & \hfill -p_0{W}_0\hfill \end{array}\right)=p_0{W}_0(p_0-x_i{y}_i),\hfill \\ \hfill \det {\mathcal{Q}}_{0,2}=& \det \left(\begin{array}{cc}\hfill -p_0{W}_0\hfill & \hfill -p_0{W}_0\hfill \\ \hfill -p_0{W}_0\hfill & \hfill -p_0{W}_0\hfill \end{array}\right)=0;\hfill \end{array}$$ (B12)

carrying out the summation, we get

$$\begin{array}{cc}\hfill b_2=& p_0{W}_0{N}_I\sum _{i=1}^{N_E}(p_0-x_i{y}_i)\hfill \\ \hfill =& p_0{W}_0{N}_I(N_E{p}_0-\mathcal{T}).\hfill \end{array}$$ (B13)

The coefficient b₃

The fourth and last nonzero coefficient is the sum over three row diagonal minors

$$\begin{array}{cc}\hfill \det {\mathcal{Q}}_{3,0}=& 0,\hfill \\ \hfill \det {\mathcal{Q}}_{2,1}=& \left(\begin{array}{ccc}\hfill x_i{y}_i\hfill & \hfill x_i{y}_j\hfill & \hfill -p_0{W}_0\hfill \\ \hfill x_j{y}_i\hfill & \hfill x_j{y}_j\hfill & \hfill -p_0{W}_0\hfill \\ \hfill p_0\hfill & \hfill p_0\hfill & \hfill -p_0{W}_0\hfill \end{array}\right)\hfill \\ \hfill =& p_0^2{W}_0(x_i{y}_i+x_j{y}_j-x_i{y}_j-x_j{y}_i),\hfill \\ \hfill \det {\mathcal{Q}}_{1,2}=& \det Q_{0,3}=0\left(\text{repeated columns}\right).\hfill \end{array}$$

Carrying out the sum,

$$\begin{array}{cc}\hfill b_3=& N_I{p}_0^2{W}_0\sum _{i<j}(x_i{y}_i+x_j{y}_j-x_i{y}_j-x_j{y}_i)\hfill \\ \hfill =& \frac{1}{2}{N}_I{p}_0^2{W}_0\sum _{i=1}^{N_E}\sum _{j=1}^{N_E}(x_i{y}_i+x_j{y}_j-x_i{y}_j-x_j{y}_i)\hfill \\ \hfill =& N_I{p}_0^2{W}_0(N_E\mathcal{T}-{\mathcal{S}}^2).\hfill \end{array}$$ (B15)

The coefficients b_k with k > 3

Now we show that b_k = 0 for k > 3. A minor representing a subnetwork of four neurons or more can have N_I = 0, N_I = 1, or N_I ≥ 2. If N_I ≥ 2 the minor is zero because of repeated columns. If N_I = 1, then N_E ≥ 3. Here, the determinant is a sum of k = N_E − 1 N −2 row diagonal minors of the form $\det {\mathcal{Q}}_{N_E-1,0}$ which is zero for _E ≥ 3. Lastly, if N_I = 0 then again we have a sum of terms of the form $\det {\mathcal{Q}}_{N_E,0}$ which is zero as discussed above.

Appendix C: Networks with Γ degree distributions

We choose a specific parametrization where the marginals of the joint in- and out-degree distribution are Γ with form parameter κ, scale parameter θ and have average correlation ρ. Owing to the properties of sums of random variables that follow a Γ distribution, we can write the random in- and out-degree sequences as

$$\begin{array}{cc}\hfill k_i^{\mathrm{in}}=k_{1i}+k_{2i},\hfill & \hfill k_{1i}\sim \Gamma (\kappa \rho ,\theta ),\hfill \\ \hfill k_i^{\mathrm{out}}=k_{1i}+k_{3i},\hfill & \hfill k_{2i},k_{3i}\sim \Gamma (\kappa (1-\rho ),\theta ),\hfill \end{array}$$ (C1)

where 1 ≤ i ≤ N_E. In this Appendix 〈·〉 will denote averages over the joint in- and out-degree distribution.

The moments of the distribution imply that, for this parametrization,

$$\langle {\left(k_i^{\mathrm{in}}\right)}^n\rangle =\langle {\left(k_i^{\mathrm{out}}\right)}^n\rangle ={\theta }^n\prod _{m=0}^{n-1}(\kappa +m).$$ (C2)

for all 1 ≤ i ≤ N_E. Here, since elements of $k_i^{\mathrm{in}}$ and $k_i^{\mathrm{out}}$ are (separately) independent and identically distributed we will suppress the subscript i and superscripts in, out when possible, and let 〈k²〉 = 〈k^in⊤kⁱⁿ〉, kⁱⁿk^out = k^in⊤k^out, etc.

One can verify that indeed the average correlation between the in- and out-degree sequences is

$$\frac{\langle k^{\mathrm{in}}{k}^{\mathrm{out}}\rangle -\langle k^{\mathrm{in}}\rangle \langle k^{\mathrm{out}}\rangle }{\sqrt{\langle k^{\mathrm{in}2}-{\langle k^{\mathrm{in}}\rangle }^2\rangle }\sqrt{\langle k^{\mathrm{out}2}-{\langle k^{\mathrm{out}}\rangle }^2\rangle }}=\rho .$$ (C3)

Using this parametrization we compute the averages $\langle \mathcal{T}\rangle$, $\langle \mathcal{S}\rangle$, etc., and express them in terms of ρ, θ, κ, and N_E.

The functional $\mathcal{T}$

$$\begin{array}{cc}\hfill \mathcal{T}=& \sum _{i=1}^{N_E}{x}_i{y}_i=\frac{1}{N_E\kappa \theta }\sum _{i=1}^{N_E}{k}_i^{\mathrm{in}}{k}_i^{\mathrm{out}},\hfill \\ \hfill \langle \mathcal{T}\rangle =& \frac{1}{\kappa \theta }\langle k^{\mathrm{in}}{k}^{\mathrm{out}}\rangle =\theta (\rho +\kappa ).\hfill \end{array}$$ (C4)

The functional $\mathcal{S}$

$$\begin{array}{cc}\hfill \mathcal{S}=& \sum _{i=1}^{N_E}{x}_i=\frac{1}{\sqrt{N_E\kappa \theta }}\sum _{i=1}^{N_E}{k}_i^{\mathrm{in}},\hfill \\ \hfill \langle \mathcal{S}\rangle =& \sqrt{\frac{N_E}{\kappa \theta }}\langle k\rangle =\sqrt{N_E\kappa \theta }.\hfill \end{array}$$ (C5)

The functional $\mathcal{U}$

$$\begin{array}{cc}\hfill \mathcal{U}=& \sum _{i=1}^{N_E}{x}_i^2=\frac{1}{N_E\kappa \theta }\sum _{i=1}^{N_E}{k}_i^{\mathrm{in}2},\hfill \\ \hfill \langle \mathcal{U}\rangle =& \frac{1}{\kappa \theta }\langle k^2\rangle =\theta (\kappa +1).\hfill \end{array}$$ (C6)

The functional $\mathcal{Z}$

To compute $\langle \mathcal{Z}\rangle$ we first derive an expression for kⁱⁿ²k^out2. Using the independence of k₁, k₂, k₃,

$$\begin{array}{cc}\hfill \langle k^{\mathrm{in}2}{k}^{\mathrm{out}2}\rangle =& \langle (k_1^2+2k_1{k}_2+k_2^2)(k_1^2+2k_1{k}_3+k_3^2)\rangle \hfill \\ \hfill =& {\theta }^4\left\{6\kappa \rho +{\kappa }^2[1+8\rho +2{\rho }^2]+2{\kappa }^3[1+2\rho ]+{\kappa }^4\right\}.\hfill \end{array}$$ (C7)

Now we can write

$$\begin{array}{cc}\hfill \mathcal{Z}=& \sum _{i=1}^{N_E}{x}_i^2{y}_i^2=\frac{1}{N_E^2{\kappa }^2{\theta }^2}\sum _{i=1}^{N_E}{k}_i^{\mathrm{in}2}{k}_i^{\mathrm{out}2},\hfill \\ \hfill \langle \mathcal{Z}\rangle =& \frac{1}{N_E{\kappa }^2{\theta }^2}\langle k^{\mathrm{in}2}{k}^{\mathrm{out}2}\rangle \hfill \\ \hfill =& \frac{{\theta }^2}{N_E}\left\{6\frac{\rho }{\kappa }+[1+8\rho +2{\rho }^2]+2\kappa [1+2\rho ]+{\kappa }^2\right\}.\hfill \end{array}$$ (C8)

The functional $\mathcal{R}$

To compute $\langle \mathcal{R}\rangle$ (and $\langle \mathcal{V}\rangle$) we first derive an expression for 〈kⁱⁿk^out2〉. Using the independence of k₁; k₂; k₃,

$$\begin{array}{cc}\hfill \langle k^{\mathrm{in}2}{k}^{\mathrm{out}}\rangle =& \langle (k_1^2+2k_1{k}_2+k_2^2)(k_1+k_3)\rangle \hfill \\ \hfill =& {\theta }^3\kappa (\kappa +1)(\kappa +2\rho ),\hfill \\ \hfill \langle k^{\mathrm{in}}{k}^{\mathrm{out}2}\rangle =& \langle (k_1+k_2)(k_1^2+2k_1{k}_3+k_3^2)\rangle \hfill \\ \hfill =& {\theta }^3\kappa (\kappa +1)(\kappa +2\rho ).\hfill \end{array}$$ (C9)

Now we can write

$$\begin{array}{cc}\hfill \mathcal{R}=& \frac{1}{N_E^3{\kappa }^3{\theta }^3}\left(\sum _{i=1}^{N_E}{k}_i^{\mathrm{in}}{k}_i^{\mathrm{out}2}\right)\left(\sum _{i=1}^{N_E}{k}_i^{\mathrm{in}2}{k}_i^{\mathrm{out}}\right),\hfill \\ \hfill \langle \mathcal{R}\rangle =& \frac{1}{N_E{\kappa }^3{\theta }^3}\langle k^{\mathrm{in}}{k}^{\mathrm{out}2}\rangle \langle k^{\mathrm{in}2}{k}^{\mathrm{out}}\rangle \hfill \\ \hfill =& \frac{{\theta }^3{(\kappa +1)}^2{(\kappa +2\rho )}^2}{N_E\kappa }.\hfill \end{array}$$ (C10)

The functional $\mathcal{V}$

$$\begin{array}{cc}\hfill \mathcal{V}=& \frac{1}{N_E^3{\kappa }^3{\theta }^3}\sum _{i=1}^{N_E}(k_i^{\mathrm{in}}{k}_i^{\mathrm{out}2}+k_i^{\mathrm{in}2}{k}_i^{\mathrm{out}}),\hfill \\ \hfill \langle \mathcal{V}\rangle =& \frac{1}{N_E^2{\kappa }^3{\theta }^3}(\langle k^{\mathrm{in}}{k}^{\mathrm{out}2}\rangle +\langle k^{\mathrm{in}2}{k}^{\mathrm{out}}\rangle )\hfill \\ \hfill =& \frac{2(\kappa +1)(\kappa +2\rho )}{N_E^2{\kappa }^2}.\hfill \end{array}$$ (C11)