Light-induced self-assembly of active rectification devices

Self-propelled particles that swim in response to light can self-assemble microfluidic rectification devices under nonuniform illumination.

Abstract

Self-propelled colloidal objects, such as motile bacteria or synthetic microswimmers, have microscopically irreversible individual dynamics—a feature they share with all living systems. The incoherent behavior of individual swimmers can be harnessed (or “rectified”) by microfluidic devices that create systematic motions that are impossible in equilibrium. We present a computational proof-of-concept study showing that such active rectification devices could be created directly from an unstructured “primordial soup” of light-controlled motile particles, solely by using spatially modulated illumination to control their local propulsion speed. Alongside both microscopic irreversibility and speed modulation, our mechanism requires spatial symmetry breaking, such as a chevron light pattern, and strong interactions between particles, such as volume exclusion, which cause a collisional slowdown at high density. Together, we show how these four factors create a novel, many-body rectification mechanism. Our work suggests that standard spatial light modulator technology might allow the programmable, light-induced self-assembly of active rectification devices from an unstructured particle bath.

INTRODUCTION

The past decade has seen a surge of interest in so-called “active” materials, whose constituent building blocks violate time-reversal symmetry on the microscopic scale by continuously converting fuel into motion (1, 2). These building blocks can be natural, such as swimming bacteria or algae (3), or synthetic, such as self-phoretic Janus swimmers (4, 5). Apart from deepening our understanding of nonequilibrium systems, and in particular about how and when concepts from equilibrium thermodynamics can (and cannot) be applied to such systems (6, 7), a strong motivation behind active matter research is that activity can be harnessed to create devices and induce phenomena that would be impossible in thermodynamic equilibrium. Examples include the flow of rotor particles around a circuit (8), steady rotation of a gear wheel in a bacterial bath (9, 10), and pumping of bacteria between chambers by “funnel gates” (11).

Here, we show how irreversible motion in a particular class of active matter (light-controlled self-propelled particles) can be used to self-assemble active “rectification devices” and circuits directly from an unstructured active-particle suspension, using only spatially controlled (but possibly incoherent) lighting. Such light-controlled motility has been experimentally demonstrated several times, both in synthetic systems (12–15) and in natural ones (strains of Escherichia coli bacteria whose motility requires illumination) (16). The possibility of such light-controlled self-assembly is far from obvious because light intensity is, for our purposes, a scalar rather than a vector field: it controls the speed of particles but not their orientation; therefore, uniform illumination does not itself create directional motion. This differs fundamentally from magnetotaxis, for example, in which a uniform vector field directs motion by aligning the propulsion direction of particles (17). Because of the ubiquity of spatial light modulator (SLM) technology (18), the ability to create active rectification devices using light-induced self-assembly could have many advantages over conventional microfluidic approaches to rectification (9–11, 19–21). In particular, it would allow real-time device reprogramming rather than mechanical interchange of fixed microfluidic elements. Our proposed strategy hinges on the tendency of motile particles to accumulate in regions where they move slowly (22–24). This allows one to use light to sculpt regions of high and low particle density. So long as the particles interact repulsively, the dense regions could be used to create the type of microfluidic obstacles previously used for rectification (11). We first develop this appealingly simple avenue before turning to other approaches that prove more efficient.

The slowing-induced accumulation of motile particles is much like the crowding of pedestrians who slow down in front of a shop window on a busy street (6). Within a wide class of models (24), it is quantified as ρ(r) ∝ 1/v(r), where ρ(r) is the steady-state mean particle density at position r and v(r) is the local swim speed (22). This result has no counterpart for nonmotile (for example, Brownian) particles in thermal equilibrium, whose steady-state density is governed solely by the Boltzmann distribution and whose speed statistics remain completely independent of their position. It applies rigorously for noninteracting particles (22, 24) and generalizes as $\mathrm{\rho }(\mathit{r})\propto 1/\overline{\mathit{v}}(\mathit{r},\mathrm{\rho })$ to cases where interactions cause the average local swim speed $\overline{\mathit{v}}(\mathit{r},\mathrm{\rho })$ to differ from the local value for an isolated particle v(r), which we assume to be illumination-controlled (23, 24).

RESULTS AND DISCUSSION

Light-controlled accumulation of active particles

For our proof-of-concept simulations, we deploy a well-studied model of “active Brownian particles” in two spatial dimensions. Each particle swims with a constant speed v along a particle-fixed axis that rotates by autonomous angular diffusion; this motion is influenced by interparticle collisions (see Methods). At a fixed, spatially uniform v, collisions cause a linear dependence of the average swim speed on density: $\overline{\mathit{v}}(\mathrm{\varphi })=\mathit{v}(1-\mathrm{\varphi }/\mathrm{\varphi }*)$, with ϕ = ρπσ²/4 being the volume fraction of particles in two dimensions, σ the particle diameter, and ϕ* ≈ 0.93 a near-close-packed volume fraction that depends on interaction details (25, 26). Thus, if a spatial speed-modulation pattern v(r) is imposed in this system, one might expect ϕ(r) to obey ϕ ∝ 1/(v(1 − ϕ/ϕ*)) everywhere. This prediction is tested in Fig. 1 for a modulation pattern comprising a lattice of 16 circular traps, each with a different uniform nominal speed v_i = v₀(1 − i/16) (i = 1, …, 16) in its interior and a larger speed v₀ between the traps. (We use periodic boundary conditions.) The agreement is excellent except at the highest densities, where, with the chosen interactions (see Methods), particles show significant overlap, invalidating the assumed linear dependence of $\overline{\mathit{v}}$ on ϕ (25).

Fig. 1. Time-averaged local volume fraction ϕ(r) of interacting and noninteracting particles in a system with spatially patterned one-particle swim speed v(r), where v = v_i = v₀(1 – i/16) in the ith well and v = v₀ between the wells.

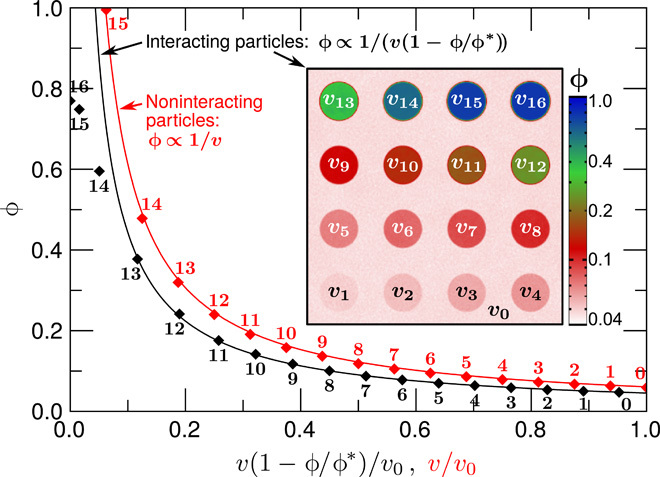
The solid lines show our predictions with a prefactor determined by least-squares fits, where we neglected the three highest density (ϕ > 0.5) data points for the interacting particles. Inset: Spatially resolved plot of ϕ(r) for the interacting particles; note the logarithmic scale on the color bar.

Self-rectification by funnel gates

The above results demonstrate that for motile particles with repulsions, just as for noninteracting ones, the density pattern ρ(r) can be rather precisely manipulated by spatial modulation of the one-particle swim speed v(r). However, Fig. 1 does not demonstrate rectification: that would require either a continuous steady-state particle current or, if the boundary conditions prevent such a current, two areas of the same v to acquire different densities. Only then can one claim to have converted incoherent particle dynamics, which by itself is responsible for the $\mathrm{\rho }\propto 1/\overline{\mathit{v}}$ behavior, into a systematic pumping effect.

A simple strategy for achieving such rectification is to create a light-guided density pattern that mimics microfluidic devices. Such devices generally operate at the one-particle level: a series of obstacles is created so that each particle is geometrically biased toward a nonzero average motion. However, when the obstacles are made of other particles, this becomes an inherently many-body mechanism that computer simulations can illuminate. In an elegant experimental demonstration of one-particle rectification, Galajda et al. (11) established that a wall of microfabricated chevron-shaped obstacles or “funnels” will rectify a suspension of swimming E. coli bacteria. Asymmetric pumping across such a wall between two chambers of the same v can yield a density difference of more than a factor of 2. The effect of additional layers of walls on the density ratio is multiplicative (11).

Inspired by these experiments, we now simulate a set of chevron-shaped “dark” regions, in which the nominal swim speed v(r) is set to zero. As can be seen in Fig. 2 and movie S1, this pattern rapidly guides the self-assembly of a set of funnel-like obstructions, which in turn cause rectification. The mechanism is almost the same as in the studies by Galajda et al. (11) and Wan et al. (19): The trajectories of motile particles tend to trace the funnel wall, making the probabilities of passing through the funnel from either side unequal. However, because our funnels assemble reversibly from the motile particles themselves, such rectification requires not only time-irreversible trajectories (wall tracing) and broken reflection symmetry of the modulation pattern (19, 27, 28) but also repulsive interparticle interactions (see Fig. 2). Unlike conventional microfabricated structures, ours could in principle be dismantled and reassembled into a completely different structure, simply by reprogramming the light intensity pattern to give a different v(r). Crucially, the mechanism requires no external or interparticle forces that align the swimming directions of the particles.

Fig. 2. Rectification through self-assembled funnels.

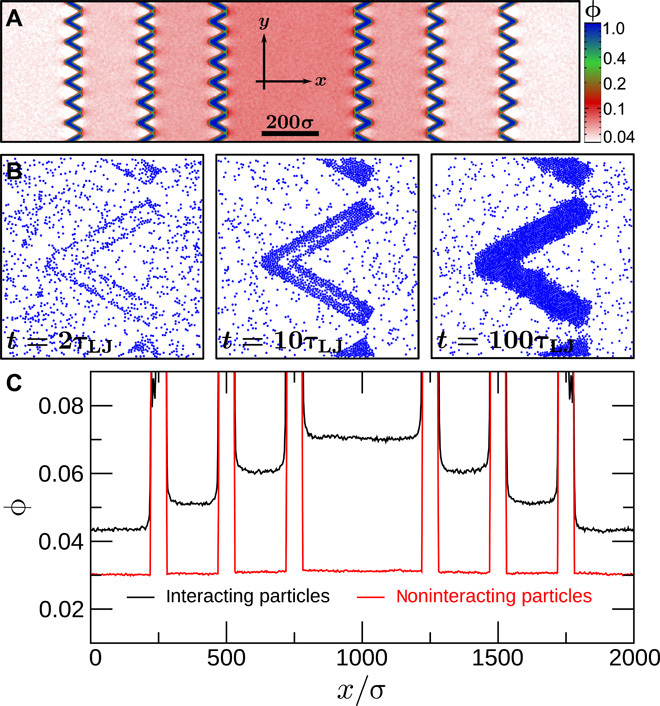
(A) Time-averaged particle packing fraction ϕ(r) at steady state in a system of self-assembled funnels. Note the logarithmic scale on the color bar. (B) Magnification of one of the funnels showing the self-assembly process at three different times starting from a homogeneous particle distribution; τ_LJ is the Lennard-Jones time (see Methods). (C) Black curve: The packing fraction ϕ from (A) but now as a function of x and averaged over y; the pumping effect (rectification) is obvious. Red curve: For noninteracting particles, rectification is not possible.

As a first proof of principle, these are striking results. However, the efficiency of our device (measured as the ratio between the density in the inner compartment and the density in the outer compartment) is modest: the density ratio induced by three pairs of funnel walls is about 1.6 (see Fig. 2C), compared to about 2.8 seen in E. coli experiments using a single microfabricated funnel wall (11) and in simulations of rod-shaped particles in a similar geometry (19). As shown in the Supplementary Materials, this is largely because our self-assembled many-particle funnels cannot prevent particles from “leaking” backward against the pumping flux, limiting their pumping efficiency.

Self-rectification by one-dimensional speed profiles

A contrasting single-particle rectification strategy deploys microfabricated wedge-shaped solid barriers with one steep side and one shallow side. Such barriers have been shown experimentally (20, 21) to make swimming bacteria preferentially transport passive tracer colloids from the shallow side and deposit them on the steep side of the barrier, leading to a significant steady-state accumulation. Loosely inspired by this, we abandoned the chevron design and imposed a simpler, one-dimensional sawtooth-shaped speed profile v(x) shown in Fig. 3. This leads to the self-assembly of an asymmetric barrier with a distinctive density profile ρ(x).

Fig. 3. Steady-state packing fraction ϕ(x) (solid curves) in a system with a modulated speed v(x) composed of two opposing sawtooth profiles (dashed curves) obtained from particle-resolved simulations and our continuum model.

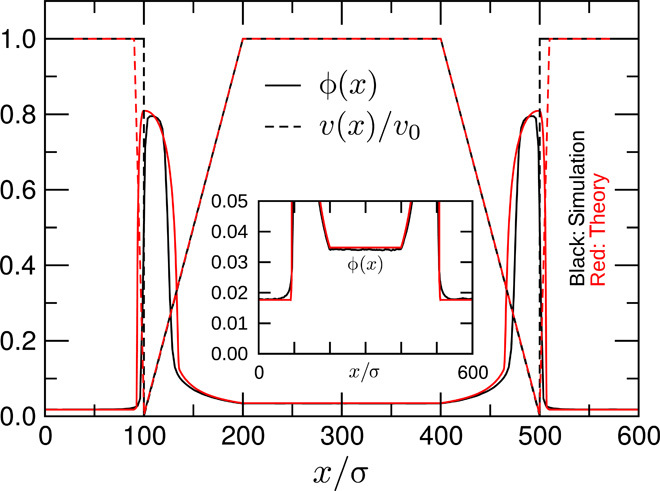
For numerical reasons, the discontinuities of v(x) are smeared out over 10σ in the continuum calculations. The inset shows ϕ(x) with a magnified y scale, clearly demonstrating the rectification.

Remarkably, this extremely simple device shows a density ratio of almost 2 and thus a strong rectification (see inset to Fig. 3). Note that particles must pass through, but not over or around, the barrier so that the “leakage” encountered earlier is being exploited here. To study this rectification, we have extended a continuum model, involving local density and orientation fields coupled in a standard manner (29), to the case where the swim speed depends on both position and density (see Methods). The rectification is found to arise from a polarization (that is, alignment of particle orientations) on the dense (steep) side of the barrier; here, the average swimming direction of the particles is oriented into the barrier (see the Supplementary Materials for details). This polarization is a straightforward consequence of the irreversible particle motion, which makes particles that swim toward a solid object such as a wall become “trapped” there until their swimming direction has rotationally diffused enough to let them escape, creating an average particle orientation pointing into the object. The polarization in turn creates a mechanical pressure that drives a particle flux from the steep side of the barrier toward the shallow side. In more mathematical terms, rectification rests on the presence of a density gradient–driven pumping effect that is nonzero only in a small region close to the barrier. Flux balance then requires a change in the uniform steady-state particle densities in the bulk regions far to the left and to the right of the barrier, where density gradients, and thus the pumping effect, approach zero. In contrast to equilibrium systems, here local gradient effects cause rectification across an interface between bulk regions, rather than merely shifting the interfacial tension (30).

Self-assembled active circuits

By using aligned (instead of opposing) barriers and applying suitable boundary conditions, either of the above devices can be reconfigured to create an “active circuit,” where motile particles flow endlessly around a closed loop at steady state. In the study by Bricard et al. (8), macroscopic circulation was achieved with field-driven autorotors with hydrodynamic alignment interactions. In Fig. 4, we give a computational proof of principle for a simpler design that uses the speed modulation from Fig. 3 but now with two aligned sawteeth. In this example, colloids are confined to an annulus by a surrounding dark region; thus, both the “circuit” itself and the rectifying elements arise solely by light-guided self-assembly.

Fig. 4. Self-assembled active circuit.

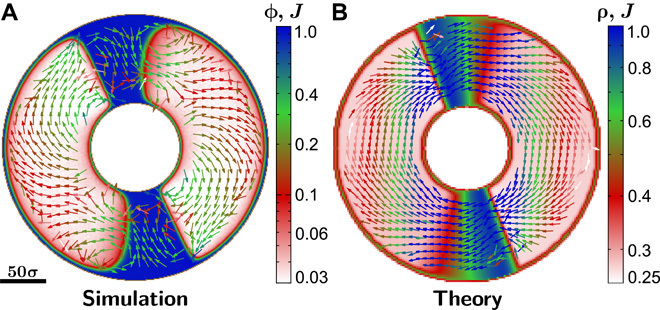
(A) Particle-resolved simulations of an annular circuit self-assembled through a prescribed speed profile v(r) with two similar sawteeth along the annulus and a very low speed outside of the annulus. The resulting dense particle packing outside of the annulus (not shown for clarity) confines the motile particles to the circuit. The color map shows the time-averaged steady-state local packing fraction ϕ(r), and vectors denote the rescaled local particle current J(r), with their colors indicating the absolute current density J(r) = |J(r)|. The logarithmic color bar applies both to the density plot and to the vector field plot. (B) Corresponding plot of the rescaled particle density ρ(r) ∝ ϕ(r) and particle current J(r) obtained from our continuum model.

CONCLUSION

In conclusion, we have given proof-of-principle evidence, using computer simulations and theoretical considerations, that self-assembled active rectification devices for motile particles can be created solely through spatial modulation of the local propulsion speed v(r). This space-dependent propulsion speed can in turn be realized by a space-dependent illumination (12, 13, 15, 16) and hence rendered programmable through the use of SLMs. A key element of the light-guided assembly strategy presented here is that the illumination supplies the particles only with scalar information, namely, the instruction to swim at a certain speed. In some experimental systems, the light also elegantly supplies the energy source for swimming (13), but this is not always the case (12) and is not an essential ingredient in our proposed strategy. Crucially, in our mechanism, the optical field does not exert directional forces directly on the particles. This differs fundamentally from, and requires much lower light intensities than, the manipulation of particles by optical tweezers; as an example, the light-propelled particles studied by Buttinoni et al. (13) require light intensities of ≤5 μW/μm², compared to intensities of 10² to 10⁴ μW/μm² typically used in optical tweezers (31, 32). Our mechanism can be easily applied to large-scale systems containing many particles, circumventing several disadvantages of traditional micromanipulation techniques (31), such as significant heating-up of the system and the need for complicated optical equipment. Indeed, although the use of SLMs would certainly be appealing, there is no requirement that the light field even be coherent.

Our work points toward a new technological opportunity in which light-guided self-assembly is not only used to make crystals and other aggregates (12, 13, 15) but also used to create programmable, active rectification devices from an initially structureless “primordial soup” of self-propelled particles. The capacity to do this stems from an interplay between microscopically irreversible particle motion, spatially asymmetric light modulation, and interparticle repulsions. These findings may also be relevant to controlling mass transport in biological systems, steering pattern formation in future applications of active particles in materials science, and deploying active particles in colloidal self-assembly.

METHODS

Particle-based model

Our particle-resolved computational studies use a simple model of swimming microorganisms (like motile bacteria and protozoa) and artificial microswimmers, known as active Brownian particles. Such particles exhibit persistent propulsion in a particle-fixed direction, which rotates through thermal rotational diffusion. This model has been shown to capture many essential features of active matter systems such as bacterial suspensions while still allowing for both the derivation of exact results from first principles and computational studies of systems containing millions of particles. The active colloids are modeled as spherical particles with diameter σ moving on a two-dimensional substrate. They interact repulsively through a truncated and shifted Lennard-Jones potential U(r) = 4ε((σ/r)¹² − (σ/r)⁶) + ε, with the center-to-center particle distance r and an upper cutoff at r = 2^1/6σ, beyond which U = 0. ε determines the interaction strength, and β = 1/(k_BT) is the inverse thermal energy. The motion of these particles is described by the overdamped Langevin equations

$${\dot{\mathit{r}}}_{\mathit{i}}=\mathit{v}({\mathit{r}}_{\mathit{i}})\widehat{\mathit{u}}({\mathrm{\theta }}_{\mathit{i}})+\mathrm{\beta }{\mathit{D}}_{\mathrm{T}}{\mathit{F}}_{\mathit{i}}(\{{\mathit{r}}_{\mathit{j}}\})+\sqrt{2{\mathit{D}}_{\mathrm{T}}}{\mathbf{\Lambda }}_{\mathrm{T}}$$ (1)

$${\dot{\mathrm{\theta }}}_{\mathit{i}}=\sqrt{2{\mathit{D}}_{\mathrm{R}}}{\mathrm{\Lambda }}_{\mathrm{R}}$$ (2)

where r_i(t) is the position and θ_i(t) is the orientation of the ith particle at time t. In our particle-resolved Brownian dynamics simulations, we solved these Langevin equations numerically using the LAMMPS molecular dynamics package (33). Here, v(r) is the nominal swim speed of an active particle at position r, û(θ) = (cos(θ), sin(θ))^T is an orientational unit vector that denotes the propulsion direction of a particle with orientation θ, and F_i({r_j}) is the total conservative force on particle i, which results from the interactions with other particles and thus depends on U(r). D_T and D_R = 3D_T/σ² denote the constant translational and rotational diffusion coefficients of the particles, respectively, and Λ_T(t) and Λ_R(t) are zero-mean, unit-variance Gaussian white noise terms. The natural time unit in this model is the Lennard-Jones time τ_LJ = σ²/(εβD_T). Further technical details about the particle-resolved simulations can be found in the Supplementary Materials.

Continuum model

In our continuum simulations, we numerically solved the following dynamic equations for the local particle density ρ(r, t) and the local polarization P(r, t)

$$\dot{\mathrm{\rho }}=-\nabla \cdot (\overline{\mathit{v}}\mathit{W})+{\mathit{D}}_{\mathrm{T}}{\nabla }^2\mathrm{\rho }$$ (3)

$$\begin{array}{cc}\dot{\mathit{W}}=& -\frac{1}{2}\nabla (\overline{\mathit{v}}\mathrm{\rho })-{\mathrm{\gamma }}_1\mathit{W}-{\mathrm{\gamma }}_2{\mathit{W}}^2\mathit{W}+\mathit{k}{\nabla }^2\mathit{W}\\ \hfill \hfill & -{\mathit{w}}_1(\mathit{W}\cdot \nabla )\mathit{W}+{\mathit{w}}_2\nabla ({\mathit{W}}^2)\end{array}$$ (4)

Here, W = ρP is a weighted local polarization with modulus W = |W|, and γ₁, γ₂, k, w₁, and w₂ are parameters. This continuum model can be obtained by an appropriate adaptation of the derivation of a mean-field theory for a suspension of active particles in the study by Farrell et al. (29). The average swim speed $\overline{\mathit{v}}(\mathit{r},\mathrm{\rho })$ of an active particle at position r in an active suspension of density ρ is known from particle-resolved simulations (25, 26) to be linearly decreasing with ρ. Nevertheless, in our numerical calculations based on the continuum model, we used the expression $\overline{\mathit{v}}(\mathit{r},\mathrm{\rho })=\mathit{v}(\mathit{r})\text{exp}(-\mathrm{\alpha }\mathrm{\rho }(\mathit{r},\mathit{t}))$, where the parameter α determines how quickly the average local swim speed decreases with density. This choice increases numerical stability without changing the qualitative conclusions drawn here.

The parameters γ₁ and γ₂ are positive and ensure that, at steady state and in the absence of any density or velocity gradients, W vanishes everywhere. k is an effective diffusion coefficient for W and ensures continuity of this field. The term proportional to w₁ encodes self-advection, whereas the term proportional to w₂ can be viewed as an “active pressure” term because it can be written as − ∇p, with p = − w₂W². Both these terms generically arise when coarse-graining models of self-propelled particles (29, 34–36); the ensuing analysis suggests that w₂ > 0 (29). Furthermore, if one considers W as a fast variable and performs a quasi-stationary approximation (24), the w₂ term leads to a term proportional to $-{\mathit{w}}_2{\nabla }^2((\nabla (\overline{\mathit{v}}\mathrm{\rho }){)}^2)$ in Eq. (3); its form is similar to that of the leading-order active contribution in the minimal field theory for active-particle phase separation (“Active Model B”) (30). Further technical details about the numerical solution of the continuum model can be found in the Supplementary Materials.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/4/e1501850/DC1

Particle leakage through the funnels

Rectification mechanism

Particle-resolved simulations

Numerical solution of the continuum model

Movie S1. Movie showing the self-assembly process of a single chevron-shaped obstacle.

Fig. S1. Steady-state density profiles for funnel-wall systems with the funnel particles either mobile or fixed.

Fig. S2. Local polarization around a sawtooth-shaped speed profile, obtained from particle-resolved simulations and the continuum model.

Fig. S3. Polarization profiles obtained from the continuum model with w₂ = 0 and w₂ > 0.

Fig. S4. Propulsion speed profiles used in simulations of “active circuits.”