Climate change can rapidly undermine ritual mechanisms that enhance social consensus, as shown for the Pueblo Southwest.
Keywords: Prehispanic Pueblo Southwest, socio-ecological cycles, Agriculture, Climate change
Abstract
Cycles of demographic and organizational change are well documented in Neolithic societies, but the social and ecological processes underlying them are debated. Such periodicities are implicit in the “Pecos classification,” a chronology for the pre-Hispanic U.S. Southwest introduced in Science in 1927 which is still widely used. To understand these periodicities, we analyzed 29,311 archaeological tree-ring dates from A.D. 500 to 1400 in the context of a novel high spatial resolution, annual reconstruction of the maize dry-farming niche for this same period. We argue that each of the Pecos periods initially incorporates an “exploration” phase, followed by a phase of “exploitation” of niches that are simultaneously ecological, cultural, and organizational. Exploitation phases characterized by demographic expansion and aggregation ended with climatically driven downturns in agricultural favorability, undermining important bases for social consensus. Exploration phases were times of socio-ecological niche discovery and development.
INTRODUCTION
In 1927, 2 years before compilation of the master chronology allowing tree-ring (t-r) dating of prehistoric habitations in the U.S. Southwest (Fig. 1), some 40 researchers converged on Pecos, New Mexico, to identify common patterns through time in regional prehistory (1). They discerned eight periods labeled Basketmaker (BM) I to BM III and Pueblo (P) I to P V, each characterized by a constellation of architecture, ceramics, and settlement configurations that was widespread across the northern Southwest (1). The development of tree-ring dating soon allowed archaeologists to assign calendar dates to these “cultural stages” (2–4). In the ensuing nine decades, those initial stage designations have undergone surprisingly few changes in the core Pueblo area (5). The peculiar resilience of this classification in the face of a flood of new data has stimulated several attempts to identify structural principles or forces underlying the classification.
Fig. 1. The rain-fed maize growing niche in the southwestern United States, A.D. 500–1400.
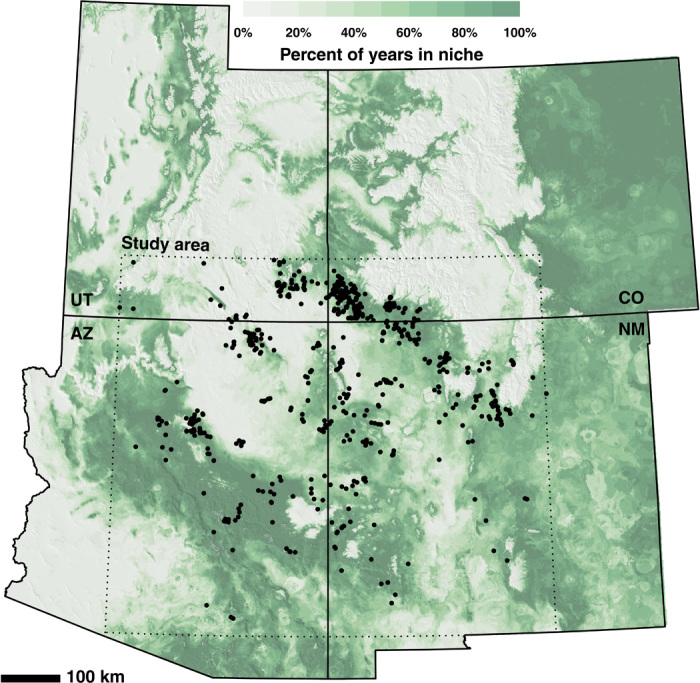
Each cell is colored by the percentage of years it is in the niche; darker green represents more years in the niche. Black dots mark the locations of tree-ring–dated sites in our database (n = 1002). Our study area is within the dotted rectangle encompassing all these sites. UT, Utah; AZ, Arizona; CO, Colorado; NM, New Mexico.
In the early 1980s, Berry (6) observed that the 6398 tree-ring cutting dates from archaeological sites then available tended to strongly cluster into four sequential peaks separated by intervals with fewer dates. He connected the periods with many cutting dates to productive periods for maize farming and the years with fewer dates to severe drought. Peaks in the histograms of counts of dates through time corresponded with the BM III, P I, P II, and P III periods of the Pecos classification. Of course, tree-ring–dated sites constitute only a small sample of the population of contemporaneously occupied habitations which is undoubtedly biased in a number of ways (7). However, patterns in the much larger sample of dates now available (Fig. 2A) remain as recognized in the 1980s, even as criteria determining the sites to be excavated have changed markedly with the explosion in cultural resource management activities (5, 8).
Fig. 2. Tree-ring date distributions and the percentage of the landscape in the rain-fed MFN where and when tree-ring dates are found, A.D. 500–1400.
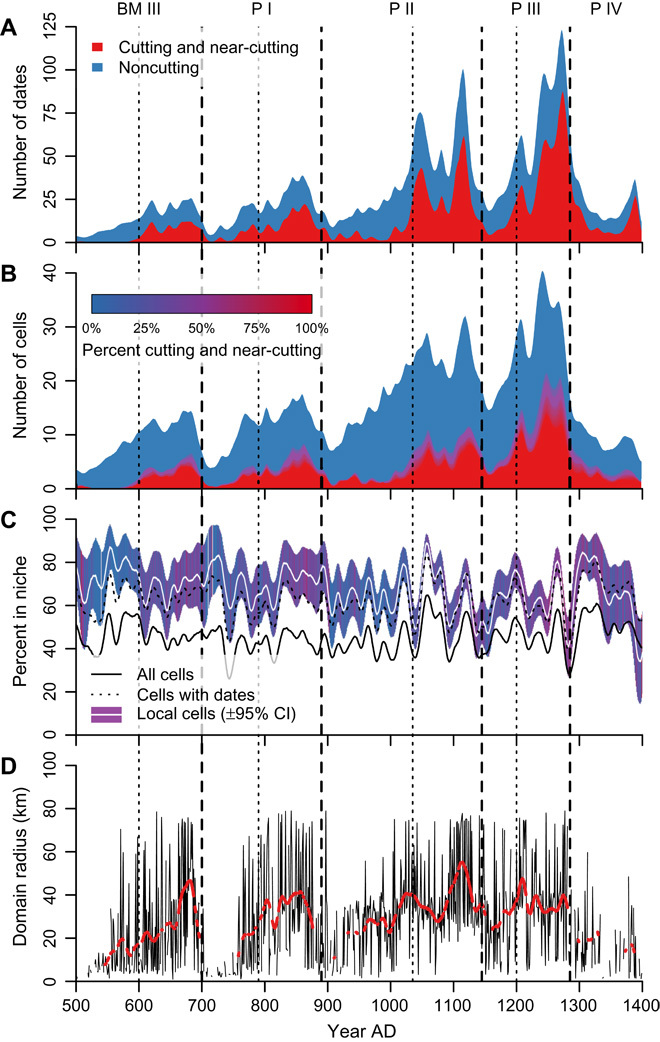
Pecos period divisions (dashed lines) and subperiod divisions (dotted lines) as rederived here are superimposed on all plots. All series are smoothed using a 21-year center-aligned Gaussian filter with a 5-year SD. (A) Stacked histogram of the number of cutting and noncutting dates through time. (B) Stacked histogram of the number of 30–arc sec cells with dates, shaded by the percentage of cutting dates in the cell. Red indicates cells with 100% cutting or near-cutting dates; blue indicates cells with 0% cutting or near-cutting dates. (C) The percentage in the niche of all 30–arc sec cells (solid black line), of all cells that ever contain tree-ring dates (dotted black line), and all local cells with 95% confidence intervals (CIs) (white line with colored bars). A local cell has a tree-ring date in the plotted year or any of the previous 3 years. The color of the confidence interval for each year indicates the unsmoothed mean of the percentages of dates in each cell that are cutting and near-cutting; the color ramp is as in (B). (D) The domain radius, or radius of maximal clustering, through time (see Materials and Methods). The black line connects true data points estimated annually; the red line is smoothed as above. Lower values indicate more dispersion between smaller clusters of occupied cells, whereas higher values indicate spatially larger clusters of occupied cells. The red line is missing in periods of no significant clustering.
We will argue that this periodic pattern reflects human organizational responses to continually changing climatic conditions that determine the spatial distribution of areas suitable for maize production. Perhaps surprisingly, peaks in the tree-ring date distribution do not correspond to extended periods of widespread agricultural opportunity, as previously proposed (6). Likewise, troughs in the distribution do not mark extended periods of aridity, uncertain production, or population retreat to high-elevation refugia (6). We propose, instead, that troughs correspond to periods of “exploration” in which dispersing populations experimented with new settlement locations and new organizational forms. Some successful trials eventually allowed farmers to settle into periods of “exploitation,” marked by intensive development of a niche that was simultaneously ecological, cultural, and organizational. In exploitation periods, newly aggregated and relatively stable populations invested in architectural infrastructure that is now visible as peaks in the tree-ring date distribution and in related aspects of the archaeological record.
Archaeological research aiming to link social and climatic variability must convincingly overcome three main obstacles. First, climate variability must be translated into variability in supply of resources critical to society. We do this by using climate proxies—tree rings sensitive to variability in precipitation and temperature—to estimate the location and extent of the maize dry-farming niche. Maize was indeed critical to all pre-Hispanic Southwestern populations considered here. From at least the first century A.D., maize constituted more than 60% of the Pueblo diet (9), increasing to 80% or more by the mid–P III period (10).
Second, precisely concomitant temporal relationships between climatic and social variability must be demonstrated. Here, using tree rings for temporal control of both the archaeological and the climate data, we develop annual estimates of when residential sites were constructed and how construction coincided with highly local maize-growing conditions.
Finally, an argument must be built linking resource variability with aspects of social variability visible in the archaeological record. We build this argument on considerable evidence from Neolithic societies in general (and from Pueblo societies in particular) that ritual practices on which agricultural success depended were critical to holding communities together. When harvests fail, ritual practices—and the leaders responsible for them—lose their ability to maintain community participation and cooperation. Critically for our model, the rapidity with which such relationships could rupture contrasts with the much slower pace of their construction.
Building the model
The tree-ring dates assembled here include 29,311 determinations between A.D. 500 and 1400, associated with 1002 unique archaeological sites in the upland Southwest. Of these, 10,489 are cutting dates (the dated tree died during the year of its outermost ring), 3661 are near-cutting dates, and 15,161 are noncutting dates (see Materials and Methods). For brevity, we group cutting and near-cutting dates as “cutting” throughout this paper, unless otherwise noted. Seventy percent of the sites (n = 706) have at least one cutting date.
For the four-state area in Fig. 1, we produced an annual reconstruction of the direct-precipitation maize farming niche (MFN) from A.D. 1 to 2000. The MFN for each year is the area in which rainfall and temperature were sufficient to grow maize successfully. Generally, following Bocinsky and Kohler (11), our retrodictions of annual water-year (previous October to current September) precipitation and May to September accumulated heat [Fahrenheit growing degree days (FGDD)] are derived from automated selection of the subset of 532 regional, climatically sensitive tree-ring chronologies that, in combination, best retrodicts these two variables for a spatially interpolated historic-period record (12). This retrodiction is done separately for each of the 2,164,084 30–arc sec cells in Arizona, Colorado, New Mexico, and Utah (691,200 within the study area, Fig. 1). These reconstructions show low cross-validated prediction error (averaging between 0 and 40 mm of precipitation and 5 and 25 GDD), and error decreases through time as more tree-ring chronologies become available (Fig. 3). Cells exceeding 30 cm of precipitation and 1800 FGDD are considered to be in the MFN (11).
Fig. 3. Average prediction error across space and through time for each climate reconstruction, A.D. 500–1400.
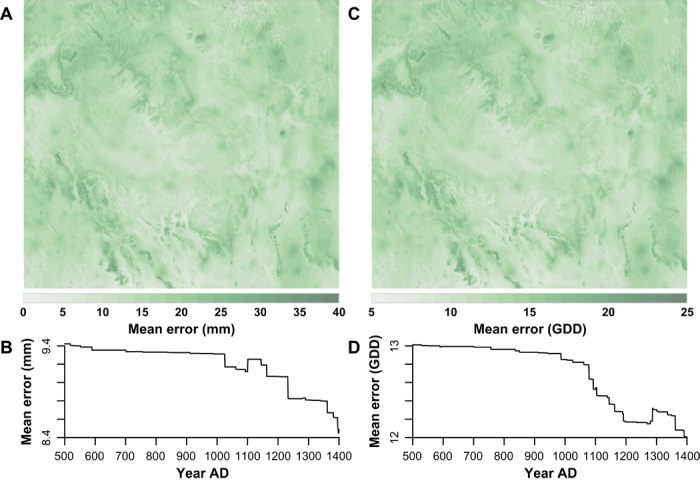
In each map, lighter (lower) values indicate a higher-quality reconstruction for that place. Declines or increases in error through time (B and D) occur when particularly important tree-ring chronologies for reconstructing each climate signal become available or unavailable, respectively. (A) Water-year precipitation, averaged through time. (B) Water-year precipitation, averaged across space. (C) Growing-season GDD, averaged through time. (D) Growing-season GDD, averaged across space.
In the remainder of this paper, we deal with the study area shown in Fig. 1—the smallest rectangle enclosing all our tree-ring–dated sites—and the period from A.D. 500 to 1400 within which tree-ring dates are numerous. For each analysis, we compare the spatiotemporal distribution of tree-ring dates to three spatiotemporal scales of the MFN reconstruction (Fig. 2C and Tables 1 and 2): “all cells” in the entire study area; “cells with dates,” only those cells that were demonstrably occupied at any point in A.D. 500–1400 (for which we have tree-ring dates); and “local cells,” consisting of only those cells that have a tree-ring date during a 4-year window ending in that year. Because all cells include large regions that were either too dry or too cold to support farmers, we view the cells with dates and local cell comparisons to be most relevant for understanding Pueblo experience. Potential sampling biases still exist because of uneven preservation and investigation; however, the size of our database and the robustness of the patterns identified by Berry (6), despite a much larger sample of dates, are reassuring.
Table 1. Summary statistics for each subperiod. The “MFN” measures are the percentage of cells in the niche as in Fig. 2C.
| Exploration | Exploitation | |||
| BM III | Years A.D. | 500–600 | Years A.D. | 600–700 |
| Cutting count, n (%) | 80 (9.3) | Cutting count, n (%) | 1012 (45.8) | |
| Noncutting count, n (%) | 782 (90.7) | Noncutting count, n (%) | 1198 (54.2) | |
| MFN—all (%) | 49.1 | MFN—all (%) | 47.2 | |
| MFN—cells with dates (%) | 65.6 | MFN—cells with dates (%) | 66.6 | |
| MFN—local (%) | 74.8 | MFN—local (%) | 68.5 | |
| P I | Years A.D. | 700–790 | Years A.D. | 790–890 |
| Cutting count, n (%) | 441 (34.9) | Cutting count, n (%) | 1402 (48.9) | |
| Noncutting count, n (%) | 822 (65.1) | Noncutting count, n (%) | 1466 (51.1) | |
| MFN—all (%) | 43.5 | MFN—all (%) | 44.7 | |
| MFN—cells with dates (%) | 63.0 | MFN—cells with dates (%) | 63.8 | |
| MFN—local (%) | 70.2 | MFN—local (%) | 71.2 | |
| P II | Years A.D. | 890–1035 | Years A.D. | 1035–1145 |
| Cutting count, n (%) | 836 (25.3) | Cutting count, n (%) | 3740 (53.7) | |
| Noncutting count, n (%) | 2470 (74.7) | Noncutting count, n (%) | 3223 (46.3) | |
| MFN—all (%) | 43.7 | MFN—all (%) | 49.8 | |
| MFN—cells with dates (%) | 61.3 | MFN—cells with dates (%) | 65.8 | |
| MFN—local (%) | 64.9 | MFN—local (%) | 64.7 | |
| P III | Years A.D. | 1145–1200 | Years A.D. | 1200–1285 |
| Cutting count, n (%) | 582 (34.7) | Cutting count, n (%) | 4523 (61.2) | |
| Noncutting count, n (%) | 1096 (65.3) | Noncutting count, n (%) | 2864 (38.8) | |
| MFN—all (%) | 46.9 | MFN—all (%) | 46.4 | |
| MFN—cells with dates (%) | 63.4 | MFN—cells with dates (%) | 61.7 | |
| MFN—local (%) | 61.7 | MFN—local (%) | 62.4 | |
| P IV | Years A.D. | 1285–1400 | — | |
| Cutting count, n (%) | 1534 (55.3) | — | ||
| Noncutting count, n (%) | 1238 (44.7) | — | ||
| MFN—all (%) | 52.1 | — | ||
| MFN—cells with dates (%) | 70.0 | — | ||
| MFN—local (%) | 66.3 | — | ||
Table 2. Summary statistics calculated from the count of years in the current and previous 3 years in which cells with tree-ring dates are in the MFN.
Calculations for cells with dates reflect the MFN status for each subperiod of all cells for which any tree-ring date between A.D. 500 and 1400 is present. Calculations for local cells are based on only those cells with tree-ring dates in a given year or any of the previous 3 years. Period boundaries are as given in the text and in Table 1. x̄ is the mean, σ is the SD, G1 is an unbiased estimator of skewness, and G2 is an unbiased estimator of kurtosis. See also Fig. 5.
| Exploration | Exploitation | |||||||
|
Cells with dates |
Local cells |
Cells with dates |
Local cells | |||||
| BM III | x̄ (σ) | 2.63 (1.39) | x̄ (σ) | 3.16 (1.11) | x̄ (σ) | 2.66 (1.40) | x̄ (σ) | 2.85 (1.37) |
| G1 | −0.64 | G1 | −1.24 | G1 | −0.69 | G1 | −0.94 | |
| G2 | −0.88 | G2 | 0.68 | G2 | −0.85 | G2 | −0.45 | |
| P I | x̄ (σ) | 2.54 (1.47) | x̄ (σ) | 2.87 (1.35) | x̄ (σ) | 2.54 (1.45) | x̄ (σ) | 2.94 (1.29) |
| G1 | −0.55 | G1 | −0.99 | G1 | −0.55 | G1 | −1.03 | |
| G2 | −1.12 | G2 | −0.30 | G2 | −1.10 | G2 | −0.12 | |
| P II | x̄ (σ) | 2.47 (1.44) | x̄ (σ) | 2.73 (1.28) | x̄ (σ) | 2.61 (1.42) | x̄ (σ) | 2.69 (1.37) |
| G1 | −0.48 | G1 | −0.71 | G1 | −0.64 | G1 | −0.70 | |
| G2 | −1.12 | G2 | −0.60 | G2 | −0.95 | G2 | −0.80 | |
| P III | x̄ (σ) | 2.53 (1.40) | x̄ (σ) | 2.60 (1.37) | x̄ (σ) | 2.50 (1.42) | x̄ (σ) | 2.65 (1.36) |
| G1 | −0.56 | G1 | −0.61 | G1 | −0.50 | G1 | −0.63 | |
| G2 | −0.98 | G2 | −0.90 | G2 | −1.09 | G2 | −0.88 | |
| P IV | x̄ (σ) | 2.79 (1.34) | x̄ (σ) | 2.81 (1.33) | — | — | ||
| G1 | −0.85 | G1 | −0.85 | — | — | |||
| G2 | −0.51 | G2 | −0.50 | — | — | |||
We now juxtapose this corpus of tree-ring dates and this novel Southwest-wide reconstruction of the annual extent of the MFN (Fig. 1 and Table 1) to answer three main questions. (i) How does the spatial distribution of tree-ring dates relate to the extent of the MFN across the nine centuries examined here? (ii) Are there differences in the size of the MFN during subperiods with relatively few dates versus those with many dates? If the MFN was generally larger during episodes when tree-ring dates were frequent, it could explain the periodicities in the date histograms noted by Berry. (iii) In a given year, were people more likely to build in a cell that is within the current MFN than in a cell that is outside it? If people are building outside the current MFN, we might infer that people were outstripping the extent of the most desirable locations near their local communities or that water-managed farming was becoming more important.
RESULTS
Our sample of tree-ring dates (Fig. 2A) exhibits the pattern with four major peaks identified by Berry (6). These peaks, driven by increased numbers of cutting and near-cutting dates shown in red, are separated by 100- to 150-year “troughs” in cutting-date frequency, during which noncutting dates increase as a proportion of all dates (Table 1). This same pattern is evident when tree-ring dates are binned into 30–arc sec (~800-m) resolution cells (Fig. 2B). Monte Carlo resampling demonstrates that the four-peak signal is robust when controlling for disparities in the number of tree-ring dates recovered from individual sites (Fig. 3; Materials and Methods).
Although the Pecos classification was originally derived from shared, widespread material characteristics of archaeological sites, its generally accepted dating coincides closely with this periodic pattern in the tree-ring dates. Nevertheless, for the analyses in this paper, we redate the Pecos periods using an explicit procedure that depends only on the frequencies of spatially binned cutting dates, necessarily ignoring some variability in period dates in various subregions [(7, 13, 14); Materials and Methods]. This method results in the period boundaries shown in Figs. 2 and 4 to 6 that are similar but not identical to traditional schemes (for example, 5). The revised Pecos periods (bounded to be within A.D. 500–1400) are as follows: BM III, A.D. 500–700; P I, A.D. 700–890; P II, A.D. 890–1145; P III, A.D. 1145–1285; and P IV, A.D. 1285–1400. Our method also identifies transitions within each Pecos period at the inflections in the cutting-date frequency distribution—we interpret predominantly concave or convex periods as periods of exploration and exploitation, respectively (see Materials and Methods). Transitions from exploration to exploitation occur at A.D. 600 (in BM III), A.D. 790 (in P I), A.D. 1035 (in P II), and A.D. 1200 (in P III). Periods of exploration tend to have higher proportions of noncutting dates.
Fig. 4. Monte Carlo resampling of tree-ring date distributions controlling sample-size disparities between sites (n = 1002), A.D. 500–1400.
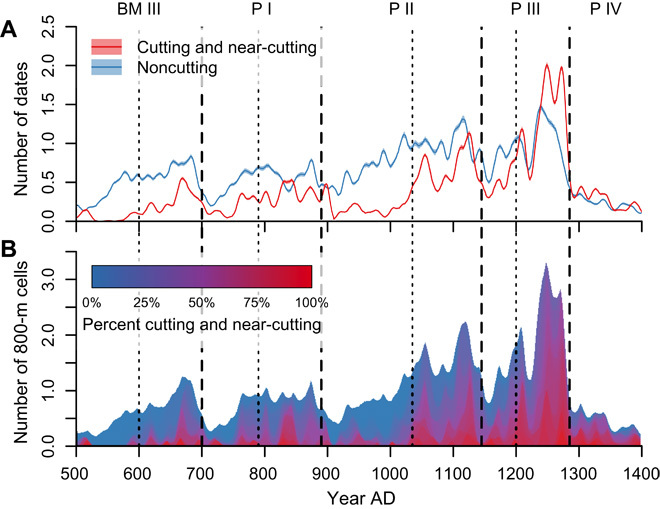
These are based on 999 replications; each replication represents a randomly selected date (cutting or noncutting) drawn from each site in the database. Pecos period divisions (dashed lines) and subperiod divisions (dotted lines) as rederived here are superimposed on all plots. All series are smoothed using a 21-year center-aligned Gaussian filter with a 5-year SD. (A) Mean number of dates through time, ±1 SD. (B) Stacked plot of the mean number of 30–arc sec cells with dates, shaded by the percentage of cutting dates in the cell. Red indicates cells with 100% cutting or near-cutting dates; blue indicates cells with 0% cutting or near-cutting dates.
Fig. 6.
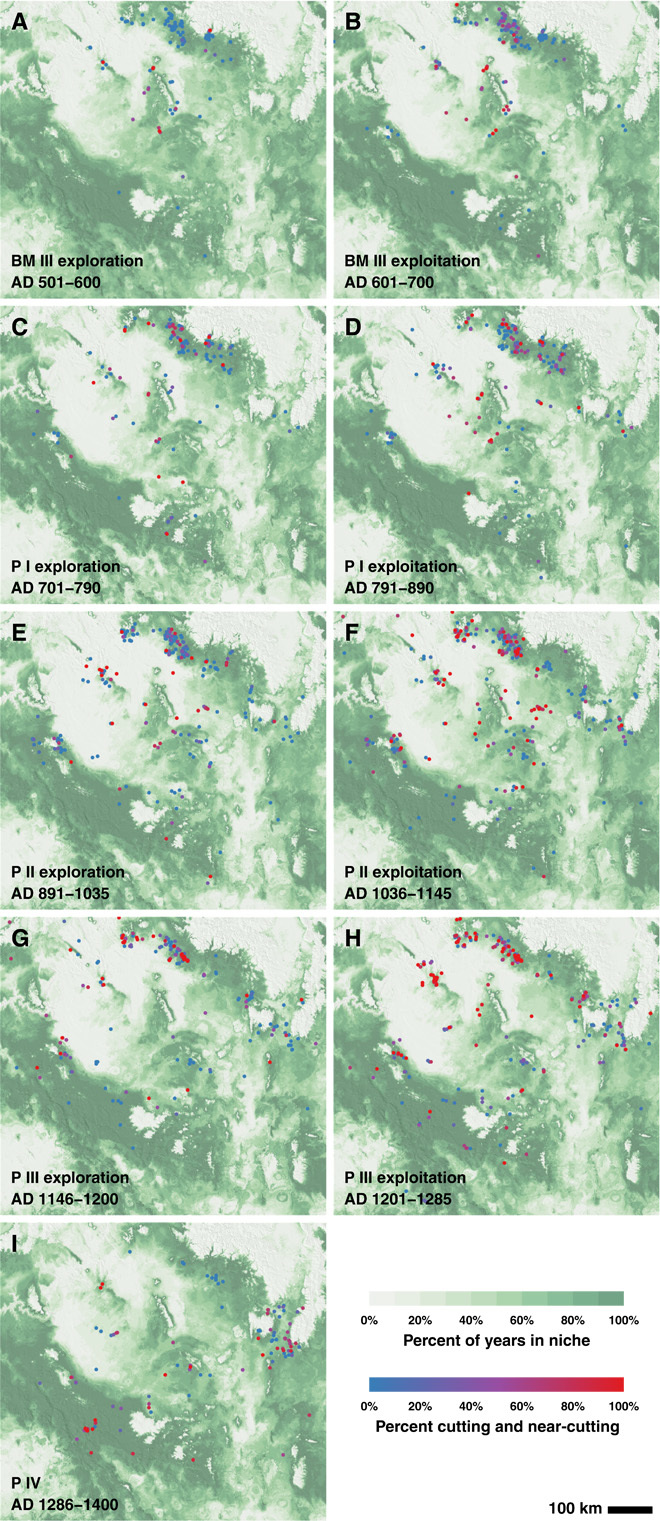
The rain-fed MFN and tree-ring dates by revised Pecos subperiod. In each panel, the green shading represents the percentage of years in that period that each 30–arc sec cell is in the MFN; darker greens reflect more years in the niche. Dots represent cells with tree-ring dates in each subperiod, shaded by the percentage of cutting dates in the cell. Red indicates cells with 100% cutting or near-cutting dates; blue indicates cells with 0% cutting or near-cutting dates. The region is as defined in Fig. 1.
With respect to our first question, inspection of Fig. 1 demonstrates that cells frequently within the MFN (darker-green cells) in this 900-year period are much more likely to contain a tree-ring–dated site than cells rarely or never within the MFN (lighter-green or white cells). Because such a relationship is to be expected, it increases our confidence in both the representativeness of the sample of tree-ring–dated sites and the relevance and accuracy of the MFN reconstruction.
Our second and third questions ask whether this correlation persists at shorter time scales. Despite reasonable expectations to the contrary (6, 15), the four primary peaks in the histogram of tree-ring dates through time do not correspond, on average, to periods with larger MFNs, nor do the troughs correspond to periods that, on average, have fewer cells in the MFN (Table 1 and Figs. 4 to 6). If the frequency of tree-ring dates responds primarily to the size of the MFN, the second subperiod (labeled Exploitation in Table 1; see Discussion), on average, should have more cells in the MFN than the first subperiod (labeled Exploration). This expectation does not generally hold up, regardless of whether one considers all cells, cells with dates, or local cells (Table 1 and Fig. 2C).
At the even finer temporal resolution required to address our third question, Fig. 5 (local cells) and Table 2 (“local” columns) summarize the MFN status of the years for which the cutting-date evidence indicates the occupation of a cell. A local cell has a tree-ring date in the plotted year or any of the previous 3 years. We chose this interval because, by P I times, households overproduced during good years to accumulate stored maize for consumption during bad years (16). However, even with storage, ethnographic evidence indicates that four sequential years with no production would have been disastrous (see Assessing storage stress section of Materials and Methods). For example, in the BM III exploration phase, the cells occupied (as indicated by a t-r date) in the current year or one of the three previous years (local cells) were, on average, in the MFN for 3.16 of those same 4 years. In contrast, the cells that were occupied (indicated by a t-r date) at any time during our 900-year frame were only in the niche for an average of 2.63 of those 4 years. This suggests that, in this subperiod, people were more likely to build in a cell within the MFN than they were to build in cells that were demonstrably habitable in the long run. In all nine subperiods, occupation was more likely in cells within the MFN at the time than in arbitrary cells occupied at some time, though the numbers are close in some subperiods (notably P IV exploration) (Table 2).
Fig. 5. For each Pecos classification subperiod, the mean number of years, within a 4-year window ending in the current year, for which a cell is in the MFN.
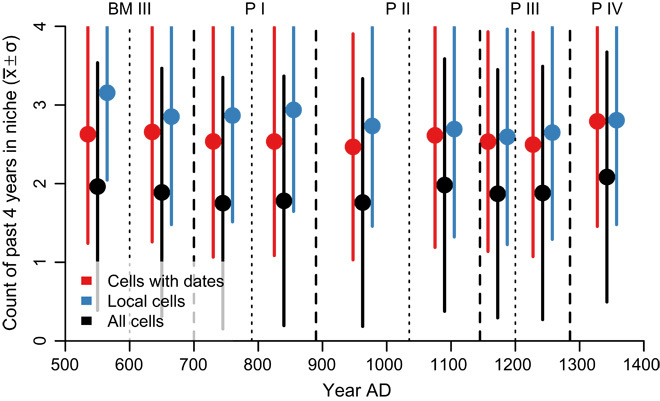
Pecos period divisions (dashed lines) and subperiod divisions (dotted lines) as rederived here are superimposed on all plots. Points represent the mean; error bars show ±1 SD.
Because the peaks in the tree-cutting distribution do not correspond to periods more favorable to agriculture (Table 1), how then can these peaks be explained? Figure 2C and Table 1 show that the trough subperiods (with fewer dates) tend to be associated with relatively higher proportions of noncutting dates (bluish CIs in Fig. 2C), whereas the second subperiod in each period, corresponding to peaks in the date distribution, contains relatively more cutting dates (resulting in reddish CIs). These changing proportions of cutting dates (among all dates) through time indicate systematic behavioral changes (13), pointing to an alternative explanation for the four-peak distribution of dates. The pattern of relatively fewer cutting dates in subperiods that have fewer dates of any kind could be due to a tendency for households in these subperiods to disperse into areas that were previously unoccupied or lightly occupied. It is possible that in such areas, initial construction would take advantage of more available deadwood (that did not have to be chopped down with stone axes) than would be available to people building structures or fires in a long-established area (where deadwood would already have been collected). Deadwood is less likely to yield cutting dates than newly cut wood because of the degradation of the outside of the log as it decays on the ground surface (17–19). It may also be true that, in subperiods with fewer dates overall, a higher proportion of those dates come from firewood given the lower overall investment in construction in such periods. On the other hand, subperiods with many dates and relatively more cutting dates likely represent a more static and intensive use of the landscape.
These interpretations are strengthened by noting that, in the subperiods with relatively few dates, cells with dates tend to occur in small, dispersed clusters if they show significant clustering at all (Fig. 2D; Materials and Methods). In subperiods with many dates, cells with dates tend to be significantly clustered at larger spatial scales. This clustering would have further diminished the ability of people to find deadwood. We argue that the cyclical pattern, the cutting/noncutting proportions, and the concomitant spatial clustering/dispersion of all dates are related.
DISCUSSION
We connect these patterns to the trade-offs between exploration and exploitation that all organizations must balance over time (20, 21). Subperiods with many tree-ring dates and high proportions of cutting dates are exploitation-dominated. In these subperiods, Pueblo societies intensively developed particular socio-environmental niches that were combinations of locations in which productive activities (especially maize farming) were generally fruitful and social and ritual organizations tuned to operate successfully given such configuration of production (Fig. 6, B, D, F, and H). Efficiency of production and competition among societies are prominent in exploitation phases. As successful clusters emerged toward the beginning of such phases, they attracted immigrants. However, niches change—as a result of both climatic and human factors—so there is a possibility of getting trapped in a suboptimal niche (21), in part because of sunk-cost dynamics following investment in particular areas or organizational modes (22). Transmission (23) within (and less commonly between) the high-density population clusters common during exploitation subperiods contributed to within-cluster behavioral and stylistic conformity, whereas competition among such clusters led to competitive emulation (24), spreading a common canon. Periods of exploitation ended with local decreases in the MFN: minimal at the end of BM III but pronounced at the ends of the following periods as shown by dips in the percentage in niche lines in Fig. 2C. These declines would have undercut prevailing social practices and tended to delegitimize the ritual practices tying people and places together productively. We assume, but cannot document at this point, that previous growth of these clusters from internal demographic processes and their attractive qualities for immigration (given their success), contributed to undermining their resilience in the face of these declines.
Some of the practices that were abandoned as exploitation subperiods terminated are quite clear. The typical practice of storing maize in underground cists outside the pit house in the BM III period gave way, in P I, to a system in which storage became concentrated in aboveground rooms integrated with other household living spaces. By inference, this reflects the demise of strong social norms seen in existing foraging societies mandating relatively unrestricted sharing within groups (25), leading to a system of more restricted reciprocal exchange emphasizing the control of resources at the levels of the household or corporate (kin) group (26, 27).
At the end of P I, the ritual system connected through oversized pit houses (“protokivas”) literally went up in flames in some areas (28) in favor, eventually, of a P II system of masonry-lined small kivas. By the beginning of the P II exploitation subperiod, larger versions of these structures (“great” kivas) were central architectural elements of the Great House (Chacoan) system shared by much of our study area. At the end of P II, the Great House system disappeared over most (but not all) of the Southwest along with nearly all of its Mesoamerican-linked ritual trappings (29).
The most sweeping delegitimization and disruption of residential location though took place at the end of P III, with the disappearance from eastern Pueblo societies of a long suite of characteristics—many reflecting practices prevalent for centuries—in conjunction with massive, long-distance migrations out of the northern area (30). Significantly—because it emphasizes the social disruption accompanying these changes—exploitation subperiods of the P I, P II, and P III periods each terminated with increases in violence that were especially marked at the end of the P II and P III periods (31).
Subperiods with fewer dates and lower proportions of cutting dates (Table 1) are exploration-dominated. Settlements in exploration phases are typically small, either unclustered or arranged within small, widely separated clusters (Fig. 2D), and often in locations not occupied in the previous subperiod (Fig. 6, A, C, E, and G). In these locations, deadwood would have been more available and large-scale construction using new wood would have been infrequent (note the higher proportion of blue-colored sites in the exploration-phase maps of Fig. 6). In general, periods of exploration were marked by disaggregation, mixing of populations, and diverse local experiments with new social forms and locations.
During the exploration phases, some settlement and ritual practices proved to be particularly successful and expanded, either because of emulation, demic expansion, or perhaps political domination in the case of P II. By the beginning of the subsequent exploitation phase, these practices—as identified by their associated architectural and ceramic styles—came to constitute the “canon” by which archaeologists since 1927 have distinguished the periods in the Pecos classification. These canons changed through time in response to changing spatial configurations of production or subsistence innovations, generally increasing population size, and incorporation of organizational forms or behaviors that became available during exploration subperiods. However, in each case, it was the partial destruction of the prevailing canon at the end of an exploitation subperiod that relaxed constraints and stimulated conceptual recombinations, permitting the emergence of the next canon (32).
The MFN analysis reveals that local niches developed by populations in all periods were substantially more productive than the study area as a whole (Table 1 and Figs. 2C and 5). Although this is not surprising, it suggests that people were responding to factors related to those we are reconstructing. However, Fig. 5 shows that starting from the exploitation subperiod of P II, the preference for areas within the MFN is reduced: an occupied cell in a 4-year window (blue dot) remains only slightly more likely to be within the MFN (higher on the graph) than an arbitrary study-area cell occupied at any time (red dot); the apparent degree of selection for cells in the MFN was reduced. We suggest that this reflects both a reduced ability to locate within the MFN given the regional population increase (33) and the fact that people in some portions of the study area were actively directing surface water to fields, thus expanding the niche for maize farming to areas outside the rain-fed limit of our reconstruction.
Our division of Southwestern (especially Puebloan) prehistory into phases dominated by exploitation or exploration is similar in some respects to an earlier suggestion that, in some periods and areas, “strong patterns” developed, marked by large, planned, centralized sites; specialized ceramic production and increased ceramic exchange; homogeneous architectural styles within larger sites; and intensive agriculture (34). In times and places dominated by “weak patterns,” by contrast, small sites with more expedient architecture, less exchange, more extensive agriculture, and more egalitarian and diverse social organization prevailed. Here, we propose a model to explain these differences.
We do not assert that no exploration-like behavior occurred in periods dominated by exploitation, or vice versa; clearly, societies must always be involved in both types of activities. It is noteworthy, though, that large-scale synthetic treatments of Pueblo prehistory tend to take the “strong patterns” (our canons) prevalent in some areas during the exploitation phase of each Pecos period as typifying that period. The great kivas and dance floors most common from A.D. 600 to 700 are used to characterize BM III; P I is connected with the villages most common between A.D. 790 and 890; P II brings to mind the peak of the Great House pattern from A.D. 1035 to 1145; and P III is most distinctively characterized by its A.D. 1200–1285 aggregations.
In addition to helping make sense of the structure of prehistory in the northern Southwest writ large, the juxtaposition of tree-ring dates and the MFN presented here can also illuminate important local aspects of Pueblo prehistory, including the initial rise of the Great House system in Chaco Canyon in the San Juan Basin during the mid–A.D. 800s. As movie S1 shows, the Chaco area was unusually favorable for rain-fed farming in this period. This movie also shows that the unprecedented expansion of this system during the P II exploitation phase took place when dry farming in and adjacent to Chaco Canyon itself was unproductive, but dry-farming prospects were often quite favorable on the periphery of the San Juan Basin. The genius of the Chaco organization was its apparent ability to tie these disparate production zones into a single system.
The emergence of stylistic and organizational canons marking each exploitation phase as a distinct Pecos period never completely erased subregional differences across the upland Southwest (7, 14), and the MFN probabilities in Fig. 1 and movie S1 suggest one reason for this. Clusters of many dated cells in Fig. 1 tend to match subregions long recognized by archaeologists as distinctive enough to warrant their own names. The cluster of dated cells in northeastern Arizona, for example, marks the Kayenta area. Its separation from neighboring clusters of cells with dates by large MFN “deserts” allowed this subregional distinction to endure for centuries, because movement and cultural transmission within the cluster was markedly easier than between clusters. These MFN deserts persist through time, as shown in the panels in Fig. 6. On the other hand, the arc of cells with dates extending from southeastern Utah through southwestern Colorado is composed of three somewhat distinct but nearby clusters, called western, central, and eastern Mesa Verde, separated from each other and from the Totah (middle San Juan) cluster just to the south in northern New Mexico by zones of decreased MFN, but not by MFN deserts. Because their spatial separation is smaller and their productive isolation is less complete, these four subregions are much more similar to each other than they are to the Kayenta subregion. Glowacki (35) notes that the Mesa Verde areas and the Totah were connected by ceramic exchange.
This analysis of cycles of tree cutting was designed to explain periodicities in societal expansion and contraction (including collapse) in the upland Southwest. Our argument, though, may apply to similar cycles seen in Neolithic societies in many areas of the world, including Europe (36) and the Near East (37). Neolithic societies everywhere shared relatively large and sedentary populations that faced two novel problems: how to coordinate ever-larger groups and how to avoid degrading local environments. Solutions to these problems inevitably involved ritually sanctioned norms and practices whose development might take generations but whose destruction could happen quickly when sets of integrated economic, organizational, and ritual practices in which people had heavily invested repeatedly failed to deliver on their constituents’ expectations that their basic subsistence needs would be met. The climatic causes for contractions in such societies may be much shorter than the exploration phases that they initiated.
MATERIALS AND METHODS
Computer code
The computer code written in the R statistical language (38) for all analyses reported here is available as data file S1. We also created a new R package, PaleoCAR (39), for producing tree-ring–based paleoclimate reconstructions over arbitrarily large geographic regions. Other essential software packages used in this analysis include care (40), FedData (41), raster (42), and rgdal (43), available at https://cran.r-project.org.
Archaeological tree-ring dates
All dates were determined by the Laboratory of Tree-Ring Research (LTRR) at the University of Arizona and indicate the analyst’s confidence that the outermost ring present marks the year in which the tree died. Here, we group these reliabilities into cutting dates (B, G, L, c, or r, with or without a “+”), near-cutting dates (v or v+, generally within 0 to 3 years of the true date of the last ring), and noncutting dates (vv, or any of the above symbols with a “++”), for which there is no way to know how many rings may be missing. The LTRR does not recognize “near-cutting dates” and would not consider any date with a “+” to be a cutting date. Because the count of cells with noncutting dates corresponds closely to high-frequency expansions and contractions of the MFN (as is most apparent in the “P II” section of Figs. 2C and 4A), we inferred that most noncutting dates in our sample were within a very few years of their true cutting. All dates represent the timing of initial use; we did not attempt to account for the reuse or stockpiling of beams, although we noted that people probably reused beams locally, rather than transporting them over long distances. Thus, local comparisons between the original dates of beam use and the MFN remain valid—we simply did not observe the latter use.
Because of the macroregional scale of our analysis, we did not entirely rule out the possibility of variability in proportions of noncutting dates due to cultural behaviors, such as beam shaping and intentional burning, or due to poor site preservation or the utilization of low-quality wood. However, widespread beam shaping and intentional burning are behaviors most commonly observed in later exploitation subperiods (see Discussion). Climate-driven preservation issues are unlikely because our MFN reconstruction did not indicate prolonged wet periods that might create long periods of poorer preservation. Also, although the proportions of cutting to noncutting dates shift between adjacent subperiods, they are surprisingly consistent between the primary Pecos periods, even given the presumably poorer preservation in BM III and P I habitations lacking stone masonry. Finally, although we did not assess patterns in the utilization of different wood species through time (or by extension, timber quality), we felt that it was unlikely that depletion of high-quality timber would have been widespread at the geographic scale of our analysis.
We performed a Monte Carlo resampling analysis to examine the sensitivity of the four-peak signal and the ratio of cutting to noncutting dates in the temporal distribution of tree-ring dates to demonstrable oversampling of certain archaeological sites. Many sites in the tree-ring database only have a single date, whereas others can have hundreds (Chetro Ketl, a Great House in Chaco Canyon, has 907 tree-ring dates between A.D. 500 and 1400). Figure 7 shows the distribution of counts of tree-ring dates across sites. For each of 999 replications, we drew a single tree-ring date from each site (n = 1002 sites) and then plotted the smoothed counts of cutting versus noncutting dates through time. This simulated what the tree-ring date distribution would look like if a dendrochronologist collected only a single date from each of the 1002 sites; replicating the process 999 times allows us to establish how different the patterns would be had different beams been selected. This method did not model the potential uncertainty in the dating of undersampled sites but controlled for the effect of oversampled sites. Results that present the mean and SD of the 999 replications are shown in Fig. 4. The four-peak signal and the cutting-to-noncutting ratio were still very evident after resampling.
Fig. 7. Histogram of the distribution of tree-ring date counts across archaeological sites.
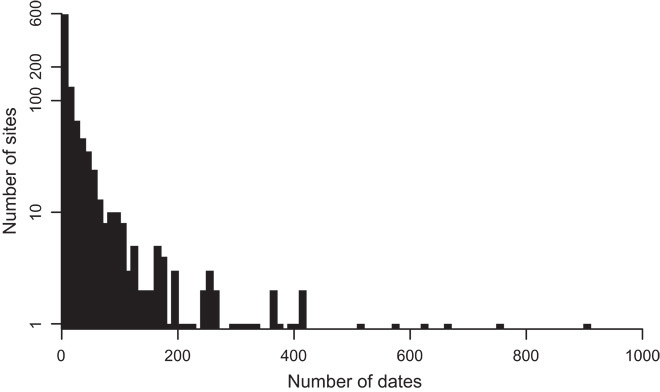
Most sites in the database only have a single tree-ring date, whereas several sites have hundreds of dates. The y axis is logarithmic.
Period/subperiod boundaries
We wanted to identify the points in time when the rate of change in the cutting-date frequency was transitioning from slowing down to accelerating, to break up Fig. 2B into five Pecos periods (and their subperiods) based on the four primary “humps” in the cutting-date frequency distribution. To do so, we calculated the modal inflection points (the points at which a continuous vector switches from being concave to being convex, or vice versa) in a series of kernel density estimates of the number of cells with cutting dates through time (Fig. 2B), each using a Gaussian kernel (that is, a normal distribution). Because the smoothness of kernel density distributions is determined by the kernel bandwidth (here, the SD of the Gaussian kernel), we estimated inflection points for density distributions with kernel bandwidths ranging from 0.01 to 50 years, in 0.01-year increments (5000 kernel density estimates). For each density distribution, we calculated a series of inflection points as the years where the second derivative of the kernel density estimate function was zero. Kernel distributions with very small bandwidths will have many inflection points, whereas those with large bandwidths (that is, very smooth distributions) will only have a few. The inflection points of each of the kernel density distributions were combined to calculate the 10 most common inflection years. Inflection years were rounded to the nearest fifth year. One break in the P IV period (at A.D. 1365) was discarded because P IV was determined to not fit the demographic and organizational pattern of the earlier periods.
Spatiotemporal clustering of occupied cells
We assessed spatial clustering through time with domain sizes derived from Ripley’s H-function, a standardized version of Ripley’s K-function (44, 45). Ripley’s K-function measured the average number of other points, N, within a radius r from a given point, over a set of radii, and was defined as
| (1) |
where λ is a circular area (πr2), pi is the ith point, and the sum is taken over n points (44).
The H-function normalized the K-function so that its expected value under a random Poisson distribution was 0, and was defined as
| (2) |
Positive values of H(r) indicated clustering, whereas negative values indicated dispersion. Statistical significance could be determined by Monte Carlo simulation of a Poisson distribution of N points over the region to generate an envelope of likely H(r) values due to random processes. Measured H(r) values that fell above or below this envelope were determined to be significantly clustered or dispersed, respectively.
We estimated the domain radius of clustering (Fig. 2D)—or the radius that jointly maximizes the point density within the radius and the separation between domains—as the radius at the minimum of the derivative of H(r), following the methodology of Kiskowski et al. (44). All clustering analyses were performed at the level of the 30–arc sec cell using the center of each cell as the point location for clustering.
MFN reconstruction
Paleoclimate reconstructions of water-year precipitation and growing-season FGDDs were performed following the methodology of Bocinsky and Kohler (11), with three important differences. First, instead of minimizing cross-validated prediction error, we selected the linear combination of tree-ring chronologies for each cell at each point in time that minimizes the corrected Akaike Information Criterion (46). Second, we did not correct for “spatial artifacts”; the data presented here are raw, independent PaleoCAR reconstructions for each cell. Finally, over the raw PaleoCAR reconstruction for each cell, we implemented a new chained mean-variance matching standardization procedure. Traditional mean-variance matching—in which each reconstruction is scaled and transformed to match the mean and variance of the calibration data over the calibration period (11)—behaves poorly when chaining together reconstructions from tree-ring chronologies that may behave differently over the calibration period. The chained approach first matches mean and variance over the calibration period for only the portion of the reconstruction that overlaps the calibration period. It then takes adjacent unadjusted sections of the reconstruction and matches their mean and variance to the already adjusted portion of the reconstruction over the 60-year period (the same length as the calibration period) immediately closer in time to the calibration period. This process continues until the entire reconstruction has been adjusted. Chained mean-variance matching allows more low-frequency variability to be retained in the reconstruction.
All analyses were performed using the PaleoCAR package for R (39), on the basis of the CAR method by Zuber and Strimmer (47). Growing-season FGDDs were estimated from monthly records of average minimum and maximum temperatures as in Bocinsky and Kohler (11).
We used the set of 532 standardized tree-ring chronologies publicly available from the International Tree-Ring Data Bank (48) as of May 2015 within a 10° distance from the borders of Arizona, Colorado, New Mexico, and Utah, calibrated using PaleoCAR to the 30–arc sec Parameter-elevation Relationships on Independent Slopes Model (PRISM) data set of modern climate (12). We calibrated to the A.D. 1924–1983 period (11), because many long chronologies in the Southwest United States only extend to the 1980s, and PRISM data degrade substantially with fewer weather stations before the 1920s.
Assessing storage stress
We transformed the rain-fed MFN reconstruction into a measure of storage stress defined as the number of years, within a 4-year window ending in the current year, for which a cell is in the MFN (Fig. 5, Table 2, and movie S1). For Table 2, we calculated sample skewness (G1) and kurtosis (G2) as the third and fourth central moments of the distribution (49). Skewness is a measure of the asymmetry of a distribution; kurtosis is a measure of its peakedness. Kurtosis was reduced by 3 so that a normal distribution would have a kurtosis of 0 (Eq. 7).
Skewness was calculated as
| (3) |
where
| (4) |
and
| (5) |
for the sample moments of order r.
Kurtosis is calculated as
| (6) |
where
| (7) |
and the sample moments were calculated as in Eq. 5.
Supplementary Material
Acknowledgments
We acknowledge assistance from J. d’Alpoim-Guedes, M. Berry, A. Brin, J. Chuipka, S. Crabtree, A. Kinzig, W. D. Lipe, B. Ludäscher, R. Higgins, J. Dean, S. Nash, T. McPhillips, S. Oas, S. Ortman, M. Peeples, K. Safi, K. Throgmorton, C. Van West, B. Vierra, and the following organizations: Compass, NMCRIS/ARMS (New Mexico Cultural Resources Information System/Archaeological Records Management Section), Utah Division of State History, and AZSITE (Arizona’s cultural resource inventory). Funding: This material is based on work supported by the NSF under grant nos. BCC-1439603, DGE-1347973, and DEB-0816400. Computation was performed in part on the ROGER (Resourcing Open Geospatial Education and Research) supercomputer, supported by NSF under grant no. ACI-1429699. Author contributions: R.K.B., T.A.K., and K.W.K. designed the research. T.A.K. assembled the tree-ring date database from the determinations generated by the LTRR, beginning from the data gathered by M. Berry and the Dominguez Anthropological Research Group (www.dargnet.org/net/TRPublic/). R.K.B. developed the paleoclimate reconstruction method. R.K.B. and J.R. performed the paleoclimate reconstructions. R.K.B. performed the concurrent analyses and created all figures and computer code. R.K.B., T.A.K., and K.W.K. wrote the paper. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data and computer code used to obtain the conclusions in this paper are archived with the Digital Archaeological Record (http://core.tdar.org/dataset/399314) and National Oceanic and Atmospheric Administration paleoclimatology repository (https://www.ncdc.noaa.gov/paleo/study/19783) or presented in the Supplementary Materials.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/4/e1501532/DC1
Data file S1. R code for all analyses reported here.
Movie S1. Annual realization of the MFN from A.D. 500 to 1400 for the study area shown within dotted lines in Fig. 1.
REFERENCES AND NOTES
- 1.Kidder A. V., Southwestern Archaeological Conference. Science 66, 489–491 (1927). [DOI] [PubMed] [Google Scholar]
- 2.Douglass A. E., The secret of the Southwest solved by talkative tree rings. Natl. Geogr. 54, 737–770 (1929). [Google Scholar]
- 3.Douglass A. E., The Central Pueblo chronology. Tree-Ring Bulletin 2, 29–34 (1936). [Google Scholar]
- 4.S. E. Nash, Time, Trees and Prehistory (University of Utah Press, Salt Lake City, UT, 1999). [Google Scholar]
- 5.W. D. Lipe, History of archaeology, in Colorado Prehistory: A Context for the Southern Colorado River Basin, W. D. Lipe, M. D. Varien, R. H. Wilshusen, Eds. (Colorado Council of Professional Archaeologists, Denver, CO, 1999), pp. 51–94. [Google Scholar]
- 6.M. S. Berry, Time, Space, and Transition in Anasazi Prehistory (University of Utah Press, Salt Lake City, UT, 1982). [Google Scholar]
- 7.Dean J. S., Reviewed work: Time, space, and transition in Anasazi prehistory. Am. Antiquity 50, 704–705 (1985). [Google Scholar]
- 8.W. H. Doelle, D. A. Phillips Jr., From the academy to the private sector: CRM’s rapid transformation within the archaeological profession, in Southwest Archaeology in the Twentieth Century, L. S. Cordell, D. D. Fowler, Eds. (University of Utah Press, Salt Lake City, UT, 2005), pp. 97–108.
- 9.Coltrain J. B., Janetski J. C., The stable and radio-isotope chemistry of southeastern Utah Basketmaker II burials: Dietary analysis using the linear mixing model SISUS, age and sex patterning, geolocation and temporal patterning. J. Archaeol. Sci. 40, 4711–4730 (2013). [Google Scholar]
- 10.Matson R. G., The nutritional context of the Pueblo III depopulation of the northern San Juan: Too much maize? J. Archaeol. Sci. Rep. 5, 622–631 (2016). [Google Scholar]
- 11.Bocinsky R. K., Kohler T. A., A 2,000-year reconstruction of the rain-fed maize agricultural niche in the US Southwest. Nat. Commun. 5, 5618 (2014). [DOI] [PubMed] [Google Scholar]
- 12.Daly C., Halbleib M., Smith J. I., Gibson W. P., Doggett M. K., Taylor G. H., Curtis J., Pasteris P. P., Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States. Int. J. Climatol. 28, 2031–2064 (2008). [Google Scholar]
- 13.Dean J. S., Euler R. C., Gumerman G. J., Plog F., Hevly R. H., Karlstrom T. N. V., Human behavior, demography, and paleoenvironment on the Colorado Plateaus. Am. Antiquity 50, 537–554 (1985). [Google Scholar]
- 14.Euler R. C., Gumerman G. J., Karlstrom T. N. V., Dean J. S., Hevly R. H., The Colorado Plateaus: Cultural dynamics and paleoenvironment. Science 205, 1089–1101 (1979). [DOI] [PubMed] [Google Scholar]
- 15.M. S. Berry, L. V. Benson, Tree-ring dates and demographic change in the southern Colorado Plateau and Rio Grande regions, in Leaving Mesa Verde: Peril and Change in the Thirteenth-Century Southwest, T. A. Kohler, M. D. Varien, A. M. Wright, Eds. (The University of Arizona Press, Tucson, AZ, 2010), pp. 53–74. [Google Scholar]
- 16.L. Sebastian, The Chaco Anasazi: Sociopolitical Evolution in the Prehistoric Southwest (Cambridge Univ. Press, New York, 1992). [Google Scholar]
- 17.R. V. N. Ahlstrom, The Interpretation of Archaeological Tree-Ring Dates, (University of Arizona, Tucson, AZ, 1985). [Google Scholar]
- 18.R. R. Lightfoot, The Duckfoot Site, Vol. 2: Archaeology of the House and Household (Crow Canyon Archaeological Center, Cortez, CO, 1994). [Google Scholar]
- 19.Towner R. H., Archeological dendrochronology in the southwestern United States. Evol. Anthropol. 11, 68–84 (2002). [Google Scholar]
- 20.J. H. Holland, Adaptation in Natural and Artificial Systems (University of Michigan Press, Ann Arbor, MI, 1975). [Google Scholar]
- 21.March J. G., Exploration and exploitation in organizational learning. Organ. Sci. 2, 71–87 (1991). [Google Scholar]
- 22.Janssen M. A., Kohler T. A., Scheffer M., Sunk-cost effects and vulnerability to collapse in ancient societies. Curr. Anthropol. 44, 722–728 (2003). [Google Scholar]
- 23.R. Boyd, P. J. Richerson, Culture and the Evolutionary Process (University of Chicago, Chicago, IL, 1985). [Google Scholar]
- 24.C. Renfrew and J. F. Cherry, Peer Polity Interaction and Socio-political Change (Cambridge Univ. Press, Cambridge, 1986). [Google Scholar]
- 25.Gintis H., van Schaik C., Boehm C., Zoon Politikon: The evolutionary origins of human political systems. Curr. Anthropol. 56, 327–353 (2015). [DOI] [PubMed] [Google Scholar]
- 26.Gilman P. A., Architecture as artifact: Pit structures and Pueblos in the American Southwest. Am. Antiquity 52, 538–564 (1987). [Google Scholar]
- 27.Hegmon M., Risk reduction and variation in agricultural economies: A computer simulation of Hopi agriculture. Res. Econ. Anthropol. 11, 89–121 (1991). [Google Scholar]
- 28.Wilshusen R. H., The relationship between abandonment mode and ritual use in Pueblo I Anasazi Protokivas. J. Field Archaeol. 13, 245–254 (1986). [Google Scholar]
- 29.S. H. Lekson, The Chaco Meridian: One Thousand Years of Political and Religious Power in the Ancient Southwest (Rowman & Littlefield, Lanham, MD, 2015). [Google Scholar]
- 30.W. D. Lipe, Lost in transit: The central Mesa Verde archaeological complex, in Leaving Mesa Verde: Peril and Change in the Thirteenth-Century Southwest, T. A. Kohler, M. D. Varien, A. M. Wright, Eds. (The University of Arizona Press, Tucson, AZ, 2010), pp. 262–284. [Google Scholar]
- 31.Kohler T., Ortman S., Grundtisch K., Fitzpatrick C., Cole S., The better angels of their nature: Declining violence through time among prehispanic farmers of the Pueblo Southwest. Am. Antiquity 79, 444–464 (2014). [Google Scholar]
- 32.R. Axelrod, M. D. Cohen, Harnessing Complexity: Organizational Implications of a Scientific Frontier (The Free Press, New York, 1999). [Google Scholar]
- 33.Kohler T. A., Reese K. M., Long and spatially variable Neolithic Demographic Transition in the North American Southwest, Proc. Natl. Acad. Sci. U.S.A. 111, 10101–10106 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.J. A. Tainter, F. Plog, Strong and weak patterning in Southwestern prehistory: The formation of Puebloan archaeology, in Themes in Southwest Prehistory, G. J. Gumerman, Ed. (School of American Research Press, Santa Fe, NM, 1994), pp. 165–181. [Google Scholar]
- 35.D. M. Glowacki, Living and Leaving: A Social History of Regional Depopulation in Thirteenth-Century Mesa Verde (University of Arizona Press, Tucson, AZ, 2015). [Google Scholar]
- 36.Shennan S., Downey S. S., Timpson A., Edinborough K., Colledge S., Kerig T., Manning K., Thomas M. G., Regional population collapse followed initial agriculture booms in mid-Holocene Europe. Nat. Commun. 4, 2486 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Rosen S. A., The desert and the pastoralist: An archaeological perspective on human-landscape interaction in the Negev over the millennia. Ann. Arid Zone 50, 1–15 (2011). [Google Scholar]
- 38.R Core Team, R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, Vienna, Austria, 2015); www.R-project.org/ [accessed March 1, 2016].
- 39.R. K. Bocinsky, PaleoCAR: Paleoclimate Reconstruction from Tree Rings using Correlation Adjusted corRelation (2015); R package version 2.1; https://github.com/bocinsky/PaleoCAR/archive/2.1.tar.gz [accessed March 1, 2016].
- 40.V. Zuber, K. Strimmer, care: High-Dimensional Regression and CAR Score Variable Selection (2014); R package version 1.1.4.
- 41.R. K. Bocinsky, FedData: Functions to Automate Downloading Geospatial Data Available from Several Federated Data Sources (2015); R package version 2.0.
- 42.R. J. Hijmans, raster: Geographic Data Analysis and Modeling (2013); R package version 2.1-66.
- 43.R. Bivand, T. Keitt, B. Rowlingson, rgdal: Bindings for the Geospatial Data Abstraction Library (2013); R package version 0.8-13.
- 44.Kiskowski M. A., Hancock J. F., Kenworthy A. K., On the use of Ripley’s K-function and its derivatives to analyze domain size. Biophys. J. 97, 1095–1103 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ripley B. D., Modelling spatial patterns. J. R. Stat. Soc. B 39, 172–212 (1977). [Google Scholar]
- 46.Akaike H., A new look at the statistical model identification. IEEE Trans. Autom. Control 19, 716–723 (1974). [Google Scholar]
- 47.Zuber V., Strimmer K., High-dimensional regression and variable selection using CAR scores. Stat. Appl. Genet. Mol. Biol. 10, 34 (2011). [Google Scholar]
- 48.Grissino-Mayer H. D., Fritts H. C., The International Tree-Ring Data Bank: An enhanced global database serving the global scientific community. The Holocene 7, 235–238 (1997). [Google Scholar]
- 49.Joanes D. N., Gill C. A., Comparing measures of sample skewness and kurtosis. J. R. Stat. Soc. D 47, 183–189 (1998). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/4/e1501532/DC1
Data file S1. R code for all analyses reported here.
Movie S1. Annual realization of the MFN from A.D. 500 to 1400 for the study area shown within dotted lines in Fig. 1.


