Discovery of natural MgSiO₃ tetragonal garnet in a shocked chondritic meteorite

A high-pressure phase is discovered in a shocked, stony meteorite.

Abstract

MgSiO₃ tetragonal garnet, which is the last of the missing phases of experimentally predicted high-pressure polymorphs of pyroxene, has been discovered in a shocked meteorite. The garnet is formed from low-Ca pyroxene in the host rock through a solid-state transformation at 17 to 20 GPa and 1900° to 2000°C. On the basis of the degree of cation ordering in its crystal structure, which can be deduced from electron diffraction intensities, the cooling rate of the shock-induced melt veins from ~2000°C was estimated to be higher than 10³°C/s. This cooling rate sets the upper bound for the shock-temperature increase in the bulk meteorite at ~900°C.

INTRODUCTION

Mineral physicists have made long-standing efforts to understand the mineralogy of Earth’s deep interior. In particular, phase equilibria studies have clarified a variety of high-pressure polymorphs of silicates and oxides (1, 2). Natural examples of such high-pressure phases from the deep Earth, including mantle xenoliths (3) and inclusions in diamond crystals, are quite rare (4, 5). However, during the past half-century, many high-pressure phases have been discovered from terrestrial and extraterrestrial rocks that have experienced high-pressure and high-temperature impact events.

Particularly, shocked chondritic meteorites yield many dense silicate minerals that are thought to compose Earth’s transition zone and lower mantle. MgSiO₃ pyroxene, which is one of the major minerals in the upper mantle, is known to transform into Mg₂SiO₄-modified spinel + stishovite (SiO₂), Mg₂SiO₄ spinel + stishovite, MgSiO₃ tetragonal garnet (at high temperatures: 1600° to 2400°C), or MgSiO₃ ilmenite (at low temperatures: 600° to 2000°C); it is also known to transform into MgSiO₃ perovskite and CaIrO₃-structured MgSiO₃ with increasing pressure (fig. S1). The CaIrO₃ phase cannot be recovered under ambient conditions as a so-called “unquenchable” phase (6). All other “quenchable” high-pressure phases of MgSiO₃ and Mg₂SiO₄ that appear in the MgSiO₃ system have been discovered in shocked meteorites, except for the tetragonal garnet phase (7–13).

In the early 1970s, MgSiO₃ garnet was identified inside and in the vicinity of shock-induced melt veins (that is, shock veins) of a chondritic meteorite; this mineral was named “majorite” (8). Meteoritic majorite contains variable amounts of Al, Ca, and Fe. Al- and Ca-deficient majorite, which forms polycrystalline aggregates, is considered to have been formed by a solid-state transformation from the host low-Ca pyroxene. On the other hand, Al-, Ca-, and Fe-rich majorite, which coexists with Fe-rich minerals such as magnesiowüstite [(Mg,Fe)O], was crystallized from shock-induced chondritic melt under high pressure (14). Both types of majorite have been reported to have a cubic symmetry. By way of contrast, here we provide unequivocal evidence for natural tetragonal majorite in the Tenham meteorite based on analytical transmission electron microscopy (ATEM).

RESULTS AND DISCUSSION

Tenham can be classified as an ordinary L6 chondrite (15). This meteorite is one of the renowned extraterrestrial samples in which most of the high-pressure polymorphs of silicate minerals have been found (7, 9, 13, 16). The major constituent minerals of the meteorite are olivine, pyroxene, plagioclase, iron-nickel alloy, and iron-sulfide. Owing to shock metamorphism that resulted from an impact event on its parental asteroid, shock veins (<1 mm in thickness) that interconnect melt pockets form a network throughout the sample (Fig. 1). These shock veins abundantly enclose fragments of mineral assemblages of host rocks. A portion of the olivine, pyroxene, and plagioclase in the fragments and on the wall of the shock veins has transformed into high-pressure phases. Concerning the two fragments within a 400-μm shock vein that are examined in the present study, the rims of the low-Ca pyroxene grains are isotropic under a polarized microscope, thereby suggesting a cubic or a pseudocubic symmetry (fig. S2). Raman spectra taken from these isotropic parts were consistent with majorite (fig. S3). The isotropic parts were processed into ultrathin foils and investigated in detail by ATEM (fig. S4).

Fig. 1. Backscattered electron image of a shock-induced melt vein in Tenham chondritic meteorite.

Fragments of minerals of the host rock are captured in the shock vein. Olivine and plagioclase (in a fragment at the center of the image) were transformed into the spinel phase (Rw, ringwoodite) and diaplectic glass (Msk, maskelynite), respectively. Low-Ca pyroxene (En) is partly transformed into the garnet phase (Maj, majorite). The rectangular hole is a portion extracted by a focused ion beam (FIB) apparatus for ATEM analysis.

The ATEM samples consist of monomineralic aggregates of euhedral or subhedral grains that are 450 ± 200 nm in size (Fig. 2). There are no interstitial phases among the grains. The chemical formula of the grains, as determined by ATEM, is approximately (Mg_0.79,Ca_0.02,Fe_0.19)Si_1.00O₃ (table S1). This composition is almost identical to that of the low-Ca pyroxene [(Mg_0.78,Ca_0.02,Fe_0.20)Si_1.00O₃] in the host rock (11). The occurrence of majorite suggests that the majorite was formed through a solid-state transformation that proceeded directly from the low-Ca pyroxene.

Fig. 2. Transmission electron micrograph of an aggregate of (Mg,Fe)SiO₃ tetragonal majorite in Tenham.

The ATEM sample consists of monomineralic aggregates of euhedral or subhedral grains. No interstitial phases are present among the majorite grains.

Concerning crystallographic analysis, tetragonal majorite was previously reported in Tenham by ATEM (17). Majorite with a Ca-rich composition [Ca/(Mg + Ca + Fe) = 0.27] was a dissociation product of CaMgSi₂O₆ clinopyroxene from a solid-state transformation. Ca-rich majorite occurred as a submicrometer-sized symplectic intergrowth with amorphous Fe-Mg silicate. Because of the extremely fine grain size, powder electron diffraction rings were taken from the aggregates. In addition, the tetragonal symmetry of majorite was determined by only one extra diffraction ring of the (011) crystallographic plane. However, in this study, we examined the symmetry of majorite by single-crystal electron diffraction of individual grains.

All the selected area electron diffraction (SAED) patterns taken from the grains were consistent with the normal cubic garnet structure with space group $Ia\overline{3}d$ (Fig. 3A). However, the diffraction patterns along the [010] zone axis showed faint extra spots, which violate the extinction rule on the Bragg diffraction for $Ia\overline{3}d$. Accumulated exposures of the diffraction patterns on a charge-coupled device camera revealed that the extra spots correspond to the diffraction of {h0l} planes, where both h and l are odd. This pattern is consistent with a tetragonal symmetry with the space group I4₁/a (Fig. 3B). The obtained unit-cell parameters and volume for a tetragonal unit cell are a = 1.152(12) nm, c = 1.151(12) nm, and 1.53(5) nm³, respectively; the calculated density is 3.72(13) g/cm³. The unit cell is metrically cubic within the analytical uncertainty associated with electron diffraction under ATEM, though the extra diffraction spots clearly showed that the symmetry of the majorite grains was tetragonal (see fig. S5).

Fig. 3. SAED patterns from single crystals of (Mg,Fe)SiO₃ tetragonal majorite.

(A) Along the [$11\overline{1}$] zone axis. (B) Along the [010] zone axis. Weak {h0l} reflections, where both h and l are odd [indicated by triangles in the magnified pattern (right)] are diagnostic reflections for the tetragonal I4₁/a symmetry.

Laboratory experiments demonstrated the stability of tetragonal majorite with the MgSiO₃ composition under high pressures and high temperatures (18). The phase appears at 16 to 22 GPa and 1600° to 2400°C in between the stability fields of high-pressure clinoenstatite and the perovskite phase (19, 20) (fig. S1). Fe incorporation affects the stability relations in MgSiO₃. Majorite with the Fe/(Mg + Fe) = 0.2 composition ratio is bounded within the pressure range of 17 to 20 GPa at 1800°C (21) and within the temperature range of 1900° to 2100°C at 20 GPa (22). The temperature conditions are further constrained by the liquidus temperature in the bulk chondritic composition at this pressure range (fig. S1). The liquidus temperature of ~2000°C at 20 GPa corresponds to the upper temperature limit for tetragonal majorite formation in a solid-state reaction because low-Ca pyroxene should be melted with coexisting minerals above this temperature. Hence, tetragonal majorite in Tenham would have formed at 1900° to 2000°C and 17 to 20 GPa, although there is some uncertainty in the pressure-temperature limits when their interdependencies are considered.

The crystal symmetry of (Mg,Fe)SiO₃ majorite is complex. Precise unit-cell determination by powder x-ray diffraction confirmed that synthetic (Mg,Fe)SiO₃ majorite has a tetragonal symmetry throughout the Fe/(Mg + Fe) range from 0 to 0.24 (21, 23). On the other hand, meteoritic (Mg,Fe)SiO₃ majorite has been reported to be cubic (24, 25). On the basis of group theory, MgSiO₃ majorite forms by means of a symmetry reduction from the space group $Ia\overline{3}d$ (cubic) to the space group I4₁/a (tetragonal) through Mg-Si ordering in the octahedral sites upon cooling (26). Pervasive modulated and twinning structures observed in synthetic (Mg,Fe)SiO₃ majorite constitute evidence for the symmetry reduction during cooling in their syntheses, when the majorite went across the cubic-tetragonal phase boundary (27, 28). The transition temperature in (Mg,Fe)SiO₃ was estimated to be lower than ~1950°C and was deduced from the density contrast of twinning structures (28).

Therefore, the discrepancy in the symmetry of (Mg,Fe)SiO₃ majorite between meteoritic and synthetic samples can be explained by the difference in cooling rates from the temperature above the phase boundary (28). In the case of the current study, both meteoritic and synthetic (Mg,Fe)SiO₃ majorites showed a tetragonal I4₁/a symmetry with diagnostic reflections ({h0l}, where both h and l are odd). However, those reflections in meteoritic majorite are significantly weaker than those of synthetic majorite (fig. S6). This suggests that cations in the octahedral sites of meteoritic majorite were less ordered, even though its symmetry became tetragonal. This difference would have been caused by different cooling rates between both samples. In high-pressure synthesis, the sample in a Kawai-type apparatus is cooled at the rate of 10³°C/s (29), whereas (Mg,Fe)SiO₃ tetragonal majorite in Tenham would have cooled more rapidly.

The cooling rate of a shock vein constrains the shock temperature of the overall meteorite sample because locally extremely heated shock veins are cooled by the surrounding host rock after the passage of the shock wave. The shock temperature of the host rock can be estimated on the basis of thermal calculations using the one-dimensional thermal conductivity model (fig. S7). As discussed above, tetragonal majorite in Tenham has a lower degree of cation ordering in the octahedral sites. This can be explained by the higher cooling rate of the shock vein as compared to its counterpart in high-pressure synthesis. The cation ordering is thought to proceed in the temperature range between the cubic-tetragonal phase boundary (~1950°C) (28) and the closure temperature of cation ordering (~1000°C), which is assumed from Mg-Ti ordering in the octahedral sites in karrooite (MgTi₂O₅) (30). When Mg, Fe, and Si ordering in octahedral sites in meteoritic majorite is hindered because of the higher cooling rate (as compared with synthetic majorite) in the above temperature range (1000° to 1950°C), the shock temperature of the host rock does not exceed ~900°C (Fig. 4). The calculated temperature is much higher than the one estimated by its shock equation of state (Hugoniot) at 25 GPa, which is 157° to 387°C (31). This Hugoniot calculation assumes that the target material is nonporous, although collapse of initial pores during shock compression largely contributes to energy increase. If our calculation is correct, some porosity in unshocked Tenham would have enhanced shock temperature.

Fig. 4. Calculated cooling history on the wall of a 400-μm-thick shock vein based on the one-dimensional thermal conductivity model.

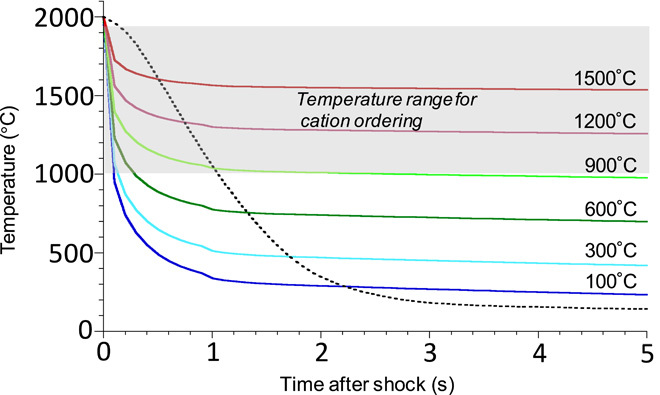
The initial temperature just after the shock wave passage was assumed to be 2000°C, corresponding to the liquidus temperature of the bulk chondritic composition at 20 GPa (37). The solid lines represent temperature paths of shock veins cooled by a shock-temperature increase in the host rock. The broken line represents the temperature path in high-pressure synthesis in the Kawai-type multianvil apparatus (29). The gray background corresponds to the temperature range where (Mg,Fe)-Si ordering occurs in the octahedral sites in the majorite structure (28, 30). When cation ordering in the octahedral sites in meteoritic majorite is hindered owing to the higher cooling rate (as compared to that of synthetic majorite), the shock-temperature increase in the host rock must be lower than ~900°C.

The present study demonstrated that majorite is one of the key minerals in meteorites that simultaneously constrain the pressure, temperature, and cooling rate in shock veins. Further experimental and theoretical evaluations of cation ordering in majorite as a function of the cooling rate contribute to a more profound understanding of the thermal history of shocked meteorites. The estimated very high cooling rate also possibly implies the new occurrence of high-pressure phases in shocked meteorites. For instance, it is believed that CaSiO₃-perovskite (stable at >18 GPa) (32) and CaCl₂-type SiO₂ (stable at >55 GPa) (33) are not experimentally recovered under ambient conditions. However, extremely rapid cooling may enable such high-pressure phases to be “frozen” in the vicinity of shock veins in Tenham.

The crystal structure of majorite is important not only for asteroidal impact events but also for mantle geophysics, because it is possible that the compressibility of mantle minerals increases as a result of cation disordering (34). Majorite in Earth’s transition zone and subducting lithospheres (410- to 660-km depth) also contains considerable amounts of Na, Al, Ca, Ti, Cr, and Fe (35). Accordingly, the symmetry of majorite in the multicomponent system needs to be reevaluated by single-crystal x-ray and electron diffractometry to achieve a better understanding of the physical properties of the mantle transition zone.

MATERIALS AND METHODS

Material

A polished thin section of the Tenham chondrite with dimensions of 21 × 16 mm², containing (Mg,Fe)SiO₃ tetragonal majorite (sample number NSM-MF15737), has been deposited at the Department of Geology and Paleontology, National Museum of Nature and Science, Japan.

Analytical transmission electron microscopy

The polished thin section of Tenham was initially examined by a scanning electron microscope (Hitachi SU1510) and a polarized microscope to observe shock-induced melt veins and fragments of host rocks therein. The rims of the low-Ca pyroxene in the fragments were optically isotropic (fig. S2) and show Raman spectra that correspond to those of majorite (fig. S3). The portion was processed into two ultrathin foils with areas of 7 × 7 and 6 × 10 μm² and with thickness of approximately 100 nm by a Ga-ion beam after deposition of carbon protection layers in an FIB apparatus (Hitachi SMI4050) (fig. S4). The ultrathin foils were mounted on Cu grids using a micromanipulator equipped with the FIB and were studied using a transmission electron microscope (JEOL ARM-200F) operated at an accelerating voltage of 200 kV at the Kochi Institute for Core Sample Research, Japan Agency for Marine-Earth Science and Technology (JAMSTEC). With ATEM, we were able to evaluate symmetry using SAED, as well as microtextures using diffraction contrast imaging. The chemical compositions of the samples were obtained using energy-dispersive x-ray spectroscopy with a 100-mm² silicon drift detector. For quantitative chemical analyses, k-factors for the major elements were determined using the standards for San Carlos clinopyroxene. The intensities of the characteristic x-rays of each element were measured using a fixed live time of 50 s, a beam spot size of 100 nm, and a beam current of 250 pA.

Symmetry diagnosis by single-crystal electron diffraction

The c/a value of MgSiO₃ tetragonal majorite is 0.9925, and this value approaches unity as the Fe content increases [c/a = 0.9936 for (Mg_0.81Fe_0.19)SiO₃ (23)]. Therefore, the a and c axes in the tetragonal unit cell could not be distinguished from each other within the accuracy of electron diffraction. In the present characterization, the symmetry of the tetragonal garnet was determined by the systematic absences in the diffraction patterns, taking into account the effects of multiple diffractions. The space group I4₁/a has a-glide planes only on the (001)_tetragonal plane, whereas $Ia\overline{3}d$ has a-glide planes on all three {100}_cubic planes. Therefore, I4₁/a requires the following diffraction conditions: for the [001] zone, h, k = even for hk0 (a-glides); for the [010] zone, h + l = even for h0l (body centering only). However, the space group $Ia\overline{3}d$ requires the same diffraction conditions for all <010> zone axes: for the [100] zone, k, l = even for 0kl; for the [010] zone, h, l = even for h0l; for the [001] zone, h, k = even for hk0 (fig. S5). Hence, these two space groups can be distinguished by inspecting the <010> zone axis diffraction patterns.

Cooling path calculation of shock veins

To evaluate the thermal history of Tenham chondrite during a shock event, we calculated the temperature paths of shock veins based on the one-dimensional thermal conduction model (fig. S7) (36). The 400-μm-thick shock vein was assumed to have been cooled by heat conduction from the shock vein to the host rock according to the following equation

$$T-T_0/(T_{}-T_0)=0.5\left\{\text{erf}\right[(a-x)/2{\left(\kappa t\right)}^{1/2}]+\text{erf}[(a+x)/2{\left(\kappa t\right)}^{1/2}\left]\right\}$$ (1)

where T is the temperature at position x measured at time t after the passage of the shock wave; T₀ is the temperature of the host rock just after shock (that is, the shock temperature); T_m is the melting temperature of the shock-induced melt vein; 2a is the width of the shock vein; x − a is the distance from the vein wall; and κ is the thermal diffusivity. The melting temperature of the vein corresponds to the liquidus temperature (2273 K) of the chondritic meteorite at 20 GPa (37) because the chemical composition of the vein is nearly the same as the bulk composition of the meteorite. The thermal diffusivity of olivine crystal under high pressures, which is the most dominant mineral in the Tenham chondrite, was estimated to be 10⁻⁶ m²/s (36). Cooling by adiabatic expansion during decompression was not considered in the calculation because its contribution is negligible (38).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/3/e1501725/DC1

Fig. S1. Pressure-temperature phase diagram of MgSiO₃.

Fig. S2. Polarized optical micrographs of a fragment of host rock captured in a shock vein.

Fig. S3. Raman spectrum of majorite at the rim of a shock vein in Tenham.

Fig. S4. Transmission electron micrograph of the entire ultrathin foil sample of a tetragonal majorite aggregate processed by an FIB.

Fig. S5. Schematic diagrams of electron diffraction patterns of cubic ($Ia\overline{3}d$) and tetragonal (I4₁/a) majorites along the <001> and <010> zone axes.

Fig. S6. One- and two-dimensional electron diffraction profiles of natural and synthetic majorites.

Fig. S7. One-dimensional thermal conductivity model used for estimating the temperature paths of a shock vein cooled by the host rock of a meteorite.

Table S1. Chemical composition of (Mg,Fe)SiO₃ tetragonal majorite.