NEIGHBORHOOD EFFECT HETEROGENEITY BY FAMILY INCOME AND DEVELOPMENTAL PERIOD: EVIDENCE FROM A COUNTERFACTUAL MODEL OF HIGH SCHOOL GRADUATION

Geoffrey T Wodtke; Felix Elwert; David J Harding

doi:10.1086/684137

. Author manuscript; available in PMC: 2017 Jan 1.

Published in final edited form as: AJS. 2016 Jan;121(4):1168–1222. doi: 10.1086/684137

NEIGHBORHOOD EFFECT HETEROGENEITY BY FAMILY INCOME AND DEVELOPMENTAL PERIOD: EVIDENCE FROM A COUNTERFACTUAL MODEL OF HIGH SCHOOL GRADUATION

Geoffrey T Wodtke ¹, Felix Elwert ², David J Harding ³

PMCID: PMC4820764 NIHMSID: NIHMS770487 PMID: 27017709

Abstract

Effects of disadvantaged neighborhoods on child educational outcomes likely depend on a family's economic resources and the timing of neighborhood exposures during the course of child development. This study investigates how timing of exposure to disadvantaged neighborhoods during childhood versus adolescence affects high school graduation and whether these effects vary across families with different income levels. It follows 6,137 children in the PSID from childhood through adolescence and overcomes methodological problems associated with the joint endogeneity of neighborhood context and family income by adapting novel counterfactual methods—a structural nested mean model estimated via two-stage regression-with-residuals—for time-varying treatments and time-varying effect moderators. Results indicate that exposure to disadvantaged neighborhoods, particularly during adolescence, has a strong negative effect on high school graduation, and that this negative effect is more severe for children from poor families.

Spatial inequality is a central dimension of social stratification. Ever since the publication of Wilson's (1987) influential treatise on urban poverty, researchers have worked to understand how concentrated neighborhood disadvantage undermines social progress (Anderson 1999; Brooks-Gunn, Duncan, and Aber 1997; Harding 2010; Jencks and Mayer 1990; Massey 2004; Massey and Denton 1993; Sampson 2001; Wilson 1987; Wilson 1996), focusing especially on educational attainment (Aaronson 1998; Brooks-Gunn et al. 1993; Crane 1991; Crowder and South 2010; Ginther, Haveman, and Wolfe 2000; Harding 2003; Sharkey and Elwert 2011; Wodtke, Harding, and Elwert 2011).

Multiple sociological theories suggest that the socioeconomic position of the family should moderate the impact of neighborhood context on educational outcomes (neighborhood effect moderation occurs when individual or family characteristics dampen or amplify the effect of some neighborhood exposure). Different theories, however, disagree on the direction of neighborhood effect moderation by family economic resources. Compound disadvantage theory contends that family poverty intensifies the harmful effects of neighborhood deprivation because children from poor families must rely more heavily on neighborhood networks and institutional resources than children from nonpoor families (Jencks and Mayer 1990; Wilson 1987; Wilson 1996). By contrast, relative deprivation theory posits that neighborhood effects may be less pronounced among children in low-income families because these children lack the personal resources needed to capitalize on the network and institutional advantages available in more advantaged neighborhoods (Crosnoe 2009; Jencks and Mayer 1990).

Although it is commonly hypothesized that neighborhood effects vary by family economic resources, previous research on this type of effect heterogeneity is rare and does not yield consistent results. Most prior studies simply constrain the effects of neighborhood context to be the same for all children, regardless of their families’ economic resources (e.g., Ginther et al. 2000; Harding 2003; Wodtke et al. 2011), and these constraints may obscure divergent consequences of growing up in disadvantaged neighborhoods among different groups of children. The few studies that do test for interactions between neighborhood context and different measures of family socioeconomic status yield inconsistent results (e.g., Brooks-Gunn et al. 1993; South and Crowder 1999; Wheaton and Clarke 2003). Furthermore, none of these studies investigate neighborhood effect moderation within a time-dependent framework that properly accounts for the dynamic coevolution of neighborhood contexts and family resources over time (Wodtke et al. 2011; Wodtke 2013).

Theories about the impact of concentrated disadvantage on child development additionally suggest that the consequences of living in a disadvantaged neighborhood depend on the developmental timing of exposure. For example, perspectives emphasizing peer socialization mechanisms anticipate more pronounced effects of adolescent, rather than early childhood, exposure to disadvantaged neighborhoods. On the other hand, research on human capital formation suggests that children are especially sensitive to environmental inputs during the early stages of developmental (Duncan and Brooks-Gunn 1998; Heckman 2006). Recent research shows that it is important to account for duration of exposure to disadvantaged neighborhoods (Crowder and South 2010; Wodtke et al. 2011; Wodtke 2013), but few prior studies examine how the effects of neighborhood deprivation vary across different developmental periods. Among these few prior studies are several that suggest heterogeneous effects for neighborhood exposures during childhood versus adolescence on childbearing risk, mental health, and cognitive development (Sastry and Pebley 2010; Wheaton and Clarke 2003; Wodtke 2013), although results are somewhat inconsistent. Moreover, none of these prior studies examine neighborhood effects on educational attainment.

This study investigates whether neighborhood effects on high school graduation are moderated by family economic resources and whether these effects depend on the timing of neighborhood exposures during different developmental stages. Specifically, it examines how exposure to disadvantaged neighborhoods during childhood versus adolescence affects the chances of high school graduation among subgroups of children with different family economic resources over time. We focus on high school graduation because it is a critical educational transition and essentially a precondition for economic security as an adult (Rumberger 1987).

Analyses of neighborhood effect moderation in the longitudinal setting are complicated by several conceptual and methodological difficulties. First, estimating neighborhood effects without regard for effect moderation is already quite challenging because families dynamically select into and out of neighborhoods on the basis of time-varying covariates that are themselves affected by prior neighborhood conditions. For example, parental income affects future neighborhood attainment; in turn, where the family lives may affect parents’ subsequent incomes. In the presence of such time-varying confounders, conventional methods of estimating neighborhood effects are biased (Wodtke et al. 2011). Second, the joint endogeneity of time-varying family income and neighborhood exposures further complicates the analysis of neighborhood effect moderation across different income subgroups. The challenge is not merely statistical but conceptual. As we elaborate below, because neighborhood conditions during childhood in part create the subgroup of interest (poor families) during adolescence, conventional and ostensibly reasonable research questions may not translate into coherent causal estimands. Furthermore, even with a set of well-defined causal estimands, conventional estimation methods remain biased for these effects when time-varying effect moderators are affected by past neighborhood conditions (Robins 1994).

To overcome these challenges, we analyze the effects of different neighborhood exposure trajectories conditional on the evolving economic position of the family using a two-stage regression-with-residuals estimator for a structural nested mean model (Almirall et al. 2011; Almirall, Ten Have, and Murphy 2010; Robins 1994). Under assumptions discussed below, these methods are unbiased for the moderated causal effects of time-varying treatments when both time-varying confounders and time-varying moderators are affected by past treatment. This approach to the analysis of causal effect moderation has the potential for wide application in sociology, wherever both treatments and moderators vary endogenously over time (e.g., classroom conditions and student attributes).

In the sections that follow, we begin with a review of the theoretical mechanisms through which neighborhood disadvantage is thought to impact high school graduation. Next, we discuss several theories positing that the effects of neighborhood disadvantage depend on the socioeconomic position of the family and the developmental timing of neighborhood exposures. Then, we outline the dynamic neighborhood selection process that complicates conventional estimation methods, present the structural nested mean model and its two-stage regression-with-residuals estimator, and estimate the moderated effects of exposure to disadvantaged neighborhoods during childhood versus adolescence on high school graduation with data from the Panel Study of Income Dynamics (PSID).

This study makes four contributions to theory and research on neighborhood effects. First, substantively, it provides evidence that exposure to disadvantaged neighborhoods during adolescence has a more pronounced negative effect on high school graduation than exposure during childhood. It also provides new evidence that this negative effect is much more severe for children whose families are poor during adolescence. Second, theoretically, these results adjudicate between compound disadvantage theory and relative deprivation theory, supporting the former. Third, conceptually, this study outlines a framework for formulating coherent causal questions about effect moderation when both treatments and moderators vary across time. Fourth, methodologically, it introduces to sociology new and readily transferable methods (structural nested mean models and two-stage regression-with-residuals) that can estimate moderated causal effects in the longitudinal context. We conclude that ecological socialization models must account for the interactions between nested social contexts, like the family and neighborhood, as well as for the dynamic coevolution of these contexts over time.

NEIGHBORHOOD EFFECT MODERATION BY FAMILY RESOURCES

Neighborhood disadvantage is thought to influence educational attainment through several different mechanisms. Social isolation theories emphasize the absence of adult role model who demonstrate the advantages of formal education (Wilson 1987; Wilson 1996) and the alternative, or heterogeneous, cultural messages about the value of schooling, which children must navigate in impoverished communities (Anderson 1999; Harding 2007; Harding 2010; Harding 2011; Massey and Denton 1993). Social disorganization models contend that poor neighborhoods have lower capacity for collective informal social control, resulting in two types of effects on educational outcomes. The first is that low social control results in more violent crime (Sampson, Raudenbush, and Earls 1997) and a breakdown of collective trust in poor communities that impacts the emotional and behavioral development of children in ways that may interfere with progression through school (Harding 2009; Sharkey 2010; Sampson 2001; Sampson, Morenoff, and Gannon-Rowley 2002). The second consequence of low informal social control is that poor neighborhoods may have lower capacity for collective supervision of youth (Coleman 1988, Browning, Leventhal and Brooks-Gunn 2005), potentially leading to greater truancy and less engagement in schooling. Institutional resource perspectives focus on the detrimental effects of low-quality schools and the limited services available to residents of disadvantaged neighborhoods (Brooks-Gunn et al. 1997; Small and Newman 2001). Environmental models posit that children living in impoverished communities are disproportionately exposed to physical hazards, such as heavy air pollution and indoor allergens, which may affect child health and thereby disrupt educational progress (Earls and Carlson 2001; Kawachi and Berkman 2003).

The effects of neighborhood disadvantage on children's educational outcomes likely depend on their families’ economic resources. Competing sociological theories, however, disagree on whether children of resource-rich or resource-poor families should be more sensitive to disadvantaged neighborhoods. These theories are structured around two phenomena that could generate this type of effect moderation: first, poor versus nonpoor children's differential exposure to neighborhood-effects mechanisms; and second, poor versus nonpoor children's differential susceptibility to the mechanisms to which they are exposed.

Compound disadvantage theory posits that the detrimental impact of exposure to poor neighborhoods is more severe among poor children for several reasons (Jencks and Mayer 1990; Wilson 1987; Wilson 1996). First, more advantaged families are likely better able to insulate their children from the negative effects of poor neighborhoods. For example, parents with greater economic resources may be able to “buy out” of the potentially harmful effects of institutional resource deprivation in disadvantaged neighborhoods. Nonpoor parents living in disadvantaged neighborhoods may be able to afford higher-quality childcare outside the neighborhood, enroll their children in private or charter schools and other supplementary educational programs outside the neighborhood, and travel beyond the neighborhood to secure other goods and services that facilitate effective parenting. Moreover, time spent outside the neighborhood may also reduce exposure to the local cultural context, thereby limiting social isolation, and provide access to other contexts with greater formal and informal social control, supervision, and monitoring. In contrast, the social networks and activity spaces of poor families may be more restricted to the local neighborhood (Jencks and Mayer 1990), which makes children from poor families more dependent on the networks and institutional resources, or lack thereof, within the neighborhood.

Second, even if children from poor and more advantaged families are equally exposed to the local neighborhood context, poor children may be more susceptible to its influences. The personal experience of family poverty and blocked opportunities may legitimize “alternative” cultures and “institutional distrust” encountered in the neighborhood (Harding 2010). Children with poor parents may also be more sensitive to the absence of successful role models and the presence of “ghetto-related” subcultures in the local neighborhood (Wilson 1996). Without parents or resident adults to signal that socioeconomic advancement is possible, poor children living in disadvantaged neighborhoods may adopt fatalistic attitudes about their life chances that diminish their educational attainment. In addition, to acquire the cultural skills that facilitate advancement in the formal education system (Carter 2005), children with poor parents must rely more heavily on resident adults and neighborhood institutions. By contrast, children with economically advantaged parents can learn these skills at home. Finally, the experience of family poverty may also make poor children less resilient to the psychological, cognitive, and health effects of exposure to violence and environmental hazards.

In sharp contrast to compound disadvantage theory, relative deprivation theory, as it relates to neighborhood effect moderation, contends that the impact of neighborhood disadvantage is less severe for children in poor families than for children in nonpoor families because poor children are ill-equipped to realize the benefits associated with residence in more advantaged neighborhoods. First, because poor families lack disposable income, they may not be able to capitalize on the availability of institutional resources in advantaged neighborhoods (Jencks and Mayer 1990). For example, living in a neighborhood with quality childcare, high-end grocery stores, and many recreational programs may be of little consequence to families that cannot afford them.

Second, according to social psychological variants of relative deprivation theory, children evaluate themselves, and are evaluated by resident adults, relative to their neighborhood or school peers (Crosnoe 2009; Marsh 1987). This suggests that poor children living in more affluent neighborhoods may suffer stigmatization or develop negative self-perceptions that interfere with their schooling. Nonpoor children in affluent neighborhoods, by contrast, would not suffer the harmful psychological and emotional effects of relative deprivation. In other words, when children from poor families live in affluent neighborhoods, they may encounter a unique set of psychosocial harms that attenuate the potential benefits of residence in these areas.

Third, living in a more affluent neighborhood may also put children with poor parents at a competitive disadvantage for access to limited educational resources, such as college preparatory courses and attention from school staff (Crosnoe 2009; Jencks and Mayer 1990). Nonpoor children tend to be better prepared for class and have parents who are better equipped to navigate the school system (Lareau 2000), while children from poor families are disproportionately placed in less rigorous courses and overlooked by instructors. If neighbors act as competitors for limited institutional resources (Jencks and Mayer 1990), children from poor families are at a disadvantage in in affluent neighborhoods.

In addition to heterogeneity by family economic resources, neighborhood effects on educational outcomes may also differ by race. Wilson (1987, 1996) argued that black families living in disadvantaged urban neighborhoods are more likely than other groups to suffer racial discrimination linked to place. Similarly, owing to racial segregation and anti-black discrimination on the part of whites in nonpoor suburban communities (Massey and Denton 1993), black families in poor neighborhoods may have less access to institutions and people outside of their neighborhood than white families. Furthermore, black families may also be more susceptible to alternative or oppositional cultural models given their long history of oppression and marginalization. In sum, theory suggests that it is important to consider not only effect moderation by family poverty but also by race because blacks and whites may have differential exposure and susceptibility to the mechanisms thought to transmit the effects of disadvantaged neighborhoods.

Despite compelling theoretical rationales, prior research on neighborhood effect moderation by family economic resources is scarce, and results are mixed. Wheaton and Clarke (2003) investigate neighborhood effects on mental health and find that children from poor families are significantly more vulnerable to disadvantaged neighborhoods than children from nonpoor families. Sucoff and Upchurch (1998) also report evidence of neighborhood effect moderation, but in the opposite direction. In their analysis, neighborhood effects on teen childbearing appear to be more consequential for children in high-income families. South and Crowder (1999), Brewster (1994), and Brewster, Billy, and Grady (1993), on the other hand, find no evidence of neighborhood effect moderation by parental socioeconomic status in their analyses of adolescent sexual activity. Finally, the only study that investigates whether neighborhood effects on educational outcomes are moderated by family economic resources finds no evidence that the impact of neighborhood disadvantage varies by family income (Brooks-Gunn et al. 1993). As we discuss below, it is possible that past studies of neighborhood effect moderation yield inconsistent results because they do not properly measure and account for the dynamic coevolution of neighborhood contexts and family resources over time.

DEVELOPMENTAL TIMING OF NEIGHBORHOOD EXPOSURES

The consequences of living in disadvantaged neighborhoods also likely depend on the developmental timing of exposure. Previous theory and research, however, provide only limited guidance about differential sensitivity to neighborhood conditions at different stages of the early life course. On one hand, since school continuation decisions typically occur during late adolescence, residence in disadvantaged neighborhoods during this developmental stage may be especially consequential for educational attainment. Social isolation and alternative subculture theories, which contend that neighborhood effects operate primarily through socialization with peers and local adults, also suggest that adolescence is the stage at which the neighborhood environment is most influential. Because adolescence is the period when neighborhood peers and adults become central to a child's social life (Darling and Steinberg 1997), neighborhood effects transmitted through socialization mechanisms may only begin to have an appreciable impact at this developmental stage. Residence in disadvantaged neighborhoods earlier during childhood, by contrast, may have a more limited impact on later outcomes because the sphere of social interaction for young children is comparatively circumscribed.

On the other hand, neighborhood-effects theories that emphasize the role of violence, resource deprivation, and environmental hazards, together with research on child development, suggest a substantial impact for early childhood exposures to disadvantaged neighborhoods on educational outcomes—even those outcomes, like the decision to drop out of high school, that are not realized until many years later. For example, research on cognitive development and academic skill formation indicates that individuals are particularly sensitive to different forms of environmental deprivation early in childhood (Duncan et al. 1998; Heckman 2006; Heckman and Krueger 2004). To the extent that later educational outcomes are affected by abilities formed during childhood, exposure to neighborhood conditions that impact these abilities at a young age may have a lasting impact on school continuation decisions during adolescence. According to this perspective, then, early childhood exposures to violence, poor schools, and environmental health hazards may set children on a long-term developmental trajectory that impedes later success in school.

Several prior studies of neighborhood effects on other dimensions of child development suggest heterogeneous effects depending on the timing of neighborhood exposures (Sastry and Pebley 2010; Wheaton and Clarke 2003; Wodtke 2013). Results, however, are inconsistent. For example, Wodtke (2013) reports some evidence that adolescent exposures to neighborhood poverty are more consequential for the risk of teen childbearing than are childhood exposures, while Wheaton and Clarke (2003) find that childhood exposures to disadvantaged neighborhoods are more consequential for mental health measured in early adulthood. Previous research has not evaluated whether neighborhood effects on educational attainment depend on the timing of exposures during the early life course.

NEIGHBORHOOD SELECTION AND FEEDBACK

As children grow up, families often move, or the social composition of their neighborhood changes around them. Decisions to depart or stay in a particular neighborhood are determined by a variety of family characteristics, such as parental income and marital status. In turn, the same family characteristics that influence future neighborhood choices are themselves influenced by past neighborhood conditions. This process of dynamic neighborhood selection and feedback, whereby time-varying characteristics of the family environment are simultaneously outcomes of prior neighborhood conditions and determinants of future neighborhood attainment, presents a difficult methodological problem for estimating how the effects of neighborhood disadvantage vary across groups: time-varying family covariates may be confounders for the effect of future exposures, mediators for the effect of past exposures, and effect moderators. To assess the effects of time-varying neighborhood conditions for subgroups of children defined in terms of family characteristics that are themselves time-varying and endogenous to past neighborhoods, knowledge of the dynamic selection process is crucial.

Previous research highlights socioeconomic position, family structure, and race as important determinants of neighborhood attainment (Charles 2003; Sampson and Sharkey 2008; South and Crowder 1997a, 1997b, 1998a, 1998b; South and Deane 1993; Speare and Goldscheider 1987). Education, income, employment status, and homeownership are all closely linked to the social composition of the neighborhood in which a family resides, where those families who are more advantaged on these characteristics are much less likely to live in disadvantaged neighborhoods (Sampson and Sharkey 2008; South and Crowder 1997a, 1998a). In addition, parental marital status and family size are associated with neighborhood socioeconomic characteristics. Specifically, single parents and larger families are more likely than smaller and intact families to live in disadvantaged neighborhoods (Sampson and Sharkey 2008; South and Crowder 1998a; Speare and Goldscheider 1987). Past research also shows that spatial attainment is largely determined by race. Because of extensive discrimination at all levels of the residential sorting process, blacks are much more likely than whites to live in disadvantaged neighborhoods, regardless of group differences in education, income, or family structure (Massey and Denton 1993; Yinger 1995). Comparative studies of residential mobility show that black families, unlike their white counterparts, often struggle to convert personal resources into improved neighborhood conditions, indicating that neighborhood selection processes operate differently for blacks and whites (Iceland and Scopilliti 2008; South and Crowder 1998b; South and Deane 1993).

While there is considerable evidence that family structure and socioeconomic characteristics influence neighborhood attainment, theory and research also suggest that these covariates are themselves affected by neighborhood context (Fernandez and Su 2004; Wilson 1987; Wilson 1996). Wilson (1987) argued that adult residents of disadvantaged neighborhoods have more difficulty finding stable employment because of the paucity of jobs at appropriate skill levels in these areas (see also Fernandez and Su 2004). Living in a disadvantaged neighborhood also affects family structure, for example, by limiting the pool of potential spouses with sufficient income to support a family (Wilson 1987). Several studies suggest that exposure to disadvantaged neighborhoods leads to delayed marriage and increases the chances of non-marital fertility (South and Crowder 1999; South and Crowder 2010). Thus, time-varying family covariates may simultaneously confound, mediate, and moderate the effects of disadvantaged neighborhoods.

DATA AND MEASURES

We assess the impact of different longitudinal patterns of exposure to disadvantaged neighborhoods among subgroups of children defined by time-varying family income using data from the PSID. The PSID is a longitudinal study of families that focuses on the dynamic aspects of economic and demographic behavior. It began in 1968 with a probability sample of about 4,800 households. From 1968 to 1997, the PSID interviewed household members annually; after 1997, interviews were conducted biennially. Families are matched to census tracts with the restricted-use PSID geocode file, which contains tract identifiers for 1968 through 2003, and data on the socioeconomic composition of census tracts come from the Geolytics Neighborhood Change Database (NCDB). The NCDB contains nation-wide tract-level data from the 1970-2000 U.S. Censuses with variables and tract boundaries defined consistently across time. Tract characteristics for intercensal years are imputed using linear interpolation. Longitudinal data from the PSID together with tract-level measures from the NCDB allow us to analyze trajectories of neighborhood conditions and putative effect moderators throughout the early life-course.

The analytic sample for this study includes the 6,137 subjects who were present in the PSID at age 2 between 1968 and 1982. We focus on this particular cohort of children because it is the group for which we can obtain annual measurements of key variables throughout childhood and adolescence. Using all available data for these subjects between age 2 and 17, measurements of neighborhood disadvantage and family-level covariates are constructed separately by developmental period, where the time index k is used to distinguish between measurements taken during childhood (k = 1) and adolescence (k = 2). The outcome of interest, high school graduation, is measured at age 20.¹

Treatment in this study refers to exposure to different levels of neighborhood disadvantage. Following Wodtke et al. (2011), principal component analysis is used to generate a composite measure of neighborhood disadvantage based on seven tract characteristics: poverty, unemployment, welfare receipt, female-headed households, education (percent of residents age 25 or older without a high school diploma, percent of residents age 25 or older with a college degree), and occupational structure (percent of residents age 25 or older in managerial or professional occupations).² The childhood measurement of neighborhood disadvantage, A₁, is based on a subject's average tract disadvantage score over the four survey years from age 6 to 9. Neighborhood disadvantage during adolescence, A₂, is based on the average tract disadvantage score between age 14 and 17. To facilitate interpretation of results and simplify notation, we recode these multi-wave averages into ordinal treatment variables coded 1 through 5 that record the neighborhood disadvantage quintile—based on the national distribution of the composite disadvantage scores—in which a subject resides.³ Lower values of A_k indicate exposure to less disadvantaged neighborhoods and higher values indicate exposure to more disadvantaged neighborhoods (see Part A of the Appendix for details).

The analysis adjusts for time-invariant and time-varying covariates. The vector of time-invariant covariates includes gender, race, birth year, mother's age and marital status at the time of childbirth, and the family head's level of education.⁴ The vector of time-varying covariates includes the family income-to-needs ratio, the family head's marital and employment status, the family head's most recent occupation, homeownership, residential mobility, and family size, all of which are measured at every wave in the PSID. At each survey wave, parental marital status is dummy-coded, 1 for married and 0 for not married; employment status is coded 1 for employed and 0 for not employed; residential mobility is coded 1 if the family moved in the previous year, and 0 otherwise; homeownership is expressed as a dummy that indicates whether the family owns the residence they occupy; and household size counts the number of people present in a subject's family at the time of the interview. Family head's most recent occupation is expressed as a series of dummy variables for “unskilled manual occupations” (excluded category), “skilled manual occupations,” “clerks and sales occupations,” and “professional and managerial occupations.” We constructed an income-to-needs ratio that is equal to a family's annual real income divided by the official poverty threshold, which is indexed to family size. For ease of interpretation, the income-to-needs ratio is centered at the poverty line, so that this variable is greater than 0 for families with incomes that exceed poverty level and is less than 0 for families with sub-poverty incomes. The income-to-needs ratio enters all analyses as a continuous measure, but in the results section, we compute and display estimates based on selected values of this variable, using the descriptors “extremely poor,” “poor,” and “nonpoor” for families with incomes at one-half the poverty line (income-to-needs = −.5), at the poverty line (income-to-needs = 0), and at three times the poverty line (income-to-needs = 2), respectively.

We construct separate multi-wave averages of time-varying covariates during childhood and adolescence. The vector of time-varying covariates during childhood, L₁, is averaged over the survey waves in which a subject is age 2 to 5—the four waves immediately preceding measurement of childhood exposure to neighborhood disadvantage. To simplify notation, L₁ also includes all time-invariant covariates measured at baseline. Similarly, the vector of time-varying covariates during adolescence, L₂, is averaged over the survey waves in which a subject is age 10 to 13—the four waves preceding measurement of adolescent neighborhood disadvantage. These variables thus have the following temporal order: (L₁, A₁, L₂, A₂, Y), where Y is the outcome coded 1 if a subject graduated high school by age 20, and 0 otherwise. We use multiple imputation with 100 replications to fill in missing values for all covariates and the outcome (Royston 2005; Rubin 1987).

Figure 1 presents a directed acyclic graph (DAG) that describes the hypothesized causal relationships between neighborhood disadvantage, family covariates, unobserved factors, and the outcome, high school graduation. With DAGs, nodes represent variables, arrows represent direct causal effects, and the absence of an arrow indicates the absence of a direct causal effect (Pearl 1995; Pearl 2000). Consistent with theory and prior research, this figure shows that time-varying characteristics of the family environment are simultaneously confounders for the effect of future exposures to neighborhood disadvantage and mediators for the effect of past exposures to neighborhood disadvantage. Theory also suggests that time-varying family covariates are effect moderators. Specifically, family income is thought to temper or exacerbate the educational effects of exposure to disadvantaged neighborhoods. While effect moderation is not explicitly indicated in a DAG, Figure 1 is consistent with neighborhood effect moderation because the outcome in this graph depends on both treatment and the hypothesized effect moderator (Elwert and Winship 2010; VanderWeele 2009; VanderWeele and Robins 2009).⁵

METHODS

In this section, we first explicate a causal model that gives precise meaning to the difficult concept of neighborhood effect moderation by time-varying family income. Next, we explain why this causal model cannot be estimated with conventional methods, such as ordinary least squares regression or propensity score matching. Finally, we introduce a new estimator that overcomes the limitations of conventional methods to estimate the causal model.

A Counterfactual Model of Moderated Neighborhood Effects

The central aims of this analysis are to estimate how the causal effects of exposure to disadvantaged neighborhoods depend on (1) timing of exposure during childhood versus adolescence and (2) the evolving economic position of the family. In this section, we use the counterfactual framework to formally define the moderated neighborhood effects of interest (Almirall et al. 2011; Almirall, Ten Have, and Murphy 2010; Holland 1986; Robins 1994; Rubin 1974). For expositional clarity, we treat L₁ and L₂ as repeated measures of a single time-varying covariate, the family income-to-needs ratio; our empirical analyses below, however, incorporate vector-valued L_k.

Let the potential outcome Y(a₁, a₂) indicate whether a subject would have graduated high school had she been exposed to the sequence of neighborhood conditions (a₁, a₂) during childhood and adolescence, possibly contrary to fact. For example, Y(2, 1) is the subject's outcome had she been exposed to the second quintile of neighborhoods during childhood and the least disadvantaged, first quintile of neighborhoods during adolescence. Similarly, let L₂ (a₁) represent the family income-to-needs ratio the subject would have experienced during adolescence had she and her family been exposed to neighborhood conditions (a₁) during childhood. Note that L₂ (a₁) is itself a potential outcome. Because subjects are exposed to one of five levels of neighborhood disadvantage at two developmental periods, there are twenty-five potential education outcomes {Y(1, 1), Y(2,1), ... , Y(4,5), Y(5,5)} and five intermediate potential income-to-needs outcomes {L₂(1), L₂(2), ... , L₂(5)}. For each subject, we only observe the potential outcomes corresponding to the neighborhood contexts actually experienced; all other potential outcomes are unobserved, or counterfactual.

In the counterfactual framework, causal effects are defined as contrasts between potential outcomes. Defining sensible contrasts for moderated neighborhood effects in the longitudinal setting poses difficult conceptual problems. For example, consider the question, “what is the effect of continuously living in the most disadvantaged quintile of neighborhoods, rather than the least disadvantaged quintile, among children whose families are continuously poor?” Causal questions compare the same individuals in different counterfactual states, but this seemingly reasonable question actually implies a nonsensical comparison because the children whose families would stay poor had they been continuously exposed to the most disadvantaged neighborhoods and the children whose families would stay poor had they been continuously exposed to the least disadvantaged neighborhoods are not the same set of individuals.⁶ Avoiding these conceptual difficulties requires careful attention to the temporal ordering of time-varying treatments and moderators.

We define two sets of moderated neighborhood effects on the risk difference scale, one set for exposure to disadvantaged neighborhoods during childhood and one set for exposure during adolescence. The first set of moderated effects is defined as

u_{1} (L_{1}, a_{1}) = E (Y (a_{1}, 1) - Y (1, 1) ∣ L_{1}),

(1)

which gives the direct causal effect of childhood exposure to neighborhood disadvantage, holding adolescent neighborhood conditions constant. Specifically, it gives the average causal effect of exposure sequence (a₁, 1) compared to sequence (1,1) within levels of L₁. In words, u₁ (L₁, a₁) compares the probability of high school graduation had subjects been exposed to neighborhoods in quintile a₁ during childhood and neighborhoods in the least disadvantaged quintile during adolescence with the probability of high school graduation had subjects been continuously exposed to the least disadvantaged quintile of neighborhoods, separately for families with baseline income-to-needs given by L₁. For example, u₁ (L₁ = 0, a₁ = 5), is the causal effect of living in the most disadvantaged, fifth quintile of neighborhoods during childhood and then in the least disadvantaged quintile of neighborhoods during adolescence, rather than sustained exposure to neighborhoods in the least disadvantaged quintile throughout childhood and adolescence, among subjects whose families had poverty-level resources, L₁ = 0, at baseline.

We use a linear function, u₁(L₁, a₁) = (a₁ − 1)(β₁ + β₂L₁), to parameterize these effects: β₁ gives the average direct causal effect on high school graduation of childhood exposure to neighborhoods located in quintile a₁, rather than the less disadvantaged quintile a₁ − 1, among subjects in families with poverty-level resources during childhood, and β₂ increments this effect for subjects in families with incomes above or below the poverty line. If β₂ = 0, then the baseline income-to-needs ratio does not moderate the impact of exposure to disadvantaged neighborhoods during childhood.

The second set of moderated neighborhood effects is defined as

u_{2} (L_{2} (a_{1}), a_{2}) = E (Y (a_{1}, a_{2}) - Y (a_{1}, 1) ∣ L_{2} (a_{1})),

(2)

which gives the causal effect of adolescent exposure to neighborhood disadvantage, holding childhood neighborhood conditions constant. Specifically, it gives the average causal effect of neighborhood exposure sequence (a₁, a₂) compared to sequence (a₁, 1) within levels of L₂(a₁).

That is, u₂(L₂(a₁),a₂) compares the probability of high school graduation had subjects been exposed to neighborhoods in quintile a₁ during childhood and then neighborhoods in quintile a₂ during adolescence with the probability of high school graduation had subjects been exposed to neighborhoods in quintile a₁ during childhood but then neighborhoods in the least disadvantaged quintile during adolescence, separately for families with income-to-needs given by L₂(a₁). For example, u₂(L₂(5) = 0, a₂ = 5) is the causal effect of living in the most disadvantaged quintile of neighborhoods during adolescence, rather than the least disadvantaged quintile, had subjects first been exposed to the most disadvantaged quintile of neighborhoods during childhood and lived in families that would have poverty-level incomes L₂(5) = 0 during adolescence under this childhood exposure.

We use a linear function, u₂(L₂(a₁),a₂) = (a₂ − 1)(β₃ + β₄L₂(a₁)), to parameterize the average causal effects of adolescent exposure to different neighborhood conditions for subgroups of individuals defined in terms of their family's income-to-needs ratio measured during adolescence: L₃ gives the average causal effect on high school graduation of adolescent exposure to neighborhoods located in quintile a₂, rather than the less disadvantaged quintile a₂ − 1, holding neighborhood conditions during childhood constant, among subjects in families that would have poverty-level resources during adolescence under the fixed childhood exposure, and L₄ increments this effect for subjects in families that would have incomes above or below the poverty line at this development stage. As above, if β⁴ = 0, then the family income-to-needs ratio does not moderate the impact of adolescent exposure to neighborhood disadvantage.⁷

The causal functions defined here describe how the effects of exposure to disadvantaged neighborhoods during childhood versus adolescence depend on the evolving economic position of the family. By including cross-product terms for the family income-to-needs ratio and neighborhood context, these functions allow us to evaluate the competing predictions of compound disadvantage theory and relative deprivation theory. In addition, by evaluating moderated neighborhood effects within a longitudinal framework, we can examine whether individuals’ sensitivity to different neighborhood conditions varies by developmental stage.

These causal functions involve conditional counterfactuals that are quite complex. For clarity, it can be helpful to explain u₁(L₁,a₁) and u₂(L₂(a₁),a₂) using the language and logic of sequential experiments. Consider a hypothetical experiment where, at baseline (i.e., childhood), the researcher would first measure the family incomes of each subject in the study. Next, the researcher would randomly assign all subjects (and their families) to neighborhoods in different quintiles of the disadvantage distribution during childhood, and then later, during adolescence, assign all subjects to neighborhoods in a single disadvantage quintile. Finally, the researcher would observe at the end of follow-up whether or not each subject graduated high school. Comparing mean outcomes for subjects assigned to different neighborhood contexts during childhood, separately by their family incomes at baseline, would be an experimental estimate of u₁(L₁,a₁), the childhood causal function.

The moderating role of family income with respect to adolescent neighborhood disadvantage would be captured by a different hypothetical experiment. In this experiment, the researcher would first assign all subjects to neighborhoods in a single disadvantage quintile during childhood and measure their family incomes only after this initial intervention. Then, the researcher would randomly assign subjects to neighborhoods in different quintiles of the disadvantage distribution during adolescence and measure high school graduation at the end of follow-up. Comparing mean outcomes for subjects assigned to different neighborhood contexts during adolescence, separately by family incomes measured just prior to adolescent treatment assignment, would be an experimental estimate of u₂(L₂(a₁),a₂), the adolescent causal function. Note that, rather than conducting two separate experiments to estimate u₁(L₁,a₁) and u₂(L₂(a₁),a₂), one could also conduct a single experiment in which subjects are randomly assigned to different neighborhood quintiles during both childhood and adolescence, and measurements of family income are taken just prior to treatment assignment at each developmental stage. Such a sequentially randomized experiment is the canonic motivation for the structural nested mean model (SNMM), which is used to simultaneously estimate the two sets of moderated causal effects identified from this research design (Almirall et al. 2010; Robins 1994).

The SNMM is a particular decomposition of the conditional expectation of Y(a₁, a₂) given (L₁, L₂(a₁)) that includes the moderated neighborhood effects of interest, u₁ (L₁,a₁) and u₂ (L₂(a₁),a₂), as well as a set of “nuisance” functions, denoted by ε₁(L₁) and ε₂(L₁,a₁,L₂(a₁)), that capture the (causal or noncausal) association of the moderator with the outcome (Almirall et al. 2010; Almirall et al. 2011; Almirall, Ten Have, and Murphy 2010; Robins 1994). These nuisance functions are not of direct substantive interest, but estimating moderated neighborhood effects requires their correct specification in the model. Specifically, in this analysis, the SNMM is expressed as

E (Y (a_{1}, a_{2}) ∣ L_{1}, L_{2} (a_{1})) = β_{0} + ε_{1} (L_{1}) + u_{1} (L_{1}, a_{1}) + ε_{2} (L_{1}, a_{1}, L_{2} (a_{1})) + u_{2} (L_{2} (a_{1}), a_{2}),

(3)

where β₀ = E(Y(1,1)) is the mean of the potential outcomes under sustained exposure to the least disadvantaged quintile of neighborhoods, ε₁(L₁) = E(Y(1,1)|L₁) − E(Y(1,1)) is the association between the childhood income-to-needs ratio, L₁, and high school graduation had all subjects lived only in the least disadvantaged quintile of neighborhoods, and ε₂(L₁,a₁,L₂(a₁)) = E(Y(a₁,1)|L₁,L₂(a₁)) − E(Y(a₁,1)|L₁) is the association between the adolescent income-to-needs ratio, L₂, and high school graduation had subjects with characteristics (a₁,L₁) lived in the least disadvantaged quintile of neighborhoods during adolescence.⁸

An important property of the nuisance functions, ε₁(L₁) and ε₂(L₁,a₁,L₂(a₁)), is that their conditional expectation zero given the past (Almirall et al. 2011; Almirall et al. 2010). Indeed, the central challenge to estimating the causal functions of the SNMM is to parameterize the nuisance functions in a way that preserves this zero conditional expectation property. To this end, ε₁(L₁) is modeled with the function η₁(L₁ − E(L₁)), and ε₂(L₁,a₁,L₂(a₁)) is modeled with the function η₂(L₂(a₁) − E(L₂(a₁)|L₁)). Note that the terms in parentheses associated the parameters η₁ and η₂ are like residuals for the childhood and adolescent measurements of the income-to-needs ratio. This property informs the two-stage estimation strategy explained below.

The causal effects defined in Equations 1 and 2 can be identified from observed data under the assumption of sequential ignorability of treatment assignment (Almirall et al. 2011; Almirall et al. 2010; Robins 1994). Formally, this condition is expressed in two parts as Y(a₁,a₂) ⊥ A₁|L₁ and Y(a₁, a₂) ⊥ A₂|L₁, A₁, L₂, where ⊥ denotes statistical independence. Substantively, this condition states that at each time period there exist no other variables that directly affect selection into different neighborhood contexts and the outcomes, high school graduation, apart from prior measured covariates and prior neighborhood context, as previously illustrated in Figure 1. Sequential ignorability is met by design in experimental studies where treatment is randomly assigned at each time point. In observational studies, however, satisfying this assumption requires data on all the joint predictors of neighborhood disadvantage and high school graduation (we present a sensitivity analysis for potential violations of this assumption below).

Limitations of Conventional Regression Estimation

Estimating how the causal effects of time-varying neighborhood conditions are moderated by time-varying family incomes is difficult. In this section, we briefly present an explanation for why traditional regression methods fail at this task. Consider the conventional linear probability model for the effects of exposure to disadvantaged neighborhoods during childhood and adolescence with a single time-varying effect moderator, the family income-to-needs ratio:

E (Y ∣ L_{1}, A_{1}, L_{2}, A_{2}) = λ_{0} + λ_{1} L_{1} + (A_{1} - 1) (λ_{2} + λ_{3} L_{1}) + λ_{4} L_{2} + (A_{2} - 1) (λ_{5} + λ_{6} L_{2}) .

(4)

Equation 4 includes “main effects” for neighborhood disadvantage and the income-to-needs ratio measured at each developmental period. The model also includes interaction terms that allow the coefficients on neighborhood disadvantage to vary for families with incomes above or below the poverty line.

Unfortunately, this model yields biased estimates of moderated causal effects even if the assumption of sequential ignorability is true. Because Equation 4 directly conditions on the adolescent income-to-needs ratio, L₂, which is affected by childhood exposure to neighborhood disadvantage, the parameters λ₂ and λ₃ do not represent the moderated causal effects of childhood exposure to neighborhood disadvantage. As depicted graphically in Figure 2, conditioning on L₂ removes the indirect effect of exposure to disadvantaged neighborhoods during childhood that is transmitted through the family income-to-needs ratio during adolescence and may induce a noncausal association between neighborhood context and unobserved determinants of high school graduation (Elwert and Winship 2012; Greenland 2003; Pearl 1995; Pearl 2000).⁹

Problems with Conventional Regression Models

In other words, even with data from an experiment that sequentially randomized exposure to disadvantaged neighborhoods, conventional regression models would fail to recover the moderated effects of neighborhood disadvantage if the moderating variable of interest were time-varying and affected by past neighborhood conditions (Almirall et al. 2011; Almirall et al. 2010; Robins 1987, 1994, 1999a, 1999b). Similar problems prevent the estimation of moderated neighborhood effects with propensity score matching.¹⁰ Thus, alternative methods are needed to estimate the effects of interest in this study.

Two-stage Regression-with-Residuals Estimation

Almirall and colleagues (2011; 2010) recently developed a novel two-stage regression estimator for the SNMM that is motivated by the zero conditional expectation property of the nuisance functions discussed previously. This approach is similar to estimating a conventional regression model, but it overcomes the problems of conventional regression by proceeding in two stages. In the first stage, all time-varying covariates are regressed on the observed past to obtain estimated residuals. For example, we regress the income-to-needs ratios in childhood and adolescence on prior neighborhood context and time-varying covariates in models with form E(L₁) = α₀ and E(L₂|L₁,A₁) = γ₀ + γ₁L₁ + (A₁ − 1)(γ₂ + γ₃L₁), and then we estimate residuals as $L_{1}^{r} = L_{1} - \hat{E} (L_{1})$ and $L_{2}^{r} = L_{2} - \hat{E} (L_{2} ∣ L_{1}, A_{1})$ . In the second stage, the SNMM is estimated by regressing the outcome on neighborhood context and the residualized time-varying covariates in an observed data model with form,

E (Y ∣ L_{1}, A_{1}, L_{2}, A_{2}) = β_{0} + η_{1} L_{1}^{r} + (A_{1} - 1) (β_{1} + β_{2} L_{1}) + η_{2} L_{2}^{r} + (A_{2} - 1) (β_{3} + β_{4} L_{2}) .

(5)

As described above, the beta coefficients estimate how the probability of high school graduation is expected to change with exposure to different neighborhood contexts during childhood versus adolescence, conditional on prior income-to-needs, and the eta coefficients capture the association between time-varying covariates and high school graduation. The crucial difference between Equation 5 and the conventional regression model in Equation 4 is that Equation 5 includes “main effects” for the residualized time-varying covariates obtained from the first-stage regressions rather than for the untransformed values of these covariates. In other words, Equation 5 uses $η_{1} L_{1}^{r}$ as the model for ε₁(L₁) and $η_{2} L_{2}^{r}$ as the model for ε₂(L₁,a₁,L₂(a₁)), which satisfy the zero conditional expectation property of these functions.

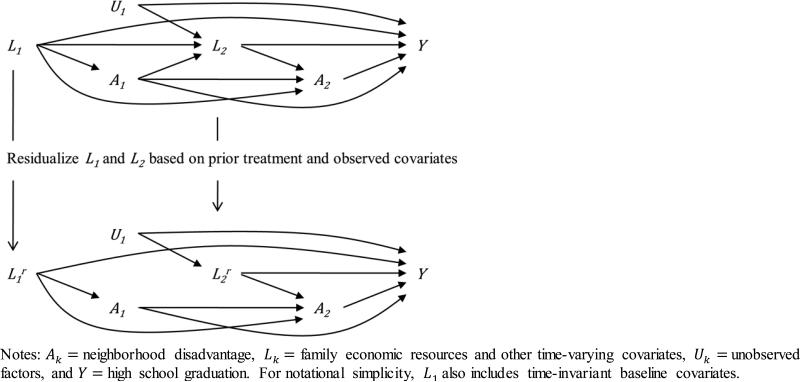
Figure 3 shows a stylized graph describing how the relationship between treatment and future time-varying covariates changes after the latter are transformed into residuals. Residualizing the adolescent income-to-needs ratio purges it of its association with neighborhood disadvantage during childhood (i.e., no arrow from A₁ to $L_{2}^{r}$ ). Conditioning on the residualized income-to-needs ratio in the second-stage regression, then, does not “control away” the indirect effect of childhood exposure to disadvantaged neighborhoods that operates through this time-varying covariate nor does it induce an association between childhood exposure status and unobserved determinants of high school graduation. Thus, unlike conventional regression, regression-with-residuals estimation avoids the problems associated with time-varying covariates affected by prior treatment, and it is unbiased for the moderated neighborhood effects of interest under the assumptions of no unobserved confounders and no model misspecification.

Consequences of Residualizing Time-varying Covariates

We compute regression-with-residuals estimates of the moderated effects of neighborhood disadvantage on high school graduation, focusing on a single time-varying moderator, the income-to-needs ratio, because theory suggests an important role for family income in dampening or amplifying the effects of neighborhood context. Other covariates are treated as controls, entering only the nuisance functions in the SNMM. Estimates are reported for the total population and also for blacks and whites separately to investigate potential differences in the severity of neighborhood effects by race.¹¹ Standard errors are estimated from 1,000 bootstrap samples (Efron and Tibshirani 1993).

The PSID oversampled low-income families, which necessitates the use of weights to generate descriptive statistics that are representative of the target population. We focus on unweighted descriptive statistics in the main text in order to document that analyses of moderated neighborhood effects do not rely on out-of-sample extrapolation, but we also report weighted descriptive statistics that adjust for the oversampling of low-income families in Part B of the Appendix. The weighted descriptive statistics represent population distributions, while the unweighted descriptive statistics indicate whether the PSID sample supports estimation of moderated neighborhood effects, which is the central concern in this analysis.

In addition, we present unweighted estimates of moderated neighborhood effects in the main text because, with regression analysis, sampling weights are unnecessary and inefficient as long as the model sufficiently controls for the design variables—in this case, family income—that determine the unequal probabilities of sample selection (Pfeffermann 1993; Winship and Radbill 1994). Comparisons of weighted and unweighted neighborhood effect estimates, which are similar, together with explicit tests demonstrating that weights can be safely ignored in the analysis of neighborhood effects, confirm that the SNMM described above sufficiently controls for all relevant aspects of the sample design (see Part B of the Appendix for details). In this situation, unweighted effect estimates are preferred because they are both representative and more efficient than the corresponding weighted effect estimates.

The SNMM, which is used in this study to analyze moderated, or subpopulation average, effects of time-varying neighborhood exposures, has a convenient functional relationship with the marginal structural model (MSM), which has been used in prior research to analyze marginal, or population average, effects of time-varying neighborhood exposures (Sampson et al. 2008; Sharkey and Elwert 2011; Wodtke et al. 2011; Wodtke 2013). Formally, the MSM is equivalent to the SNMM when averaged over the time-varying moderators—that is, E(Y(a₁,a₂) = E(E(Y(a₁,a₂)|L₁,L₂(a₁))). Substantively, this equivalence reflects a similar logic to that underlying the relationship between marginal versus moderated, or population versus subpopulation average, effects in the point-in-time setting. There, the population average effect is equivalent to the weighted mean of the subpopulation average effects with weights equal to the relative size of each subpopulation (Morgan and Winship 2007). This relationship indicates that marginal effects can be obtained from a SNMM via post-processing of the moderated effects. The converse, however, is not true: one cannot recover the moderated effects in an SNMM from the population average effects in an MSM. In other words, SNMMs extend MSMs by additionally permitting an analysis of whether the population average effects of a time-varying treatment obscure (i.e., average over) important differences across time-varying subpopulations.

RESULTS

Sample Characteristics

Time-invariant sample characteristics are summarized in Table 1, revealing considerable racial disparities. Overall, 80 percent of the total sample graduated high school by age 20, but only 74 percent of black subjects are high school graduates compared to 85 percent of white subjects. Parents of black subjects are also much more disadvantaged than parents of white subjects. For example, black subjects are more likely than white subjects to have been born to young unmarried mothers, and black heads of household have much lower educational attainment than their nonblack counterparts. Table 2 presents descriptive statistics for time-varying covariates, which further document sizeable racial disparities in the analytic sample.

Table 1.

Time-invariant Covariates

Variable	Total		Blacks		Whites
Variable	mean	sd	mean	sd	mean	sd

S - high school graduate	.80	(.40)	.74	(.44)	.85	(.36)
S - female	.48	(.50)	.49	(.50)	.48	(.50)
M - age at childbirth	24.79	(5.56)	23.79	(5.63)	25.71	(5.27)
M - married at childbirth	.71	(.45)	.50	(.50)	.91	(.29)
H - high school graduate	.24	(.43)	.25	(.43)	.25	(.43)
H - some college	.26	(.44)	.20	(.40)	.33	(.47)
H - college graduate	.09	(.29)	.02	(.13)	.16	(.37)

Open in a new tab

Notes: Results are combined estimates from 100 multiple imputation datasets. S, M, and H indicate subject, mother of subject, and household head, respectively.

Table 2.

Time-varying Covariates

Variable	Total		Blacks		Whites
Variable	mean	sd	mean	sd	mean	sd

Childhood
H - married	.73	(.40)	.58	(.45)	.88	(.28)
H - employed	.79	(.35)	.67	(.40)	.90	(.23)
H - skilled manual occupations	.47	(.50)	.46	(.50)	.48	(.50)
H - clerks and sales occupations	.11	(.32)	.11	(.31)	.12	(.33)
H - prof. and managerial occupations	.16	(.37)	.05	(.22)	.27	(.44)
FU - owns home	.46	(.45)	.30	(.41)	.63	(.43)
FU - size	4.85	(1.78)	5.23	(2.06)	4.47	(1.32)
FU - number of moves	1.15	(1.13)	1.20	(1.12)	1.08	(1.13)
FU - inc-to-needs ratio	.89	(1.22)	.35	(.92)	1.42	(1.26)
Adolescence
H - married	.67	(.44)	.49	(.47)	.83	(.34)
H - employed	.78	(.37)	.65	(.42)	.90	(.25)
H - skilled manual occupations	.42	(.49)	.42	(.49)	.41	(.49)
H - clerks and sales occupations	.13	(.33)	.14	(.35)	.11	(.32)
H - prof. and managerial occupations	.22	(.41)	.09	(.28)	.35	(.48)
FU - owns home	.57	(.46)	.40	(.46)	.74	(.40)
FU - size	4.86	(1.57)	5.09	(1.84)	4.63	(1.21)
FU - number of moves	.76	(1.01)	.83	(1.03)	.68	(.97)
FU - inc-to-needs ratio	1.28	(1.65)	.54	(1.14)	2.00	(1.77)

Open in a new tab

Notes: Results are combined estimates from 100 multiple imputation datasets. H and FU indicate household head and family unit, respectively.

Neighborhood Conditions during Childhood and Adolescence

Table 3 describes exposure to different levels of neighborhood disadvantage during childhood and adolescence for black and white subjects. The main diagonal cells show the extent of continuity in neighborhood conditions, while the off-diagonal cells describe upward and downward neighborhood mobility.

Table 3.

Joint Treatment Distribution

n row cell		Blacks					Whites
		NH disadvantage quintile - adolescence					NH disadvantage quintile - adolescence
		1	2	3	4	5	1	2	3	4	5
NH disadvantage quintile - childhood	1	35	11	7	7	2	336	52	23	15	3
		.56	.18	.11	.11	.03	.78	.12	.05	.04	.01
		.01	.00	.00	.00	.00	.11	.02	.01	.01	.00
	2	20	29	25	10	6	160	257	81	31	7
		.22	.32	.28	.11	.07	.30	.48	.15	.06	.01
		.01	.01	.01	.00	.00	.05	.09	.03	.01	.00
	3	16	39	59	41	33	47	224	360	104	31
		.09	.21	.31	.22	.18	.06	.29	.47	.14	.04
		.01	.01	.02	.01	.01	.02	.08	.12	.03	.01
	4	12	29	73	182	162	29	58	217	404	112
		.03	.06	.16	.40	.35	.04	.07	.26	.49	.14
		.00	.01	.03	.06	.06	.01	.02	.07	.14	.04
	5	12	32	80	235	1744	6	13	42	123	247
		.01	.02	.04	.11	.83	.01	.03	.10	.29	.57
		.00	.01	.03	.08	.60	.00	.00	.01	.04	.08

Open in a new tab

Notes: Results are combined estimates from 100 multiple imputation datasets.

Among black subjects, 60 percent are exposed to the most disadvantaged quintile of American neighborhoods during both childhood and adolescence. While the majority of black subjects grow up in highly disadvantaged neighborhoods, a nontrivial number live in less disadvantaged areas and some of these individuals are upwardly mobile. For example, among black subjects living in third quintile neighborhoods during childhood, about 30 percent remain in these neighborhoods and another 30 percent move to less disadvantaged neighborhoods during adolescence. Downward neighborhood mobility is also common, however, with about 40 percent of black subjects in third quintile neighborhoods during childhood moving to more disadvantaged neighborhoods in adolescence.

Compared to their black counterparts, white subjects grow up in much less disadvantaged neighborhoods. Only 8 percent of white subjects live in the most disadvantaged, fifth quintile of neighborhoods throughout childhood and adolescence, and upward mobility from these areas is more common. About 11 percent of white subjects live in the least disadvantaged, first quintile of neighborhoods throughout the early life course, and nearly 30 percent are continuously exposed to either first or second quintile neighborhoods. By contrast, only about 3 percent of black subjects live in either first or second quintile neighborhoods during childhood and adolescence. Most white subjects live in second through fourth quintile neighborhoods during childhood, and many transition upward to less disadvantaged neighborhoods in adolescence. The frequent mobility between different neighborhood contexts among both black and white subjects underscores the importance of longitudinal measurement and dynamic modeling strategies in research on neighborhood effects.

Table 4 describes differences in exposure to neighborhood disadvantage during childhood and adolescence by prior family resources among the total sample of children. The rows in this table define different levels of the income-to-needs ratio, where values below zero represent sub-poverty incomes and values greater than zero represent incomes above the poverty line. Family income during childhood and adolescence are strongly related to neighborhood context, where those with higher income-to-needs ratios are much less likely to live in the most disadvantaged neighborhoods and much more likely to live in the least disadvantaged neighborhoods, compared to those with lower income-to-needs ratios, as expected.

Table 4.

Treatment Distribution at Childhood and Adolescence by Prior Family Income

n row cell		Childhood					Adolescence
		NH disadvantage quintile					NH disadvantage quintile
		1	2	3	4	5	1	2	3	4	5
Family income-to-needs ratio	>2	273	220	183	178	129	485	373	322	237	195
		.28	.22	.19	.18	.13	.30	.23	.20	.15	.12
		.04	.04	.03	.03	.02	.08	.06	.05	.04	.03
	(1,2]	121	217	325	342	343	132	213	321	330	383
		.09	.16	.24	.25	.25	.10	.15	.23	.24	.28
		.02	.04	.05	.06	.06	.02	.03	.05	.05	.06
	[0,1]	92	163	386	571	976	62	148	259	406	858
		.04	.07	.18	.26	.45	.04	.09	.15	.23	.50
		.01	.03	.06	.09	.16	.01	.02	.04	.07	.14
	<0	25	58	96	246	1193	23	41	100	236	1013
		.02	.04	.06	.15	.74	.02	.03	.07	.17	.72
		.00	.01	.02	.04	.19	.00	.01	.02	.04	.17

Open in a new tab

Notes: Results are combined estimates from 100 multiple imputation datasets. Income-to-needs ratio is centered around 1 such that values less than zero represent sub-poverty incomes, values equal to 0 represent poverty-level incomes, and values greater than 0 represent incomes above the poverty line.

Poor families, however, are not restricted to living in disadvantaged neighborhoods, and families of greater means are not bound to more advantaged communities. For example, Table 4 shows that 13 percent of subjects in families with income-to-needs ratios greater than two during childhood (i.e., with incomes more than three times the poverty line) are exposed to the most disadvantaged quintile of neighborhoods during the same developmental period. Among subjects in families with incomes at or just above the poverty line during childhood, 4 percent and 7 percent live in less disadvantaged first and second quintile neighborhoods, respectively. Even among subjects in extremely poor families with sub-poverty incomes, a nontrivial number live in less disadvantaged first and second quintile neighborhoods, and many subjects at all income-to-needs levels reside in third quintile neighborhoods.

In sum, the descriptive statistics presented in Tables 3 and 4 show that most transitions between neighborhood quintiles from childhood to adolescence, and all combinations of family incomes and neighborhood exposures at different development periods, are well represented in the analytic sample. These unweighted sample distributions document that this analysis avoids out-of-sample extrapolation—that is, the extent of variation in neighborhood exposures both over time and at different levels of the family income distribution allows for the estimation of moderated neighborhood effects in the longitudinal setting.

Moderated Neighborhood Effects

Table 5 presents two-stage regression-with-residuals estimates for the SNMM causal function parameters. The first column contains results from the total sample. Estimates for the direct effect of childhood exposure to neighborhood disadvantage are highly imprecise and fail to reach conventional thresholds of statistical significance. The point estimates suggest a negligible direct impact of exposure to neighborhood disadvantage during childhood ( ${\hat{β}}_{1} = - .005$ , p = .674) and provide little evidence of effect moderation by prior levels of the family income-to-needs ratio ( ${\hat{β}}_{2} = .005$ , p = .256). For example, among individuals in poor families, even the most extreme treatment contrast—exposure to the most disadvantaged quintile of neighborhoods during childhood and then exposure to the least disadvantaged quintile of neighborhoods during adolescence, compared to sustained residence in the least disadvantaged quintile of neighborhoods—is estimated to reduce the probability of high school graduation by only 2 percentage points (i.e., ${\hat{u}}_{1} (L_{1} = 0, a_{1} = 5) = \hat{E} (Y (5, 1) - Y (1, 1) ∣ L_{1} = 0) = 4 ({\hat{β}}_{1} + {\hat{β}}_{2} L_{1}) = 4 (- .005 + .005 (0)) = - .020$ , where L₁ = 0 indicates that a subject's family is at the poverty line during childhood). Among individuals in families above or below the poverty line, the direct effects of neighborhood disadvantage during childhood are also modest. Thus, regardless of family income, results indicate that childhood exposure to different neighborhood contexts has a minimal impact on high school graduation if adolescent neighborhood conditions are held constant.

Table 5.

Moderated Effects of Neighborhood Disadvantage on High School Graduation

Model	Total			Blacks			Whites
Model	coef	se		coef	se		coef	se
Intercept	.884	(.021)	^***	.915	(.046)	^***	.885	(.019)	^***
Childhood
NH dadvg	–.005	(.011)		–.004	(.019)		–.008	(.015)
NH dadvg × inc-to-needs	.005	(.004)		.005	(.008)		.006	(.005)
Adolescence
NH dadvg	–.041	(.010)	^***	–.054	(.016)	^***	–.025	(.013)	^†
NH dadvg × inc-to-needs	.012	(.003)	^***	.016	(.006)	^*	.006	(.004)

Open in a new tab

Notes: Results are combined estimates from 100 multiple imputation datasets. Standard errors are based on 1000 bootstrap samples. The income-to-needs ratio is centered at the poverty line.

^†

p < 0.10

p < 0.05

**p < 0.01, and

^***

p < 0.001 for two-sided tests of no effect.

Estimates for the effect of adolescent neighborhood context, by contrast, indicate that exposure to disadvantaged neighborhoods during this developmental period has a strong and statistically significant negative effect on high school graduation ( ${\hat{β}}_{3} = - .041$ , p < .001) and that this effect is moderated by the family income-to-needs ratio ( ${\hat{β}}_{4} = .012$ , p < .001).

Consistent with compound disadvantage theory, these estimates indicate that disadvantaged neighborhoods are especially harmful for individuals from poor families. For example, among individuals in families living at the poverty line during adolescence, exposure to the most disadvantaged quintile of neighborhoods, rather than the least disadvantaged quintile, is estimated to reduce the probability of high school graduation by about 16 percentage points. For individuals in families who are extremely poor during adolescence, exposure to the most disadvantaged quintile of neighborhoods, compared to the least disadvantaged quintile, is estimated to reduce the probability of high school graduation by about 19 percentage points (i.e., ${\hat{u}}_{2} (L_{2} (a_{1}) = - .5, a_{2} = 5) = \hat{E} (Y (a_{1}, 5) - Y (a_{1}, 1) ∣ L_{2} (a_{1}) = - .5) = 4 ({\hat{β}}_{3} + {\hat{β}}_{4} L_{2}) = 4 (- .041 + .012 (- .5)) = - .188$ , where L₂ = −.5 indicates that a subject's family has an income equal to one-half the poverty line during adolescence).

The effects of adolescent exposure to disadvantaged neighborhoods for nonpoor individuals, on the other hand, are much less severe. Among individuals from nonpoor families with incomes equivalent to three times the poverty line during adolescence, exposure to the most, compared to the least, disadvantaged quintile of neighborhoods during the same developmental period only reduces the probability of high school graduation by about 7 percentage points. In sum, these results indicate that an individual's chance of high school graduation is most sensitive to neighborhood context during adolescence, and that family poverty intensifies the negative effects of adolescent exposure to disadvantaged neighborhoods.

Separate effect estimates from black and white subjects are reported in the second and third columns of Table 5. These estimates are comparable to those from the total sample, indicating that adolescent exposure to disadvantaged neighborhoods is highly consequential, while the direct effect of earlier exposure during childhood is negligible, and that effects are most severe for subjects living in poor families. Among blacks, exposure to the most disadvantage quintile of neighborhoods during adolescence, compared to the least disadvantaged quintile, is estimated to lower the probability of high school graduation by 25 percentage points for subjects whose families are extremely poor, by 22 percentage points for subjects in families at the poverty line, and by only 9 percentage points for subjects in nonpoor families during adolescence.

Among whites, estimates associated with adolescent neighborhood context are smaller and only marginally significant, but they too suggest harmful effects for disadvantaged neighborhoods during this developmental stage that are amplified by family resource deprivation. Specifically, adolescent exposure to the most disadvantaged quintile of neighborhoods, rather than the least disadvantaged quintile, is estimated to reduce the probability of high school graduation by 10 percentage points for whites in poor families and by 5 percentage points for whites in families with resources equivalent to three times the poverty line.

Figure 4 displays probabilities of high school graduation for blacks with different neighborhood and family income histories computed from the SNMM estimates. The graph shows how the probability of high school graduation would be expected to change if black subjects that had lived in middle class, third quintile neighborhoods during childhood were later exposed to different levels of neighborhood disadvantage in adolescence. Estimates are plotted separately for subjects living in families that were extremely poor, poor, or nonpoor during both childhood and adolescence to illustrate the magnitude of effect moderation by family income.

Predicted Probability of High School Graduation by Adolescent Exposure to Neighborhood Disadvantage and Family Poverty History, Black Respondents

Results indicate that if black subjects in both poor and extremely poor families had lived in third quintile neighborhoods during childhood and then moved to a neighborhood in the least disadvantaged quintile during adolescence, about 91 percent would have graduated high school by age 20. If, on the other hand, these same individuals had moved from third quintile neighborhoods in childhood to the most disadvantaged quintile of neighborhoods during adolescence, only an estimated 70 percent of poor subjects and 66 percent of extremely poor subjects would have graduated high school. For blacks living with nonpoor families, an estimated 92 percent would have graduated had they moved, between childhood and adolescence, from third quintile neighborhoods to neighborhoods in the least disadvantaged quintile. About 83 percent of nonpoor blacks would be expected to graduate had they instead moved to the most disadvantaged quintile of neighborhoods during adolescence.

Figure 5 displays predicted probabilities of high school graduation for whites by neighborhood and family income history. These estimates indicate that had white subjects in poor and in nonpoor families been exposed to third quintile neighborhoods during childhood and then later moved to the least disadvantaged, first quintile of neighborhoods during adolescence, about 88 percent of both groups would be expected to graduate from high school. If, on the other hand, these same individuals had moved to neighborhoods in the most disadvantaged quintile during adolescence, an estimated 78 percent of whites in poor families and 84 percent of those in nonpoor families would have graduated high school.

Predicted Probability of High School Graduation by Adolescent Exposure to Neighborhood Disadvantage and Family Poverty History, White Respondents

Sensitivity Analyses

Under the assumptions of no unobserved confounding (i.e., sequential ignorability) and no model misspecification (i.e., correct functional form), the estimates presented previously can be interpreted as average causal effects of neighborhood context among different subgroups of children defined by their time-varying family income history. These assumptions are strong, and their violation would invalidate inferences about the moderated effects of disadvantaged neighborhoods. First, if either the causal or nuisance functions of the SNMM were incorrectly specified, then neighborhood-effect estimates would be biased. Experimentation with a wide variety of specifications for both the causal and nuisance functions, however, indicates that the reported estimates are robust (see Part C of the Appendix for details).

Second, if there were unmeasured factors that simultaneously affect neighborhood selection and the probability of high school graduation, then effect estimates would be biased due to unobserved confounding of neighborhood context. The assumption of no unobserved confounding is not directly testable, but we measure and adjust for an extensive set of confounders to mitigate this problem as much as possible. Furthermore, we formally investigate the sensitivity of our effect estimates to hypothetical patterns of unobserved confounding. Results from this formal sensitivity analysis, summarized in Part D of the Appendix, indicate that the magnitude of unobserved confounding would have to be extremely large to alter our inferences about the effects of adolescent exposure to disadvantaged neighborhoods. For example, among individuals in poor families, we find that the effect of adolescent neighborhood disadvantage remains statistically significant even in the situation where unobserved confounding is assumed to be twice as strong as the amount of confounding due to all observed covariates included in the empirical analysis.

Finally, because subjects may drop out of the PSID before the end of follow-up, some are missing covariate and outcome data. To account for the uncertainty associated with missing information, we report combined estimates based on multiple imputation. In Part E of the Appendix, we additionally compute estimates using multiple imputation with deletion (von Hippel 2007), single regression imputation (Longford 2005), and complete case analysis to investigate whether our estimates are sensitive to different methods of missing data adjustment. Results indicate that estimates of moderated neighborhood effects are quite stable under different procedures for handling missing data.

DISCUSSION

Research on the spatial dimensions of social stratification is central to understanding the reproduction of poverty and persistent educational inequality in the U.S. Although the educational consequences of disadvantaged neighborhoods are extensively studied, previous research has not rigorously investigated whether neighborhood effects on high school graduation are moderated by the evolving state of a child's family resources or depend on the timing of exposure to different neighborhood contexts during childhood versus adolescence. Using novel methods that properly account for dynamic neighborhood selection, this study finds that exposure to concentrated disadvantage, particularly during adolescence, has a strong negative effect on the chances of high school graduation, and it reveals that the consequences of adolescent exposure to disadvantaged neighborhoods are more severe for individuals whose families are also economically disadvantaged. By contrast, the effect of neighborhood disadvantage is less pronounced for those exposed earlier during childhood and among adolescents whose families live well above poverty level. Neighborhood effects are thus moderated, time-dependent contextual determinants of high school graduation.

A potentially important practical implication of these findings is that moving children from poor families to less disadvantaged neighborhoods, and children from nonpoor families to more disadvantaged neighborhoods, in an effort to reduce aggregate levels of spatially concentrated disadvantage may result in educational benefits for poor children without significantly harming the educational prospects of nonpoor children. These results also suggest that the often vigorous resistance among high-income residents of advantaged neighborhoods to housing policies aimed at neighborhood integration is misplaced or may be motivated by concerns other than the supposedly harmful impact of integration on their children's educational opportunities. While it is extremely difficult to infer housing policy outcomes from observational research on neighborhood effects, our findings raise the possibility that, at least for certain aspects of child development like high school graduation, residential integration may have considerable benefits without any serious negative consequences.

Neighborhoods are important to “ecological” socialization models that describe how interconnected social contexts influence child development (Brooks-Gunn et al. 1993). This study demonstrates that ecological socialization models must account for interactions between nested social contexts, like the family environment and neighborhood. Specifically, our results support compound disadvantage theory and are difficult to reconcile with relative deprivation theory. Consistent with Wilson's (1987) seminal arguments about spatially concentrated poverty, this study suggests that the “truly disadvantaged” are indeed children simultaneously embedded in impoverished families and impoverished neighborhoods.

In addition to neighborhood effect moderation by family income, this study shows that it is essential to account for the longitudinal sequence of neighborhood contexts experienced by individuals throughout the course of development. While previous research documents the importance of duration of exposure to different neighborhood conditions (Crowder and South 2010; Wodtke et al. 2011; Wodtke 2013), results presented here elaborate these findings by demonstrating that neighborhood effects on high school graduation also depend on the timing of exposure during childhood versus adolescence. Point estimates indicate that exposure at both developmental periods reduces the probability of high school graduation, but the effects of adolescent exposure are considerably larger and highly significant. These findings add to the growing body of research indicating that neighborhood effects should be studied within a longitudinal and developmental framework (Sampson et al. 2008; Sharkey and Elwert 2011; Wodtke et al. 2011; Wodtke 2013).

Investigating moderated contextual effects within a temporal framework, however, requires new methods that overcome critical limitations of more conventional approaches to estimation, which cannot appropriately incorporate time-varying moderators that are affected by prior treatment. We use the SNMM and two-stage regression-with-residuals estimator (Almirall et al. 2010, 2011; Robins 1994) to analyze neighborhood effect moderation by family economic resources, a time-varying attribute that simultaneously confounds, mediates, and moderates effects of past and future neighborhood exposures. The regression-with-residuals estimator is unbiased for moderated neighborhood effects under a weaker set of assumptions than is required for conventional regression or propensity score matching, and analyses of potential violations of these assumptions indicate that our results are robust. These methods can be easily and productively adapted for analyzing whether the effects of other time-varying social contexts (e.g., classrooms, families, or firms) are moderated by the evolving characteristics of the individuals embedded in these contexts (e.g., students, children, or workers).

Although this study extends previous work on neighborhood effects in the longitudinal setting, it is not without limitations. First, because the requisite data is unavailable for our sample from the PSID, we are not able to investigate the specific mechanisms through which neighborhood characteristics impact children's education progress. An important task for future research will be to conduct mediation analyses of neighborhood effects within an appropriate temporal framework.

Second, this study only examines a single educational outcome, high school graduation. Our conclusions about exposure to disadvantaged neighborhoods should not be extrapolated to other educational outcomes or transitions, especially those that occur during earlier or later stages of development. To better understand how neighborhood effects depend on the timing of exposure and family environment, future research should examine a variety of outcomes related to school progression and achievement measured throughout the early life course.

In addition, this study uses a measure of high school graduation that does not account for school quality, which differs systematically across neighborhood contexts. Graduating from a low-quality high school in a poor neighborhood, rather than an elite high school in an advantaged community, may provide a more limited set of academic skills and may not facilitate future educational attainment (e.g., college admission and completion) to the same extent. Estimates of neighborhood effects that ignore school quality may understate the educational disadvantages that children in poor neighborhoods encounter.

These limitations notwithstanding, the present study provides important new evidence about temporal dependency and family resource moderation of neighborhood effects on high school graduation. With both income inequality and income segregation increasing in America (Reardon and Bischoff 2011), the devastating impact of spatially concentrated disadvantage on high school graduation for children from poor families suggests that these broad social trends are mutually reinforcing: income inequality begets income segregation, and income segregation facilitates the reproduction of poverty.

Acknowledgments

*The authors would like to thank Daniel Almirall and participants in the Michigan Inequality Workshop for their comments on previous drafts on this study. This research was supported by the National Science Foundation Graduate Research Fellowship under Grant No. DGE 0718128 and by the National Institute of Child Health and Human Development under Grant Nos. T32 HD007339 and R24 HD041028 to the Population Studies Center at the University of Michigan.

APPENDIX

Part A: Neighborhood Disadvantage Index

Table A.1.

Principal Component Weights and Correlations

Variable	1st PC
Variable	Weight	Corr
Percent poverty	.408	.861
Percent unemployed	.371	.783
Percent receiving welfare	.412	.868
Percent female-headed households	.337	.711
Percent without high school diploma	.378	.798
Percent college graduates	–.348	–.735
Percent mgr/prof workers	–.385	–.812

Component variance	4.449
Proportion total variance explained	.636

Open in a new tab

Notes: Principal component analysis based on correlation matrix. Analysis includes all tract-year observations from the 1970 to 2000 U.S. censuses.

Figure A.1 — Neighborhood Socioeconomic Characteristics by Disadvantage Index Quintile

Part B: Weighted Estimates

This section reports estimates that are weighted to adjust for the oversampling of low-income families in the PSID (as well as for nonrandom patterns of initial nonresponse among sampled families). Specifically, we use the original 1968 family weights, which represent the inverse probability of selection and participation in the survey. Tables B.1 to B.4 report weighted descriptive statistics that parallel the unweighted descriptive statistics reported in the main text. The weighted descriptive statistics reported here approximate population distributions for the target cohort of children born between 1966 and 1980, although they are still not strictly representative of this cohort because the PSID sample design systematically excludes the children of immigrants who entered the U.S. during this period.

Table B.5 reports weighted estimates of moderated neighborhood effects on high school graduation. The weighted point estimates are similar to the unweighted point estimates reported in the main text, which suggests that the SNMM sufficiently controls for the relevant design variables without the use of weights. The standard errors for the weighted estimates are notably larger than those for the unweighted estimates, as expected. This reflects the inefficiency of additionally using weights to adjust for features of the survey design that the model adjusts for directly (Pfeffermann 1993; Winship and Radbill 1994).

Table B.5 also contains results from formal design tests that evaluate whether the weights can be ignored given the covariates in the model (DuMouchel and Duncan 1983; Nordberg 1989; Pfeffermann 1993). Specifically, this design test evaluates null hypotheses of the form: $H_{0} : {plim}_{n \to \infty, N \to \infty} (\hat{β} - {\hat{β}}^{w t}) = 0$ , where $\hat{β}$ is an unweighted estimator and ${\hat{β}}^{w t}$ is the corresponding weighted estimator (Pfeffermann 1993). In words, the null hypothesis states that the weighted and unweighted estimators converge in probability. This test is performed by estimating an unweighted model that includes interaction terms between the weights and covariates and then evaluating the significance of these interactions using conventional heteroscedasticity-robust test statistics. P-values from these tests are reported in Table B.5. They show that we fail to reject the null hypothesis for every coefficient of interest, indicating that the sampling weights can be safely ignored in this analysis of moderated neighborhood effects.

Table B.1.

Weighted Descriptive Statistics for Time-invariant Covariates

Variable	Total		Blacks		Whites
Variable	mean	sd	mean	sd	mean	sd

S - high school graduate	.85	(.36)	.77	(.42)	.87	(.34)
S - female	.48	(.50)	.48	(.50)	.49	(.50)
M - age at childbirth	25.52	(5.36)	23.91	(5.57)	25.86	(5.25)
M - married at childbirth	.86	(.35)	.53	(.50)	.92	(.27)
H - high school graduate	.25	(.43)	.24	(.43)	.25	(.43)
H - some college	.32	(.47)	.23	(.42)	.34	(.47)
H - college graduate	.15	(.36)	.03	(.18)	.18	(.38)

Open in a new tab

Notes: Results are weighted to adjust for oversampling of low-income families in the PSID and combined across 100 multiple imputation datasets. S, M, and H indicate subject, mother of subject, and household head, respectively.

Table B.2.

Weighted Descriptive Statistics for Time-varying Covariates

Variable	Total		Blacks		Whites
Variable	mean	sd	mean	sd	mean	sd

Childhood
H - married	.84	(.32)	.61	(.45)	.89	(.27)
H - employed	.88	(.27)	.67	(.40)	.92	(.21)
H - skilled manual occupations	.47	(.50)	.44	(.49)	.46	(.50)
H - clerks and sales occupations	.13	(.33)	.14	(.34)	.13	(.33)
H - prof. and managerial occupations	.25	(.43)	.08	(.26)	.29	(.45)
FU - owns home	.60	(.44)	.35	(.43)	.65	(.42)
FU - size	4.54	(1.43)	5.04	(1.99)	4.43	(1.26)
FU - number of moves	1.07	(1.12)	1.20	(1.13)	1.03	(1.11)
FU - inc-to-needs ratio	1.33	(1.28)	.47	(.99)	1.51	(1.27)
Adolescence
H - married	.79	(.38)	.50	(.47)	.84	(.33)
H - employed	.87	(.29)	.65	(.42)	.91	(.23)
H - skilled manual occupations	.40	(.49)	.41	(.49)	.40	(.49)
H - clerks and sales occupations	.12	(.33)	.16	(.37)	.11	(.32)
H - prof. and managerial occupations	.32	(.47)	.11	(.31)	.36	(.48)
FU - owns home	.70	(.42)	.45	(.46)	.75	(.39)
FU - size	4.67	(1.32)	5.01	(1.83)	4.60	(1.19)
FU - number of moves	.68	(.97)	.83	(1.06)	.64	(.95)
FU - inc-to-needs ratio	1.86	(1.77)	.65	(1.17)	2.10	(1.77)

Open in a new tab

Notes: Results are weighted to adjust for oversampling of low-income families in the PSID and combined across 100 multiple imputation datasets. H and FU indicate household head and family unit, respectively.

Table B.3.

Weighted Joint Treatment Distribution

n row cell		Blacks					Whites
		NH disadvantage quintile - adolescence					NH disadvantage quintile - adolescence
		1	2	3	4	5	1	2	3	4	5
NH disadvantage quintile - childhood	1	25	8	4	12	1	372	50	20	14	4
		.49	.16	.09	.25	.02	.81	.11	.04	.03	.01
		.01	.00	.00	.00	.00	.12	.02	.01	.00	.00
	2	26	28	34	7	10	173	281	82	26	6
		.24	.27	.33	.06	.10	.30	.49	.14	.04	.01
		.01	.01	.01	.00	.00	.06	.09	.03	.01	.00
	3	19	37	64	37	26	49	239	376	95	28
		.10	.20	.35	.20	.14	.06	.30	.48	.12	.04
		.01	.01	.02	.01	.01	.02	.08	.13	.03	.01
	4	9	41	88	185	185	30	55	215	390	101
		.02	.08	.17	.36	.36	.04	.07	.27	.49	.13
		.00	.01	.03	.06	.06	.01	.02	.07	.13	.03
	5	6	47	106	223	1675	7	14	39	108	208
		.00	.02	.05	.11	.81	.02	.04	.10	.29	.55
		.00	.02	.04	.08	.58	.00	.00	.01	.04	.07

Open in a new tab

Notes: Results are weighted to adjust for oversampling of low-income families in the PSID and combined across 100 multiple imputation datasets.

Table B.4.

Weighted Treatment Distribution at Childhood and Adolescence by Prior Family Income

n row cell		Childhood					Adolescence
		NH disadvantage quintile					NH disadvantage quintile
		1	2	3	4	5	1	2	3	4	5
Family income-to-needs ratio	>2	482	381	287	252	115	818	625	481	317	158
		.32	.25	.19	.17	.08	.34	.26	.20	.13	.07
		.08	.06	.05	.04	.02	.13	.10	.08	.05	.03
	(1,2]	194	356	520	468	281	200	306	449	378	264
		.11	.20	.29	.26	.15	.13	.19	.28	.24	.17
		.03	.06	.08	.08	.05	.03	.05	.07	.06	.04
	[0,1]	113	233	521	627	501	75	190	329	391	428
		.06	.12	.26	.31	.25	.05	.13	.23	.28	.30
		.02	.04	.08	.10	.08	.01	.03	.05	.06	.07
	<0	15	50	83	190	465	20	37	86	182	401
		.02	.06	.10	.24	.58	.03	.05	.12	.25	.55
		.00	.01	.01	.03	.8	.00	.01	.01	.03	.07

Open in a new tab

Notes: Results are weighted to adjust for oversampling of low-income families in the PSID and combined across 100 multiple imputation datasets. Income-to-needs ratio is centered around 1 such that values less than zero represent sub-poverty incomes, values equal to 0 represent poverty-level incomes, and values greater than 0 represent incomes above the poverty line.

Table B.5.

Weighted Neighborhood Effect Estimates and Design Ignorability Tests

Model	Total				Blacks				Whites
Model	coef	se		Design Test	coef	se		Design Test	coef	se		Design Test
Intercept	.899	(.018)	^***		.932	(.061)	^***		.906	(.017)	^***
Childhood
NH dadvg	–.011	(.013)		.337	–.015	(.028)		.526	–.014	(.015)		.560
NH dadvg × incneeds	.006	(.005)		.245	.008	(.013)		.753	.007	(.005)		.901
Adolesence
NH dadvg	–.029	(.012)	^*	.125	–.045	(.024)	^†	.431	–.027	(.014)	^†	.363
NH dadvg × incneeds	.009	(.004)	^*	.271	.014	(.011)		.454	.008	(.004)	^†	.862

Open in a new tab

Notes: Coefficient estimates are weighted to adjust for oversampling of low-income families in the PSID and combined across 100 multiple imputation datasets. Standard errors are based on 500 bootstrap samples. The income-to-needs ratio is centered at the poverty line. The design test column reports p-values from a hypothesis test that evaluates whether the sampling weights are ignorable, that is, a test of $H_{0} : {plim}_{n \to \infty, N \to \infty} (\hat{β} - {\hat{β}}^{w t}) = 0$ .

^†

p < 0.10

p < 0.05

**p < 0.01, and

^***

p < 0.001 for two-sided tests of no effect.

Part C: Model Specification

This section investigates the sensitivity of our estimates to different specifications of the causal and nuisance functions of the SNMM. Table C.1 presents two-stage estimates for models that allow the effect of neighborhood disadvantage to vary across not only family economic resources but also all other family-level covariates as well as prior neighborhood context. Model A is the base model reported in the main text of the paper. Model B extends the base model by including a cross-product term between childhood and adolescent neighborhood context. This model provides no evidence that the effect of later exposure to disadvantaged neighborhoods is moderated by earlier neighborhood conditions. Models C and D allow the effect of neighborhood context to vary across a variety of different family-level covariates, including parental education, marital status, and employment status, in addition to family resources. These models do not reveal any significant interactions between neighborhood context and family covariates apart from the income-to-needs ratio, and point estimates of the focal moderated neighborhood effects are highly stable across the different specifications of the SNMM causal functions considered here. Thus, these analyses indicate that the causal functions of our base model are well specified.

Table C.2 presents two-stage estimates of SNMMs that have the same causal functions but use different specifications for the nuisance functions. Model A is the base model reported in the main text of the paper. The nuisance functions in this model include “main effects” for time-invariant covariates, denoted by V; time-varying family covariates measured during childhood, L₁; and time-varying family covariates measured during adolescence, L₂. Models B, C, and D use progressively more complex specifications for the nuisance functions, including all two-way interactions between time-invariant covariates, between time-varying covariates measured during childhood, and between time-varying covariates measured during adolescence. Models E, F, and G include nuisance functions with all two-way interactions between time-varying covariates measured during childhood and adolescence, as well as cross-time interactions between these covariates. Estimates of the moderated neighborhood effects of interest are relatively invariant and remain statistically significant across the different specifications for the SNMM nuisance functions.

Table C.1.

Regression-with-residuals Estimates based on Different Specifications of the SNMM Causal Functions

Model	A (base)			B			C			D
Model	coef	se		Coef	se		coef	se		coef	se
Intercept	.884	(.021)	^***	.885	(.024)	^***	.880	(.023)	^***	.877	(.025)	^***
Childhood
NH dadvg	–.005	(.011)		–.005	(.013)		.005	(.017)		.028	(.034)
NH dadvg × inc-to-needs	.005	(.004)		.005	(.004)		.007	(.005)		.007	(.005)
NH dadvg × H-less than HS							–.015	(.021)		–.011	(.022)
NH dadvg × H-some college							–.021	(.020)		–.017	(.021)
NH dadvg × H-college grad							–.013	(.023)		–.006	(.025)
NH dadvg × H-married										.005	(.018)
NH dadvg × H-employed										–.039	(.026)
NH dadvg × H-skilled mnl occ										–.004	(.016)
NH dadvg × H-clerk/sales occ										.009	(.019)
NH dadvg × H-prof/mgr occ										–.007	(.019)
NH dadvg × H-homeowner										.007	(.013)
NH dadvg × family size										.004	(.004)
Adolescence
NH dadvg	–.041	(.010)	^***	–.041	(.016)	^**	–.043	(.015)	^**	–.051	(.028)	^†
NH dadvg × inc-to-needs	.012	(.003)	^***	.012	(.003)	^***	.012	(.004)	^***	.010	(.004)	^*
NH dadvg × H-less than HS							.001	(.020)		–.001	(.019)
NH dadvg × H-some college							.007	(.018)		.005	(.018)
NH dadvg × H-college grad							.000	(.020)		.002	(.022)
NH dadvg × H-married										.008	(.014)
NH dadvg × H-employed										–.006	(.018)
NH dadvg × H-skilled mnl occ										.003	(.015)
NH dadvg × H-clerk/sales occ										.018	(.017)
NH dadvg × H-prof/mgr occ										–.006	(.018)
NH dadvg × H-homeowner										.012	(.013)
NH dadvg × family size										–.005	(.004)
Chld × Adl NH dadvg				.000	(.004)

Open in a new tab

Notes: Results are combined estimates from 100 multiple imputation datasets. Standard errors are based on 1000 bootstrap samples.

^†

p < 0.10

p < 0.05

^**

p < 0.01, and

^***

p < 0.001 for two-sided tests of no effect.

Table C.2.

Regression-with-residuals Estimates based on Different Specifications of the SNMM Nuisance Functions

Model	A (base)			B			C			D			E			F			G
Model	coef	se		coef	se		coef	se		coef	se		coef	se		coef	se		coef	se
Intercept	.884	(.021)	^***	.883	(.021)	^***	.879	(.022)	^***	.874	(.022)	^***	.881	(.022)	^***	.882	(.022)	^***	.880	(.022)	^***
Childhood
NH dadvg	–.005	(.011)		–.005	(.011)		–.002	(.012)		–.006	(.012)		–.002	(.011)		–.007	(.011)		–.007	(.012)
NH dadvg × inc-to-needs	.005	(.004)		.006	(.004)		.003	(.005)		.005	(.005)		.003	(.004)		.006	(.005)		.006	(.005)
Adolescence
NH dadvg	–.041	(.010)	^***	–.041	(.010)	^***	–.040	(.010)	^***	–.032	(.011)	^**	–.040	(.010)	^***	–.036	(.010)	^***	–.034	(.011)	^**
NH dadvg × inc-to-needs	.012	(.003)	^***	.012	(.003)	^***	.012	(.003)	^***	.007	(.004)	^*	.011	(.003)	^***	.009	(.003)	^**	.008	(.004)	^*
Description
Num. of 2^nd stage parameters	30			48			102			156			56			82			108
Nuisance functions	main effects for V, L₁ and L₂			A + all two-way interactions btw elements of V			B + all two-way interactions btw V and L₁			C + all two-way interactions btw V and L₂			A + all two-way interactions btw elements of L₁			E + all two-way interactions btw elements of L₂			F + all two-way interactions btw L₁ and L₂

Open in a new tab

Notes: Results are combined estimates from 100 multiple imputation datasets. Standard errors are based on 1000 bootstrap samples. For this analysis, V denotes time-invariant baseline characteristics. L₁ and L₂ denote time-varying factors measured during childhood and adolescence, respectively.

†p < 0.10

p < 0.05

^**

p < 0.01, and

^***

p < 0.001 for two-sided tests of no effect.

Part D: Sensitivity Analysis

In this section, we implement a formal sensitivity analysis to test the robustness of our estimates to unobserved confounding, a violation of the sequential ignorability assumption. Unobserved confounding would occur if families select different neighborhood contexts on the basis of unmeasured factors that affect the chances of high school graduation. We consider unobserved confounding of the following type: children currently living in more disadvantaged neighborhoods may have lower graduation rates regardless of where they live, while children currently living in less disadvantaged neighborhoods may have higher graduation rates regardless of neighborhood context. This may occur because subjects living in disadvantaged neighborhoods, compared to those living in more affluent communities, have parents that are less “ambitious” or “skilled” when it comes to raising children or because they come from families with less accumulated wealth. Since we lack reasonable measures of parental skill or ambition, as well as family wealth, our neighborhood-effect estimates would be downwardly biased if these characteristics are in fact confounders, indicating a negative impact of concentrated disadvantage even if there is no such effect.

Following Sharkey and Elwert (2011), we implement a sensitivity analysis for time-varying neighborhood treatments that models bias due to unobserved confounding as a function of potential outcomes (Brumback, Hernan, Haneuse, and Robins 2004; Robins 1999a; Robins 1999b). With this approach, a selection function is used to summarize the relationship between observed and counterfactual outcomes and then to compute bias-adjusted effect estimates. If inferences about the negative effect of neighborhood disadvantage on high school graduation do not change across a range of substantively reasonable confounding scenarios, as defined by different values of the selection function, we conclude that our results are robust to unobserved confounding.

To illustrate the logic behind this type of sensitivity analysis, consider a point-in-time experiment that randomized a sample of families and their children to neighborhoods in each of the five quintiles of the disadvantage distribution. Table D.1 provides a cross-tabulation of the potential outcomes for this hypothetical experiment. The main diagonal cells give the observed proportion of high school graduates in neighborhood quintile a for subjects that were in fact assigned to a neighborhood in quintile A = a of the composite disadvantage distribution. The off-diagonal cells in parentheses are unobserved, or counterfactual, graduation rates. For example, cell (EE) is the graduation rate in the most disadvantaged quintile of neighborhoods for individuals actually assigned to live in the least disadvantaged quintile of neighborhoods. In an optimal randomized experiment, the potential outcome for a given treatment is the same for members of all treatment groups, such that the observed and counterfactual graduation rates are equal within columns: E = (F) = (G) = (H) = (I), (J) = K = ··· = (N), and so on. In other words, with perfect randomization, the observed mean potential outcome among subjects living in quintile a should equal the unobserved mean potential outcome of living in quintile a among subjects randomized to live in some other quintile a′. If the probability of high school graduation is a linear function of neighborhood disadvantage, a regression of the observed outcome, Y, on the treatment variable, A, would provide a valid estimate of the average causal effect of neighborhood disadvantage.

In this framework, unobserved confounding can be thought of as a departure from perfect randomization of neighborhood context. Specifically, bias due to unobserved confounding occurs if E ≠ (F) ≠ ··· ≠ (I), (J) ≠ K ≠ ··· ≠ (N), and so on. That is, if the observed mean outcome in one treatment group is not exchangeable with the counterfactual mean outcome in the other treatment groups, estimates are biased due to unobserved confounding. Based on this relationship between observed mean outcomes and counterfactual mean outcomes, unobserved confounding can be summarized by the following parsimonious selection function,

s (a, a^{'}) = E (Y (a) ∣ A = a) - E (Y (a) ∣ A = a^{'}),

(6)

where, for example, s(0,1) = E − (F). Different values of s(a,a′) correspond to varying types and degrees of unobserved confounding.

For the present analysis, we adopt one particular specification of the selection function: s(a,a′) = (a − a′)α, where α ≤ 0 is a sensitivity parameter that specifies the magnitude of bias confounding. We use a linear model for unmeasured confounding because our empirical analysis of neighborhood effects is focused on estimating the parameters of a linear SNMM. In this model, α = 0 implies no unobserved confounding of neighborhood context, and α < 0 defines the type of confounding described previously: children currently living in more disadvantaged neighborhoods have lower graduation rates regardless of where they live, and children currently living in less disadvantaged neighborhoods have higher graduation rates regardless of neighborhood context. For computational simplicity, this selection function constrains the magnitude of hypothetical unobserved confounding to be the same across levels of observed covariates and moderators.

Based on this selection function, a bias-adjusted estimate for the average treatment effect in the point-in-time context can be obtained from the following calculations. First, we compute the proportion of subjects in each neighborhood quintile, denoted by P(A) for A = 1,2, ... ,5. Second, we subtract the bias term, $B = \sum_{A^{'} = 1}^{A^{'} = 5} (A - A^{'}) α P (A^{'})$ , from the observed outcome, Y, to obtain a bias-adjusted outcome Y^c = Y − B. Finally, we estimate a bias-adjusted treatment effect by regressing the corrected outcome, Y^c, on the treatment variable, A. By selecting a range of plausible values for the sensitivity parameter, α, and estimating bias-adjusted effects for each of those values, we are able to assess the robustness of our results to different degrees of unobserved confounding.

For the present analysis where treatment is time-varying, separate selection functions, $s_{k} a_{k}, a_{k}^{'})$ , are used to model unobserved confounding in childhood (k = 1) and adolescence (k = 2). The formula for the bias term is modified to account for the total bias accumulated across developmental periods, $B = \sum_{k = 1}^{k = 2} \sum_{A_{k}^{'} = 1}^{A_{k}^{'} = 5} (A_{k} - A_{k}^{'}) α_{k} P (A_{k}^{'})$ , and then the adjusted outcomes are computed as above. To incorporate effect moderation and controls for observed confounders, we simply refit the SNMM using the adjusted outcomes, and this yields bias-adjusted estimates for the impact of neighborhood disadvantage on high school graduation. Following Sharkey and Elwert (2011), the sensitivity parameter, α_k, is calibrated such that a one unit change corresponds to the amount of bias eliminated from our main effect estimates in the childhood and adolescent causal functions after adjusting for all observed confounders. The sensitivity of neighborhood effect estimates is thus interpreted in terms of multiples of observed confounding bias.

Figures D.1 and D.2 display the results from this sensitivity analysis for the effects of childhood and adolescent exposure to neighborhood disadvantage, respectively. In both figures, separate bias-adjusted effect estimates are presented for children in poor and in nonpoor families. The value of the sensitivity parameter, α, is plotted on the horizontal axis. A value of α = 0 indicates no unobserved confounding and simply reproduces the estimates reported in Table 5.

For α = −1, unobserved factors are assumed to confound the effect of neighborhood disadvantage on high school graduation to the same extent as all observed covariates already controlled for in the regression, including race, parental education, occupation, marital status, employment status, family structure, and so on. Because we adjust for a large and relevant set of observed confounders, we judge values of α < −1 to be implausible unobserved confounding scenarios.

The results of this sensitivity analysis indicate that our estimates and main substantive conclusions are robust to unobserved confounding: across a wide range of values for α, we conclude that the direct effect of exposure to disadvantaged neighborhoods during childhood is small and not statistically significant for both poor and nonpoor children, while the effect of adolescent neighborhood disadvantage is severe and remains statistically significant under a moderate degree of unobserved confounding (α > −.5) for nonpoor children and under a high degree of unobserved confounding (α > −1) for poor children. Even in the most extreme situation where unobserved confounding is assumed to be twice as strong as that already controlled for through observed covariates (α = −2), the negative effect of neighborhood disadvantage on high school graduation among children in poor families remains substantively large and statistically significant. Thus, based on the results in Figures D.1 and D.2, we conclude that the neighborhood effect estimates presented in Table 5 are highly robust to unobserved confounding.

Table D.1.

Potential Outcomes from a Hypothetical Neighborhood Experiment

Observed Treatment	Mean Potential Outcome, E(Y(a)\|A)
Observed Treatment	E(Y(1)\|A)	E(Y(2)\|A)	E(Y(3)\|A)	E(Y(4)\|A)	E(Y(5)\|A)
A = 1	E	(J)	(O)	(T)	(EE)
A = 2	(F)	K	(P)	(U)	(FF)
A = 3	(G)	(L)	Q	(V)	(GG)
A = 4	(H)	(M)	(R)	W	(HH)
A = 5	(I)	(N)	(S)	(X)	II

Open in a new tab

Figure D.1 — Sensitivity of Effect Estimates for Childhood Neighborhood Disadvantage to Hypothetical Unobserved Confounding

Figure D.2 — Sensitivity of Effect Estimates for Adolescent Neighborhood Disadvantage to Hypothetical Unobserved Confounding

Part E: Missing Data

The analyses in this study suffer from a nontrivial amount missing data, summarized here in Table E.1, due primarily to attrition from the PSID. This section investigates whether results change considerably using different methods of adjustment for missing data. The first column of Table E.2 shows the combined estimates reported in the main text from 100 multiple imputation (MI) samples. Under the assumption that data are “missing at random” (MAR), specifically, that conditional on observed covariates, the mechanism governing missingness does not depend on unobserved factors that also affect the variable in question, combined effect estimates and standard errors based on MI are unbiased and valid, respectively. The second column contains combined estimates based on multiple imputation with deletion (MID), a procedure where all missing data are multiply imputed but cases with missing values for the outcome variable are deleted prior to estimation (von Hippel 2007). This approach offers greater statistical efficiency than MI but requires slightly more stringent assumptions about the missing data mechanism. The third column contains estimates based on single regression imputation (SI) for which missing values are replaced with the conditional sample mean. Under the MAR assumption, this procedure yields unbiased effect estimates but understates their variance. Finally, the last column presents estimates from a complete case analysis (CC) that simply deletes all observations with any missing data. This procedure is unbiased only if data are “missing completely at random” (MCAR), that is, only if the mechanism governing missingness does not depend on observed or unobserved factors that affect the variable in question. Combined estimates based on conventional MI are very similar to those obtained from MID, SI, and CC. We report MI estimates because this approach requires the weakest assumptions for unbiased estimation and valid inference.

Table E.1.

Missing Data

Variable	Childhood		Adolescence
Variable	% miss	N miss	% miss	N miss

S - high school graduation	-	-	43	(2,636)
H - marital status	0	(0)	24	(1,461)
H - employment status	0	(0)	24	(1,461)
H - occupation	21	(1,310)	41	(2,489)
FU - homeownership	0	(0)	24	(1,461)
FU - size	0	(0)	24	(1,461)
FU - residential mobility	13	(802)	30	(1,830)
FU - inc-to-needs ratio	0	(0)	24	(1,461)

Open in a new tab

Notes: S, H, and FU indicate subject, household head, and family unit, respectively.

Table E.2.

Regression-with-residuals Estimates Under Different Methods of Adjusting for Missing Data

Model	MI (base)			MID			SI			CC
Model	coef	se		coef	se		coef	se		coef	se
Intercept	.884	(.021)	^***	.906	(.018)	^***	.904	(.015)	^***	.889	(.016)	^***
Childhood
NH dadvg	–.005	(.011)		–.008	(.012)		–.009	(.008)		–.008	(.013)
NH dadvg × inc-to-needs	.005	(.004)		.007	(.005)		.005	(.003)		.008	(.005)
Adolesence
NH dadvg	–.041	(.010)	^***	–.040	(.010)	^***	–.041	(.007)	^***	–.053	(.012)	^***
NH dadvg × inc-to-needs	.012	(.003)	^***	.011	(.004)	^**	.011	(.002)	^***	.013	(.004)	^***
Description
Num. of observations	6137			3501			6137			1891
Num. of replications	100			100			1			0

Open in a new tab

Notes: MI = multiple imputation, MID = multiple imputation then deletion, SI = single imputation, and CC = complete case analysis. Standard errors are based on 1000 bootstrap samples.

*p < 0.05

^**

p < 0.01, and

^***

p < 0.001 for two-sided tests of no effect.

Footnotes

Due to measurement limitations in the PSID, subjects with a general equivalency degree (GED) are coded as high school graduates. In addition, for subjects with item-specific missing data on educational attainment at age 20, we use measures of educational attainment taken at age 21, if available, to construct our indicator of high school graduation.

By focusing on the census tract of residence, this analysis eschews an investigation of extra-local neighborhood effects, which recent evidence links to educational outcomes (Crowder and South 2010; Sampson et al. 2002). Investigating moderation of both local and extra-local neighborhood effects within a longitudinal framework would require strong additional assumptions and a notable increase in free parameters, neither of which we deem defensible with current data.

Classifying neighborhoods into quintiles results in some information loss about neighborhood context. Measurement error in treatment would be particularly concerning if it were linked to family poverty because this might lead to inappropriate inferences about the degree of effect moderation. To investigate this issue, we also conduct analyses with the raw disadvantage index scores. Results (not reported) are similar to those based on the quintile treatment definition. Because the quintile classification of neighborhoods greatly simplifies notation and facilitates a clean interpretation of effect estimates, we report results based on this treatment definition.

⁴

Parental education is treated as time-invariant because the PSID does not measure this factor at regular intervals, thereby limiting our ability to track changes over time. We use measurements of parental education taken when a child is age two or, if that is not available, the most recent measurement prior to age two.

⁵

Effect moderation is sometimes depicted with a stylized graph that includes an arrow from the moderator variable into an arrow representing the effect of treatment on the outcome. In DAGs, however, these “arrows into arrows” have no meaning, and their inclusion would invalidate the formal rules by which one can determine identification and non-identification of causal effects in a DAG.

⁶

Alternatively, consider the subtly different but still problematic question, “what is the effect of continuously living in the most disadvantaged quintile of neighborhoods, rather than the least disadvantaged quintile, among subjects whose families would stay poor regardless of treatment received?” Translated into potential outcomes notation, this question is expressed as E(Y(5,5) – Y(1,1)|L₁ = 0, L₂(5) = L₂(1) = 0)). This is a well-defined causal contrast, but it cannot be identified because it is impossible to determine which families would stay poor regardless of prior treatments. Furthermore, it is unclear whether this effect is even a substantively interesting quantity, since it involves an unobservable subpopulation for which one of the mechanisms thought to mediate neighborhood effects is inoperative.

⁷

Models that permit the effect of adolescent neighborhood disadvantage to vary by the childhood measurements of neighborhood context and family income are also considered in supplemental analyses (see Table C.1 in the Appendix). There is no evidence that the effect of exposure to disadvantaged neighborhoods during adolescence interacts with earlier neighborhood exposures or is moderated by family income during childhood.

⁸

Equation 3 is an unsaturated linear probability SNMM. The particular decomposition of the conditional mean on which this model is based does not directly translate to nonlinear models, such as logit or probit regressions. Unsaturated linear probability models can be problematic because they allow predicted values outside the logical [0,1] range, but they generally perform well when used for estimating average casual effects (Angrist and Pischke 2009). We find that this model provides a reasonable fit to the data with few nonsensical predicted probabilities, and more complex models that relax a number of additivity and linearity constraints by including polynomial and additional interaction terms yield substantively similar results.

⁹

Prior research suggests that these biases lead conventional estimation methods to understate the harmful impact of neighborhood disadvantage on adolescent outcomes (Wodtke et al. 2011; Wodtke 2013), but this pattern need not hold true in all studies of contextual effects. In general, the direction of bias due to over-control and collider-stratification is difficult to determine because it depends on the nature of the treatment-to-moderator-to-outcome indirect effect and on the nature of unobserved confounding for the moderator-to-outcome direct effect.

¹⁰

Similar to conventional regression, propensity score stratification and matching estimators adjust for observed confounding by conditioning—via the propensity score—on a function of covariates that predict future treatment and the outcome. In the time-varying context, if propensity scores for future treatments are a function of time-varying confounders affected by prior treatments, then matching and stratification estimators will be biased due to collider stratification and over-control of intermediate pathways.

¹¹

Measurement and sample size limitations in the PSID preclude separate estimates for other racial and ethnic groups.

Contributor Information

Geoffrey T. Wodtke, University of Toronto

Felix Elwert, University of Wisconsin-Madison and Social Science Research Center Berlin.

David J. Harding, University of California-Berkeley

REFERENCES

Aaronson Daniel. Using Sibling Data to Estimate the Impact of Neighborhoods on Children's Educational Outcomes. Journal of Human Resources. 1998;33:915–46. [Google Scholar]
Almirall Daniel, Coffman Cynthia J., Yancy William S., Murphy Susan A. Structurnal Nested Models. In: Faries D, Leon AC, Haro JM, Obenchain RL, editors. Analysis of Observational Health Care Data Using SAS. SAS Institute; Cary, NC: 2010. pp. 231–61. [Google Scholar]
Almirall Daniel, McCaffrey Daniel F., Ramchand Rajeev, Murphy Susan A. Subgroups Analysis when Treatment and Moderators are Time-varying. Prevention Science. 2011 doi: 10.1007/s11121-011-0208-7. (electronic publication ahead of print): http://dx.doi.org/10.1007/s11121-011-0208-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Almirall Daniel, Ten Have Thomas, Murphy Susan A. Structural Nested Mean Models for Assessing Time-Varying Effect Moderation. Biometrics. 2010;66:131–9. doi: 10.1111/j.1541-0420.2009.01238.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Anderson Elijah. Code of the Street: Decency, Violence, and the Moral Life of the Inner City. Norton; New York: 1999. [Google Scholar]
Angrist Joshua D., Pischke Jorn-Steffen. Mostly Harmless Econometrics: An Empiricist's Companion. Princeton University Press; Princeton, NJ: 2009. [Google Scholar]
Brewster Karin L. Neighborhood Context and the Transition to Sexual Activity among Young Black Women. Demography. 1994;31:603–14. [PubMed] [Google Scholar]
Brewster Karin L., Billy John O. G., Grady William R. Social Context and Adolescent Behavior: The Impact of Community on the Transition to Sexual Activity. Social Forces. 1993;71:713–40. [Google Scholar]
Brooks-Gunn Jeanne, Duncan Greg J., Lawrence Aber J. Neighborhood Poverty (Vol. 1): Context and Consequences for Children. Russell Sage; New York: 1997. [Google Scholar]
Brooks-Gunn Jeanne, Duncan Greg J., Klebanov Pamela K., Sealand Naomi. Do Neighborhoods Influence Child and Adolescent Development? American Journal of Sociology. 1993;99:353–95. [Google Scholar]
Brumback Babette A., Hernan Miguel A., Haneuse Sebastien J. P. A., Robins James M. Sensitivity Analyses for Unmeasured Confounding Assuming a Marginal Structural Model for Repeated Measures. Statistics in Medicine. 2004;23:749–67. doi: 10.1002/sim.1657. [DOI] [PubMed] [Google Scholar]
Carter Prudence L. Keepin' It Real: School Success Beyond Black and White. Oxford University Press; New York: 2005. [Google Scholar]
Charles Camille Z. The Dynamics of Racial Residential Segregation. Annual Review of Sociology. 2003;29:167–207. [Google Scholar]
Crane Jonathan. Effects of Neighbohoods on Dropping Out of School and Teenage Childbearing. In: Jencks C, Peterson PE, editors. The Urban Underclass. Brookings; Washington, D.C.: 1991. pp. 299–320. [Google Scholar]
Crosnoe Robert. Low-Income Students and the Socioeconomic Composition of Public High Schools. American Sociological Review. 2009;74:709–30. doi: 10.1177/000312240907400502. [DOI] [PMC free article] [PubMed] [Google Scholar]
Crowder Kyle, South Scott J. Spatial and Temporal Dimensions of Neighborhood Effects on High School Graduation. Social Science Research. 2010;40:87–106. doi: 10.1016/j.ssresearch.2010.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
Darling Nancy, Steinberg Laurence. Community Influences on Adolescent Achievement and Deviance. In: Brooks-Gunn J, Duncan GJ, Aber JL, editors. Neighborhood Poverty (Vol. 2): Policy Implications in Studying Neighborhoods. Russell Sage; New York: 1997. pp. 120–31. [Google Scholar]
DuMouchel William H., Duncan Greg J. Using Sample Survey Weights in Multiple Regression Analysis of Stratified Samples. Journal of the American Statistical Association. 1983;78:535–543. [Google Scholar]
Duncan Greg J., Brooks-Gunn Jeanne. Consequences of Growing Up Poor. Russell Sage; New York: 1997. [Google Scholar]
Duncan Greg J., Jean Yeung W, Brooks-Gunn Jeanne, Smith Judith R. How Much Does Childhood Poverty Affect the Life Chances of Children? American Sociological Review. 1998;63:406–23. [Google Scholar]
Earls Felton, Carlson Mary. The Social Ecology of Child Health and Well-being. Annual Review of Public Health. 2001;22:143–66. doi: 10.1146/annurev.publhealth.22.1.143. [DOI] [PubMed] [Google Scholar]
Efron Bradley, Tibshirani Robert J. An Introduction to the Bootstrap. Chapman and Hall; New York: 1993. [Google Scholar]
Elwert Felix, Winship Christopher. Effect Heterogeneity and Bias in Main-Effects-Only Regression Models. In: Dechter R, Geffner H, Halpern JY, editors. Probability and Causality: A Tribute to Judea Pearl. College Publications; London: 2010. pp. 327–36. [Google Scholar]
Elwert Felix, Winship Christopher. Endogenous Selection Bias. University of Wisconsin-Madison; 2012. Unpublished Manuscript. [Google Scholar]
Fernandez Roberto M., Su Celina. Space in the Study of Labor Markets. Annual Review of Sociology. 2004;30:545–69. [Google Scholar]
Ginther Donna, Haveman Robert, Wolfe Barbara. Neighborhood Attributes as Determinants of Children's Outcomes: How Robust are the Relationships? Journal of Human Resources. 2000;35:603–42. [Google Scholar]
Greenland Sander. Quantifying Biases in Causal Models: Classical Confounding vs Collider-stratification Bias. Epidemiology. 2003;14:300–6. [PubMed] [Google Scholar]
Harding David J. Counterfactual Models of Neighborhood Effects: The Effect of Neighborhood Poverty on Dropping Out and Teenage Pregnancy. American Journal of Sociology. 2003;109:676–719. [Google Scholar]
Harding David J. Cultural Context, Sexual Behavior, and Romantic Relationships in Disadvantaged Neighborhoods. American Sociological Review. 2007;72:341–64. [Google Scholar]
Harding David J. Collateral Consequences of Violence in Disadvantaged Neighborhoods. Social Forces. 2009;88:757–84. doi: 10.1353/sof.0.0281. [DOI] [PMC free article] [PubMed] [Google Scholar]
Harding David J. Living the Drama: Community, Conflict, and Culture among Inner-City Boys. University of Chicago Press; Chicago: 2010. [Google Scholar]
Harding David J. Rethinking the Cultural Context of Schooling Decisions in Disadvantaged Neighborhoods: From Deviant Subculture to Cultural Heterogeneity. Sociology of Education. 2011;84:322–39. doi: 10.1177/0038040711417008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Heckman James J. Skill Formation and the Economics of Investing in Disadvantaged Children. Science. 2006;312:1900–1. doi: 10.1126/science.1128898. [DOI] [PubMed] [Google Scholar]
Heckman James J., Krueger Alan B. Inequality in America: What Role for Human Capital Policies? The MIT Press; Boston, MA: 2004. [Google Scholar]
Holland Paul W. Statistics and Causal Inference. Journal of the American Statistical Association. 1986;81:945–60. [Google Scholar]
Hong Guanglei, Raudenbush Stephen W. Causal Inference for Time-Varying Instructional Treatments. Journal of Educational and Behavioral Statistics. 2008;81:333–362. [Google Scholar]
Iceland John, Scopilliti Melissa. Immigrant Residential Segregation in US Metropolitan Areas, 1990-2000. Demography. 2008;45:79–94. doi: 10.1353/dem.2008.0009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Jackson Margot I., Mare Robert D. Cross-Sectional and Longitudinal Measurements of Neighborhood Experience and Their Effects on Children. Social Science Research. 2007;36:590–610. doi: 10.1016/j.ssresearch.2007.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
Jencks Christopher, Mayer Susan E. The Social Consequences of Growing Up in a Poor Neighborhood. In: Lynn LE, McGreary MGH, editors. Inner-City Poverty in the United States. National Academy Press; Washington, D.C.: 1990. pp. 111–86. [Google Scholar]
Kawachi Ichiro, Berkman Lisa F. Neighborhoods and Health. Oxford University Press; New York: 2003. [Google Scholar]
Lareau Annette. Home Advantage: Social Class and Parental Intervention in Elementary Education. Rowan and Littlefield; New York: 2000. [Google Scholar]
Longford Nicholas T. Single Imputation and Related Methods. In: Fienberg S, van der Linden W, editors. Missing Data and Small-Area Estimation: Modern Analytical Equipment for the Survey Statistician. Springer; New York: 2005. pp. 37–58. [Google Scholar]
Marsh Herbert. The Big Fish Little Pond Effect on Academic Self-Concept. Journal of Educational Psychology. 1987;79:280–95. [Google Scholar]
Massey Douglas S. Segregation and Stratification: A Biosocial Perspective. Du Bois Review. 2004;1:7–25. [Google Scholar]
Massey Douglas S., Denton Nancy A. American Apartheid: Segregation and the Making of the Underclass. Harvard University Press; Cambridge, MA: 1993. [Google Scholar]
Mayer Susan. What Money Can't Buy: The Effect of Parental Income on Children's Outcomes. Harvard University; Cambridge, MA: 1997. [Google Scholar]
Morgan Stephen L., Winship Christopher. Counterfactuals and Causal Inference: Methods and Principals for Social Research. Cambridge University Press; New York: 2007. [Google Scholar]
Nordberg Lennart. Generalized Linear Modeling of Sample Survey Data. Journal of Official Statistics. 1989;5:223–239. [Google Scholar]
Pearl Judea. Causal Diagrams for Empirical Research. Biometrika. 1995;82:669–710. [Google Scholar]
Pfeffermann Danny. The Role of Sampling Weights When Modeling Survey Data. International Statistical Review. 1993;61:317–337. [Google Scholar]
Pearl Judea. Causality: Models, Reasoning, and Inference. Cambridge University Press; Cambridge: 2000. [Google Scholar]
Quillian Lincoln. How Long Are Exposures to Poor Neighborhoods? The Long-Term Dynamics of Entry and Exit from Poor Neighborhoods. Population Research and Policy Review. 2003;22:221–49. [Google Scholar]
Reardon Sean F., Bischoff Kendra. Income Inequality and Income Segregation. American Journal of Sociology. 2011;116:1092–153. doi: 10.1086/657114. [DOI] [PubMed] [Google Scholar]
Robins James M. A New Approach to Causal Inference in Mortality Studies with a Sustained Exposure Period--Application to Control of the Healthy Worker Survivor Effect. Mathematical Modeling. 1987;7:1393–512. [Google Scholar]
Robins James M. Correcting for Noncompliance in Randomized Trials Using Structural Nested Mean Models. Communications in Statistics-Theory and Methods. 1994;23:2379–412. [Google Scholar]
Robins James M. Association, Causation, and Marginal Structural Models. Synthese. 1999a;121:151–79. [Google Scholar]
Robins James M. Marginal Structural Models versus Structural Nested Models as Tools for Causal Inference. In: Halloran E, editor. Statistical Models in Epidemiology. Springer-Verlag; New York: 1999b. pp. 95–134. [Google Scholar]
Robins James M., Hernan Miguel A., Brumback Babette A. Marginal Structural Models and Causal Inference in Epidemiology. Epidemiology. 2000;11:550–60. doi: 10.1097/00001648-200009000-00011. [DOI] [PubMed] [Google Scholar]
Royston Patrick. Multiple Imputation of Missing Values: Update. The Stata Journal. 2005;5:1–14. [Google Scholar]
Rubin Donald B. Estimating Causal Effects of Treatments in Randomized and Nonrandomized Studies. Journal of Educational Psychology. 1974;66:688–701. [Google Scholar]
Rubin Donald B. Multiple Imputation for Nonresponse in Surveys. J. Wiley & Sons; New York: 1987. [Google Scholar]
Rumberger Russell W. High-School Dropouts: A Review of Issues and Evidence. Review of Educational Research. 1987;57:101–21. [Google Scholar]
Sampson Robert J. How Do Communities Undergird or Undermine Human Development? Relevant Contexts and Social Mechanisms. In: Booth A, Crouter N, editors. Does It Take a Village? Community Effects on Children, Adolescents, and Families. Erlbaum; Mahwah, N.J.: 2001. pp. 3–30. [Google Scholar]
Sampson Robert J., Morenoff Jeffrey D., Gannon-Rowley Thomas. Assessing “Neighborhood Effects”: Social Processes and New Directions in Research. Annual Review of Sociology. 2002;28:443–78. [Google Scholar]
Sampson Robert J., Sharkey Patrick. Neighborhood Selection and the Social Reproduction of Concentrated Racial Inequality. Demography. 2008;45:1–29. doi: 10.1353/dem.2008.0012. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sampson Robert J., Sharkey Patrick, Raudenbush Stephen W. Durable Effects of Concentrated Disadvantage on Verbal Ability among African-American Children. Proceedings of the National Academy of Sciences. 2008;105:845–52. doi: 10.1073/pnas.0710189104. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sastry Narayan, Pebley Anne R. Family and Neighborhood Sources of Socioeconomic Inequality in Children's Achievement. Demography. 2010;47:777–800. doi: 10.1353/dem.0.0114. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sharkey Patrick. The Acute Effect of Local Homicides on Children's Cognitive Performance. Proceedings of the National Academy of Sciences. 2010;107:11733–38. doi: 10.1073/pnas.1000690107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sharkey Patrick, Elwert Felix. The Legacy of Disadvantage: Multigenerational Neighborhood Effects on Cognitive Ability. American Journal of Sociology. 2011;116:1934–81. doi: 10.1086/660009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Small Mario L., Newman Katherine. Urban Poverty After The Truly Disadvantaged: The Rediscovery of the Family, the Neighborhood, and Culture. Annual Review of Sociology. 2001;27:23–45. [Google Scholar]
South Scott J., Crowder Kyle D. Escaping Distressed Neighborhoods: Individual, Community, and Metropolitan Influences. American Journal of Sociology. 1997a;102:1040–84. [Google Scholar]
South Scott J., Crowder Kyle D. Residential Mobility Between Cities and Suburbs: Race, Suburbanization, and Back-to-the-City Moves. Demography. 1997b;34:525–38. [PubMed] [Google Scholar]
South Scott J., Crowder Kyle D. Avenues and Barriers to Residential Mobility among Single Mothers. Journal of Marriage and the Family. 1998a;60:866–77. [Google Scholar]
South Scott J., Crowder Kyle D. Housing Discrimination and Residential Mobility: Impacts for Blacks and Whites. Population Research and Policy Review. 1998b;17:369–87. [Google Scholar]
South Scott J., Crowder Kyle D. Neighborhood Effects on Family Formation: Concentrated Poverty and Beyond. American Sociological Review. 1999;64:113–32. [Google Scholar]
South Scott J., Crowder Kyle D. Neighborhood Poverty and Nonmarital Fertility: Spatial and Temporal Dimensions. Journal of Marriage and Family. 2010;72:89–104. doi: 10.1111/j.1741-3737.2009.00685.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
South Scott J., Deane Glenn D. Race and Residential Mobility: Individual Determinants and Structural Constraints. Social Forces. 1993;72:147–67. [Google Scholar]
Speare Alden, Goldscheider Frances K. Effects of Marital Status Change on Residential Mobility. Journal of Marriage and the Family. 1987;49:455–64. [Google Scholar]
Sucoff Clea A., Upchurch Dawn M. Neighborhood Context and the Risk of Childbearing among Metropolitan-area Black Adolescents. American Sociological Review. 1998;63:571–85. [Google Scholar]
Timberlake Jeffrey M. Racial and Ethnic Inequality in the Duration of Children's Exposure to Neighborhood Poverty and Affluence. Social Problems. 2007;54:319–42. [Google Scholar]
VanderWeele Tyler J. On the Distinction between Interaction and Effect Modification. Epidemiology. 2009;20:863–71. doi: 10.1097/EDE.0b013e3181ba333c. [DOI] [PubMed] [Google Scholar]
VanderWeele Tyler J., Robins James M. Minimal Sufficient Causation and Directed Acyclic Graphs. The Annals of Statistics. 2009;37:1437–65. [Google Scholar]
von Hippel Paul T. Regression with Missing Ys: An Improved Strategy for Analyzing Multiply Imputed Data. Sociological Methodology. 2007;37:83–117. [Google Scholar]
Wheaton Blair, Clarke Philippa. Space Meets Time: Integrating Temporal and Contextual Influences on Mental Health in Early Adulthood. American Sociological Review. 2003;68:680–706. [Google Scholar]
Wilson William J. The Truly Disadvantaged: The Inner City, the Underclass, and Public Policy. University of Chicago Press; Chicago: 1987. [Google Scholar]
Wilson William J. When Work Disappears: The World of the New Urban Poor. Vintage Books; New York: 1996. [Google Scholar]
Winship Christopher, Radbill Larry. Sampling Weights and Regression Analysis. Sociological Methods & Research. 1994;23:230–257. [Google Scholar]
Wodtke Geoffrey T., Harding David J., Elwert Felix. Neighborhood Effects in Temporal Perspective: The Impact of Long-term Exposure to Concentrated Disadvantage on High School Graduation. American Sociological Review. 2011;76:713–36. doi: 10.1177/0003122411420816. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wodtke Geoffrey T. Duration and Timing of Exposure to Neighborhood Poverty and the Risk of Adolescent Parenthood. Demography. 2013;50:1765–88. doi: 10.1007/s13524-013-0219-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
Xie Yu, Brand Jennie E., Jann Ben. Estimating Heterogeneous Treatment Effects with Observational Data. Sociological Methodology. 2012;42:314–47. doi: 10.1177/0081175012452652. [DOI] [PMC free article] [PubMed] [Google Scholar]
Yinger John. Closed Doors, Opportunities Lost: The Continuing Costs of Housing Discrimination. Russell Sage; New York: 1995. [Google Scholar]

[R1] Aaronson Daniel. Using Sibling Data to Estimate the Impact of Neighborhoods on Children's Educational Outcomes. Journal of Human Resources. 1998;33:915–46. [Google Scholar]

[R2] Almirall Daniel, Coffman Cynthia J., Yancy William S., Murphy Susan A. Structurnal Nested Models. In: Faries D, Leon AC, Haro JM, Obenchain RL, editors. Analysis of Observational Health Care Data Using SAS. SAS Institute; Cary, NC: 2010. pp. 231–61. [Google Scholar]

[R3] Almirall Daniel, McCaffrey Daniel F., Ramchand Rajeev, Murphy Susan A. Subgroups Analysis when Treatment and Moderators are Time-varying. Prevention Science. 2011 doi: 10.1007/s11121-011-0208-7. (electronic publication ahead of print): http://dx.doi.org/10.1007/s11121-011-0208-7. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R4] Almirall Daniel, Ten Have Thomas, Murphy Susan A. Structural Nested Mean Models for Assessing Time-Varying Effect Moderation. Biometrics. 2010;66:131–9. doi: 10.1111/j.1541-0420.2009.01238.x. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] Anderson Elijah. Code of the Street: Decency, Violence, and the Moral Life of the Inner City. Norton; New York: 1999. [Google Scholar]

[R6] Angrist Joshua D., Pischke Jorn-Steffen. Mostly Harmless Econometrics: An Empiricist's Companion. Princeton University Press; Princeton, NJ: 2009. [Google Scholar]

[R7] Brewster Karin L. Neighborhood Context and the Transition to Sexual Activity among Young Black Women. Demography. 1994;31:603–14. [PubMed] [Google Scholar]

[R8] Brewster Karin L., Billy John O. G., Grady William R. Social Context and Adolescent Behavior: The Impact of Community on the Transition to Sexual Activity. Social Forces. 1993;71:713–40. [Google Scholar]

[R9] Brooks-Gunn Jeanne, Duncan Greg J., Lawrence Aber J. Neighborhood Poverty (Vol. 1): Context and Consequences for Children. Russell Sage; New York: 1997. [Google Scholar]

[R10] Brooks-Gunn Jeanne, Duncan Greg J., Klebanov Pamela K., Sealand Naomi. Do Neighborhoods Influence Child and Adolescent Development? American Journal of Sociology. 1993;99:353–95. [Google Scholar]

[R11] Brumback Babette A., Hernan Miguel A., Haneuse Sebastien J. P. A., Robins James M. Sensitivity Analyses for Unmeasured Confounding Assuming a Marginal Structural Model for Repeated Measures. Statistics in Medicine. 2004;23:749–67. doi: 10.1002/sim.1657. [DOI] [PubMed] [Google Scholar]

[R12] Carter Prudence L. Keepin' It Real: School Success Beyond Black and White. Oxford University Press; New York: 2005. [Google Scholar]

[R13] Charles Camille Z. The Dynamics of Racial Residential Segregation. Annual Review of Sociology. 2003;29:167–207. [Google Scholar]

[R14] Crane Jonathan. Effects of Neighbohoods on Dropping Out of School and Teenage Childbearing. In: Jencks C, Peterson PE, editors. The Urban Underclass. Brookings; Washington, D.C.: 1991. pp. 299–320. [Google Scholar]

[R15] Crosnoe Robert. Low-Income Students and the Socioeconomic Composition of Public High Schools. American Sociological Review. 2009;74:709–30. doi: 10.1177/000312240907400502. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R16] Crowder Kyle, South Scott J. Spatial and Temporal Dimensions of Neighborhood Effects on High School Graduation. Social Science Research. 2010;40:87–106. doi: 10.1016/j.ssresearch.2010.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R17] Darling Nancy, Steinberg Laurence. Community Influences on Adolescent Achievement and Deviance. In: Brooks-Gunn J, Duncan GJ, Aber JL, editors. Neighborhood Poverty (Vol. 2): Policy Implications in Studying Neighborhoods. Russell Sage; New York: 1997. pp. 120–31. [Google Scholar]

[R18] DuMouchel William H., Duncan Greg J. Using Sample Survey Weights in Multiple Regression Analysis of Stratified Samples. Journal of the American Statistical Association. 1983;78:535–543. [Google Scholar]

[R19] Duncan Greg J., Brooks-Gunn Jeanne. Consequences of Growing Up Poor. Russell Sage; New York: 1997. [Google Scholar]

[R20] Duncan Greg J., Jean Yeung W, Brooks-Gunn Jeanne, Smith Judith R. How Much Does Childhood Poverty Affect the Life Chances of Children? American Sociological Review. 1998;63:406–23. [Google Scholar]

[R21] Earls Felton, Carlson Mary. The Social Ecology of Child Health and Well-being. Annual Review of Public Health. 2001;22:143–66. doi: 10.1146/annurev.publhealth.22.1.143. [DOI] [PubMed] [Google Scholar]

[R22] Efron Bradley, Tibshirani Robert J. An Introduction to the Bootstrap. Chapman and Hall; New York: 1993. [Google Scholar]

[R23] Elwert Felix, Winship Christopher. Effect Heterogeneity and Bias in Main-Effects-Only Regression Models. In: Dechter R, Geffner H, Halpern JY, editors. Probability and Causality: A Tribute to Judea Pearl. College Publications; London: 2010. pp. 327–36. [Google Scholar]

[R24] Elwert Felix, Winship Christopher. Endogenous Selection Bias. University of Wisconsin-Madison; 2012. Unpublished Manuscript. [Google Scholar]

[R25] Fernandez Roberto M., Su Celina. Space in the Study of Labor Markets. Annual Review of Sociology. 2004;30:545–69. [Google Scholar]

[R26] Ginther Donna, Haveman Robert, Wolfe Barbara. Neighborhood Attributes as Determinants of Children's Outcomes: How Robust are the Relationships? Journal of Human Resources. 2000;35:603–42. [Google Scholar]

[R27] Greenland Sander. Quantifying Biases in Causal Models: Classical Confounding vs Collider-stratification Bias. Epidemiology. 2003;14:300–6. [PubMed] [Google Scholar]

[R28] Harding David J. Counterfactual Models of Neighborhood Effects: The Effect of Neighborhood Poverty on Dropping Out and Teenage Pregnancy. American Journal of Sociology. 2003;109:676–719. [Google Scholar]

[R29] Harding David J. Cultural Context, Sexual Behavior, and Romantic Relationships in Disadvantaged Neighborhoods. American Sociological Review. 2007;72:341–64. [Google Scholar]

[R30] Harding David J. Collateral Consequences of Violence in Disadvantaged Neighborhoods. Social Forces. 2009;88:757–84. doi: 10.1353/sof.0.0281. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R31] Harding David J. Living the Drama: Community, Conflict, and Culture among Inner-City Boys. University of Chicago Press; Chicago: 2010. [Google Scholar]

[R32] Harding David J. Rethinking the Cultural Context of Schooling Decisions in Disadvantaged Neighborhoods: From Deviant Subculture to Cultural Heterogeneity. Sociology of Education. 2011;84:322–39. doi: 10.1177/0038040711417008. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R33] Heckman James J. Skill Formation and the Economics of Investing in Disadvantaged Children. Science. 2006;312:1900–1. doi: 10.1126/science.1128898. [DOI] [PubMed] [Google Scholar]

[R34] Heckman James J., Krueger Alan B. Inequality in America: What Role for Human Capital Policies? The MIT Press; Boston, MA: 2004. [Google Scholar]

[R35] Holland Paul W. Statistics and Causal Inference. Journal of the American Statistical Association. 1986;81:945–60. [Google Scholar]

[R36] Hong Guanglei, Raudenbush Stephen W. Causal Inference for Time-Varying Instructional Treatments. Journal of Educational and Behavioral Statistics. 2008;81:333–362. [Google Scholar]

[R37] Iceland John, Scopilliti Melissa. Immigrant Residential Segregation in US Metropolitan Areas, 1990-2000. Demography. 2008;45:79–94. doi: 10.1353/dem.2008.0009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R38] Jackson Margot I., Mare Robert D. Cross-Sectional and Longitudinal Measurements of Neighborhood Experience and Their Effects on Children. Social Science Research. 2007;36:590–610. doi: 10.1016/j.ssresearch.2007.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R39] Jencks Christopher, Mayer Susan E. The Social Consequences of Growing Up in a Poor Neighborhood. In: Lynn LE, McGreary MGH, editors. Inner-City Poverty in the United States. National Academy Press; Washington, D.C.: 1990. pp. 111–86. [Google Scholar]

[R40] Kawachi Ichiro, Berkman Lisa F. Neighborhoods and Health. Oxford University Press; New York: 2003. [Google Scholar]

[R41] Lareau Annette. Home Advantage: Social Class and Parental Intervention in Elementary Education. Rowan and Littlefield; New York: 2000. [Google Scholar]

[R42] Longford Nicholas T. Single Imputation and Related Methods. In: Fienberg S, van der Linden W, editors. Missing Data and Small-Area Estimation: Modern Analytical Equipment for the Survey Statistician. Springer; New York: 2005. pp. 37–58. [Google Scholar]

[R43] Marsh Herbert. The Big Fish Little Pond Effect on Academic Self-Concept. Journal of Educational Psychology. 1987;79:280–95. [Google Scholar]

[R44] Massey Douglas S. Segregation and Stratification: A Biosocial Perspective. Du Bois Review. 2004;1:7–25. [Google Scholar]

[R45] Massey Douglas S., Denton Nancy A. American Apartheid: Segregation and the Making of the Underclass. Harvard University Press; Cambridge, MA: 1993. [Google Scholar]

[R46] Mayer Susan. What Money Can't Buy: The Effect of Parental Income on Children's Outcomes. Harvard University; Cambridge, MA: 1997. [Google Scholar]

[R47] Morgan Stephen L., Winship Christopher. Counterfactuals and Causal Inference: Methods and Principals for Social Research. Cambridge University Press; New York: 2007. [Google Scholar]

[R48] Nordberg Lennart. Generalized Linear Modeling of Sample Survey Data. Journal of Official Statistics. 1989;5:223–239. [Google Scholar]

[R49] Pearl Judea. Causal Diagrams for Empirical Research. Biometrika. 1995;82:669–710. [Google Scholar]

[R50] Pfeffermann Danny. The Role of Sampling Weights When Modeling Survey Data. International Statistical Review. 1993;61:317–337. [Google Scholar]

[R51] Pearl Judea. Causality: Models, Reasoning, and Inference. Cambridge University Press; Cambridge: 2000. [Google Scholar]

[R52] Quillian Lincoln. How Long Are Exposures to Poor Neighborhoods? The Long-Term Dynamics of Entry and Exit from Poor Neighborhoods. Population Research and Policy Review. 2003;22:221–49. [Google Scholar]

[R53] Reardon Sean F., Bischoff Kendra. Income Inequality and Income Segregation. American Journal of Sociology. 2011;116:1092–153. doi: 10.1086/657114. [DOI] [PubMed] [Google Scholar]

[R54] Robins James M. A New Approach to Causal Inference in Mortality Studies with a Sustained Exposure Period--Application to Control of the Healthy Worker Survivor Effect. Mathematical Modeling. 1987;7:1393–512. [Google Scholar]

[R55] Robins James M. Correcting for Noncompliance in Randomized Trials Using Structural Nested Mean Models. Communications in Statistics-Theory and Methods. 1994;23:2379–412. [Google Scholar]

[R56] Robins James M. Association, Causation, and Marginal Structural Models. Synthese. 1999a;121:151–79. [Google Scholar]

[R57] Robins James M. Marginal Structural Models versus Structural Nested Models as Tools for Causal Inference. In: Halloran E, editor. Statistical Models in Epidemiology. Springer-Verlag; New York: 1999b. pp. 95–134. [Google Scholar]

[R58] Robins James M., Hernan Miguel A., Brumback Babette A. Marginal Structural Models and Causal Inference in Epidemiology. Epidemiology. 2000;11:550–60. doi: 10.1097/00001648-200009000-00011. [DOI] [PubMed] [Google Scholar]

[R59] Royston Patrick. Multiple Imputation of Missing Values: Update. The Stata Journal. 2005;5:1–14. [Google Scholar]

[R60] Rubin Donald B. Estimating Causal Effects of Treatments in Randomized and Nonrandomized Studies. Journal of Educational Psychology. 1974;66:688–701. [Google Scholar]

[R61] Rubin Donald B. Multiple Imputation for Nonresponse in Surveys. J. Wiley & Sons; New York: 1987. [Google Scholar]

[R62] Rumberger Russell W. High-School Dropouts: A Review of Issues and Evidence. Review of Educational Research. 1987;57:101–21. [Google Scholar]

[R63] Sampson Robert J. How Do Communities Undergird or Undermine Human Development? Relevant Contexts and Social Mechanisms. In: Booth A, Crouter N, editors. Does It Take a Village? Community Effects on Children, Adolescents, and Families. Erlbaum; Mahwah, N.J.: 2001. pp. 3–30. [Google Scholar]

[R64] Sampson Robert J., Morenoff Jeffrey D., Gannon-Rowley Thomas. Assessing “Neighborhood Effects”: Social Processes and New Directions in Research. Annual Review of Sociology. 2002;28:443–78. [Google Scholar]

[R65] Sampson Robert J., Sharkey Patrick. Neighborhood Selection and the Social Reproduction of Concentrated Racial Inequality. Demography. 2008;45:1–29. doi: 10.1353/dem.2008.0012. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R66] Sampson Robert J., Sharkey Patrick, Raudenbush Stephen W. Durable Effects of Concentrated Disadvantage on Verbal Ability among African-American Children. Proceedings of the National Academy of Sciences. 2008;105:845–52. doi: 10.1073/pnas.0710189104. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R67] Sastry Narayan, Pebley Anne R. Family and Neighborhood Sources of Socioeconomic Inequality in Children's Achievement. Demography. 2010;47:777–800. doi: 10.1353/dem.0.0114. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R68] Sharkey Patrick. The Acute Effect of Local Homicides on Children's Cognitive Performance. Proceedings of the National Academy of Sciences. 2010;107:11733–38. doi: 10.1073/pnas.1000690107. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R69] Sharkey Patrick, Elwert Felix. The Legacy of Disadvantage: Multigenerational Neighborhood Effects on Cognitive Ability. American Journal of Sociology. 2011;116:1934–81. doi: 10.1086/660009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R70] Small Mario L., Newman Katherine. Urban Poverty After The Truly Disadvantaged: The Rediscovery of the Family, the Neighborhood, and Culture. Annual Review of Sociology. 2001;27:23–45. [Google Scholar]

[R71] South Scott J., Crowder Kyle D. Escaping Distressed Neighborhoods: Individual, Community, and Metropolitan Influences. American Journal of Sociology. 1997a;102:1040–84. [Google Scholar]

[R72] South Scott J., Crowder Kyle D. Residential Mobility Between Cities and Suburbs: Race, Suburbanization, and Back-to-the-City Moves. Demography. 1997b;34:525–38. [PubMed] [Google Scholar]

[R73] South Scott J., Crowder Kyle D. Avenues and Barriers to Residential Mobility among Single Mothers. Journal of Marriage and the Family. 1998a;60:866–77. [Google Scholar]

[R74] South Scott J., Crowder Kyle D. Housing Discrimination and Residential Mobility: Impacts for Blacks and Whites. Population Research and Policy Review. 1998b;17:369–87. [Google Scholar]

[R75] South Scott J., Crowder Kyle D. Neighborhood Effects on Family Formation: Concentrated Poverty and Beyond. American Sociological Review. 1999;64:113–32. [Google Scholar]

[R76] South Scott J., Crowder Kyle D. Neighborhood Poverty and Nonmarital Fertility: Spatial and Temporal Dimensions. Journal of Marriage and Family. 2010;72:89–104. doi: 10.1111/j.1741-3737.2009.00685.x. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R77] South Scott J., Deane Glenn D. Race and Residential Mobility: Individual Determinants and Structural Constraints. Social Forces. 1993;72:147–67. [Google Scholar]

[R78] Speare Alden, Goldscheider Frances K. Effects of Marital Status Change on Residential Mobility. Journal of Marriage and the Family. 1987;49:455–64. [Google Scholar]

[R79] Sucoff Clea A., Upchurch Dawn M. Neighborhood Context and the Risk of Childbearing among Metropolitan-area Black Adolescents. American Sociological Review. 1998;63:571–85. [Google Scholar]

[R80] Timberlake Jeffrey M. Racial and Ethnic Inequality in the Duration of Children's Exposure to Neighborhood Poverty and Affluence. Social Problems. 2007;54:319–42. [Google Scholar]

[R81] VanderWeele Tyler J. On the Distinction between Interaction and Effect Modification. Epidemiology. 2009;20:863–71. doi: 10.1097/EDE.0b013e3181ba333c. [DOI] [PubMed] [Google Scholar]

[R82] VanderWeele Tyler J., Robins James M. Minimal Sufficient Causation and Directed Acyclic Graphs. The Annals of Statistics. 2009;37:1437–65. [Google Scholar]

[R83] von Hippel Paul T. Regression with Missing Ys: An Improved Strategy for Analyzing Multiply Imputed Data. Sociological Methodology. 2007;37:83–117. [Google Scholar]

[R84] Wheaton Blair, Clarke Philippa. Space Meets Time: Integrating Temporal and Contextual Influences on Mental Health in Early Adulthood. American Sociological Review. 2003;68:680–706. [Google Scholar]

[R85] Wilson William J. The Truly Disadvantaged: The Inner City, the Underclass, and Public Policy. University of Chicago Press; Chicago: 1987. [Google Scholar]

[R86] Wilson William J. When Work Disappears: The World of the New Urban Poor. Vintage Books; New York: 1996. [Google Scholar]

[R87] Winship Christopher, Radbill Larry. Sampling Weights and Regression Analysis. Sociological Methods & Research. 1994;23:230–257. [Google Scholar]

[R88] Wodtke Geoffrey T., Harding David J., Elwert Felix. Neighborhood Effects in Temporal Perspective: The Impact of Long-term Exposure to Concentrated Disadvantage on High School Graduation. American Sociological Review. 2011;76:713–36. doi: 10.1177/0003122411420816. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R89] Wodtke Geoffrey T. Duration and Timing of Exposure to Neighborhood Poverty and the Risk of Adolescent Parenthood. Demography. 2013;50:1765–88. doi: 10.1007/s13524-013-0219-z. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R90] Xie Yu, Brand Jennie E., Jann Ben. Estimating Heterogeneous Treatment Effects with Observational Data. Sociological Methodology. 2012;42:314–47. doi: 10.1177/0081175012452652. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R91] Yinger John. Closed Doors, Opportunities Lost: The Continuing Costs of Housing Discrimination. Russell Sage; New York: 1995. [Google Scholar]

PERMALINK

NEIGHBORHOOD EFFECT HETEROGENEITY BY FAMILY INCOME AND DEVELOPMENTAL PERIOD: EVIDENCE FROM A COUNTERFACTUAL MODEL OF HIGH SCHOOL GRADUATION

Geoffrey T Wodtke

Felix Elwert

David J Harding

Abstract

NEIGHBORHOOD EFFECT MODERATION BY FAMILY RESOURCES

DEVELOPMENTAL TIMING OF NEIGHBORHOOD EXPOSURES

NEIGHBORHOOD SELECTION AND FEEDBACK

DATA AND MEASURES

Figure 1.

METHODS

A Counterfactual Model of Moderated Neighborhood Effects

Limitations of Conventional Regression Estimation

Figure 2.

Two-stage Regression-with-Residuals Estimation

Figure 3.

RESULTS

Sample Characteristics

Table 1.

Table 2.

Neighborhood Conditions during Childhood and Adolescence

Table 3.

Table 4.

Moderated Neighborhood Effects

Table 5.

Figure 4.

Figure 5.

Sensitivity Analyses

DISCUSSION

Acknowledgments

APPENDIX

Part A: Neighborhood Disadvantage Index

Table A.1.

Figure A.1.

Part B: Weighted Estimates

Table B.1.

Table B.2.

Table B.3.

Table B.4.

Table B.5.

Part C: Model Specification

Table C.1.

Table C.2.

Part D: Sensitivity Analysis

Table D.1.

Figure D.1.

Figure D.2.

Part E: Missing Data

Table E.1.

Table E.2.

Footnotes

Contributor Information

REFERENCES

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases