ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB

Abstract

Molecular mechanics is powerful for its speed in atomistic simulations, but an accurate force field is required. The Amber ff99SB force field improved protein secondary structure balance and dynamics from earlier force fields like ff99, but weaknesses in side chain rotamer and backbone secondary structure preferences have been identified. Here, we performed a complete refit of all amino acid side chain dihedral parameters, which had been carried over from ff94. The training set of conformations included multidimensional dihedral scans designed to improve transferability of the parameters. Improvement in all amino acids was obtained as compared to ff99SB. Parameters were also generated for alternate protonation states of ionizable side chains. Average errors in relative energies of pairs of conformations were under 1.0 kcal/mol as compared to QM, reduced 35% from ff99SB. We also took the opportunity to make empirical adjustments to the protein backbone dihedral parameters as compared to ff99SB. Multiple small adjustments of φ and ψ parameters were tested against NMR scalar coupling data and secondary structure content for short peptides. The best results were obtained from a physically motivated adjustment to the φ rotational profile that compensates for lack of ff99SB QM training data in the β-ppII transition region. Together, these backbone and side chain modifications (hereafter called ff14SB) not only better reproduced their benchmarks, but improved secondary structure content in small peptides, and reproduction of NMR χ1 scalar coupling measurements for proteins in solution. We also discuss the Amber ff12SB parameter set, a preliminary version of ff14SB that includes most of its improvements.

TOC figure

Introduction

Computational studies of biopolymers such as proteins have become commonplace, supplementing experimental information with models that provide simultaneous resolution in time, space and energy. The results, however, strongly depend on the accuracy of the computed energies and forces. The constant chemical topology prescribed by molecular mechanics (MM) leads to dramatically enhanced efficiency over quantum mechanics (QM). As wide application of even the most approximate quantum methods to solvated biomolecular simulations remains computationally prohibitive, development of accurate force fields is a critical problem for in silico biomolecular studies. Polarizable force fields¹ in principle should be more accurate than fixed charge force fields, but for many systems of interest current fixed-charged models may provide results that are comparably reasonable in aqueous solution to polarizable contemporaries². This is particularly important as these fixed-charge models also typically have lower computational overhead, allowing for improvements to the conformational sampling that often limits comparison to experiment. We believe that there is still room for improvement in fixed-charge biomolecular MM force fields. Such optimization is the focus of this work, where we focus on improving accuracy where needed most, without adding additional computational complexity over the widely used ff99SB model³.

ff99SB uses the functional form and many of the parameters derived in ff94⁴ and ff99⁵, largely associated with the Amber software⁶. A key difference in these force fields is the parameters in Fourier series adjusting energy profiles for rotation around bonds. These corrections account for key orbital effects or weaknesses in other terms like 1B4 non-bonded interactions, typically the last step in fitting force field parameters. A key assumption in these force fields is that the dihedral corrections are uncoupled, and thus have no explicit dependence on values of neighboring dihedrals. In ff94, “generic”’ torsions applying to all sets of four atoms around a bond between two atom types (using a wildcard for the outer 2 atoms) were fit to a set of experimental small molecule barrier heights. In ff99⁵, multiple-periodicity specific torsional parameters applicable to protein side chains were fit to a larger set of small molecules.

An important component of protein force fields is the “backbone” dihedral parameters that can alter secondary structure preferences. ff94 and ff99SB leverage unique corrections to multiple sets of 4 atom dihedral terms around φ and ψ, describing the multiple combinations of atoms bonded to the central 2 atoms. In ff94, the baseline backbone dihedral profile for φ (C–N–Cα–C) and ψ (N–Cα–C–N) dihedral corrections were fit to glycine dipeptide conformation energies from QM. Then, the influence of the side chain was added to other amino acids by fitting parameters for the so-called φ′ (C–N–Cα–Cβ) and ψ′ (Cβ–Cα–C–N) based on alanine dipeptide QM conformational energies. Importantly, the φ′ and ψ′ were fit as a correction on top of the φ and ψ parameters that had already been fit to glycine. Thus all amino acids except glycine had 2 full sets of “backbone” dihedral contributions, one using only backbone atoms and a second correction set using the Cβ atom. The ubiquity of force fields based on ff94 shows its overall effectiveness, despite specific weaknesses in performance for proteins, such as exaggerated helical propensity³. With ff99SB³, protein backbone dihedrals were refit by expanding upon the methods used in ff94 and ff99. A larger set of alanine tetrapeptide conformations was used in fitting φ′ and ψ′, as well as introducing glycine tetrapeptide conformations for fitting φ and ψ. The relative energies of conformations control populations and barriers in an MM model, and thus they were used as the direct targets in parameter optimization. The conformations were limited to local minima because of computational expense, but the fitting struck a balance of secondary structure suitable for a range of systems^{3, 7}. ff99SB became widely adopted in the simulation community, and thus the same approach of conformation pair energy fitting is used in the present work for optimization of side chain dihedral parameters.

Limitations in ff99SB

Limitations in models often only become apparent after extensive use and testing. One advantage of the wide adoption of ff99SB is that trends in the weaknesses were noted, in contrast to single anecdotal failures for which the cause may be difficult to determine, or unknown weaknesses in force fields that are not widely distributed.

Most notably, rotamer preferences for several side chains were observed to be less accurate than others⁸. This likely arose since ff99SB inherited amino acid side chain dihedral parameters from ff99, which were derived against a limited set of relative energies for small organic compounds⁵. The transferability of energy correction parameters for small molecules with relatively simple energy landscapes to amino acids may be an issue. The atoms in the amino acids typically have different partial atomic charges than the reference compounds, as well as more complex coupling to neighboring fragments. Due to recent increases in computational power, more extensive calculations (including full rotational energy profiles rather than selected stable conformations) can now be used to train side chain parameters directly against QM data on complete amino acids^8–9.

Several studies noted room for improvement in the secondary structure preferences of ff99SB, and this is also investigated here. After ff99SB was published, solution scalar coupling data for short peptides¹⁰ became available, against which ff99SB and other force fields were compared¹¹, and the potential for improvement was discussed^11a. NMR scalar coupling constants, especially three-bond scalar ³J couplings, are particularly relevant for evaluation of dihedral distributions, as ³J couplings measure spin-spin interactions across three bonds. This allows one to utilize the simple Karplus relation¹²—a third order cosine series—to convert directly from dihedral angles to scalar couplings. In practice, however, the Karplus relation fails to account for other features that may affect scalar coupling, such as bond length or angle, or neighboring spin systems. Recent DFT calculations suggest that nearly all peptide backbone scalar couplings may in fact depend on both φ and ψ, for example¹³. Furthermore, scalar couplings calculated by a Karplus relation are sensitive to which empirical Karplus parameters are used^{11a, 11b}. It also has been suggested that helical structures are not stable enough in ff99SB^{11b, 11c, 14}.

We hypothesize that two potential weaknesses in the ff99SB backbone parameter fitting strategy may be the dominant factors limiting accuracy: (1) the lack of backbone fitting data outside gas-phase minima and (2) using pre-polarized MM partial charges intended for aqueous solution simulations while fitting dihedral parameters against gas-phase QM data. Limiting the backbone parameter training to gas-phase local minima left potentially arbitrary energies for transition barriers or, importantly, in regions that become minima in solution or in the complex landscape of the protein interior. Additionally, the additive ff99SB model employs HF/6-31G* RESP partial atomic charges¹⁵ that overestimate gas-phase dipoles by a similar amount as obtained in water models such as TIP3P¹⁶, thus approximating the polarization expected in aqueous solution¹⁵. However, subsequent refitting of dihedral energy profiles to more accurate gas-phase energies calculated at the MP2 level results in dihedral parameters that may partially counteract the contribution of implicit polarization effects on the rotational energy profiles. Thus empirical corrections may provide additional benefit in reproducing experiments in water. While an alternative strategy to account for solvation effects in a more consistent way might be to develop an entirely new charge model¹⁷, the original ff94 RESP charge model^{4, 15} developed by Peter Kollman has been extensively tested, and retaining it also maintains compatibility with many other parameter sets such as those modeling nucleic acids and carbohydrates¹⁸. Likewise, refitting the entire backbone dihedral profile rather than just minima would potentially lose the advantage of extensive studies^{7, 11a, 11b, 19} evaluating ff99SB’s strengths and weaknesses. Here, we investigate the simpler strategy of developing a small empirical adjustment to the ff99SB backbone parameters to improve reproduction of the experimental data in solution.

We show below that ff14SB, the combination of ff99SB with these new QM-based side chain dihedral parameters and a small empirical adjustment to the backbone φ energy profile, improves upon ff99SB in ensemble distributions for short polyalanine conformations (backbone scalar couplings), protein side chains (χ1 scalar couplings), and secondary structure balance for peptides adopting α-helical and β-hairpin conformations, while maintaining the quality of ff99SB local dynamics (Lipari-Szabo S² order parameters). Recently, we also showed that updating the side chain parameters with those reported here results in a model that is able to accurately fold a wide variety of protein topologies up to nearly 100 amino acids²⁰. It has also been shown that ff14SB maintains the crystal lattice and protein conformations of triclinic lysozyme better than ff99SB, ff14ipq, or CHARMM36²¹. We recommend use of ff14SB for protein simulations in Amber as well as in other biomolecular simulation software.

Fitting Strategy and Goals

Side chains

For the side chain update, we focus on improving the aspects that we feel are most likely to be the greatest weaknesses in the current model. Several recent reports of force field training have focused on application of more accurate quantum theory^{3, 8–9, 22}. Although the level of theory is certainly important, we feel that focusing on the conformational diversity and consistency in the training data set is more likely to improve the model. In principle, dihedral parameters account for orbital effects missing in a classical model for bond rotation, but in practice also serve as empirical corrections for all differences between the QM and MM models, including lack of charge polarization changes during rotation, as well as dihedral-dependent errors in other (bond, angle, and nonbonded) terms in the force field. As a result, the appropriate correction needed to match the MM torsion rotation energy profile to that obtained using QM may differ depending on chemical or conformational context, such as backbone conformation or other side chain torsions. In most biomolecular MM force fields, however, each rotatable bond is described by parameters that are independent of the conformation of the rest of the molecule (though exceptions exist where a subset of dihedral pairs are explicitly coupled, such as the CHARMM CMAP²³). As a result, while the net energy profile for rotating about a given bond will likely depend on other dihedrals (through steric effects, for example), the lack of explicit coupling in dihedral parameters limits the parameters to an implicit account for any coupling missing in the classical model. Therefore, it is important that the structures used for dihedral fitting include neighboring regions of the molecule where the parameters will be used. It is paramount to include conformational variety in those regions to avoid implicit coupling to a limited subset of their phase space, for example, a single rotamer or backbone conformation. In the present case, this led us to follow previous work^8–9 and use complete amino acids in the QM calculations for the side chain training data, as opposed to the small organic compounds used in ff99⁵ and carried over to ff99SB. It is also crucial to ensure that the appropriate molecular degrees of freedom are consistent between the QM and MM, whereas other degrees of freedom may need to be optimized for each model. Thus we explored different restraints and optimization schemes.

Furthermore, implicit coupling was incorporated by fitting a single set of dihedral parameters using a large set of conformations that included multidimensional scans of all side chain χ rotatable bonds, with both α and β backbone conformations for the dipeptide. Thus, while the model lacks explicit coupling, the correction parameters for each dihedral are optimized in a mean field of extensive conformational variability for the remainder of the molecule. In a recent revision of a small number of ff99SB side chain torsions that were identified by comparison of rotamer preferences in a helical context against the PDB, training against quantum mechanics energies for conformations with extended backbone improved χ1 rotamer preferences in β-rich proteins. However, while two of four amino acids showed considerable improvement in the helical test case, the other two showed more modest reduction in errors⁸. Our goal is to derive parameters that are transferable across chemical and conformational diversity, thus we explicitly included dipeptide conformations with both α and β backbone when sampling side chain rotational profiles. Given the weaknesses associated with scalar couplings, we did not fit to side chain scalar coupling data, but used them only to evaluate results of parameter changes that were fit using QM. This differentiates our approach from CHARMM36⁹, for example, where side chain parameters were finally adjusted to better reproduce χ1 scalar couplings.

Another choice concerns the importance of conformational diversity in the side chain rotamer training set. One option is to scan each dihedral rotamer separately, but as discussed above, this approach can fail to incorporate coupling needed in the correction terms, and may provide parameters that work well for some rotamer combinations, but fail for others that were absent in the training data. Since including coupling via multidimensional scans can generate large numbers of conformations, one option to reduce the size of the training set is to include only minima. However, the exact locations of side chain χ minima can depend on backbone conformation, solvent, and packing with nearby residues. We thus decided to sample side chain conformations via full two-dimensional scans for the thirteen amino acids (counting different protonation states for Asp and His) with two side chain dihedrals (Table S1). For larger amino acids, conformational diversity was generated via symmetry considerations or dynamics simulations (described below). Because positions of minima may change in the context of a more complex system, and because energies for transitions may be relevant, each point in these scans was considered equally important as compared to weighting data points by their energy. As side chain preferences are coupled to the backbone²⁴, we performed these scans at both α (φ,ψ = −60°, −45°) and β (−135°, 135°) backbone conformations. Although additional backbone conformations could be employed, we considered only the archetypal α and β secondary structures due to computational cost. A separate ppII conformation (−75°, 150°) was not included, as the interaction of the side chain with the N-terminal peptide group is comparable in ppII and α conformations, while the interaction of the side chain with the C-terminal peptide is comparable in ppII and β conformations, thus these interactions are represented in the two backbone conformations already included in our set.

Our fitting targets for the side chains were gas-phase ab initio energies, as in ff99SB. To accommodate the 15082 dipeptide conformations in our training set, we employed a relatively modest level of theory, with geometries calculated at HF/6-31G* and single point energies calculated at MP2/6-31+G**. Given the fundamental approximations, such as additivity, fixed partial charges, r⁻¹² repulsion, and harmonic bond and angle vibrations, we do not expect the quantum theory to be the limiting factor in improving our model and focused on increasing the conformational diversity in the training set.

Additional choices that must be made relate to the generation of the QM and MM energies for conformations in the training set. First, we investigated what restraints to use in potential energy surface scans. Restraining the 4-atom set defining each χ dihedral, as well as those for φ and ψ, is natural given the goal of scanning combinations. Less obvious is whether other dihedral restraints should be included for the rotatable bond being scanned, such as those sharing the same 2 atoms defining the central bond, but varying the outer atoms. For example, the restraint for χ1 in Val is defined using N-Cα-Cβ-Cγ1, but the dihedral N-Cα-Cβ-Cγ2 could either be restrained or allowed to freely optimize in the presence of the χ1 restraint. Another choice is whether (and how strongly) to restrain other parts of the molecule, such as methyl rotations, or the peptide ω rotation. Next, given the fundamental differences in QM and MM models, and weakness in MM description of energetics beyond dihedral profiles, we investigated whether to optimize geometries once—calculating molecular mechanical energies of quantum mechanical structures—or to re-optimize the QM structures with the MM model prior to comparing energies. The energies could be calculated for identical structures, for example the quantum mechanical structures. An advantage of this approach is that all coordinates and non-bonded distances would be identical. Alternatively, energies could be compared for structures optimized with the corresponding method (i.e. MM energies for MM-optimized structures). The MM model may not reproduce small changes in bond and angle geometries for different rotamers in the QM model, and the stiffness of the MM quadratic function could result in these differences making large contributions to the errors in relative energies of conformation pairs that could be relaxed with MM re-optimization (or dynamics), thus focusing the resulting energy profile on the rotamer changes rather than MM covalent structure approximations.

Like several other MM force fields, the Amber-related models have traditionally used atom types to apply a small number of bond, angle and dihedral parameters to similar fragments in different amino acids. Ideally, the parameters would be highly transferable, and show accuracy for a variety of contexts. This approach reduces the number of parameters needed, but also limits the accuracy of the model as the implicit coupling we seek is worsened when the parameters are averaged over too great a variety of neighboring functional groups that can influence charge distribution. More specifically, the dihedral parameters are added to the energy calculated using the 1–4 electrostatics, but the partial charges are atom-specific and need not be the same for atoms with the same atom type. Yet, many sets of four atoms in the amino acid backbone and side chains shared the same atom types (and therefore the same dihedral corrections) with each other and also with nucleic acids in ff99SB. To overcome this, new atom types were created when needed to improve specificity. For example, asparagine χ2 (Cα-Cβ-Cγ-Nδ), glutamine χ3 (Cβ-Cγ-Cδ-Nɛ), and ψ′ (Cβ-Cα-C-N) all shared atom types CT-CT-C -N, and therefore the same dihedral corrections applied to all three bonds. Here, additional atom types were created to allow independent adjustment of backbone parameters and different side chain parameters. A new atom type for the α carbon (CX) was created to separate main chain, χ1, χ2, and other χ parameters, as the backbone and side chain were corrected separately. Where cross-referencing simulation data and errors fitting quantum energies suggested that solving corrections for particular amino acids together led to inaccuracies that solving separately would alleviate, additional atom types were also introduced to segregate them. Within the side chains, atom types 2C and 3C were developed for carbons bound to two or three heavy atoms, respectively, more thoroughly describing branched amino acids while isolating the revisions to amino acids (and preventing application to nucleic acids, which was possible in previous models). The CO atom type was introduced to distinguish carboxylate carbon from other carbonyl carbons. The C8 atom type was added for arginine and lysine sp3 carbons, to distinguish them from glutamate, glutamine, and methionine. Each side chain atom type was added only if it had some chemical justification, allowed better reproduction of both quantum mechanics fitting targets, and improved dynamic properties, to verify that additional parameters are appropriate. Tables S1 and S2 provide atom types for all atoms in the amino acids.

Backbone

Another goal of this work is to develop empirical adjustments to the dihedral parameters in order to improve secondary structure balance, and agreement with NMR scalar coupling data for short peptides in solution. Particularly, HN–Hα scalar couplings calculated from the MD ensemble were too high^11a, suggesting too much sampling in the region between β and ppII, where the Karplus curve suggests coupling constant values greater than the values observed in the NMR experiments (Figure 1A). Despite this region being a formal barrier region, and therefore not represented by the minimized ff99SB training set conformations (Figure 1A), free energy profiles for alanine dipeptide suggest that the barrier is low enough that population of the region can contribute significantly to the ensemble averaged coupling constant at 300K (Figure 1B). It seems reasonable that the optimized ff99SB energy profile may have been too low in this region yet still provided a good fit to the training data that lacked structures in the transition region. Rather than attempting to generate additional unminimized training data and refitting the entire backbone dihedral profile, we took the approach of developing a small empirical correction aimed at reducing the population in the transition region in order to improve the correspondence between the simulations and experiments. Importantly, while much of the rest of the force field (and certainly the other dihedral parameters) was fit to physics-based, QM data, this backbone dihedral adjustment is an empirical correction based on data obtained from simulations carried out in TIP3P explicit water. Therefore, transferability of this correction term to other implicit or explicit solvent models may need evaluation prior to production use.

Figure 1.

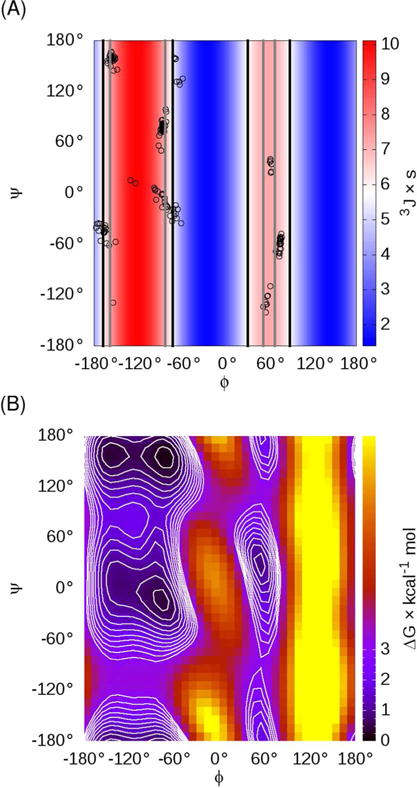
(A) Ramachandran plot with the structures in the ff99SB Ala₃ training set³ shown as circles, with the Hu and Bax²⁵ H-Hα Karplus curve data shown in the background as a color gradient. Vertical lines indicate the φ values where the Karplus curve matches the scalar coupling value from either NMR¹⁰ (black) or ff99SB simulations (gray). Note that ff99SB training data were limited near the maximum of the Karplus curve (φ=−120°), suggesting that the ff99SB energies may be poorly defined in this region. (B) Free energy surface for alanine dipeptide in ff99SB, showing that the β-ppII transition region near φ,ψ=−120°,160° has significant population despite lack of training data in Figure 1A.

We therefore developed modifications to φ′ and ψ′ torsional parameters to specifically address agreement between NMR and MD for short alanine peptides (see Supporting Information for complete details). We hypothesized that the main problem is that the β-ppII barrier is too low due to lack of fitting data, but as described below, we tested alternative strategies as well. Some modifications raise the barriers between β and ppII basins or between ppII and α basins. Other modifications stabilize ppII and α relative to β or stabilize α relative to β and ppII to account for the solvation inconsistencies described above (since aqueous solvation stabilizes the α-helical macrodipole). All pairs of individual φ and ψ modifications were combined and tested. To isolate backbone errors from side chain refitting, we continued to use alanine as a model system, and evaluated thirty candidate force fields against Ala₅ scalar couplings. Besides decoupling the backbone and side chain, Ala₅ is small, facilitating generation of precise conformational ensembles in explicit water, with error bars smaller than the differences resulting from changing the backbone parameters. Such reduction of precision errors to lower than the accuracy errors is crucial for quantitative force field validation. Scalar couplings were evaluated using multiple sets of Karplus parameters to seek consensus. But due to the limitations discussed above, evaluation of these coupling constants gives a qualitative guide to force field quality; we use this to filter parameters sets for more extensive (and computationally expensive) testing on larger systems. One potential strength of our approach is that we do not fit to scalar couplings directly (particularly since the values depend on the Karplus parameters selected), but use them to select a limited set among many physically-motivated empirical modifications. This differs from recent work that has focused on modifying a single torsional term to reproduce solution measurements directly^{11c, 26} or deriving coupled corrections against protein chemical shifts²⁷. We also desired parameters that were transferable between short disordered peptides (such as Ala₅) and larger peptides with propensity to adopt stable secondary structure. This puts our approach between that of Nerenberg and Head-Gordon²⁶ and those of Best and Hummer^11c, and Li and Brüschweiler²⁷.

Potential limitations in our approach

We retain many of the approximations present in ff99SB, such as weaknesses in the harmonic description of covalent bonds and angles, as well as the 6–12 Lennard-Jones function. We also retained the same 1–4 nonbonded scaling factors employed with ff99SB. We refit all side chain dihedral parameters except the “generic” terms applied to nonpolar hydrogens, which were left at the values from ff99. We continue to assume that backbone corrections for alanine are appropriate for all amino acids except glycine, and that explicit coupling between dihedral pairs can be neglected. For going beyond the fine-tuning applied here, this might not be the case, and per-residue, explicitly coupled backbone corrections may provide better accuracy. We also assume that comparing to scalar couplings by Karplus relations is rigorous enough to identify the best force field candidates for further screening. This naturally depends on errors in the approximate and empirical Karplus parameters or the experimentally measured scalar couplings. We additionally assume that gas-phase comparison against MP2/6-31+G**//HF/6-31G* quantum energies is sufficient to improve the side chain parameters. A brief test on aspartate conformations spaced every 60° indicated that our chosen level of theory agrees with MP2/aug-cc-pVTZ to within less than 0.3 kcal/mol average normalized error³ (ANE, described below) for both α and β backbone conformations. Ultimately, improving the level of theory or adding solvent in QM may alleviate some errors or inconsistencies in this approach. These assumptions, however, allowed us to overhaul the side chain dihedral parameters that had been carried over from ff94, in the context of the RESP charge model used in many force fields, and also to further refine the ff99SB protein backbone parameters.

Methods

Backbone dihedral empirical adjustment

Backbone parameter modifications were based on conformational ensembles for Ala₃ in TIP3P explicit water at 300 K that we published previously^11a. These ensembles were used to predict shifts in populations with dihedral parameter modification, and to predict the resulting change in ensemble-averaged scalar coupling values. A grid with 5° spacing was generated for both φ and ψ dihedral angles and calculated the normalized population and relative free energy of each grid bin using the ff99SB simulation ensemble. Next, the expected J value contribution for each grid bin was calculated using the population and Karplus parameters²⁸. A spreadsheet was used to calculate ff99SB dihedral energies for each grid bin, as well as dihedral energies calculated with a Fourier series with altered amplitudes for backbone dihedrals. For each grid bin, the free energy was reweighted by the difference between the energies calculated using ff99SB and modified dihedral parameters. These altered free energies for the bins were converted to normalized populations, and then back to expected J values using the Karplus curve. Thus the potential impact on the agreement between simulated and measured ³J(H_NH_α) from candidate dihedral parameter amplitude adjustments could be interactively estimated. The details of each modification to phase, periodicity and amplitude are provided in Tables S5 and S6, and the rationale for each change is discussed in the Supporting Information.

Side chain dihedral training

Dipeptide structure generation

Acetyl and N-methyl capped dipeptides of the natural amino acids, except proline, alanine, and glycine, were built using LEaP²⁹ at α (−60°, −45°) and β (−135°, 135°) backbone conformations. $\overrightarrow{\chi }$ was explored by rotating in 10° increments, re-optimizing at each step, or by high temperature simulation (described in Results).

Quantum mechanics optimizations were performed with RHF/6-31G*. Scanned residues were optimized using GAMESS (US)³⁰ with default options. Optimization continued until the RMS gradient was less than 1.0 × 10⁻⁴ Hartree Bohr⁻¹, with an initial trust radius of 0.1 Bohr that could then adjust between 0.05 and 0.5 Bohr. Minimization proceeded by the quadratic approximation. Residues sampled by high temperature simulations were optimized using Gaussian98³¹ with VTight convergence criteria. Quantum mechanics energies for training data were calculated with MP2/6-31+G**. Molecular mechanics re-optimizations were performed in the gas phase with ff99SB for a maximum of 1.0 × 10⁷ cycles or until the RMS gradient was less than 1.0 × 10⁻⁴ kcal mol⁻¹ Å⁻¹, with a non-bonded cutoff of 99.0 Å and initial step size of 10⁻⁴. Dihedral restraint force constants were 2.0 × 10⁵ kcal mol⁻¹ rad⁻². Minimization employed 10 steps of steepest descent followed by conjugate gradient. Molecular mechanics energies were calculated from the last step of ff99SB minimization.

Dipeptide energy calculations

Generating conformational diversity in the training set

To maximize transferability of the parameters, multidimensional structure scans were employed to generate conformational diversity. For smaller side chains, grid scans in dihedral space were used to generate side chain variety, including both α and β backbone conformations for each side chain rotamer. Grid scans were generated for Val in one dimension, as it only has χ1, at an interval of 10°. Grids were generated for Asp⁻, Asn, Cys, Phe, His (δ-, ɛ-, and doubly-protonated), Ile, Leu, Ser, Thr, and Trp in two dimensions, as they have χ1 and χ2, at intervals of 20°, yielding 324 structures per amino acid.

We were unable to exhaustively explore side chain conformational space side chains with more than two rotatable bonds. Tyrosine has 3 rotatable χ bonds, but dihedral space is reduced as 180° rotation of either the phenol (χ2) or of the hydroxyl produce the same effect when accounting for symmetry of the ring. We therefore fully scanned each tyrosine dihedral when the other two were at a stable rotamer defined as any instance of that value in the rotamer library for this amino acid, rounded to the nearest 10° and limiting χ2 to (−90°, 90°] to account for symmetry. Stable rotamers for the hydroxyl, not in the rotamer library, were inferred from the QM energy profiles discussed above. Stable rotamers were 180° or ±60° for χ1, ±30° or 90° for χ2, and 0° or 180° for the hydroxyl. Conformations were generated using a full scan for each dihedral (at 20° increments), repeated for every combination of stable rotamer values for the other two dihedrals. As protonated aspartate has nearly the same dihedrals as Tyr (χ1, χ2 and hydroxyl), it was scanned in the same manner, but without χ2 restriction because aspartate does not have the same symmetry properties.

Cysteine presents a special case, as it can form disulfide bonds that bridge two amino acids. In addition to developing parameters for reduced Cys (no disulfide), a pair of Cys dipeptides with a disulfide bond was employed to scan the S-S energy profile. However, a disulfide between Cys_A and Cys_B has a total of five dihedrals: χ1_A, χ2_A, χ_SS, χ2_B, and χ1_B. As full sampling across five dihedrals is clearly intractable, conformation space was reduced by applying the same χ1 / χ2 values to both dipeptides. Using this symmetry, a two-dimensional scan was performed for all χ1 / χ2 combinations using 20° spacing; this scan was repeated with χ_SS restrained to 180°, ±60°, or ±90° (five 2D scans). Separately, the χ_SS profile was scanned with 20° spacing using χ1 of 180° or ±60° and χ2 of 180° or ±60° (nine 1D scans total). As with the other amino acids, the entire procedure was repeated with the backbone in α and β conformations; here, both dipeptides adopted the same backbone conformation.

The remaining side chains, Arg⁺, Gln, Glu (protonated), Glu⁻,Lys⁺, and Met, have at least three side chain dihedrals (Table S1). Rather than performing a grid search, MD simulations were used to generate diverse conformations of these side chains. Each dipeptide was simulated twice, with α or β backbone restraints, for 100 ns each. To overcome kinetic traps, these simulations were performed at 500 K and the dielectric was set to 4r. Next, a diverse subset was generated by mapping each conformation to a multidimensional grid spaced 10° in each χ. The five lowest energy conformations at each grid point were saved. From each simulation grid, five hundred structures were randomly selected (comparable to the number generated by the grid procedure described above for Tyr). Because the longer, more flexible side chains of these amino acids can adopt conformations with strong interactions between backbone and side chain, conformations where we suspected the in vacuo MM description may produce fitting artifacts were excluded, using electrostatic and distance cutoffs defined in the Supporting Information.

Objective function for parameter optimization

As in ff99SB, the errors in relative energies between all pairs of conformations were evaluated to alleviate the bias of a single, potentially arbitrary reference conformation. We first defined the relative energy error (REE) between a single pair of conformations i and j:

$$\text{REE}(i,j)=(E_{\text{QM},i}-E_{\text{QM},j})-(E_{\text{MM},i}-E_{\text{MM},j})$$ (1)

where E_QM,i and E_MM,i are the quantum and molecular mechanics energies of conformation i. E_MM is calculated either as ff99SB, or, during parameter search as the ff99SB energy with the dihedral energy replaced using the candidate dihedral parameters, E_{ff_new}:

$$E_{\text{ff\_new}}=E_{\text{ff99SB}}+{\displaystyle {\sum }_{\chi }\left(E_{\chi }^{\text{ff\_new}}-E_{\chi }^{\text{ff99SB}}\right)}$$ (2)

Where the sum is taken over all side chain rotatable bonds χ. $E_{\chi }^{\mathit{ff}}$ is the sum of dihedral energy contributions of N_χ 4-atom sets around each rotatable bond, excluding those containing nonpolar hydrogens (Table S2), which remained at the values from ff99SB. For each dihedral, the periodicity n=1–4 Fourier series contributions with amplitude $V_{\chi \left[c\right],n}^{\mathit{ff}}$ and phase ${\gamma }_{\chi \left[c\right],n}^{\mathit{ff}}$ were summed:

$$E_{\chi }^{\text{ff}}={\displaystyle \sum _{c=1}^{N_{\chi }}{\displaystyle \sum _{n=1}^4{V}_{\chi \left[c\right],n}^{\text{ff}}\left(1+\cos \left(n{\phi }_{\chi \left[c\right]}-{\gamma }_{\chi \left[c\right],n}^{\text{ff}}\right)\right)}}$$ (3)

We note that this equation is consistent with the Amber standard and lacks a factor of 1/2, and thus the true range of the energy for each term is twice V^ffχ. The fitting was limited to the fourth order term in each correction, consistent with ff99SB. Test fits using more terms resulted in noisier corrections without significantly improving fit quality (data not shown).

To focus the energy differences on side chain rotamer profiles, comparisons between structures pairs with different backbone conformations, or of different amino acids, were excluded. Alternate protonation states for ionizable amino acids were summed separately. For each amino acid, in either α or β backbone conformation, the magnitudes of REE over all pairs of N side chain conformations were summed, dividing by the number of pairs to obtain the average absolute error (AAE, as defined in Hornak et al.³) for this amino acid, in a given protonation state, in a specific backbone conformation:

$$\text{AAE}=\frac{2}{N(N-1)}{\displaystyle \sum _i{\displaystyle \sum _{j<i}\left|\text{REE}(i,j)\right|}}$$ (4)

The average of the AAEs for each residue and backbone conformation was minimized by adjusting the amplitude and phase parameters for all terms in Eqn. 3. Formally, optimization was performed by minimizing the objective function:

$$O=\frac{1}{n_{\mathit{profiles}}}{\displaystyle \sum _{r=1}^{\text{amino}\text{acid}}{\displaystyle \sum _{bb=\alpha ,\beta }{\text{AAE}}_{r,bb}}}$$ (5)

where n_profiles is the number of AAE profiles, resulting in a normalized O value that represents the error in energy differences for conformation pairs, averaged over all backbone contexts, amino acids and protonation states.

The parameters for all non-hydrogen dihedrals in the protein side chains describing rotation around single bonds, as well as hydroxyl or sulfhydryl torsions are presented in Table S2. As discussed above, our structure training set was designed to include amino acid conformation pairs with simultaneous changes to more than one rotatable bond, thus necessitating concurrent optimization of parameters for multiple dihedrals (rather than the simpler approach³² of scanning parameter space one rotatable bond at a time). This enables the optimized energy corrections for each rotatable bond to incorporate implicit coupling to nearby conformational diversity. Furthermore, the presence of similar local structure (as described by atom types) in multiple amino acids often led to the requirement for fitting parameters using data from all amino acids where that functionality exists. This provides parameters that implicitly account for nearby chemical diversity, as opposed to training in a single amino acid and use in others. As a result of these two design factors, the parameter space for optimization is considerable.

To reduce problem size and accelerate convergence, amino acids were separated into the solving groups listed in Table S3 based on shared dihedral atom types, and a separate objective function (Equation 6) was constructed for each of the solving groups. Specific tables of dihedrals in each solving group are provided in Table S2. As each group shares no four-atom dihedrals with other groups, the full parameter space could be partitioned, with each solving group providing all conformations and energies necessary for separate optimization of each parameter subset. Optimized values of the objective function for each solving group are provided in Table S3.

Our goal was to use the AAEs to optimize a single set of parameters that minimizes the REE for multiple backbone conformations. However, the AAE for α and β are averages over all side chain pairs, while the ability of the optimization procedure to maximize transferability hinges on the backbone dependence of the QM-MM energy error for pairs of side chain conformations. Greater similarity of REEs among backbone conformations would indicate a better likelihood of being able to optimize a single set of parameters that is transferable among said backbone conformations. To quantify this, we subtracted the β REE from the α REE for each pair i,j of side chain conformations, averaging the magnitudes of these differences to obtain the intrinsic backbone dependence (BBD):

$$\text{BBD}=\frac{2}{N(N-1)}{\displaystyle {\sum }_i{\displaystyle {\sum }_{j<i}\left|\text{REE}{(i,j)}_{\alpha }-\text{REE}{(i,j)}_{\beta }\right|}}$$ (6)

Where the same notation is used as defined for Eqn. 4. We note that the BBD does not report on how well the QM and MM energies match, only on whether the differences are consistent as the backbone conformation changes. Thus BBD for each amino acid is a measure of the ultimate ability of side chain dihedral parameters to match QM data in the absence of explicit coupling between backbone and side chain par ameters; any difference cannot be corrected with side chain dihedral parameters.

The ANEs were minimized using a genetic algorithm to perturb the amplitudes V and phase shifts γ in Eqn. 3. Full details are provided in the Supporting Information, but the procedure is briefly outlined here. Two populations each for ff99SB, zeroed force field parameters, and random force field parameters were generated with 63 individuals, and evolved independently. For the first 200000 generations, the amplitude was allowed to be perturbed by any value between −0.5 and 0.5 kcal/mol. Then, to focus the search, amplitude changes were restricted to 0.002 kcal/mol for another 100000 generations and then 0.001 kcal/mol until an ff99SB-initialized population found the same solution as populations starting with zero or random force field parameters. Phase shifts were restricted to 0° or 180° to produce parameters applicable for alternate enantiomers.

Simulation protocols

Initial helical conformations were defined as all amino acids having (φ, ψ)=(−60°, −40°). Initial extended conformations were defined as all (φ, ψ)=(180°, 180°). Native conformations, as appropriate, were defined for each system as below. Explicit solvation was achieved with truncated octahedra of TIP3P water¹⁶ with a minimum 8.0 Å buffer between solute atoms and box boundary. All structures were built via the LEaP module of Ambertools. Except where otherwise indicated, equilibration was performed with a weak-coupling (Berendsen) thermostat³³ and barostat targeted to 1 bar with isotropic position scaling as follows. With 100 kcal mol⁻¹ Å⁻² positional restraints on protein heavy atoms, structures were minimized for up to 10000 cycles and then heated at constant volume from 100 K to 300 K over 100 ps, followed by another 100 ps at 300 K. The pressure was equilibrated for 100 ps and then 250 ps with time constants of 100 fs and then 500 fs on coupling of pressure and temperature to 1 bar and 300 K, and 100 kcal mol⁻¹ Å⁻² and then 10 kcal mol⁻¹ Å⁻² Cartesian positional restraints on protein heavy atoms. The system was again minimized, with 10 kcal mol⁻¹ Å⁻² force constant Cartesian restraints on only the protein main chain N, C_α, and C for up to 10000 cycles. Three 100 ps simulations with temperature and pressure time constants of 500 fs were performed, with backbone restraints of 10 kcal mol⁻¹ Å⁻², 1 kcal mol⁻¹ Å⁻², and then 0.1 kcal mol⁻¹ Å⁻². Finally, the system was simulated unrestrained with pressure and temperature time constants of 1 ps for 500 ps with a 2 fs time step, removing center-of-mass translation and rotation every picosecond.

SHAKE³⁴ was performed on all bonds including hydrogen with the AMBER default tolerance of 10⁻⁵ Å for NVT and 10⁻⁶ Å for NVE. Non-bonded interactions were calculated directly up to 8 Å. Beyond 8 Å, electrostatic interactions were treated with cubic spline switching and the particle-mesh Ewald approximation³⁵ in explicit solvent, with direct sum tolerances of 10⁻⁵ for NVT or 10⁻⁶ for NVE. A continuum model correction for energy and pressure was applied to long-range van der Waals interactions. The production timesteps were 2 fs for NVT and 1 fs for NVE.

System-specific details

Ala5

Ala5 was simulated with protonated N- and C-termini under NVT conditions. 891 water molecules were used to solvate the system. Equilibration was performed as previously^11a. The structures were saved every 20ps. mod1ψ, mod2ψ, mod3ψ, mod4ψ, mod1φ, mod1φ1ψ, mod1φ2ψ, mod1φ3ψ, mod1φ4ψ, mod2φ, mod2φ1ψ, mod2φ2ψ, mod2φ3ψ, mod2φ4ψ, mod3φ, mod3φ1ψ, mod3φ3ψ, mod3φ4ψ, mod4φ, mod4φ1ψ, mod4φ3ψ, and mod5φ3ψ were run for 160 ns. ff99SB, mod3φ2ψ, mod4φ2ψ, mod4φ4ψ, mod5φ, mod5φ1ψ, and mod5φ2ψ were run for 320 ns. mod5φ4ψ was run for 480 ns.

Helices

Simulations were performed for two helical peptide systems: a hydrogen bond surrogate peptide (HBSP) and K19. The HBSP sequence denoted 3a by Wang et al.³⁶ (Ac-GQVARQLAEIY-NH₂) was chosen, as it had the greatest measured helical content³⁶. HBSP has a covalently pre-organized α turn, with the O of the first CO and the H of the NH of residue 5 substituted by carbons, with a covalent single bond between the substituted carbons. Modeling of this covalent modification was approximated by a harmonic distance restraint between the CO of the acetyl cap and the NH of A5 with force constant 100 kcal mol⁻¹ Å⁻². This restraint was chosen as it well reproduced the distribution of hydrogen bond distances present in a crystal structure of aquaporin (PDB ID: 3ZOJ³⁷) (see Supporting Information). For K19, we chose the sequence Ac-GGG(KAAAA)₃K-NH₂, consistent with previous work³⁸.

HBSP and K19 were solvated with 2643 and 3427 TIP3P water molecules, respectively, and simulated for 1.6 μs in the NVT ensemble. Each system had two independent runs. Initial structures were either all helical (as defined in Initial Structures) or semi-extended conformations. The HBSP semi-extended conformation was built with the first five residues helical to satisfy the covalent modification in the experiment, with the remaining residues extended. The K19 semi-extended conformation was a random coil conformation extracted from simulation using ff99SB in which helical content was absent.

Cln025

As a model system to carry out initial tests of secondary structure balance, we turned to CLN025, an engineered fast-folding hairpin that is a thermally optimized variant of Chignolin³⁹. CLN025 contains N- and C-terminal glycine-to-tyrosine substitutions from Chignolin. Thus the CLN025 sequence was YYDPETGTWY. The native conformation was chosen as the fifth conformation in the NMR ensemble^39b, as that conformation was closest to the average of the NMR ensemble.

Proteins

We simulated four folded proteins for comparison of dynamic properties to NMR. First was the third Igg-binding domain of protein G (GB3). The native structure was defined as a liquid crystal NMR structure (PDB ID: 1P7E⁴⁰). Second was the bovine pancreatic trypsin inhibitor (BPTI). The native structure was defined as a joint neutron/X-ray diffraction structure (PDB ID: 5PTI⁴¹). Third was ubiquitin (Ubq), with the native structure defined as a crystal structure (PDB ID: 1UBQ⁴²). Fourth was hen egg white lysozyme (HEWL), with the native structure defined as a crystal structure (PDB ID: 6LYT⁴³). Owing to their larger size, the proteins were equilibrated as above, but with the unrestrained step extended to a full nanosecond, rather than 500 ps.

Analysis

Calculation of NMR observables

Scalar couplings were calculated from simulations using Karplus relations¹². Backbone scalar couplings were calculated as by Best et al.^11b: using the Orig parameters^{25, 44} also used by Graf et al.¹⁰ and the DFT1 and DFT2 parameters from Case et al.⁴⁵. Side chain scalar couplings were calculated using Ile, Thr, and Val C/N-Cγ Karplus parameters from Chou et al.⁴⁶, and Perez et al. Karplus parameters⁴⁷ for all other χ1 scalar couplings. Backbone NH Lipari-Szabo S² order parameters were calculated using the iRED method⁴⁸ via cpptraj⁴⁹.

NOE reproduction in CLN025 was evaluated by computing r⁻⁶ for all interproton vectors and comparing ${\langle r^{-6}\rangle }^{-\frac{1}{6}}$ of each vector with the NOE-based restraints published by Honda et al.^39b, downloaded from the BMRB⁵⁰. For ambiguous restraints, contributions from each proton pair to the NOE were summed⁵¹. For each force field we generated two ensembles, one combining structures from the 4 initially folded simulations and the other combining the 4 initially extended simulations. These were used to calculate NOE deviations, with the difference between ensembles from different initial structures used to quantify precision.

Calculation of helical content

When comparing to CD (as for HBSP), helical content was defined as the fraction of residues in α-helix (H) or 3–10 helix (G) as defined by DSSP⁵² as implemented in cpptraj⁴⁹, with simulation averages calculated for the whole trajectory. DSSP is used for comparison to CD, since both are sensitive to formation of complete helical turns, rather than local backbone dihedral angles. When comparing to CSDs (as for K19), helical content was defined based on the Ramachandran surface, as done previously³⁸, with the α basin encompassing φ ∈ [−90°, −30°] and ψ ∈ [−77°, −17°]. HBSP helical content included all amino acids, whereas K19 helical content was averaged over residues 8,10,11,12,16, and 17 to correspond to experimental helical measurements.³⁸

Hairpin clustering, etc

First, representative structures were extracted from each simulation to make the cluster analysis tractable, selecting frames spaced every 5 ns. For each 5 μs trajectory, this selected 1000 frames, yielding 16000 total frames for the two force fields, two initial structures, and four independent simulations for each force field and initial structure. The combined trajectories were clustered together to allow direct comparison of clusters between them. Clusters were formed using the hierarchical/agglomerative algorithm implemented in cpptraj⁴⁹, with a 3 Å cutoff. The mask included all non-symmetric atoms to avoid the need to account for differences between clusters arising from symmetry. Thus atom names N, Cα, C, H, O, Cβ, Cγ, Cγ2, Cζ, Oγ1, Hγ1, Oη, Hη, all tryptophan non-hydrogens, and proline Cδ were included in the cluster analysis. Finally, the counts of each cluster were divided into four quarters representing each force field and initial structure. Hence, each cluster count accounts for four independent simulations with each force field/initial structure combination. The average values for each force field were computed, and the difference across initial structures was used to calculate uncertainties for each force field.

Further Methods details are provided in the Supporting Information.

Results

Reproduction of Ala5 NMR scalar coupling data is improved

We tested ff99SB and 29 backbone parameter modifications (Figure 2) by simulating Ala₅ in explicit water, with each combination of φ and ψ modifications. We calculated scalar couplings from each ensemble using the Orig, DFT1, and DFT2 parameters used by Best et al.^11b and us^11a previously^{25, 45}. We quantified the deviations between simulations and NMR using Best et al.’s χ² metric^11b:

$${\chi }^2=\frac{1}{N}{\displaystyle {\sum }_i^N\frac{{\left({\langle J_i\rangle }_{\text{sim}}-J_{i,\text{NMR}}\right)}^2}{{\sigma }_i^2}}$$ (7)

where σ_i is the estimated systematic error in experimental constant i. The χ² for each force field, according to each set of Karplus parameters, are provided in Tables 1–3. Consistent with our previous report^11a, our starting point of ff99SB had χ² of 1.89±0.09, 1.45±0.04, and 1.70±0.09 according to Orig, DFT1, and DFT2 parameters, respectively (error bars are from independent simulations using different initial structures). Two modified force fields achieved χ² less than 1.0, both with the Orig parameters—mod1φ had a χ² of 0.89±0.04 and mod1φ2ψ had χ² = 0.93±0.02. Significantly, none of the force fields tested by Best et al. had achieved χ² values under 1.0.^11b The mod1φ and mod1φ2ψ modifications also improved DFT2-based χ² to 1.22±0.03 (comparable to 1.2 reported for C36 using DFT2-based parameters⁹) and 1.41±0.06, but actually worsened agreement according to DFT1 parameters. In fact, none of the modifications improved agreement via the DFT1 parameters. Potential sensitivity of Karplus parameter derivation to peptide length may be a relevant discrepancy between Ala₅ and the DFT1 parameters trained against Ac–Ala–Nme²⁶. The force field best reproducing Ala₅ scalar couplings with the DFT2 parameters is mod3φ, with χ² of 1.11±0.01, once again improved compared to all of the force fields tested by Best et al.^11b and slightly improved relative to C36.⁹

Figure 2.

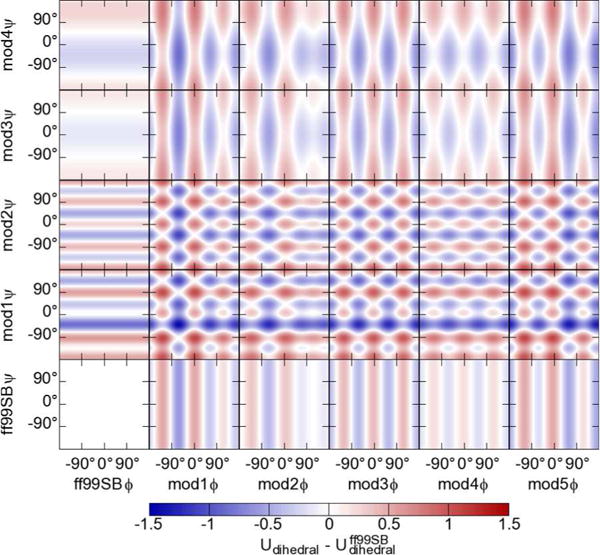
Ramachandran heat maps showing energy differences between ff99SB (lower left, all values 0) and each of the five φ (across) and the four ψ (up) modifications, and all combinations. Note that while these surfaces are graphed with φ and ψ axes, many modifications adjust the φ′ and ψ′ corrections, some with phase shifts, and thus the graphs may not be symmetric about the x and y axes. See main text for definition of “prime” dihedrals.

Table 1.

Scalar coupling χ² using the “Orig” Karplus parameters for Ala_5, in each backbone parameter combination, with error bars from independent simulations

	ff99SBφ	mod1φ	mod2φ	mod3φ	mod4φ	mod5φ
ff99SBψ	1.89±0.09	0.89±0.04	1.09±0.14	1.17±0.01	1.38±0.04	1.78±0.02
mod1ψ	1.77±0.07	1.26±0.04	1.07±0.10	1.35±0.01	1.48±0.10	1.58±0.11
mod2ψ	2.11±0.30	0.93±0.02	1.19±0.07	2.26±0.59	1.99±0.33	1.65±0.22
mod3ψ	1.89±0.02	1.13±0.03	1.52±0.20	1.45±0.01	1.77±0.06	2.27±0.09
mod4ψ	2.23±0.21	1.49±0.02	1.56±0.08	1.51±0.12	2.11±0.06	2.51±0.35

Table 3.

Scalar coupling χ²using DFT2 parameters for Ala₅ in each backbone parameter combination

	ff99SBφ	mod1φ	mod2φ	mod3φ	mod4φ	mod5φ
ff99SBψ	1.70±0.09	1.22±0.03	1.20±0.08	1.11±0.01	1.20±0.02	1.51±0.02
mod1ψ	1.59±0.05	1.79±0.03	1.31±0.02	1.39±0.03	1.40±0.05	1.41±0.05
mod2ψ	1.89±0.30	1.41±0.06	1.31±0.05	2.14±0.64	1.79±0.35	1.45±0.16
mod3ψ	1.71±0.03	1.46±0.03	1.52±0.19	1.36±0.04	1.56±0.05	2.03±0.05
mod4ψ	2.04±0.21	1.76±0.08	1.66±0.05	1.46±0.13	1.89±0.04	2.25±0.37

We selected parameter combinations for further testing in larger systems according to the best performing in each Karplus parameter set —mod1φ for Orig, ff99SB for DFT1, and mod3φ for DFT2. We also carried over mod1φ2ψ because it achieved χ² < 1.0 with Orig and was nearly within error bars of the performance with mod1φ; this also allowed us to include a ψ modification in further testing. While results for some other parameter sets are very close when considering uncertainties, we needed to limit the number of combinations carried over to testing of converged ensembles for larger systems in explicit water.

Side chain rotamer energies show improved match to QM data and better transferability between backbone conformations

Whereas the initial tests of backbone parameter improvement focused on the highly flexible alanine, testing with systems exhibiting more well-defined structural propensity requires use of sequences that include side chains with rotatable bonds. Therefore, we next derived new side chain parameters to provide a more accurate model for testing the impact of the backbone parameter changes.

An important question is how to define E_QM,i and E_MM,i used for calculating REE in Eqn. 1. As discussed above, restraints could be applied to dihedrals other than the specific 4-atom set defining the φ, ψ, and χ rotatable bonds. We tested several choices, including restraining only the 4-atom sets defining φ, ψ, and χ, as well as restraining all possible 4-atom dihedrals, or restraining all dihedrals in the backbone but only the defining dihedrals in the side chains (see Table S1 for dihedral classifications). We also tested the impact of MM re-optimization of QM geometries. As discussed above, these choices in the generation and comparison of structures can introduce artifacts in the energy profiles that hamper parameter optimization and weaken transferability. We evaluated the impact of these choices by calculating the intrinsic BBD as well as the AAE for various restraint and structure optimization options, using ff99SB as a baseline MM model. Restraining all possible backbone dihedrals and re-optimizing the QM structure with MM before calculating energy yielded both the lowest AAE (2.55±0.09 kcal mol⁻¹ for Asp and 1.98±0.01 kcal mol⁻¹ for Asn, error bars reflect difference between α and β backbone context) and lowest BBD (1.35±0.01 kcal mol⁻¹ for Asp and 1.42±0.03 kcal mol⁻¹ for Asn). Thus we restrained all possible backbone dihedrals and re-optimized QM structures with MM when building our training set. Further analysis of different options can be found in the Supporting Information.

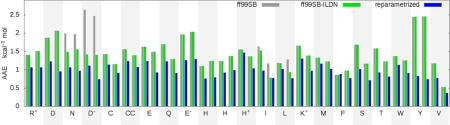
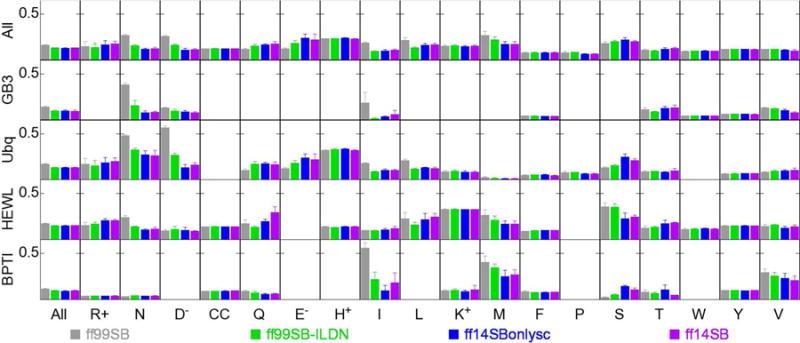
As discussed in Methods, each solving group was optimized separately (values for each solving group are provided in Table S3), but here we average the individual objective function O values, weighted by the number of profiles, to facilitate their comparison between different parameter sets. The resulting O values quantify the magnitude of error in energy differences for conformation pairs, averaged over all amino acids and backbone conformations. In ff99SB, O was 1.52 kcal mol⁻¹, while O for the final optimization parameter set was 0.98 kcal mol⁻¹. This 35% improvement is decomposed by residue and by backbone conformation in Figure 3, and the distribution of all pair energy errors (REEs) is shown in Table S4. All of the amino acids with errors larger than 2 kcal/mol in ff99SB (tyrosine and protonated or deprotonated aspartic acid) were significantly improved with the new parameters. In addition to improvement for the ILDN residues previously addressed by Lindorff-Larsen et al.⁸, we observed better agreement with the QM training data for every residue compared to ff99SB. The only profile that didn’t improve was α-backbone Phe, in which the initial ff99SB error was close to the average final AAE, limiting the potential for improvement. It is remarkable to see that the optimization procedure was able to find a solution that simultaneously improved performance for all amino acids, and with little resulting backbone dependence.

Figure 3.

The AAE of each force field for each amino acid (single letter codes), with data for both α and β backbone conformation. For ionizable residues, the ionic form is indicated by a charge superscript. CC indicates the disulfide bridge. Data are shown for ff99SB, ff99SB-ILDN, and ff99SB with the reparametrized side chain corrections obtained using the procedure described in the text.

Although we noted improvement in the reproduction of QM results for Arg and Lys side chains (Figure 3), further testing of the type discussed later in this article showed that scalar coupling agreement was slightly worsened by application of the new Arg and Lys parameters. Given the risk of overfitting for amino acids with four side chain dihedrals, especially given the ability of these side chains to form hydrogen bonds with the backbone that may affect the fitting, we decided that arginine and lysine may need a stronger effort, with more conformations, perhaps with implicit solvent at the QM stage. We therefore decided not to include the refit parameters for Arg and Lys in the final ff14SB parameter set or in the further testing discussed below.

We refer to the combination of ff99SB with new side chain dihedral parameters as ff14SBonlysc; adding the updated backbone parameters (discussed below) will result in the ff14SB model. Although it is promising that the ff14SBonlysc parameters show improved reproduction of the QM data, several caveats apply. First, the performance in Figure 4 measures the ability of the parameters to reproduce energies for structures that were used in the training shown above, but not for the other force fields, thus better performance on the training data is expected. Second, closely reproducing gas-phase QM data does not guarantee reliable simulation properties⁵³. As discussed above, it is possible that training against gas-phase QM data might counteract some of the influence of the “pre-polarized” partial charges in our model, potentially worsening performance for simulations in aqueous solution. Thus we followed the training against QM data with more rigorous testing in solution simulations, with comparison to experiments also in solution.

Figure 4.

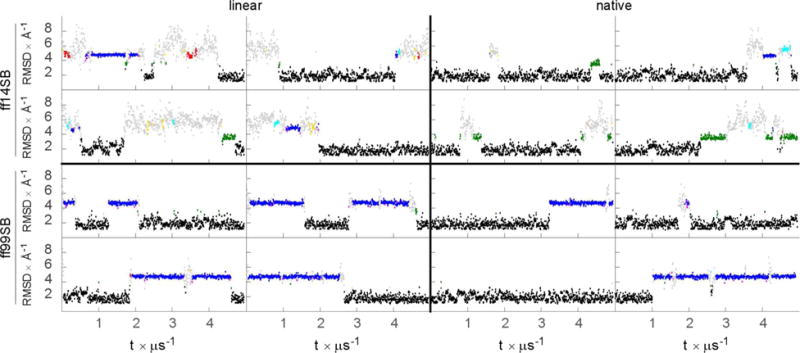
RMSD to the NMR structure vs time for the four linear and four native runs of CLN025 with ff14SB and ff99SB, colored by cluster being sampled: black=0, blue=1, green=2, cyan=3, red=4, fuchsia=5, gold=6, and all other clusters light gray.

Testing Strategy

The fitting just presented rests on several key assumptions that raise important questions. One question is whether the backbone corrections that reproduce Ala₅ scalar couplings through empirical Karplus equations will improve secondary structure balance in larger systems with more complex (and well-defined) structure than Ala₅. Since the computational cost is greater for these longer peptides, and transition rates are slower between more stable minima, we utilized small test systems when possible. To test the impact of the backbone parameter changes on secondary structure balance, we first simulated several peptides that adopt modest amounts of helical structure, comparing results from simulation and experiment. Since we did not want to increase helical stability at the cost of destabilizing β structures, we also simulated a short β-hairpin system to evaluate the ability of the force field to provide balance in sequence-dependent secondary structure content. These peptides have more complex side chains than alanine, thus some of the tests also incorporated the updated side chain parameters described above.

A second question is whether the diversity and planned backbone-independence of our side chain training set will improve side chain rotamer preferences for proteins in solution, despite training against in vacuo dipeptide energies at a modest level of QM theory. To investigate the accuracy of side chain rotamer sampling, we compared against χ1 scalar couplings for a set of folded proteins including GB3, ubiquitin, lysozyme, and BPTI (collated by Lindorff-Larsen et al.^{8, 25, 46, 54}). Importantly, we considered the performance of the new model relative to ff99SB and ff99SB-ILDN⁸ (ff99SB with new (I)le, (L)eu, Asp (D), and As(n) parameters) in different secondary structure contexts, to evaluate whether inclusion of multiple dipeptide backbone conformations in side chain training improved transferability between different backbone conformations in proteins. We also tested the benefit of re-optimizing parameters for side chains other than ILDN.

These side chain parameter evaluations are subject to all the caveats of scalar couplings outlined in Fitting Strategy. In fact, many reported experimental scalar couplings lie outside the range of the relevant Karplus curves, suggesting that reproducing the experimental observations using these curves would be impossible regardless of the ensemble of conformations sampled in simulation. In these cases, we adjusted the target value by adopting the value on the Karplus curve lying closest to the experimental value; otherwise, the experimental value was used as the target:

$${ }^3{J}_{i,\text{NMR}}^{\ast }=\{\begin{array}{c}\min \left(J_{i,\text{Karplus}}\right),{}^3{J}_{i,\text{NMR}}<\min \left(J_{i,\text{Karplus}}\right)\\ \max \left(J_{i,\text{Karplus}}\right),{}^3{J}_{i,\text{NMR}}<\max \left(J_{i,\text{Karplus}}\right)\\ { }^3{J}_{i,\text{NMR}},\text{otherwise}\end{array}$$ (8)

Additionally, because H-H scalar couplings reporting on some residues have a much larger range than C-C scalar couplings reporting on others, deviations were normalized by the magnitude of the Karplus curve range. The errors are summarized in terms of the average normalized error ANE:

$$\text{ANE}=\frac{1}{N}{\displaystyle {\sum }_i^N\frac{\left|{\langle J_i\rangle }_{\text{sim}}{-}^3{J}_{i,\text{NMR}}^{\ast }\right|}{\text{max}(J_{i,\text{Karplus}})-\text{min}(J_{i,\text{Karplus}})}}$$ (9)

The resulting metric is more intuitive than average error, as 0 indicates best possible agreement, while 1 indicates maximum deviation.

In the peptides and proteins tested here, backbone and side chain dihedrals are coupled to each other within and between residues, making it difficult to determine exactly why a particular scalar coupling may disagree with experiment (assuming the error is not because of the experimental measurement or the Karplus curve). Likewise, this hinders ascribing credit for improvement to any specific backbone or side chain update. To help aid in the decomposition, we therefore tested helical content in a model peptide with just backbone parameter updates, and then introduced the side chain modifications. For protein side chains, we tested χ1 scalar couplings with just side chain modifications and then introduced backbone updates, to help isolate the effects of intended and secondary changes. On the other hand, this dihedral coupling can mean that χ1 scalar couplings implicitly report on backbone, χ2 or χ3 torsions; thus reproducing χ1 data may suggest reasonable accuracy in other parameters as well.

Lastly, after testing whether ff14SB achieves its design goals of improving secondary structure balance and side chain dynamics, we tested the final combination of backbone and side chain improvements on folded proteins to ensure that the new force field maintained reasonably accurate protein order parameter reproduction as reported previously for ff99SB³. We calculated backbone NH order parameters using the same simulations used to analyze χ1 scalar couplings.

Testing Results

Helical stability is improved

For testing helical propensity, we employed the hydrogen bond surrogate peptide (HBSP) of Arora and colleagues^{36, 55}. With a covalently pre-organized nucleus that avoids the limiting entropic cost of helix initiation, experiments indicate the presence of significant helical content despite the short length of only 10 amino acids, providing an ideal initial model system. A covalent link replaces what would be the first helical hydrogen bond between residues 1 and 5, but we wanted to avoid introducing additional new parameters other than those described above. We created a model for the HBSP by including only natural amino acids, but using a H-bond distance restraint as an analog for the covalent bond used in experiments (see Methods and Supporting Information); the sequence was otherwise the same in order to allow comparison of helix propagation propensity. We generated ensembles for the system using the backbone parameter modifications that performed well for the Ala₅ scalar couplings, as discussed above, and compared helical content calculated with DSSP to that from experiment. Wang et al. reported ~46% helical content in PBS^55c, but due to the potential for aggregation in that experiment, we followed the suggestion⁵⁶ of the authors and used the value of 70.13% helical content in 10% TFE, adjusted downward by ~ 5–10% to obtain an estimate in water of ~ 65%.

Simulations with ff99SB exhibited 0.17±0.01 fraction helix (Table 4; uncertainties represent data from independent runs), compared with the 0.65 target value discussed above. The mod1φ correction, which had the lowest Ala₅ χ² among all parameter sets, tripled the helical content to 0.51±0.01. Adding the mod2ψ correction, mod1φ2ψ, yielded 0.72±0.01 helical content. This number is somewhat higher than experiment, suggesting that this ψ modification, introduced to improve helical stability, may do so too strongly. This is notable because the results show that improvements in helical content are already achieved through modification of only the φ energy profile, which was designed to improve Ala₅ scalar couplings. The other parameter set that was carried over from the Ala₅ test, mod3φ, showed a more modest improvement relative to ff99SB, with 0.26 ± 0.01 fraction helix.

Table 4.

Helical content of HBSP and K19, from experiments and force fields, namely ff99SB and our modifications chosen based on Ala₅ results. Simulated helical content was determined based on DSSP and Ramachandran analyses for HBSP and K19, respectively. The force field uncertainties were obtained from two independent simulations (see Methods).

	HBSP (only updated backbone parameters)	HBSP (adding updated sidechain parameters)	K19
Experimental	0.65	0.65	0.31
ff99SB	0.17±0.01	0.26±0.01	0.08±0.01
mod1ϕ	0.51±0.01	0.60±0.01	0.26±0.05
mod1ϕ2ψ	0.72±0.01	0.79±0.01	0.87±0.03
mod3ϕ	0.26±0.01	0.46±0.01	0.10±0.01

Since HBSP contains non-Ala amino acids, we next combined these backbone adjustments with the new side chain parameters discussed above (ff14SBonlysc). When combined with mod1φ, we obtained a further increase in HBSP helical content, with 0.60±0.1 helix (compared to the experimental estimate of 0.65). Adding the new side chain parameters to mod1φ2ψ and mod3φ resulted in 0.79±0.01 and 0.46±0.01helix, respectively; in both cases the fractions were again higher than obtained with the backbone adjustments alone. Indeed, simply updating the side chain parameters for the ff99SB backbone parameters (ff14SBonlysc) nearly doubled the helical content to 0.26±0.02. Previous studies have modified the ff99SB backbone parameters to quantitatively match experimental observations^{11c, 27}. Our data suggests that doing so, without considering side chain errors, could lead to a non-transferable cancellation of error between side chain and backbone effects; updating side chain parameters in those models may actually worsen agreement with experiment.

Although reproduction of Ala₅ scalar couplings and HBSP helicity is promising, we also performed tests on a longer peptide without covalent modification, the K19 Baldwin-type peptide that we had simulated previously in implicit solvent³⁸. For this peptide sequence, none of the side chain parameters differ from those in ff99SB. K19 simulations with ff99SB produced very low helical content (average of 0.08±0.01 for residues with measured CSDs, see Methods), in disagreement with the experimental estimate of 0.31 (Table 4). With mod1φ, K19 helical content was significantly improved at 0.26±0.05. Moreover, examination of per-residue helicity for amino acids with measured CSDs (Figure S4) shows that the largest difference between the error bar range from mod1φ MD and the experimental value is 3% (absolute error). The other backbone modifications did not perform as well as mod1φ, with trends similar to those obtained for HBSP; use of mod1φ2ψ resulted in too much helix (0.87±0.03), while mod3φ resulted in small improvement over ff99SB (0.10±0.01).

Overall, mod1φ has three advantages: it was physically motivated based on analysis of the ff99SB training data, it provides the best reproduction of Ala₅ scalar coupling data among the combinations that we tested, and when combined with the QM-based side chain parameters the helical content also reasonably matches experiment for two different systems. mod1φ was thus selected as the backbone parameter update for ff14SB.

Testing hairpin stability and structure

We next tested whether the improvement in helical content was obtained at the cost of less accurate performance on β systems. As a model system to carry out initial tests of secondary structure balance, we turned to CLN025³⁹, an engineered fast-folding hairpin that is a thermally optimized variant of Chignolin³⁹. CLN025 contains N- and C-terminal glycine-to-tyrosine substitutions from Chignolin, which already possesses one tyrosine and one tryptophan. The presence of four aromatic side chains in a short peptide suggests the potential for strong sensitivity of observed stability to accurate treatment of side chain conformational energy profiles, as well as of hydrophobicity. The system also presents a challenge due to the relatively slow folding of β-sheets compared to the helical systems (although estimates of 100 ns for CLN025 were obtained from T-jump IR experiments), and obtaining precise measures of population may be difficult. Still, use of CLN025 as a model presents a reasonable route to obtaining a qualitative view of whether ff14SB’s increased helical propensity also compromises β stability.

For each of ff99SB and ff14SB, we performed four MD runs starting from the NMR-based structure closest to the ensemble average, and four additional runs starting from fully linear structures to quantify convergence. We compared simulation snapshots against the initial NMR structure using all non-symmetric atoms (Figure 4). We also performed cluster analysis on the combined trajectories from both force fields so that the influence of force field on cluster populations could be directly compared. Simulations with ff99SB predominantly sampled structures within cluster 0 at around 3 Å RMSD (59±10%), or within cluster 1 at around 4.8 Å RMSD (34±9%; all error bars were calculated from the difference between initially extended/hairpin ensembles). Compared to ff99SB, the ff14SB simulations sampled cluster 0 with similar frequency (57±14%), but sampled cluster 1 much less than ff99SB (5±3%), though the comparisons are somewhat qualitative due to the uncertainties. Instead, the ff14SB simulations are more diverse when unfolded, sampling structures ranging from 4 Å to just over 9 Å RMSD. ff99SB simulations sampled 194 clusters with non-zero frequency, whereas ff14SB simulations sampled 843.

Inspection of the second major cluster of ff99SB (cluster 1, blue in Figure 4) reveals a hairpin with shift of the C-terminal strand one residue out of phase relative to the N-terminal strand (representative structures for clusters 0 and 1 are shown together with the NMR-derived structure in Figure S5). The populations suggest that ff14SB destabilizes this alternate conformation, although the populations are not well converged; however the difference is also qualitatively apparent in observing that this cluster is significantly sampled in 6 of 8 ff99SB simulations, but only 2–3 of 8 ff14SB simulations, with typically shorter persistence time than with ff99SB (Figure 4). Whether the ff14SB parameter changes favor the native-like cluster over the alternate cluster can be probed by decomposing the dihedral energies of each cluster according to each force field. In particular, we evaluated how the difference in energies of the two main clusters depends on the force field:

$$\mathrm{\Delta }\mathrm{\Delta }E=\left({\langle U_{\text{ff14SB}}\rangle }_{\text{cluster}0}-{\langle U_{\text{ff14SB}}\rangle }_{\text{cluster}1}\right)-\left({\langle U_{\text{ff99SB}}\rangle }_{\text{cluster}0}-{\langle U_{\text{ff99SB}}\rangle }_{\text{cluster}1}\right)$$ (10)

Analysis using Eqn. 10 indicates that the dihedral changes in ff14SB favor the native cluster over the alternate by 2.9 kcal mol⁻¹ relative to ff99SB. Further decomposition of this difference suggests that parameter changes applied to Asp3 χ2 favor this native structure by 1.2 kcal mol⁻¹, and then φ modifications favor the native structure by 0.5 kcal mol⁻¹ in the backbone of Glu5. This is especially promising because the same modifications also improved agreement with experiment for the helical systems.

Although it may appear desirable for ff14SB to favor the native conformation more than in ff99SB, presence of a similar strand-shifted structured in the simulated ensemble for the Chignolin hairpin was reported to improve agreement of simulations with experimental NOEs for that system⁵⁷. We therefore calculated distances corresponding to NOEs from our CLN025 simulations, using the ‘naïve’ approach⁵⁸ that was used for Chignolin⁵⁷. The sum of all NOE deviations was 2.8±0.2 Å for ff99SB and 2.1±0.4 Å for ff14SB. Furthermore, NOE agreement is better for ff99SB native run 3, which sampled only the native cluster, than for ff99SB native runs 1 and 4 or extended runs 2 through four, which sampled comparable amounts of the two clusters (Table S7). This suggests that in our simulations of CLN025, reduction in population of the non-native hairpin improves agreement with experiment. Although no definitive conclusions can be drawn about improvements of ff14SB based on these simulations alone, the simulations together with energy analysis suggest that ff14SB is at least as reasonable as ff99SB at hairpin modeling, and thus the desirable increase in α-helical content with ff14SB did not worsen β-hairpin simulation accuracy.

Agreement with side chain NMR scalar couplings is improved with ff14SB

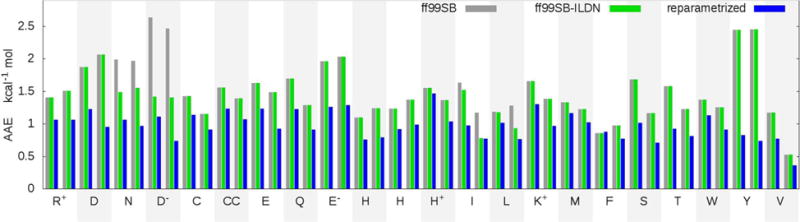
In addition to indirectly testing side chains sampling accuracy in the context of overall conformational propensities, it is appropriate to evaluate side chain parameter changes more directly by comparing to experimental measures of side chain dynamics. We therefore simulated GB3, ubiquitin, lysozyme, and bovine pancreatic trypsin inhibitor (BPTI) to compare against experimental scalar couplings aggregated by Lindorff-Larsen et al.^{8, 25, 46, 54}.

We tested ff99SB and ff99SB-ILDN as references, ff14SB which includes the backbone and side chain parameter updates described above, and also ff14SBonlysc, which includes the side chain updates described above while retaining the ff99SB φ and ψ parameters. This allows us to partially deconvolute the influence of improvements to the side chain and backbone. Simulations of each protein were carried out using each force field, and the ANE (Eqn. 9) was calculated for each amino acid where experimental data is available (Figure 5). The average error was 0.160±0.004 with ff99SB, 0.129±0.003 with ff99SB-ILDN, 0.127±0.003 with ff14SBonlysc, and 0.129±0.003 with ff14SB. The average figures were within statistical uncertainty for ff99SB-ILDN, ff14SBonlysc, and ff14SB, which show measurable improvement over ff99SB. Not surprisingly for these stably folded proteins, there is little difference between ff14SB and ff14SBonlysc, suggesting that the improvement over ff99SB observed in this test is largely due to side chain parameter updates.

Figure 5.

Average normalized errors (ANE) in side chain scalar couplings for all amino acids in GB3, ubiquitin (Ubq), lysozyme (HEWL), and bovine pancreatic trypsin inhibitor (BPTI), according to ff99SB, ff99SB-ILDN, ff14SBonlysc, and ff14SB. Amino acids are shown with single letter code, with charge state noted for ionizable side chains. Error bars are calculated from four independent simulations.

All of the variants significantly improved upon ff99SB in average, however the specific improvements of each force field differed. For example, the errors obtained using ff14SB (ff99SB-ILDN values given in parentheses after ff14SB values) in isoleucine, leucine, aspartate, and asparagine—the four residues modified by ff99SB-ILDN—were 0.11±0.01 (0.091±0.005), 0.16±0.02 (0.13±0.01), 0.111±0.009 (0.16±0.02), and 0.12±0.02 (0.154±0.009), respectively—slightly improved in 2 cases, and slightly worsened in 2 others.

As discussed above, ff99SB-ILDN was fit using β backbone conformations, while our fitting procedure was designed to improve side chain energetics for multiple backbone conformations. We investigated whether explicit inclusion of dipeptide α backbone conformations for QM calculations in the gas phase was successfully translated to improvement in scalar couplings of helical residues in larger proteins. We performed further fitting, simulations and analysis in order to gain insight into the impact of these choices in the quality of reproduction of experimental data, with an aim toward guiding future optimization efforts. We found that the choice of restraints during the QM and MM optimizations played an important role, which became more important when only a single backbone conformation was used during fitting of side chain parameters (see Supporting Information for more details). Overall, the results suggest that more careful consideration of these issues should be a factor in future force field efforts, as these measures can impact performance of simulations using the resulting parameters. These choices include how finely geometric changes outside the scan region are controlled, what level of variation in this geometry is desirable between QM and MM energy evaluations, and how these decisions are affected by intentional inclusion of diversity in neighboring regions.

We analyzed residues refit by both ff99SB-ILDN and ff14SB that matched the following criteria: in a helix, solvent-exposed and therefore likely to represent the intrinsic preferences of the amino acid, and experimentally characterized by χ1 scalar couplings. Only three residues fit these criteria, N35 of GB3, D32 of ubiquitin, and N97 of lysozyme. Of the three, all are better reproduced with ff14SB than ff99SB-ILDN, with ANEs for N35, D32 and N93 of 0.11±0.03/0.22±0.09 (ff14SB/ff99SB-ILDN), 0.15±0.04/0.47±0.02, and 0.16±0.02/0.31±0.04, respectively (although the N35 differences are within uncertainty ranges). We investigated these results further, and found that differences at the level of the QM and MM energy calculations are likely responsible for these differences, and that the ability to accurately predict quantum mechanics training energies correlates with reproduction of χ1 scalar couplings. See the Supporting Information for detailed analysis.

High quality of backbone dynamics in the native state is maintained

We also evaluated the ability of ff14SB to reproduce local dynamics in well-folded proteins as measured by backbone NH S² Lipari-Szabo order parameters. We calculated NH order parameters from the same simulations used for side chain scalar coupling evaluation. This calculation was performed using iRED, which does not require separability of local and global motions⁴⁸. For this analysis, we averaged iRED results calculated for windows of length 5 times the tumbling correlation time (τ_C), as has been suggested to best reproduce the model-free S² order parameters⁵⁹. This analysis was also repeated with window lengths found in previous publications, to facilitate comparison of results (see Supporting Information). The iRED-calculated order parameters, shown in Figure 6, are comparable among the different force fields, as indicated by low RMSD between simulation results. The greatest differences among simulations occurs for GB3, where the calculated ff99SB-ILDN and ff14SB order parameters differ by 0.05 RMSD. With ff14SB, order parameters are slightly improved with lysozyme (0.055±0.004 RMSD against NMR⁶⁰, versus 0.07±0.01 for ff99SB and 0.065±0.004 for ff99SB-ILDN), and slightly worsened with GB3 (0.08±0.01 RMSD against NMR⁶¹, versus 0.060±0.005 for ff99SB and 0.061±0.004 for ff99SB-ILDN), though the statistical significance of these differences is limited. Meanwhile, ubiquitin S² RMSDs were between 0.045 and 0.050 against NMR⁶² with all three force fields. We conclude that the high quality order parameter reproduction previously reported for ff99SB³ is maintained with ff14SB. There are, however, subtle differences worth noting.

Figure 6.

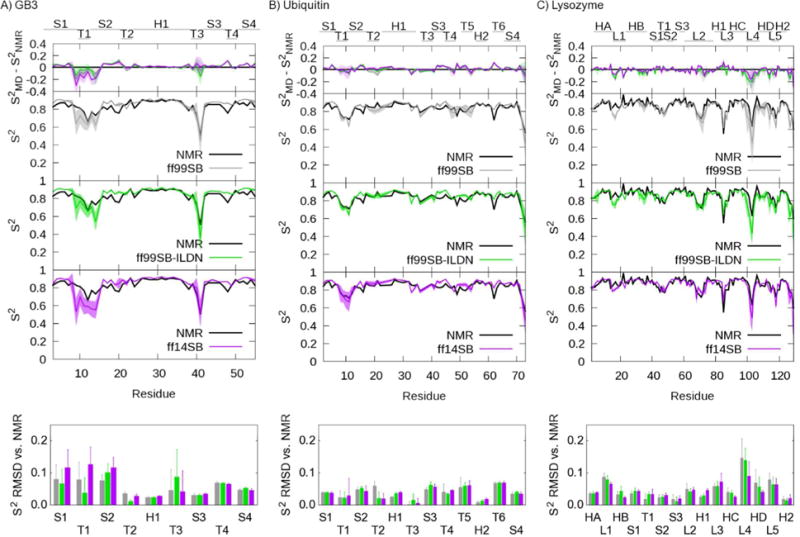
Order parameters from NMR compared to those back calculated by iRED for ff99SB, ff99SB-ILDN, and ff14SB simulations of GB3, ubiquitin, and lysozyme. Error bars represent the standard deviation of average values from four independent runs. The top panels show differences between simulation and experiment, while the lowest panels show average data for each secondary structure region, following Hornak et al.³.

Firstly, loop 4 in lysozyme is better reproduced with ff14SB on average (0.09±0.05 RMSD against NMR versus 0.15±0.06 and 0.14±0.04 for ff99SB and ff99SB-ILDN). As with the overall S² RMSDs, these differences are not highly statistically significant. But it is interesting that L4 connects two helices, and thus enhanced rigidity could stem from our goals of improving helical stability. On the other hand, the first hairpin in GB3 is reproduced with ff14SB less well on average (0.12±0.02 RMSD for residues 1–20 versus 0.08±0.01 for both ff99SB and ff99SB-ILDN). Although the RMSDs considered don’t vary largely when considering uncertainties, ff14SB may model the stability of some hairpins slightly less accurately. Evaluating whether ff14SB reproduces S² across different secondary structures more equitably in the general case would require a more comprehensive examination. Nonetheless, the differences between force fields are not very significant. Thus, although ff14SB may slightly improve modeling of helical regions, yet may slightly worsen modeling of hairpins, we conclude that ff14SB maintained ff99SB’s excellent order parameter reproduction overall.

Conclusion

The weaknesses of ff99SB addressed in this work are the less than ideal agreement with polyalanine scalar couplings, helical propensity, and side chain preferences. We tackled the former two weaknesses with the best of an array of empirical tweaks to the backbone potentials (here denoted mod1phi) and the latter by de novo fitting against a backbone-independent MP2 training set. The successor to ff99SB, ff14SB, augmented helical content of HBSP and K19 and improved side chain rotamer distributions as suggested by scalar couplings, while maintaining the reasonable reproduction of order parameters and hairpin structure characteristic of ff99SB. Interestingly, we were able to continue to improve the force field in solution by training against an in vacuo quantum mechanics benchmark, with performance that is similar between α and β contexts when compared against QM or against NMR scalar couplings. The ubiquity of ff14SB improvements and more thorough description of potential limitations will require further testing than possible here. But based on the benchmark reported, we recommend ff14SB for the simulation of proteins and peptides.

Table 2.

Scalar coupling χ² using DFT1 parameters for Ala₅ in each backbone parameter combination

	ff99SBφ	mod1φ	mod2φ	mod3φ	mod4φ	mod5φ
ff99SBψ	1.45±0.04	2.71±0.15	2.21±0.08	1.83±0.01	1.47±0.08	1.53±0.03
mod1ψ	1.63±0.01	3.60±0.02	2.61±0.13	2.33±0.08	1.94±0.14	1.76±0.16
mod2ψ	1.69±0.15	3.16±0.13	2.37±0.01	2.56±0.58	1.96±0.31	1.70±0.10
mod3ψ	1.65±0.03	2.92±0.15	2.31±0.15	1.99±0.12	1.71±0.02	1.96±0.09
mod4ψ	1.91±0.09	3.12±0.27	2.61±0.05	2.19±0.15	1.96±0.04	2.12±0.26

ABBREVIATIONS

ff99SB

force field 99 Stony Brook

ff14SB

force field 14 Stony Brook

NMR

nuclear magnetic resonance

CD

circular dichroism

CSD

chemical shift deviation(s)

iRED

isotropic reorientational eigenmode dynamics

GB3

third immunoglobin-binding domain of protein G

BPTI

bovine pancreatic trypsin inhibitor

Ubq

ubiquitin

HEWL

lysozyme

HBSP

hydrogen bond surrogate peptide

QM

quantum mechanics

MM

molecular mechanics

MD

molecular dynamics

REMD

replica exchange MD

MP2

Møller-Plesset Perturbation Theory of the Second Order

HF

Hartree-Fock

RHF

restricted Hartree-Fock

6-31G*

6-31G(d)

ESP

electrostatic potential

AAE

average absolute error

BBD

backbone dependence

ANE

average normalized error

CMAP

correction map

PDB

protein data bank

RMS

root mean square

REE

relative energy error

Orig

“original” Karplus parameters

DFT1

density functional theory-based Karplus parameters, derived from Ala₁

DFT2

density functional theory-based Karplus parameters, derived from Ala₂

NOE

nuclear overhauser effect

BMRB

Biological Magnetic Resonance Bank

ILDN

isoleucine, leucine, aspartate, and asparagine

ppII

polyproline helix, type II

K19

ac-G₃(KAAAA)₃K-NH2

ff14SBonlysc

ff99SB with the updated ff14SB side chain corrections

BB

backbone

RMSD

root mean squared deviations