Stability and Change in Executive Function Abilities From Late Adolescence to Early Adulthood: A Longitudinal Twin Study

Abstract

Executive functions (EFs) –– the higher-level cognitive abilities that enable us to control our own thoughts and actions –– continue to develop into early adulthood, yet no longitudinal study has examined their stability during the important life transition from late adolescence to young adulthood. In this twin study (total N=840 individuals from 424 families), we examined the stability of individual differences in three EF components across a six-year period, from approximately age 17 years (Wave 1) to 23 years (Wave 2). Specifically, we address the following questions: 1) How stable are individual differences in multiple EFs across this time period? And 2) What (genetic and/or environmental) influences affect stability and change in EFs? Results indicated that individual differences in EFs are quite stable across this time 6-year period (phenotypic latent variable correlations ranged from 0.86 to 1.0). However, there was evidence for change, particularly in the factor common to multiple EFs (Common EF). Multivariate twin models suggested that stability was due almost entirely to high genetic correlations across time; there was no new genetic variance at Wave 2. Change in Common EF was due to small but significant nonshared environmental influences at Wave 2 (15%). The results suggest that individual differences in EFs are quite heritable and stable by late adolescence, yet are still sensitive to environmental influences.

A broad literature on cognitive development and aging suggests changes in mean levels of performance across the life span coupled with considerable stability in individual differences, especially in adulthood (e.g., Larsen, Hartmann, & Nyborg, 2008; Tucker-Drob & Briley, 2014). However, most longitudinal research studies, particularly genetically informative studies, have focused on children/adolescents or older adults, reflecting the prevalent assumption that cognition is stable in early adulthood. For example, in a recent meta-analysis of genetic and environmental influences on stability and change in cognition (Tucker-Drob & Briley, 2014), no studies measured changes from late adolescence to early adulthood. Yet, there may be good reasons to study the transition from adolescence to young adulthood: This time period captures the entry into adulthood, which can include a number of important life transitions. This barrage of new environmental influences occurs at a time when the brain, particularly the frontal-parietal network (e.g., Fuster, 2002) that underlies executive functions (EFs), is still developing (e.g., Giedd, 2008; Lebel & Beaulieu, 2011; Sowell, Thompson, Holmes, Jernigan, & Toga, 1999). In this twin study, we examine the stability of individual differences in multiple EFs –– the higher-level cognitive abilities that enable us to control our own thoughts and actions –– across a 6-year period, from late adolescence (Wave 1; mean age 17.2 years) to early adulthood (Wave 2; mean age 22.8 years). Specifically, we address the following questions: 1) How stable are individual differences in multiple EFs across this time period? And 2) What (genetic and environmental) influences affect stability and change in EFs? Included in this latter question is whether there are new genetic and/or environmental influences in early adulthood.

Development of Executive Functions

The transition from adolescence to adulthood is a particularly interesting time for EF development, because it is a period during which performance matures. Some cross-sectional studies suggest that peak performance occurs sometime between 20 and 29, although other studies estimate that adult-level performance occurs in later adolescence (e.g., Luciana, Conklin, Hooper, & Yarger, 2005; see also Best & Miller, 2010). These developmental changes are often discussed in the context of neural changes, because performance improvements coincide with synaptic pruning and myelination throughout the brain (Fuster, 2002; Giedd et al., 1999; Lebel & Beaulieu, 2011; Sowell et al., 1999).

Some functional neuroimaging studies of EF tasks suggest that children and adolescents use the same circuitry as adults, just less efficiently (Luna, Garver, Urban, Lazar, & Sweeney, 2004; Luna et al., 2001; Scherf, Sweeney, & Luna, 2006). For example, Luna et al. (2001) reported that adolescents, compared to adults, showed more dorsolateral prefrontal cortex activation and less activation of other areas during an antisaccade task. They interpreted these results as evidence that the development of response inhibition "is influenced by the maturation of integrated function among the neocortex, striatum, thalamus, and cerebellum" (p. 791).

This protracted development in the neural circuitry/organization of EFs occurs in the context of a major life transition period from adolescence to adulthood (emerging adulthood), wherein individuals experience myriad new environments and social roles (Arnett, 2000; Schulenberg, Sameroff, & Cicchetti, 2004). This period is also characterized by high variability in the range of experiences (e.g., in terms of residence, education/work, responsibilities, and experimentation with substances and risky behavior). Thus, both biological and environmental changes associated with emerging adulthood (or their combination) could be candidates for changes in EFs.

However, mean changes in performance across developmental periods do not necessitate that individual differences are unstable. For example, if everyone improves to the same extent, rank ordering within the distribution would be perfectly stable, and cross-time correlations would approach unity. If some individuals improve while others remain the same or even decline, the pattern might be one of instability. Thus, longitudinal studies are needed to determine how stable individual differences are in the course of these developmental transitions identified by cross-sectional studies.

Stability of Individual Differences in Cognition Across the Lifespan

Investigations of stability in cognitive ability (including EFs and general cognitive ability) have typically focused on childhood and later adulthood. Stability tends to be lower in childhood (Bayley, 1949; Polderman et al., 2007) than in adulthood (Larsen et al., 2008; Lessov-Schlaggar, Swan, Reed, Wolf, & Carmelli, 2007). In their meta-analysis, Tucker-Drob and Briley (2014) reported increases in stability across the lifespan, starting around .30 in very early life and increasing to .70 by age 16 years.

Genetically informative studies examine the sources of stability and change in terms of additive genetic influences (A), common or shared environmental influences (C; those shared by family members; e.g., socioeconomic status), and nonshared environmental influences (E; those not shared by family members, e.g., peer influences, unique experiences). Tucker-Drob and Briley (2014) found that early in life, stability is primarily due to environmental influences shared by family members, but these shared environmental influences quickly decrease and genetic influences increase to account for the bulk of stability in general intelligence. Stability after childhood is primarily due to genetic influences (Deary et al., 2012; Lyons et al., 2009; Tucker-Drob & Briley, 2014), with nonshared environmental influences (those not shared by family members) contributing largely to change.

Taken together, this literature indicates that cognitive abilities become increasingly heritable through the lifespan, and these genetic influences seem to make them more stable. However, there is also a significant gap in the literature on adolescent to early adult stability, limiting power to detect discontinuities between childhood and old age (Tucker-Drob & Briley, 2014). Moreover, few studies have examined EFs, and those that have have done so at the level of individual tasks rather than aggregate measures of separable EFs. The current study is the first to investigate genetic and environmental contributions to stability and change in multiple EFs in emerging adulthood.

This prior literature suggests that we would be unlikely to find new genetic influences on cognitive measures in adulthood. Although it is possible that the protracted development of EFs might produce a parallel extension of new genetic influences, it is more likely that new nonshared environmental influences may come into play, contributing to instability. In most studies, such nonshared environmental influences would be confounded with measurement unreliability, but in the current study we use latent variables, which are relatively free from measurement error (Bollen, 1989). Given that the EFs measured in this study showed very little environmental variance in late adolescence (Friedman et al., 2008, 2011; see also Engelhardt, Briley, Mann, Harden, & Tucker-Drob, 2015, for similarly high heritability estimates in a younger sample), even a small amount of reliable new environmental variance would be notable.

The Current Study

We examine stability in three latent EF variables derived from a unity/diversity framework (Friedman et al., 2008; Miyake & Friedman, 2012). This model is based on nine tasks measuring three separable EF factors (Miyake et al., 2000): prepotent response inhibition (Inhibiting), working memory updating (Updating), and task shifting (Shifting). In our original "correlated factors" model, each task loads on one of the three correlated EF latent variables. More recently (Friedman et al., 2008), we have focused on a re-parameterization of the data that shows similar fit. In this "nested factors" (or bifactor) model, all tasks load on a common factor (Common EF), and the updating and shifting tasks also load on "nested" specific factors (Updating-Specific and Shifting-Specific, respectively) that capture correlations among the updating and shifting tasks once Common EF variance is removed. There is no Inhibiting-Specific factor because we have found in several independent datasets that once the Common EF factor is estimated, there are no longer significant positive correlations among the inhibiting tasks (i.e., the Common EF variable captures all the variance in inhibiting abilities).

At the genetic level, these EF variables, measured at Wave 1, were highly heritable at the latent variable level (96% for Common EF, 100% for Updating-Specific, and 79% for Shifting-Specific; Friedman et al., 2011). None of the EFs showed evidence for shared environmental influences, and the Shifting-Specific variable was the EF with significant nonshared environmental influences (21%).

For the current study, we tested 749 individual twins on the same EF tasks approximately six years after the initial assessment at Wave 1 (Friedman et al., 2008, 2011). In designing the retest, we were faced with two options: retain identical measures to maximize the similarity of the measures across time (making it possible to look at mean changes), or make changes to accommodate age-related improvements (i.e., to avoid ceiling effects and maximize individual differences). We opted for the latter approach for two main reasons.

First, we were primarily interested in stability of individual differences, rather than mean change across this time period. Within a longitudinal study, mean change is confounded with practice effects (e.g., Salthouse & Tucker-Drob, 2008). General improvements in EF in this age group have already been established in cross-sectional studies (De Luca et al., 2003), and we also observed mean differences in our own tasks between Wave 1 of the current sample (average age 17 years) and a separate population sample of twins tested at a mean age of 21 (unpublished data). Moreover, some of our tasks in the Wave 1 sample were already showing signs of ceiling effects and benefited from transformation (see Friedman et al., 2008). Ceiling effects would restrict our ability to detect changes in rank order. Hence, we endeavored in the new battery to keep the tasks largely the same, but adjust difficulty. Because of this similarity in requirements, and because we look at variance common to multiple tasks, our changes should not alter the basic abilities measured. Second, we wanted to have measures of EF at this age that could stand alone as an age-appropriate assessment within this large longitudinal sample. With this goal in mind, we also sought to also improve the reliability of the measures.

We addressed the first goal of the study (stability of EFs) by examining the latent variable correlations of the EF factors measured at each age at the phenotypic (i.e., unpaired) level. This analysis asks to what extent individuals retain their rank order in the distribution, rather than whether they improve across time. To address the second goal (sources of stability and change), we first used a multivariate ACE twin model to examine the extent to which Wave 2 EFs reflected genetic and environmental influences. We were particularly interested in whether there is any evidence for increased environmental effects at the level of latent variables, given the somewhat striking lack of these influences on the Common EF and Updating-Specific factors in late adolescence (Friedman et al., 2008). We then used cross-wave models to partition the Wave 2 ACE variance into that shared with Wave 1 and that new to Wave 2.¹

Method

Participants

Monozygotic (MZ) and dizygotic (DZ) same-sex twins were recruited through the Colorado Longitudinal Twin Sample (see Rhea, Gross, Haberstick, & Corley, 2013 for more information on this sample). Wave 1 (M = 17.25 years, SD = 0.64, range = 16.51 to 20.08 years) EF data were available for 786 individuals from 401 families (415 female, 371 male; from 214 MZ and 187 DZ pairs; see Friedman et al., 2011 for more information). Wave 2 (M = 22.84 years, SD = 1.29, range = 21.11 to 28.03 years) EF data were available for 749 individuals (400 female, 349 male; from 205 MZ, and 181 DZ pairs). An additional 2 participants' Wave 2 EF data were unusable because one had problems completing the tasks due to brain surgery and the other fell asleep during multiple tasks. Of the 749 individuals with data for Wave 2, 695 also had Wave 1 data; the average interval between the two testing waves was 5.57 years (SD = 1.01, range = 4.47 to 10.38 years). The total sample size with data for at least one wave was 840 individuals from 424 families (435 female, 405 male; from 229 MZ and 195 DZ pairs).

Of the 749 participants with usable data for the Wave 2 testing session, 30 were missing data for one or more EF task because of color blindness, equipment malfunction, failure to understand or follow task instructions, or chance-level accuracy (following the same criteria used by Friedman et al., 2008; see Table 1 for ns). Zygosity was determined through repeated tester ratings combined with DNA genotyping.

Table 1.

Descriptive Statistics

Task	N	Mean	SD	Min	Max	Skewness	Kurtosis	Reliability
Wave 1
Antisaccadea	779	1.04	0.20	0.47	1.57	−0.12	−0.26	.89b
Stop-signal	741	282 ms	63	151	489	1.13	1.51	.75b
Stroop	759	214 ms	90	0	488	0.59	0.19	.91b
Keep tracka	774	0.94	0.18	0.38	1.49	0.31	0.56	.65c
Letter memorya	785	1.09	0.25	0.38	1.57	0.29	−0.20	.62c
Spatial 2-backa	777	1.17	0.17	0.65	1.57	−0.93	1.65	.90c
Number–letter	776	331 ms	183	–14	923	1.04	1.12	.86b
Color–shape	768	331 ms	189	–196	916	0.76	0.75	.85b
Category-switch	766	333 ms	181	–34	899	0.98	0.92	.83b
Wave 2
Antisaccade	748	0.62	0.16	0.20	0.96	–0.13	–0.67	.90c
Stop-signal	735	215 ms	30	116	315	–0.23	0.25	.63c
Stroop	737	156 ms	74	–73	387	0.71	0.71	.96b
Keep track	749	0.72	0.09	0.44	0.96	–0.36	0.11	.66c
Letter memory	749	0.70	0.13	0.38	1.00	0.22	–0.64	.92c
Spatial n-backd	749	–0.01	0.91	–2.74	2.70	–0.31	–0.03	.75b
2-backa	745	1.08	0.17	0.64	1.45	–0.53	–0.24	.92c
3-backa	745	0.97	0.11	0.62	1.40	0.03	0.45	.78c
Number–letter	748	246 ms	157	–241	735	0.91	0.92	.91b
Color–shape	743	221 ms	182	–239	792	1.05	1.19	.90b
Category-switch	747	198 ms	161	–81	735	1.14	1.28	.94b

Note. Min = minimum; Max = maximum.

^aAccuracy scores were arcsine transformed.

^bInternal reliability was calculated by adjusting split-half or part1–part2 correlations with the Spearman–Brown prophecy formula.

^cInternal reliability was calculated using Cronbach’s alpha.

^dAverage of z-scores for the 2- and 3-back tasks.

All research protocols were reviewed and approved by the University of Colorado’s Institutional Review Board. Parental permission and informed consent or assent was obtained from each participant or parent, as appropriate, at each assessment.

Materials, Design, and Procedure

Wave 1 measures were described in Friedman et al. (2008). Here we describe the Wave 2 measures in detail and note the primary differences from the Wave 1 versions.

The nine Wave 2 tasks were programmed in PsyScope X Build 51 (Cohen, MacWhinney, Flatt, & Provost, 1993) and administered on Macintosh computers, except for stop signal at Wave 2 (executable program run from a Windows XP partition). Reaction times (RTs) were measured with a millisecond-accurate button box or Empirisoft keyboard (stop-signal only); a headset attached to the button box was used to collect voice key responses (Stroop only).

Antisaccade

This response inhibition task required participants (seated 18 inches from the monitor) to avoid the reflexive tendency to look at a cue and instead look in the opposite direction to see a briefly presented target stimulus. In this version of the task, eye movements were not measured, but the timing of the task was set so that it would not be possible for the participant to see the target if he or she first saccaded to the cue.

The task began with a prosaccade block (18 trials) to introduce the task and increase prepotency of the prosaccade response, followed by three antisaccade blocks of increasing difficulty (each 36 trials). Each trial began with a centered fixation cross. After a variable duration (one of nine durations from 1500 to 3500 ms at 250-ms intervals), the fixation disappeared and the cue (a black 1/8 in. square, inner edge 3.375 in. from the center) appeared on the left or right of the screen (with equal probability). The cue remained on the screen for 233 ms in the first antisaccade block, 200 ms in the second, and 183 ms in the third and the initial prosaccade blocks. Once it disappeared, a numeric target (a digit 1-9, 26 pt Helvetica font, presented in a 7/16 in. square with its inner edge 3.25 in. from the fixation) appeared for 150 ms before being masked with gray cross-hatching, on the same side as the cue for prosaccade block and on the opposite for the antisaccade blocks. The participant verbalized the target number (or guessed), and the experimenter entered the response, initiating the next trial. The prosaccade and first antisaccade blocks were each preceded by 12 practice trials, and each block contained two "warm up" trials that were not included in the analyses. The dependent measure was average accuracy for the three antisaccade blocks.

The Wave 1 version differed primarily in that it did not include a prosaccade block; its targets were left, right, and up arrows that were identified with participants' button-press responses; and all trials had the same timing (150 ms cue, 183 ms target). We included more difficult to discriminate and guess targets and multiple blocked cue-to-target intervals to increase range and avoid the slight ceiling effect seen in Wave 1.

Stop-signal

In this response inhibition task, participants completed a simple categorization task (indicate whether centrally presented green arrows were pointing to the left or right with keyboard responses) as quickly and accurately as possible on the majority of trials, but had to withhold the response if the arrow turned red during the trial (25% of trials). The program (van den Wildenberg et al., 2006) used a staircase algorithm for adjusting the stop-signal delay (the amount of time the arrow was green before turning red) so that participants would be able to stop on approximately 50% of the stop trials. Specifically, the first stop-signal delay was 200 ms, which was reduced or increased by 50 ms on the next stop trial if the participant did not stop or did stop on the prior stop trial, respectively. This algorithm continued across blocks including the practice (i.e., the delay did not reset to 200 ms at the beginning of each block).

The task began with an all-go block (50 trials, preceded by 10 practice trials) to set up the prepotent response. Then the instructions for the stop-signal were given, and the participants practiced on 48 trials, then completed three blocks of 80 trials each. At the end of each block, participants were given feedback on their accuracy, go RT, and percentage stopping. The experimenter went over this information with them and if they showed substantial slowing, they were reminded to try to go as quickly and accurately as possible. If the participant's percentage of stopping fell outside of 40-60%, the experimenter ran additional blocks until three were usable (18% of participants); if the experimenter failed to do so or the participant did not follow instructions so that there were not three usable blocks, the data were excluded. The dependent measure was the stop-signal RT (SSRT; the time at which the stopping process completes), calculated as the difference between the median go RT (RT on trials in which the arrow remained green) and the mean stop-signal delay across all trials (separate SSRTs for each block were used to calculate reliability but were not used to compute the overall SSRT).

The Wave 1 version differed primarily in that it did not use the staircase algorithm; rather, three stop-signal delays were calculated for each participant based on his or her mean RT in the initial go block. The categorization task was also more complex (categorize 24 words as animals or not), and the signal was a beep rather than a color change. The primary reason for the changes implemented at Wave 2 was to increase the prepotency of the primary task and to reduce the impact of strategic slowing (the staircase algorithm adjusts for slowing).

Stroop

In this response inhibition task, participants avoided the prepotent tendency to read color words and instead named the colors (red, blue, or green) in which they were printed. On each trial, a 750 ms blank period was followed by a 250 ms white fixation cross (the background was black throughout the task), then a colored stimulus, which remained on the screen until the participant reported the color. The task began with a block of 42 trials with colored strings of 3-5 asterisks (no response conflict), followed by a block of 42 trials of color words (RED, BLUE, and GREEN) printed in the congruent color (response facilitation), and ended with two blocks of 42 trials of color words printed in incongruent colors (response conflict). The first two blocks were preceded by 10 practice trials each, and every block included two "warm-up" trials that were not included in the analyses. The dependent measure was the difference in mean RTs for correct responses (i.e., excluding errors, stuttering, and hybrid responses such as “blred”) in the incongruent vs. asterisks blocks.

The primary difference from the Wave 1 version is that we used fewer colors, and the conditions were blocked versus mixed. We decided to use a blocked design based on previous work with this EF battery. Specifically, the Stroop task loads on a Common EF factor, which Miyake and Friedman (2012) characterized as tapping active goal maintenance and top-down biasing. Individual differences in this ability are best measured when the baseline condition does not also heavily involve this kind of goal maintenance. Because mixing easier trials with harder trials can make the easier trials more demanding (perhaps because participants continue to maintain the color-naming goal at a higher level than necessary for non-conflict trials, because interference effects from previous conflict trials carry over into subsequent trials, or other reasons), we decided that a blocked presentation would be a more appropriate baseline.

Keep track

This updating task requires participants to keep track of the last instances of two to five categories (animals, colors, countries, distances, metals, and relatives) in a stream of words from six categories. Each trial began with category list, which remained at the bottom of the screen while 15-25 words appeared for 2 s each. At the end of the trial, the categories disappeared from the screen and "???" appeared, signaling the participant to recall the last word from each target category. After two practice trials with two categories to remember, there were four blocks, each containing a two-, a three-, a four-, and a five-category trial, randomly ordered within each block. The dependent measure was proportion of words recalled across all trials.

The primary difference from the Wave 1 version was the inclusion of 5-category trials, and increased variability of the trial lengths and number of updates within trials. For example, in the Wave 1 version, each trial had 15 words, with two to three exemplars of each category, whereas in the Wave 2 version, trials were variable length and contained one to four exemplars of each category. These changes made the trials more unpredictable in terms of when they would end and when the target words might appear, encouraging participants to update each word. To accommodate this increased difficulty, we increased the duration of each word to 2 s each (from the 1.5 s used before).

Letter memory

In this updating task, participants had to continuously rehearse the last four letters in a series of unpredictable length (9, 11, or 13 letters). Each letter (consonants only) appeared for 3 s, allowing time for the participant to say the last four letters, including the current letter, aloud. Participants accumulated letters until the fourth letter was reached, after which the fifth letter back was dropped (i.e., “L”, “L-S”, “L-S-K”, “L-S-K-D”, ”S-K-D-H”, etc.). One point was given for each correctly reported set (i.e., the last four letters reported in the correct order). At the end of each letter series, subjects were asked to repeat the final four letters, but this final recall was not scored because it was already captured in the set score for the last letter. There were 12 trials total, and the dependent measure was the proportion of sets correctly rehearsed.

The primary difference from the Wave 1 version was the requirement to update four letters instead of three, and the scoring of the updating portion of the task. In the Wave 1 version, participants were required to update the last three letters aloud, but only final recall was scored. To allow time to report more letters, we increased the duration of each letter to 3 s vs. the 2.5 s used at Wave 1.

Spatial n-back

In this updating task, participants saw 12 open 5/8-in. squares fixed in pseudorandom locations on the monitor. In each of six blocks, 24 squares flashed (i.e., became solid black for 500 ms and then returned to open for 1500 ms), one at a time, and for each flash, the participant had to report via button press whether it was the same as the one that had flashed n-trials (i.e., two or three trials) before. The 2-back and 3-back conditions were presented as separate tasks (one near the start of the session and the other near the end) to minimize interference between the conditions. Each block had 25% "yes" (match) trials, and 30% of the 2-back and 20% of the 3-back "no" trials were "lures": flashes that matched the square from three or four flashes back in the 2- and 3-back tasks, respectively. Participants completed a practice block of 20 flashes prior to the six blocks for each condition. The dependent measure was average of the z-scores for arcsined proportion correct scores in each condition, with omissions counted as errors.

The primary difference from the Wave 1 version is the addition of the 3-back condition, and the addition of lures to increase difficulty. In addition, this version used 12 locations instead of the 10 used at Wave 1.

Switch tasks

The three task- or set-switching tasks all required participants to switch back and forth between two subtasks. In each trial of the number–letter, participants saw a number-letter or letter-number pair in one quadrant of a box and categorized the number (2-9) as odd or even if the pair appeared in one of the top two quadrants, but categorized the letter (A, E, I, U, G, K, M, or R) as consonant or vowel if the pair appeared in one of the bottom two quadrants. In each trial of the color–shape task, participants saw a colored (red or green) shape (circle or triangle) and categorized the shape or color depending on a cue (C or S) that appeared above the stimulus. In each trial of the category-switch task, participants saw a word (alligator, bicycle, cloud, coat, goldfish, knob, lion, lizard, marble, mushroom, oak, pebble, shark, snowflake, sparrow, or table) and categorized it as describing something that is smaller or bigger than a soccer ball or living or nonliving, depending on a symbol (heart or crossed arrows) that appeared above the stimulus. In each trial (except for the number–letter single-task and predictable-switch blocks), the cue (darkening of the quadrant, letter, or symbol) started 350 ms before the target stimulus appeared. The cue and stimulus remained on the screen until the participant responded with one of two button presses (left indicated odd or consonant, red or circle, and small or nonliving, and right indicated even or vowel, green or triangle, and big or living), which triggered the next trial after a 350 ms response-to-cue interval. A 200 ms buzz sounded for errors.

Each task began with single-task blocks in which only one task was required (number then letter; color then shape; and animacy then size) for 24 trials each in the color–shape task and 32 trials each in the number–letter and category-switch tasks (block length differed slightly due to counterbalancing considerations). Each of these single-trial blocks was preceded by a 12-trial practice block and included two extra "warm-up" trials that were not analyzed. After these single-task blocks, participants completed two mixed blocks (56 trials each for color–shape, and 64 trials each for the other tasks), in which the two subtasks were pseudo-randomly mixed such that half the trials required switching subtasks. In the number–letter task they also completed two 64-trial predictable-switch blocks (not analyzed here) prior to the random mixed blocks, in which the stimuli circled the box in a clockwise pattern. The first of each type of switch block was preceded by a 24-trial practice block, and each switch block included four extra "warm-up" trials. The dependent measure for each task was the local switch cost: the difference between average RTs for switch trials and repeat trials in the random mixed blocks.

The primary change from the Wave 1 versions was the addition of the error signal (to further improve accuracy), the single-task blocks, the use of a 350-ms cue-to-stimulus interval throughout the mixed blocks, and the elimination of longer cue-to-stimulus interval blocks. In the Wave 1 version, participants completed four blocks that alternated between a 150 ms cue-to-stimulus interval and a 1,500 ms cue-to-stimulus interval (used to calculate residual switch costs); however, the blocks with the longer interval were not analyzed for the primary report (Friedman et al., 2008). The single-task blocks gave participants practice with the subtasks and response mappings and provided a baseline for calculating global switch costs and mixing costs (not analyzed here).

General Procedure

In both waves of testing, the EF tasks were administered as part of a larger battery of individual differences measures (interviews/questionnaires and cognitive tasks). Within each task (and whenever possible, within each task block), stimuli were appropriately counterbalanced and randomized. The order of stimuli within each task and the order of tasks were fixed for all participants to avoid participant by order interactions. Tasks were arranged so that no two sequential tasks tapped the same EF construct. At Wave 2, participants completed ½ hour of questionnaires on a separate computer and then received a 5-10 minute break between sets of EF tasks (generally after every three cognitive tasks); they also took a lunch break halfway through the session. This intermixing of tasks and questionnaires was intended to break up the cognitive demands of the testing session. The tasks described in the current study took approximately two hours to complete. Participants received $100 for completing the entire Wave 2 battery.

Statistical Procedures

Data transformation and trimming

To improve normality of the distributions, we implemented appropriate trimming and transformations, as described in detail in Friedman et al. (2008). Briefly, for the Wave 1 data, we used the arcsine of the proportion correct for accuracy measures to improve normality, and RT measures depending on mean RTs (all except stop signal) were subjected to within-subject trimming robust to nonnormality (Wilcox & Keselman, 2003) to obtain the best measures of central tendency. RTs for error trials and RTs < 200 ms were eliminated, and for the three shifting tasks, RTs for trial following errors were also eliminated (because the correct set might not have been achieved on the previous trial, making it ambiguous whether the current trial was a switch or repeat trial). To reduce the influence of extreme scores at the between-subject level, we replaced observations farther than 3 SDs from the group mean with values 3 SDs from the mean. This procedure affected no more than 2.0% of the observations for any measure at either wave of assessment. The same procedures were followed for the Wave 2 data, except that the arcsine transformation was not necessary for any task besides spatial 2-back due to reduction of ceiling effects (we also transformed 3-back before z-scoring and averaging for consistency). Average accuracy was greater than 92% in all RT tasks in both waves. After these transformations and trimming, the variables showed acceptable skewness and kurtosis (see Table 1). In all analyses, the directionality of the RT measures was reversed so that for all measures, higher scores indicated better performance.

Model estimation

We used Mplus 7.3 (Muthén & Muthén, 1998–2012) for the analyses, which included participants with missing data for one or more measures. All analyses were conducted on raw data, rescaled when appropriate to avoid ill-scaled covariance matrices. Because the chi-square (χ²) is sensitive to sample size, we also used confirmatory fit index (CFI) < .95 and root-mean-square error of approximation (RMSEA) < .06 as indicators of good fit (Hu & Bentler, 1998). Statistical significance of parameters of interest was tested with chi-square difference (Δχ²) tests. To correct for the nonindependence of the twin pairs in the phenotypic analyses, we used Mplus’s TYPE = COMPLEX option to obtain a scaled χ² and standard errors robust to nonindependence, and we used scaled Δχ² tests (Satorra & Bentler, 2001) for nested model comparisons.

Twin analyses

The ACE model partitions phenotypic variance into additive genetic (A), shared environmental (C), and nonshared environmental (E) components. The A components correlate 1.0 in MZ twins, who share the same genes, and they correlate 0.5 in DZ twins, who share on average half their segregating genes; the C variables correlate at 1.0 in both types of twins because they are reared together; the E variables do not correlate by definition, because they represent environmental influences unique to each twin (and measurement error for observed variables). We present standard errors for all ACE parameters, but when significance tests based on these standard errors disagree with Δχ² tests, we only interpret the latter.²

Possible covariates

We considered whether to control for sex and testing age within wave as covariates in the models (or regress them out of the measures). After examination of the patterns of effects, described in this section, we decided against doing so. Thus, none of the analyses reported consider testing age or sex.

As reported in Friedman et al. (2011), sex differences in Wave 1 EF task performance were inconsistent within constructs (e.g., males were more accurate on the antisaccade task but showed larger interference effects on the Stroop task), so task differences did not result in sex differences at the latent variable level. Wave 1 sex differences were significant for the following tests: antisaccade (arcsined accuracy for males = 1.09 [SD = 0.18] > females = 0.99 [SD = .20], p < .001); Stroop (males = 223 ms [SD = 95] > females = 206 ms [SD = 85], p = .025); color–shape (males = 348 ms [SD = 197] > females = 316 ms [SD = 182], p = .039); and category-switch (males = 314 ms [SD = 179] < females = 350 ms [SD = 182], p = .017). At Wave 2, we observed a similar pattern: Sex differences in Wave 2 EF task performance were significant for the following tests: antisaccade (accuracy for males = 0.67 [SD = 0.16] > females = 0.58 [SD = .15], p < .001); color–shape (males = 238 ms [SD = 189] > females = 206 ms [SD = 174], p = .032); and category-switch (males = 183 ms [SD = 154] < females = 210 ms [SD = 165], p = .043). Given that these sex differences were not consistent within constructs and did not appear for most of the tasks, we did not regress out sex.

Wave 1 testing age was not significantly related to any of the nine EF tasks (all p > 0.152). Wave 2 testing age was significantly related to Wave 2 antisaccade (standardized beta = –0.12, p = .005); stop-signal (standardized beta = 0.09, p = .027); Stroop (standardized beta = 0.08, p = .048); keep track (standardized beta = –0.10, p = .002); and letter memory (standardized beta = –0.10, p = .005). All of these differences were in the direction that older participants performed less accurately/more slowly. However, the older participants may not have been tested until that later age because they were difficult to schedule; this difficulty may have been at least partially due to difficulties keeping the meeting, which in turn may have been related to EF ability. Indeed, Wave 2 testing age was significantly related to Wave 1 Common EF (standardized beta = –0.16, p = .031). Given that these apparent age differences may not have been reflecting true age differences, we decided not to regress them out.

Results and Discussion

Phenotypic Stability of Executive Functions

Table 2 presents the correlation matrix for Waves 1 and 2. As can be seen in the boxed cells, the Wave 1 to Wave 2 correlations for the individual tasks ranged from .21 to .56 (M = .45, SD = .12). The lowest correlation (.21) was for stop-signal, which generally correlated less with the other EF measures at Wave 2 than it did at Wave 1, followed by spatial n-back. The remaining correlations were moderate (.43 to .56).

Table 2.

Phenotypic Correlations

Task	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
Wave 1
1. Antisaccade	--
2. Stop-signal	.26	--
3. Stroop	.17	.15	--
4. Keep track	.19	.23	.21	--
5. Letter memory	.25	.16	.25	.46	--
6. Spatial 2-back	.22	.24	.13	.26	.26	--
7. Number–letter	.15	.26	.23	.13	.19	.15	--
8. Color–shape	.16	.22	.27	.14	.15	.12	.41	--
9. Category-switch	.22	.28	.25	.17	.16	.19	.48	.43	--
Wave 2
10. Antisaccade	.54	.25	.18	.19	.21	.20	.27	.20	.34	--
11. Stop-signal	.17	.21	.17	.05	.08	.02	.11	.16	.12	.23	--
12. Stroop	.21	.23	.45	.19	.23	.15	.16	.10	.23	.32	.13	--
13. Keep track	.18	.22	.21	.56	.45	.25	.14	.09	.19	.25	.13	.24	--
14. Letter memory	.28	.19	.26	.47	.54	.28	.12	.14	.18	.40	.12	.30	.52	--
15. Spatial n-back	.29	.19	.15	.35	.30	.33	.10	.12	.15	.37	.05	.18	.33	.40	--
16. Number–letter	.14	.15	.19	.08	.06	.07	.51	.39	.48	.26	.09	.18	.11	.10	.04	--
17. Color–shape	.11	.14	.22	.16	.15	.07	.32	.43	.37	.17	.01	.17	.15	.12	.10	.43	--
18. Category-switch	.23	.27	.26	.19	.12	.15	.46	.34	.53	.36	.15	.30	.23	.21	.15	.50	.41	--

Note. Correlations are maximum likelihood estimates (from Mplus) based on all data, adjusted for missing observations and nonindependence. Boxed cells are Wave 1 with Wave 2 correlations for the same tasks. Total N = 840. Directionality of the reaction time measures was reversed so that for all tasks, higher scores indicate better performance. Boldface type indicates p < .05.

Wave 2 factor structure

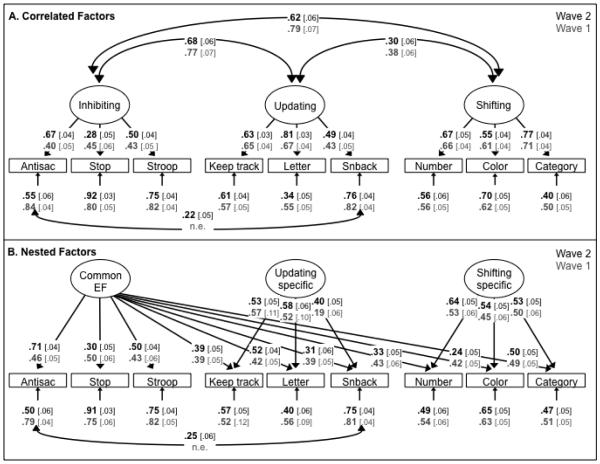
Before examining cross-wave latent variable correlations, we first examined whether we obtained the same factor structure (i.e., configural invariance) at Wave 2. As shown in Figure 1 (black font), the basic pattern of unity and diversity was replicated at Wave 2, and the correlations of the Inhibiting, Updating, and Shifting variables were very similar to what we found at Wave 1 (gray font). Both the correlated factors model (Figure 1A), χ²(23) = 54.94, p < .001; CFI = .971; RMSEA = .043, and the nested factors model (Figure 1B), χ²(20) = 41.41, p = .003; CFI = .981; RMSEA = .038, showed good fits to the data.³ As with the Wave 1 data, there was no evidence of an Inhibiting-Specific variable in the nested factors model.⁴

Figure 1.

Two complementary parameterizations of the EF data (Wave 2 parameters on top in black font, Wave 1 below in gray font; Waves 1 and 2 estimated in separate models). Numbers on arrows are standardized factor loadings, those under the smaller arrows are residual variances, and those on curved double-headed arrows are inter-factor correlations. Numbers in brackets are standard errors. In the correlated factors model (Panel A), there are three correlated EF latent variables predicting three tasks each. In the nested factors model (Panel B), there is a Common EF latent variable on which all nine EF tasks load, as well as two "nested" latent variables on which the updating and shifting tasks, respectively, also load. The Common EF variance is isomorphic with the Inhibiting latent variable, so there was no inhibiting-specific variance at either time point. Because the Common EF factor captures the variance common to all three EFs, the Updating-Specific and Shifting-Specific factors capture the variance that is unique to Updating and Shifting, respectively. Hence, they are uncorrelated with the Common EF factor and with each other. All parameters were statistically significant (p < .05). Antisac = antisaccade, Stop = stop-signal, Letter = letter memory, Snback = spatial n-back, Number = number–letter, Color = color–shape, Category = category-switch; n.e. = not estimated at Wave 1.

Cross-wave correlations

To examine stability, we added the Wave 2 model to the Wave 1 model and allowed the latent variables to correlate across waves. We also allowed the residuals for each task to correlate across waves, as task-specific variance might be somewhat stable. We tested for measurement invariance in the factor loadings, but, as expected given the changes we made for Wave 2, we could not constrain the standardized loadings to be equal across waves for either the correlated factors model, Δχ² (9) = 35.16, p < .001, or the nested factors model, Δχ² (15) = 50.24, p < .001. However, for the correlated factors model we could constrain the latent variable correlations to be equal across waves while allowing the factor loadings to differ, Δχ² (3) = 5.64, p = .131, which suggests measurement invariance at the second-order level.

In the correlated factors model (all correlations freely estimated), χ²(110) = 224.00, p < .001; CFI = .964; RMSEA = .035, the cross-wave correlations for the Inhibiting, Updating, and Shifting latent variables were .83 [s.e. = .07], .93 [s.e. = .03], and .90 [s.e. = .03], respectively, all ps < .001. Collapsing any of these latent variables into a single factor across waves significantly reduced fit, all Δχ² (5) > 23.77, p < .001, suggesting that there was significant variance that did not overlap across waves in all three factors. From a unity/diversity perspective, we were interested in whether this separable variance occurred at the unity level, the diversity level, or both. The cross-wave correlations for the nested factors model, χ²(110) = 212.23, p < .001; CFI = .968; RMSEA = .033, are informative in this regard: they were .86 [s.e. = .03], 1.0 [s.e. = .05], and .91 [s.e. = .05] for the Common EF, Updating-Specific, and Shifting-Specific variables, respectively, all ps < .001. The correlation of 1.0 for Updating-Specific indicates that the two waves were not distinguishable on this variable. The same was true for the Shifting-Specific factor; Waves 1 and 2 could be collapsed without a significant decrement in model fit, Δχ² (1) = 2.75, p = .097. However, the two waves of the Common EF factor could not be collapsed, Δχ² (1) = 66.24, p < .001. These results suggest that most of the change seen in the correlated factors was attributable to the unity portion of the model. The remaining analyses are conducted with the nested factors model, as this model isolates what changed across waves.

Genetic and Environmental Stability and Change in Executive Functions

Wave 2 only

Results of univariate ACE models for the Wave 2 tasks are shown in Table 3. Estimates were generally similar to those at Wave 1, with the exception of stop-signal: Most tasks showed moderate heritability and no significant shared environmental variance.

Table 3.

Univariate Task Twin Correlations and ACE Estimates

	Twin Correlationsa		Variance Components (%)			Model Fit
Task	MZ	DZ	A	C	E	χ2 (6)	p	RMSEA	CFI
Wave 1
Antisaccade	.55*	.22*	54* [5]	0 [.00]	46* [5]	3.21	.782	.000	1.00
Stop-signal	.51*	.08	44* [6]	0 [.00]	56* [6]	10.41	.109	.061	.911
Stroop	.48*	.29*	38* [17]	9 [.14]	53* [5]	5.57	.473	.000	1.00
Keep track	.54*	.25*	53* [5]	0 [.00]	47* [5]	1.89	.930	.000	1.00
Letter memory	.57*	.18*	55* [5]	0 [.00]	45* [5]	7.50	.277	.035	.983
Spatial 2-back	.29*	.14	25 [20]	2 [.17]	73* [6]	4.56	.602	.000	1.00
Number–letter	.51*	.29*	48* [16]	4 [.14]	48* [5]	2.99	.810	.000	1.00
Color–shape	.34*	.21*	34 [19]	3 [.15]	63* [6]	5.60	.469	.000	1.00
Category-switch	.53*	.33*	39* [16]	13 [.14]	47* [5]	3.47	.748	.000	1.00
Wave 2
Antisaccade	.61*	.40*	42* [14]	19 [.13]	39* [4]	2.05	.915	.000	1.00
Stop-signal	.27*	.22*	12 [20]	15 [.16]	73* [7]	3.74	.712	.000	1.00
Stroop	.52*	.08	49* [5]	0 [.00]	51* [5]	8.72	.190	.049	.956
Keep track	.60*	.15	57* [5]	0 [.00]	43* [5]	6.34	.387	.017	.996
Letter memory	.69*	.34*	69* [3]	0 [.00]	31* [3]	0.81	.992	.000	1.00
Spatial 2-back	.55*	.16*	53* [5]	0 [.00]	47* [5]	9.13	.167	.052	.957
Number–letter	.51*	.17*	53* [5]	0 [.00]	47* [5]	11.29	.080	.068	.917
Color–shape	.32*	.23*	28 [19]	7 [.15]	66* [7]	4.91	.556	.000	1.00
Category-switch	.50*	.21*	48* [5]	0 [.00]	52* [5]	5.23	.514	.000	1.00

Note. Standard errors in brackets. Variance components sum to 100%, within rounding error. MZ = monozygotic; DZ = dizygotic; A = additive genetic variance; C = shared environmental variance; E = nonshared environmental variance; RMSEA = root-mean-square error of approximation. CFI = confirmatory fit index. χ²/df < 2, RMSEA < .06, and CFI > .95 indicate good fit.

^aCorrelations are maximum likelihood estimates (from Mplus) based on all data, adjusted for missing observations.

^*p < .05, determined with chi-square difference tests for the ACE models and with z-values for the correlations.

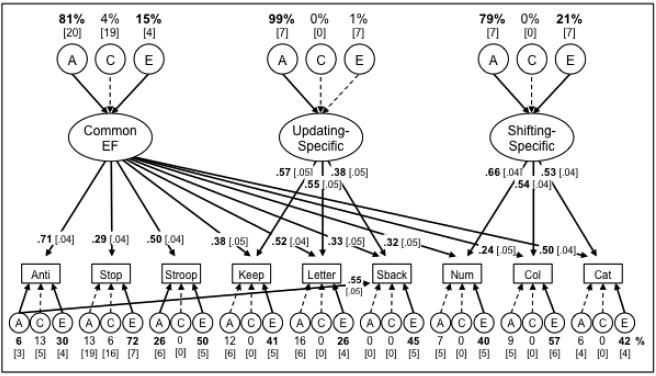
As reported in Friedman et al. (2011), the only latent construct showing significant environmental variance at Wave 1 was Shifting-Specific (A = 79% and E = 21%). Common EF was 96% heritable (E = 4%, not significant), and Updating-Specific was estimated as 100% heritable. Figure 2 shows the ACE components of the EF model for Wave 2, χ²(320) = 420.26, p < .001; CFI = .945; RMSEA = .040. The three EF latent variables were still highly heritable, but the nonshared environmental variance for Common EF was also significant, Δχ² (1) = 21.00, p < .001. Although small (15%), this variance is notable because it signifies environmental influences that are shared among all nine tasks, and represents the only notable change from the Wave 1 results.

Figure 2.

Nested factors ACE genetic model of the Wave 2 EF data. Numbers on arrows are standardized factor loadings, those above the top ACEs are the percentages of the Common EF, Updating-Specific, and Shifting-Specific factors’ variances due to genetic and environmental influences, and those below the lower ACEs are estimates for the remaining nonexecutive variances in individual tasks. Numbers in brackets are standard errors. Boldface type and solid lines indicate statistical significance (p < .05), determined with chi-square difference tests for the ACE variances. Anti = antisaccade, Stop = stop-signal, Keep = keep track; Letter = letter memory, Sback = spatial n-back, Num = number–letter, Col = color–shape, Cat = category-switch.

Cross-wave

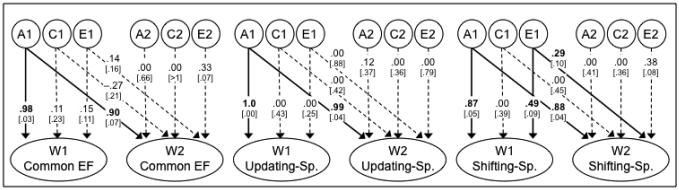
To examine the cross-wave genetic and environmental stability and change in the EFs, we estimated the Cholesky decomposition depicted in Figure 3 (only the latent variables are shown; cross-wave task-unique A, C, and E covariances were also modeled, but are not shown for simplicity). For each EF component (Common EF, Updating-Specific, and Shifting-Specific were estimated in the same model, but because they are uncorrelated, their Wave 1 to Wave 2 Cholesky decompositions can be shown as bivariate), this decomposition partitions the variance in Wave 2 EF scores into that shared with Wave 1 scores (paths to Wave 2 from A1, C1, and E1) and that unique to Wave 2 (paths from A2, C2, and E2). Squaring the standardized path estimates in Figure 3 provides the proportion variance accounted for by each variable (i.e, to obtain percentages analogous to those in Figure 2). The full model showed an acceptable fit, χ²(1253) = 1607.90, p < .001; CFI = .922; RMSEA = .037.

Figure 3.

Cholesky decomposition of the nested factors EF model for the cross-wave data (individual tasks not shown for simplicity). Each Wave 2 latent variable is decomposed into additive genetic (A), shared environmental (C), and nonshared environmental (E) variance shared with Wave 1 (paths to Wave 2 from A1, C1, and E1), and that unique to Wave 2 (paths from A2, C2, and E2). Squaring the path estimates provides the proportion variance accounted for by each variable (i.e, to obtain the percentages depicted in Figure 2). Common EF, Updating-Specific, and Shifting-Specific were estimated in the same model, but are orthogonal. Numbers on arrows are standardized regression coefficients predicting Common EF, Updating-Specific, and Shifting-Specific factor with the genetic and environmental latent variables. Numbers in brackets are standard errors. Boldface type and solid lines indicate statistical significance (p < .05), determined with chi-square difference tests. Note that when the chi-square difference tests disagreed with the standard errors, only the results for the difference tests were interpreted. W1 = Wave 1; W2 = Wave 2; Common EF = Common Executive Function; Updating-Sp. = Updating-Specific; Shifting-Sp. = Shifting-Specific.

As indicated by the zero or near-zero path estimates from the A2 variables, there was no significant genetic variance unique to Wave 2 for any of the EF latent variables. There were also no significant shared environmental influences (indicated by the nonsignificant paths from C1 and C2 variables). For the Common EF variable, most of the nonshared environment variance was estimated as being new to Wave 2. Dropping either the cross-wave E1 to Wave 2 Common EF path or the Wave 2-unique E2 path separately did not result in a significant fit decrement, both Δχ² (1) < 0.84, p > .360. However, the E variance for Wave 1 was essentially zero (squaring the .15 path from E1 to W1 Common EF gives only 2%); when the E variance unique to Wave 2 was fixed at zero, the Wave 2 E variance moved into the cross path and the E1 to Wave 1 path became even smaller so that there was essentially no environmental correlation; thus this model was equivalent to a model with no E variance at Wave 1, no cross path, but E variance at Wave 2. When both E paths to Wave 2 were dropped, there was a significant decrement in fit, Δχ² (2) = 18.86, p < .001, indicating that there was significant E variance at Wave 2. We interpret the results as showing new nonshared environmental variance at Wave 2.

For the Shifting-Specific variable, Wave 2 nonshared environmental variance was estimated at 22% total (i.e., summing the squared paths from E1 and E2 to Wave 2). The 8% in common with Wave 1 was significant, Δχ² (1) = 7.44, p = .006, and the 14% unique to Wave 2 did not reach significance, Δχ² (1) = 2.83, p = .093 (but see footnote 1 for information about the power of this test).

These results can also be described with cross-wave genetic and environmental correlations (e.g., the genetic correlation, rA, is the correlation between the A variances for Waves 1 and 2 when there is no cross-path; that is, A1 only predicts Wave 1 but is allowed to correlate with A2, which captures all the genetic variance at Wave 2). These correlations, calculated from the Cholesky model shown in Figure 3, are presented in Table 4 for the latent variables. The genetic correlations were 1.0, .99, and 1.0 for the Common EF, Updating-Specific, and Shifting-Specific variables, respectively. The nonshared environmental correlations were .40 and .61 for the Common EF and Shifting-Specific variables, respectively.

Table 4.

W1 to W2 Genetic and Environmental Correlations and Stabilities

	ACE Correlations			Standardized Stabilities
Task	rA	rC	rE	Phenotypic	A	C	E
EF Latent Variables
Common EF	1.0* [.00]	–1.0 [.06]	.40 [.43]	.87* [.03]	.88* [.05]	–.03 [.04]	.02 [.02]
Updating-Specific	.99* [.04]	--	--	.99* [.04]	.99* [.04]	.00 [.00]	.00 [.00]
Shifting-Specific	1.0* [.00]	--	.61* [.18]	.91* [.04]	.77* [.06]	.00 [.00]	.14* [.06]
EF Tasks
Antisaccade	.78* [.10]	1.0 [.00]	.20* [.07]	.54* [.03]	.38* [.09]	.07 [.08]	.08* [.03]
Stop-signal	1.0* [.00]	--	–.02 [.07]	.21* [.04]	.24* [.08]	–.01 [.06]	–.01 [.04]
Stroop	.90* [.24]	--	.16* [.07]	.45* [.03]	.37* [.07]	.00 [.05]	.08* [.04]
Keep track	.90* [.05]	--	.12 [.07]	.55* [.03]	.50* [.04]	.00 [.00]	.05 [.03]
Letter memory	.90* [.11]	--	.04 [.07]	.54* [.03]	.53* [.06]	.00 [.05]	.01 [.03]
Spatial 2-back	1.0* [.00]	--	.05 [.07]	.33* [.04]	.32* [.06]	–.02 [.04]	.03 [.04]
Number–letter	.96* [.17]	--	.09 [.07]	.52* [.03]	.47* [.06]	.00 [.04]	.05 [.04]
Color–shape	.74 [.17]	1.0 [.00]	.24* [.07]	.44* [.03]	.21 [.13]	.08 [.10]	.15* [.05]
Category-switch	1.0* [.00]	1.0 [.00]	.05 [.06]	.53* [.03]	.42* [.10]	.09 [.10]	.02 [.03]

Note. Stability = (W1/W2 correlation) * √(W1 variance*W2 variance). A+C+E stabilities sum to phenotypic stability, within rounding error. Estimates are derived from W1/W2 Cholesky decompositions (one model for the three EF latent variables; a separate model for each EF task). rC not presented if one of the C variances was estimated at less than 1% in the bivariate model. W1 = wave 1; W2 = wave2; A = additive genetic; C = shared environment; E = nonshared environment. Standard errors in brackets.

^*p < .05, determined with chi-square difference tests on the cross paths for the Cholesky decompositions.

The extent to which these genetic and environmental correlations account for overall phenotypic stability is also presented in Table 4, both for the latent variables and the individual EF tasks (the latter were calculated for each task separately, in nine different models). Following Tucker-Drob and Briley (2014), the total phenotypic stability (i.e., the correlation between Wave 1 and Wave 2) is decomposed into that due to the A, C, and E components. For example, the phenotypic stability of Shifting-Specific (.91) that is attributable to genetic influences is .77, calculated as the product of rA (1.0) and the paths from A1 to Wave 1 and A2 to Wave 2 when there is no cross path in the model (the square roots of the A variances at Wave 1 [.87] and Wave 2 [.88]). The portion attributable to nonshared environmental influences is .14, calculated as the product of rE (.61) and the square roots of the E variances at Wave 1 (.49) and Wave 2 (.48). None of the stability is attributable to shared environmental influences because the C variances were zero. Thus, the total phenotypic stability (.91) of Shifting-Specific is 85% genetic (.77/.91) and 15% nonshared environmental (.14/.91).

As shown in Table 4, Shifting-Specific was the only latent variable for which nonshared environment contributed to stability; the Common EF and Updating-Specific stabilities were 100% genetic. At the individual task level, genetic influences also accounted for the majority of the stability in the individual task correlations (70% to 100%), with the exception of color–shape (48%). Only three tasks (antisaccade, Stroop, and color–shape) showed significant nonshared environmental stability (accounting for 15 to 34% of the phenotypic stability).

General Discussion

We examined genetic and environmental stability and change in three EF components, measured with latent variables, from late adolescence to early adulthood (ages 17 to 23 years). The factor structure of the EFs was similar across waves, but in Wave 2, there was significant nonshared environmental variance for Common EF at the latent variable level, which was not true of Wave 1. Common EF was the only factor with a cross-wave correlation significantly lower than 1.0. Genetic analyses indicated that for the Common EF variable, stability was due to genetic influences, and change was due to new nonshared environmental influences. For the Updating-Specific variable, stability was due to genetic influences, and there was no significant change. Finally, for the Shifting-Specific variable, stability was due primarily to genetic influences but also to a small extent to nonshared environmental influences, and change was not significant.

These results are consistent with the existing literature on stability and change in cognitive ability, which suggests that most stability is genetic and change is environmental (Lyons et al., 2009; Tucker-Drob & Briley, 2014). Our results augment this literature by covering an understudied interval, examining EF latent variables, and examining stability and change within a multiple-component, unity/diversity framework.

Unity and Diversity Components of EF

The use of a unity/diversity framework (Miyake & Friedman, 2012) to examine stability and change provides a new perspective on the development of EFs, and may also provide some insight into what mechanisms may be changing the most during this late stage of development. When we examined the latent constructs of Inhibiting, Updating, and Shifting (correlated factors), we saw considerable stability, but none of the three EF factors could be collapsed across waves. This result suggests that all three EFs showed some change. However, because these EFs are correlated, this analysis could not really inform us as to whether the change in each variable reflected the same variance. Repartitioning the variance into that common to these three EFs and that unique to Updating and Shifting suggested that the change was primarily occurring in the common (unity) portion of the model.

We have proposed that Common EF may reflect individual differences in the ability to actively maintain goals and use them to bias lower-level processing (Herd et al., 2014; Miyake & Friedman, 2012). This proposal is consistent with other characterizations of executive and frontal lobe functioning (Miller & Cohen, 2001). Moreover, some accounts have conceptualized inhibitory control as a by-product of such goal maintenance (e.g., Munakata et al., 2011), a view that is consistent with the lack of inhibiting-specific variance that we observed at both waves and in other samples (Miyake & Friedman, 2012). Active goal maintenance is usually attributed to the prefrontal cortex, which works together with numerous cortical and subcortical areas during executive control (Miller & Cohen, 2001; Stoet & Snyder, 2009). Though the general structures that support this ability are in place relatively early in childhood, adult performance is distinguished from adolescent and childhood performance by more efficient use of this existing circuitry (Luna et al., 2001; 2004; Scherf et al., 2006). This refinement of existing circuitry could explain the pattern of better mean performance that others have observed (e.g., De Luca et al., 2003), combined with the high stability we observed.

In contrast to these Common EF mechanisms, we have proposed that the Updating-Specific factor may tap individual differences in working memory gating (subserved by the basal ganglia) and long-term memory retrieval, whereas the Shifting-Specific factor may reflect individual differences in flexibility –– specifically, the ease of replacing no longer relevant goal information (Herd et al., 2014). The results of the current study suggest that these factors, though differentially influenced by environment (i.e., the Updating-Specific shows no environmental variance whereas the Shifting-Specific factor shows robust nonshared environmental variance), are both stable in terms of individual differences during this period.

Environmental Change

Despite the marked stability across this 6-year time period, we did find some evidence for change due to new nonshared environmental influences on Common EF at Wave 2. Though small, this new environmental variance is notable because Common EF showed a striking lack of environmental influences at Wave 1 (Friedman et al., 2008, 2011). Thus, the presence of such influences at Wave 2 represents a change in the genetic and environmental structure and, importantly, evidence of increased impact of the environment on individual differences in EF.

What specific environmental factors might this new variance reflect? As mentioned earlier, most individuals experience considerable life changes during this transition (Arnett, 2000), including changes to residence, education, social and employment roles, and also changes in behaviors like substance use. These new contexts and stressors could be reasonably expected to introduce some new environmental influences on EFs. It will be important to explore whether measured differences between twins in behavior and/or experiences can account for this variance.

Such an exploration is beyond the scope of the current study, in part because we suspect that environmental variance reflects numerous different influences that additively (and potentially nonadditively) combine. It has been notoriously difficult to account for nonshared environmental variance with specific measured variables (see Turkheimer & Waldron, 2000), despite the fact that nonshared environment, estimated as a statistical component with family studies, accounts for large amounts of variance in childhood outcomes (Plomin & Daniels, 1987). One explanation is that a number of different environments are important, but any one only accounts for a small fraction of variance (Plomin, Asbury, & Dunn, 2001). That is, nonshared environment might be highly poly-environmental, just as genetic effects on cognitive ability seem to be highly polygenic.

If so, it may take a somewhat extensive program of research to fully account for the nonshared environmental variance we identified for Wave 2 Common EF. However, we believe that this variance is "real" (i.e., not just measurement error), because it emerged at the latent level. Had we found this result only at the individual task level, it could represent task-specific effects, changes to the tasks that we intentionally made, and/or measurement error. The fact that we found this result at the latent level suggests that these influences are affecting all nine tasks in the same direction, ruling out task-specific effects and measurement error.

Genetic Stability

Although the environmental influences on Wave 2 Common EF were notable because they were absent at Wave 1, they only accounted for a small fraction of the overall variance. Genetic influences dominated individual differences in all three EFs and accounted for all of the stability in the Common EF and Updating-Specific factors, and 85% of the stability in the Shifting-Specific factor. Thus, understanding individual differences in these EFs may depend on understanding the specific genetic variants that relate to these performance differences.

To date, very little genetic variance in EF tasks has been accounted for with measured genotypes that reach genome-wide significance. It appears that genetic variance in behavioral traits reflects highly polygenic effects, with each measured polymorphism accounting for only a small fraction of one percent of the overall variance (see, e.g., Davies et al., 2011). These small effects sizes have meant that gene hunting necessitates much larger samples (that can only be achieved by combining datasets) than originally hoped. Indeed, the largest genome-wide association study of EF tasks to date (Ibrahim-Verbaas et al., 2015), with discovery sample sizes up to greater than 13,000 subjects, yielded no genome-wide significant hits for any EF measure.

However, some promising results have been obtained with larger samples of general cognitive ability data. Fortunately, there is moderate genetic overlap between general cognitive ability or IQ and the Common EF and Updating-Specific factors (Friedman et al., 2008), so it makes sense to test genome-wide significant hits for IQ as candidate genes in smaller samples with EF data. Several such candidate regions were suggested in a recent genome-wide analysis study (Davies et al., 2015) of general cognitive function in approximately 54,000 middle-aged and older adults, which found 13 significant single-nucleotide polymorphisms (SNPs). Because this study focused on older adults, some of these SNPs (such as those associated with Alzheimer's dementia and non-pathological cognitive aging) may be specific to later ages (indeed, one of the effects was correlated with age). Other SNPs, in genes associated with brain development and neurological function, may be associated with stable variance across adulthood.

While recognizing that our data suggest that identifying genes for EF ability is important, we also caution that high heritability does not mean that environmental influences do not or could not have large influences on EF abilities. One possibility that may be particularly important in this context is that environmental influences for EF are difficult to detect because they are correlated with genetic propensities. Gene-environment correlations (rGE; Plomin, DeFries, & Loehlin, 1977) can occur in multiple ways (e.g., individuals who have high EF seek out activities that practice and improve those abilities, or benefit more from such activities when they happen to experience them). In these scenarios, some of this environmental variance would actually be included in the genetic estimate, as it would not be separable from the genetic variance. These rGEs may be important to consider not because they would inflate our estimates of heritability (one could argue that genes are the ultimate cause of these environmental influences, and so this variance actually does belong in the genetic estimate; Plomin et al.; 1977), but because they have important implications for future research on environmental influences and interventions. In particular, if the high heritability and stability we observed for EFs reflects substantial rGEs , it may be productive to search for environments that are genetically correlated with EFs in addition to controlling for genetic influences by focusing on nonshared environments.

Limitations

Though our modification of the tasks for the Wave 2 tests was strategic, it can be considered a limitation of the current study. We were thoughtful about the changes so that individual differences at the latent level would not reflect new cognitive processes required at Wave 2. However, although we think it unlikely, it is possible that the changes to the individual tasks did somehow manifest at the latent level to contribute to the new environmental variance we observed. It is also possible that instability might arise from measurement variance (i.e., different factor loadings across waves), though if so, we might expect to see this show up in multiple factors rather than only in the common factor as we observed.

The new environmental variance in the Common EF factor may reflect transient factors such as motivation or fatigue, rather than more long-term environmental effects. If so, we likely should have seen such influences at Wave 1 as well, which involved a similar testing situation, but we did not. Of course, it is possible that such factors have genetic influences, and so would contribute to the genetic variance.

Conclusions

The finding of new variance for the Common EF factor in early adulthood suggests that this component, which we have found is associated with a number of important behaviors (Friedman et al., 2007, 2011; Miyake & Friedman, 2012; Young et al., 2009), shows some change, despite the prevalent assumption that cognitive abilities stabilize in adolescence. It also demonstrates the principle that high heritability does not imply immutability: Despite the nearly 100% heritability observed at Wave 1, we saw evidence for change at Wave 2. Important future directions are to investigate what specific genetic influences lead to the high stability of EFs, and what new environmental influences have significant effects on Common EF in adulthood, both of which may provide some insight into the underlying mechanisms.