An algorithm for synchronizing a clock when the data are received over a network with an unstable delay

Abstract

A method is presented for synchronizing the time of a clock to a remote time standard when the channel connecting the two has significant delay variation that can be described only statistically. The method compares the Allan deviation of the channel fluctuations to the free-running stability of the local clock, and computes the optimum interval between requests based on one of three selectable requirements: (1) choosing the highest possible accuracy, (2) choosing the best tradeoff of cost vs. accuracy, or (3) minimizing the number of requests to realize a specific accuracy. Once the interval between requests is chosen, the final step is to steer the local clock based on the received data. A typical adjustment algorithm, which supports both the statistical considerations based on the Allan deviation comparison and the timely detection of errors is included as an example.

I. Introduction

The Time and Frequency Division of the National Institute of Standards and Technology (NIST) operates public servers that are connected to the Internet and that respond to requests for time in a number of different formats. See [1] for a list. The two-way message protocol plays a central role in the operation of these servers – the servers that are not located at one of the NIST time and frequency laboratories in Colorado are synchronized to UTC(NIST) by the use of a two-way message exchange over telephone lines, and the delay in the network link between the public clients and these servers is also estimated by using a two-way protocol. (The telephone-line connection and the network messages are based on different data formats, but they share the common feature of estimating the one-way time delay between the transmitter and the receiver as one-half of the measured round-trip delay. The details of this method are described below.) In both cases, the goal is to synchronize the time of the clock in a client system to the time of a remote server. The design of the synchronization process depends on statistical estimates of the characteristics of both the client system and the network that links it to the remote reference, with a goal of realizing a system that incorporates the best properties of both contributions and therefore has better overall statistical properties than either the network or the local clock taken separately. The Allan variance plays a central role in this estimation process, and I will describe this role in the next sections. The focus is on the usefulness of the Allan variance in this application, and the discussion is not intended to be a complete survey of the various synchronization algorithms and message formats that could be used for this purpose. Although there is no detailed discussion of these possibilities, the general statistical considerations that are discussed below do not depend on the detailed contents of the messages that are exchanged between the client and the server to implement the synchronization process.

The public time servers operated by NIST act as clients with respect to the time scale that realizes UTC(NIST), and they simultaneously act as servers with respect to the systems that send them requests for time. The client and server modes are realized by separate, distinct processes that are completely independent and are linked only through the system clock; the client process adjusts the system clock based on a message exchange with the atomic clock ensemble in Boulder, and the server process uses the system clock to construct the replies to queries from remote systems. This separation simplifies the design of each process, which can be optimized based on the statistics of the corresponding channel. In addition, although the time server is simultaneously a client with respect to the NIST time scale and a server with respect to public users, these two roles do not interact with each other and the following discussion would apply to either of them. A discussion of the overall synchronization pyramid between the NIST atomic clock ensemble and the final client system would generally be realized by several synchronization segments and is outside of the scope of this discussion.

An optimum synchronization algorithm will combine the statistics of the local clock with the characteristics of the network link. The goal is to realize a combination that is better than either component by itself. The method is based on the two-sample Allan deviation [2] to characterize both the stochastic variations in the frequency of the clock in the client, (the local clock), and the variation in the two-way estimate of the network delay. In most cases, the stochastic variations in the remote reference clock are small enough to be ignored relative to the other contributions. From this perspective, the intent is that the Allan deviation of the synchronized clock should be better than the Allan deviation of both the free-running local oscillator and the link to the remote reference time.

In general, the use of the Allan deviation to characterize the frequency of the local clock oscillator is quite successful in modeling its stochastic behavior; the network delay is more difficult to characterize in this way, especially when the connection is implemented over a packet-switched network such as the Internet, because it is generally not stationary, so that no statistical estimator can fully describe its behavior. In addition, the Allan deviation characterizes the RMS stability of a system, and the statistic provides no information on the system accuracy. The Allan deviation is also not sensitive to a constant offset in frequency. This is generally not a serious limitation because this offset is estimated and removed by the steering algorithm. Also, it does not provide any insight into the worst-case measurement, so that it must be combined with a non-statistical method for handling outliers. Any method for handling outliers is outside of a statistical description by definition and is therefore always somewhat subjective.

The first step is to describe the basic operation of the two-way message exchange between a client system that requests the time and a remote server. The client and the server are linked by a telephone connection or a network such as a local area network or the Internet. An important aspect of the discussion will be estimating the time difference between the client and the server in the presence of stochastic variations in the characteristics of the network link. The discussion will only briefly consider the much simpler configuration in which the reference clock is local and is connected directly to the client system or where it is not local but is connected by a channel that has a negligible stochastic variation in its delay.

II. THE TWO-WAY METHOD

The fundamental two-way method treats the two systems that use it as equal partners in the message exchange. In principle, either partner can initiate the message exchange or both can transmit asynchronously. In practice, digital networks are generally configured in a client-server mode; one system always initiates the exchange and the other responds. The remote client generally initiates the conversation in packet-switched networks, while the exchange between the NIST time servers and the clock ensemble that realizes UTC(NIST) is initiated from the NIST-clock-ensemble end of the connection. There can be subtle differences between these two implementations, as will be discussed below. The following discussion will use a client-server model in which the client initiates the conversation, because this is the configuration that is most commonly used for digital time transfer. However, the basic method would be unchanged if the roles of the client and the server were interchanged.

The client initiates the conversation by sending a request to the server at time t₁ as measured by its local clock. The message is received by the server when its time is t₂ and it sends a reply at time t₃, where both of these times are measured by the clock on the server. The response reaches the client at time t₄ as measured by its clock. The round-trip travel time is given by

$$\mathrm{\Delta }=(t_4-t_1)-(t_3-t_2)$$ (1)

where the first term is the total elapsed time for the round-trip message exchange as measured by the client and the second term is the time delay in the server, as measured by its clock, between when it received the request and when it responded. The method assumes that the one-way transmission delay, d, is the same in both directions, so that the one-way delay in either direction is given by

$$d=\frac{\mathrm{\Delta }}{2}$$ (2)

The time difference between the client and the server is,

$$T_{cs}=(t_1+d)-t_2,$$ (3)

where the first term on the right-hand side is the time of the client when the outbound message was received by the server, and the second term is the time of the server at that instant. A positive value implies that the client system time is fast with respect to the time of the server. Substituting eq. 1 into eq. 2 and then eq. 2 into eq. 3, the time difference between the client and the server is given by

$$T_{cs}=\frac{t_1-t_2}{2}+\frac{t_4-t_3}{2}.$$ (4)

The two-way message exchange described by the preceding equations is asynchronous, and can be initiated at any time.

The link between the NIST time servers and the atomic clock ensemble that realizes UTC(NIST) operates “backwards” – the interface to the clock ensemble, which is acting in the role of the server, initiates the conversation. The message exchange is synchronous – the server transmits one message per second, and advances the transmission time (relative to the time stamp in the message) so that the on-time marker in the message will arrive at the client system on time. The advance in the transmission time is computed from the round-trip delay measurement, so that the client system must participate in the two-way message exchange, but need not do any calculations. The advance computed by the server is included in each message. In addition, when the NIST time servers act as clients to the NIST clock ensemble, the software is configured so that there is a negligible delay between when a message was received and when the reply was sent back to the application linked to the atomic clock ensemble. That is, t₂=t₃=t_s. This is an important design constraint in the client software because the server linked to the atomic clock ensemble assumes that it is true. With this simplification, eq. 4 becomes

$$T_{cs}=\frac{t_1+t_4}{2}-t_s.$$ (5)

A. Limitations Of The Two-Way Method

The accuracy of the two-way method depends on the validity of the assumption that the path delay is symmetric, and eq. 4 and eq. 5 incorporate this assumption explicitly. If the delay is not symmetric then the outbound delay between the client and the server is given by

$$d=k\mathrm{\Delta }$$ (6)

where 0 ≤ k ≤ 1. The outbound delay is greater than the delay in the reverse direction when k > 0.5, and the opposite is true when k < 0.5. The two-way method calculates the time difference by substituting eq. 2 into eq. 3, but, when the path delay is not symmetric, the actual time difference should use eq. 6 instead of eq. 2. The difference between the true time difference and the value calculated on the assumption that the path is symmetric is given by

$$\epsilon =((t_1+k\mathrm{\Delta })-t_2)-((t_1+0.5\mathrm{\Delta })-t_2).$$ (7)

$$\epsilon =(k-0.5)\mathrm{\Delta }$$

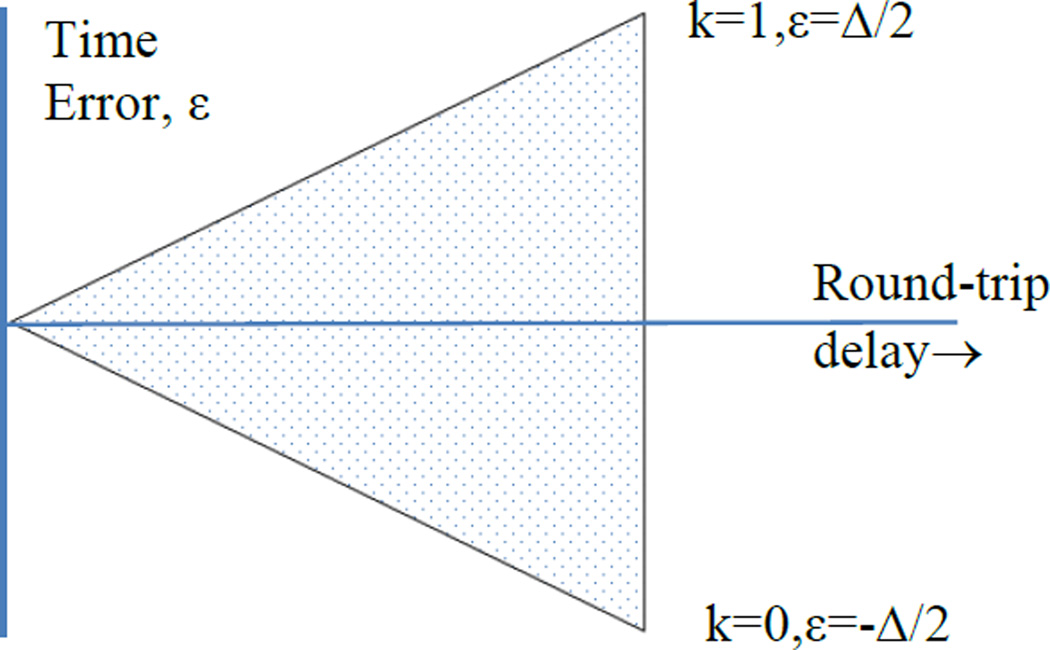
Eq. 7 shows that the maximum possible error due to a path asymmetry is given by ±0.5Δ, so that a path with a smaller round-trip delay is guaranteed to have a smaller maximum possible error. This point is illustrated in fig. 1.

Fig. 1.

The error in the time difference, ε, computed by the use of the two-way message exchange as a function of the measured round-trip delay, Δ. The maximum error is bounded by the two lines with slopes of +0.5Δ and −0.5Δ as described in the text. The x and y axes are in identical but arbitrary units.

In general, the time difference computed with the two-way method has two correlated unknowns: the time difference, T_cs and the asymmetry parameter, k, and the correlation is removed by simply assuming that k=0. Although there is no way of detecting a constant asymmetry, which introduces a constant bias into all of the time differences, it is often possible to estimate and remove the stochastic variability of the asymmetry, as discussed below.

It is often the case that the stability of the oscillators in both the client and the server over a relatively short time interval is much better than the stability of the network delay or its asymmetry over the same interval. This is almost always the case for sufficiently short intervals because in many systems the local oscillator and the process that requests the system time and uses it to estimate the time difference both have small white phase noise that is much smaller than the transfer noise. Therefore, the time differences computed from the data in several closely-spaced messages should have the same value because the stochastic frequency fluctuations of the oscillator result in only a small time dispersion over the short interval. With this assumption, any variation in the computed time difference between consecutive, rapid measurements must have been caused by a change in the asymmetry parameter, since the time difference of the physical devices has not changed and the round-trip path delay has been estimated and its effect has been removed. The “rapid” interval between measurements is defined by the assumption that the time dispersion of the clocks in the client and the server are both negligible relative to the stochastic behavior of the network link over the same interval. The validity of this assumption can be evaluated by noting that the rapidly-measured time differences do or do not correlate with changes in the measured round-trip delay. If a strong positive or negative correlation is detected then the change in the measured round-trip delay is probably largely a change in the symmetry of the delay, because the total round-trip delay itself has been measured and its effect has been removed on the assumption that the asymmetry is zero. This is the general situation with the telephone links between the NIST time servers and the reference time scale.

If there is a significant variation in the measured time differences but no significant variation in consecutive measurements of the round-trip delay or if the variation in the round-trip delay measurements does not correlate with the variation in the measured time differences then the situation is ambiguous. It can result from a change in the symmetry of the round-trip delay, especially if the change in symmetry did not significantly change the overall round-trip delay. One possible cause, especially if the system is heavily loaded or if it supports a graphical user interface, is that the values of t₂ and t₃ do not represent the actual times at which the message was received and the reply sent, respectively. (If the link is to the NIST time scale, the analogous problem is that the assumption that t₂=t₃ does not describe the actual situation.) This is discussed below in more detail. Another possible cause is that the variation in the time differences is caused by a time step or by a real variation in the frequency of the local clock. In other words, the assumption that the stochastic variations in the true time difference is much smaller than the variation in the network delay is not true. There is no unique way of dealing with this situation. The three possibilities are (1) the time-differences should be accepted because the variation in the measured time differences results from low-probability events that conform to the statistical model; (2) the values should not be accepted because the variation results from a one-time glitch; (3) the values should be accepted and they indicate that the model of the clock behavior should be revised. The revision would include either a change to the estimate of the deterministic frequency offset of the client oscillator, a change to the magnitude of the stochastic parameter or both.

The NIST servers use assumption (1) for variations that are less than or equal to twice the assumed statistical noise parameter. They use assumption (3) for variations that are between two and three times the statistical noise parameter and assumption (2) for larger variations. A one-time glitch is the most common reason for the problem, and this assumption is validated when the measured time difference returns to a normal value on a subsequent measurement cycle. Subsequent time differences will continue to have problems if there is a change in the underlying deterministic frequency value or a change in the magnitude of the stochastic parameter. The incremental differences between the expected and measured time differences will tend to have the same value if there has been a change in the deterministic frequency of the client oscillator, and this will not be true if the stochastic amplitude has changed.

The success of models based on the Allan deviation (or on any other statistical estimator, for that matter) depend on the fact that glitches are relatively rare events. If this is not the case, then it is probable that the data are not stationary, and a statistical analysis may not be appropriate in this situation. In some cases, it is possible to use a time-varying Allan deviation to model the data or by “pre-whitening” the data by removing a non-stationary contribution such as a diurnal effect. Diurnal (or nearly diurnal) contributions often occur for message exchanges that use the Internet or when the frequency of the oscillator in the client system has a significant admittance to temperature variations.

B. Advantages Of The Two-Way Method

Even when the path delay has a static asymmetry, the two-way method can be useful in attenuating the resulting time error. For example, suppose that the round-trip delay is measured as 1 s, but the outbound and inbound delays are 0.6 s and 0.4 s, respectively; therefore k=0.6/1= 0.6. The cause of this static asymmetry is not important. The asymmetry can be caused by a distributed inbound-outbound difference in delays or by a completely symmetric network coupled to a piece that is essentially completely asymmetric because it has a much greater delay in one direction than in the other one. The difference between these two path delays is 0.2 s, but from eq. 6 we see that the error in the estimate of the time difference is only 0.1 s. The application of the two-way method has reduced the impact of the static time asymmetry by a factor of 2. The error with no correction at all would have been much larger, of course.

If the round-trip delay due to the completely symmetric portion of a connection is 0.8 s, and a completely asymmetric outbound segment adds a variable delay, δ, the measured round-trip delay is 0.8+δ and the outbound delay is 0.4+δ. The value of k is given by

$$k=\frac{d}{\mathrm{\Delta }}=\frac{0.4+\delta }{0.8+\delta }.$$ (8)

From eq. 7, the error due to this asymmetry is

$$\epsilon =(k-0.5)\mathrm{\Delta }=0.5\delta .$$ (9)

The time error caused by the variable asymmetry has been attenuated by a factor of 2 – the same result as for a static asymmetry. The statistics of the measurement process would be degraded by only one-half of the varying asymmetry.

If it is recognized that the asymmetric portion of the delay is confined to a single segment of the network path, the asymmetric portion might be moved outside of the two-way measurement loop in an attempt to improve the statistics of the synchronization process. As I will discuss, this may not improve the accuracy of the actual time transfer.

To see this, suppose that the two-way protocol was implemented as a user process on a system, and both the jitter and the asymmetric contribution to the delay were caused by a variable latency in the response time of the operating system to a request for a time stamp by this process. Then the statistics of the process that controls the system clock could be improved by implementing it as a low-level process within the operating system instead of as a normal user process. The jitter and the variable asymmetric portion of the delay are no longer in the measurement loop, and the statistics of the measurement process have improved. In this simple model where there are no other noise sources and the delay in the path has become completely symmetric, the errors in the measurement process have been reduced to zero. However, the user process still sees the variable latency in the response of the operating system to a request for a time stamp, and this variable latency is no longer attenuated. In this situation, improving the apparent statistics of the process that measures the time difference of the client clock actually makes things worse, by a factor of 2, from the perspective of a user application running on the same system if that application requests time stamps from the kernel.

The lesson of the preceding discussion is clear: the process that controls the system time and the process that uses the time should run at the same level – either both should be user processes or both should run as low-level processes in the kernel of the operating system. The second configuration, in which the application runs as a low-level process in the kernel of the operating system, makes it difficult to change the application that uses the system time, so that synchronizing a computer clock by means of a low-level process may not be optimum from the perspective of a user application that will use the time. The magnitude of this problem depends on the jitter and latency within the operating system, and can be significant if the system is heavily loaded, if it supports a graphical user interface with a large number of open windows, or if it supports a process like a web server that presents an inherently asymmetric load to the network interface.

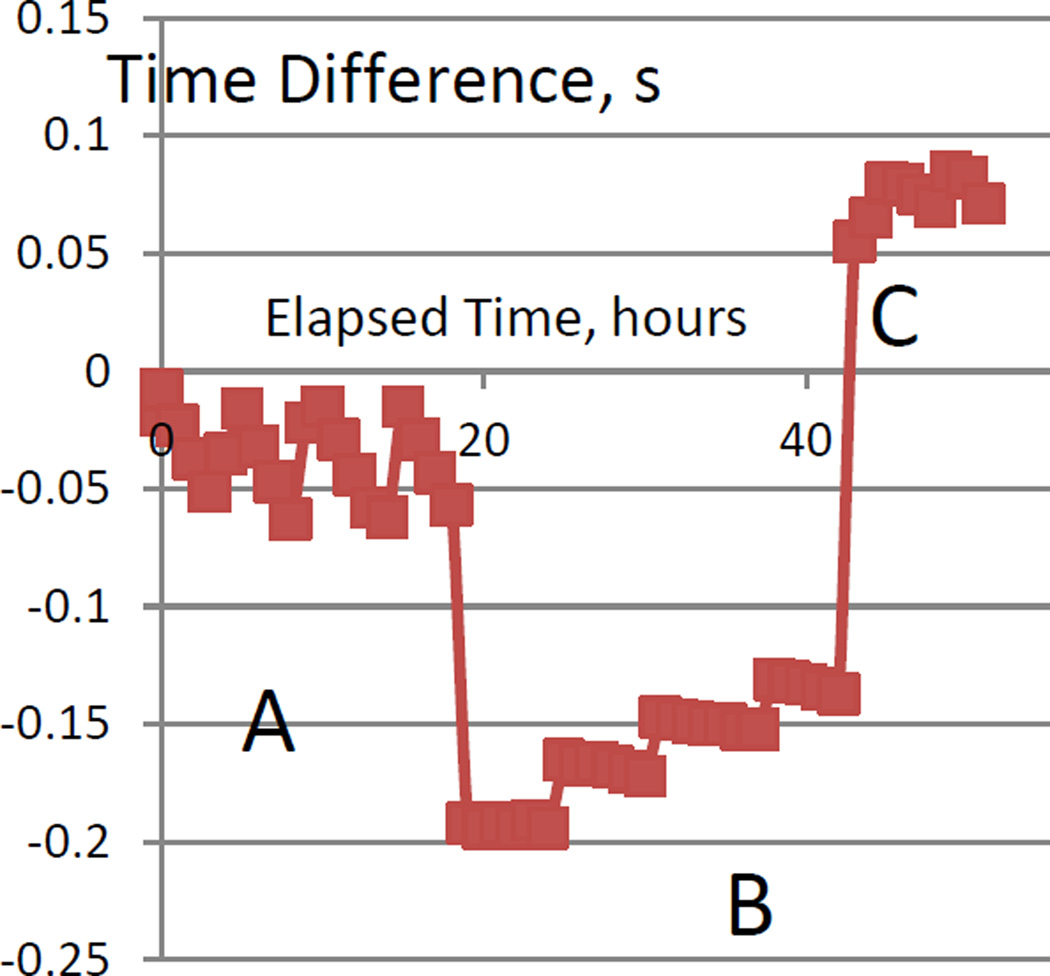
The results of a series of experiments designed to demonstrate the potential magnitude of this problem are shown in fig. 2.

Fig. 2.

The time difference, in seconds, as a function of elapsed time, in hours, between a computer configured with a common operating system that includes a graphical interface and a NIST time server located on an adjacent subnet of a Class B network. The data identified as “A” (the first 20 hours of the data set) were acquired when the client computer had no other processes running; The data identified as “B” (from hour 21 to hour 42) were acquired when the client computer had a simulated asymmetric network load, and the data identified as “C” (from hour 43 to the end of the measurements) were acquired when the network segment that linked the client computer also had a heavy load. An overall rate offset has been removed. The significance is discussed in the text.

The figure shows the hourly time differences between a PC with a common operating system that includes a graphical user interface and a NIST time server located (in an adjacent room) on a different subnet of the Class B network of the University of Colorado. The time differences were acquired by means of the two-way Network Time Protocol (NTP) format as described in the preceding text. The clock in the client system was not adjusted, and a constant rate offset has been removed from all of the data to make the variation easier to display.

The data segment identified as “A” in the figure (the first 19 hours of the experiment) was acquired when the system had only the NTP client process running, which is as close to a single-user environment as is possible in that kind of system. The data exhibit a quasi-periodic variation with an amplitude of about 50 ms peak-to-peak and a period of about 5 hours. This variation is caused by an unknown combination of the varying asymmetry of the network link, the fluctuations in the frequency of the oscillator that drives the clock in the client system, and any variation in the time-dependent background processes that are part of the operating system.

In the data segment identified as “B” in the figure, a second user process that presented a very asymmetric load to the operating system was added starting at hour 20. The intent was to simulate the effect of a process that provided web service. This additional process introduced an immediate time step with an amplitude of approximately −150 ms, caused by a change to the static asymmetry within the operating system. There is also a change in average frequency offset relative to the previous segment and smaller time steps. The time steps would be particularly difficult to deal with in an actual synchronization process. A time step that is confined to a single measurement is treated as an outlier and ignored; the persistent time steps in the figure would be taken as real, but only after some delay that would verify that they were not single-point outliers.

In the data segment identified as “C” in the figure, another system was added to the local network segment at hour 43. This additional system increased the load on the local network, which increased both the delay and its asymmetry. This resulted in another immediate time step and another change in the average rate relative to the previous segment.

These results confirm the previous discussion that it can be quite difficult for a user-level application to realize accurate millisecond-level timing in a computer system of this type, and that there can be a significant asymmetry in the time delay in the network link and in the kernel of the operating system. There may be no easy fix for this problem.

III. SYNCHRONIZING THE CLIENT SYSTEM CLOCK

The two-way message protocol can be used to synchronize a client clock to a remote time reference. Configurations where the reference clock is directly connected to the system or when it is connected by a channel that has negligible stochastic delay variations do not require any complex analysis because the effective stability of the reference clock is so much better than the local system time. The simple strategy in these configurations is to use the time of the reference clock either directly by tightly coupling the local clock to the reference time. The free-running frequency stability of the local clock becomes irrelevant in this configuration, and the local clock will follow the remote reference unconditionally.

A configuration when the channel to the reference clock has significant stochastic variation in its delay or in its symmetry is more complex; this is the usual situation when the channel is realized by means of telephone circuits, a local packet network, or the Internet. The goal of the synchronization process is to improve both the accuracy and the stability of the client clock. The improvement in the accuracy depends on the validity of the assumption that the delay is symmetrical on the average, and that the asymmetry in the delay is small for every message. The requirement that the delay is symmetrical on the average is needed to guarantee that the average of a sequence of round-trip delay measurements can be used to compute an accurate estimate of the one-way delay. The magnitude of the delay is not important. The requirement that the asymmetry in the delay is small for every message is needed to improve the probability that only a relatively small number of round-trip delay measurements is needed to obtain an accurate estimate of the one-way delay. When these conditions are satisfied, the measured channel delay can be divided into two contributions: a symmetric, noiseless physical delay, and a stochastic contribution that has a mean of zero for relatively short time intervals. The average of the delay over a relatively small number of time-difference measurements converges to the true noiseless value in this case.

Asymmetric delays are much more difficult to deal with. It is generally not possible to detect a constant asymmetry or one that has a very long-period variation unless the time difference computed from the message exchange can be compared to data acquired via an independent channel. Therefore, a static asymmetry will compromise the accuracy of the synchronization process, but will not impair the stability. As a practical matter, it can be difficult to estimate a static or nearly-static slowly varying asymmetry in the presence of a large stochastic variation in the delay estimate.

To improve the stability of the client clock, the time dispersion that results from the frequency variations of the local oscillator and the fluctuations in the process that requests the time from the operating system must be separated from the apparent fluctuations in the measured time differences due to the stochastic variation in the reference device and the channel that links the two systems. The method will degrade the stability of the local clock if it adjusts its time or frequency based on these latter time differences – the local clock would have been more stable if it had been left alone. In most cases, this variation can be attributed solely to the network because the native stability of the remote reference system is very small compared to the instability of the channel delay. This is always true if the reference device is linked to the atomic clock ensemble of a National Metrology Institute or timing laboratory and the channel is implemented by means of a packet network such as the Internet or the telephone system.

A. Characterizing the clock stability

The first step in the separation of variance described in the previous paragraph is to estimate the free-running stability of the clock in the client system. The standard two-sample Allan deviation is used to evaluate the synchronization process; the more complicated relatives of the simple variance (Mod AVAR, TVAR, ToTvar, …) [3][4] include an averaging of the time-difference data in the computation, and this averaging is generally not incorporated into the synchronization process. The simple two-sample Allan variance, on the other hand, is closer to how the time-difference data are actually used in the synchronization algorithm.

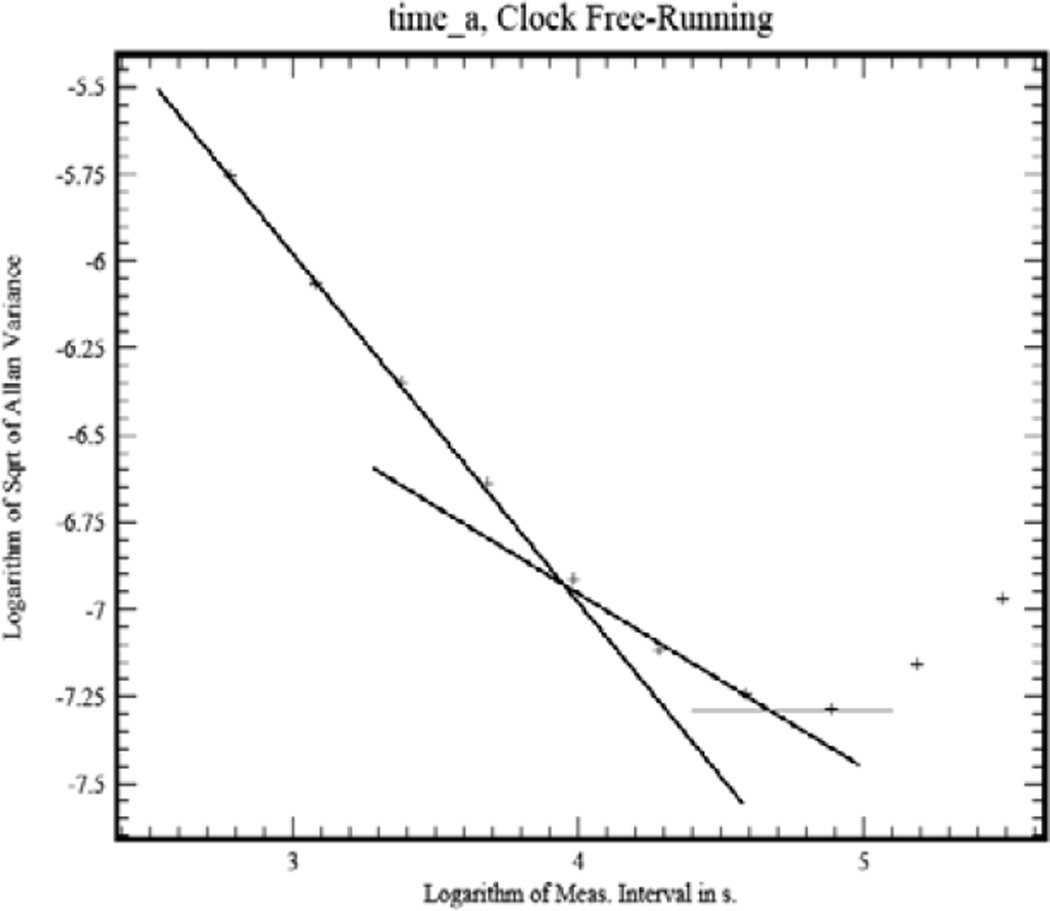
Fig. 3 shows a log-log display of the two-sample Allan deviation for the clock oscillator in a typical general-purpose computer system. The points in the figure were computed by using an external atomic clock to generate a system interrupt every second and then reading the system time on every interrupt. This procedure evaluates the oscillator as it is seen by a user process. The system under test did not use a graphical user interface, and the measurement process was started from the command line. It was the only user process running on the system during the evaluation. The statistics of the bare physical oscillator are not observable. The latency of the measurement process itself was tested and found to be on the order of a few microseconds, which is negligible in this configuration.

Fig. 3.

The two-sample Allan deviation (square root of the Allan Variance) of the free-running stability of the clock in a typical general-purpose computer. The points are the measured time-difference values and the straight lines help to identify the underlying noise types as described in the text. The arrows near the bottom of the figure at averaging time of about 50 000 seconds and 1 day, identify the range of averaging times that maximize the benefit to cost ratio as described in the text.

The three straight lines in the figure help to identify the noise processes that are important for different averaging time domains. For averaging times, τ, less than about 10⁴ s, the Allan deviation, σ_y(τ), is approximately 0.0011/τ; it is approximately 1.1×10⁻⁵/√τ for averaging times between 10⁴ s and 5×10⁴ s and approximately 5×10−⁸ for averaging times between 5×10⁴ s and 1 day. The Allan deviation increases as a power of the averaging time for times greater than 1 day, but synchronization algorithms generally do not operate in this region, so that the behavior there is not important. The time dispersion resulting from this frequency noise is approximately given by τ × σ_y(τ); the magnitude of the time dispersion is a few milliseconds for any averaging time less than about 1 day (10⁵ s). For comparison, the deterministic frequency offset for this device is about 2.5 s/day – almost a factor of 500 times larger than the stochastic time variation. The large difference between deterministic and stochastic frequency contributions is true for many types of oscillators.

There is some variability among different computer models, and even among different computers of the same model. The variability is most significant at shorter averaging times. The best system that was tested (evaluated in the same as described above) had a short-term stability of 8.9×10⁻⁵/τ – significantly better than the more typical system described above. However, its performance at longer averaging times was about a factor of 3 worse than the values quoted above. The transition between the 1/τ and 1/√τ dependence occurs at an averaging time of about 100 s. The minimum value of the Allan deviation is about the same as for the previous device, so that this device would also have a stochastic time dispersion of only a few milliseconds for any averaging time less than about 1 day. The deterministic frequency offset for this device was about 4 s/day. As above, the deterministic frequency offset is much larger than the stochastic variation.

The measured stability at the shortest averaging times includes the jitter and latency in the communication between the user process and the operating system. This is only a few microseconds in the configuration used for the tests, but it could be significant if the system were heavily loaded. It would be possible to realize greater time stability by moving the measurement process into the operating system kernel. Unfortunately, this may not be of much help to a user-level process that depends on the system clock, which is why this configuration has not exploited for these evaluations.

The noise process at averaging times less than about 10⁴ s is approximately white phase noise, so that the Allan deviation in fig. 3 implies a time dispersion of approximately 0.0011/√3 = 0.64 ms independent of the averaging time. A more conservative estimate would be about 1 ms. It would be possible to improve this time dispersion by averaging consecutive time-difference measurements, but the improvement that could result from averaging would probably not be available to a process that associated a time stamp to a single non-recurring event. Averaging consecutive measurements is never optimum from a cost/benefit perspective, since the cost increases linearly with the number of measurements that are included in the average, while the standard deviation of the average improves only as the square root of that number.

B. Characterizing The Channel Delay

The second step in the design of a synchronization algorithm is to estimate the statistical characteristics of the data channel back to the reference clock. The discussion is limited to the situation where the communications channel that links the client to the server has a symmetrical delay on the average, but both the delay and its asymmetry vary in time. A static asymmetry generally cannot be detected or removed.

The variations in the channel delay are characterized by means of the Allan variance formalism; this result is compared with the free-running stability of the local oscillator as shown in fig. 3, and the averaging time is set to the point at which the variance of the remote clock seen through the noisy channel is more stable than the performance of the local clock oscillator.

The method can be illustrated by considering the statistics of the telephone connections that are used to link the NIST time servers to the atomic clock ensemble [5][6]. A typical connection lasts about 30 s, and the statistics of these connections can be characterized as white phase noise for the duration of the connection, with the exception of the first few seconds during which the line delay is stabilizing. The magnitude of the Allan deviation for these data was approximately 3×10⁻³/τ. Comparing this value with the values shown in fig. 3, the measurements show that at short times the NIST atomic clock ensemble as seen through the telephone line was noisier than the stability of the local clock oscillator, and the stability of the local oscillator would be degraded if the interval between calibration queries was too short.

The telephone link will be less stable than the local clock oscillator for all times in the 1/τ domain, since both contributions vary as the same function of the averaging time in this domain. The two noise contributions will be equal when

$$\frac{3\times {10}^{-3}}{\tau }=\frac{1.1\times {10}^{-5}}{\sqrt{\tau }}$$

$$\tau ~74000s$$ (10)

and the remote reference clock seen through the communication channel will be more stable for all averaging times greater than this value. The performance of the synchronization algorithm is now defined: the stability of the local clock will be determined by its free-running stability for averaging times less than the value in eq. 10, and will be given by the stability of the reference clock as seen through the telephone line for longer periods. The longer period divergence in the free-running stability of the client clock for averaging times greater than one day has been removed and the overall stability is better than either contribution.

To express this result in more general terms, consider the somewhat idealized situation where the statistics of the local clock are dominated by white frequency noise with no appreciable white phase noise (due to measurement jitter, for example), and where the statistics of the remote clock and the channel can be characterized as simple white phase noise with no glitches, periodic delay variation, or any of the other problems that can occur with real channels. In that case, the Allan deviation of the local clock as a function of averaging time can be characterized as

$${\sigma }_y^L(\tau )=\frac{L}{\sqrt{\tau }},$$ (11)

where L is the magnitude of the Allan deviation for the local clock. The Allan deviation of the remote reference clock as seen through the channel can be characterized as

$${\sigma }_y^R(\tau )=\frac{R}{\tau },$$ (12)

where R is the magnitude of the channel deviation. If we combine eq. 11 and eq. 12, the averaging time at which the cross-over occurs is

$$\tau ={\left(\frac{R}{L}\right)}^2.$$ (13)

The counter-intuitive result is that decreasing the averaging time does not improve the stability of the local clock because the free-running stability of the local clock is corrupted by noise from the channel connection to the remote reference. In fact, the optimum averaging time or polling interval should be increased as the channel becomes less stable. As a practical consequence of this result, a clock synchronized by means of messages transmitted over the wide-area Internet should almost always have a longer polling interval and averaging time than the same clock synchronized by means of messages transmitted over a local, more stable network.[7] Most synchronization algorithms use much shorter averaging times in this situation, suggesting that they probably introduce network noise into the local clock oscillator.

The algorithm that is used to synchronize the NIST public NTP servers [7][8] is based on these considerations, with the averaging time of the clock control loop decoupled from the polling interval as I discuss in the following paragraphs. The control loops in the NIST time servers average five consecutive one-second time differences, so that the effective value of R is improved by a factor of somewhat more than two with respect to the value that is characteristic of a single one-second measurement. However, the averaging time is much longer and is set based on the considerations I discussed in the previous paragraphs with this improved value of R.

The model for the statistics of the local clock is reasonable if it does not have a graphical user interface, is not heavily loaded, and does not support a web service. However, real channels, especially those that communicate using the public Internet, tend to have larger jitter in the asymmetry than would be predicted from eq. 12. A channel may also have longer-period symmetry variations, especially at diurnal or near-diurnal periods. These problems will increase the value of the estimate of the two-sample Allan deviation over the value predicted by eq. 12, and will tend to require even longer averaging times than would be predicted from eq. 13.

On the other hand, the averaging time should be decreased as the channel becomes more stable, and there will come a point where the analysis of the previous paragraphs no longer works. With the Allan deviation shown in fig. 3, this point will occur when the averaging time computed above drops below 10⁴ s. The Allan deviation of the local clock changes to a 1/τ dependence in this case. The remote and local clocks have the same dependence on averaging time in the simple model discussed above, and the ratio of the two Allan deviations becomes independent of averaging time. The time differences are completely characterized by white phase noise in this domain, and the variance of the time differences can be improved by decreasing the polling interval and averaging more and more measurements. The variance of the time differences will improve as the reciprocal of the number of measurements that contribute to the average. In the limit of an extremely short polling interval, the remote clock seen through the channel is always more stable than the local clock, and the local clock is simply locked to the remote time differences. The time dispersion of the local clock can be made arbitrarily small on a stable, quiet network or when the reference clock is a locally-connected device that is linked to the system by a method that has negligible measurement noise. The tight coupling of the local system to the remote clock drives the estimate of the effective offset frequency of the local clock to zero, since the rapid polling interval results in the time dispersion due to the frequency becoming negligible relative to the white phase noise of the measurement process. Therefore, although the time stability of the local clock is improved, we no longer have any information at all about the static frequency offset of the local clock oscillator or the characteristics of its stability. The time accuracy of the local clock will be rapidly compromised if the reference signal is lost since we can no longer flywheel on its previously estimated offset frequency. This very rapid polling interval is an acceptable solution if the goal is to have the local and remote clocks on the same time without regard to whether this time is or is not correct and if the reliability of the data stream from the remote clock is not a significant concern.

These two situations suggest two different synchronization strategies. In the more common situation described by eqs. 11, 12, and 13, the cross-over between the stabilities of the remote and local devices will always occur in the white frequency noise domain of the local clock, so that the optimum strategy will be based on averaging the frequency of the local clock and using the average to drive the time dispersion to zero. [8] On the other hand, when the dominant noise source is white phase noise, the optimum strategy will be based on averaging the time difference directly. This latter situation would be appropriate for a directly-connected reference clock or one that is remote and linked by a channel with a very stable delay.[9] These stable delays can be realized when the link is implemented by a physical circuit that has no packet-switching elements or if these elements are present but the propagation delays through them are measured by special-purpose “boundary clock” hardware. See, for example, the description of the IEEE 1588 standard, commonly referred to as the Precise Time Protocol (PTP) [10].

IV. Cost – Benefit Analysis

Consider the situation where the object is to adjust the interval between queries so as to maximize the Benefit/Cost ratio of the synchronization process. This might be an appropriate analysis when it was expensive to query the remote server, and the goal is to minimize the cost by minimizing the number of such queries. If the cost of a single query (measured in units of network bandwidth, computer cycles, …) is C, then the total cost of synchronizing the clock for a time T seconds with messages every τ seconds is proportional to the number of messages that will be transmitted in time T, and is given by

$$\mathit{\text{Cost}}=C\frac{T}{\tau }.$$ (14)

The benefit will be proportional to the reciprocal the time deviation computed from the Allan deviation of the process – a smaller Allan deviation implying a greater benefit. The benefit is approximated by

$$\mathit{\text{Benefit}}=B\frac{1}{\tau {\sigma }_y(\tau )}$$ (15)

where B is a proportionality constant. The goal is then to maximize the ratio of Benefit and Cost per second, which is given by Cost/T

$$\frac{\mathit{\text{Benefit}}}{\mathit{\text{Cost}}}=\frac{B}{C}\frac{1}{{\sigma }_y(\tau )}.$$ (16)

The Allan deviation can be modeled as a power, k, of the averaging time, so that

$${\sigma }_y(\tau )=S{\tau }^k$$

$$\frac{\mathit{\text{Benefit}}}{\mathit{\text{Cost}}}=\frac{B}{CS}{\tau }^{-k}.$$ (17)

The fraction on the right-hand side of eq. 17 is a constant that is a characteristic of the stability of the clock and the characteristics of the network link, so that the benefit/cost ratio continues to improve as long as the polling interval between queries is increased and parameter k, the slope of the Allan deviation, remains negative. In this domain the cost is decreasing faster than the stability is degrading. From fig. 3, the optimum averaging time from this perspective is between about 50 000 s and 1 day. The Benefit/Cost ratio starts to degrade at averaging times longer than about 1 day. The cost would continue to decrease as the reciprocal of the averaging time for longer averaging times, but the stability degrades more rapidly, so that the benefit/cost ratio becomes less favorable. However, these longer averaging times might possibly still be acceptable if only modest timing accuracy was required.[11]

For example, consider the last point in the free-running stability statistic show in fig. 3. The measurement interval for that data point is approximately 10^5.5 s or about 88 hours. If a clock had been set on time and on frequency at the start of the interval, its time dispersion after 88 hours would be approximately given by τ×σ_y(τ)=10^−6.95+5.5 =0.035 s. A practical algorithm would not use a polling interval this long because it would not provide a timely detection of outliers or other problems; the actual polling interval would be driven by concerns about outliers and errors and not by considerations of statistical stability, but a polling interval this long might be appropriate for a system that was connected to a network only occasionally.

V. CLOCK ADJUSTMENT AND ERROR CORRECTION

The intervals between calibration queries derived in the preceding sections were based on statistical considerations and were generally quite long – at least several thousand seconds and possible even longer. This has the disadvantage that an error in the local clock may persist for some time before it is detected and removed. A timely detection of errors would require a much shorter polling interval, but the time-difference data acquired in this way should not be used to discipline the local clock directly without some method of detecting and removing outliers if the optimum statistical performance is to be maintained. For the purposes of error detection, the interval between calibration requests is set as a compromise between shorter polling intervals, which would provide more rapid response to time errors, and longer polling intervals, which would be less expensive in terms of connection charges and computer cycles. Time errors in the system clock are relatively rare events, whereas problems with the stability of the network link to the remote server are much more common. Therefore, it is important to process the measurements with an algorithm that detects and ignores outliers.

A. Kalman Algorithms

Determining the optimum clock adjustment based on a time-difference measurement is difficult because the problem is fundamentally under-determined. The variance in the measured time differences must be apportioned among the deterministic and stochastic parameters of both the clock and the network and there is no unique way of doing this without some ancillary information. The deterministic parameters are not known a priori, and must be estimated from the data. A Kalman algorithm [12] is an example of a method that provides the statistical machinery to calculate the clock correction and to estimate the evolution of the model parameters.

The algorithm requires initial estimates of the variances and co-variances of the stochastic parameters of the clock and the network, and these are often derived from the Allan variance of the each contribution separately. The statistical characteristics of the network are particularly difficult to specify because the stochastic variation in the network delay is often not stationary so that it cannot be described by a statistical variance, and this is one of the primary weaknesses of the Kalman method. A related weakness is that Kalman algorithms generally do not have a robust method for detecting and ignoring outliers, which do not conform to the assumed statistical model by definition. A Kalman algorithm for estimating the stochastic performance of clocks is in [12].

On each cycle, the algorithm combines the current time-difference measurement with the value expected based on the previous solution, the deterministic parameters of the clock model, and the elapsed time since the last calculation. The outputs of the calculation are updated values of the various deterministic and stochastic parameters.

In addition to the difficulty of specifying the statistical characteristics of the network in a format that can be used by a Kalman algorithm, the calculation is rather involved, and is difficult to implement on a very busy time server. Therefore, we have used the simpler algorithm to be described in the next section.

B. Averaging and Exponential Filters

The basic assumption of the simpler averaging algorithms is that it is possible to choose a polling interval in which the measurements are dominated by a single stationary random process with a white spectrum. With this simplification, the parameter that has the white spectrum can be averaged for a time interval determined by the range of validity of the spectrum characteristic. The two common choices are a polling interval where the measurements are dominated by white phase noise and an interval where the dominant contribution is white frequency noise. The time difference can be averaged in the first domain and the frequency in the second one. Instead of a specific moving average of the appropriate parameter over the domain of validity, it is easier to use an exponential filter, with a time constant determined from the variance, which determines the averaging time, and the polling interval.

If the optimum averaging time, computed using the statistical considerations discussed above, is T, and if the interval between time-difference measurements is a shorter interval, Δt, then the dimensionless constant, κ is defined as

$$\kappa =\frac{T}{\mathrm{\Delta }t}.$$ (18)

The estimate of the control parameter, P, at time jΔt, is computed as a running average based on the computed value of P at the previous time and the value estimated from the current measurement, p:

$$P_j=\frac{\kappa P_{j-1}+p}{\kappa +1}.$$ (19)

In the time domain, Eq. 19 is equivalent to a running average of κ measurements [13]. From the Fourier analysis perspective, eq. 19 is a low-pass filter with unity gain at a Fourier frequency of zero and a roll-off at higher Fourier frequencies determined by 1/κΔt.

The client algorithm of the NIST time serves operate in the white-frequency-noise domain, so that the control parameter, P, is the estimate of the frequency offset of the client clock. The frequency control loop uses κ equal to 3 or 4. The analogous running average of the time differences would be appropriate if the control loop is operating in the domain where white phase noise dominates the noise spectrum. The value of κ would be chosen based on the considerations discussed above, and would generally be of order 10 when the channel between the client and the server is realized with a connection through the public Internet. As discussed in [11], the value of κ would be chosen dynamically based on a real-time estimate of the Allan deviation of the channel between the client and the server.

A better choice is to use two averaging domains with two exponential filters – a rapid polling interval where the noise spectrum is white phase noise and the output estimate is the average time difference, and a longer interval in the white frequency domain where these time differences are averaged again to estimate the optimum average frequency.

VI. SUMMARY

The Allan deviation has been applied to the design of methods for synchronizing computer clocks by the use of data transmitted over digital networks. The strategy is to design a synchronization algorithm so that the resulting time has the best characteristics of the local clock and the remote clock seen through the communications channel. In the simplest case where the cost of calibrations is not an issue and where the overall synchronization process can be characterized by white phase noise for all averaging times, then the optimum strategy is simply to query the remote server as rapidly as possible and average the time differences. This configuration will have poor hold-over performance if the link to the reference is lost, and is generally limited to a directly-connected reference time source.

In general, some combination of determining the average time difference in the white phase noise domain combined with determining the average frequency in the (generally longer) white frequency noise domain provides the best balance between accuracy and hold-over performance. Finally, the Allan deviation has been applied to estimating the optimum benefit/cost ratio of a synchronization algorithm, which would be appropriate when querying the remote system is expensive in terms of computer cycles, network bandwidth or some other parameter.

In applications where only modest stability is required, the Allan deviation of the free-running system clock could be used to calculate an increased interval between queries to the server so as to realize this requirement. This would be particularly useful in systems that are only occasionally connected to a network that can communicate with a time server.

Biography

Judah Levine is a Fellow of the National Institute of Standards and Technology and is the leader of the Network Synchronization Project in the Time and Frequency Division, located in Boulder, Colorado. Dr. Levine is responsible for the design and implementation of the time scales AT1 and UTC(NIST), which provide the reference signals for all of the NIST time and frequency services. In addition, he designed and built the servers that support the Automated Computer Time Service (ACTS) and the Internet Time Service, which provide time and frequency information in a number of different digital formats. These services receive about 15500 million requests per day. He received his Ph.D. in Physics from New York University in 1966. Dr. Levine is a member of the IEEE and a Fellow of the American Physical Society.