Automated assessment of hemodynamics in the conjunctival microvasculature network

Abstract

The conjunctival microcirculation is accessible for direct visualization and quantitative assessment of microvascular hemodynamic properties. Currently available methods to assess hemodynamics in the conjunctival microvasculature use manual or semi-automated algorithms, which can be inefficient for application to a large number of microvessels within the microvascular network. We present an automated image analysis method for measurements of diameter and blood velocity in microvessels. The method was applied to conjunctival microcirculation images acquired in 15 healthy human subjects. Frangi filtering, thresholding, and morphological closing were applied to automatically segment microvessels, while variance filtering was used to detect blood flow. Diameter and blood velocity were measured in arterioles and venules within the conjunctival microvascular network, and blood flow and wall shear rate were calculated. Repeatability and validity of hemodynamic measurements were established. The automated image analysis method allows reliable, rapid and quantitative assessment of hemodynamics in the conjunctival microvascular network and can be potentially applied to microcirculation images of other tissues.

I. Introduction

The bulbar conjunctiva is a densely vascularized tissue covering the sclera of the eye. It is one of a limited number of locations in the human body where red blood cell movement within the microcirculation can be directly and non-invasively visualized. Due to this characteristic, the conjunctival microcirculation has been utilized to assess microvascular alterations due to systemic disorders, such as sickle cell disease [1]–[4], Alzheimer’s disease [5], hypertension [6], hypotension [7], and diabetes mellitus [8], [9]. Furthermore, previous studies have found correlations between conjunctival microvascular hemodynamics and cerebral blood flow in dogs [10], and alterations in the conjunctival microcirculation in subjects with unilateral stroke [11] and during internal carotid artery surgery [12]. Hence, quantification of conjunctival microvasculature hemodynamics may be of value for evaluating microvascular alterations in other tissues of the body.

Several commercial instruments designed for evaluation of the retinal circulation have been modified for assessment of hemodynamic properties of the conjunctival microvasculature, including the Heidelberg Retinal Flowmeter [13] and Retinal Functional Imager [14]. However, these instruments do not provide absolute measurements of retinal blood flow [13] or evaluate vessel caliber [14]. Other techniques such as Orthogonal Polarization Spectral Imaging [15], slit lamp biomicroscopy [16]–[18], and intravital microscopy [3], [19] utilize semi-automated image analysis algorithms to measure blood velocity and diameter of microvessels, but require selection of vessels of interest, which may be subjective and time consuming.

Due to the large number of microvessels and physiologic variability of blood flow in the conjunctival microvascular network, there is a need for an automated image analysis method to comprehensively and quantitatively assess hemodynamics. Recently, a study evaluating the number of vessels required to reliably characterize the hemodynamic properties of the conjunctival microvasculature was published, reporting the need to obtain measurements in more than 15 venules [20]. In the current study, a fully automated algorithm is reported that provides a comprehensive hemodynamic assessment of the conjunctival microvascular network.

II. Methods

A. Subjects

The research study was approved by an Institutional Review Board of the University of Illinois at Chicago. Prior to subject enrollment, the research study was explained to the subjects, and informed consents were obtained according to the tenets of the Declaration of Helsinki. Conjunctival microcirculation imaging was performed in 15 healthy subjects (age; 61 ± 11 years) who did not have a history of ocular or systemic diseases. Data was obtained from one eye of each subject (11 right and 4 left eyes). To assess measurement repeatability, in a separate group of 5 healthy subjects, repeated imaging was performed in one conjunctival region. During imaging, subjects were seated with their head stabilized with a chin and forehead support. An external fixation target was presented to the subjects to minimize eye movement and allow acquisition of images at several conjunctival regions temporal to the limbus.

B. Image Acquisition

Images of the conjunctival microcirculation were acquired with the use of our previously described non-contact optical imaging system (EyeFlow) [16]. EyeFlow was comprised of a slit lamp biomicroscope and a digital charged coupled device camera (Prosilica GT, AVT, Exton, PA) to capture image sequences of red blood cell movement within the conjunctival microcirculation. Several 1-second image sequences were acquired at a rate of 50 frames per second and an exposure of 20 ms. Each image consisted of 1360 × 550 pixels and each pixel was 1.25 µm on the object plane. The magnification of the system was 5.1× and the active camera sensor size was 8.8 mm × 6.6 mm (6.45 µm pixel size). The fill factor and quantum efficiency (at the imaging wavelength of 540 nm) were 100% and approximately 50%, respectively.

C. Image Processing and Analysis

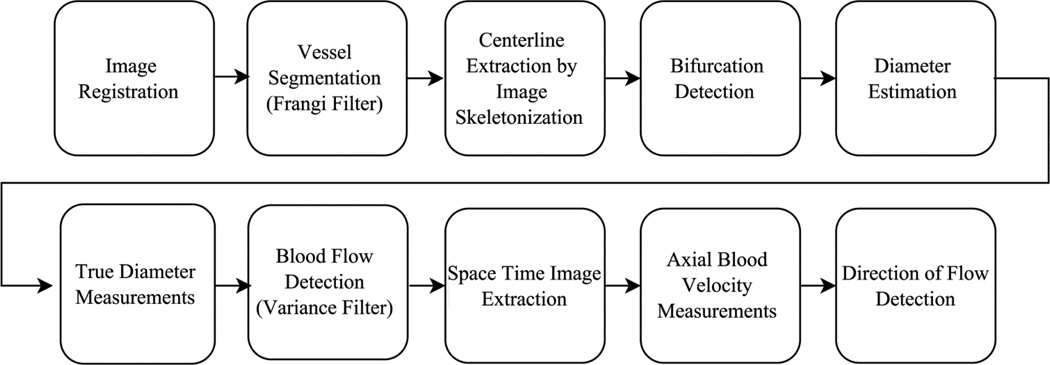
The automated technique for hemodynamic assessment of the conjunctival microvascular network consisted of several image processing steps, as depicted in the flow chart of Fig. 1. Briefly, the automated approach consisted of image registration for correction of eye movement, image segmentation to identify vessels, centerline extraction and bifurcation detection to define centerlines of individual vessel segments, diameter measurement, detection of blood flow, and measurement of axial blood velocity. All image processing and analysis algorithms were developed in Matlab (Release 2014a, MathWorks, Inc., Natick, MA, USA) with image processing toolbox version 9.0. Further detail on the analysis steps is provided below.

Fig. 1.

Flow chart depicting steps for automated image registration, vessel segmentation and hemodynamic measurements of the conjunctival microvasculature network.

D. Image Registration

Image sequences were processed to remove frames corresponding to blinks and correct for eye movement by image registration. Image frames were first examined for the presence of saturated pixels, which were removed by automated cropping of the image frames to the largest rectangular area with non-saturated pixels. For each image, a sharpness score was quantified by calculating the average magnitude of the horizontal and vertical intensity gradients, which were calculated by determining pixel-to-pixel intensity changes. To eliminate frames with insufficient sharpness due to blinks and rapid eye motion, the longest consecutive series of image frames that had sharpness scores above a threshold were extracted. This threshold was computed for each image sequence as the mean minus half the standard deviation of the sharpness scores. A reference frame was then assigned based on the highest sharpness score and the remaining frames were automatically registered to this frame by translation using the Matlab function imregister. This intensity-based image registration function uses an optimization algorithm to find the best transform to align two images. The minimum and maximum numbers of consecutive automatically registered image frames were 6 and 40, respectively.

E. Vessel Segmentation

Vessel segmentation was performed using Frangi filtering on the time-averaged image generated from the registered images. This filtering method involved computing eigenvalues of the Hessian matrix over multiple image scales (blur levels) for the detection of vessel-like structures within the image, as previously described [21]. Briefly, a vesselness measure (V_o) was derived for each pixel based on the normalized and sorted eigenvalues (λ₁ and λ₂) of the Hessian matrix computed over multiple image scales (σ) as shown in (1):

$$V_0(\sigma )=\{\begin{array}{cc}\hfill 0\hfill & \hfill \mathit{\text{if }}{\lambda }_2>0\hfill \\ \hfill \mathit{\text{exp }}(-\frac{R_B^2(\sigma )}{2{\beta }^2})\hfill & \hfill (1-\mathit{\text{exp }}(-\frac{S^2(\sigma )}{2C^2}\left)\right)\hfill \end{array}$$ (1)

where R_B (σ) = λ₁ (σ) / λ₂ (σ), S(σ) = (λ₁ (σ) + λ₂ (σ))^0.5, and β and C were constants set to the value of 1. A vesselness image was then generated by assigning the maximum vesselness measure over the image scales to each pixel, as indicated in (2).

$$V_0={\mathit{\text{MAX}}}_{{\sigma }_{\mathit{\text{min}}}\le \sigma {\le }_{\mathit{\text{max}}}}\{V_0(\sigma )\}$$ (2)

To eliminate user interaction, the minimum (σ_min) and maximum (σ_max) image scales were set to 1 and 7, respectively. To increase computation efficiency, σ varied between σ_min and σ_max using only odd values. By varying σ in steps of 2 rather than 1, the computation time for Frangi filtering was reduced by approximately a factor of 2. The vesselness image was then binarized using an empirically derived threshold value of 0.1, thereby providing segmentation of the conjunctival vessels. This binary image was further processed by counting the number of connected pixels in each binary object and removing objects smaller than 50 pixels in size. To fill holes in the vessels and smooth edges, a single step morphological closing operation was also performed using a disk shape structuring element with a radius of 4 pixels.

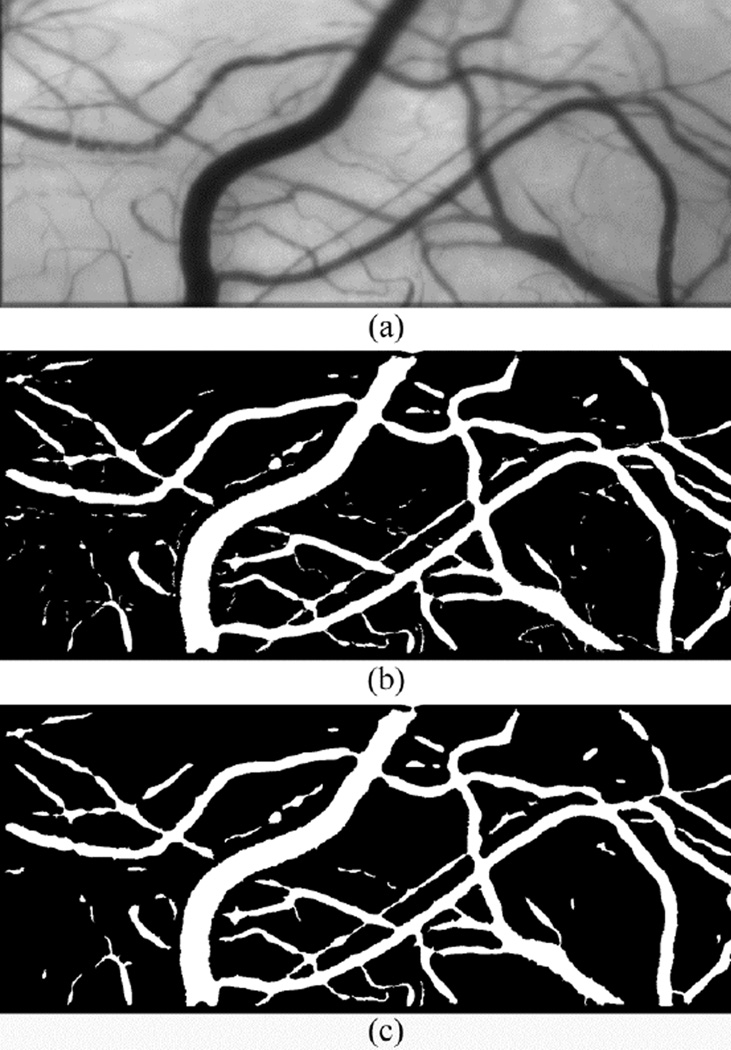
An example of a mean conjunctival microcirculation image, derived by averaging 12 registered images is shown in Fig. 2(a). Vessel segmentation results obtained by Frangi filtering using a threshold of 0.1 and the minimum and maximum image scales of 1 and 7, respectively, are shown in Fig. 2(b). The final binary image after removing small objects and morphological closing is shown in Fig. 2(c). As shown in Fig. 2, Frangi filtering was able to detect small and large caliber microvessels of the conjunctival microvasculature.

Fig. 2.

(a) Mean conjunctival microcirculation image generated by averaging consecutive registered image frames; (b) Vessel segmentation by Frangi filtering of the mean image. (c) After removing small objects and a morphological closing operation.

F. Centerline Extraction and Bifurcation Detection

To extract centerlines and detect bifurcations of the vessel segments, several steps were performed. An iterative morphological thinning algorithm [22] was used to create a skeleton image by shrinking the segmented vessels to single lines corresponding to the centerlines of the vessel segments. Small spurs created during the thinning procedure were removed by determining the number of connected neighbor pixels in a 3 × 3 kernel for each pixel in the centerline. The spurs were removed by repeatedly (20 times) eliminating pixels that only had one connected neighbor, thereby removing spurs less than 20 pixels in length. A value of 20 pixels was selected since this is approximately equal to the radius of the largest conjunctival vessels, and the length of spurs should not exceed the radius of the vessels. Intersection points of the vessel centerlines at crossovers and bifurcations were detected to obtain the centerlines associated with each vessel segment. The intersection points were found by first performing convolution of the skeleton image with a 3 × 3 unity kernel, then multiplying the result by the skeleton image and detecting pixel locations that had a value greater than three [23]. Finally, centerlines of the vessel segments were labeled automatically based on the number of connected pixels of each centerline. The lengths of the vessel segments were between 21 and 1078 pixels.

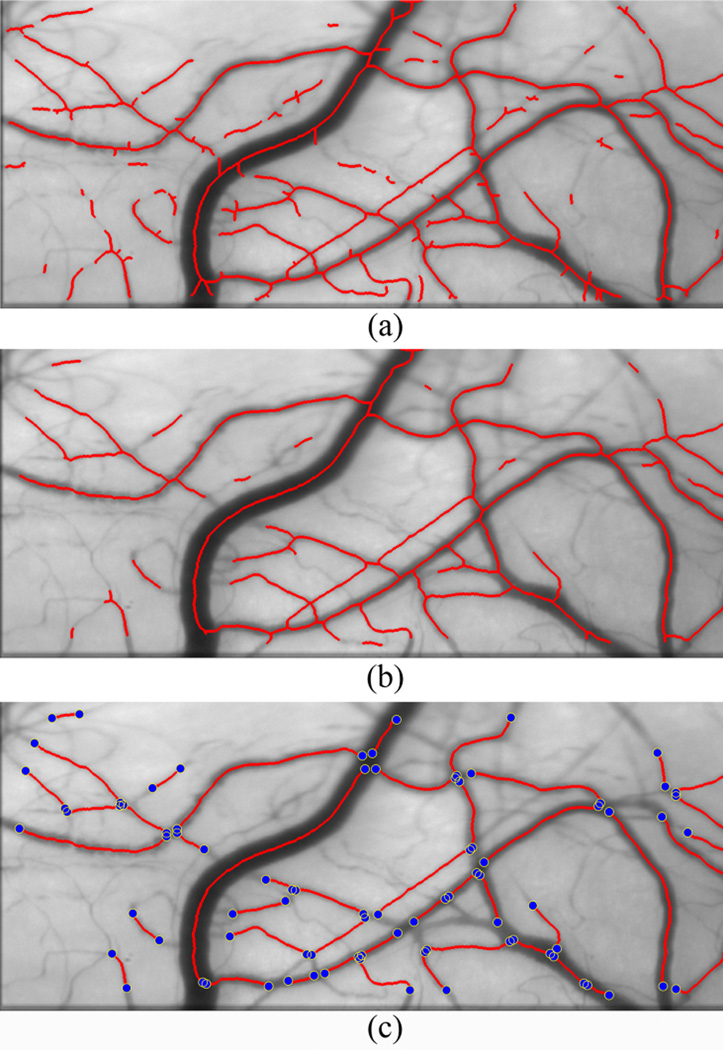
Images of the conjunctival microcirculation displaying the detected centerlines after morphological thinning and spur removal are shown in Fig. 3(a) and Fig. 3(b), respectively. Vessel intersection and bifurcation points are displayed in Fig. 3(c). In this example, 45 vessel segments in the conjunctival network were identified after centerline extraction and bifurcation detection. Hemodynamic properties of the vessel segments were then evaluated individually, as described below.

Fig. 3.

Conjunctival microcirculation image displaying detected centerlines after (a) morphological thinning (b) spur removal (c) detection of bifurcations and intersection points (blue dots).

G. Diameter Measurement

Diameter (D) and boundaries of vessel segments were automatically determined by calculating the full width at half maximum (FWHM) of intensity profiles of lines perpendicular to the vessel centerline, as previously described [24]. For each vessel segment, the length of the perpendicular lines were set to three times an approximated vessel diameter value, which ensured the perpendicular lines extended beyond the vessel walls by 1 diameter length in both directions. The approximated vessel diameter was determined by plotting 3 perpendicular lines with a length of 80 pixels (~ 100 microns) at three equally spaced points along each vessel centerline on final binary image. The perpendicular lines were established automatically by calculating the line normal to the centerline direction, which was determined based on linear regression of 5 local vessel centerline points. The perpendicular line was computed by the negative inverse of the slope of the best fit regression line. The number of pixels (length) on the 3 perpendicular lines within the vessel segment on the binary image were counted using Bresenham algorithm [25], then averaged to approximate the vessel diameter. To determine the true vessel diameter and vessel boundaries, intensity profiles of lines perpendicular to the vessel centerline were established by averaging intensity data every 5 pixels (~ 6 microns) along the centerline on the mean registered image. This spacing was empirically determined to reduce noise in the profiles but allow sufficient number of measurements along the vessel length, thereby increasing the reliability of diameter measurements. FWHMs were calculated using a previously described method [16] thereby determining the vessel diameter. Vessel diameter measurements were then averaged to generate a mean D for each vessel segment.

H. Blood Flow Detection

Variance filtering was performed on each vessel segment in the registered image sequence to identify vessels that had detectable blood flow. In general, vessels with detectable blood flow had centerline pixels with large temporal variance due to the motion of red blood cells as compared to surrounding tissue. To evaluate the local temporal variation, the standard deviation (SD) of intensity for each pixel along the centerline was computed as a function of time over which the registered images were acquired. These values were then averaged to calculate the mean SD of intensity values along the vessel segment (μ_vessel). Similarly, the mean SD of intensity values of non-vessel pixels (μ_background) was computed over time with the exclusion of vessel pixels detected by Frangi filtering. The standard deviation of the SD values (σ_background) were computed to determine a threshold value (Th_background = μ_background − σ_background). Vessel segments with a μ_vessel greater than Th_background were considered to have detectable blood flow and were included for axial blood velocity measurement.

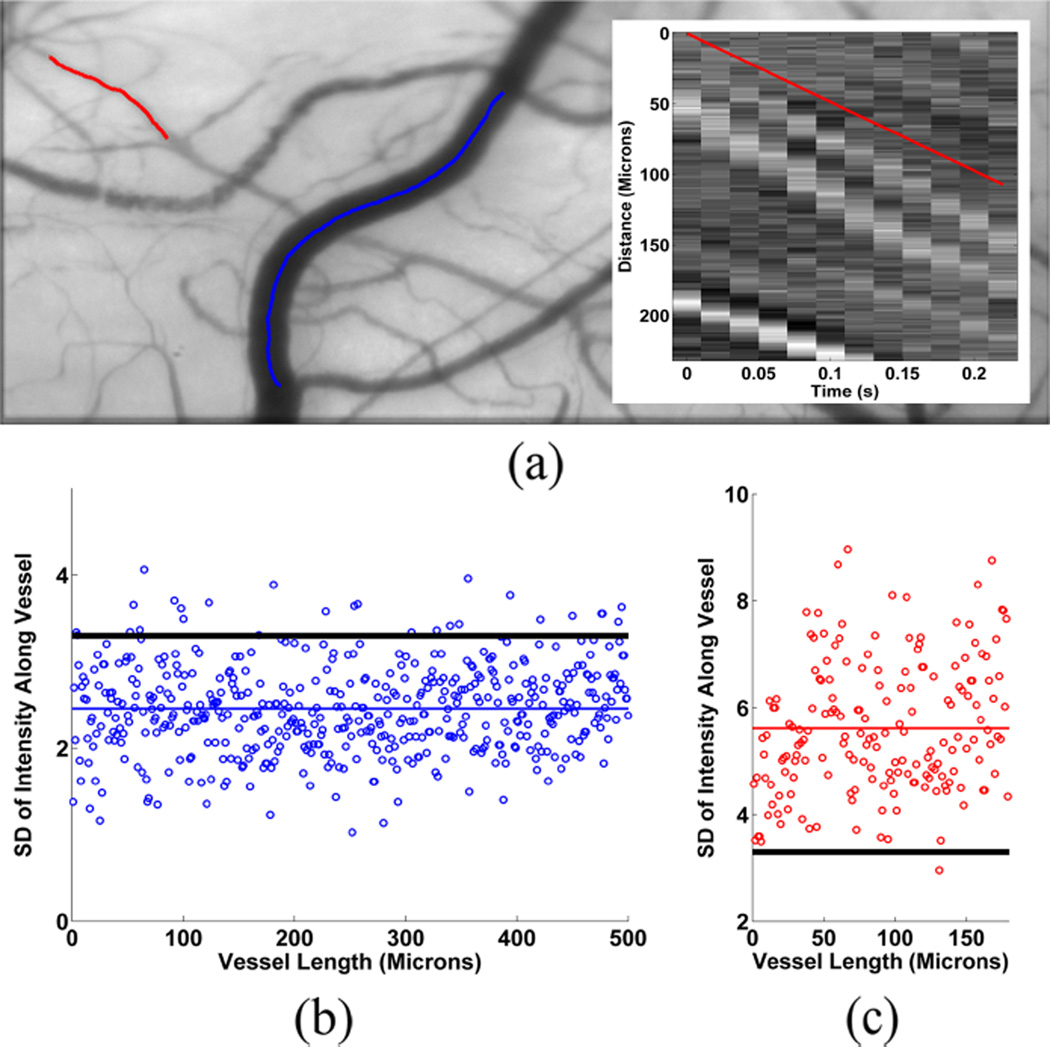
Fig. 4(a) displays an example of a conjunctival microcirculation image with two selected vessel segments. Fig. 4(b) shows the SD of intensity values plotted as a function of length for the vessel indicated by the blue centerline. In this vessel, μ_vessel was lower than Th_background, indicating the lack of discernable blood flow. In contrast, Fig. 4(c) shows the SD of intensity values plotted as a function of length for the vessel indicated by the red centerline. The mean SD (μ_vessel) exceeded Th_background, indicating detectable blood flow.

Fig. 4.

(a) Conjunctival microcirculation image displaying the centerlines of two selected vessel segments. (b) SD of intensity values plotted as a function of length for the vessel indicated by the blue centerline. Mean SD (μ_vessel) (blue horizontal line) is lower than the threshold (Th_background) (black horizontal line), indicating the lack of discernable blood flow. (c) SD of intensity values plotted as a function of length for the vessel indicated by the red centerline. Mean SD (μ_vessel) (red horizontal line) is greater than the threshold (Th_background) (black horizontal line), indicating detectable blood flow. Fig 4 (a) Insert: Spatial-temporal image (STI) generated for the vessel segment indicated by the red centerline. The red line superimposed on the STI displays the calculated slope based on the prominent bands in the STI.

I. Axial Velocity Measurement/Direction of flow

Axial blood velocity (V) was measured in each vessel segment by tracking the motion of red blood cells along the centerline in consecutive registered image frames. Tracking was performed by creating a spatial-temporal image (STI) that displayed the intensity variation along the length of the vessel segment as a function of time. Axial blood velocity was derived by determining the slope of the prominent bands in the STI which was automatically determined by 1D cross-correlation between intensity data in the columns of the STI image. For pairs of columns in the STI, 1D cross-correlation was performed, and the shift in position of the aggregated red blood cells between columns (RBC_shift) was estimated based on the maximum of the cross correlation, as shown in (3):

$$RB{C}_{\mathit{\text{shift}}}=\mathit{\text{argmax}}\{(f*g)(i)\}$$ (3)

where * denotes the cross-correlation operator, f and g are the intensity signals along the vessel centerline in two adjacent columns of the STI, and i indicates the lag in position of one intensity signal with respect to the other. The slope of the STI (velocity) was obtained by averaging the RBC_shift values derived from the column pairs, then dividing by the time increment (20 ms) between image frames. A line with the calculated slope was superimposed on the STI for visual verification by the user. An example of a STI for one vessel segment is shown as an insert in Fig. 4(a).

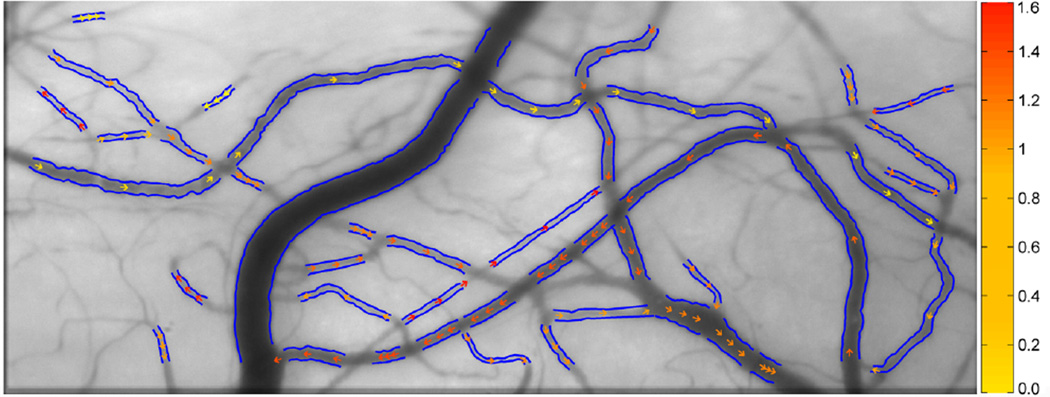
Blood flow (Q) and wall shear rate (WSR) were computed based on D and V measurements using formulas previously published by Koutsiaris et al. [17]. Flow direction in each vessel segment was determined based on the sign of the slope of the prominent bands in the space time images. Fig. 5 displays an example of vessel diameter and axial blood velocity measurements derived from a registered image sequence. The detected boundaries of the vessels are shown in blue. The magnitude and direction of axial blood velocity are depicted by color-coded arrows. Vessels were classified as arterioles or venules by visualizing the direction of blood velocity within the vessel and determining whether blood collected into another vessel (venules) or diverged into vessel branches (arterioles).

Fig. 5.

Conjunctival microcirculation image displaying vessel boundaries (blue lines) and the magnitude and direction of axial blood velocity (color-coded arrows). Color bar represents velocity in units of mm/s.

J. Statistical Analysis

Statistical analyses were performed using SPSS software (version 22, SPSS, Chicago, IL, USA). Multiple measurements at different locations along the same microvessel were removed to obtain one measurement per microvessel.

Measurement repeatability was assessed by the mean SD of repeated measurements averaged over all subjects. Hemodynamic measures were averaged over each subject and compared between arterioles and venules using paired t-tests. Arterioles and venules were categorized into 1 of 4 diameter groups based on the 25%, 50%, and 75% quartiles of diameter measurements in all vessels, yielding cut points at 11 µm, 16 µm, and 22 µm. Hemodynamic measures obtained in each diameter group were averaged per subject and compared among diameter groups with one-way ANOVA. Relationships between hemodynamic measures and D were determined by linear regression analysis. Significance was accepted at P < 0.01 to correct for multiple comparisons.

III. Results

Repeated measurements were obtained in 43 microvessels of 5 subjects (8 to 10 microvessels per subject). Repeatability (SD) of conjunctival D and V measurements were 0.7 µm (range: 0.6 – 1.0 µm) and 0.17 mm/s (range: 0.11 – 0.21 mm/s), respectively.

Conjunctival D and V measurements were obtained in a total of 204 arterioles. On average, measurements were obtained in 14 arterioles per subject (range: 3 – 27). The minimum and maximum of conjunctival D measurements were 5.9 µm and 42.9 µm, respectively. Conjunctival V ranged between 0.08 mm/s and 2.5 mm/s in arterioles.

Conjunctival D and V measurements were obtained in a total of 836 venules. On average, measurements were obtained in 56 venules per subject (range: 14 – 87). The minimum and maximum D measurements were 6.0 µm and 51.6 µm, respectively. Conjunctival V ranged between 0.07 mm/s and 3.4 mm/s in venules.

The mean and SD of conjunctival hemodynamic measures in arterioles and venules in all subjects are listed in Table I. Conjunctival D and Q were significantly higher in venules than arterioles (P ≤ 0.003). Conjunctival V was lower in venules than arterioles, but this difference was marginally significant (P = 0.05). Conjunctival WSR was significantly lower in venules than arterioles (P = 0.001).

TABLE I.

Conjunctival hemodynamic descriptors.

Vessel Type	N	D (µm)	V (mm/s)	Q (pl/s)	WSR (s−1)
Arterioles	15	15 ± 3	0.63 ± 0.17	86 ± 33	320 ± 132
Venules	15	18 ± 2	0.54 ± 0.13	140 ± 55	190 ± 46
P-value		<0.001	0.046	0.003	0.001

Mean and SD of conjunctival hemodynamic measures in arterioles and venules, categorized by diameter groups, are provided in Table II and III, respectively. Conjunctival V was not statistically different among diameter groups in arterioles (P = 0.1), but increased with larger diameter groups in venules (P < 0.001). As expected, in both arterioles and venules, Q increased with larger diameter groups (P < 0.001). WSR was higher in the small diameter group in both arterioles and venules (P < 0.001). Conjunctival V was linearly correlated with D in venules (P < 0.001), but not in arterioles (P = 0.6). Q and WSR were correlated with D in both arterioles and venules (P < 0.001).

TABLE II.

Conjunctival hemodynamic descriptors in arterioles, stratified by diameter groups.

ARTERIOLES
Diameter Groups (µm)	N	D (µm)	V (mm/s)	Q (pl/s)	WSR (s−1)
< 11	13	9 ± 1	0.70 ± 0.3	40 ± 27	488 ± 194
11 – 16	13	14 ± 1	0.62 ± 0.2	69 ± 26	279 ± 99
16 – 22	13	19 ± 1	0.54 ± 0.2	111 ± 45	163 ± 77
> 22	10	26 ± 3	0.87 ± 0.5	299 ± 155	193 ± 117
P-value		<0.001	0.125	<0.001	<0.001

TABLE III.

Conjunctival hemodynamic descriptors in venules, stratified by diameter groups.

VENULES
Diameter Groups (µm)	N	D (µm)	V (mm/s)	Q (pl/s)	WSR (s−1)
< 11	14	9 ± 1	0.41 ± 0.1	23 ± 7	281 ± 65
11 – 16	15	14 ± 1	0.44 ± 0.1	51 ± 16	194 ± 57
16 – 22	15	19 ± 1	0.50 ± 0.1	103 ± 26	147 ± 38
> 22	15	28 ± 2	0.80 ± 0.4	356 ± 181	162 ± 87
P-value		<0.001	<0.001	<0.001	<0.001

IV. DISCUSSION

Due to physiological variations in microvascular blood flow, comprehensive assessment of a large number of microvessels is required to fully characterize the hemodynamic properties of the conjunctival microvascular network. In the current study, an automated image analysis method for quantitative assessment of hemodynamics in the conjunctival microvasculature network was reported.

In conjunctival venules of similar diameter, blood velocity measurements were in agreement with our previous published values obtained semi-automatically [1], and values reported by Jiang et al. [18], but were slightly lower than values reported by Koutsiaris et al. [26], which may be attributable to differences in techniques. The maximum velocity that can be measured by our system is estimated to be approximately 3.8 mm/sec, based on tracking movement of aggregated red blood cells along a 0.3 mm vessel segment over 4 consecutive image frames acquired at 50 Hz.

Previous studies have reported pulsation in conjunctival arterioles [27–28]. In these studies, a significantly larger number of frames were acquired at a higher frame rate which allowed measurements of velocity variations in arterioles during a complete cardiac cycle. However, in the current study, this velocity variation was not observed in the STI (as evident by the presence of linear bands rather than curved bands), which is likely attributed to the limited imaging time interval. Although image sequences were acquired over a 1 second time interval, the number of consecutive image frames that could be registered was limited by eye motion and blinks. Therefore, velocity measurements were obtained from different intervals of the cardiac cycle over an average time interval of 0.3 sec, which was less than a complete cardiac cycle. Lack of synchronization of image acquisition with the cardiac cycle may have increased the variability of velocity measurements. However, within subject variability was reduced by averaging data obtained in multiple same size vessels in each subject.

Currently available techniques for assessment of hemodynamics in conjunctival microvasculature utilize manual or semi-automated methods [16]–[19] that necessitate user input and interaction. Therefore, application of these techniques to evaluate a large number of microvessels may be inefficient and time consuming. In contrast, fully automated vessel segmentation and blood flow detection by our method allows rapid and objective measurements of conjunctival hemodynamic properties in both arterioles and venules within the conjunctival microvascular network.

Assessment of microvascular hemodynamics has been reported in non-ocular tissues, including nail fold [29], sublingual [30], and buccal mucosa [31] with the use of CapiScope, a commercially available device. Although, this device is capable of automated blood vessel diameter measurements, evaluation of blood velocity requires manual drawing of a line along a target vessel. Automated hemodynamic assessment of human sublingual microcirculation was demonstrated [32], but there are no reports of automated assessment of the conjunctival microvasculature network. The automated method for vessel segmentation and blood flow detection presented in the current study allows quantitative assessment of hemodynamics in the conjunctival microvascular network and can be potentially applied to microcirculation images of other tissues.

V. CONCLUSION

An automated image analysis method for comprehensive and quantitative assessment of hemodynamics in the conjunctival microvascular network was demonstrated. Due to the inherent heterogeneity in hemodynamics of the microcirculation, this method is well suited for detection of microvascular hemodynamic abnormalities and advancing our understanding of microvascular pathophysiology.