Presence-Only Data and the EM Algorithm

Summary

In ecological modeling of the habitat of a species, it can be prohibitively expensive to determine species absence. Presence-only data consist of a sample of locations with observed presences and a separate group of locations sampled from the full landscape, with unknown presences. We propose an expectation–maximization algorithm to estimate the underlying presence–absence logistic model for presence-only data. This algorithm can be used with any off-the-shelf logistic model. For models with stepwise fitting procedures, such as boosted trees, the fitting process can be accelerated by interleaving expectation steps within the procedure. Preliminary analyses based on sampling from presence–absence records of fish in New Zealand rivers illustrate that this new procedure can reduce both deviance and the shrinkage of marginal effect estimates that occur in the naive model often used in practice. Finally, it is shown that the population prevalence of a species is only identifiable when there is some unrealistic constraint on the structure of the logistic model. In practice, it is strongly recommended that an estimate of population prevalence be provided.

1. Introduction

Modeling wildlife habitat selection is important for effective ecological management of a species. Logistic models are typically used to estimate species distribution, ideally based on records of presences or absences collected at randomly sampled locations. However, obtaining such presence–absence data may be difficult or expensive, and often records of species presence are easier to obtain than definitive absences. For example, herbaria and museums have extensive historical occurrence records (Elith et al., 2006) and radiotelemetry provides a rich source of range locations for mobile species (Frair et al., 2004). Environmental information can be collected for these recorded presence locations using geographical information system (GIS) technology.

Some methods use only these presences to estimate a species range; for example, habitat (Walker and Cocks, 1991) estimates the range of a species via a convex hull defined in environmental space. However, many methods also require a background sample or pseudo-absences—a random sample of locations taken from the region or landscape of interest. Although the presence or absence of a species at the background locations is unknown, they provide a summary of the landscape, against which we can compare the observed presences. Indeed, using these data can considerably increase prediction accuracy (Elith et al., 2006). This combination of a sample of locations with observed presences, and a background sample of locations from the landscape is what we will refer to as presence-only data.

The model construction in this article is based on strict assumptions about the sampling mechanisms. In particular, we assume that the observed presences in the presence-only sample are taken at random from all locations where the species is present. For mobile species, where presence or absence may change over time, we assume that this random sampling is at a rate proportional to the proportion of time the species is present at that location. Additionally, we assume that the background sample is sampled at random from the full landscape of locations. In practice, this second assumption is often approximately true; GIS provides an easy way to generate environmental covariates for locations chosen at random. However, the presence-only sample is often biased. Records at herbaria or museums are typically ad hoc records of species occurrence collected by individuals, and may be biased, for example, toward more accessible locations (Reese et al., 2005).

Such bias in observed presences may be counteracted by sampling the background data with the same bias. For example, ecologists have used for background data the presence records for different species in the same region (e.g., Dudík, Schapire, and Phillips, 2006). Taking this a step further, Zaniewski, Lehmann, and Overton (2002) use the recorded presences of other species to build a statistical model of sampling rate, given environmental covariates. Predicted probabilities for this sampling bias model are then used as weights in sampling the background data. These same techniques can be used with the expectation–maximization (EM) procedure described in this article. However, a more thorough treatment of this bias is beyond the scope of this article.

The modeling of presence-only data in ecology is reviewed in Keating and Cherry (2004), where it is referred to as use-availability data, and Pearce and Boyce (2006). Typically a logistic model is fit to the recorded presences and background data; we refer to this as the naive model. If a species is rare, the background data will resemble the true absences and the naive model will be close to the true model. However, for more common species, the naive model can be highly biased (Keating and Cherry, 2004); we explore the form of that bias later in this article. An alternate procedure, the exponential model of Manly et al. (2002), uses a log-linear model of the presence–absence probability, which is easy to estimate via existing modeling procedures. However, this approach does not attempt to estimate the true presence–absence logistic model, and has other recorded failings (Keating and Cherry, 2004). An ad hoc method of Engler, Guisan, and Rechsteiner (2004) uses an initial model to discover background locations where there is a low predicted probability of species presence. These locations are then used as absences in a second presence–absence logistic model. In essence this is the aim of our procedure—to label background data as true presences or absences—however, we approach this in a more rigorous manner.

Lancaster and Imbens (1996) provide an exact method for estimating a logistic regression model with presence-only data. It uses direct maximization of a likelihood based on the presence-only data to estimate the linear predictor for the presence–absence logistic regression model. However, this technique is rarely used in practice as there is no easily available implementation, and convergence problems have been reported. Our method indirectly maximizes this same presence-only likelihood in a way that is more robust, can easily incorporate more flexible models, and is straightforward to implement using existing statistical software.

Typical presence–absence methods attempt to model the probability of presence conditional on environmental covariates. In contrast, Maxent (maximum entropy modeling; Phillips, Anderson, and Schapire, 2006) estimates the density of environmental covariates conditional on species presence. This has been shown to be equivalent to a Gibbs density with certain constraints, which implies a log-probability model as used by Manly. Although Maxent has been shown to perform well in practice (Elith et al., 2006), in this article we concentrate instead on improving the logistic regression model.

Within ecology the presence-only problem arises in paradigms with subtle distinctions. In “use-availability” modeling, we are interested in the relative frequency of use of an area by wide-ranging animals; for less mobile species, “presence–absence” is modeled. However, for both these cases it is possible to arrive at a unique definition. We define the probability of presence of a species as measured across a certain time window. For nonmobile species, this time window is irrelevant, up to the lifetime of the species. Typically, for mobile species, the window is implicitly defined by the sampling mechanism, for example, by the length of time a site was observed, or by the discretization of radiotelemetry data. Any reference to a probability of presence in this article thus implicitly refers to such a time window.

2. The Presence-Only Problem and the EM Algorithm

A common aim of ecological studies is to model the probability that a species of interest is present, y = 1 (versus absent, y = 0), conditional on some ecological covariates x, ℙ(y = 1 | x). This probability is usually modeled via its logit

$$\text{logit }\mathbb{P}(y=1|\mathbf{x})=\eta (\mathbf{x})\Rightarrow \mathbb{P}(y=1|\mathbf{x})=\frac{e^{\eta (\mathbf{x})}}{1+e^{\eta (\mathbf{x})}},$$ (1)

where η(x) can be linear in x (as in logistic regression) or a nonlinear function of x, e.g., generalized additive models (GAMs; Hastie and Tibshirani, 1990) or boosted trees (Friedman, 2001). In studies where the true presences and absences of a species are known for a random sample of locations, these models are fit using established methods. We will refer to these as presence–absence data and methods.

However, in the presence-only problem, we know only where the species was present, not where it was absent. Along with these observed presences we can generate background data, which are locations where the true presence or absence is unknown. Ideally this background data set should be larger than the number of observed presences and large enough to provide a good representation of the landscape. We denote these observed presences and background data by z = 1 and z = 0, respectively. Note that when z = 1, we know y = 1. However, when z = 0 we do not know whether y is 0 or 1. For both our observed presences and background data, we have measurements of environmental variables or covariates x.

Using this notation, we can clearly state the presence-only problem. We wish to estimate ℙ(y = 1 | x), the probability of a true presence y, given covariates x. However, the observed presences and background data are generated by ℙ(x | z = 1) and ℙ(x) = ℙ(x | z = 0), respectively. Using a case–control approach (McCullagh and Nelder, 1989, p. 111), we can turn these probabilities around to obtain ℙ(z = 1 | x, s = 1), the conditional probability of an observed presence z = 1. The notation s = 1 is a construct of case–control modeling and indicates that this observation is in our presence-only data sample.

What we refer to as the naive model attempts to fit the logistic model (1) directly to the observed z:

$$\text{logit }\mathbb{P}(z=1|s=1,\mathbf{x})={\eta }_{\text{naive}}(\mathbf{x}).$$ (2)

The primary difference between the presence–absence (1) and naive presence-only (2) models is that the background data z = 0 include some true presences y = 1 as well as true absences y = 0. This creates bias in the naive presence-only model, which we illustrate through a simple example in Section 2.2 and further investigate in Section 3.2.

The aim of this article is to estimate the presence–absence model (1) using presence-only data. We start by giving an overview of our new modeling procedure (Section 2.1), then fill in the details later (Section 3). We also provide a simple example that illustrates the naive and new models, and the differences between them (Section 2.2). Throughout these sections we assume that we know the overall population prevalence of the species π = ℙ(y = 1). Later we look at an example of sensitivity analysis of the uncertainty in π (Section 4), and illustrate under what conditions we can also estimate π directly from these data (Section 5).

2.1 The EM Procedure

In fitting a model to the presence-only data, we consider two possibilities: where the background data z = 0 are assumed to have either known or unknown y:

1. If we knew the true y for the background data z = 0, then we could estimate the presence-only logistic model (1) by fitting a model directly to the y given x. As the true y = 0, 1 in these data occur in different proportions to the overall landscape, we also make a simple “case–control” adjustment to the intercept of the fitted model.

2. As we do not know the true y for the background data z = 0, we can think of these y as missing data. We use an iterative procedure that tries to estimate or impute the unknown y at each iteration and then fits a model using these imputed y. At each iteration we apply the following two steps, until subsequent iterations result in the same model:

   1. We replace the unknown y’s with our best estimate ŷ = ℙ̂(y = 1 | x) estimated from the model fit in the previous iteration.
   2. We assume that we “know” these y’s and thus apply the procedure described in (1).

The procedure in (2) is an implementation of the EM algorithm of Dempster, Laird, and Rubin (1977).

We provide a more mathematical description of the algorithm in Figure 1. The initial estimate of y for z = 0 is π = ℙ(y = 1) because this is our best guess prior to fitting any model. We provide the exact form for the intercept adjustment of the fitted models, where n_p is the number of observed presences (z = 1) and n_u is the number of background data (z = 0). For logistic procedures used in the maximization step that cannot handle noninteger responses, a workaround is illustrated in Web Appendix B. Details and derivation of this algorithm are given in Section 3.

Figure 1.

The EM algorithm for presence-only data.

2.2 A Simple Example

To illustrate the bias in the naive model and the mechanism of the EM procedure, we present a simple example where the probability of true presence y depends only on elevation:

$$\text{logit }(\mathbb{P}(y=1|\mathbf{x}))={\beta }_0+{\beta }_1\times \text{elevation}.$$

We take β₁ to be positive, so the species prefers higher elevations, and set π = 0.4. There are 10 data points with z = 1 and 20 data points with z = 0. If we knew the true y (Figure 2a) we could obtain a good estimate of the underlying logistic regression model. However, if we fit the same model to the observed z (Figure 2b) then the slope β̂₁ of the estimated model is too shallow.

Figure 2.

A simple example where species presence depends only on elevation. A logistic regression model estimated using y (a) and a naive logistic regression model estimated using z (b) are illustrated by the lines. The vertical location of data points (crosses and circles) indicates the value of the outcome as used in the fitting procedure.

The EM algorithm for this example uses a logistic regression fit at each iteration; the outcomes for these fits are 1 for z = 1 but for z = 0 they depend on the fitted model from the previous iteration. In the first iteration, the outcome is set to π for each z = 0 (Figure 3a). In the second iteration (Figure 3b), outcomes for z = 0 are set to the predicted values from the first iteration. This is repeated for subsequent iterations and the EM algorithm terminates when the models estimated in the previous and current iterations are the same (Figure 3d). In this example, the resulting fitted model is very close to that obtained using the true y (Figure 2a).

Figure 3.

Iterations of the EM algorithm using a logistic regression model as applied to the simple elevation example. The vertical location of data points (crosses and circles) indicate the value of the outcome as used in the fitting procedure and lines indicate models estimated from these data.

3. Details and Development of the Algorithm

To estimate η for the presence–absence model (1) we wish to maximize the likelihood for the presence-only data, with respect to η.We first derive the form of this observed likelihood, which is based on ℙ(z | s = 1, x). We can then derive the steps of the EM algorithm applied to this likelihood. To do this we first calculate a slightly different full likelihood based on ℙ(y, z | s = 1, x). We provide the derivation of the observed likelihood in this section, as we believe it can help the reader understand the structure of this presence-only problem. All other propositions are proved in Web Appendix A.

Proposition 1

Given the usual logistic model (1), we can use a case–control style adjustment to show

$$\text{logit }(\mathbb{P}(y=1|\mathbf{x},s=1))=\eta (\mathbf{x})+\text{log }(\frac{n_p+\pi n_u}{\pi n_u}),$$ (3)

where n_p and n_u are the number of observed presences z = 1 and background data z = 0, respectively.

Proposition 2

The observed likelihood for the presence-only data is given by

$$L(\eta |\mathbf{z},X)=\prod _i\mathbb{P}(z_i|s_i=1,{\mathbf{x}}_i)=\prod _i{\left(\frac{\frac{n_p}{\pi n_u}{e}^{\eta ({\mathbf{x}}_i)}}{1+(1+\frac{n_p}{\pi n_u})e^{\eta ({\mathbf{x}}_i)}}\right)}^{z_i}\times {\left(\frac{1+e^{\eta ({\mathbf{x}}_i)}}{1+(1+\frac{n_p}{\pi n_u})e^{\eta ({\mathbf{x}}_i)}}\right)}^{1-z_i}.$$ (4)

Proof

We will prove the form of the probability ℙ(z = 1 | s = 1, x); the construction of the observed likelihood from these probabilities follows immediately. We start with a totalprobability argument across y = 0, 1:

$$\mathbb{P}(z=1|s=1,\mathbf{x})=\mathbb{P}(z=1|y=1,s=1,\mathbf{x})\mathbb{P}(y=1|s=1,\mathbf{x})+\mathbb{P}(z=1|y=0,s=1,\mathbf{x})\mathbb{P}(y=0|s=1,\mathbf{x}).$$ (5)

Note that ℙ(z = 1 | y = 1, s = 1, x) is a sampling probability of whether true presences (y = 1) in our presence-only data were observed (z = 1) or not (z = 0). The random sampling assumptions outlined in the introduction imply that the sampling of the observed presences is independent of x, given the true presence or absence. Thus we use an application of Bayes’ rule to show

$$\mathbb{P}(z=1|y=1,s=1,\mathbf{x})=\mathbb{P}(z=1|y=1,s=1)=\frac{\mathbb{P}(z=1,y=1|s=1)}{\mathbb{P}(y=1|s=1)}.$$ (6)

The expected number of true presences (y = 1) in our data is n_p + πn_u—all data with z = 1 plus a proportion π of z = 0—and so ℙ(y = 1 | s = 1) = (n_p + πn_u)/(n_p + n_u). Also, by definition of z and y, ℙ(z = 1, y = 1 | s = 1) = ℙ(z = 1 | s = 1) = n_p/(n_p + n_u). Plugging these into (6) we get

$$\mathbb{P}(z=1|y=1,s=1,\mathbf{x})=\frac{n_p}{n_p+\pi n_u}.$$ (7)

Further, ℙ(z = 1 | y = 0, s = 1) = 0 because all y = 0 in the data must occur for z = 0.

From Proposition 1, we know ℙ(y = 1 | s = 1, x) = e^η*(x) / (1 + e^η*(x)) where η^*(x) = η(x) + log ((n_p + πn_u)/(πn_u)). Substituting all the probabilities in (5) we have

$$\mathbb{P}(z=1|s=1,\mathbf{x})=\frac{n_p}{n_p+\pi n_u}\frac{e^{{\eta }^{*}(\mathbf{x})}}{1+e^{{\eta }^{*}(\mathbf{x})}}+0$$ (8)

$$=\frac{\frac{n_p}{\pi n_u}{e}^{\eta (\mathbf{x})}}{1+(1+\frac{n_p}{\pi n_u})e^{\eta (\mathbf{x})}},$$ (9)

after some manipulation.

Direct maximization of this likelihood is difficult, though Lancaster and Imbens (1996) have implemented this for η linear in x. We continue by providing the full likelihood, which also depends on the unknown y.

Proposition 3

The full likelihood for the presence-only data, in terms of both z and y is:

$$L(\eta |\mathbf{y},\mathbf{z},X)\propto \prod _i\mathbb{P}(y_i|s_i=1,{\mathbf{x}}_i)=\prod _i{\left(\frac{e^{{\eta }^{*}({\mathbf{x}}_i)}}{1+e^{{\eta }^{*}({\mathbf{x}}_i)}}\right)}^{y_i}{\left(\frac{1}{1+e^{{\eta }^{*}({\mathbf{x}}_i)}}\right)}^{1-y_i},$$ (10)

where η^* (x_i) = η(x_i) + log ((n_p + πn_u)/(πn_u)).

Note that in equations (4) and (10) we assume that π is known. Note also that with y known, the full likelihood (10) for η does not depend on z. In the next proposition we use this full likelihood in applying the EM (Dempster et al., 1977) to the observed likelihood.

Proposition 4

The observed likelihood (4) can be maximized using the EM algorithm. The algorithm uses alternate maximization and expectation steps as outlined in Figure 1. In the E-step, the unknown y’s are estimated using the model from the previous fit. The M-step involves maximization of the full likelihood (10) with the estimated y’s imputed.

Thus we have shown that the EM algorithm for presence-only data (Figure 1) maximizes the observed likelihood (4). In other words, this new approach is estimating the underlying logistic model η(x) of the probability of interest ℙ(y = 1 | x).

3.1 Stepwise Procedures and the EM Method

Recent work in ecological modeling has seen a move toward more flexible models, such as GAMs and boosted trees (e.g., Leathwick et al., 2005, 2006). Both GAM and boosted trees can be the logistic model of choice in the maximization step of this EM algorithm (Figure 1). However the stepwise nature of the boosted trees model suggests an improvement; interleaving expectation steps with every few boosting steps will decrease the time to convergence of the EM algorithm. In practice this decrease can be an order of magnitude. In Web Appendix C, we show how to implement this interleaving using the boosted trees package GBM in R (Ridgeway, 2004). Although we use boosted trees as an example, this could be implemented for any stepwise procedure.

3.2 The Naive Logistic Model

In recent literature (e.g., Ferrier et al., 2002) one approach to the presence-only problem has been to fit a logistic model directly to the observed presences and background data. We refer to this as a naive logistic model and use η_naive to refer to the linear predictor of this model, as defined in equation (9).

The naive logistic model is doubly problematic. Assuming that the background data are all absences ignores the “contamination” with true but unknown presences. Further, the true (but in part unknown) presences and absences are not sampled proportionally to their prevalence in the landscape. We can improve the naive model by using a case–control adjustment for η_naive to account for the differing sampling rates (e.g., Mace et al., 1996). We then show how this adjusted η_naive is related to the true η. All proofs for these propositions are provided in Web Appendix A.

Proposition 5

The case–control adjusted naive model ${\eta }_{\text{naive}}^{\text{adj}}(\mathbf{x})$ is

$${\eta }_{\text{naive}}^{\text{adj}}(\mathbf{x})={\eta }_{\text{naive}}(\mathbf{x})-\text{log }\left(\frac{(1-\pi )n_p}{\pi n_u}\right).$$

Proposition 6

The case–control adjusted naive model ${\eta }_{\text{naive}}^{\text{adj}}(\mathbf{x})$ can be written in terms of the presence–absence model η(x) as follows:

$${\eta }_{\text{naive}}^{\text{adj}}(\mathbf{x})=-\text{log }(1-\pi )-\text{log}(e^{-\eta (\mathbf{x})}+1).$$ (11)

Note that when π is small, most η are large and negative, thus −log (e^−η(x) + 1) ≈ η(x) and the naive model is similar to the true model. More generally, the adjusted naive model ${\eta }_{\text{naive}}^{\text{adj}}$ is increasing in the true η, but nonlinearly (Figure 4). Although the true and naive predictors are similar up to a constant for η ≪ 0, when η > 0 the naive model considerably underestimates the rate at which η is increasing. In particular, the naive linear predictor is bounded above: η_naive ≪ −log (1 − π). Hence the estimated probabilities for the naive model will be underestimated for locations with higher probabilities of presence.

Figure 4.

The case–control adjusted η_naive from the naive logistic regression is an increasing but nonlinear function of the linear predictor from the true model of interest, η, and the population prevalence π. Thick lines indicate typical values of η for each π.

In practice, this bias has considerable effect on logistic regression estimates: if the true η is linear in x, i.e., η(x) = x^T β, then any naive logistic regression model must be biased. In particular, the estimates for the naive model β_naive will tend to underestimate the slopes β. This is illustrated in simulations of presence-only data (Figure 5). Although the estimates for the EM procedure are approximately unbiased, the naive model estimates are shrunk to zero, with more shrinkage for larger π. However, note that even for π = 0.1, the naive estimates are noticeably different from the truth. We will see that this underestimation of effect size also occurs for more complex models (Figure 6). This shrinkage of effect size occurs because of the contamination of true presences y = 1 in the background data z = 0. Because of this contamination, the z = 1 and z = 0 are more similar to each other than the y = 1 and y = 0. It is easy to see how this shrinkage may impact variable selection, e.g., important variables may not appear statistically significant.

Figure 5.

Parameter estimates for the naive logistic regression model are biased toward the origin, with increased bias for larger π. These estimates are from 100 simulations of presence-only data, generated from the model η(x) = α + x₁β₁ + x₂β₂, where β₁ = 1 and β₂ = −2. The x are independent and identically distributed standard normals and n_p = 300 and n_u = 1000. Note that the variance of the EM estimates increase with π.

Figure 6.

The marginal effect of each variable on η for the EM and naive models and for the full model based on the true presences (mean and ±1 pointwise standard errors). The boxplot in (a) indicates the distribution of the summer temperature across all locations in the sample; 15% of these locations had a dam downstream.

For flexible modeling procedures it may seem tempting to use the relationship between the true and naive models (11) to make a post hoc transformation of the naive model. However, from model (11) we see there is an implicit constraint of ${\eta }_{\text{naive}}^{\text{adj}}<-\text{log }(1-\pi )$; exceeding this value results in undefined η. In practice this constraint is not observed, nor is there an easy way to enforce this, though a post hoc replacement of any undefined η with η = ∞ may be a good approximation for data with few such locations.

4. Example: The Longfin Eel

Assessing models based on presence-only data is difficult, because there is typically no validation data with true presences and absences. Although simulated data are a useful tool, they typically do not reflect the noise and complex structure inherent in ecological data. To overcome these issues, we have generated presence-only data sets from presence–absence data of diadromous fish in the rivers of New Zealand (more details are given in Leathwick et al., 2005, and in the acknowledgements). In particular we looked at the Longfin Eel Anguilla dieffenbachii, which has a high prevalence, occurring at 51.3% of all locations sampled. To reduce spurious effects, we repeated the presence-only data generation 10 times, with different random seeds; the results provided are amalgamated across these repetitions. There are 21 environmental covariates describing conditions at the sampled site as well as up- and downstream. This includes some variables omitted from Leathwick et al. (2005), in particular, the presence of a dam downstream, as this provides a clear illustration of the difference in the naive model and EM procedure. In the full data set, eels were present in 20% of locations with a dam downstream.

The presence-only samples were generated according to the sampling assumptions set out in this article. Ideally the background data should be a random sample from all river locations in New Zealand; here we assume that the fish data set consists of such a sample, so we can compare performances of different models. Hence the sample of background data was generated by sampling randomly from all available data. Then the naive presences sample was generated by sampling from the remaining presence locations. A random sample of one quarter of the data were set aside as a validation set and the rest were used to train the models. These training sets contained around 4400 and 1300 background data and observed presences, respectively. The validation set contained one third of these numbers, of which around 1200 were true presences and 700 were true absences.

We fitted a boosted trees model to these data, using the EM procedure (Figure 1), which we will call the EM model, with π = 0.513. This is compared to the naive model, fitting boosted trees directly to the presence-only data with a case–control adjustment to enable a fair comparison with the EM model. Additionally, as a measure of an optimal result, we calculated the full model, a boosted trees model calculated on the same data, but using the full knowledge of the true presences and absences. A total of 10,000 trees were fitted for each model, each with a depth of 4, allowing four-way interaction terms. In practice, the optimal number of trees for a model would be chosen by minimizing a prediction set deviance using the observed likelihood (4). However, here the deviance was calculated using the full likelihood (equation 10) of the true presences, so that the EM and naive models could be compared with the full model. As the validation set was not a random sample from all locations, a further case–control adjustment was made in calculating deviances. In general, the full and observed likelihoods generate similar shaped curves that are minimized at a similar number of trees. The naive model required the fewest trees (Figure 7), whereas the EM models were optimized at around 3000 trees, similar to the optimal number of trees for the full model.

Figure 7.

The EM model has a lower validation set deviance (a) and less shrinkage in η (b) than the naive model, when predicting the presence of the Longfin Eel. The average validation set deviance is calculated from the likelihood of the true presences (mean and ±1 pointwise standard errors). The predicted η in (b) are the best fitting EM and naive models, versus the best fitting model based on the true presences.

The two most important predictors in modeling the true presences were the summer temperature and the presence of a dam downstream. Figure 6 illustrates that the naive model tends to underestimate the range of the effect that each of these predictors has on η. This is particularly noticeable in the binary downstream dam variable, and echoes the pattern in Figure 5 that the naive logistic regression model shrinks the parameter estimates toward zero. This leads to the effect seen in Figure 7, that the predicted η for the naive model tends to be shrunk to zero in comparison to the model based on the true presences.

The performance of the EM model lies somewhere between that of the naive and true models. There is some shrinkage of the marginal effects and estimated η’s, though it is not as pronounced as for the naive model. This occurs because the presence probabilities imputed at the E-steps are estimates of the true model, thus introducing an averaging effect on the estimated presences/absences for the background data. Figure 7 illustrates that the EM model also has lower deviance than the naive model (calculated on a validation set where the true presences and absences are known). In this case, with π = 0.513, the EM model considerably reduces the excess in deviance over the model based on the true presences, compared to the naive model. Although these results are exploratory, these effects were seen across other species of fish with π > 0.2, but with less of an effect for smaller π. It should be noted, however, that these results were for data that were sampled according to the assumptions set out in this article; in practice, sampling of presences may be very ad hoc.

Finally, we ran a sensitivity analysis of the model, for 1 of the 10 sampling repetitions, to determine the effect of differing prior beliefs of π. The EM model was fitted using a range of different π’s between 0.3 and 0.8, in increments of 0.05. The validation set deviance was calculated for each model, using the observed likelihood (4), and the minimum deviance recorded. Figure 8a illustrates that these minimum deviances are themselves minimized around π = 0.6, with low minimum deviances for values of π between 0.5 and 0.7. Thus there is only a small change in predictive ability when increasing π slightly. However, if the prior belief was that the true π was smaller than 0.513, then the choice of π would influence the prediction deviance considerably. It should be noted here that although Figure 8a suggests we could estimate π as that which minimizes the deviance, this would be incorrect; in the next section, we show that π is not estimable when fitting a boosted trees model.

Figure 8.

A sensitivity analysis for π indicates that the minimum validation set deviance for the EM model is smallest for π ≈ 0.6 (a). The effect on η of average summer temperature has a consistent shape across all π, but the estimated effect magnitude increases with π (b). The validation set deviance is calculated using the presence-only likelihood, so is not comparable with Figure 7.

The marginal effects on η of all variables follow a pattern similar to that in Figure 8b. Across different values of π, the shape of the marginal effect is relatively constant, with the magnitude of the effect increasing with π. Unsurprisingly, as π gets smaller the effect size tends to resemble that of the naive model (not shown), as we are assuming that there are few presences in the background data. Thus, in our example, the shapes of the marginal effects are not sensitive to changes in π, but the magnitudes of the effects are.

5. Estimating π

Ideally we would like π to be identifiable; in other words, that we can estimate π, as well as η, from presence-only data. However, in the following proposition we show that this is not feasible in practice. Proofs of the first two parts of this proposition are given in Web Appendix A; the third part is illustrated using a simple example.

Proposition 7

Identifiability of π can be summarized as follows:

1. π is not identifiable if we make no assumptions about the structure of η.

2. π is identifiable only if we make unrealistic assumptions about the structure of η(x) such as in logistic regression where η(x) linear in x: η(x) = x^T β.

3. Even when π is identifiable, the estimate is highly variable.

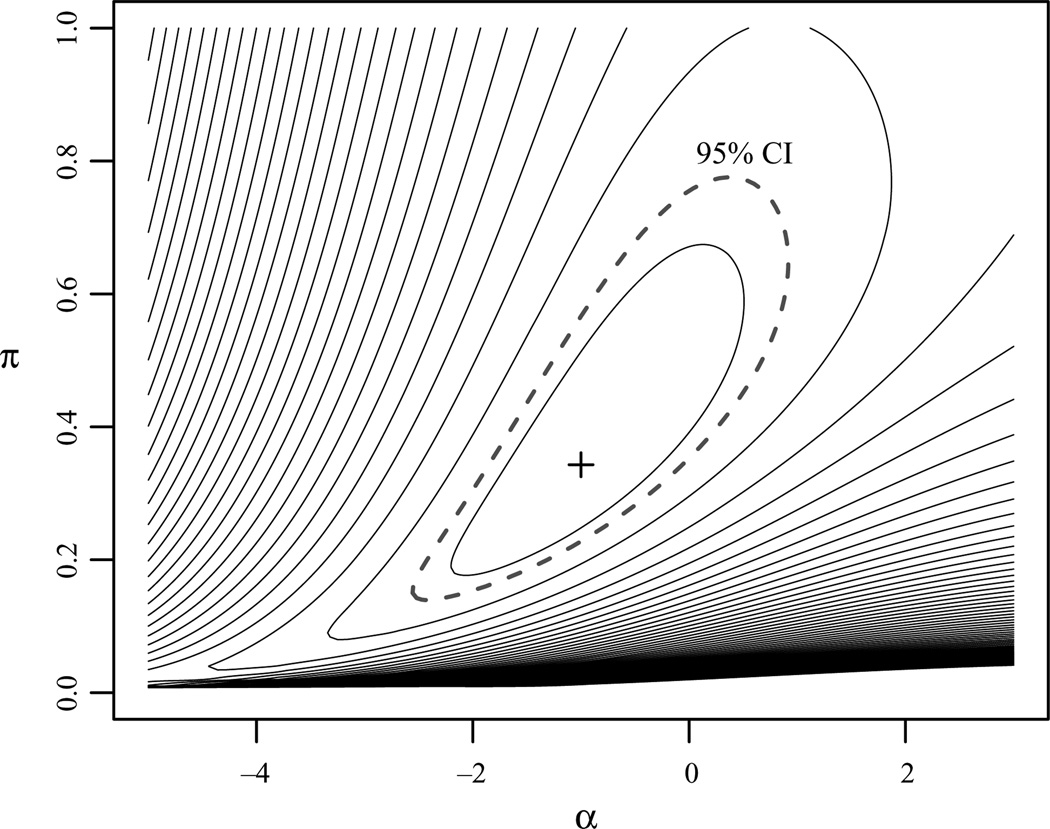
We illustrate the high variability in estimated π using an example where data are simulated from a simple logistic model (Figure 9). (Details of this estimation procedure are given in Web Appendix D.) Even in this simple example, where the assumed structure of η is correct (and linear), the 95% confidence interval for π is large (0.15–0.75) and π is highly correlated with the intercept α. Where the true model deviates from the assumed structure, the estimates are highly unstable; Lancaster and Imbens (1996) report failure of convergence of the direct maximization of the observed likelihood in several examples. These results strongly contraindicate estimating π from presence-only data in any situation.

Figure 9.

The likelihood surface, and a 95% confidence interval (dashed line), for π and the intercept α at the true β for a simulation of 200 observed presences and 1000 background data. The generative model is η(x) = α + βx, where α = −1.0, β = 2, π = 0.34 and the x are independent and identically distributed standard normals.

6. Conclusions

We have proposed an application of the EM algorithm that provides a flexible method of estimating the underlying presence–absence model from presence-only data. It can work as a wrapper to (almost) any logistic regression modeling procedure. At each iteration the probabilities of presence are calculated, given the current model, for the background data (E-step) and the case–control logistic model is reestimated using these new weighted or nonbinary outcomes (M-step). For stagewise logistic modeling procedures, such as boosted trees, E-steps may be interleaved within the procedure to save computation time.

This EM model gives approximately unbiased estimates in a simple linear logistic regression simulation study. In comparison, there is considerable shrinkage toward zero in the estimates from the naive logistic regression model, fitted directly to the presence-only data. In our more complex example, a boosted trees EM model outperforms the naive boosted trees model; there is less shrinkage of the marginal effects and the prediction deviance for the presence–absence validation set is smaller for the EM model. Unsurprisingly, the EM model still has higher prediction deviance than the boosted trees model fitted using the true presence–absence data.

Previous work in estimating the presence–absence model from presence-only data has attempted to simultaneously estimate the population prevalence π. However, we have shown that π is not identifiable when no assumptions are made about the structure of η, such as in boosted trees models. In addition, even when unrealistic assumptions are made about the structure of η, e.g., linear, the resulting estimate of π is highly variable and heavily dependent on that assumption. We recommend obtaining an estimate of π from some other source and using sensitivity analysis to assess the dependence of the results on this estimate. If no estimate of π is available, then the naive model is the only logistic model available.

Alternatively, a Bayesian approach could be considered in situations when π is not precisely known. As π is not realistically identifiable in the presence-only framework, an informative prior should be used to summarize the strength of the knowledge of π. Standard errors of the fitted model resulting from such an analysis would be larger than in the EM approach described in this article; this increase would reflect the uncertainty inherent in the prior for π.

This application of the EM algorithm provides a flexible way of estimating species distribution from the extensive records of species presence in herbaria and museums, and from radiotelemetry studies. Because of its simplicity, we believe it can be easily adopted by anyone working in this field.