Dynamics of the Human Structural Connectome Underlying Working Memory Training

Abstract

Brain region-specific changes have been demonstrated with a variety of cognitive training interventions. The effect of cognitive training on brain subnetworks in humans, however, remains largely unknown, with studies limited to functional networks. Here, we used a well-established working memory training program and state-of-the art neuroimaging methods in 40 healthy adults (21 females, mean age 26.5 years). Near and far-transfer training effects were assessed using computerized working memory and executive function tasks. Adaptive working memory training led to improvement on (non)trained working memory tasks and generalization to tasks of reasoning and inhibition. Graph theoretical analysis of the structural (white matter) network connectivity (“connectome”) revealed increased global integration within a frontoparietal attention network following adaptive working memory training compared with the nonadaptive group. Furthermore, the impact on the outcome of graph theoretical analyses of different white matter metrics to infer “connection strength” was evaluated. Increased efficiency of the frontoparietal network was best captured when using connection strengths derived from MR metrics that are thought to be more sensitive to differences in myelination (putatively indexed by the [quantitative] longitudinal relaxation rate, R₁) than previously used diffusion MRI metrics (fractional anisotropy or fiber-tracking recovered streamlines). Our findings emphasize the critical role of specific microstructural markers in providing important hints toward the mechanisms underpinning training-induced plasticity that may drive working memory improvement in clinical populations.

SIGNIFICANCE STATEMENT This is the first study to explore training-induced changes in the structural connectome using a well-controlled design to examine cognitive training with up-to-date neuroimaging methods. We found changes in global integration based on white matter connectivity within a frontoparietal attention network following adaptive working memory training compared with a nonadaptive comparison group. Furthermore, the impact of different diffusion MR metrics and more specific markers of white matter on the graph theoretical findings was evaluated. An increase in network global efficiency following working memory training was best captured when connection strengths were weighted by MR relaxation rates (influenced by myelination). These results are important for the optimization of cognitive training programs for healthy individuals and people with brain disease.

Introduction

Graph theory is a powerful mathematical framework for quantifying topological properties of networks (Sporns, 2014). In recent years, it has emerged as a useful tool for characterizing brain network (“connectome”) changes during development, maturation, and aging (Collin and van den Heuvel, 2013). Life-span connectome changes appear to follow an inverted U-shaped pattern, with an increasingly integrated topology during development, a plateau during adulthood, and an increasingly localized topology in later life (Fair et al., 2008, 2009). These dynamic changes are thought to contribute to critical changes in cognitive ability across the life-span.

Brain plasticity can also be demonstrated over a much shorter time period in response to cognitive training interventions (Taya et al., 2015). For example, working memory training induces changes in brain activity in frontal and parietal cortex (e.g., Klingberg, 2010; Jolles et al., 2013; Kundu et al., 2013; Olesen et al., 2004). Attentional training produced increased resting cerebral blood flow in prefrontal cortex (Mozolic et al., 2010). Memory training modified cortical thickness in the right fusiform gyrus and lateral orbitofrontal cortex in the elderly (Engvig et al., 2010), whereas mental calculation training induced gray matter volume changes in bilateral frontoparietal regions and left superior temporal gyrus (Takeuchi et al., 2011). Thus, there is ample evidence of changes in specific, isolated brain regions in response to various cognitive training interventions.

However, in examining plasticity, it is important to move beyond isolated brain regions and consider the impact of cognitive training interventions on brain networks (Bressler and Menon, 2010). A network perspective is crucial in understanding the factors that drive training-induced changes, ultimately leading to more effective treatment of neurological disorders. It is also important and necessary for capturing learning processes of cognitive functions that underpin training-induced changes in cognition (Taya et al., 2015). This approach facilitates the integration of multiple sources of information, accounting for the highly interconnected nature of brain, and is necessary because intensive practice of higher-order cognitive skills (e.g., working memory), may have a broader impact on neuronal integration, which cannot be fully captured by analyzing single brain regions or tracts. To date, only one study has used a connectome approach exploring training-induced brain changes (Langer et al., 2013), albeit studying function (using fMRI). However, whether and how intensive training activities produce measurable and durable changes in structural brain integration is unclear.

Here, we investigated the effects of 2 months of adaptive memory training and nonadaptive control activities on structural networks. There is evidence from diffusion tensor MRI studies that cognitive training can modify white matter fractional anisotropy (FA), a quantitative index of tissue microstructural organization (e.g., Scholz et al., 2009; Takeuchi et al., 2010; Wolf et al., 2014). For example, working memory training has been shown to result in increased FA in the intraparietal sulcus and anterior corpus callosum (Takeuchi et al., 2010). Although frequently concluded that increased myelination underpins training-induced FA changes, FA can be modulated by a variety of biological factors, including myelination, packing density, and diameter of the axonal fibers (Jones et al., 2013).

We examined for the first time white matter plasticity in 40 healthy adults with novel in vivo white matter imaging techniques beyond diffusion tensor MRI, which offer enhanced specificity to distinct attributes of white matter microstructure, such as myelination with MR relaxometry-based metrics (Deoni et al., 2008) and axonal morphometrics (using advanced models of diffusion) (Assaf and Basser, 2005). This study not only provides a compelling demonstration of structural network plasticity for the very first time but also offers insight into the underlying mechanisms.

Materials and Methods

Participants.

Forty-six healthy participants between the ages of 19 and 40 years were recruited from the Cardiff University School of Psychology Community Panel and via poster advertisements in local shopping and leisure centers. Participants were assigned to one of the two training groups (adaptive or nonadaptive group) pseudo-randomly with the provision to match the groups for age, sex, and handedness (only one participant was left-handed). All participants were blind to their training condition. All participants had normal or corrected vision, and none had a history of neurological or psychiatric illness or reported recent drug or alcohol abuse. All participants were carefully screened for MRI contraindications, such as pacemakers, metal contamination, or claustrophobia. Participants had to have a good command of the English language and had to have access to a computer and internet connection at home to be able to perform the working memory training (see below). All participants gave written informed consent to participate in this study under a protocol approved by Ethics Committee of the School of Psychology at Cardiff University. For various reasons, such as dropout and moving away from the area, 6 participants were discarded from further analysis (3 from the adaptive and 3 from the nonadaptive group), leading to a total of 40 remaining datasets (20 per group, 19 males and 21 females). The two groups did not differ in terms of gender distribution, handedness, or age (t₍₃₈₎ = 0.44, p = 0.67) (Table 1).

Table 1.

Summary of demographic variables and performance in working memory and executive function benchmark tests of the two groups at baseline and results of independent t test^a

	Training	Controls	t(38)	p
n	20	20	—	—
Age (years)	26 (6.2)	27 (6.8)	0.44	0.67
Females	11	10	—	—
Right-handed	19	20	—	—
Forwards digit span	5.3 (0.8)	5.2 (0.7)	−0.67	0.51
Backwards digit span	4 (1.4)	4 (1.4)	−0.01	0.99
Spatial span	5 (0.5)	4.9 (0.5)	−0.97	0.34
Double trouble	22.8 (13.6)	25.9 (15.4)	0.69	0.49
Grammatical reasoning	0.79 (0.2)	0.73 (0.2)	−0.97	0.34
Tree task	23.7 (8.7)	19.8 (7.2)	−1.54	0.13
Odd one out	9.5 (3.2)	9.1 (4.3)	−0.37	0.71
Self-ordered spatial span	6.2 (1.1)	5.5 (1.4)	−1.90	0.07
Automated symmetry span	25.3 (6.5)	22.6 (7.9)	−1.18	0.25
No. of training sessions	40	40	—	—

^aData are mean ± SD.

Training.

Participants trained extensively for 8 weeks, ∼45 min in each session (40 sessions in total). Training was self-administered at home via the software Cogmed RM. For full details and in-depth description of this training program, the interested reader is referred to previous studies (Klingberg et al., 2002; Astle et al., 2015) (or www.Cogmed.com/rm). In brief, working memory capacity was trained with computerized exercises of verbal (e.g., digits) and spatial (e.g., flashing lights) span tasks under various conditions, such as repeating sequences in forwards or backwards order, repeating auditory verbal information with or without visual cues, repeating sequences of flashing lights in stationary or rotating displays. In the high-capacity training condition, task difficulty increased or decreased adaptively depending on the trainee's level of performance. The participants assigned to the nonadaptive training group trained on a level of difficulty of three item spans independently of their performance throughout the 40 training days.

Tasks for pretraining and post-training assessment.

To assess near- and far-transfer training effects, participants were assessed before and after the training in a number of computerized working memory and executive function tasks from the Cambridge Brain Sciences Laboratory (www.cambridgebrainsciences.com) (Owen et al., 2010).

Verbal and spatial working memory spans were assessed with computerized versions of the digit span forwards and backwards and the spatial span task (Wechsler, 1999). In each version, the task difficulty was adjusted by increasing the number of span items by one following a successful trial and decreasing by one following an unsuccessful trial. Outcome measures were the average number of digits or spatial locations, respectively, in all successfully completed trials. Participants were allowed to make three errors in total before the task was discontinued.

The ability to maintain and manipulate spatial information was assessed with the self-ordered spatial span task (Owen et al., 2010). In this task, a number of boxes appear on the screen and a token is hidden in one of the boxes. Participants were instructed to find the token by clicking on the boxes and to remember the location of the token because novel tokens were never hidden in previously occupied boxes. Searching a box twice or clicking on a box that previously contained a token was penalized and the task discontinued after three such errors. Participants completed a trial successfully when all targets had been found with the outcome measures being the average number of successfully completed trials.

The ability to suppress distracting and response conflicting information was assessed with the double trouble task, a version of the Stroop task (Stroop, 1935). Participants were presented with a target color word at the top and two response color words at the bottom of the screen and were instructed to select with a mouse click the word that correctly described the target font color. Task difficulty was manipulated by varying the congruency between the font color and color meaning of the target and response words. The outcome measure was the number of correct responses within 90 s.

Complex verbal reasoning was assessed with an adapted version of the grammatical reasoning test (Baddeley, 1968), whereby participants have to determine, as quickly as possible, whether grammatical statements (e.g., the circle is not smaller than the square) about a presented figure (a large square and a smaller circle) were correct or false and to complete as many trials as possible within 90 s. The outcome measure was the total number of trials answered correctly minus the number answered incorrectly.

Nonverbal abstract reasoning was assessed with the odd one out task, an adaptation of the Raven's Progressive Matrices (Raven, 1942), in which participants are presented with nine patterns on the screen, each made up of color, shape, and number features. Participants had to find the one pattern that differed from the others according to a single feature or a combination of features. The task difficulty increased with performance improvements. The outcome measure was the number of correctly solved trials within 3 min.

The ability to plan and think forward was assessed with the Hampshire tree task, a version of the Tower of London/Hanoi test (Shallice, 1982). Participants were presented with a tree-shaped frame with nine numbered balls slotted onto the branches and were instructed to rearrange the balls so that they were ordered numerically with as few moves as possible. Participants could only move one ball at a time and only move balls that were not blocked by another ball. The time limit for this task was 3 min, and the outcome measure was the number of correctly executed moves with fewer moves reflecting better performance.

Finally, the ability to multitask was assessed with the automated symmetry span task (Unsworth et al., 2005), which requires participants to alternate rapidly between repeating spatial spans of increasing length and symmetry judgments for patterns of increasing complexity. The outcome measure used in this study was the total number of correctly completed trials.

We found no significant baseline differences for working memory and executive function performance in the pretraining session between the two groups: digit span forwards (t₍₃₈₎ = −0.67, p = 0.51), digit span backwards (t₍₃₈₎ = −0.01, p = 0.99), spatial span (t₍₃₈₎ = −0.97, p = 0.34), double trouble (t₍₃₈₎ = 0.69, p = 0.49), grammatical reasoning (t₍₃₈₎ = −0.97, p = 0.34), tree task (t₍₃₈₎ = −1.54, p = 0.13), odd one out (t₍₃₈₎ = −0.37, p = 0.71), self-ordered search (t₍₃₈₎ = −1.90, p = 0.07), and automated symmetry span task (t₍₃₈₎ =1.18, p = 0.25).

MRI data acquisition.

We captured multiple attributes of brain tissue structure through the use of different types of MRI scans acquired on a 3T HDx MRI system (General Electric Medical Systems) using an eight channel receive-only RF head coil. The MRI sessions were interleaved for the adaptive and nonadaptive groups to avoid any potential confounds between the experimental conditions and scanner-related changes in data acquisition, such as scanner drift effects.

Specifically, we combined well established (although nonspecific) diffusion tensor MRI metrics with both MR relaxometry-based metrics (Deoni et al., 2008) and metrics derived from advanced models of diffusion (Assaf and Basser, 2005). Relaxometry-based quantitative metrics, including the “myelin water fraction,” have been shown to have high qualitative and quantitative correspondence with the degree of myelination, as measured by more direct histological means, and thus can be used as an indirect measure of myelin (MacKay et al., 1994; Mottershead et al., 2003; Schmierer et al., 2008; Hurley et al., 2010; Deoni et al., 2011, 2012; Kitzler et al., 2012; Kolind et al., 2012). Complementing these relaxometry-based markers, the advanced models of diffusion (Assaf and Basser, 2005) yield proxy estimates of axonal density.

Diffusion-weighted data were acquired using a cardiac-gated single-shot spin-echo EPI sequence using the following parameters: 60 axial slices; slice thickness: 2.4 mm; echo time (TE): 89.1 ms; number of diffusion directions 60 (using an optimized gradient vector scheme) (Jones et al., 1999); b-value: 1200 s/mm²; six non–diffusion-weighted scans; FOV: 230 mm × 230 mm; acquisition matrix: 96 × 96 (total acquisition time TA ∼30 min depending on their heart rate). High-resolution T₁-weighted anatomical images were acquired using a fast-spoiled gradient recalled echo (FSPGR) sequence (172 slices; slice thickness: 1 mm; acquisition matrix: 256 × 256; TE: 2.9 ms; TR: 7.8 ms; flip angle: 20°; FOV: 230 mm × 230 mm; TA: 7 min). Quantitative maps indexing axonal morphology were acquired using the CHARMED protocol (Assaf and Basser, 2005) (slice thickness: 2.4 mm; TE: 126 ms; TR: 17,000 ms; 45 gradient orientations distributed on 8 shells)/(Santis et al., 2014) (maximum b-value: 8700 s/mm²; FOV: 230 mm × 230 mm, acquisition matrix: 96 × 96; TA = 13 min). Finally, maps of putative indices of myelin were acquired using the mcDESPOT protocol (Deoni et al., 2008) that comprised spoiled gradient recalled (SPGR) acquisitions: TE: 2.1 ms; TR: 4.7 ms; flip angles: (3, 4, 5, 6, 7, 9, 13, 18°); and balanced Steady-State Free Precession (bSSFP) acquisitions: TE: 1.6 ms; TR: 3.2 ms; flip angles: (10.6, 14.1, 18.5, 23.8, 29.1, 35.3, 45, 60°); spatial resolution: 1.7 mm isotropic; TA: 12 min. bSSFP acquisitions were repeated with and without 180° RF phase alteration to remove SSFP banding artifacts, B₀- and B₁-induced errors in the derived myelin water fraction estimates (Deoni et al., 2011).

Analyses of neuroimaging data.

Eleven different kinds of networks were generated using the subject's diffusion MRI, CHARMED, mcDESPOT, and T₁-weighted data (Fig. 1). A network was defined as a set of nodes (denoting anatomical regions of the parcellation scheme) and interconnecting edges (denoting tractography-reconstructed fiber trajectories that interconnect the nodes). The reconstructed graphs were all undirected as tractography does not differentiate between efferent and afferent fibers. Moreover, different quantitative white metrics were assigned to the edges of the graph, resulting in weighted graphs. We now describe the processing steps starting from analyses of the neuroimaging data to computation of the topological metrics of the graph.

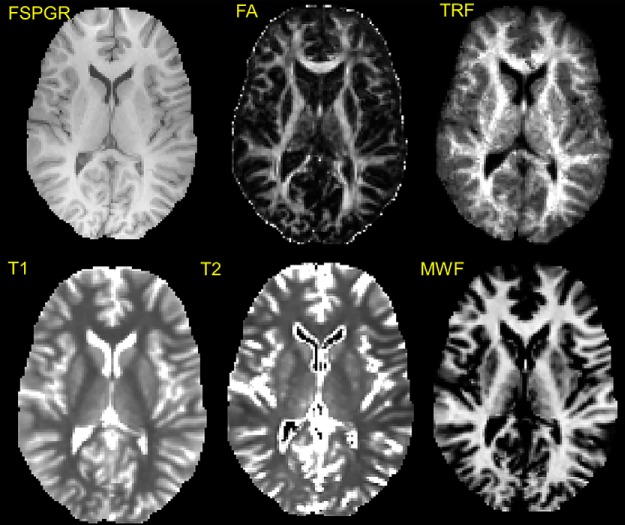
Figure 1.

Multimodal characterization of the tissue structure, combining diffusion tensor MRI-based indices (including FA) with those derived from multicomponent relaxometry as putative measures of myelin (MWF), intrinsic relaxation rates R₁ and R₂, and the TRF derived from the CHARMED pipeline as a putative measure of axonal density, together with Freesurfer-derived estimates of volume derived from the FSPGR T₁-weighted anatomical data.

The diffusion-weighted data were corrected for distortions induced by the diffusion-weighted gradients, artifacts due to head motion and due to the EPI-induced geometric distortions by registering each image volume to the high-resolution T₁-weighted anatomical images (Irfanoglu et al., 2012), with appropriate reorientation of the encoding vectors (Leemans and Jones, 2009). A two compartment model using the Free Water Elimination approach (Pasternak et al., 2009) was then fitted to derive maps of FA, mean diffusivity, radial diffusivity, and axial diffusivity (Pierpaoli et al., 1996), corrected for partial volume contamination of CSF, together with a map of the tissue volume fraction in each voxel (Metzler-Baddeley et al., 2012).

CHARMED data were corrected for motion and distortion artifacts according to Ben-Amitay et al. (2012) and were corrected for CSF-partial volume contamination with the Free Water Elimination method. The number of distinct fiber populations (1, 2, or 3) in each voxel was determined using a model selection approach (Santis et al., 2014), and the total restricted fraction (TRF, i.e., the fraction of the signal assigned to restricted diffusion) was calculated per voxel with in-house software coded in MATLAB (The MathWorks) (Santis et al., 2014).

The spoiled gradient recalled echo (SPGR) and balanced steady-state free precession (bSSFP) images acquired as part of the mcDESPOT pipeline (Deoni et al., 2008) were corrected for motion using the FMRIB Linear Image Registration Tool (Smith et al., 2001) to align all images to the first in the acquisition series. The mcDESPOT model was fitted to the data using in-house software coded in C++ (Deoni et al., 2008) to obtain maps of the myelin water fraction and of the intrinsic relaxation times T₁ and T₂ (subsequently used to derive R₁ and R₂ maps). All quantitative maps were coregistered to the T₁-weighted anatomical images. The TRF maps (derived from CHARMED) were coregistered using the Elastix registration toolbox (Klein et al., 2010), whereas the myelin water fraction (MWF), R₁, and R₂ maps (derived from mcDESPOT) were coregistered to the T₁-weighted anatomical image using the FMRIB nonlinear registration tool FNIRT.

Whole-brain tractography was performed for each participant and each time point in the participant's native space using the damped Richardson-Lucy algorithm (Dell'acqua et al., 2010), which (in contrast to diffusion tensor MRI) allows for recovery of multiple fiber orientations within each voxel. The tracking algorithm estimated peaks in the fiber orientation density function (fODF) using each voxel as a seed point and propagated in 0.5 mm steps along these axes reestimating the fODF peaks at each new location (Jeurissen et al., 2010). Tracks were terminated if the fODF amplitude fell <0.05 or the direction of pathways changed through an angle >45° between successive 0.5 mm steps. This procedure was then repeated by tracking in the opposite direction from the initial seed point.

Freesurfer analyses.

FreeSurfer (http://surfer.nmr.mgh.harvard.edu) was used for cortical reconstruction and volumetric segmentation reconstruction of the brain's surface to compute cortical thickness using a semiautomated approach described in detail previously (Jovicich et al., 2009; Fischl, 2012), with use of additional computing resources from the high performance computing TIER1 cluster at the University of Gent (http://www.ugent.be/hpc/). Images were processed automatically using the FreeSurfer longitudinal stream (Reuter et al., 2012). Specifically, an unbiased within-subject template space and image were created using robust, inverse consistent registration. Several processing steps, such as skull stripping, Talairach transforms, atlas registration, spherical surface maps, and parcellations, were then initialized with common information from the within-subject template, resulting in increased reliability and statistical power. Coregistered and segmented images were inspected visually for quality assurance purposes. Automated cortical parcellation and ROI labeling were performed to obtain (sub)cortical volume measures for the nodes of interest (see below).

Nodes.

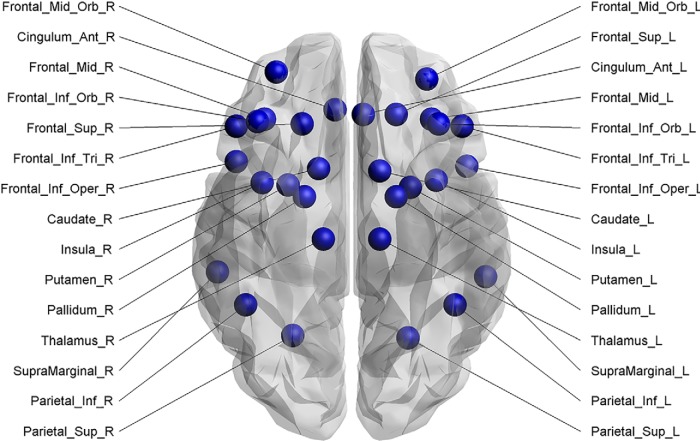
ROIs were defined based on previous fMRI studies in children, young adults, and older adults undergoing Cogmed training (e.g., Olesen et al., 2004; Klingberg, 2010; Ullman et al., 2014). Thirty regions from the automated anatomical labeling atlas (AAL) (Tzourio-Mazoyer et al., 2002) were selected to define the nodes of the network (Fig. 2). The areas constituting this network included the inferior and superior parietal cortex, supramarginal gyrus, caudal and rostral middle dorsolateral prefrontal cortex, superior frontal cortex, inferior ventrolateral prefrontal cortex (pars opercularis, pars triangularis, and pars orbitalis), insula, and anterior cingulate cortices. In addition, subcortical regions of the basal ganglia (i.e., caudate, putamen, and globus pallidum) as well as the thalamus were included in the analyses. Each ROI of the AAL template represented a node of the network.

Figure 2.

Cortical and subcortical regions (30 in total) as defined anatomically by the AAL template image in standard stereotaxic space.

White matter tractography networks.

The connection strengths for the white matter networks were defined by the quantitative metrics derived from the diffusion tensor MRI, CHARMED, and mcDESPOT pipelines, including the following: (1) diffusion MRI measures of average FA, tissue volume fraction, the number of reconstructed fibers, axial diffusivity, and the inverse of the mean and radial diffusivity; (2) myelin water fraction and the inverse of the intrinsic relaxation times T₁ (R₁) and T₂ (R₂) from the mcDESPOT pipeline; and (3) the total restricted fraction from the CHARMED pipeline (Fig. 1). As a result, for each participant, there were 10 different kinds of weighted white matter networks, each of which was represented by a symmetric 30 × 30 connectivity matrix.

Gray matter covariance networks.

The gray matter volumes of the 30 anatomical regions of interest (as described above) were used to construct structural correlation networks. For each group and each time point, a 30 × 30 correlation matrix R was generated with each entry r_ij defined as the Pearson correlation coefficient between the gray matter volume measures of regions i and j, across participants (He et al., 2007; Bernhardt et al., 2011; Fan et al., 2011).

Graph theoretical network analysis.

We quantified measures of network integration (characteristic path length) and segregation (clustering) for each network (Rubinov and Sporns, 2010). The characteristic path length L of a network is the average shortest path (distance) between all pairs of nodes in the network. It is defined as follows:

where d_ij is the shortest path length (distance) between nodes i and j. The global efficiency (Latora and Marchiori, 2001) is the average inverse shortest path length in the network and is inversely related to the characteristic path length. In other words, networks with a small average characteristic path length have higher efficiency than those with large average characteristic path length.

The clustering coefficient of a node is a measure of the number of edges that exist between its nearest neighbors and is quantified by counting the numbers of triangles, t, formed around a node (Onnela et al., 2005; Opsahl and Panzarasa, 2009). The clustering coefficient C of the network is the average clustering coefficient across all nodes and is quantified as follows:

where k_i is the number of connections (degree) for node i and t_i is the number of triangles around node i.

Statistical analysis.

It is important to recognize that the various cognitive measures (tasks for pretraining and post-training) may not be independent and could well all be impure measures of overlapping latent constructs. To account for this, an exploratory principal component analysis was run within the complete dataset of the pretraining cognitive data (including the subjects that did not complete the training; i.e., N = 46), to obtain composites to reduce the number of measures before conducting further analyses (ANOVAs and correlation analyses) on those composites (see below). Here, a procedure was used with Varimax rotation of the factor matrix to minimize the complexity of the components, whereby each factor has a small number of large loadings and a large number of zero (or small) loadings. Factor pattern matrices were identified using the Kaiser criterion (i.e., factors with Eigenvalues >1 were regarded significant). The factor loadings reflect the strength of each variable in defining the factor with negative loadings indicating that a variable related negatively to the other components. Per convention, variables were included when their loading exceeded a value of 0.5. This principal component analysis revealed three significant behavioral components that together accounted for 59% of the total variance (Table 2). More specifically, all of the tasks in which information had to be actively maintained in short-term memory, for example, the automated symmetry span task, the spatial span task, and the odd one out task loaded heavily on the first component. This complex span working memory factor accounted for 34% of the variance. The second component (accounting for 13% of the variance) was associated with tasks involving a verbal component, including the double trouble task, digit span tasks, and the grammatical reasoning task. Tasks requiring general reasoning, including the Hampshire tree task and the self-ordered spatial span, loaded heavily on the third component, accounting for 12% of the variance. Second, we computed composite scores by converting the raw test scores of these tasks to z-scores. Then, we summed the z-scores for each component per time point to create a composite for that time point. Finally, we used the composite scores as dependent variables in a 3 × 2 × 2 (factor × group × time) repeated-measures ANOVA to investigate training effects.

Table 2.

Rotated component matrix of the principal component analysis within the complete dataset of the pretraining cognitive data (N = 46)^a

Cognitive task	Component
	1	2	3
Spatial span	0.761	0.067	0.355
Odd one out	0.738	0.028	0.03
Automated symmetry span	0.648	0.256	0.085
Double trouble	−0.012	0.777	−0.009
Digit span backwards	0.418	0.688	0.137
Grammatical reasoning	−0.03	0.551	0.292
Digit span forwards	0.26	0.543	0.065
Hampshire tree	0.196	0.017	0.872
Self-ordered spatial span	0.128	0.276	0.821

^aRotation method: Varimax with Kaiser normalization.

Interaction effects between group and time for the graph metrics were analyzed using the longitudinal plugin of the Graph Analysis Toolbox (Kesler et al., 2013). Specifically, each edge weight was first normalized by the mean edge weight across the network, and graph metrics were computed for the normalized networks. A nonparametric permutation test with 1000 repetitions was then used to test the statistical significance of the effects of time course and group (adaptive and nonadaptive group) on the graph metrics (Bassett et al., 2008; Hosseini et al., 2012). In each permutation, the residuals of each participant were randomly assigned to one of the two groups so that each randomized group had the same number of subjects as in the original groups. Finally, the actual difference in the slope between the original groups was compared with the distribution of difference in slope between randomized groups (obtained through the permutation procedure) to obtain the p value. The same permutation procedure was used to test the significance of the differences in regional network measures. In this step, we compared regional clustering coefficient for the networks thresholded at the minimum density in which the networks of both groups were not fragmented. We obtained false discovery rate (FDR)-corrected p values as measures of significance for the regional measures comparisons. In the present study, the p values reported for regional differences between groups are FDR-corrected for multiple comparisons (30 comparisons, each corresponding to one of the anatomical nodes).

Finally, Pearson product correlation coefficients were calculated between the change in global efficiency of the network and (1) the three composite scores derived from the principal component analysis of the cognitive measures and (2) the scores from the CogMed measures. FDR corrections for multiple comparisons were made.

Results

Training-related changes in tasks of working memory and executive function tasks

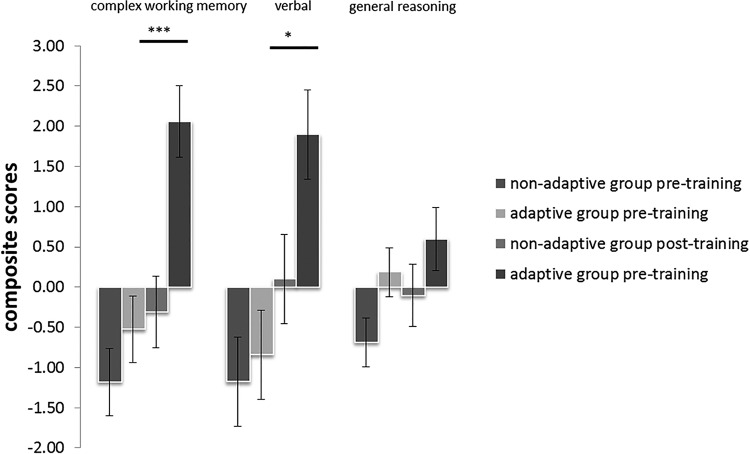
Using a 3 × 2 × 2 repeated-measures ANOVA, analysis of the composite scores revealed a main effect of time (F_(1,38) = 96.59, p < 0.001) and group (F_(1,38) = 5.94, p = 0.02). The main effect of factor was not significant. No significant interaction effect was found between factor and group. However, the time × group interaction (F_(1,38) = 12.19, p < 0.001) and the time × factor interaction (F_(2,37) = 10.07, p < 0.001) were significant. The three-way interaction between factor, group, and time was also significant (F_(2,37) = 4.07, p = 0.021). Post hoc t testing showed a superior performance on the complex working memory score factor (p = 0.001) and the verbal factor (p = 0.028) in the post-training session for the adaptive group compared with the nonadaptive group, as shown in Figure 3.

Figure 3.

Cognitive changes for the adaptive and nonadaptive group. Performance improvements in the adaptive group were significant on the complex working memory factor (Component 1) and the verbal factor (Component 2). *p < 0.05 (post hoc test). ***p < 0.001 (post hoc test). Error bars indicate SE.

Graph theoretical network analysis of the working memory training effects

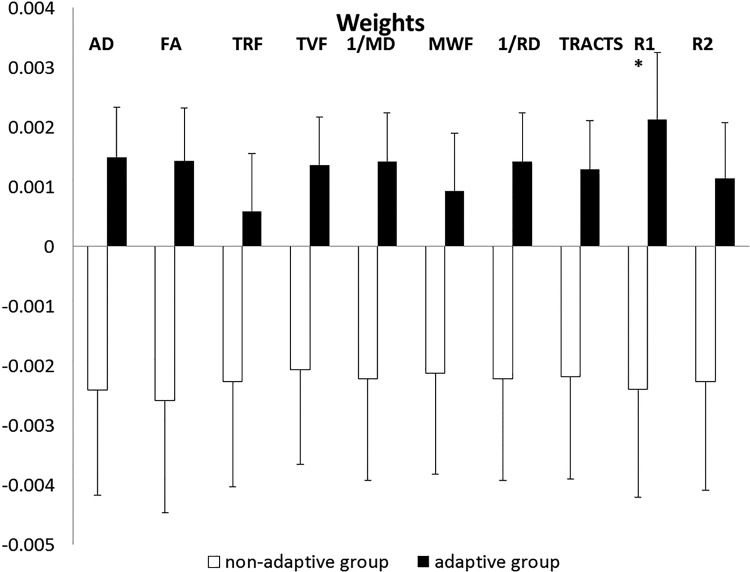
We found a significant group × time interaction effect when the network edges were weighted by the intrinsic longitudinal relaxation rate, R₁ (1/T₁), derived from the mcDESPOT protocol (F_(1,38) = 4.50, p < 0.04; as shown in Fig. 4). The post hoc two-sided t tests demonstrated an increase in global efficiency (i.e., more global integration) between nodes of the network in the adaptive group from the presession to the postsession (p < 0.04). This group difference was not seen at pretest.

Figure 4.

Difference scores (postassessment − preassessment) in global efficiency of the different weighted networks. *An increase in global efficiency following working memory training was best captured by the network weighted by the longitudinal relaxation rate (R₁). TVF, Tissue volume fraction; AD, axial diffusivity; RD, radial diffusivity.

Marginal significant interaction effects were observed for the global efficiency of the graphs weighted by diffusion-derived parameters, including FA (p = 0.057), 1/mean diffusivity (MD) (p = 0.063), axial diffusivity (p = 0.052), tissue volume fraction (p = 0.056), 1/radial diffusivity (p = 0.061), and number of streamlines (p = 0.073). No significant interaction effects were observed for the graph weighted by the total restricted fraction derived from the CHARMED protocol (p = 0.15) or in the graph derived from the covariance of gray matter volumes (p = 0.35).

Regional analyses

Clustering coefficient was evaluated at the nodal level, to identify the nodes in the network that are responsible for the working memory training effects. The FDR was used to correct for multiple comparisons. The clustering coefficient of the right anterior rostral cingulate gyrus showed a significant (group × time) interaction for the volume-weighted networks (F_(1,38) = 13.58, p < 0.05, FDR-corrected). Moreover, for the intrinsic relaxation rate, R₂, of the mcDESPOT protocol, we observed a significant (group × time) interaction effect for the clustering coefficient of the right inferior ventrolateral prefrontal cortex (F_(1,38) = 9.94, p < 0.05, FDR-corrected; Fig. 5).

Figure 5.

Change in clustering coefficient from preassessment (left) to postassessment (right). Size of the ROIs (spheres) represents the clustering coefficient. Magenta represents the node in the network that is significant after FDR correction.

The post hoc two-sided t tests of the clustering coefficient of the right anterior cingulate gyrus (volume-weighted networks) and the right inferior ventrolateral prefrontal cortex (R₂-weighted networks) revealed a significant increase (i.e., more functional segregation) from the pretraining to the post-training session in the adaptive group (p values <0.05). This difference was not apparent in the baseline session (p values >0.10).

Correlations between changes in global efficiency and improved performance on Cogmed tasks and cognitive tasks

The analyses of correlations between the changes in global efficiency from pretraining to post-training and the composite scores of the behavioral parameters showed little direct association between changes in structural network metrics and the improved performance on cognitive tests or Cogmed tasks. Using an exploratory uncorrected threshold of p < 0.05, we observed correlations between the changes in Cogmed tasks and changes in global efficiency of the R₁-weighted networks (data room, r = 0.46; rotating dots, r = 0.43), pairing better working memory performance on the Cogmed with higher efficiency of information transfer (i.e., more global integration). None of the correlations survived the necessary correction for multiple comparisons.

Correlations between global efficiency across the different parameters

The scores of global efficiency of the networks constructed with different metrics as “connection strengths” were highly intercorrelated at baseline and thus represent nonindependent observations (Table 3, lower triangle). For example, global efficiency of the network whose connections strengths were defined by the quantitative relaxation rate R₁ (1/T₁) derived from the mcDESPOT pipeline correlated strongly with global efficiency of the network weighted by the TRF derived from the CHARMED pipeline (r = 0.55, p < 0.01). There were also strong correlations between the difference scores (post-training vs pretraining) in global efficiency of the networks constructed with the different weights. Importantly, the difference scores in global efficiency of the networks weighed by R₁ were not correlated significantly with difference scores in efficiency of the network weighted by the TRF metric (r = 0.42, p = 0.063). Similarly, difference scores in efficiency of the R₁-weighted network did not correlate significantly with difference scores of the MWF-weighted network (r = 0.44, p = 0.051). Thus, although all metrics correlate at baseline, the reduction in correlation post-training suggests that the white matter network undergoes changes that are more sensitively detected with R1 and that these different metrics index different aspects of white matter microstructure (Table 3, upper triangle). Important to note, these reductions in correlation were not significant using the Fisher r-to-z transformation (all p values >0.10).

Table 3.

Correlations between global efficiency of networks weighted by different metrics, including (1) diffusion tensor MRI measures of average FA, TVF, the number of reconstructed fibers (tracts), axial diffusivity (AD), the inverse of the mean (MD), and radial diffusivity (RD); (2) MWF and the inverse of the intrinsic relaxation times T₁ (R₁) and T₂ (R₂) derived from mcDESPOT; and (3) the TRF of the CHARMED data^a

Weights	Group	AD	FA	TRF	TVF	1/MD	MWF	1/RD	TRACTS	R1	R2
AD	Adaptive		0.977*	0.851*	0.995*	0.996*	0.847*	0.996*	0.994*	0.784*	0.896*
	Nonadaptive		0.995*	0.972*	0.996*	0.999*	0.971*	0.999*	0.998*	0.994*	0.979*
FA	Adaptive	0.976*		0.873*	0.983*	0.975*	0.863*	0.975*	0.975*	0.777*	0.896*
	Nonadaptive			0.979*	0.994*	0.996*	0.981*	0.996*	0.994*	0.994*	0.983*
TRF	Adaptive	0.921*	0.924*		0.860*	0.848*	0.978*	0.848*	0.850*	0.423	0.632*
	Nonadaptive				0.978*	0.977*	0.990*	0.977*	0.977*	0.984*	0.984*
TVF	Adaptive	0.995*	0.977*	0.929*		0.998*	0.856*	0.998*	0.994*	0.788*	0.906*
	Nonadaptive					0.999*	0.972*	0.999*	0.997*	0.993*	0.976*
1/MD	Adaptive	0.997*	0.974*	0.924*	0.999*		0.849*	1.000*	0.997*	0.788*	0.904*
	Nonadaptive						0.974*	1.000*	0.999*	0.995*	0.980*
MWF	Adaptive	0.898*	0.907*	0.970*	0.904*	0.901*		0.849*	0.849*	0.442	0.643*
	Nonadaptive							0.974*	0.973*	0.983*	0.993*
1/RD	Adaptive	0.997*	0.974*	0.924*	0.999*	1.000*	0.901*		0.997*	0.788*	0.904*
	Nonadaptive								0.999*	0.995*	0.980*
TRACTS	Adaptive	0.994*	0.976*	0.924*	0.996*	0.998*	0.903*	0.998*		0.782*	0.901*
	Nonadaptive									0.995*	0.982*
R1	Adaptive	0.765*	0.756*	0.553*	0.777*	0.776*	0.545*	0.776*	0.777*		0.960*
	Nonadaptive										0.991*
R2	Adaptive	0.836*	0.846*	0.692*	0.856*	0.855*	0.700*	0.855*	0.856*	0.954*
	Nonadaptive

^aLower triangle represents pretraining (total group). Upper triangle represents difference scores.

*Correlation is significant at the 0.01 level (two-tailed).

Discussion

This is the first study to explore training-induced changes in the structural connectome using a well-controlled design to examine cognitive training with up-to-date neuroimaging methods. Our findings showed that improved performance on tasks of working memory (i.e., near-transfer effects) and executive function tasks (i.e., far-transfer effects) occur alongside an increase of global efficiency (i.e., more global integration) of the network in the adaptive group. More importantly, the relaxation rate-weighted networks provided enhanced sensitivity to training-induced white matter changes compared with other weighted networks. Furthermore, the increased efficiency was related to improved performance on Cogmed tasks.

Near-transfer effects together with more general effects on reasoning and inhibition

Significant practice-induced improvements in working memory tasks and executive functioning tests were observed in the adaptive group. Intensive adaptive training of working memory has been shown to enhance individual working memory capacity in healthy adults, in older adults, and in clinical populations, such as children with ADHD and stroke patients (for review, see Takeuchi et al., 2010). Here, we made use of an internet-based training program, originally developed by Klingberg et al. (2002, 2005) for children with ADHD, which enabled storage of training information at the trial-by-trial level and allowed us to include a nonadaptive group. The effective training time was 40–50 min per day, 5 d a week for 8 weeks (totaling ∼30 h).

Specifically, we found that performance improvements in the adaptive group were significant on two components, which loaded on tasks of working memory span (i.e., the digit span, spatial span, and automated symmetry span task), reasoning (i.e., odd one out, grammatical reasoning), and inhibition (i.e., double trouble task). In other words, the training led to improvement on tests of the same domain (near-transfer) and generalized to tasks, such as (non)verbal reasoning and inhibition (far-transfer). The near-transfer results have also been confirmed in several recent meta-analyses of working memory training using Cogmed or other training programs (e.g., Melby-Lervåg and Hulme, 2013; Peijnenborgh et al., 2015; Schwaighofer et al., 2015; Spencer-Smith and Klingberg, 2015; Cortese et al., 2015). Moreover, our results are consistent with previous studies that have demonstrated transfer to other cognitive constructs that were not part of the training program (Klingberg et al., 2002, 2005; Westerberg et al., 2007; Holmes et al., 2009). It is important to note that, in the present study, we did not observe a general training effect across all three factors (i.e., our training effects were selective to some outcome measures). We note that, in the previous reports, the participants were either very young or from a clinical cohort, as opposed to our cohort of fully mature and healthy adults (mean age: 26.5 years). It is possible, therefore, that there is less capacity for general training effects in our cohort than in clinical groups/young participants. It is also possible that our study lacked the statistical power to detect the more general training effects (Au et al., 2014; Karbach and Verhaeghen, 2014).

Working memory training modified the structural connectome

Our key graph metrics showed consistent increases in the adaptive group between the pretraining and post-training assessments indicating that mean network connectivity increased significantly in the context of adaptive training of working memory. Specifically, increases in global efficiency suggest that training resulted in increased integration in the examined network. Similarly, increases in clustering coefficient in the adaptive group, suggest that the network in the adaptive group became more closely connected at a regional level following the 8 week training regimen. This was especially the case for the right anterior cingulate gyrus and the right inferior ventrolateral prefrontal cortex. The right anterior cingulate gyrus is often associated with attentional control and mental effort (Buschkueh et al., 2012). The right inferior ventrolateral prefrontal cortex is hypothesized to play an important role in attentional orienting processes (Corbetta et al., 2008). As task difficulty was adaptively increased, the Cogmed tasks required more attentional control and deployment with training, resulting in increase in functional segregation in the adaptive group.

Our results are consistent with a previous EEG study of Langer et al. (2013), who reported increased small-worldness within frontoparietal regions of the functional network in high performers with working memory training. The combined interpretation of this previous finding with the present result that network metrics increase in the adaptive group indicates that graph theoretical analysis can capture the dynamics of both the functional and structural connectome.

Multicomponent relaxometry approach as a sensitive weight

To our knowledge, this is the first time that differently weighted structural brain networks were compared, in which the edges of the brain graphs had continuously variable weights representing potentially more specific markers of white matter than diffusion-tensor MRI indices or number of streamlines. Until recently, the question about which quantitative metric would be most useful as a weight to probe connectivity remained open (Fornito et al., 2013). The majority of connectome studies using weighted graph metrics have used diffusion tensor MRI-derived measures that reflect the local anisotropy or overall rate of diffusion (e.g., FA and MD, respectively). These FA- or MD-weighted connectomics should be interpreted with caution. Such metrics are sensitive to manifold properties of tissue (e.g., myelination, axonal density, axon diameter, intravoxel orientational dispersion) that cannot be reliably distinguished with diffusion tensor MRI (Jones et al., 2013). Other definitions of edge weight, such as the level of myelination as inferred through the magnetization transfer ratio, have been used previously (van den Heuvel et al., 2010). However, multicomponent relaxometry metrics (such as those derived from the mcDESPOT protocol used here) have been shown to have greater myelin-specificity than diffusion anisotropy or magnetization transfer imaging (Madler et al., 2008; Vavasour et al., 2011).

Our results showed that changes in global efficiency in the adaptive group could be demonstrated for the network weighted by the quantitative R₁ relaxation rate. Moreover, a significant interaction effect was reported for the clustering coefficient when using R₂ to weight the network. No significant differences were found for the network weighted by the MWF. These results suggest that these different relaxometry-derived metrics inform on different complementary aspects of tissue microstructure and biochemical features (Alexander et al., 2011; Deoni et al., 2012, 2015). Both T₁ and T₂ are affected by changes in water, lipid, and protein content. T₂ is also sensitive to changes in iron within the oligodendrocytes. MWF is thought to be more specific to changes in lipid myelin content. The results shown herein, specifically the lack of significant training-related changes of MWF versus R₁ or R₂ alterations in the adaptive group, suggest that iron, water, lipid, and protein content is altered with working memory training.

Compelling evidence from previous studies (Ortiz et al., 2004; Holmes-Hampton et al., 2012) suggests that iron accumulation by oligodendrocytes may contribute to training-induced changes in brain white matter (Zatorre et al., 2012). These alterations in iron are essential for myelin production and can influence the cholesterol and lipid biosynthesis. This induced myelin formation is probably a process of myelin remodeling in healthy adults, whereby additional myelin internodes are added to partially myelinated axons in such a way that the total number of myelinating cells increases without a concomitant increase in the total length of myelin sheath (Young et al., 2013; Wang and Young, 2014). Thus, iron accumulation by oligodendrocytes in the preparation of myelination may have caused the changes in the R₁ and R₂ relaxation rates over 2 months of training. Further exploratory analyses revealed a high correlation at baseline between global efficiency of the networks weighted by R₁ and by the TRF, but no correlation in the difference scores in the adaptive training group. In short, we suggest that our observed structural changes in the healthy young adults are underpinned by subtle changes in microscopic structures, such as oligodendrocytes, rather than changes in the number of axons or axon diameter.

Relationship between changes in the structural connectome and behavior

No correlations were found between improvements on the cognitive tasks over the training period and degree of change of graph metrics. We only observed a positive correlation between change in the Cogmed tasks and change in global efficiency in the adaptive training group. This suggests that training-induced improvements of Cogmed tasks were associated with increases in global efficiency. Our findings further support associations between working memory improvements over time and changes in graph metrics, which provides potential new insights into the mechanisms underpinning training-induced plasticity that may drive memory improvement in clinical populations.