Skip to main content
PMC home page
Nature Communications logoLink to Nature Communications
. 2016 Apr 4;7:11213. doi: 10.1038/ncomms11213

In situ microscopy of the self-assembly of branched nanocrystals in solution

Eli Sutter 1,a, Peter Sutter 2, Alexei V Tkachenko 3, Roman Krahne 4, Joost de Graaf 5, Milena Arciniegas 4, Liberato Manna 4,b
PMCID: PMC4822026  PMID: 27040366

Abstract

Solution-phase self-assembly of nanocrystals into mesoscale structures is a promising strategy for constructing functional materials from nanoscale components. Liquid environments are key to self-assembly since they allow suspended nanocrystals to diffuse and interact freely, but they also complicate experiments. Real-time observations with single-particle resolution could have transformative impact on our understanding of nanocrystal self-assembly. Here we use real-time in situ imaging by liquid-cell electron microscopy to elucidate the nucleation and growth mechanism and properties of linear chains of octapod-shaped nanocrystals in their native solution environment. Statistical mechanics modelling based on these observations and using the measured chain-length distribution clarifies the relative importance of dipolar and entropic forces in the assembly process and gives direct access to the interparticle interaction. Our results suggest that monomer-resolved in situ imaging combined with modelling can provide unprecedented quantitative insight into the microscopic processes and interactions that govern nanocrystal self-assembly in solution.

Inline graphicUnderstanding the structure and transformation of colloidal matter requires probing configurations from monomers to extended assemblies. Here, the authors use liquid-cell electron microscopy to elucidate the nucleation and growth properties of linear chains of branched nanocrystals in solution.

The self-assembly of nanocrystals into ordered superstructures promises access to photonic1,2, plasmonic3, electronic4,5, magnetic6 and catalytic7 functionalities that are tunable and may even be reconfigurable in real time8. Besides technological interest, research on crystallization of colloids is driven by the recognition that they are not simply large atom equivalents but represent a form of matter with complex collective behaviour that can be controlled via the interplay of entropic, van der Waals, steric and dipolar interactions9,10,11, by attaching molecular linkers such as coordinated ligands or DNA12,13,14, or by using shaped particles15. Understanding the structure, formation and transformation of colloidal matter requires probing particle configurations from monomers to extended periodic or aperiodic assemblies. Computer simulations provide this capability16,17, but experiments are complicated by the need to interrogate processes in liquids that allow suspended particles to diffuse and interact freely. Larger micro-colloids can be imaged with single-particle resolution by optical microscopy18,19, but offer limited diversity of materials and shapes20. For nanocrystals, in situ measurements have largely been restricted to reciprocal space techniques14,21, which yield little information on the assembly process or the underlying forces. Liquid-cell electron microscopy (LCEM) has recently been developed into a tool capable of imaging processes in liquids with nanometre resolution22,23,24. LCEM has been used previously to study single-layer assembly of compact nanocrystals driven by convective transport during solvent drying25. A large class of self-assembly processes, for instance the entropy-driven assembly of polyhedral nanocrystals15 or the DNA-guided crystallization12,13,14,26 and reconfiguration27 of spherical nucleic acid conjugates occurs in bulk solutions with transport by Brownian motion.

Using the example of the one-dimensional (1D) self-assembly of CdSe/CdS octapods, we demonstrate the ability of LCEM to dynamically probe such solution-phase self-assembly processes in real space with nanometre resolution. Octapods, branched nanocrystals with a complex but still highly symmetric shape28,29,30, have been found to self-assemble into a variety of superstructures: interlocked 1D chains in bulk liquid, two-dimensional square lattices on substrates31 or micron-sized three-dimensional (3D) structures of aligned 1D chains21. Strongly anisotropic interactions are thought to be key to their rich set of accessible superstructures. By real-time imaging with monomer resolution, the in situ LCEM observations reported here establish several key aspects of the self-assembly of ordered linear chains of octapods in solution. The trimer, that is, a three-octapod chain, is the shortest stable chain of interlocked octapods. Two-octapod chains (dimers) are suppressed, which implies that they are unstable. Dynamic fluctuations and the incorporation of trimers and of longer oligomers are mostly responsible for the growth of the interlocked chains, which in this way can reach up to ∼20 octapods in length. Besides tracking nucleation and growth, the need for in situ observations is illustrated by measurements of important properties, such as the interparticle spacing in the chains. In their native solution environment, the octapod chains are much less densely packed than observed in conventional ex situ analysis after drying or vitrification of the solvent. On the basis of the characteristics obtained from in situ microscopy, a statistical mechanics model is built that explains the chain-length distribution (notably the absence of stable dimers), establishes the relative importance of van der Waals and entropic forces in the self-assembly, and determines the strength of the particle–particle interaction. Our findings illustrate the ability of in situ microscopy combined with modelling to obtain detailed quantitative insight into nanocrystal self-assembly processes in solution.

Results

In situ liquid-cell electron microscopy

In situ microscopy was performed by scanning transmission electron microscopy (STEM) using solutions of CdSe/CdS octapods (pod length L∼(47±3) nm, L/Dp∼4.2; see Fig. 1) in toluene with a nominal particle concentration of 10−8 M, prepared according to reported methods21.

Figure 1. CdSe/CdS octapods.

Figure 1

Open in a new tab

(a) Schematic representation of geometry of a single octapod-shaped CdSe/CdS nanocrystal. (b) TEM image of a group of CdSe/CdS octapods drop-cast onto amorphous carbon film. Scale bar, 200 nm. (c,d) High-magnification TEM images of octapods with different orientations. Scale bar, 20 nm. TEM, transmission electron microscopy.

The solution was loaded in the liquid cell and observed within a viewing area where it was held between two electron transparent SiNx membranes (see Methods). Immediately after starting the observations, there was a higher concentration of octapods near the corners of the cell (for example, Supplementary Figs 1 and 6) and along the edges of the window, whereas the centre of the cell remained less populated.

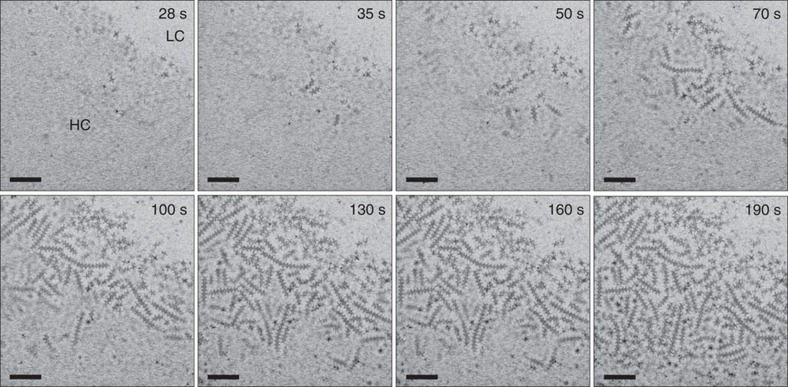
Figure 2 shows a representative sequence of liquid-cell STEM images of octapods in toluene (extracted from Supplementary Movie 1) that follows the time evolution near the boundary between high and low concentration. Initially (observation time t<30 s) the solution within these areas appears homogeneous, with diffuse contrast and streaking suggesting dispersed individual octapods and possibly chains submerged in the bulk solvent. As the self-assembly progresses, octapods and linear chains are clearly observed (t⩾35 s). Chains of interlocked octapods form exclusively in the region with higher concentration near the edges and corners of the viewing window (Supplementary Fig. 7). The first clear contrast is due to two short-chain segments, each containing three interlocked octapods (t=35 s). In the next ∼20 s, additional short chains become visible and the first longer chains appear; surrounding diffuse contrast indicates continuing rapid motion in the solvent. During the further evolution, the existing chains grow longer so that the field of view becomes progressively crowded with interlocked octapod chains of different length. An overall downward directionality might be interpreted as a sign of progressive drying of the solvent and concomitant increase of the octapod density in the remaining solution, such as in evaporative self-assembly processes32,33. Further examination shows, however, that the formation of octapod chains occurs in a 3D solution environment of constant thickness, and is not significantly influenced by evaporation of the toluene solvent (see Supplementary Note 1 and Supplementary Figs 3–6,8 and 9).

Figure 2. In situ LCEM of the assembly of octapods into linear chains.

Figure 2

Open in a new tab

Selected inverted dark-field STEM images from Supplementary Movie 1 showing the formation of ordered chains of octapods in toluene. Scale bar, 500 nm. The images show the evolution of the system starting from single octapods dispersed in the entire liquid volume (for t<30 s, ‘HC'/‘LC': high/low concentration of octapods) to interlocked chain-like structures that aggregate near the top membrane of the liquid cell.

Analysis of real-time image sequences allows us to develop a detailed picture of the self-assembly of 1D octapod chains in solution. Important elements, such as image contrast, predominant octapod orientations and a limited 3D imaging capability in STEM are discussed in the Methods and Supplementary Fig. 2. Figure 2 and additional data (Supplementary Movies 2–6; extracted images in Fig. 3 and Supplementary Figs 10–14) document the assembly mechanism. The process is initiated by the emergence of short segments of tightly interlocked octapod chains. The majority of chains are built from interlocked units, similar to those analysed ex situ in vitrified solvent21, but observations of pairs or larger numbers of monomers interacting tip-to-tip and diffusing as a non-interlocked cluster (Supplementary Movies 2 and 3) suggest a richer set of interactions between monomers than the pod-to-pod van der Waals forces invoked so far.

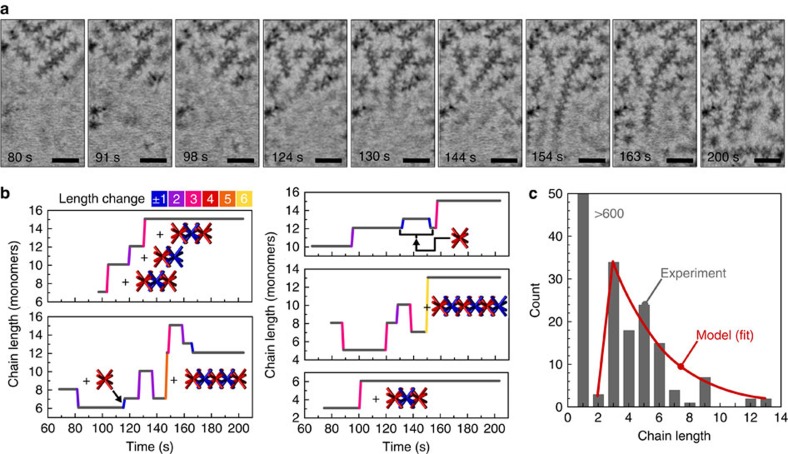
Figure 3. Imaging octapod chains and tracking their growth with monomer resolution; modelling of the assembly process.

Figure 3

Open in a new tab

(a) Representative time-lapse series of inverted dark-field STEM images showing the growth of a long chain of interlocked octapods. Scale bar, 200 nm. (b) Representative traces of the chain length as a function of time, showing length changes occurring only in exceptional cases by addition or removal of monomers, but instead mostly via incorporation and detachment of longer oligomers. Length changes are colour coded as shown. Longer horizontal lines imply that the length stays unchanged for extended time periods. (c) Length distribution of interlocked octapod chains, determined by ex situ STEM after opening the liquid cell (grey bars; total sample size: 752 objects, of which 642 were individual octapods). Note the absence of interlocked dimers. Red line: best fit of the length distribution within the statistical mechanics model described in the text.

Short interlocked octapod chains typically emerge from the bulk solution, which indicates that they are formed there. Observations of the fluid with focal plane near the top SiNx membrane show the attachment and detachment of such short-chain segments as the predominant process of forming long 1D chains (Fig. 2). Chain growth is clearly a dynamic process, subject to fluctuations that add and remove segments of varying length (Fig. 3a,b). The smallest interlocked oligomer unit observed in our experiments is the trimer, that is, consists of three octapods. A survey of a large number of chains ex situ after opening the liquid cell (Fig. 3c) and in situ at different stages of the assembly (Fig. 4a) shows only isolated instances of interlocked dimers, whereas trimers and longer chains are much more abundant. The addition of trimers and longer oligomers is also the predominant elementary step in chain growth (Fig. 3b), while monomer incorporation is quite rare and is often followed by detachment of the same unit, suggesting incomplete locking (for example, Fig. 3b). Two-octapod increments are occasionally seen (Fig. 3b) but the absence of stable dimers in the solution suggests that these instances may actually represent a sequential addition of monomers or of non-interlocked dimers.

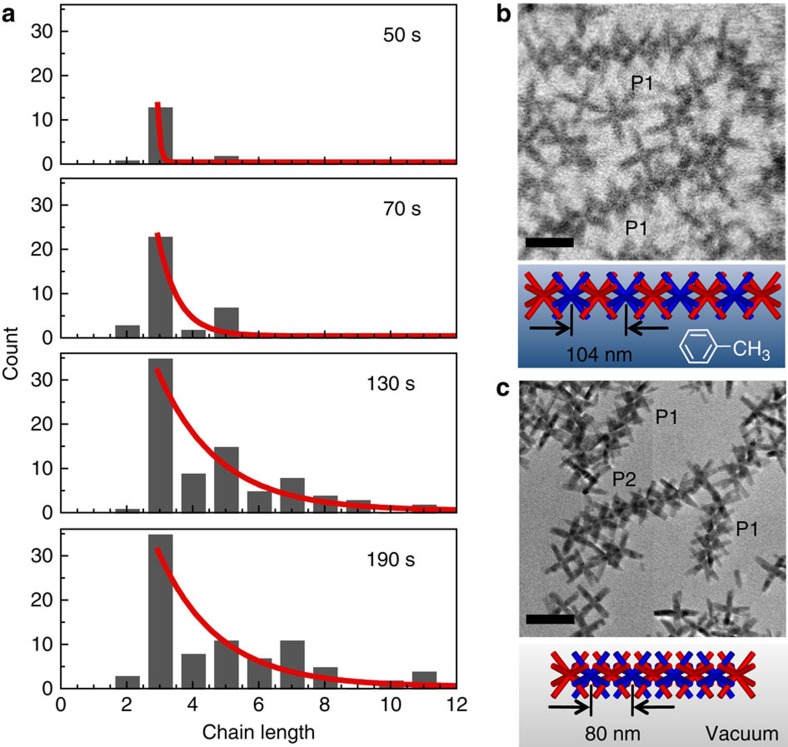
Figure 4. Characteristics of octapod chains determined in situ.

Figure 4

Open in a new tab

(a) Length distribution at different times during the self-assembly. Red lines are exponential fits for chain lengths ⩾3. (b) Octapod chains in toluene, imaged in situ by liquid-cell STEM. Two longer chains are imaged in projection P1 (see Methods and Supplementary Fig. 2). (c) Octapod chains in projections P1 and P2 imaged by TEM in vacuum after opening the liquid cell, shown at the same scale as b. Scale bars, 100 nm. Note the substantially larger interparticle spacing observed in toluene (52±2 nm) compared with the dried assemblies (40±2 nm), which suggests that capillary forces upon drying (and during freezing for cryo-TEM)21 cause a significant tightening of the chains. TEM, transmission electron microscopy.

The observed solution-phase self-assembly deviates from a classic nucleation and growth scenario, which presumes the formation of a stable nucleus followed by attachment of monomer units34. While there appears to be a stable nucleus, the trimer, the further growth in most cases does not involve the incorporation of individual octapods, even though monomers are abundant and show extensive Brownian motion (Supplementary Note 2 and Supplementary Fig. 16). Instead, the stable nucleus grows primarily by attachment of other supercritical units, all of which are mobile in the solution. Attachment is facilitated by a considerable bending flexibility of the chains, which, for instance, allows long chains near the membrane to reach into the bulk liquid to capture a diffusing segment (Fig. 3a, Supplementary Fig. 10 and Supplementary Movie 4).

Statistical mechanical model

We constructed a model to probe the physical origin of the striking suppression of dimers and the prevalence of trimers as the shortest chain of interlocked octapods in solution. Using the measured chain-length distribution and other characteristics identified uniquely by in situ microscopy, the model provides insight into the interactions underlying the self-assembly process. In equilibrium, the probability of finding a chain of length n can be determined from the grand canonical distribution function:

graphic file with name ncomms11213-m1.jpg

Here the chemical potential of octapods is determined by the monomer concentration, C1, as μ=kT In C1; H is the interaction Hamiltonian of the system, β=1/kT and dΓ represents an integration over internal degrees of freedom of the chain, that is, positions and orientations of n−1 octapods. If we neglect physical binding between the octapods (that is, assume H=0, but exclude their mutual overlap), the confinement of a single octapod within a cage made by two of its neighbours can be represented as a factor v. This factor has the meaning of an effective localization volume and it accounts for the loss of translational and orientational entropies of the confined octapod. If Δ is a typical range of translational fluctuations, the corresponding amplitude of the angular degrees of freedom is Δ/R, where R is a characteristic radius of the octapod. Therefore an integration over three translational and three orientational degrees of freedom gives an effective localization volume v∼Δ6/R3.

We can now take into account mutual binding of the octapods. In our model, two octapods in contact create reversible bonds, each having the same characteristic binding energy 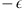Inline graphic and localization range δ (∼2.5 nm, set by the length of the ligands). We represent these bonds as a collection of two-state systems that can be in a bound or an unbound state independently of each other. This leads to the following distribution function:

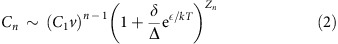graphic file with name ncomms11213-m3.jpg

An alternative, more detailed derivation of this result is presented in Supplementary Note 3. Zn is the total number of contacts between the octapods that can be independently formed within the chain. This parameter is of crucial importance for understanding the observed chain statistics, in particular the substantial suppression of dimers compared with longer chains. We assume the maximum number of contacts that can be made between nearest neighbours to be 4. This implies that a tighter interlocking of two octapods with eight mutual contacts is not sterically allowed, presumably because of the geometry of their octahedral cores. This is consistent with the experimental observations (see below). In addition to the interactions with its nearest neighbours, it is assumed that fluctuations in the chain allow an octapod to create up to four contacts with any of its next-nearest neighbours. This consideration sets an upper bound to the number of contacts in a chain: Zn≤4(n−1)+4(n−2)=8n−12. However, this is not the only limitation. Each octapod has six degrees of freedom: three translational and three rotational. This means that for trimers (n=3) the number of possible contacts (12) is exactly equal to the number of internal degrees of freedom of the chain, 6(n−1). For dimers (n=2), the number of contacts is less than the number of degrees of freedom (4 and 6, respectively), while for chains longer than (n⩾3), the situation is opposite. The maximally connected structure with Zn=8n−12 would be over-constrained, and can only exist if the shapes are identical and symmetric to a very high precision. Any imperfection would lead to a loss of some of the contacts. We therefore postulate that the number of internal degrees of freedom sets another bound on the value of Zn, that is,

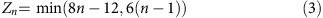graphic file with name ncomms11213-m4.jpg

This model can successfully describe the observed chain statistics, including the suppression of dimers. In fact, its major predictions are very robust with respect to the choice of the model parameters. For n⩾3, Zn=6(n−1), that is, the overall distribution function is proportional to an exponential, Cn∝pn−1, where 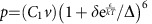Inline graphic. For n=2, Zn=4, that is, dimers are suppressed by a factor (C1v)1/3.

As far as the specific parameters are concerned, the characteristic radius R of the octapod is set to ∼30 nm, half the pod length; Δ≈15 nm was estimated as the difference between the apparent interparticle distance in the chain (50 nm) and its minimal value allowed geometrically (35 nm). The estimated average concentration of free octapods in the area in which self-assembly takes place is C1∼10−6 M∼10−6 nm−3, so that C1ν∼C1Δ6/R3 is of order 10−3.

Discussion

Once the geometrical parameters are fixed, the only free parameter of the model is the energy per contact, 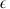Inline graphic. The value of the energy that gives the best fit to the experimental data is 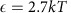Inline graphic (Fig. 3c), approximately twice the energy expected for a pure van der Waals interaction between two crossed pods21. The difference may be due to effects of inter-digitation of the ligands. The robustness of our model can be illustrated by the fact that changing C1v by a factor of 2 leads to a correction to the binding strength 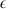Inline graphic of 0.1kT, and to a relative change of the dimer fraction of only 25%. Additional molecular dynamics simulations also show that a pure van der Waals interaction is not sufficient to induce assembly (see Supplementary Note 4, Supplementary Methods and Supplementary Figs 17–19). Adding a short-range attraction does lead to chain formation.

In our model the assembly is driven not only by the energy gained because of binding. The fact that each contact fluctuates between bound and unbound states results in an additional entropic-free energy contribution 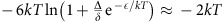Inline graphic per particle that stabilizes the chain. A final piece of evidence that supports the proposed mechanism stems from measurements of the octapod spacing in chains, determined in situ to avoid uncertainties due to capillary forces that may affect ex situ measurements of the lattice constant of dried or vitrified assemblies. The observed next-nearest neighbour octapod distance in solution (≈100 nm, Fig. 4b) is in fact greater than the one needed for physical contact between four tips of the two octapods (≈85 nm, close to the value found ex situ in vacuum (Fig. 4c) or vitrified solvent21). This distance is however sufficient to make up to two simultaneous contacts upon some rotation. In this way, the system can achieve the required value of Zn (6 per particle) without paying an excessive entropic penalty for the extra confinement. The loose packing in solution also rationalizes characteristics important to chain growth, such as the facile addition and removal of segments and the bending of chains in tight radii, involved in capturing chain segments at later growth stages.

By imaging the self-assembly of branched nanocrystals with monomer resolution in solution, our experiments have pointed out a novel avenue for studying key aspects of self-assembly, such as the mechanism of formation and growth of ordered nanocrystal arrays and the interparticle spacing in solution. On the basis of characteristics obtained from in situ microscopy, a statistical mechanics model could be built that established the relative importance of van der Waals and entropic forces and determined the strength of the particle–particle interaction. A similar approach can be applied to other systems, such as spherical or polyhedral particles that arrange in two-dimensional or 3D assemblies, binary or more complex nanocrystal mixtures, or the folding and assembly of suitably tagged proteins. Once cells are developed that allow for controlled mixing of different liquids, external stimuli (for example, changes in PH, addition of co-solvents or depletants and so on.) may be used to actively change the assembly process while observing the outcome in real time.

Methods

Materials preparation

CdSe/CdS octapod-shaped nanocrystals were synthesized following a procedure based on the growth of CdS pods on cuboctahedral CdSe seeds that are prepared after a cation exchange process from Cu2−xSe nanocrystals. Briefly, a reaction flask was loaded with 120 mg of CdO and various surfactants (6 g of trioctylphosphine oxide, 160 mg of hexylphosphonic acid and 580 mg of octadecylphosphonic acid). The flask was kept under vacuum at 150 °C for 120 min. The temperature was increased to 350 °C and 1.6 g of trioctylphosphine was injected. After the recovery of the temperature, an aliquot of previously prepared Cu2−xSe nanocrystals with a concentration of 0.3 × 10−9 M was quickly injected in the flask after the addition of 16:0.5 mg S/trioctylphosphine solution. The reaction was run for 10 min and cooled down to the room temperature. After several washing steps with an anti-solvent, the final product was dispersed in 5 ml of toluene.

In situ liquid-cell STEM experiments

The liquid-cell experiments were carried out in a dedicated specimen holder (Hummingbird Scientific) using micro-fabricated liquid cells, consisting of two 30-nm-thick SiNx membrane windows with 50 μm × 50 μm window area supported by Si frames. The spacing between the windows was controlled using 200 and 300 nm polystyrene beads or 100 and 200 nm SiO2 spacers. STEM imaging was performed in a FEI Titan 80–300 environmental Cs image corrected microscope operated at 300 kV. Low-loss electron energy loss spectra (EELS) were acquired using a Gatan Enfina spectrometer with an entrance aperture semi-angle of 5 mrad. The weighted average of the ratio of the thickness and the inelastic mean free path for the toluene and the two SiN membranes (each 30 nm thick) was determined from low-loss EELS, and the toluene thickness was calculated from it according to ref. 35 (Supplementary Figs 3,5 and 6). Typically, ∼1 μl of the octapod-containing solution with an initial concentration of particles of 10−8 M was introduced in the liquid cell. The holder was inserted in the microscope immediately after loading of the cell. The time delay between loading of the solution and initiating the observations was ∼10–20 min. STEM imaging was performed with ∼2 Å probe size and∼0.2–0.3 nA beam current, measured in vacuum before introduction of the liquid cell. Time-lapse series of STEM images were acquired at several positions along the cell window, and at all positions the assembly of octapods was observed in real time. The results of the observations at two different areas are shown in Supplementary Movies 1 and 8. For Supplementary Movies 1–7 time-lapse STEM images of the assembly of the octapods were recorded with frame interval of 1 s and 3.96 μs dwell time/pixel. The conditions for the acquisition of STEM images were: electron dose rate of 1.35 e− Å−2 s−1, electron dose per image of 1.35 e− Å−2, total electron dose for the movie (204 frames) of 275.4 e− Å−2. The Supplementary Movies 1–7 are played at 20 frames per second. The original STEM images are shown in Supplementary Fig. 1. The STEM images in which the octapods appear dark on a light background have been inverted (in the program ImageJ) to facilitate visual perception and analysis. Supplementary Movie 8 is a series of time-lapse images recorded at a frame interval of 9 s.

Image contrast in in situ liquid STEM of octapod assemblies

The use of a focused probe in STEM, whose focal plane coincides with one of the membranes (for example, the top membrane) of the liquid cell, implies a limited 3D imaging capability. As an octapod chain transits from the bulk solution towards the membrane (Supplementary Fig. 2a, top), it initially appears with soft contrast that progressively sharpens (Supplementary Fig. 2a, bottom). Electron beam exposure generally induces octapods and chains to move from the interior of the solution towards the SiNx membrane, possibly as a result of a beam-induced charging of the membrane and interaction with the tips of the polar (wurtzite) CdS pods via Coulomb or higher order multipole forces. While this behaviour facilitates high-resolution imaging by concentrating material near the focal plane, which allows to clearly distinguish individual octapods and their orientation in solution and within 1D chains, the attraction to the membrane is sufficiently weak that free octapod monomers can move via Brownian motion in the solution (see Supplementary Note 2 and Supplementary Fig. 16) with a substantially larger diffusion coefficient (Dt∼10−15 m2 s−1) than found previously for particles in ultrathin liquid layers36. Octapod chains also show significant freedom of motion, including in-plane and out-of plane bending (Supplementary Fig. 10) and diffusion (Supplementary Fig. 11).

The interaction with the SiNx membrane also acts to reduce the phase space of possible orientations of octapod chains (Supplementary Figs 2d,e and 15), which aids in the analysis of the chain length and allows counting the number of octapods in interlocked 1D chains with monomer resolution. Surveying a large number of chains, a large majority appears in projection P1, in which the pods of neighbouring nanoparticles project symmetrically towards the membrane. A minority of chains shows projection P2, in which they are rotated by 22.5° around their axis relative to P1. Occasionally, octapod chains with mixed appearance (that is, partial P1 and P2) are observed. While still interlocked, these chains contain a stacking defect in which one section (a four-octapod segment in orientation P2, in Supplementary Fig. 2e) is rotated by 22.5° relative to the remainder of the chain (a five-octapod segment in projection P1, Supplementary Fig. 2e).

Additional information

How to cite this article: Sutter, E. et al. In-situ microscopy of the self-assembly of branched nanocrystals in solution. Nat. Commun. 7:11213 doi: 10.1038/ncomms11213 (2016).

Supplementary Material

Supplementary Information

Supplementary Figures 1-19, Supplementary Notes 1-4, Supplementary Methods and Supplementary References

ncomms11213-s1.pdf (17.9MB, pdf)
Supplementary Movie 1

Time-lapse sequence #1 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene.

Download video file (13.3MB, avi)
Supplementary Movie 2

Time-lapse sequence #2 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene

Download video file (1.7MB, avi)
Supplementary Movie 3

Time-lapse sequence #3 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene.

Download video file (1.6MB, avi)
Supplementary Movie 4

Time-lapse sequence #4 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene.

Download video file (2.2MB, avi)
Supplementary Movie 5

Time-lapse sequence #5 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene

Download video file (4.6MB, avi)
Supplementary Movie 6

Time-lapse sequence #6 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene.

Download video file (715KB, avi)
Supplementary Movie 7

Time-lapse sequence #7 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene.

Download video file (5.7MB, avi)
Supplementary Movie 8

Time-lapse sequence #8 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene.

Download video file (9.7MB, avi)

Acknowledgments

This research has been carried out in part at the Center for Functional Nanomaterials, Brookhaven National Laboratory, which is supported by the US Department of Energy, Office of Basic Energy Sciences, under Contract No. DE-SC0012704. L.M. and M.A. acknowledge financial support from the European Union through the FP7 starting ERC grant NANO-ARCH (contract number 240111). We thank K. Jungjohann for participating in some of the experiments and measuring EELS spectra, and E. Krings for analysing the chain-length distributions. J.d.G. acknowledges financial support from the NWO Rubicon grant (#680501210) and Prof. A. Arnold and Dr O. Hickey for useful discussions.

Footnotes

Author contributions E.S. conceived the study, performed in situ microscopy experiments, analysed the data and co-wrote the paper. P.S. analysed the data and co-wrote the paper. R.K. conceived the experiment and contributed to data analysis, discussion, interpretation of data and paper writing. J.d.G. performed numerical simulations, contributed to the discussion of the results and paper writing. A.T. conceived the statistical mechanical model explaining the octapod chain-length distribution. A.T. contributed to discussion, interpretation of the data, and writing of the paper. M.A. contributed to the data analysis, discussion, interpretation of the data and paper writing. L.M. contributed to the data analysis, discussion, interpretation of the data and paper writing. All authors commented on the manuscript.

References

  1. Konstantatos G., Clifford J., Levina L. & Sargent E. H. Sensitive solution-processed visible-wavelength photodetectors. Nat. Photon. 1, 531–534 (2007) . [Google Scholar]
  2. Sun L. et al. Bright infrared quantum-dot light-emitting diodes through inter-dot spacing control. Nat. Nanotechnol. 7, 369–373 (2012) . [DOI] [PubMed] [Google Scholar]
  3. Tao A., Sinsermsuksakul P. & Yang P. Tunable plasmonic lattices of silver nanocrystals. Nat. Nanotechnol. 2, 435–440 (2007) . [DOI] [PubMed] [Google Scholar]
  4. Dong A., Jiao Y. & Milliron D. J. Electronically coupled nanocrystal superlattice films by in situ ligand exchange at the liquid–air interface. ACS Nano 7, 10978–10984 (2013) . [DOI] [PubMed] [Google Scholar]
  5. Choi J.-H. et al. Bandlike transport in strongly coupled and doped quantum dot solids: a route to high-performance thin-film electronics. Nano Lett. 12, 2631–2638 (2012) . [DOI] [PubMed] [Google Scholar]
  6. Cheon J. et al. Magnetic superlattices and their nanoscale phase transition effects. Proc. Natl Acad. Sci. USA 103, 3023–3027 (2006) . [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Yamada Y. et al. Nanocrystal bilayer for tandem catalysis. Nat. Chem. 3, 372–376 (2011) . [DOI] [PubMed] [Google Scholar]
  8. Kim Y., Shah A. A. & Solomon M. J. Spatially and temporally reconfigurable assembly of colloidal crystals. Nat. Commun. 5, 3676 (2014) . [DOI] [PubMed] [Google Scholar]
  9. Collier C. P., Vossmeyer T. & Heath J. R. Nanocrystal superlattices. Annu. Rev. Phys. Chem. 49, 371–404 (1998) . [DOI] [PubMed] [Google Scholar]
  10. Shevchenko E. V., Talapin D. V., Kotov N. A., O'Brien S. & Murray C. B. Structural diversity in binary nanoparticle superlattices. Nature 439, 55–59 (2006) . [DOI] [PubMed] [Google Scholar]
  11. Frenkel D. Entropy-driven phase transitions. Phys. A Stat. Mech. Appl. 263, 26–38 (1999) . [Google Scholar]
  12. Mirkin C. A., Letsinger R. L., Mucic R. C. & Storhoff J. J. A DNA-based method for rationally assembling nanoparticles into macroscopic materials. Nature 382, 607–609 (1996) . [DOI] [PubMed] [Google Scholar]
  13. Park S. Y. et al. DNA-programmable nanoparticle crystallization. Nature 451, 553–556 (2008) . [DOI] [PubMed] [Google Scholar]
  14. Nykypanchuk D., Maye M. M., van der Lelie D. & Gang O. DNA-guided crystallization of colloidal nanoparticles. Nature 451, 549–552 (2008) . [DOI] [PubMed] [Google Scholar]
  15. Damasceno P. F., Engel M. & Glotzer S. C. Predictive self-assembly of polyhedra into complex structures. Science 337, 453–457 (2012) . [DOI] [PubMed] [Google Scholar]
  16. Auer S. & Frenkel D. Prediction of absolute crystal-nucleation rate in hard-sphere colloids. Nature 409, 1020–1023 (2001) . [DOI] [PubMed] [Google Scholar]
  17. Cacciuto A., Auer S. & Frenkel D. Onset of heterogeneous crystal nucleation in colloidal suspensions. Nature 428, 404–406 (2004) . [DOI] [PubMed] [Google Scholar]
  18. Gasser U., Weeks E. R., Schofield A., Pusey P. N. & Weitz D. A. Real-space imaging of nucleation and growth in colloidal crystallization. Science 292, 258–262 (2001) . [DOI] [PubMed] [Google Scholar]
  19. Yethiraj A. & van Blaaderen A. A colloidal model system with an interaction tunable from hard sphere to soft and dipolar. Nature 421, 513–517 (2003) . [DOI] [PubMed] [Google Scholar]
  20. Vutukuri H. R., Imhof A. & van Blaaderen A. Fabrication of polyhedral particles from spherical colloids and their self-assembly into rotator phases. Angew Chem. Int. Ed. Engl. 53, 13830–13834 (2014) . [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Miszta K. et al. Hierarchical self-assembly of suspended branched colloidal nanocrystals into superlattice structures. Nat. Mater. 10, 872–876 (2011) . [DOI] [PubMed] [Google Scholar]
  22. Williamson M. J., Tromp R. M., Vereecken P. M., Hull R. & Ross F. M. Dynamic microscopy of nanoscale cluster growth at the solid-liquid interface. Nat. Mater. 2, 532–536 (2003) . [DOI] [PubMed] [Google Scholar]
  23. Zheng H. M. et al. Observation of single colloidal platinum nanocrystal growth trajectories. Science 324, 1309–1312 (2009) . [DOI] [PubMed] [Google Scholar]
  24. Sutter E. et al. In situ liquid cell electron microscopy of Ag-Pd galvanic replacement reactions on Ag nanoparticles. Nat. Commun. 5, 4946 (2014) . [DOI] [PubMed] [Google Scholar]
  25. Park J. et al. Direct observation of nanoparticle superlattice formation by using liquid cell transmission electron microscopy. ACS Nano 6, 2078–2085 (2012) . [DOI] [PubMed] [Google Scholar]
  26. Rogers W. B. & Manoharan V. N. Programming colloidal phase transitions with DNA strand displacement. Science 347, 639–642 (2015) . [DOI] [PubMed] [Google Scholar]
  27. Maye M. M. et al. Switching binary states of nanoparticle superlattices and dimer clusters by DNA strands. Nat. Nanotechnol. 5, 116–120 (2010) . [DOI] [PubMed] [Google Scholar]
  28. Li H., Kanaras A. G. & Manna L. Colloidal branched semiconductor nanocrystals: state of the art and perspectives. Acc. Chem. Res. 46, 1387–1396 (2013) . [DOI] [PubMed] [Google Scholar]
  29. Glotzer S. C. & Solomon M. J. Anisotropy of building blocks and their assembly into complex structures. Nat. Mater. 6, 557–562 (2007) . [DOI] [PubMed] [Google Scholar]
  30. Conca E. et al. Charge separation in Pt-decorated CdSe@CdS octapod nanocrystals. Nanoscale 6, 2238–2243 (2014) . [DOI] [PubMed] [Google Scholar]
  31. Qi W. et al. Ordered two-dimensional superstructures of colloidal octapod-shaped nanocrystals on flat substrates. Nano Lett. 12, 5299–5303 (2012) . [DOI] [PubMed] [Google Scholar]
  32. Brinker C. J., Lu Y., Sellinger A. & Fan H. Evaporation-induced self-assembly: nanostructures made easy. Adv. Mater. 11, 579–585 (1999) . [Google Scholar]
  33. Rabani E., Reichman D. R., Geissler P. L. & Brus L. E. Drying-mediated self-assembly of nanoparticles. Nature 426, 271–274 (2003) . [DOI] [PubMed] [Google Scholar]
  34. De Yoreo J. J., Vekilov P. in Biomineralization eds Dove P.M., De Yoreo J.J., Weiner S. 57–93Mineralogical Society of America (2003) . [Google Scholar]
  35. Egerton R. F. Electron Energy Loss Spectroscopy in the Electron Microscope Plenum Press (1996) . [Google Scholar]
  36. Lu J. Y., Aabdin Z., Loh N. D., Bhattacharya D. & Mirsaidov U. Nanoparticle dynamics in a nanodroplet. Nano Lett. 14, 2111–2115 (2014) . [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures 1-19, Supplementary Notes 1-4, Supplementary Methods and Supplementary References

ncomms11213-s1.pdf (17.9MB, pdf)
Supplementary Movie 1

Time-lapse sequence #1 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene.

Download video file (13.3MB, avi)
Supplementary Movie 2

Time-lapse sequence #2 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene

Download video file (1.7MB, avi)
Supplementary Movie 3

Time-lapse sequence #3 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene.

Download video file (1.6MB, avi)
Supplementary Movie 4

Time-lapse sequence #4 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene.

Download video file (2.2MB, avi)
Supplementary Movie 5

Time-lapse sequence #5 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene

Download video file (4.6MB, avi)
Supplementary Movie 6

Time-lapse sequence #6 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene.

Download video file (715KB, avi)
Supplementary Movie 7

Time-lapse sequence #7 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene.

Download video file (5.7MB, avi)
Supplementary Movie 8

Time-lapse sequence #8 of liquid cell STEM images following the self-assembly of branched octapod nanocrystals in toluene.

Download video file (9.7MB, avi)

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES