Removal of between-run variation in a multi-plate qPCR experiment

Abstract

Quantitative PCR (qPCR) is the method of choice in gene expression analysis. However, the number of groups or treatments, target genes and technical replicates quickly exceeds the capacity of a single run on a qPCR machine and the measurements have to be spread over more than 1 plate. Such multi-plate measurements often show similar proportional differences between experimental conditions, but different absolute values, even though the measurements were technically carried out with identical procedures. Removal of this between-plate variation will enhance the power of the statistical analysis on the resulting data. Inclusion and application of calibrator samples, with replicate measurements distributed over the plates, assumes a multiplicative difference between plates. However, random and technical errors in these calibrators will propagate to all samples on the plate. To avoid this effect, the systematic bias between plates can be removed with a correction factor based on all overlapping technical and biological replicates between plates. This approach removes the requirement for all calibrator samples to be measured successfully on every plate. This paper extends an already published factor correction method to the use in multi-plate qPCR experiments. The between-run correction factor is derived from the target quantities which are calculated from the quantification threshold, PCR efficiency and observed C_q value. To enable further statistical analysis in existing qPCR software packages, an efficiency-corrected C_q value is reported, based on the corrected target quantity and a PCR efficiency per target. The latter is calculated as the mean of the PCR efficiencies taking the number of reactions per amplicon per plate into account. Export to the RDML format completes an RDML-supported analysis pipeline of qPCR data ranging from raw fluorescence data, amplification curve analysis and application of reference genes to statistical analysis.

1. Introduction

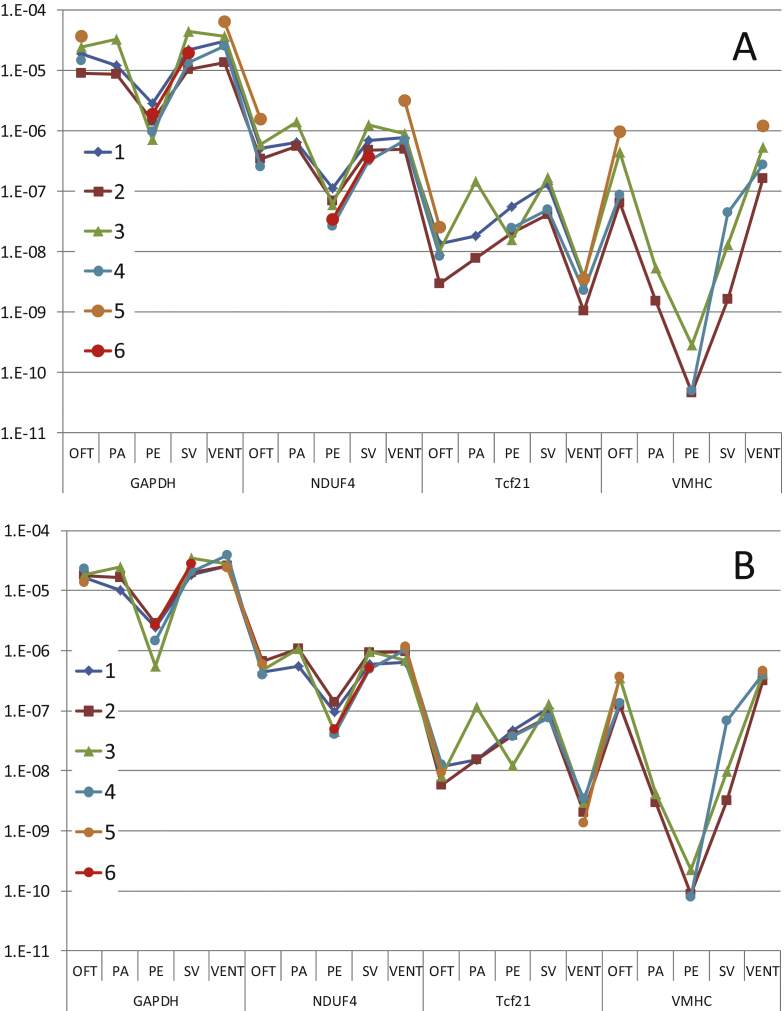
In experimental biology, replicating a series of measurements under presumably identical circumstances often leads to results that show the same proportional differences between experimental groups, disease states or treatments, but different absolute values within each of the conditions in the different measurement sessions [1]. A quantitative PCR (qPCR) analysis also often requires more than one run, each run consisting of one plate with measurements for every well on the plate. In such a multi-plate qPCR analysis, between-run variation may result from small, but systematic, differences in cDNA, primer and reagent concentrations, reaction temperatures and timing of denaturing, annealing and elongation phases. Apart from this, the yield of the RT-reaction and handling of the plates prior to running the PCR are systematically affecting the results per run. The fact that a logarithmic plot of replicated measurements shows parallel lines per run (Fig. 1A) indicates that these variation sources together proportionally increase or decrease the outcome of the amplification reaction for all samples on the plate. Therefore, this between-run variation is commonly removed using calibrator samples. In this correction, every observed target quantity on the plate is divided by the geometric mean of the target quantities of the calibrator samples on that plate [2]. Consequently, all observations on a plate are divided by a constant, the so-called calibration factor; the between-run variation is thus assumed to result from a multiplicative factor that affects the whole plate in a similar way. A drawback of the calibrator sample approach is that it requires the successful measurement of all calibrator samples because missing values will bias the calibration factor. Moreover, the calibrator samples cannot be used in further statistical analysis because their residual error is artificially reduced compared to other samples. In the extreme case, with only one calibrator sample per plate, the calibrator samples are without variation after the correction [1]. As no measurement is free of error, the error in the calibrator samples are propagated to all samples in the plate and is, therefore, still present as between-run variation in all non-calibrator samples.

Fig. 1.

Between-run variation in quantitative PCR experiments. (A) Target quantities of 4 genes measured in 5 different parts of the embryonic chicken heart in 6 plates. Note the 6-times difference between runs 2 and 5 and the missing overlap between runs 5 and 6. The parallel lines per plate indicate that between-plate variation is multiplicative. (B) Data from panel A corrected for the multiplicative difference between runs. Note that there is no longer a systematic difference between the runs and that the scaling of the Y-axis has not changed. Abbreviations: OFT, outflow tract; PA, pharyngeal arches; PE, pro-epicardium; SV, sinus venosus; VENT, ventricle.

Factor correction was proposed as a method to determine the multiplicative factors that enable the removal of the systematic bias between measurement sessions without the use of calibrators [1]. As stated in that paper, “for a correction method to be effective, the correction factors should be based on all observations in the session and the estimation of these factors should not be affected by incomplete data sets”. The current paper describes the use of factor correction in the analysis of qPCR data. In terms of quantitative PCR, the above quote means that an optimal estimation of factors to correct between-run differences requires a maximum overlap between plates. This overlap can be reached with respect to conditions, being the unique combinations of targets, experimental treatments or biological variables in the study. The statistical model is not based strictly on technical replicates, as is the case for calibrator samples, but also on biological replicates. It will be shown that all target quantities that have technical or biological replicates between plates can serve to estimate the factor per run. The described program, Factor-qPCR, imports analysed qPCR data, consisting of C_q, PCR efficiency, quantification threshold and target quantity values, and performs the correction between plates. The corrected target quantities can directly be used to calculate relative gene expression levels [3] which can further be analysed with standard statistical software. Alternatively, to calculate efficiency-corrected relative gene expression ratios [4] and to perform further statistical analysis with software commonly used in qPCR analysis [2], the corrected target quantities can be converted into efficiency-corrected C_q values, using a PCR efficiency per target. Factor-qPCR supports import of data and export of corrected values in spreadsheet or RDML format [5].

2. Methods and results

2.1. Factor correction model

As described, measurements that result from multi-session experiments can be considered to result from a mixed additive and multiplicative model [1]. This is also true for multi-plate qPCR experiments. The equations in this paper refer to a multi-plate experiment with N runs, J conditions and K measurements per target; the lowercase characters are used as indexes in the equations.

The multiplicative nature of the between-run variation in the data set is illustrated by the approximately parallel lines that connect the data points per run in a logarithmic plot of the data (Fig. 1A). In a multi-plate experiment with such a multiplicative between-run variation, the observations can, therefore, be described with Eq. (1)

$$Y_{nj}=F_n\times (Y_{\text{mean}}+C_j+\text{error})$$ (1)

The additive part of this model, between parentheses, states that the result of a measurement in condition j is the sum of the population mean (Y_mean), the effect of condition j (C_j), and a technical error and/or biological variation. Note that the condition effect C in this model represents the effect of a combined condition consisting of the target and the biological conditions in which the samples are collected. For each run n, the additive part of the observation Y_.j is multiplied by plate factor F_n. This factor affects every target and sample in a plate in the same way.

In this model the biological error is normally distributed with mean 0 and standard deviation σ. This biological error reflects the variance within a condition, whereas the condition effects reflect the differences between conditions. As in standard statistics, the sum of the condition effects is 0. The product of the session factors equals 1, which, together with the condition effects sum of 0, ensures that in a complete and balanced design the mean of all observations Y_nj is equal to the overall Y_mean.

2.2. Estimation of the session factors with the ratio approach

The run factors F can be determined by the described ratio approach [1]. This approach is based on the fact that a between-run ratio for a pair of observations from different runs (a and b) but for the same condition (C_j) can be written as Eq. (2):

$${\text{Between-run ratio}}_{a/b}=\frac{Y_{a,j}}{Y_{b,j}}=\frac{F_a}{F_b}\times \frac{(\overline{Y}+C_j+\text{error})}{(\overline{Y}+C_j+\text{error})}$$ (2)

In this between-run ratio, the ratio of the two normally distributed additive parts of the multi-run model (Eq. (1)) has a Cauchy distribution. Theoretically speaking, the Cauchy distribution has no mean but it has a median of zero and a symmetrical clock shape [6]. Because more pairs of observations overlap between plate a and plate b, the average of the last term in Eq. (2) will approach zero and cancel out. This makes every between-run ratio an unbiased estimate of the ratio of the two run factors [1]. Because of this, the best estimate of a ratio of two run factors can be determined by calculating the geometric mean for all pairs of observations that have conditions in common in each pair of two runs.

To derive run factors from this between-run ratio matrix, the matrix has to be complete. When a pair of runs has no conditions in common, the between-run ratio will be missing (e.g. runs 5 and 6 in Fig. 1, Fig. 2). Such a missing between-run ratio can be substituted. To this end, the quotients of the other ratios in the column of the missing ratio and those in each of the other columns of the matrix are calculated. Their geometric mean is the fold difference between the columns in the matrix (Fig. 2B). An estimate of the missing ratio can then be calculated by dividing the observed ratio in the row of the missing ratio (Fig. 2A) by this fold difference. The geometric mean of these N − 1 estimates, one per column, is then the best substitute for the missing ratio (Fig. 2C). Eq. (3) shows the nested geometric means that are applied in this calculation.

$$R_{c/r}\hspace{0.17em}=\hspace{0.17em}\sqrt[N-1]{\prod _{n=1}^{N-1}\left(R_{n/r}/\sqrt[N-1]{\prod _{i=1}^{N-1}\left(\frac{R_{i/n}}{R_{c/n}}\right)}\right)}$$ (3)

In Eq. (3), N is the number of runs; n and i range from 1 to N − 1, excluding row r and column c, respectively. The inner geometric mean calculates the fold difference between matrix columns. The observed ratios in the affected row are divided by this difference to obtain substitutes and the outer geometric mean then results in the best substitute. Substitution can be applied repeatedly. However, when more than 2 rounds of substitution are required, the design of the experiment is clearly incomplete and it is recommended to run another plate to fill in the missing overlap.

Fig. 2.

Factor estimation from the between-run ratio matrix. (A) Each cell in the between-run ratio matrix is the geometric mean of all ratios that can be calculated between observations in the same conditions from each pair of runs and is an estimate of the column and row run factors. Runs 5 and 6 have no conditions in common (Fig. 1) and the F6/F5 ratio is missing. (B) Divide each ratio in a column by the ratio in the column with the missing ratio and take the geometric mean to obtain a fold-difference between the columns. (C) Divide each observed ratio in the row of the missing ratio by the fold difference in (B) to obtain an estimate of the missing ratio. The geometric mean of these estimates completes the between-run ratio matrix (D). (E) Because in each column of this completed matrix the denominator in the ratio is a different run factor, these factors cancel out in the geometric mean of a column of ratios, resulting in the run factor (Eq. (4)).

From the matrix in which the missing between-run ratios are substituted (Fig. 2D), the run factors can be determined. In the matrix of between-run ratios every cell is an estimate of the factor of the run in the column divided by the factor of the run in the row (Fig. 2D). Because in the factor correction model (Eq. (1)), the product of all session factors equals 1, the geometric mean of column i in this between-run ratio matrix is an estimate of the correction factor for run i (Fig. 2E; as shown in Eq. (4), in which n ranges over the N rows in the matrix).

$${\text{Geometric mean column}}_i\hspace{0.17em}=\hspace{0.17em}\sqrt[N]{\prod _{n=1}^N\left(\frac{F_i}{F_n}\right)}=\sqrt[N]{\frac{{F_i}^N}{{\prod }_{n=1}^N(F_n)}}=F_i$$ (4)

The between-run variation in the original data set can now be removed by dividing each measured target quantity (N₀) in each plate by the corresponding run factor (Eq. (5)).

$$\text{Corrected}{N}_{0,n}=\frac{N_{0,n}}{F_n}$$ (5)

The corrected data of Fig. 1A are shown in Fig. 1B. After factor correction, the average of the between-run ratios has become 1.

2.3. Application of factor correction to qPCR data: Factor-qPCR

Analysis of qPCR data starts with raw fluorescence values which can either be processed by the software of the qPCR system, resulting in a PCR efficiency per target derived from a dilution series and a C_q value per target and sample, or be exported as raw data. In the latter case, the amplification curves can be analysed with other programs mostly resulting in the PCR efficiency per target and a target quantity per sample and target [7], [8] (Fig. 3). The qPCR systems or analysis programs export these data per run to a table, in text or spreadsheet format, or to an XML-based hierarchical tree structure defined as RDML (www.rdml.org) [5], [9]. During the import of the data of every run into Factor-qPCR, the program creates a variable that identifies the plate. The user has to select the variables that identify the targets, group and treatment annotations which serve to set the combined condition. When the target quantity (N₀), that has to be corrected, is not reported in the input file, it has to be calculated from the quantification threshold (N_q) and PCR efficiency value (both per target) and C_q value (per sample) (Eq. (6)).

$$N_0=\frac{N_q}{E^{C_q}}$$ (6)

After these user choices, the correction factor per run can be determined (Fig. 3). Dividing each target quantity by the correction factor has removed the between-run variation (Eq. (5)).

Fig. 3.

Flowchart of a multi-run quantitative PCR experiment. The raw fluorescence values can be analysed by the qPCR system or exported and analysed with an amplification curve analysis program and saved in spreadsheet or RDML format. The resulting data can be imported into Factor-qPCR (shaded part of the flow chart). After substitution of missing between-run ratios, the run factors are determined and applied. The program then exports the corrected target quantities (N₀) to a spreadsheet or, after their conversion into efficiency-corrected C_q values, to RDML for normalisation and further statistical analysis.

The corrected N₀ values can then be saved into a spreadsheet format that can be read by standard statistical packages. However, the use of the corrected target quantity by statistical packages used in qPCR analysis requires its conversion into an efficiency-corrected C_q value. To this end, the PCR efficiency per target that was reported per plate has to be converted into a PCR efficiency per target that is representative for the multi-plate experiment. Because the individual PCR efficiencies, as reported by amplification curve analysis programs, are normally distributed when pooled over runs, the mean of those values can be used to estimate the mean PCR efficiency for each target for the combined runs (Eq. (7))

$$E_{\text{mean}}=\sum _{n=1}^N\left(\sum _{k=1}^{K_n}{E}_{k,n}\right)/\sum _{n=1}^N(K_n)$$ (7)

In Eq. (7), N is the number of plates and K_n is the number of observations for the specific target on plate n. However, when only the PCR efficiency per target is reported for each plate, e.g. derived from a dilution series included in every plate, the sum of the PCR efficiency values for the multi-plate experiment is calculated by multiplying the reported value (E_n) by the number of observations for the target on the plate (K_n); the mean PCR efficiency can then be calculated (Eq. (8)).

$$E_{\text{mean}}=\sum _{n=1}^N(K_n{E}_n)/\sum _{n=1}^N(K_n)$$ (8)

Export to RDML requires that a standard error (SE) for these PCR efficiency values is reported. This SE can be determined from the residual variation (SS_res). In case of individual efficiencies, this residue is determined with respect to the PCR efficiency per target per plate (Eq. (9)).

$$S{S}_{res}=\sum _{n=1}^N\left(\sum _{k=1}^{K_n}{(E_n-E_{n,k})}^2\right)$$ (9)

In Eq. (9), E_n is the PCR efficiency of the target on plate n and E_n,k are the individual efficiencies observed for the K_n samples in which the target was amplified. When only an SE of the PCR efficiency per plate is reported in the input files, these SEs have to be converted into the variation per plate and summed over plates (Eq. (10)).

$$S{S}_{res}=\sum _{n=1}^N((K_n-1){(S{E}_n\times \sqrt{K_n})}^2)$$ (10)

The SE of the mean PCR efficiency for the combined runs can be calculated from the SS_res as usual (Eq. (11)).

$$S{E}_{E_{\text{mean}}}=\sqrt{S{S}_{res}/\sum (K_n-1)}/\sqrt{\sum (K_n)}$$ (11)

In Eq. (11), Σ(K_n) is the sum of the number of observations for each target per plate.

An efficiency-corrected C_q value per sample can be calculated with the PCR efficiency per target (E_mean) and the corrected target quantity (r_N₀). To this end, the inverse of the logarithmic version of Eq. (6) is applied (Eq. (12)).

$$C_{q,Ecorr}=\frac{\log (1)-\log (r\_N_0)}{\log (E_{\text{mean}})}$$ (12)

The quantification threshold is set to 1. Factor-qPCR enables the export of the corrected data to a spreadsheet or RDML for further statistical analysis. The original plate differences were removed and can, therefore, be ignored in these analyses. Factor-qPCR was specifically implemented to perform factor correction on multi-run quantitative PCR experiments. The program and a demonstration dataset can be downloaded from http://HFRC.nl.

3. Discussion

Between-run correction in qPCR data analysis assumes a multiplicative difference between plates in a multi-plate qPCR experiment. After division by a constant factor per plate, all between-run differences that are not multiplicative will still be present. The latter is true, irrespective of the method used to determine the correction factor: restricted to calibrator samples or including all overlapping technical and biological replicates. The advantage of using all overlap between plates is that measurements that have failed for technical reasons can be replicated easily in a new run and then added to the experiment.

Factor correction requires overlap between plates. Although this overlap can be reached by spreading replicate measurements over different plates, the required overlap is not restricted to such technical replicates. The statistical model on which the correction is based requires maximum overlap between plates with respect to targets and samples collected under the same biological or experimental conditions. In the ratio approach (Eq. (2)), the biological and technical errors, both normally distributed with a mean of zero, cancel out (Eq. (2)). Overlap between plates can, therefore, be based on biological and technical replicates. The design of the experiment should preferably be balanced and complete: a similar number of samples coming from every condition on each of the required plates. Because every target and condition then has the same influence on the between-run correction, the loss of condition effects through the correction is avoided.

Plate design in qPCR experiments often aims at sample maximisation: biological or medical samples that have to be compared are measured all in 1 plate, limiting the number of targets that can be measured on that plate [2]. This approach allows comparison between samples, but not between targets. Alternatively, target maximisation enables comparison between genes but not between samples. The maximum overlap design that is basic in Factor-qPCR allows comparison of samples and genes and thus enables the study of gene expression pathways.

Competing interests

The authors declare that they have no competing interests.