Abstract
Aggregates of amyloid-β (Aβ) peptide are known to be the key pathological agents in Alzheimer disease (AD). Aβ aggregates to form large, insoluble fibrils that deposit as senile plaques in AD brains. The process of aggregation is nucleation–dependent in which the formation of a nucleus is the rate–limiting step, and controls the physiochemical fate of the aggregates formed. Therefore, understanding the properties of nucleus and pre-nucleation events will be significant in reducing the existing knowledge–gap in AD pathogenesis. In this report, we have determined the plausible range of critical nucleation number (n*), the number of monomers associated within the nucleus for a homogenous aggregation model with single unique nucleation event, by two independent methods: A reduced-order stability analysis and ordinary differential equation based numerical analysis, supported by experimental biophysics. The results establish that the most likely range of n* is between 7 and 14 and within, this range, n* = 12 closely supports the experimental data. These numbers are in agreement with those previously reported, and importantly, the report establishes a new modeling framework using two independent approaches towards a convergent solution in modeling complex aggregation reactions. Our model also suggests that the formation of large protofibrils is dependent on the nature of n*, further supporting the idea that pre-nucleation events are significant in controlling the fate of larger aggregates formed. This report has re-opened an old problem with a new perspective and holds promise towards revealing the molecular events in amyloid pathologies in the future.
Keywords: Amyloid-β, Aggregation, Oligomers, Simulation, Nucleation, Stability analysis
1. Introduction
Aggregates formed by misfolded proteins called amyloids have emerged as the primary neurotoxic agents in neurodegenerative diseases. In Alzheimer disease (AD), amyloid-β (Aβ) peptide aggregates that eventually deposit as insoluble plaques observed in the brains of AD patients. Aggregates of Aβ are responsible for synaptic dysfunction and neuronal death that consequently leads to cognitive decline [1]. Among the various aggregate forms of Aβ, low-molecular weight forms ranging between dimers and 100mers are implicated as the primary toxic agents along the aggregation pathway [1–3]. Therefore, there is an increased interest in understanding the precise mechanism of aggregation leading to various toxic forms. Several aspects of Aβ aggregation are well understood over two decades of research. For example, Aβ aggregation towards large fibrillar deposits is a nucleation-dependent phenomenon that follows a sigmoidal growth pattern involving a lag phase prior to fibril growth (Fig. 1). The lag-phase is a rate-limiting step during which an important process of nucleation occurs [4,5]. Analogous to crystal growth, the formation of nucleus dictates the outcome of the fibrils in terms of their rate of formation, structure and morphology [4,6]. It is widely known that the pre-nucleation events involve both conformational change and self-assembly of monomers to a certain critical mass, which may form the ‘gatekeeper’ for the entire aggregation pathway. However, precise understanding of aggregation especially during the pre-nucleation phase that defines parameters such as the number of monomers associated in the nucleus (nucleation number, n*) and physiochemical nature of nucleus are far from clear.
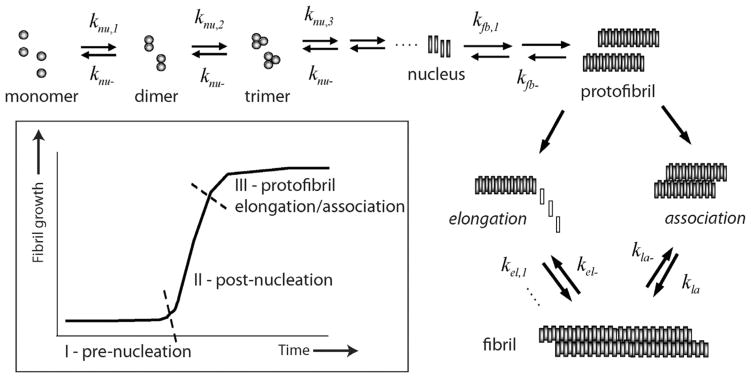
Fig. 1.
Aβ aggregation pathway. Schematic diagram indicating the salient aspects of Aβ aggregation towards fibril formation. Important rate constants that are considered in the model are shown. (Inset) The sigmoidal aggregation growth curve indicating three important phases of the reaction.
During the past two decades, kinetics and thermodynamics of Aβ aggregation have been intensely studied, and a number of approaches and mathematical models have been developed (reviewed in [7–10]). The molecular complexities involved in aggregation process especially during the pre-nucleation stage, and those in detecting and monitoring the process experimentally, necessitate modeling approaches that go beyond brute-force methodologies. Unlike the widely believed thought, emerging evidence based on coarse-grained simulations indicate that the pre-nucleation itself may involve multiple steps and intermediates to reach the critical nucleus size [11,12]. Previously, n* value for amyloid protein, huntingtin was calculated to be ~ 0.98 (for polyglutamine, Q28 peptide) homogenous association [13]. Upon incorporating conformational heterogeneity among the monomers assembled within the nucleus, the values of n* were observed to take on negative values [14]. Lee and co-workers adopted an ordinary differential equation (ODE)-based simulation to model insulin aggregation and utilized the previously predicted n* value of 6 [15]. More recently, Saric and co-workers determined that plausible nucleation size may range between 6 and 14 depending on the initial monomer concentration [11].
The main reason for the paucity in nucleation-related information that precludes experimental characterization and conventional modeling is the complexity of the Aβ aggregation mechanism that has led to a confounding understanding of the pre-nucleation events. Accurate biophysical analysis is difficult due to the dynamic nature of the process that precludes precise experimental characterization. In particular, the lack of sufficiently sensitive experimental probes that could detect the presence of a range of oligomers including those that are less populated has further hindered experimental validation of the simulated models. Detection of intermediate oligomers poses great difficulty to detect, let alone to isolate and characterize. Not surprisingly, only a few stable large (> 1500mers) intermediates along the pathway such as protofibrils (PFs) have been isolable, which are soluble fibril-like species formed during the post-nucleation stage (Fig. 1). PFs are biophysically well-characterized and show propensity to both elongate and laterally associate to grow into mature fibrils [16]. Only a handful of low-molecular weight oligomers have been successfully isolated [17–19]. However, the inability to isolate bonafide on-pathway intermediates as well as the lack of extrinsic molecular probes to precisely monitor the dynamics during pre-nucleation have impeded the progress towards understanding the process of nucleation. Furthermore, stochasticity causes variations in nucleation rates even among identical microscopic molecules. Therefore, molecular-level simulations are essential as they cater to the different temporal scales along the aggregation pathway that can create modeling stiffness.
In this report, we provide insights into Aβ aggregation by modeling key elements of the process involved based on a simple homogenous aggregation of Aβ molecules with a single unique nucleation event using two independent approaches with converging solutions: (i) a reduced order stability argument and (ii) a mass action kinetics based numerical simulation, supported by experimental biophysical data. Using such an approach, we have previously modeled reactions involving PFs, and established that the parameter sweep for rate constants could be dramatically reduced based on the stability argument [20]. Though employed on a simpler model system, the stability argument relies on a key physical requirement that the correct choice of nucleus, and hence n*, renders the equilibria stable. The ODE-based numerical simulations were employed using a divide-and-conquer strategy by segmenting the sigmoidal fibril-growth curve into three stages (Fig. 1; inset) as previously reported [21]. The data indicate a narrow range of critical nucleation number for Aβ aggregation that is in close agreement to other reports. More importantly, this report sheds insights into understanding the critical nucleation event during Aβ aggregation from a new approach and methodology.
2. Experimental methods
Aβ42 peptide was synthesized at the peptide synthesis facility core at Mayo Clinic, Rochester, MN. Thioflavin-T (ThT) and other chemicals were purchased from VWR Inc.
Aβ monomer preparation and aggregation
Lyophilized Aβ peptide was stored at −20 °C until use. Aβ monomers, free of any preformed aggregates were prepared as previously described [22]. Briefly, the peptide stocks were dissolved in 50 mM NaOH that was left to stand at room temperature for 15 min before fractionating using Superdex-75 size exclusion chromatography column. The samples were collected as 0.5 mL fractions upon isocratic elution in 20 mM Tris, pH 8.0 buffer with a flow-rate of 0.5 mL/min. The fractions corresponding to monomers were collected individually and were used as such. The concentrations were determined using UV–Vis absorbance at 280 nm and with an extinction coefficient of 1450 cm−1 M−1 (www.expasy.org) corresponding to a tyrosine residue. All the experiments were performed either with freshly purified monomers or monomers not more than two day old stored at 4 °C. Aggregation of Aβ at different concentrations were initiated using freshly purified Aβ42 (20 mM Tris, 50 mM NaCl, pH 8.0) was incubated quiescently at 37 °C, and the aggregation kinetics was monitored by ThT fluorescence and MALDI-ToF mass spectrometry at different time points as described below.
Thioflavin-T fluorescence
Fluorescence experiments were performed on a Cary Eclipse spectrometer (Varian Inc). Samples were excited at 452 nm and the emission at 482 nm was monitored in kinetic mode for one minute with a band width of 10/10 nm. The averaged data point was considered for the overall kinetic plot. Aggregation parameters were obtained by monitoring the reaction with ThT fluorescence and fitting the data points to the sigmoidal curve in Eq. (1) using Origin 8.5 software.
| (1) |
In this equation t is time, a and b are fixed parameters, and t0.5 is the time to reach half-maximal ThT fluorescence. Lag times are equal to t0.5 − 2b for each fitted curve.
Mass spectrometry
Monomer depletion during aggregation was monitored using MALDI-ToF mass spectrometry (Bruker Inc). Insulin sample were used as internal standards to calculate the absolute concentrations of Aβ42 in the sample as previously shown [23]. Typically, 2 μL aliquot of sample from each incubations at different time points (20–100 pmol of samples for 10–50 μM Aβ incubations) and mixed with 16 pmol of insulin (1 μL sample) for each sample in the matrix. The solution was mixed with a saturated solution of α-Cyano-4-hydroxycinnamic acid (CHCA) matrix in acetonitrile and water before spotting on a MSP AnchorChip 600/96 plate (Bruker Daltonics Inc, Germany). Prior to the start of each experiment, parameters in MALDI-ToF instrument were optimized and calibrated using molecular weight standards (Protein Calibration Standard-1; Bruker Daltonics). The detection limit in the spectrometer was set at 2X with a laser power of 51% in reflectron mode. For each spot/time points, 700 shots were collected and averaged to obtain the final plot. The plots were normalized based on insulin intensity shown in Eq. 2 as previously reported [23].
| (2) |
3. Preliminary observations: stability analysis
As a first step towards validating our hypothesis that the critical nucleation number, n*, falls within a narrow range of molecular mass in a homologous single nucleation model, the stability analysis was performed on a simplified, reduced order mass action based model. The rate constants derived from this study was used as a preliminary lead for a more detailed numerical model presented in the second part of this section to determine n*. The equilibria obtained from the numerical model were also employed in the perturbation analysis resulting in an optimal feedback between perturbation and numerical arguments.
In order to see whether the molecular weight of nucleus is conserved or confined within a narrow range of masses, a linear stability analysis was employed on a simple three-species model containing monomers (A1), nucleus (An*) and fibrils (F). Since the rate constants for the system of equations are not known at the outset, the system remains unsolvable. We argue that after perturbing the system, the rate constants involved in the dissapearance of the perturbed species must reflect those involved in the formation of the species. In terms of the energetics involved in aggregation, it can be said that at any point in time, any stable perturbation that drives the system off course will eventually die and bring the system back to its course. This is mathematically tractable only in the equilibrium state and could yield valuable information about the system. Our earlier analysis using such an algorithm has yielded important information on PFs [20], and this has been used to reduce the parameter search space in our numerical simulations as discussed later.
Mathematically, we represent the three-species system by:
In accordance with this simplistic scheme, a critical number (n*) monomers aggregate to form the nucleus and a certain number of nuclei (denoted s*), in turn aggregate to form the fibrils. For sake of simplicity, any combination of monomers and nuclei which could result in the formation of the fibrils is disregarded here. As in our previous reports, PFs, which are smaller than fibrils are assumed to be composed of 1600mers [24], and for simplicity, in this analysis we have assumed fibrils (F) to be of the same size too. This allows us to estimate the critical number of nuclei required to form the fibril, namely . The terms kij (i,j = m,n,p) refer to the forward and backward reaction rates. It must be noted that the nucleation number, n* is unknown at this stage and is the key parameter to be determined. In order to find n*, we test the differential equation resulting from the above scheme (Eq. (3)–(5) below) for all integers, n, in a large range dictated by the biophysics. The set of n* values is then a special subset of n and chosen based on which n yields physically meaningful results as discussed in detail below.
The corresponding nonlinear differential equations for our model system, based upon mass action kinetics, are then given by
| (3) |
| (4) |
| (5) |
Here An results from the aggregation of n monomers and F from the aggregation of ‘s’ An ‘s’. The objective of this study was to find the optimal set of n*, by varying 1 ≤ n ≤ |F| (where |F| refers to the magnitude of the fibrils or the number of monomeric units that compose fibrils) that keeps the equilibrium concentration of the various species stable for sufficiently small perturbations applied to the system. Let Me, Fe, Ne be the equilibrium concentrations of the monomers, fibrils and nucleus, respectively, corresponding to the steady state version of the Eqs. (3)–(5). For the Eqs. (3)–(5) to be physically meaningful, the equilibrium state for this system must be mathematically stable, and any perturbation to the system, if sufficiently small, must eventually disappear. Therefore, stable equilibria conditions were derived upon linear perturbation of the stable solutions Me, Fe, Ne. Based on the above mentioned mathematical treatment, the concentrations of the different species can be written in the form
| (6) |
where M1, F1, N1 represent perturbed concentrations and ε is the magnitude or order of the perturbation. The above expression Eq. (6) for A1, An, F were placed into Eq. (3)–(5) and the O(ε) were collected, giving the perturbed system
| (7) |
| (8) |
| (9) |
To see whether the perturbations disappear, these equations were written in the operator form
| (10) |
Where the matrices [X], [Y] are respectively represented by
| (11) |
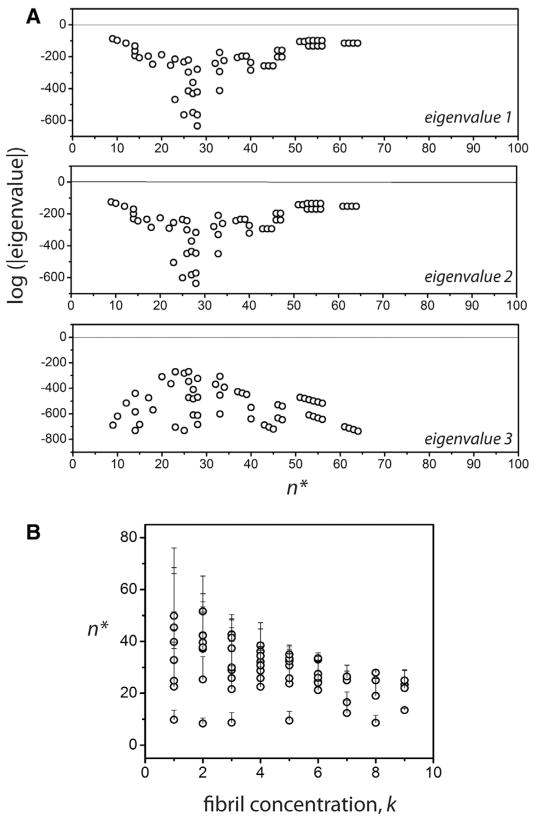
Our objective was to seek the range of the rate constants in which the real part of all the eigenvalues of the matrix [Y] remain simultaneously negative (i.e. the perturbations eventually vanish). Due to the presence of several parameters, some restrictions were imposed for computation based on experimental data. This included the assumption that at thermodynamic equilibrium after infinite time, 99.9% of the monomers are depleted and 98.9% of the initial monomers are converted into fibrils leaving 1% to remain as the nuclei. In other words, Me = 0.001Fe and Ne = 0.001Fe. The value of knp was assumed to be knp = 0.9 s−1 based on our previous report [20]. The parameters, n, kmn, Fe along with the fibril size were then varied. The reverse rates, and were obtained from equilibrium conditions. By sweeping over n and fixing all the other parameters, the eigenvalues of the perturbed system were analyzed for those values that were simultaneously negative, which would render the equilibrium state, stable. The n’s corresponding to the stable states are denoted n*. Fig. 2 shows a plot of the logarithm of the absolute values of the three eigenvalues of the system versus n*. The interesting aspect of the plot is that this select group of ‘stable’ n* values is small and finite and confined to a narrow range 10 < n* < 60 for the most part. For all other cases of n, at least one of the eigen values becomes positive making the perturbation unstable. The range of n* is sensitive to the choice of fibril size and the order of magnitude of Fe, namely k (such that Fe = 10−k), which is one of the primary variables in our study. The magnitude of n* increases with increasing magnitude of the fibrils and decreases with increasing values of k (Fig. 2B). However, the key observation here is that no matter the size of the fibrils, which can range between 3000 and 5000mers, n* is restricted to a fairly tight range (10–60). This mathematical analysis support our hypothesis that the n* could be narrow in range that could potentially play a significant role in the fate of the overall aggregation process.
Fig. 2.
Prediction of n* by stability analysis. (A) Logarithm of the absolute values of real parts of the three eigenvalues of the perturbed system Eq. (7)–(9). The graph shows the eigenvalues only when all three values are simultaneously negative, suggesting linear stability. The n* values corresponding to the open circles are the allowable values for the nucleation size. (B) The variations in the n* as a function of fibril concentration index k, where the concentration is taken to be Pe = 10−k. Note that for any given value of k, fibril size, several n*’s are mathematically permissible, indicated by the error bars in the plot.
Based on perturbation analysis described above, having observed that the nucleation event is not random but could be tightly-controlled with a narrow range of molecular mass in a homologous mechanism, we sought to determine more rigorously, how many monomers are associated within the nucleus (n*) by experimental and computational methods. First, the concentration dependence of Aβ42 aggregation was experimentally established. Four different concentrations, 20, 30, 40 and 50 μM of freshly purified, buffered Aβ42 monomers were subjected to aggregation in quiescent conditions at 37 °C. The reactions were monitored using the ThT fluorescence assay. All the samples exhibited a sigmoidal growth curve with a lag time, growth phase and saturation, indicative of a nucleation-dependent process (Fig. 3A). As expected, increase in monomer concentration resulted in increased rate of aggregation and consequently reduced the lag-times. The data were fit with Eq. (1) revealed the lag times of 28.3, 22.1, 18.3 and 16.9 h for 20, 30, 40 and 50 μM reactions, respectively. The semi-log plot of Aβ concentration and the calculated lag-time showed an expected linear dependency (Fig. 3B). In addition, a linear relationship was also observed between Aβ concentration and saturating values of ThT fluorescence (Fig. 3C).
Fig. 3.
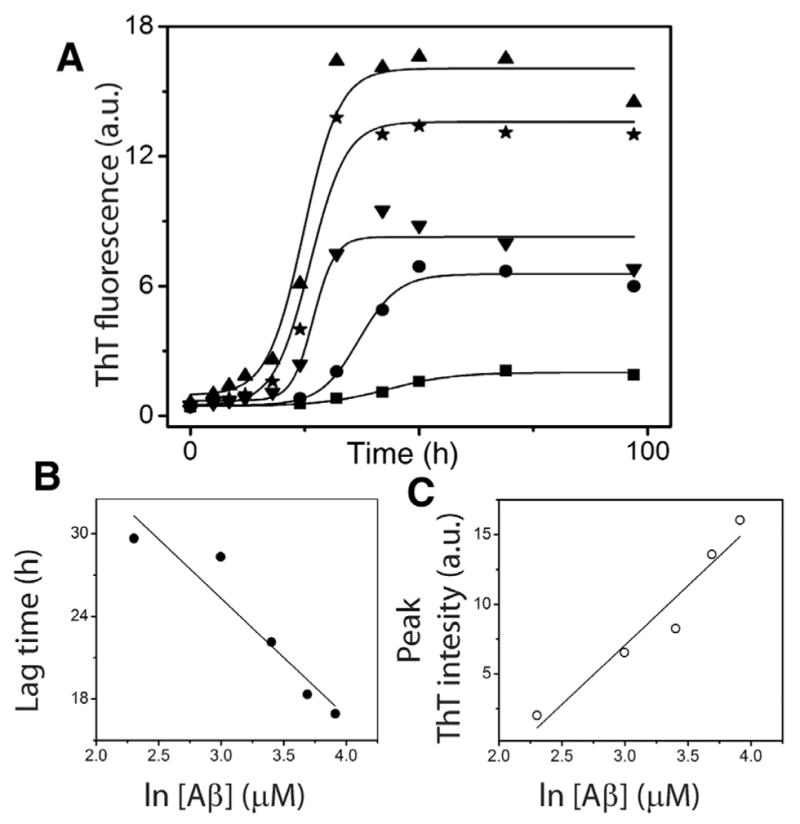
Aβ aggregation reactions. (A) Aliquots of Aβ aggregation reactions with 20 (■), 30 (●), 40 (▲), and 50 μM (★) monomer concentrations in 20 mM Tris, 50 mM NaCl at pH 8.0 were periodically removed and analyzed by ThT fluorescence assay. The data were fit to sigmoidal equation (Eq. (1)). (B) and (C) The lag time and peak intensity were plotted against Aβ concentration to obtain the expected linear fits.
4. ODE-based simulations
Modeling approach
A ‘divide and conquer’ strategy was adopted by simplifying the overall aggregation into three experimentally and computationally-viable parts such as pre-nucleation (Stage I), post-nucleation (Stage II) and protofibril reactions (Stage III) (Fig. 1), without compromising the reactions involved in aggregation. Needless to say, it is imperative to compute the kinetic rate constants involved in all the different stages to simulate the overall aggregation process. Pre-nucleation events, which are subjected to intense scrutiny lately and are the focus of this report, occur at Stage I. The forward and backward rate constants in this Stage are designated as knu,i and knu−, respectively. The rate-limiting step of nucleation is followed by a growth phase, which is dominated by aggregation reactions (Stage II) [4,25]; the forward and backward rate constants in this stage are designated by kfb,i and kfb− respectively. Stage III involves the formation of PFs that are known to follow elongation (forward and backward rate constants designated as kel, and kel− respectively) and association mechanisms (forward and backward rate constants designated by kla and kla− respectively) towards fibrils [16,26–30] (Fig. 1). Using ODE-based approach, we have previously modeled Stage III of aggregation involving PF elongation and lateral association, and obtained key rate constants for the reactions [24]. It is noteworthy that for the reactions involved in Stage III fixed rate constants were used primarily to reduce the number of parameters. However, this strategy did not affect our simulation because within this stage, as the size of aggregates involved in these reactions are large, only negligible differences in reaction rates occur due to their respective diffusivities. Our divide and conquer approach will help reduce the number of parameters that need to be computed simultaneously (forward and backward rate constant pairs for every reaction, as well as the n*). However, to facilitate the computation further, the following specific rational assumptions were made based on established experimental and theoretical evidence. Energetically, during the pre-nucleation phase (Stage I), the concentration of monomers and low-molecular weight oligomers (dimers, trimers etc.) are in a dynamic flux with each other until the formation of the nucleus [7,9,31–33]. The pre-nucleation reactions constitute the rate-limiting events during aggregation and hence, generate the observed lag times during sigmoidal fibril growth. Based on the observed experimental bulk rates of reaction, we assume that for pre-nucleation reactions, the forward rate constants of formation become progressively larger for larger aggregates towards the nucleus (knu,1 < knu,2 < ···< knu,n*). Furthermore, for simplicity sake, a single backward rate constant, knu− was considered during this Stage based on the assumption that the backward rate constant is independent of the aggregate size. The basis for such an assumption comes from the previous report by Serio and colleagues, who showed that increasing the number of seeding fibril ends by sonication could increase the reaction rates significantly [34]. This suggests that the detachment of monomers mostly occur at the terminal rather than in the internal segment of the aggregate. Hence, we assumed that the number of monomers within an oligomer does not affect the backward rates significantly. Described below are the two closely-related modeling paradigms called modified and detailed models that will be utilized in this work.
The modified model
Our proposed model is based on the one that was developed for insulin aggregation by Lee and co-workers [15], and has been modified specifically for the Aβ. Aggregation pathway has been characterized by a set of biochemical reactions (Fig. 4A) for which the corresponding reaction fluxes were computed and differential equations were formulated for each oligomer concentration as a function of time (Eq. 12). Solving the set of homogeneous ODEs allows us to study the temporal dynamics (in terms of concentration change) of each oligomer in the system.
Fig. 4.
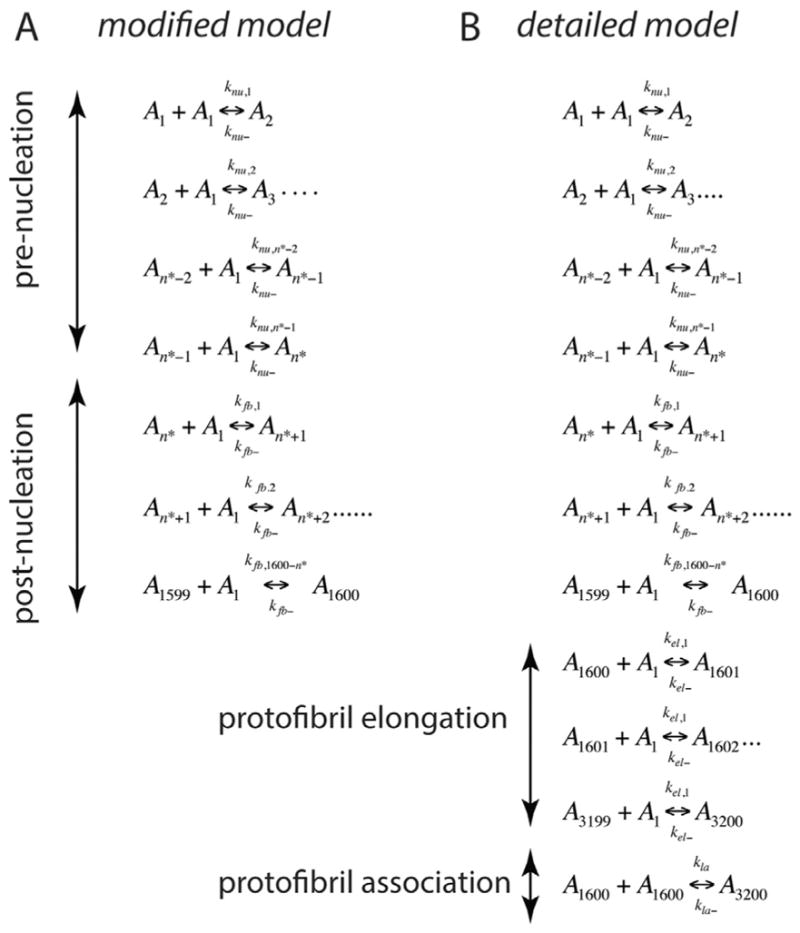
(A) Reactions considered during the pre- and post-nucleation stages in the modified model. (B) Reactions considered for Stages I, II and III in the detailed model. In these equations, Ai represents the aggregate of ith order, for example, A1 is monomer, A2 is dimer etc. and n* the nucleation number.
| (12) |
Here, Ai’s denote i-mers, n* is the nucleation number, Jnu,i and Jfb,i refer to the fluxes for nucleus and fibrils respectively, and F is a fibril. The following assumptions were made for aggregation involving homogenous, single nucleation mechanism: (a) monomer adds to i-mers until fibril formation, (b) nucleation involves monomer addition as well as a structural change in the aggregate, An* (this conformational change is implicit), (c) post-nucleation events are relatively faster, as the forward rate constants for post-nucleation are much higher than those in pre-nucleation (i.e., knu,n*+i≫knu,i) (~108 fold difference was reported in [15] for insulin aggregation), (d) the reverse reaction rate constants are assumed to be independent of size i, and abbreviated as knu− and kfb− and, (e) aggregation under agitation conditions are known to drastically decrease the lag-times. Therefore, knu,i and kfb,i are assumed to be diffusion-limited; using the Stokes–Einstein equation, the diffusivity is proportional to the inverted cubic root of i, resulting in:
| (13) |
Based on these assumptions, the reaction fluxes and differential equations are derived as shown in Eq. 12. Note that assumption (e) mentioned above helps in drastically reducing the number of parameters to be estimated in the pathway by relating all the forward rate constants in Stages I and II to the first rate constant for each respective stage (i.e., knu,1 and kfb,1). Importantly, it greatly reduces the complexity involved in incorporating PF as a parameter. This model, however, does not include the dynamics of Stage III, protofibril-to-fibril transitions.
The detailed model
A complete simulation of the Aβ aggregation requires an estimate of the following six parameters: knu,1, kfb,1, knu−, kfb−, n* and b (see Fig. 1), where b is the mapping constant that helps correlate the experimental ThT fluorescence data to concentration estimates as we have shown previously [24]. It is a daunting task to make parameter sweep for individual reactions with different values for each of these variables to accurately simulate the experimental plots due to the large solution space. Hence, as mentioned earlier, the sigmoidal fibril-growth curve was dissected in three simplified stages as mentioned before to bring down the number of parameters to be estimated together [24]. The pre- and post-nucleation stages are well-approximated by the set of equations shown in Eq. 12. However, the stage involving PF dynamics (Stage III) requires reactions from both post-nucleation (Stage II) and PF elongation/lateral associations to be combined. Assuming that fibrils can potentially reach up to about at least 3200-mers (they can range much more than this but this conservative lower limit is appropriate for our models), 3200 different species have to be considered within the simulation and hence, a similar number of differential equations have to be included to study their change with concentration. Furthermore, many aggregates along the pathway could potentially interact with one another, one needs to consider 3200C2 combinations of possible reactions between them, which renders the problem mathematically intractable. A viable approach would be to consider monomer addition reactions until the formation of 1600-mers in the system (which is approximated to be the average PF size (19)), and then to include our previously established PF elongation and lateral association reactions. We call this as the detailed model for which the complete set of reactions is shown in Fig. 4B. Such an endeavor then necessitates the estimation of four more bulk rate constants: the forward and backward rate constants for the PF elongation and lateral association stage denoted by kel,1, kel−, kla and kla−, respectively. In our previous report [24], we estimated the rate constants (kel,1, kel−, kla and kla−) separately and verified them with in vitro experiments as follows: kel,1 = 9.0 × 103 (h−1 μM−1), kel− = 4.5 × 102 (h−1), kla = 9.0 × 10−1 (h−1 μM−1), kla− = 6.0 × 10−3 (h−1). Note that the estimation of kfb,1 (in Stage II) automatically allows the calculation of kfb, 1600−n* using Eq. (13); also, the PF elongation is considered to be merely a continuation of the post-nucleation phase with kel,1= kfb, 1600−n* and kel− = kfb. Hence, the detailed model as shown in Fig. 4B can now be simulated to obtain the lag-times.
Rationale for simulation with modified and detailed models
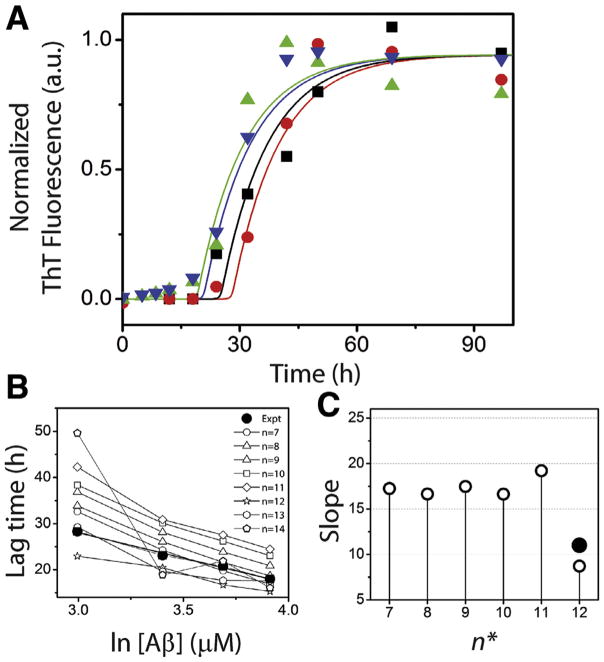
In order to achieve both simulation accuracy and ease, both the modified model and the detailed model were used in tandem for Aβ aggregation. Since the primary objective of this report is estimating n*, the modified model is adequate, which computes Stages I and II. Our rationale to incorporate the detailed model are (a) to investigate the dependence of n* on PF size observed from stability analysis described above, and (b) to validate our simulation by accounting monomer depletion, which will require simulation of the entire aggregation pathway. Therefore, modified model was used to study the lag times of aggregation exclusively, generated for different values of n* as presented in Fig. 5, while the detailed model was used for validation.
Fig. 5.
Overall simulation of aggregation. (A) Normalized ThT fluorescence data shown in Fig. 3 with 20 (
 ), 30 (■), 40 (
), 30 (■), 40 (
 ) and 50 (
) and 50 (
 ) μM Aβ. Corresponding lines are obtained from the modified model (with a scaling factor, b of 6) for respective concentrations for n* = 12; 20 (red), 30 (black), 40 (navy) and 50 (green) μM Aβ. (B) Lag time data obtained from the modified simulations for n* = 7–14 (Regimes 1 and 2) for these Aβ concentrations are compared to that obtained from the experiment (●). (C) Slope derived from panel (B) (○) are plotted against the corresponding n* values (●). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
) μM Aβ. Corresponding lines are obtained from the modified model (with a scaling factor, b of 6) for respective concentrations for n* = 12; 20 (red), 30 (black), 40 (navy) and 50 (green) μM Aβ. (B) Lag time data obtained from the modified simulations for n* = 7–14 (Regimes 1 and 2) for these Aβ concentrations are compared to that obtained from the experiment (●). (C) Slope derived from panel (B) (○) are plotted against the corresponding n* values (●). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
5. Results
5.1. Lag time correlations derived from modified model
Based on the stability analysis shown in Fig. 2, the parameter sweep for rate constants were greatly reduced to the plausible range, 10 < n* < 60 as mentioned above, which was computed using the modified model. Table 1 shows the simulated lag times for different n* and initial Aβ concentration. In order to find the pre-nucleation rate constants along with n*, the rate constants that give the maximum lag times for each value of n* were estimated. Note that, changing the rate constants further to achieve higher lag times render the system of differential equations unstable. Hence, they were considered unrealistic and hence, discarded. Interestingly, the modified model shows four distinctly different regimes of lag times corresponding to four different pairs of rate constants in pre-nucleation (highlighted in Table 2). In parallel, this also characterizes four different regimes of n* values associated with Aβ aggregation that are summarized as follows: Regime 1: n* = 7–11; Regime 2: n* = 12–14; Regime 3: n* = 15–17; Regime 4: n* = 18–21. The rate constants for each of these regimes are shown in Table 2.
Table 1.
Lag times from simulation for various estimates of n*.
| n* | 20 μM (h) | 30 μM (h) | 40 μM (h) | 50 μM (h) |
|---|---|---|---|---|
| 7 | 32.60 | 24.24 | 19.76 | 16.88 |
| 8 | 33.85 | 26.05 | 21.59 | 18.67 |
| 9 | 36.85 | 28.14 | 23.84 | 20.86 |
| 10 | 38.35 | 30.12 | 26.19 | 23.04 |
| 11 | 42.26 | 30.87 | 27.54 | 24.44 |
| 12 | 22.93 | 20.45 | 16.70 | 15.29 |
| 13 | 29.27 | 19.65 | 17.68 | 17.59 |
| 14 | 49.62 | 18.88 | 21.89 | 16.06 |
| Expt | 28.32 | 23.13 | 20.70 | 18.00 |
Table 2.
Forward and backward rate constant values used in simulation. knu,1 is the forward rate constant value for the first reaction during the Stage I, and rest of the forward rate constants are computed based on Stokes–Einstein equation (Eq. (13)). For each simulation these combinations of knu,1, and the backward rate constant, knu− were fixed.
| Nucleation number (n*) | Knu,1 (h−1 m M−1) | Knu− (h−1) | |
|---|---|---|---|
| 7 | 1.38 × 100 | 9.5 × 10−1 | |
| 8 | 1.38 × 100 | 5.6 × 10−1 | |
| Regime 1 | 9 | 1.38 × 100 | 3.7 × 10−1 |
| 10 | 1.38 × 100 | 2.3 × 10−1 | |
| 11 | 1.38 × 100 | 1.9 × 10−1 | |
| Regime 2 | 12 | 4.6 × 100 | 2.9 × 10−1 |
| 13 | 4.6 × 100 | 2.8 × 10−1 | |
| 14 | 4.6 × 100 | 9.0 × 10−2 | |
| Regime 3 | 15 | 1.38 × 101 | 1.4 × 10−2 |
| 16 | 1.38 × 101 | 1.0 × 10−2 | |
| 17 | 2.1 × 101 | 1.1 × 10−2 | |
| Regime 4 | 18 | 2.1 × 101 | 1.1 × 10−2 |
| 19 | 2.4 × 101 | 1.1 × 10−2 | |
| 20 | 2.6 × 101 | 1.5 × 10−2 | |
| 21 | 2.8 × 101 | 1.2 × 10−2 |
Note that the forward rate constant, (knu,1) was fixed for each n*, while the others and backward rate constant were varied to achieve the highest lag times as reported in Table 1. It is noteworthy that all the other n* values, i.e. n* < 7 and n* > 21 resulted in either (i) negative/ discontinuous simulations or (ii) oscillatory nature of the fibril growth curve (instead of the expected sigmoidal behavior). Both of these are indicative of poor convergence or in other words, physiochemically invalid possibilities (data not shown). Fig. 5A shows the simulations (solid lines) of Aβ aggregation for n* = 12 for 20, 30, 40 and 50 μM monomer concentrations that showed canonical sigmoidal growth curves. Overlay of the normalized experimental data obtained from Fig. 3A shows a very good correspondence between the simulation and experimental data (Fig. 5A). The bulk lag times for each initial monomer concentration and for each n* value were then calculated using t0.5 − 2b term upon fitting the curves with Eq. (1) (Table 1). One of the important properties of Aβ aggregation is the linear correlation between Aβ concentrations and lag times (Fig. 3B). By plotting the lag times values obtained for various n* simulations, largely linear correlations were obtained for n* = 7–13, and among them n* = 12 and 13 showed the best correlation with the experimental data (Fig. 5B and C). None of the simulations above n* = 13 yielded meaningful data suggesting those values could be improbable (data not shown).
5.2. Comparison of the simulated and experimental lag times
The experimental ThT fluorescence plots provide an ensemble-averaged, cumulative effect of all aggregated forms. Hence, from the simulation, one has to plot the cumulative effects from all the nucleated oligomers that can be mapped directly to the experimental results. For the modified model, we assume that all nucleated species are ThT positive; hence the concentration of fibrils, [F], at each time point was simply multiplied by a mapping constant b to see if they were in agreement with the experimental data. The model however, needs to account for the oligomer sizes as each of the oligomers at the post-nucleation stage such as, An*, An*+1,…,A3200 would contribute to the bulk ThT fluorescence differently. In order to do this, the individual oligomer contributions to ThT at each value of the simulation time were computed to a weighted average as shown below:
| (14) |
where [An*+i] denotes the concentration of each nucleated species, i denotes the number of Aβ molecules by which the oligomer has elongated beyond n* and hence, the contribution of the corresponding oligomer towards the fluorescence, and b is a constant scaling factor to map to the fluorescence sensitivity estimates. The simulation curves shown in Fig. 5 plot the concentration of F based on the assumption that all nucleated oligomers display ThT fluorescence. The lag times estimated from the modified model were still higher than that observed experimentally for Regimes 1, 3 and 4 as the rate constants were selected based on those that could achieve maximum lag time for each n*. Hence, it can be argued that Regime 2 (showing lower lag times than the experimental data) might allow for more rate constant combinations to serve as valid solutions and simulate the experimental growth curves better. Also, it is difficult to know what the minimum size of oligomers that show ThT fluorescence from the experimental data and hence, the experimental estimates are at best the maximum limits of the lag times for each initial Aβ concentration reported here. The data obtained from the modified model however, provides a plausible range of n* and generate important rate constants that could be utilized in the detailed model.
5.3. Monomer depletion as model validation using the detailed model
The detailed model was used to simulate the monomer depletion, which requires the knowledge of dynamics along the entire pathway. While simple monomer additions were assumed for Stages I and II, the following conditions were considered for the reactions within the Stage III: The last forward rate constant at Stage II was used as the starting point for each of the PF elongation reactions (kfb,1600−n* = kel,1). As mentioned before, due to their large size, rate constants involving individual PF reactions were assumed not to vary much owing to small differences in their respective diffusivities. In addition, the lateral association reactions used in the abstraction scheme (Fig. 4A) consider A3200 as the fibril size (for simplicity). We treat all the reactions alike or in other words, lateral association of A1600 + i, (i = 0,…,1599) and A1600 will still produce an A3200. A similar strategy was used in our previous report (19). Rate constant values derived from the mathematical stability argument were also utilized to narrow the parameter space. The rate constants thus obtained were directly incorporated within the detailed model to generate the monomer depletion curves for validation.
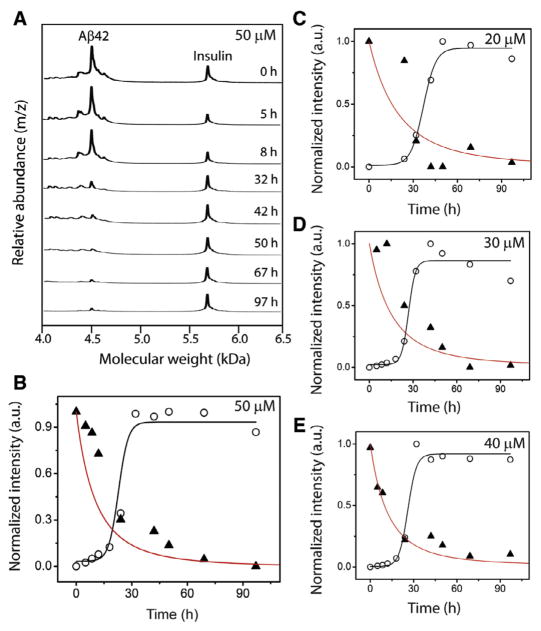
Although ThT fluorescence has served as a benchmark for analyzing amyloid aggregation, binding of ThT to amyloid fibrils is poorly characterized. Precise stoichiometry of ThT-to-Aβ is unclear and hence, quantitative assessments could not be made accurately. Since the aggregation data shown in Fig. 3 will be used for our computational analyses described below, we wanted to ensure a precise quantitative evaluation of the aggregation process. Generation and quantitative analysis of any homogeneous aggregate along the aggregation pathway is nearly impossible to achieve, as the dynamic nature of aggregation precludes experimental isolation of specific aggregates for quantitative measurements. However, quantitative assessment can be made on monomers by monitoring their disappearance during aggregation. To do so, we employed matrix-assisted laser desorption ionization-time of flight (MALDI-ToF) mass spectrometric technique. MALDI-ToF is uniquely suited for this experiment as this soft ionization technique ensures no dissociation of preformed aggregates and hence enables quantification of unreacted monomers exclusively. As described in Experimental Methods, aliquots of the samples from Aβ reactions shown in Fig. 3 were plated on a MALDI plate along with a constant amount of insulin as an internal standard. A similar method for quantifying monomeric Aβ using insulin as internal standard was adopted by Zovo and co-workers [23]. As shown in Fig. 6A, a 50 μM Aβ reaction analyzed by MALDI-ToF at various time points of incubation showed two major peaks corresponding to the unreacted Aβ42 monomer (4513 a.m.u) along with the insulin standard (5808 a.m.u). Over time, the intensity of Aβ42 monomers diminished correlating with aggregation. A plot of monomer intensities normalized based on intensities of insulin standards (see Experimental Methods) against incubation times resulted in monomer depletion curve (▲; Fig. 6B). It is interesting to note that the monomer depletion curve did not display a sigmoidal pattern of decay with a lag phase observed for the corresponding aggregation reaction (○; Fig. 6B). Instead, an exponential pattern was observed without any observable lag times. This pattern was consistent for the rest of the aggregation reactions (20–40 μM Aβ42; Figs. 4C–E). Using the same parameters for the detailed model, plots for monomer disappearance were obtained for n* =12. The red lines in Figs. 6B–E indicate these simulate curves obtained from the detailed model, which correlate well with the experimental monomer depletion data obtained. Higher rates of monomer depletion observed for the simulated curves is expected as the simulation using detailed model is able to account for every individual reaction than the experimentally observed ones, which the ThT is incapable of capturing. This is the likely reason for the absence of a complete overlap between the experimental and the simulation data. Nevertheless, the exponential decay of monomer depletion observed from the mass spectrometric analysis is captured within the simulation by the detailed model.
Fig. 6.
Monomer depletion data along with simulation overlap. (A) Analysis of Aβ aggregation (50 μM) shown in Fig. 3A by MALDI-ToF mass spectrometry containing an internal standard, insulin at the indicated times of incubation. (B–E) Normalized ThT intensities (○) along with quantitative monomer depletion data obtained from MALDI-ToF (▲). Black line is the sigmoidal fit from the detailed simulation to the data points shown in Fig. 3A. The red line is monomer depletion data obtained from detailed simulation. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
6. Discussion
In this report, we have investigated the range of monomers that can associate to form a nucleus during Aβ aggregation–in other words, the nucleation number, n*, for a homogenous, single nucleation model. As mentioned earlier, many groups have attempted to identify the critical mass of the nucleus for amyloid proteins by a variety of different approaches. More importantly, the pre-nucleation dynamics has been under intense debate and the presence of secondary nucleation, heterogeneity in both conformation and molecular mass and even conformationally-changed monomer as a nucleus have been proposed [11,35–37]. Here, we have adopted a simplistic model of homogenous Aβ aggregation involving single unique nucleation event, and delineated the process by modeling key elements by two independent approaches with converging solutions: a reduced order stability argument and ODE-based numerical simulations, supported by experimental data. First, the reduced-order model stability analysis yielded a range between 10 and 60 mers to be the possible range of n*. The subsequent numerical simulation provided a range between 7 and 21 mers for n*. The larger range of n* from the stability argument could be attributed to its simplistic form in comparison to the numerical simulations. However, the overlap of 7–21 range is noteworthy. Furthermore, keeping in mind the sizes of PFs and fibrils, which are in the order of 1600 and 5000mers, the estimates of n* from the two evaluations seem to be in good agreement. Furthermore, the reduced-order stability analysis enables us to reduce the parameter sweep for the subsequent analysis as we reported earlier [20]. Secondly, within the narrow n* range determined by numerical analyses, the value of 12 shows good correlation with the experimental values. Shoghi-Jadid and co-workers approximately determined the n* value for Aβ to be 6 [38]. It is also noteworthy that Saric and co-workers elegantly demonstrated the significance of non-specific interactions during the pre-nucleation phase [11]. More importantly, via atomistic and coarse-grained models, the authors established a plausible size nucleus to range between 6 and 14 depending on the initial monomer concentration. The results derived from these reports are in good agreement with our conclusions despite the differences in the approaches. It has to be borne in mind that simulation curves that we generated are not ‘model fits’ to the experimental data but simply an overlay of the two independent data. In other words, the experimental data were not subject to curve fitting methods, and n* was obtained and verified by two independent approaches.
It is also interesting to observe the variations in n* as a function of PF concentration as modeled by our reduced order approach (Fig. 2B). Similar results were obtained from numerical analysis also (data not shown). Since only nucleus could have manifestations on the fate of PFs and not the other way around, the change in PF concentrations as a function of n* suggest that the physiochemical or molecular nature of the nucleus could be responsible for dictating the fate on the downstream events such as PF formation. This also brings up the possibility of the nucleus being heterogeneous, as has been proposed for poly-Q aggregates [39]. Heterogeneity could arise from conformation, overall structure of the oligomeric assembly or critical nucleation number, n*. It may not be necessary to have n* to be conserved for Aβ aggregation and could vary depending on the aggregation condition and environmental factors. A more likely scenario could be that n* may never be a single value but rather, a range between specific values similar to the one we have presented in this report (n* = 7 and 14). Within the numerical heterogeneity, the nucleus could also be conformationally heterogeneous. Nevertheless, our simplified homogenous, single nucleation model has provided key insights in the dynamics of the system. It is clear that the nucleation number could only be within a tight range of values as determined in this report. The effects of physiochemical and structural nature of nucleus on aggregation are currently being investigated and will be reported at a later date. Nevertheless, the current report presents the dynamics of Aβ aggregation from a different approach and opens the door in investigating the other possibilities of multiple nuclei and heterogeneous nucleation during Aβ aggregation in the future.
Acknowledgments
This work was partly funded by National Center for Research Resources (5P20RR016476-11) and the National Institute of General Medical Sciences (8P20 GM103476-11) from the National Institutes of Health for funding through INBRE (to VR) and the National Science Foundation grant (NSF 1351786) for PG.
Footnotes
Author contributions
VR, PG and AV conceptualized and designed the idea behind the project, and contributed equally in preparing the manuscript. AV conducted mathematical stability analysis work, PG conducted simulations while AK and VR conducted the biophysical experiments.
References
- 1.Selkoe DJ, Schenk D. Alzheimer’s disease: molecular understanding predicts amyloid-based therapeutics. Annu Rev Pharmacol Toxicol. 2003;43:545–584. doi: 10.1146/annurev.pharmtox.43.100901.140248. [DOI] [PubMed] [Google Scholar]
- 2.Mattson MP. Pathways towards and away from Alzheimer’s disease. Nature. 2004;430:631–639. doi: 10.1038/nature02621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Walsh DM, Selkoe DJ. Oligomers on the brain: the emerging role of soluble protein aggregates in neurodegeneration. Protein Pept Lett. 2004;11:213–228. doi: 10.2174/0929866043407174. [DOI] [PubMed] [Google Scholar]
- 4.Harper JD, Lansbury PT., Jr Models of amyloid seeding in Alzheimer’s disease and scrapie: mechanistic truths and physiological consequences of the time-dependent solubility of amyloid proteins. Annu Rev Biochem. 1997;66:385–407. doi: 10.1146/annurev.biochem.66.1.385. [DOI] [PubMed] [Google Scholar]
- 5.Jarrett JT, Berger EP, Lansbury PT., Jr The C-terminus of the beta protein is critical in amyloidogenesis. Ann N Y Acad Sci. 1993;695:144–148. doi: 10.1111/j.1749-6632.1993.tb23043.x. [DOI] [PubMed] [Google Scholar]
- 6.Jarrett JT, Lansbury PT., Jr Seeding “one-dimensional crystallization” of amyloid: a pathogenic mechanism in Alzheimer’s disease and scrapie? Cell. 1993;73:1055–1058. doi: 10.1016/0092-8674(93)90635-4. [DOI] [PubMed] [Google Scholar]
- 7.Morris AM, Watzky MA, Finke RG. Protein aggregation kinetics, mechanism, and curve-fitting: a review of the literature. Biochim Biophys Acta. 2009;1794:375–397. doi: 10.1016/j.bbapap.2008.10.016. [DOI] [PubMed] [Google Scholar]
- 8.McLaurin J, Yang D, Yip CM, Fraser PE. Review: modulating factors in amyloid-beta fibril formation. J Struct Biol. 2000;130:259–270. doi: 10.1006/jsbi.2000.4289. [DOI] [PubMed] [Google Scholar]
- 9.Murphy RM. Peptide aggregation in neurodegenerative disease. Annu Rev Biomed Eng. 2002;4:155–174. doi: 10.1146/annurev.bioeng.4.092801.094202. [DOI] [PubMed] [Google Scholar]
- 10.Thirumalai D, Klimov DK, Dima RI. Emerging ideas on the molecular basis of protein and peptide aggregation. Curr Opin Struct Biol. 2003;13:146–159. doi: 10.1016/s0959-440x(03)00032-0. [DOI] [PubMed] [Google Scholar]
- 11.Saric A, Chebaro YC, Knowles TP, Frenkel D. Crucial role of nonspecific interactions in amyloid nucleation. Proc Natl Acad Sci U S A. 2014;111:17869–17874. doi: 10.1073/pnas.1410159111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Garai K, Frieden C. Quantitative analysis of the time course of Abeta oligomerization and subsequent growth steps using tetramethylrhodamine-labeled Abeta. Proc Natl Acad Sci U S A. 2013;110:3321–3326. doi: 10.1073/pnas.1222478110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen S, Ferrone FA, Wetzel R. Huntington’s disease age-of-onset linked to polyglutamine aggregation nucleation. Proc Natl Acad Sci U S A. 2002;99:11884–11889. doi: 10.1073/pnas.182276099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Vitalis A, Pappu RV. Assessing the contribution of heterogeneous distributions of oligomers to aggregation mechanisms of polyglutamine peptides. Biophys Chem. 2011;159:14–23. doi: 10.1016/j.bpc.2011.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lee CC, Nayak A, Sethuraman A, Belfort G, McRae GJ. A three-stage kinetic model of amyloid fibrillation. Biophys J. 2007;92:3448–3458. doi: 10.1529/biophysj.106.098608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nichols MR, Moss MA, Reed DK, Lin WL, Mukhopadhyay R, Hoh JH, Rosenberry TL. Growth of beta-amyloid(1–40) protofibrils by monomer elongation and lateral association. Characterization of distinct products by light scattering and atomic force microscopy. Biochemistry. 2002;41:6115–6127. doi: 10.1021/bi015985r. [DOI] [PubMed] [Google Scholar]
- 17.Barghorn S, Nimmrich V, Striebinger A, Krantz C, Keller P, Janson B, Bahr M, Schmidt M, Bitner RS, Harlan J, Barlow E, Ebert U, Hillen H. Globular amyloid beta-peptide oligomer - a homogenous and stable neuropathological protein in Alzheimer’s disease. J Neurochem. 2005;95:834–847. doi: 10.1111/j.1471-4159.2005.03407.x. [DOI] [PubMed] [Google Scholar]
- 18.Klein WL. Abeta toxicity in Alzheimer’s disease: globular oligomers (ADDLs) as new vaccine and drug targets. Neurochem Int. 2002;41:345–352. doi: 10.1016/s0197-0186(02)00050-5. [DOI] [PubMed] [Google Scholar]
- 19. Kumar A, PL, Lyons D, Morgan SE, Correia JJ, Rangachari V. Specific soluble oligomers of amyloid-β peptide undergo replication and form non-fibrillar aggregates In interfacial environments. J Biol Chem. 2012;287:21253–21264. doi: 10.1074/jbc.M112.355156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ghag G, Ghosh P, Mauro A, Rangachari V, Vaidya A. Stability analysis of 4-species Aβ aggregation model: a novel approach to obtaining physically meaningful rate constants. Appl Math Comput. 2013;224:205–215. doi: 10.1016/j.amc.2013.08.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ghosh P, Datta B, Rangachari V. Computational predictions for the lag-times and nucleation mass involved in Aβ42 peptide aggregation. Bioinformatics Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms; 2012; pp. 312–316. [Google Scholar]
- 22.Kumar A, Rice BL, Patel P, Paslay LC, Singh D, Bienkiewicz EA, Morgan SE, Rangachari V. Non-esterified fatty acids generate distinct low-molecular weight amyloid-b (Ab42) Oligomers along pathway different from fibril formation. PLoS One. 2011;6:e18759. doi: 10.1371/journal.pone.0018759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zovo K, Helk E, Karafin A, Tougu V, Palumaa P. Label-free high-throughput screening assay for inhibitors of Alzheimer’s amyloid-beta peptide aggregation based on MALDI MS. Anal Chem. 2010;82:8558–8565. doi: 10.1021/ac101583q. [DOI] [PubMed] [Google Scholar]
- 24.Ghosh P, Kumar A, Datta B, Rangachari V. Dynamics of protofibril elongation and association involved in Abeta42 peptide aggregation in Alzheimer’s disease. BMC Bioinf. 2010;11(Suppl 6):S24. doi: 10.1186/1471-2105-11-S6-S24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lomakin A, Teplow DB, Kirschner DA, Benedek GB. Kinetic theory of fibrillogenesis of amyloid beta-protein. Proc Natl Acad Sci U S A. 1997;94:7942–7947. doi: 10.1073/pnas.94.15.7942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Walsh DM, Lomakin A, Benedek GB, Condron MM, Teplow DB. Amyloid beta-protein fibrillogenesis. Detection of a protofibrillar intermediate. J Biol Chem. 1997;272:22364–22372. doi: 10.1074/jbc.272.35.22364. [DOI] [PubMed] [Google Scholar]
- 27.Murphy RM, Pallitto MM. Probing the kinetics of beta-amyloid self-association. J Struct Biol. 2000;130:109–122. doi: 10.1006/jsbi.2000.4253. [DOI] [PubMed] [Google Scholar]
- 28.Harper JD, Wong SS, Lieber CM, Lansbury PT., Jr Assembly of A beta amyloid protofibrils: an in vitro model for a possible early event in Alzheimer’s disease. Biochemistry. 1999;38:8972–8980. doi: 10.1021/bi9904149. [DOI] [PubMed] [Google Scholar]
- 29.Blackley HK, Sanders GH, Davies MC, Roberts CJ, Tendler SJ, Wilkinson MJ. In-situ atomic force microscopy study of beta-amyloid fibrillization. J Mol Biol. 2000;298:833–840. doi: 10.1006/jmbi.2000.3711. [DOI] [PubMed] [Google Scholar]
- 30.Harper JD, Wong SS, Lieber CM, Lansbury PT. Observation of metastable Abeta amyloid protofibrils by atomic force microscopy. Chem Biol. 1997;4:119–125. doi: 10.1016/s1074-5521(97)90255-6. [DOI] [PubMed] [Google Scholar]
- 31.Powers ET, Powers DL. Mechanisms of protein fibril formation: nucleated polymerization with competing off-pathway aggregation. Biophys J. 2008;94:379–391. doi: 10.1529/biophysj.107.117168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Shvadchak VV, Claessens MM, Subramaniam V. Fibril breaking accelerates alpha-synuclein fibrillization. J Phys Chem B. 2015;119:1912–1918. doi: 10.1021/jp5111604. [DOI] [PubMed] [Google Scholar]
- 33.Powers ET, Powers DL. The kinetics of nucleated polymerizations at high concentrations: amyloid fibril formation near and above the supercritical concentration. Biophys J. 2006;91:122–132. doi: 10.1529/biophysj.105.073767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Serio TR, Cashikar AG, Kowal AS, Sawicki GJ, Moslehi JJ, Serpell L, Arnsdorf MF, Lindquist SL. Nucleated conformational conversion and the replication of conformational information by a prion determinant. Science. 2000;289:1317–1321. doi: 10.1126/science.289.5483.1317. [DOI] [PubMed] [Google Scholar]
- 35.Ferrone FA. Assembly of Abeta proceeds via monomeric nuclei. J Mol Biol. 2015;427:287–290. doi: 10.1016/j.jmb.2014.10.028. [DOI] [PubMed] [Google Scholar]
- 36.Cohen SI, Linse S, Luheshi LM, Hellstrand E, White DA, Rajah L, Otzen DE, Vendruscolo M, Dobson CM, Knowles TP. Proliferation of amyloid-beta42 aggregates occurs through a secondary nucleation mechanism. Proc Natl Acad Sci U S A. 2013;110:9758–9763. doi: 10.1073/pnas.1218402110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jeong JS, Ansaloni A, Mezzenga R, Lashuel HA, Dietler G. Novel mechanistic insight into the molecular basis of amyloid polymorphism and secondary nucleation during amyloid formation. J Mol Biol. 2013;425:1765–1781. doi: 10.1016/j.jmb.2013.02.005. [DOI] [PubMed] [Google Scholar]
- 38.Shoghi-Jadid K, Barrio JR, Kepe V, Wu HM, Small GW, Phelps ME, Huang SC. Imaging beta-amyloid fibrils in Alzheimer’s disease: a critical analysis through simulation of amyloid fibril polymerization. Nuclear Med Biol. 2005;32:337–351. doi: 10.1016/j.nucmedbio.2005.02.003. [DOI] [PubMed] [Google Scholar]
- 39.Pappu AVARV. Assessing the contribution of heterogeneous distributions of oligomers to aggregation mechanisms of polyglutamine peptides. Biophys Chem. 2011;159:14–23. doi: 10.1016/j.bpc.2011.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]