Predictability decomposition detects the impairment of brain–heart dynamical networks during sleep disorders and their recovery with treatment

Abstract

This work introduces a framework to study the network formed by the autonomic component of heart rate variability (cardiac process η) and the amplitude of the different electroencephalographic waves (brain processes δ, θ, α, σ, β) during sleep. The framework exploits multivariate linear models to decompose the predictability of any given target process into measures of self-, causal and interaction predictability reflecting respectively the information retained in the process and related to its physiological complexity, the information transferred from the other source processes, and the information modified during the transfer according to redundant or synergistic interaction between the sources. The framework is here applied to the η, δ, θ, α, σ, β time series measured from the sleep recordings of eight severe sleep apnoea–hypopnoea syndrome (SAHS) patients studied before and after long-term treatment with continuous positive airway pressure (CPAP) therapy, and 14 healthy controls. Results show that the full and self-predictability of η, δ and θ decreased significantly in SAHS compared with controls, and were restored with CPAP for δ and θ but not for η. The causal predictability of η and δ occurred through significantly redundant source interaction during healthy sleep, which was lost in SAHS and recovered after CPAP. These results indicate that predictability analysis is a viable tool to assess the modifications of complexity and causality of the cerebral and cardiac processes induced by sleep disorders, and to monitor the restoration of the neuroautonomic control of these processes during long-term treatment.

1. Introduction

In the emerging field of network physiology [1], the human body is seen as an integrated network composed of different organ systems, which have their own internal regulatory mechanisms, but also interact with each other to preserve the physiological function. In addition to other important physiological systems subjected to neural regulation, such as the circulatory and respiratory systems, two crucial nodes of the human physiological network are the brain and cardiac systems. The dynamical states of these systems are continuously modulated by the rhythmic activity of brain structures devoted to visceral control (i.e. the autonomic nervous system). This modulation is clearly visible in the time course of the physiological variables measured as output of the cardiac and central brain systems. For instance, the analysis of low-frequency (LF) and high-frequency (HF) oscillatory components of heart rate variability (HRV) is ubiquitously used to assess autonomic control in a variety of physiological conditions and pathological states [2]. The continuous modulation of brain activity is reflected in the amplitude of electroencephalographic (EEG) rhythms oscillating in the δ, θ, α, σ, β, and γ frequency bands that cover the whole spectral EEG variability. In particular, the modulating activity of the autonomic function is known to have an impact on the five frequency bands that characterize in detail the EEG during sleep (i.e. δ, θ, α, σ and β) [3]. Sleep is a physiological state that has a significantly more complex and important impact on the neural regulation of cardiac and cerebral physiological variables [3–6]. The stage organization of sleep reflects modulations in the autonomic activity such that an increase in the balance between the variance of the autonomic components of HRV in the LF and HF bands (LF/HF ratio) is known to occur with the transition from non-random eye movement (NREM) sleep to REM sleep [4,7]. Sleep state-related variations are also observed in the spectral power of the sleep EEG, with wave amplitude decreasing significantly in the slower δ, θ and α bands, and increasing in the faster σ and β bands, during REM sleep compared with NREM stages [3,8].

In more recent years, the research on brain and cardiovascular dynamics during sleep has seen a shift of paradigm from the study of individual EEG or HRV activity to the investigation of the relationships between specific EEG wave amplitudes and HRV dynamical indexes. Initially, brain and cardiovascular interactions during sleep were studied only indirectly, correlating indexes of cardiac and cerebral variability to each other through simple non-dynamical analyses [9–14]. Dynamic approaches to the joint characterization of cardiac and neural time series were introduced only recently, and were based on bivariate and non-causal analyses [15–22]. However, complex physiological networks are composed of multiple nodes, where each node may represent the activity of a specific physiological system that exhibits autonomous dynamics but is also connected to other diverse systems. A proper analysis of these networks necessitates the introduction of fully multivariate and causal methods for time-series analysis, to guarantee a faithful reconstruction of the network structure based on the detection of direct and directional effects. To meet this need, we have recently proposed an integrated framework for multivariate time-series analysis, essentially based on information-theoretic and predictability measures, that led us to evidence for the first time the existence during sleep of a structured network of brain–heart interactions, sustained both by the internal dynamics of the various cardiac and brain processes and by the causal interactions between them [23,24]. In this study, we pursue the twofold aim of completing the methodological formulation of this framework, and of advancing its utilization in the clinical description of sleep disorders.

Methodologically, the analysis of how information is processed inside a network of multiple interacting processes is often performed under the perspective of distributed computation, whereby the general concept of ‘information processing’ is dissected into the basic components of information storage, transfer and modification [25]. Information storage and transfer refer respectively to how much the uncertainty about the present state of a dynamical system can be resolved by the knowledge of its own past states [26], and by the additional knowledge of the past states of the systems potentially connected to it [27]. Following our recent developments in the detection of information storage and information transfer in brain–heart networks [23,24], in this study, we embed in the framework the concept of information modification, relevant to how two (groups of) source systems interact redundantly or synergistically with each other when they contribute to resolve the uncertainty about the states of the assigned target system [28,29]. The complete framework is formulated, in the context of multivariate linear prediction models, devising a predictability decomposition strategy that leads to decompose the full predictability of the target process into measures of self-predictability, causal predictability and interaction predictability which reflect the notions of information storage, transfer and modification. This opens the way to the thorough investigation of how different cardiac and brain processes retain the information that they produce, transfer information to each other, and mutually interact while they transfer information.

From a clinical point of view, a pathological condition that leads to a re-organization of the network of physiological interactions between the cardiovascular and brain rhythms is the sleep apnoea–hypopnoea syndrome (SAHS). This syndrome is a common medical problem that dramatically affects the quality of life, and is associated with hypertension, heart failure, myocardial infarction, stroke and vascular complications [30,31]. SAHS has been associated with significant alterations of the rhythmic autonomic activity during sleep, with blunted shifts of the alternating predominance of cardiac vagal and sympathetic activities during NREM and REM sleep [32], increased δ EEG activity during NREM apnoea [33], and impaired link between cardiac parasympathetic and delta EEG activities [34]. Moreover, the treatment of severely apnoeic patients with nasal continuous positive airway pressure (CPAP), a respiratory therapy which consists in applying mild air pressure to keep the airways continuously open during night-time, has been proven effective in improving sleep architecture and cardiovascular parameters, as well as in reducing some comorbidities of SAHS [35–37]. It has been recently shown that long-term CPAP therapy produces a subtle but clinically important restoration of the neuroautonomic joint regulation of different organ systems: in the presence of similar sleep characteristics and spectral profiles of cardiac variability, patients with severe SAHS exhibiting a weakened link between the cardiac vagal component of HRV and the sleep delta EEG amplitude partially recovered such a link after more than 1 year of nasal CPAP treatment [38]. In this study, we delve into these modified brain–heart interactions, according to the broader perspective of multivariate analysis of network processes, through the evaluation of the patterns of self-predictability, causal predictability and interaction predictability.

2. Linear prediction of multivariate stochastic processes

Let us consider a multivariate stochastic process Ω={Y,X} composed by a predefined ‘target’ process, Y , and by M other possibly interacting processes, X={X₁,…,X_M}, which are considered as ‘sources’. In this context, we deal with the description of the dynamics of the target process performed in the framework of linear prediction. Setting a temporal frame where n represents the present time, the random variable associated with the present of the target, Y _n, is described as resulting from a linear combination of the p past target variables, Y _n−1,…,Y _n−p, and of the past variables of the source processes, X_m,n−τm,…,X_m,n−p (m=1,…,M), according to the autoregressive (AR) model of order p and with M inputs

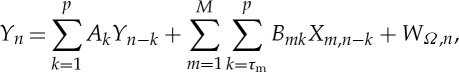2.1

where A_k and B_mk are linear regression coefficients, τ_m is the minimum delay of the interaction from X_m to Y , and W_Ω is a scalar zero-mean innovation process uncorrelated and X₁,…,X_M. The variance of W_Ω, denoted as ε(Y |Ω)=ε(Y |Y,X), is a measure of the unpredictability of Y given Ω={Y,X}, and is bounded between 0 and the variance of Y , ε(Y).

Starting from the most complete model structure of equation (2.1), simplified structures that disregard some of the source processes can be obtained as follows. Disregarding all possible sources, the description of Y can be performed by a simple linear AR model

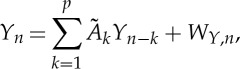2.2

where the regression coefficients 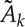are generally different from the A_k in (2.1), and the variance of the innovation process W_Y, denoted as ε(Y |Y), is a measure of the unpredictability of the present of the target process given its past. Moreover, considering two disjoint sets of Q and M–Q source processes, i.e. V={V ₁,…,V _Q} and Z={Z₁,…,Z_M−Q} such that X={V,Z}, the linear prediction of Y can be performed considering as exogenous inputs only one of these two subsets by setting the models

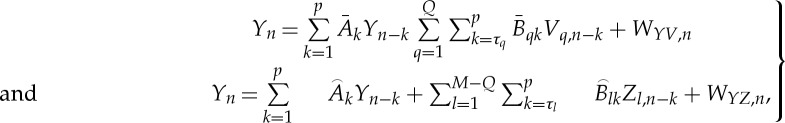2.3

In equation (2.3), the variances of the innovation processes W_YV and W_YZ, denoted as ε(Y |Y,V) and ε(Y |Y,Z), can be taken as measures of the unpredictability of the present of Y given its past and the past of V, or given its past and the past of Z, respectively.

Based on the representations above, we provide the following definitions of full predictability of Y , self-predictability of Y and causal predictability from X to Y

2.4

2.5

2.6

The full predictability P_{Y |Ω} quantifies the portion of the variance of the target process Y that can be predicted from the knowledge of the whole set of available processes Ω={Y,X}. Similarly, the self-predictability P_{Y |Y} quantifies the portion of the variance of Y that can be predicted from the exclusive knowledge of its own dynamics. These predictability measures are inversely related to the complexity of the target time series, which is defined in this study as the degree of unpredictability of the series measured through the prediction error variance [39]. The causal predictability P_X→Y measures the portion of the variance of Y that can be predicted from the knowledge of the source process X above and beyond the portion that can be predicted from Y considered alone. Quantifying predictability improvement, this last measure is in agreement with the concept of Wiener–Granger causality [40,41]. Combining equations (2.4)–(2.6), one can easily show that the measures of full, self- and causal predictability are related to each other by the equation: P_{Y |Y,X}=P_{Y |Y}+P_X→Y (figure 1). Moreover, separating the source process X into the subsets V and Z, we define the partial causal predictability from V to Y given Z as

2.7

Quantifying the portion of the variance of Y that can be predicted from the knowledge of V above and beyond the portion that can be predicted from Y and Z, the measure defined in equation (2.7) reflects the concept of (multivariate) partial Granger causality [41–44].

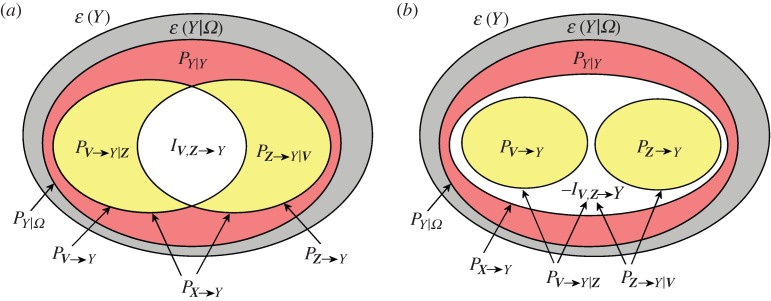
Figure 1.

Variance decomposition for the multivariate process Ω={Y,X}= {Y,V,Z}. The diagrams show how the variance of the target process Y (ε(Y), total area) is decomposed in an unpredictable part (ε(Y |Ω), grey area) plus a predictable part P_{Y |Ω}, denoting full predictability. The latter further splits in two parts evidencing the self-predictability of the target (P_{Y |Y}, red area) and the causal predictability from all sources to the target (P_X→Y, yellow+white areas). Then, the overall causal predictability can be decomposed: (a) as the sum of the partial causal predictabilities (P_{V→Y |Z} and P_{Z→Y |V}, yellow) plus the interaction predictability (I_Z,V→Y, white) in the case of redundancy or (b) as the sum of the causal predictabilities (P_V→Y and P_Z→Y, yellow) minus the interaction predictability (−I_Z,V→Y, white) in the case of synergy. (Online version in colour.)

The concepts of causal predictability and partial causal predictability can be combined together to investigate how the sources interact with each other in the prediction of the target dynamics. Specifically, defining a so-called interaction predictability as

2.8

it is easy to show that it quantifies the difference between the causal predictability and the partial causal predictability from one source process to the target process as

2.9

Then, one can show that the ‘collective’ causal predictability from X={V,Z} to Y can be decomposed as

2.10

The predictability decomposition of equation (2.10) is illustrated graphically in figure 1, showing how it allows to quantify the character (redundant or synergistic) of the interaction between V and Z when they are used to predict Y [45]. Specifically, if the causal predictability from V to Y is larger than the partial causal predictability from V to Y given Z, the interaction predictability is positive. In this case, we have that considering the two sources together yields a worse prediction of the target than summing up the individual predictabilities from each source (P_X→Y<P_V→Y+P_Z→Y); this situation denotes redundancy between the sources (figure 1a). If, on the contrary, the causal predictability from V to Y is smaller than the partial causal predictability from V to Y given Z, the interaction predictability is negative. In this case, we have that considering the two sources together yields a better prediction of the target than summing up the individual predictabilities from each source (P_X→Y>P_V→Y+P_Z→Y); this situation denotes synergy between the sources (figure 1b).

It is worth noting that the predictability measures introduced above are strictly related to a set of corresponding information-theoretic measures defined for vector AR processes. Specifically, exploiting the close correspondence between conditional entropy and prediction error variance that holds for linear processes, one can show that the measures of full predictability, self-predictability, (partial) causal predictability and interaction predictability defined in this study are directly related to the linear AR definition of the measures of prediction entropy [46], self-entropy [46], (partial) transfer entropy [43,46] and interaction transfer entropy [47], respectively. The theoretical concepts underlying these measures and their practical implementation in simulated time series have been thoroughly tested in a number of recent studies [43,46–48].

3. Experimental protocol and data analysis

This study considers a database previously collected [38], including eight patients (45.6±6.7 years) who were admitted in the Sleep Laboratory for two consecutive nights and were diagnosed as suffering from severe SAHS, detected measuring an apnoea–hypopnoea index (AHI) more than 30 events per hour. The same patients were admitted again (49.9±7.0 years) after at least 1 year of treatment with the CPAP therapy (range: 1.8–7.8 years; mean±s.d.: 4±3 years), which was maintained for at least 5 h every night and led to adjustments documented by the significant reduction of apnoea episodes (AHI<10 events per hour). Moreover, 14 healthy age-matched subjects (44.0±6.2 years), admitted to the Sleep Laboratory for three consecutive nights, were considered as the control group. Participants were not allowed to take any medication, and were instructed to limit alcohol and caffeine consumption and to respect a regular sleep–wake cycle.

We analysed the ECG and EEG recordings of the SAHS patients, both before and during CPAP treatment, and of the healthy controls, acquired during the second or third night of their hospitalization. The measurement procedure resembled that of our previous studies [23,24] and consisted in the following processing of ECG and EEG signals, digitized simultaneously with 200 Hz sampling frequency and 12-bit amplitude resolution. The analysis of the EEG recordings (Cz-Ax derivation, with Ax mastoid reference) was performed first applying a fast Fourier transform (FFT) to each consecutive window of 5 s, and then computing the spectral power inside each of the five conventional frequency bands (δ: 0.5–3 Hz; θ: 3–8 Hz; α: 8–12 Hz; σ: 12–16 Hz; β: 16–25 Hz) traditionally explored in sleep studies [1,3,15–17,34,49]. In this study, we stick to these five bands, excluding the dynamics of the EEG amplitude in the γ band (greater than 25 Hz) which are commonly associated with sensory and cognitive functions and during sleep are partly synchronous with β dynamics (γ₁ band, 25–35 Hz) and partly correlated only to muscle tone artefacts ((γ₂ band, 35–45 Hz) [50]. The time-series representative of the δ, θ, α, σ and β wave amplitudes were finally obtained averaging the power values for the relevant frequency band over non-overlapping windows of 60 s. The ECG (lead V4 or V6) was first up-sampled to 400 Hz to increase precision in the location of the R-peaks, which were used to measure HRV through the sequence of the durations of the time intervals between consecutive R-peaks (RR intervals). Premature ventricular contractions, ectopic beats and other artefacts were automatically detected when RR<0.35 s or RR>1.5 s, and were then removed and linearly interpolated with the surrounding values. The resulting RR time series was interpolated and resampled uniformly to 8 Hz, and then subdivided in consecutive windows of 120 s overlapped by half. For each window, the RR interval series was in turn detrended, Hanning windowed and FFT transformed. Finally, the time-series representative of the cardiac parasympathetic activity was obtained as the sequence of the spectral power values taken in the HF band (0.15–0.4 Hz) divided to the power contained in the LF+HF band (0.04–0.4 Hz). With this overall procedure, six synchronous time series, describing the variability of the five brain wave amplitudes and of the cardiac parasympathetic component, were obtained with sampling frequency of 1 min. In this way, one multivariate time series was collected from the full night polysomnographic recordings of each individual subject.

Before predictability analysis, each time series was normalized to zero-mean and unit variance. The six normalized time series measured for each subject were then considered as realizations of the overall stochastic process Ω={Φ,η}, composed by the five-dimensional vector process Φ={δ,θ,α,σ,β} describing the dynamics of the different brain rhythms and by the scalar process η describing the cardiac dynamics. The analysis was then performed, following the derivations presented in §2, as described in the following. In the study of cardiac dynamics, the role of the target Y was assumed by the cardiac process η, whereas the sources X were represented by the brain process Φ. We computed the full, self- and causal predictability measures P_η|Ω, P_η|η, and P_Φ→η; further, causal predictability decomposition was performed computing the interaction predictability between each single brain process and the remaining brain processes as I_{x,Φ∖x→η}, with x taking the role of any process δ, θ, α, σ or β. In the study of brain dynamics, each single brain process was considered as the target and the full, self- and causal predictability were computed as P_x|Ω, P_x|x, and P_{η,Φ∖x→x}; predictability decomposition was then performed computing the interaction predictability between the cardiac process and the brain processes other than the target as I_{η,Φ∖x→x}, (here x was equal to δ, θ, α, σ or β). All indexes were computed from the prediction error variances obtained from the linear regressions described in equations ((2.1)–(2.3)). Regressions were performed through the standard least-squares approach, after optimizing the model order p in the range from 2 to 12 according to the Bayesian information criterion (BIC) applied to the full multivariate AR model fitting the six series. The reduced model structures were separately identified from the data using the same model order obtained through the BIC for the full structure. In the study of cardiac dynamics, the minimum interaction delays τ_m were set equal to 1 for all sources. In contrast, in the study of brain dynamics, the minimum interaction delay from the cardiac source process η to the considered brain target process x, with x=δ, θ, α, σ or β, was set to 0 to account for the partial overlap of the time series owing to the measurement convention, which introduces ‘causal’ information with no delay from heart to brain (i.e. because the HF power of HRV was measured on windows of 120 s overlapped in the second half with the measurement windows of the EEG bandpowers, the nth sample of the cardiac series is built including HRV points that occur in time before the EEG points forming the nth sample of any brain series) [24].

To test the hypothesis that an individual observed process (i.e. the cardiac rhythm η or one of the brain rhythms δ, θ, α, σ, β) is significantly predictable given either the past of the full process Ω, its own past, or the past of all other processes, we assessed the statistical significance of the measures of full, self- and causal predictability (equations (2.4)–(2.7)); this was performed for each individual subject applying the Fisher F-test with significance p<0.01: the test compares the variances of the residuals obtained from the unrestricted and restricted model structures relevant to the model-based computation of the considered predictability measure. To test the hypothesis that the brain rhythms interact significantly with each other while they contribute to improve the predictability of the cardiac rhythm, and the hypothesis that the cardiac rhythm interacts significantly with the brain rhythms while contributing to improve their predictability, we assessed the statistical significance of the interaction predictability measure (equations (2.8) and (2.9)) on a group basis, by testing whether the causal predictability and partial causal predictability measures computed across subjects come from a distribution with the same median; this was done using the Wilcoxon signed-rank test for paired data, and correcting for multiple comparisons (i.e. setting statistical significance p<0.01). To test the hypothesis that each assigned predictability measure varied significantly when computed before and during the CPAP treatment, we used the Wilcoxon signed-rank test for paired data with significance p<0.05. To test the hypothesis that each assigned predictability measure varied significantly between untreated SAHS patients and controls, or between patients treated with CPAP therapy and controls, we used the Mann–Whitney U-test with significance p<0.05.

4. Results

The length of the time series analysed in this study (from the onset of sleep until the end of the last REM sleep state) was 418±60 min for the control group, 419±55 min for the SAHS patients and 410±81 min for the same patients studied after prolonged CPAP treatment. Complete sleep and demographic parameters for these groups are reported in [38]. The model order estimated for the full multivariate model using the BIC was 3.52 (average for all groups and time series), and did not vary significantly across the three groups (CTRL: 3.4±1.3 for η, 3.8±1.9 for Φ; SAHS: 3.9±2.6 for η, 3.5±1.8 for Φ; CPAP: 2.5±0.5 for η, 3.2±1.9 for Φ).

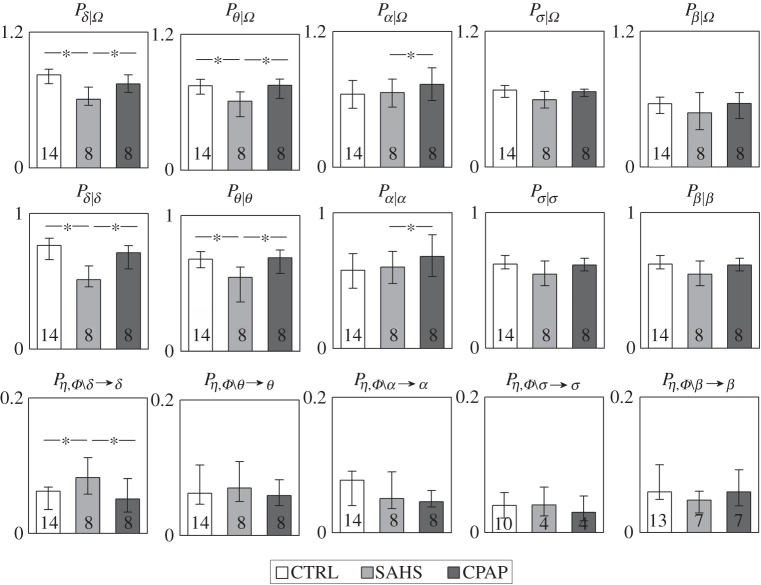
The results of the predictability decomposition of the cardiac dynamics are reported in figure 2, showing the distribution in the three groups of the full predictability of the process η and of its constituent terms, i.e. the self-predictability and the causal predictability derived from the brain process Φ. In the group of healthy subjects, about 50% of the variance of the cardiac dynamics during sleep could be predicted from their past and from the dynamics of the brain processes. This full predictability was significantly lower (36.9%, p=0.007) in patients suffering from SAHS, and remained at lower levels (38.4%, p=0.012) also after the CPAP treatment. This higher complexity exhibited by apnoeic patients compared with healthy controls was the result of a decrease of both the self-predictability of the cardiac dynamics and of the causal predictability brought by the brain dynamics. The indexes of full and self-predictability were statistically significant in all groups, whereas the causal predictability was not significant in three out of eight patients before CPAP treatment, and one patient after the treatment.

Figure 2.

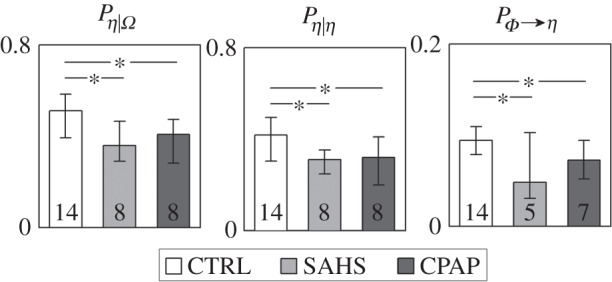
Distribution of the measures of full predictability (P_η|Ω), self-predictability (P_η|η) and causal predictability (P_Φ→η) assessed for the cardiac parasympathetic component of HRV in the network Ω={Φ,η} formed by cardiac process η and the brain process Φ, and expressed as median and quartiles computed in healthy controls (CTRL), in patients with severe sleep apnoea–hypopnoea syndrome (SAHS), and in the same patients studied after prolonged continuous positive airway pressure therapy (CPAP). For each measure, the number of subjects for which it was detected as statistically significant is reported inside the bar. *p<0.05 CTRL versus SAHS or CTRL versus CPAP (Mann–Whitney U-test).

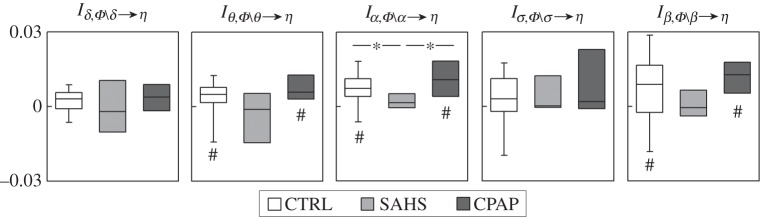
Figure 3 reports the distributions of the measures of interaction predictability reflecting how each single brain process δ, θ, α, σ or β interacts with the other brain processes in the prediction of the cardiac process η. In the group of healthy subjects, the θ, α and β brain wave amplitudes interacted redundantly with the other EEG waves (the interaction predictabilities I_{θ,Φ∖θ→η}, I_{α,Φ∖α→η} and I_{β,Φ∖β→η} were significantly different from zero). This redundant interaction disappeared in SAHS patients, and was restored after CPAP treatment. Notably, in the SAHS group, the interaction predictability was never significantly different from zero, documenting the absence of any significant interaction between the brain processes while they contribute to the prediction of the cardiac dynamics.

Figure 3.

Box plots of the measures of interaction predictability, I_{x,Φ∖x→η}, quantifying the degree of interaction between each brain process (x=δ, θ, α, σ, β) and the remaining brain processes in the prediction of the cardiac process η, computed in healthy controls (CTRL), in patients with severe sleep apnoea–hypopnoea syndrome (SAHS), and in the same patients studied after prolonged continuous positive airway pressure therapy (CPAP). For each measure, significantly non-zero interaction predictability is denoted by the hash symbol (p<0.01, Wilcoxon signed-rank test). *p<0.05 CTRL versus SAHS (Mann–Whitney U-test) or CTRL versus CPAP (Wilcoxon signed-rank test).

Figure 4 depicts the results of predictability decomposition applied to the five brain processes, reporting how the predictable dynamics of each process broke down into components related to the self-predictability of the process and to its predictability arising from the other processes of the brain–heart network. In the control group, the full predictability of the brain processes ranged from 81% for the δ wave dynamics to 73% for the θ waves, approximately 65% for the α and σ waves, and 73% for the β waves, resulting higher than that of the cardiac process (approx. 50%). While these full predictability values and their self- and causal constituents did not differ significantly in the untreated and treated patients compared with the controls when considering the faster α, σ and β waves, important modifications were noted for the slower δ and θ waves. Specifically, the predictability was markedly decreased in SAHS patients for the δ dynamics (62%, p=0.005) and the θ dynamics (59%, p=0.003), but was restored at values comparable to those of the healthy controls after long-term CPAP treatment (74% for δ and 71% for θ, p=n.s.). The drop of predictability and its recovery with treatment were entirely owing to the self-predictability of these brain rhythms, whereas the causal predictability was unchanged across the three groups for the θ wave, and was even showing an opposite trend for the δ wave.

Figure 4.

Distribution of the measures of full predictability (P_x|Ω), self-predictability (P_x|x) and causal predictability (P_{η,Φ∖x→x}) assessed for the amplitude of each EEG brain wave (x=δ, θ, α, σ, β) in the network Ω={Φ,η} formed by cardiac process η and the brain process Φ, and expressed as median and quartiles computed in healthy controls (CTRL), in patients with severe sleep apnoea–hypopnoea syndrome (SAHS), and in the same patients studied after prolonged continuous positive airway pressure therapy (CPAP). For each measure, the number of subjects for which it was detected as statistically significant is reported inside the bar. *p<0.05 CTRL versus SAHS (Mann–Whitney U-test) or CTRL versus CPAP (Wilcoxon signed-rank test).

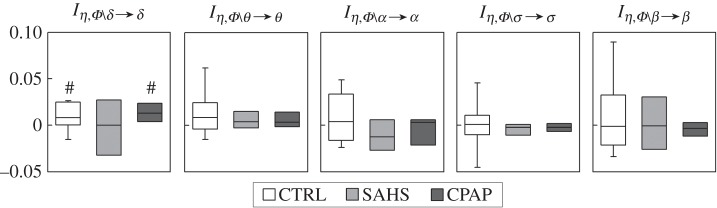
The higher causal predictability of the sleep EEG amplitude in the δ frequency band observed in untreated SAHS patients (8.3% versus 5.7% of healthy controls, p=0.044), as well as its decrease with CPAP treatment (5.6% versus 8.3%, p=0.039) documented in figure 4, can be related to how the brain and heart processes interact in contributing to the predictability of the δ waves. Figure 5 shows indeed that the interaction predictability between the cardiac dynamics and the brain dynamics other than δ is significantly positive in the control group, cannot be distinguished from zero in the SAHS patients, and is again significantly positive during long-term CPAP treatment. Such a redundant interaction between brain and cardiac dynamics for healthy subjects and treated patients was a peculiarity of the δ waves, as it was not observed for any of the other brain wave amplitudes.

Figure 5.

Box plots of the measures of interaction predictability, I_{η,Φ∖x→x}, quantifying how the prediction of each brain process (x=δ, θ, α, σ, β) results from the interaction between the remaining brain processes and the cardiac process η, computed in healthy controls (CTRL), in patients with severe sleep apnoea–hypopnoea syndrome (SAHS), and in the same patients studied after prolonged continuous positive airway pressure therapy (CPAP). For each measure, significantly non-zero interaction predictability is denoted by the symbol hash (p<0.01, Wilcoxon signed-rank test).

5. Discussion

This study deals with the characterization of the physiological network of brain–heart interactions during sleep, extending the methodology and the results of our previous works in this field [23,24] in several respects. First, complexity and causality of the brain and cardiovascular dynamics during sleep are investigated exploring predictability measures rather than information measures. Complexity is a defining feature of physiological systems, and is commonly quantified as the departure of a signal from a fully predictable time course [39,51]; in this study, we assessed complexity through the full and self-predictability measures, quantifying respectively how much of the unpredictability of an observed signal can be reduced by the knowledge of its own dynamics, or by the knowledge of the dynamics of the whole set of signals composing the observed physiological network [39]. Causality is a concept related to the existence of directed interactions between the observed signals, and is often associated with the physiological mechanisms of joint modulation of interconnected organ systems [52]; here, causality was assessed in agreement with the well-known Wiener–Granger concept of predictability improvement [41]. Furthermore, in this work, the notion of causality is broken down by exploring, for the first time, to the best of our knowledge, in the study of brain–heart networks, the concept of source interaction: defining the novel measure of interaction predictability, we investigate whether two (groups of) source signals act redundantly or in synergy while they contribute to reduce the unpredictability of the target signal. The complete framework, investigating the concepts of complexity and causality from a different perspective than in [23,24] and including the new concept of redundancy/synergy, is applied for the first time on brain–heart networks assessed in pathological states, considering a group of severely apnoeic patients before and after their treatment with the ventilation therapy. When applied to these unique data, our comprehensive approach for the prediction of multivariate time series led to the following original findings: (i) the proposed framework detected consistently the presence of structured dynamics in the nocturnal time course of the cardiac parasympathetic component of HRV and of the EEG wave amplitudes, documented by the statistically significant predictability measures which explained, in all subjects and patients, more than 50% of the variability of heart and brain dynamics during sleep; (ii) severe apnoea–hypopnoea increased the complexity of the nocturnal dynamics of the brain and cardiovascular systems, significantly reducing the predictability of the time courses of the parasympathetic component of HRV and of the δ and θ EEG bandpowers; (iii) this higher complexity of cardiac and slow-wave brain rhythms was due in its largest part to a marked reduction of the self-predictability of these rhythms; (iv) prolonged treatment of SAHS patients with the CPAP therapy restored the full and self-predictability of the δ and θ brain wave amplitudes, but not those of the cardiac parasympathetic component; (v) the magnitude of the causal effects sustaining the network of physiological brain–heart interactions during sleep decreased along the brain-to-heart direction, and increased significantly towards the δ brain process, in apnoeic patients compared with healthy subjects; and (vi) brain–heart communications during normal sleep were characterized by redundant interactions between different brain rhythms contributing to the cardiac dynamics, and between brain and cardiac rhythms contributing to the δ EEG dynamics, which were lost in severe SAHS and were restored by long-term nasal CPAP.

The analysis framework introduced in this study was designed to quantify together different aspects of the dynamics of networks composed by multiple interacting dynamical processes, i.e. the reduction in uncertainty about an assigned target process that results from its own dynamics, from the dynamics of the other processes in the network, and from the interaction between these other processes. The relevant quantitative measures are the self-predictability, causal predictability and interaction predictability, and are intimately related to the information-theoretic concepts of information storage, transfer and modification [25]. While traditionally these concepts are quantified through entropy-based functionals such as the storage entropy [43], the transfer entropy [27] and a dynamical formulation of the interaction information [53], in this work, we adopted predictability-based functionals essentially exploiting the prediction error variance. The information-theoretic and predictability frameworks are closely connected as regards the estimation of information storage and information transfer, as the self- and transfer entropies are strictly related to self- and causal predictability, and are formally equivalent in the linear Gaussian approximation [42,46]. An important advantage of the predictability framework regards the evaluation of information modification: the information-theoretic formulation of the interaction information, which for dynamical systems reflects the synergy or redundancy between two sources transferring information to a target process [53], leads to a distorting effect that may produce net synergy in the presence of statistically independent sources [48]. This confusing behaviour, which leads to the prevalence of synergy over redundancy in multivariate Gaussian systems, is avoided if one quantifies information as reduction in variance rather than reduction in entropy. Thus, also according to recent studies [45,48], our formulation based solely on subtracting prediction error variances allows an unbiased evaluation of how information is modified when comparing the combined contribution of two sources with the sum of the individual contributions in the formula for the interaction predictability.

In agreement with our previous findings obtained applying the information-theoretic framework in a different group of healthy subjects [23], the results of this work confirm that during undisturbed sleep each node of the brain–heart physiological network displays structured dynamics that can be significantly predicted from the past activity at the node, as well as from the past activity at the other nodes of the network. These structured physiological dynamics are likely the result of changes in the regulation of sleep that determine fluctuations in the autonomic nervous activity. In turn, these fluctuations induce dynamical changes in the activity of both the brain and cardiac systems [3,5,54], which are manifested at multiple time scales [21]. The characteristic scales explored in this and previous works [15,16,23,24,34] are relevant to brain and cardiovascular oscillations occurring with periods longer than 15 min. In a previous study, we documented that this network of brain–heart interactions is sustained mostly by the transitions across the different sleep states, because it is much less connected when assessed for specific individual sleep stages [23]. This study documents that these brain–heart dynamics are also detectable in the sleep recordings of patients with severe SAHS. More importantly, we observe a number of significant alterations in the temporal structure of these dynamics, which were quantified by our measures of full, self-, causal and interaction predictability. First, we found that cardiac dynamics (η rhythm) and slow wave brain dynamics (δ and θ rhythms) are significantly more complex during disturbed apnoeic sleep (figures 2 and 4). SAHS induces sudden surges in sympathetic and vagal cardiac activity [55] as well as in NREM EEG δ activity [33] and, as a result, suppresses the nocturnal rhythmic physiological shifts in the sympathovagal balance. In turn, this suppression likely induces a weakened autonomic control of the heart and brain rhythms and may thus explain their higher complexity, which we measured in this study in terms of markedly reduced values of full and self-predictability.

After long-term CPAP treatment, the differences in full and self-predictability observed in SAHS patients compared with healthy controls were maintained for the cardiac dynamics (figure 2) and disappeared for the δ and θ brain dynamics (figure 4). A factor that may contribute to the restoration of the predictability of the brain dynamics is the fact that in this group of SAHS patients the duration of REM sleep, which was significantly lower before the CPAP treatment, increased to values comparable to those of the healthy controls after the treatment [38]. Because the slow wave EEG activity was found to be much more irregularly affected by apnoeas during NREM sleep compared with REM [33], the restoration of REM duration favoured by the treatment may be helpful to restore also the complexity of the dynamical structure of the EEG waves. In contrast, the absence of any difference in all sleep parameters between treated patients and controls, documented in reference [38], was not sufficient to recover the drop in complexity of the dynamics of the HF component of HRV (see figure 2, showing that the drop in complexity documented by lower predictability of η for SAHS was not restored after CPAP). The higher complexity of the cardiac dynamics displayed by SAHS patients both before and after prolonged CPAP treatment documents an important and peculiar alteration of the neural regulation of the heart, because it was observed in the absence of any significant change of the mean and spectral HRV components across the same three groups [38]. A possible factor related to this higher complexity observed for the cardiac time series even after treatment may be the presumed increase of the cardiac vagal tone induced by CPAP, that was documented in previous studies [37,56] and only partially observed in the patients of this work [38]. Nevertheless, future studies are needed to investigate the underlying pathophysiological mechanisms and clinical relevance of this lack of recovery of the predictability of cardiac dynamics.

The analysis of the dynamical interactions in the brain–heart physiological network was performed in this study by exploring the intertwined concepts of information transfer and information modification through the measures of causal predictability and interaction predictability. Focusing on the network nodes for which the patterns of predictability changed significantly across groups, i.e. the cardiac η node and the δ brain node, we observed opposite changes of the full causal predictability comparing SAHS patients and healthy subjects: the causal interactions were weaker when directed to the η node (figure 2), and stronger when directed to the δ node (figure 4). This suggests that in apnoeic patients the network of physiological interactions re-organizes its sleep topology in a way such that information flows more towards the δ brain node and less towards the cardiac node. After prolonged CPAP treatment, the information flowing to the δ brain node decreased to values comparable with the healthy controls (figure 4), whereas the flow towards the cardiac node showed only a tendency to increase to the level of the controls (figure 2). These results extend to a broader perspective the findings of a previous study [38], and agree in suggesting that long-term CPAP treatment restores some aspects, but not the full connectivity structure of brain–heart interactions.

Contrary to causal predictability, the measure of interaction predictability revealed a common pattern in the comparison among healthy controls and untreated/treated patients, i.e. the loss of redundant interactions in the brain–heart network associated with SAHS and their recovery with CPAP. This was documented by the interactions between each of the θ, α and β waves and the other brain waves when predicting the cardiac activity (figure 3), and between the cardiac dynamics and the brain dynamics when predicting the δ wave activity (figure 5), that were significantly positive for the controls (indicating redundant cooperation), non-significant for the SAHS group (indicating statistical independence), and again significantly positive for the CPAP group. These results suggest that redundancy is a prevailing feature of correctly working brain–heart networks, and its loss during SAs generates a kind of segregation of the network nodes which are still transferring information to each other but perform this task in isolation.

Limitations of this work regarding the study design include the small size of the considered group of patients, the fact that patients and controls, though being matched in almost all demographic parameters, differed in the body mass index [38], and the highly variable duration of the CPAP treatment. Combined with the small population size, the different time at which follow-up measurements were taken may have an impact on the interpretation of our results. Nevertheless, because the CPAP therapy was prolonged up to the achievement of beneficial effects in terms of sleep efficiency, duration and quality, its different duration was unavoidable and in some sense purposeful to the formation of a group of treated patients for which therapy was really effective [38]. Given the size and characteristics of our group of patients, our results should be confirmed by larger population studies in which they can be tested also across the duration of long-term treatments.

Methodologically, the linear parametric approach adopted in this work guarantees the full detection of the system dynamics only when these dynamics are distributed as a jointly Gaussian process. While we have shown in a recent comparative study that linear and nonlinear estimators detect similar brain–heart networks in normal undisturbed sleep [24], we cannot exclude that nonlinear dynamics which cannot be fully disclosed by our linear approach may significantly contribute to self-, causal and interaction predictability during SAHS and after CPAP treatment. Thus, it may be possible that some of the results presented in this study would change when the same measures are computed relaxing the assumption of linearity. Therefore, we advocate studies comparing the linear approach proposed in this study with model-free nonlinear prediction methods [43,52] to assess the actual contribution of nonlinear dynamics to full night brain–heart interactions during apnoeic sleep and after long-term treatment. As to the theoretical development, the proposed measure of interaction predictability may be compared with novel concepts of information modification based on the simultaneous evaluation of redundant and synergistic contributions to a given target [48]. Finally, the approach proposed here could be extended in future studies to the identification of larger physiological networks comprising different physiological systems. This is particularly important given the known relevance to physiological interactions of variables not considered in the present study such as respiration, arterial pressure or cerebral blood flow [57,58]; in particular, the inclusion of respiratory dynamics would allow to relate the alterations of the brain–heart dynamics observed in this study to the cardiopulmonary instability which breaks down the scaling function of HRV in SA patients [59]. The network size can be enlarged even more within an individual complex system such as the brain, e.g. extending the intrachannel EEG network to the inclusion of the γ frequency band [19,20] and including a new subnetwork which explores the spatial level through the simultaneous interchannel analysis of the EEG at different scalp locations [20].

In conclusion, we have documented specific alterations of the sleep dynamics of the cardiac parasympathetic and brain wave activities in patients with SAHS, which are evident even in the absence of substantial modifications in the sleep characteristics or in the cardiovascular parameters. These alterations, documented for the first time using our predictability framework, are manifested through the falloff of the regularity of cardiac activity and slow wave brain activity, and of the redundant information shared within the network of brain–heart physiological interactions. We documented also that prolonged treatment of apnoeic patients with nasal CPAP is effective in restoring almost completely the sleep dynamics of the slow EEG waves as well as the links of the brain–heart network, but is unable to recover the structure of the cardiac dynamics. These findings help in elucidating how the complex influence of the autonomic nervous system on the sleep physiological dynamics is modified by sleep disorders, and may contribute to assess the efficacy of therapeutic approaches as well as to adjust the delivery of such therapies.

Ethics

All participants gave written informed consent to the procedure that was approved by the Ethical Committee of the Erasme Academic Hospital of Brussels.

Data accessibility

The datasets supporting this article have been uploaded as part of the electronic supplementary material, in the file Faes_etal-PTRSA2015-data.zip.

Author' contributions

L.F.: conception and design of the work, analysis of data, interpretation of data, drafting of the manuscript, final approval of the version to be published; F.J.: acquisition of data, critical revision of the work, final approval of the version to be published; D.M., S.S., A.P., G.N.: interpretation of data, critical revision of the work, final approval of the version to be published.

Competing interests

We have no competing interests.

Funding

This work was supported by the Healthcare Research Implementation Programme (IRCS), Provincia Autonoma di Trento and Bruno Kessler Foundation, Italy.