The pulsatility volume index: an indicator of cerebrovascular compliance based on fast magnetic resonance imaging of cardiac and respiratory pulsatility

Abstract

The influence of cardiac activity on the viscoelastic properties of intracranial tissue is one of the mechanisms through which brain–heart interactions take place, and is implicated in cerebrovascular disease. Cerebrovascular disease risk is not fully explained by current risk factors, including arterial compliance. Cerebrovascular compliance is currently estimated indirectly through Doppler sonography and magnetic resonance imaging (MRI) measures of blood velocity changes. In order to meet the need for novel cerebrovascular disease risk factors, we aimed to design and validate an MRI indicator of cerebrovascular compliance based on direct endogenous measures of blood volume changes. We implemented a fast non-gated two-dimensional MRI pulse sequence based on echo-planar imaging (EPI) with ultra-short repetition time (approx. 30–50 ms), which stepped through slices every approximately 20 s. We constrained the solution of the Bloch equations for spins moving faster than a critical speed to produce an endogenous contrast primarily dependent on spin volume changes, and an approximately sixfold signal gain compared with Ernst angle acquisitions achieved by the use of a 90° flip angle. Using cardiac and respiratory peaks detected on physiological recordings, average cardiac and respiratory MRI pulse waveforms in several brain compartments were obtained at 7 Tesla, and used to derive a compliance indicator, the pulsatility volume index (pVI). The pVI, evaluated in larger cerebral arteries, displayed significant variation within and across vessels. Multi-echo EPI showed the presence of significant pulsatility effects in both S₀ and 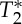signals, compatible with blood volume changes. Lastly, the pVI dynamically varied during breath-holding compared with normal breathing, as expected for a compliance indicator. In summary, we characterized and performed an initial validation of a novel MRI indicator of cerebrovascular compliance, which might prove useful to investigate brain–heart interactions in cerebrovascular disease and other disorders.

1. Introduction

Cerebrovascular disease is a significant human, social and economic burden worldwide. In the USA, it is the fourth leading cause of death and a leading cause of permanent disability. The current total annual cost of cerebrovascular disease is $105 billion in the USA, and it is expected to increase to $240 billion in 2030 [1]. Despite the usefulness of global risk assessment, it is estimated that only a fraction of cerebrovascular disease risk is explained by currently observable risk factors such as hypertension, dyslipidaemia, diabetes, smoking and arterial compliance in systemic circulation [2]. Hence, there is an urgent need for novel, individualized cerebrovascular risk signatures capable of detecting additional risk factors such as intima-media thickening, atherosclerotic plaques and stiffening of cerebral arteries. Because these goals could be achieved through early, selective detection of decreased cerebrovascular compliance, the central aim of this work was to design and validate novel, non-invasive, magnetic resonance imaging (MRI)-based biomarkers to evaluate cerebrovascular compliance through direct measures of blood volume changes with high sensitivity and speed.

Compliance is an important marker of the biomechanical properties of human tissues in normal as well as disease states. When considering a tissue compartment (e.g. blood, cerebrospinal fluid—CSF—or brain parenchyma), compliance can be quantified by the magnitude of change in the compartment volume owing to a given change in pressure, and is inversely related to the stiffness of the structure that bounds the compartment. In the human body, such pressure changes are commonly effected by travelling pressure waves, such as endogenous cardiac and respiratory pulse waves, and are one of the mechanisms through which brain–heart interactions occur.

Ageing and pathologies such as hypertension, dyslipidaemia and diabetes mellitus can cause stiffening of the aorta and other large arteries of the human body, resulting in an increase in pulse pressure in central and peripheral arteries [2]. In turn, increased pulse pressure can induce local changes in compliance by influencing local arterial remodelling in the brain such as increased wall thickness and stiffness, the development of stenosis and plaques and/or a higher likelihood of plaque rupture. Accordingly, several studies conducted on large and small artery disease suggest that increased arterial stiffness may be predictive of cerebrovascular events, with a local increase of pulse pressure in large (e.g. carotids) as well as small (e.g. arterioles) cerebral arteries [3–5] as the underlying mechanism. In this context, arterial stiffness (or its inverse, compliance) has been characterized extensively in systemic circulation, and these studies have been crucial to the understanding of key haemodynamic parameters such as vessel wall compliance, impedance and reflection coefficients in both health and disease. The most simple, robust, reproducible and widely employed non-invasive marker of systemic compliance is the aortic pulse wave velocity, i.e. the speed at which the peak (or the ‘foot’) of the cardiac pulse wave moves between the carotid and the femoral arterial sites. Importantly, aortic pulse wave velocity has proven to be an important cardiovascular risk factor in patients with cardiovascular disease (e.g. myocardial infarction, coronary artery disease, stroke and heart failure [6]).

Nevertheless, in spite of its potential usefulness as an early biomarker of cerebrovascular disease, cerebrovascular compliance is currently estimated through indirect Doppler sonography and MRI measurements (e.g. pulsatility and resistivity index) of blood velocity (rather than blood volume) changes. Such measurements are performed mainly in the carotid arteries and larger intracranial arteries. Because of limited access to intracranial tissue encased by the bony skull, grayscale, colour and spectral Doppler sonography only allow the investigation of morphological (intima-media thickness, plaque location) and functional (blood flow) abnormalities of extracranial arteries, and are usually employed to detect carotid stenosis with high sensitivity but moderate specificity [7]. Transcranial Doppler ultrasound (TCD) can measure functional bulk flow velocity changes in few large intracerebral vessels, although with reduced spatial resolution. TCD is also limited by anatomical variance in the population—10% of individuals lack the necessary ‘acoustic window’ that enables successful intracerebral vessel insonation [8]. Further, a few MRI techniques are currently used to study vascular integrity. Magnetic resonance angiography [3] can be employed to investigate structural abnormalities of extracranial and intracranial arteries in a non-invasive manner. Gated CINE-MRI [9] is a functional technique that has been mainly used to measure intracranial compliance to cardiac pulsatility in the ventricles and CSF spaces by measuring CSF velocity across the cardiac cycle [10,11]. Gated CINE-MRI has also been employed for imaging of the cardiac function [12], but is not currently employed to measure cerebrovascular compliance, most probably because of limited speed and spatial coverage (few minutes per slice to quantify bulk flow velocity in three directions).

In summary, there is an unmet need for novel non-invasive functional methods to assess cerebrovascular compliance through direct measures of blood volume changes with high spatio-temporal resolution, sensitivity and spatial (e.g. whole-brain) coverage.

The central aim of this work was to provide a novel MRI-based endogenous method to assess cerebrovascular and brain parenchymal compliance by exploiting the vessel wall mechanical response to cardiac and respiratory pressure waves. This was achieved as follows. First, we solved the Bloch equation for non-stationary (flowing) spins in a steady state during the MRI acquisition and constrained the sequence parameters to produce a novel endogenous MRI contrast dependent primarily on cerebral blood volume changes. The endogenous contrast for non-stationary spins was optimized to achieve an approximately sixfold gain compared with Ernst angle acquisitions. Then, a fast MRI sequence based on echo-planar imaging (EPI), implemented on high-field scanners, was employed along with dedicated processing to compute an average cardiac and respiratory MRI pulse waveform in each voxel of the brain, representing the brain response to physiological pressure waves. The MRI pulse waveform was obtained for several cerebral arteries, veins, voxels within the CSF and voxels within the brain parenchyma. Notably, in cerebral vessels, this waveform was expected to be directly related to blood volume changes in response to physiological pressure waves, and was used to derive a novel indicator of cerebrovascular compliance, the pulsatility volume index (pVI). In a group of healthy subjects, the pVI owing to the cardiac pulse wave was measured for several cerebral arteries; further, the origin of the MRI signal changes underlying the pVI was investigated, by characterizing the contribution of the signal changes at echo-time equal to zero (S₀) and of 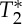signals (including possible blood oxygenation level-dependent—BOLD—effects) by multi-echo EPI; finally, we studied the performance of the pVI as a compliance biomarker, sensitive to the dynamics of cerebrovascular viscoelastic properties during breath-holding experiments.

2. Theory: contrast optimization and modelling

The aim of this work was to solve the Bloch equation for non-stationary (i.e. flowing/moving) spins in a steady state throughout the acquisition, and constrain the sequence parameters to produce an endogenous MRI contrast: (i) dependent primarily on changes in total spin concentration (i.e. volume) and (ii) optimized for non-stationary spins under certain conditions (fast-flowing spins—see definition of regime 3 below) in order to achieve a large (sixfold) gain compared with Ernst angle acquisitions, which instead provide the maximum signal for stationary spins.

In general, for a given compartment k in the brain, the gradient-echo MRI signal changes over time (M(t)) owing to the propagation of physiological pulse waves are related to both changes in the velocity (v(t)) and in the total concentration (V (t)) of moving/flowing spins (e.g. blood flow velocity and blood volume for blood compartments, respectively) as follows:

2.1

where M_xy represents the spoiled equilibrium transversal magnetization, T₁ and 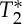the longitudinal and transversal relaxation times, respectively, M₀ the equilibrium longitudinal magnetization, TR and TE the repetition and echo times, respectively, and FA the flip angle. To separate changes in the signal at echo-time zero (S₀) from those related to 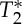, we also rewrite equation (2.1) as: M^k(t)=S₀(V ^k(t), .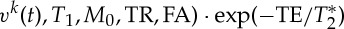

The MRI signal dependence on these two parameters (v(t),V (t)) was inspected in three regimes: regime 1, stationary spins (with velocity v=0 cm s⁻¹); regime 2, non-stationary spins flowing/moving at a velocity smaller than the critical speed v_C (i.e. the speed at which there is complete inflow of new spins and thus complete spin replacement in the slice, where v_C=ST/TR, with ST=slice thickness); regime 3, non-stationary spins flowing at a velocity greater than or equal to the critical speed (v≥v_C). Specifically, in this work, we reported on the solution of the Bloch equations under steady-state acquisitions in regimes 1 and 2 [13], explicitly investigating its dependence on spin velocity, rather than, for example, on the FA as previously shown [13]; further, we extended the solution of the Bloch equations to regime 3.

In the three regimes, for a short-TR two-dimensional (slice-selective) gradient-echo imaging method, under steady-state conditions (i.e. after the delivery of p radiofrequency or RF pulses, p depending on the regime, see below), the expected M_xy, solution of the Bloch equations, is (see figure 1 for a plot of M_xy in the three regimes for blood) as follows.

Figure 1.

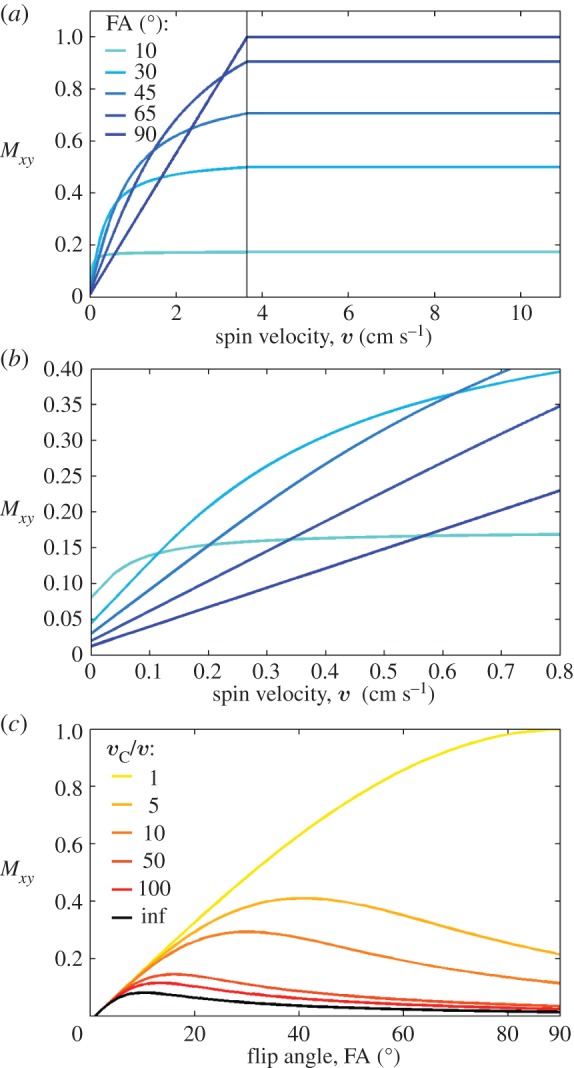
Theoretical predictions on the expected transversal magnetization M_xy for stationary (regime 1) and non-stationary spins with velocity lower (regime 2) and greater than or equal (regime 3) to the critical speed v_C. We computed M_xy (equations (2.2), (2.4), (2.7) in ‘Theory’ section for regimes 1–3, respectively) for spin velocities spanning the three regimes (regime 1, velocity=0 cm s⁻¹; regime 2, spins with velocity range= [0.36 1.8] cm s⁻¹ obtained using v_C/v in the range=[2 100]; regime 3, spins with velocity≥3.6 cm s⁻¹ (critical speed v_C= 3.6 cm s⁻¹) obtained with a ST=1.2 mm and a TR= 33 ms). We varied the FA (range [0° 90°]) and focused on the blood compartment, assuming M₀=1, and T_1blood=2.5 s at 7 Tesla [14]. We show in (a) M_xy for velocities between 0 and 11 cm s⁻¹ (at five different FA); (b) a zoomed view of (a) displaying M_xy for velocities between 0 and 0.8 cm s⁻¹; (c) the dependence of M_xy on the FA, as usually reported in MRI textbooks [9,13] (for the sake of simplicity, M_xy in (a)–(c) is displayed for TE=0, i.e. excluding possible 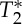effects, and for G=1). As shown in the plot, the theory predicts that compared with regime 1 the magnetization is enhanced by flowing/moving spins in regime 2–3 and crucially reaches a plateau (i.e. the signal is independent of spin velocity) in regime 3. This implies that for spins in regime 3 any change in spin velocity owing to pulsatile physiological pulse waves will not produce any change in the MRI signal. Our predictions also show that compared with Ernst angle acquisitions (e.g. approx. 10° for blood at 7 Tesla) a 90° FA is advantageous to image non-stationary spins because it enables: first, a many-fold gain in signal for non-stationary spins in regime 3 (see (a)); and second, a ‘background’ suppression of stationary spins (regime 1; see (b)). For a 90° FA compared to the Ernst angle, the gain in regime 3 was equal to 6.2 for blood at 7 Tesla (4.3, 5.7 and 8.2 respectively for WM, GM and CSF, using a T_1WM=1.2 s, T_1GM=2.1 s, T_1CSF=4.4 s [14]) and 5.1 at 3 Tesla (3.6, 4.5 and 8.2 respectively for WM, GM and CSF, using a T_1WM=0.8 s, T_1GM=1.3 s, T_1CSF=4.4 s and T_1blood= 1.7 s [14]). The background suppression in regime 1 was equal to 6.2 for blood (4.3 for WM, 5.7 for GM, 8.2 for CSF) at 7 Tesla, and 6.1 for blood (4.2 for WM, 5.5 for GM, 8.2 for CSF) at 3 Tesla. (Online version in colour.)

(1) Stationary (v=0) spins (regime 1):

2.2

where G is a gain factor, and M_z(v=0) is the longitudinal magnetization for stationary spins equal to

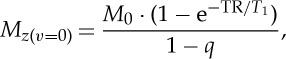2.3

where q equals 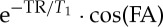. The number, p, of RF pulses needed to achieve the steady state decreases when increasing the TR/T₁ ratio, and when increasing the FA (range [0° 90°], reaching it immediately, i.e. p=1, for FA=90°). In this regime, the magnetization is independent of spin velocity (v=0 only), is larger for longer TR/T₁ ratio and the maximum magnetization is achieved at the Ernst angle .

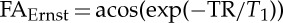(2) Non-stationary spins flowing at v<v_C (regime 2):

2.4

M_z(v=0) and q as defined above. To achieve the steady state, the number p of RF pulses needs to be greater than or equal to v_C/v (so that the velocity segment that last entered the slice experienced 1 RF pulse, whereas the first entered segment experienced v_C/v RF pulses—note that for the sake of simplicity, we assumed integer values of v_C/v). Crucially, the magnetization in regime 2 depends on spin velocity, is greater than in regime 1 (M_xy(0<v<vc)>M_xy(v=0), a phenomenon usually reported as ‘flow-related enhancement’), decreasing with the spin velocity, and reducing to M_xy(v=0) for v→0; further, the optimal FA depends on the spin velocity (figure 1). Interestingly, in this regime, for FA=90°, q is equal to zero and M_xy(0<v<vc) increases linearly with the spin velocity v:

2.5

which after replacing equation (2.3) in equation (2.5) (with q=0) reduces to

2.6

(3) Non-stationary spins flowing at v≥v_C (regime 3):

2.7

For v=v_C, this equation can be derived considering that spins flowing/moving at v_C experience only one RF pulse (all spins at the v_C that enter a slice at one RF pulse leave the slice by the next RF pulse); as a result, the transverse magnetization relates only to the projection of M₀ in the transverse plane after the application of the RF pulse, and to 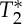relaxation (note that when v=v_C, M_xy(v=vc) in equation (2.7) can also be derived from equation (2.4), replacing the quotient v/v_C with 1). Considering that there is complete spin replacement at each TR also for v>v_C, M_xy(v>vc) is equal to M_xy(v=vc). In this regime, the steady state is reached for p=1. Further, interestingly, the maximum magnetization is expected for FA=90° (maximum of cos(FA)), and the magnetization is independent of TR/T₁ and crucially of spin velocity (see also figure 1).

In summary, the theory predicts that pulsatile MRI signal changes during physiological cycles are expected to be related to both v(t) and V (t) in regime 2, and, crucially, primarily to V (t) (mostly irrespective of pulsatile changes in v(t), as well as of TR and T₁) in regime 3 (see M_xy in figure 1):

2.8

and

2.9

We therefore hypothesized to produce an endogenous MRI contrast in several blood compartments, which would be dependent primarily on cerebral blood volume (rather than velocity) changes owing to physiological pulse waves by constraining the sequence parameters (TR, ST) to obtain a critical speed (e.g. approx. 3.6 cm s⁻¹, vertical line in figure 1) lower than for instance the (diastolic) blood velocity in large and middle cerebral vessels.

Further, the theory predicts that compared with Ernst angle acquisitions (approx. 10° for blood and the short TR employed) a 90° FA enables a many-fold gain (equal to 6.2 for blood) in endogenous signal of fast flowing/moving spins (regime 3), and a many-fold ‘background suppression’ (equal to 6.2 for blood) of stationary spins (regime 1) (see also figure 1); thus, we hypothesized that the use of a 90° FA would be optimal to investigate pulsatile signal changes of fast flowing/moving spins, without the need of using an exogenous contrast agent.

3. Material and methods

We performed four MRI experiments in order to (i) verify theoretical predictions on the optimal use of a 90° FA to study non-stationary spins in regime 3, (ii) estimate the MRI pulse waveform in response to cardiac and respiratory effects in several brain compartments and extract an indicator of cerebrovascular compliance, the pVI, in larger cerebral arteries, (iii) investigate the origin of the MRI pulse waveform, namely S₀ and possible effects related to the phase of physiological cycles, and (iv) validate the pVI by demonstrating its capability of following the dynamics of cerebrovascular viscoelastic properties during a breath-holding challenge. In each experiment, MRI was performed on a group of healthy subjects at 7 Tesla (except for one subject at 3 Tesla in experiment 2) using a detunable band-pass birdcage coil for RF transmission, and a custom-built 32-channel RF loop coil head array for reception. To limit motion, subjects were instructed to keep their head still as much as possible during MRI, and the subject's head was constrained by the use of foam pads and by the internal lining of the RF coil; data with visible head-motion were discarded from the analysis. We implemented a non-gated fast MRI technique, namely an EPI sequence with the repetition loop within the slice loop (as opposed to standard EPI used for fMRI), which uses very short TRs (approx. 30–50 ms) and steps through slices every 20–30 s (see details in each experiment). Schematics of the sequence are provided in the electronic supplementary material. The subject age/gender and additional MRI parameters are specified below for each experiment. During MRI, signals of cardiac pulsation and respiration were recorded (1 kHz sampling rate) by a piezoelectric finger pulse sensor (ADInstruments, Colorado Springs, CO, USA) and a piezoelectric respiratory bellow (UFI, Morro Bay, CA, USA) positioned around the chest, respectively. Physiological recordings were employed to identify the timing of cardiac and respiratory events (systole in peripheral finger artery and end of inhalation, respectively) and used to obtain in the brain an average MRI pulse waveform across cycles. Note that in several brain compartments (e.g. larger arteries, scalp arteries, ventricles) it was feasible to extract the timing of these events directly from the EPI data; therefore, the use of physiological recordings might be redundant in studies using single slice acquisitions covering these compartments. Nevertheless, physiological recordings are advisable for EPI acquisitions stepping through several slices (as in most of our experiments) to enable the extraction of the timing of physiological events from the same external reference signal across slices, rather than from EPI signals obtained in different slices (i.e. different brain locations and timing of the travelling pulse wave). The study was approved by the Institutional Review Board of the Massachusetts General Hospital, and written informed consent was obtained from the subjects before participation. The analyses were carried out using Matlab v. 8.4 (Natick, MA, USA).

(a). Experiment 1. On the optimal use of a 90° flip angle to image non-stationary spins in regime 3

Gradient echo (GE) single-echo EPI was performed on three subjects (3f, age 24±2 years) with the following parameters: TR/TE/FA=33 ms/18 ms/90°, inplane voxel size=1.2×1.2 mm², ST=1.2 mm (v_C=3.6 cm s⁻¹), N_scans=625, GRAPPA factor=5, bandwidth (BW)=1666 Hz per pixel, one coronal slice, acquisition time (TA) per slice ≅20 s. To scrutinize changes in M_xy of spins in regime 3, the same slice was repeatedly acquired while varying the FA (FA∈[10° 30° 45° 65° 90°]). For each subject and FA, the signal in a manually defined region of interest (ROI; nine voxels) within the right internal carotid artery (regime 3, v≥v_C) was averaged across time (after linear detrending), and then the ratio of M_xy(v≥vc) obtained with an FA=90° and 10° was calculated. Finally, we performed a similar study using a readout scheme other than EPI, and acquired on one subject (female 23 years) cardiac-gated GE CINE images (without flow-encoding gradients to quantify bulk flow) with FA=10° and 90° (in two separate acquisitions) and the following parameters: nominal TR/TE=38.12 ms/5.78 ms, voxel size=1.15×1.15 mm², ST = 1.2 mm, GRAPPA factor=2, BW=775 Hz per pixel, 22 phases (i.e. time-points during one cardiac cycle), TA equal to 49 s and 52 s for each acquisition.

(b). Experiment 2. The cardiac and respiratory magnetic resonance imaging pulse waveform and the pulsatility volume index

GE single-echo EPI was performed on three subjects (2m/1f, age 30±6 years) with the following parameters: TR/TE/FA=51 ms/22 ms/90°, inplane voxel size=1.2×1.2 mm², ST = 1.2 mm (v_C=2.4 cm s⁻¹), N_scans=600, BW=1645 Hz per pixel, GRAPPA factor=4. The acquisition was stepped through 25 spatially contiguous axial slices (axial slab, TA/slice approx. 30 s, total TA/slab approx. 12.5′) covering the occipital/temporal/frontal poles (including larger cerebral arteries, the sagittal sinus, and the lateral and third ventricles). To better cover the carotid arteries, similar GE single-echo EPI measures were performed on four subjects (4f, age 24±2 years) with the following parameters: TR/TE/FA=33 ms/18 ms/90°, inplane voxel size=1.2×1.2 mm², ST = 1.2 mm (v_C=3.6 cm s⁻¹), N_scans=625, GRAPPA factor=5, BW=1666 Hz per pixel, TA/slice≅20 s, acquisition stepped through seven coronal slices (TA∼2.5′) covering the carotid arteries. Finally, to prove the feasibility of performing such measures at 3 Tesla, one subject (m, 20 years) performed the last MRI protocol on the carotid arteries at 7 Tesla as well as at 3 Tesla (3 Tesla parameters: same TR/TE/FA/N_scans/GRAPPA factor as at 7 Tesla, inplane voxel size = 1.7×1.7 mm², ST=1.7 mm, BW=1786 Hz per pixel). In each voxel, magnitude EPI signals were converted to % signal changes by dividing the signal at each time-point by the mean signal across time; temporal drifts (third-order polynomials) were removed.

(i). Spatial distribution of effects owing to cardiac and respiratory pulsatility in the brain

To investigate which areas of the brain are mainly affected by cardiac and respiratory pressure waves, a second-order Fourier series was employed to model the effects in EPI time-courses related to the phase of the cardiac pulsation and respiration, respectively (four cardiac and four respiratory RETROICOR regressors [15]). The RETROICOR regressors, which are commonly used in fMRI [15,16], were adopted to map both the first and the second harmonics of pulsatility effects, as well as both in-phase and out-of-phase effects in our EPI data. The EPI signal variance explained (%) by cardiac and respiratory RETROICOR regressors was computed as the R²-value adjusted for the degrees of freedom, multiplied by 100 (as in [16]).

(ii). Computation of the cardiac and respiratory magnetic resonance imaging pulse waveform

To analyse respiratory effects in MRI data, EPI time-courses were low-pass filtered (cut-off frequency 0.6 Hz). To analyse cardiac effects, EPI time-courses were band-pass filtered between 0.9 and 1.4 Hz. For each voxel, and for each (cardiac or respiratory) peak detected in physiological recordings, we considered a window of N. wave cycles N_c=3 (e.g. approx. 3 s and approx. 13 s, respectively, for cardiac and respiratory effects) of the EPI time-course; we then averaged this window across temporally consecutive peaks to obtain an average cardiac and an average respiratory MRI waveform (the number of consecutive averaged peaks, N_av, was the maximum achievable in the TA).

(iii). Computation of the pulsatility volume index

With the aim of computing the pVI on the carotid arteries, we manually segmented the carotid arteries, and from each average MRI waveform and each voxel of the carotid arteries, we obtained voxel-wise estimates of the signal at systole (S(t_systole)) and at diastole (S(t_diastole)) as the maximum and minimum signal of the average MRI waveform, respectively. We then computed the average of S(t_systole)/S(t_diastole) on an ROI, namely on a voxel-by-voxel basis (pVI_voxel, ROI=single voxel), across a vessel cross section (pVI_{cross section}, ROI=vessel cross section) or across an entire segmented vessel (pVI_segment, ROI=entire vessel):

3.1

(c). Experiment 3. On the origin of the magnetic resonance imaging pulse waveform, scrutinizing S₀ and possible 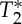effects owing to physiological pulse waves

GE multi-echo EPI was performed on four subjects (1m/3f, age 26±3) using the following parameters: TR/TEs/FA=69 ms/[18 40] ms/90°, three coronal slices, inplane voxel size=1.5×1.5 mm², ST=1.5 mm (v_C=2.2 cm s⁻¹), N_scans=300, GRAPPA factor=4, BW=2056 Hz per pixel, acquisition stepping through three spatially contiguous coronal slices covering the carotid arteries, with TA/slice≅20 s. To investigate the reproducibility of the results, we repeated the GE multi-echo acquisition for a different temporal resolution (and v_C=0.7 cm s⁻¹), with the acquisition parameters as above except for an approximately three times longer TR (TR=205 ms), N_scans=100 (to have a similar TA as the shorter TR acquisition) and three spatially contiguous slices covering the carotid arteries acquired with the traditional scheme (slice loop inside the repetition loop). For both acquisitions (shorter and longer TR), for each voxel and repetition, 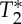and S₀ (the estimated signal at TE=0 ms) values were linearly fitted from first (E1) and second (E2) echo signals. For E1, E2, 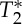and S₀ signals in each voxel the cardiac MRI pulse waveform (N_c=2) and the pVI_voxel were estimated as described in experiment 2. A mask of the carotid arteries (mask_CA) was automatically generated by applying a threshold to the average E1 signal across repetitions (E1_meanReps, threshold=five times the average of E1_meanReps across voxels). The cardiac MRI pulse waveform and the pVI_segment of the carotid arteries were then computed averaging, respectively, the cardiac MRI pulse waveform and the pVI_voxel across voxels pertaining to mask_CA.

(d). Experiment 4. The dynamics of pulsatility volume index during a breath-holding challenge

To study the dynamics of the pVI in response to changes in cerebrovascular viscoelastic properties, three subjects, who participated in experiment 3 (1m/2f, age 27±3), also performed a self-paced breath-holding task (normal breathing for approx. 30 s, then breath-hold for approx. 30 s, and then normal breathing again) during the acquisition of GE multi-echo EPI with the following parameters: TR/TEs/FA=69 ms/[18 40] ms/90°, inplane voxel size=1.5×1.5 mm², ST=1.5 mm (v_C=2.2 cm s⁻¹), GRAPPA factor=4, N_scans=1350, one coronal slice covering the carotid arteries, with TA/slice≅93 s. From inspection of the respiratory recordings, we found that one subject did not correctly perform the task, and therefore the data of this subject were excluded from further analysis. For each voxel and repetition, and S₀ values were linearly fitted from E1 and E2 signals. To study the dynamics of pVI during the breath-holding challenge, we computed a time-course of the pVI_segment of the carotid arteries sampled at each cardiac peak. The pVI was estimated from the MRI signal recorded during five cardiac cycles following each cardiac peak, namely for each cardiac peak and each voxel, the cardiac MRI pulse waveform (N_c=1) and the pVI_voxel were estimated as described in experiment 2, using a N_av value of 5; a mask of the carotid arteries (mask_CA) was automatically generated as in experiment 3, and pVI_segment of the carotid arteries was then computed as the average pVI_voxel across voxels pertaining to mask_CA. pVI_segment was finally re-sampled at each TR. This analysis was repeated for E1, E2, 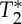and S₀ signals. In order to assess the timing of the self-paced breath-holding task, the respiratory recording was inspected; as a surrogate marker of minute ventilation [17], the respiration volume per unit time (RVT) signal was computed (similarly to [18]) from the respiratory recordings, as the difference between consecutive maxima and minima of the respiratory signal divided by the time between maxima and minima. RVT was then re-sampled at each TR.

4. Results

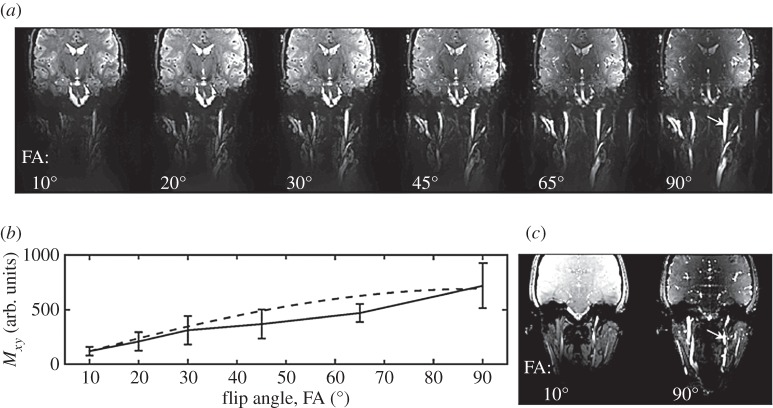
In agreement with the theoretical predictions (figure 1), our results from experiment 1 (figure 2) for both EPI and CINE MRI showed an approximate sixfold signal gain when imaging non-stationary spins in regime 3 (flow velocity>v_C, example provided for the carotid arteries) with an FA equal to 90° compared with an FA equal to the Ernst angle.

Figure 2.

On the optimal use of a 90° flip angle (FA) to image non-stationary spins in regime 3 (experiment 1). In (a), we show, for an example dataset, an EPI image (mean across time, TA≅20 s, v_C=3.6 cm s⁻¹) acquired with several FA. The dependence of the signal in the carotid artery (v≥v_C, regime 3) with the FA, displayed in (b), shows good agreement with the predictions (equation (2.7), contrast increasing with sin(FA)). In particular, for subjects 1–3, the use of a FA=90° enabled a gain in signal of fast-flowing spins (v≥v_C, regime 3) of the carotid artery equal respectively to 5.7, 6.7, 6.1 compared with FA=10°, in agreement with the expected theoretical gain equal to 6.2. Note that the use of a 90° FA is advantageous for EPI as well as for any image read-out scheme; to provide an example, we show in (c) a coronal slice (averaged across 22 time-points across the cardiac cycle) covering the carotid artery and acquired with the cardiac-gated CINE technique with 10° and 90° FA (TA=[49 52] s, respectively). The ratio of the average CINE-MRI signal measured in the carotid artery at 90° versus 10° was 5.93.

The areas of the brain mainly affected by cardiac and respiratory pulsatility are shown in figure 3a–d (experiment 2). These included: larger intracortical arteries (e.g. the carotid arteries, the anterior cerebral artery (ACA), the middle cerebral artery (MCA)), veins (notably the sagittal sinus), smaller intracortical (e.g. smaller sulcal arteries) and scalp vessels, CSF spaces (e.g. the lateral and third ventricles, the sulcal CSF), as well as—although to a smaller extent—the brain parenchyma (especially grey matter neighbouring cerebral vessels and the CSF). Examples of the raw MRI time-courses and of the MRI pulse waveform estimated in different compartments are also shown in figure 3e and f, respectively.

Figure 3.

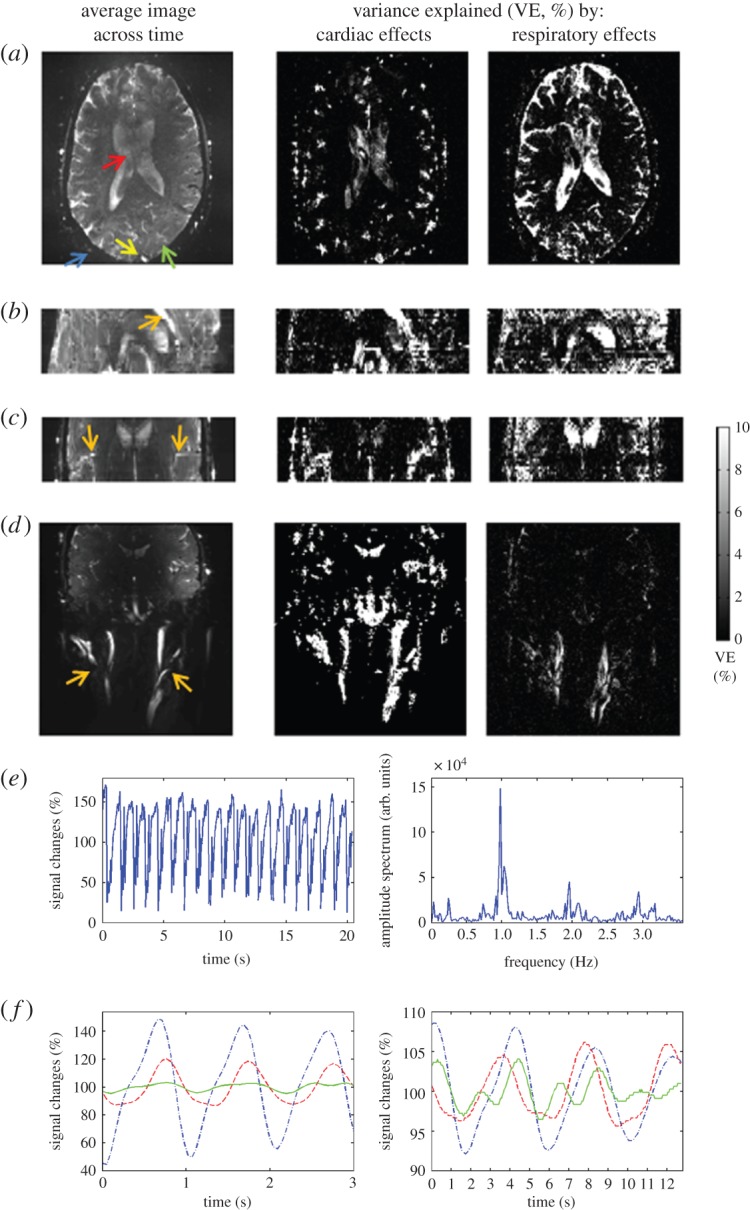
Thespatial distribution of cardiac and respiratory pulsatility effects in the brain and the MRI pulse waveform (experiment 2). For an example dataset, in (a–d), we show the average EPI image across 600 time-points (TR= 51 ms) on the left column, and the variance explained by the cardiac and respiratory RETROICOR regressors on the middle and right columns, respectively. Note that in (a) we display an axial slice (out of 25 slices) of the acquired axial slab (TA∼12.5′) showing pulsatility effects in the lateral ventricles (top–red–arrow), scalp arteries (bottom left–blue–arrow), sagittal sinus (bottom middle–yellow–arrow) and brain parenchyma (bottom right–green–arrow); in (b,c), we show a reformatted sagittal and coronal view of the axial slab (note the good spatial coverage across slices, i.e. no visible head motion) displaying pulsatility effects in the ACA and the MCA, respectively (orange arrows); further, in (d), we show a coronal image of a coronal slab (TA∼2.5′) centred on the carotid arteries (orange arrows). The signal time-course (only 20 s) from a scalp vessel (bottom left–blue–arrow in (a)) and its amplitude spectrum are plotted in (e) (left and right panels, respectively): note the presence of respiratory (approx. 0.24 Hz), cardiac (approx. 0.98 Hz, and higher harmonics) components, and also of interaction terms (approx. 0.98±0.24 Hz, and higher harmonics), the latter probably related to the respiratory sinus arrhythmia. Finally, in (f), we show the average cardiac (left) and respiratory (right) MRI pulse waveforms in three voxels (blue dashed-dot line, scalp vessel; red dashed line, lateral ventricle; green solid line, grey matter, see arrows in (a)). The MRI pulse waveforms were used to estimate the proposed biomarker of compliance, the pulsatility volume index (pVI). (Online version in colour.)

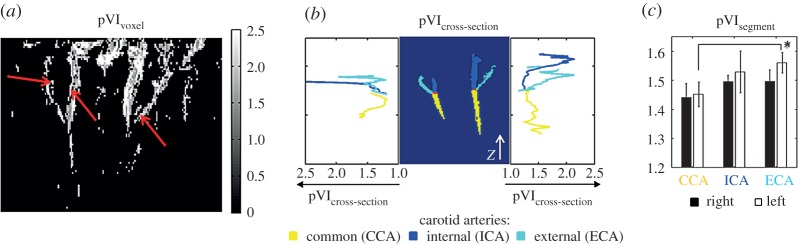
The MRI pulse waveform was employed to compute a novel indicator of cerebrovascular compliance, the pVI, which, in this work, was mainly investigated and preliminarily validated for the carotid arteries. For an example dataset, in figure 4a–c, we show respectively the computed pVI_voxel (maximum intensity projection across slices), pVI_{cross section} and pVI_segment (mean±s.e. across subjects) for the carotid arteries.

Figure 4.

The pulsatility volume index (pVI) of the carotid arteries (experiment 2). The cardiac pVI of the carotid arteries was evaluated from the cardiac MRI pulse waveform at different spatial scales: (a) at the voxel level (pVI_voxel, example dataset displayed), (b) across their cross section (pVI_{cross section}, example dataset displayed, cross section defined perpendicular to the z-axis indicated by a white arrow) and (c) across each entire segmented artery (pVI_segment, mean s.e. across subjects). Note that in (b) the pVI_{cross section} of the segmented left carotid arteries (displayed on the left part of the central panel) is shown on the left panel, and the pVI_{cross section} of the segmented right carotid arteries (displayed on the right part of the central panel) is shown on the right panel. Interestingly, pVI_voxel was lower for voxels inside or containing the arterial lumen (note in (a) a darker stripe inside the arteries, indicated by three red arrows), and higher for voxelscovering the arterial wall, as expected for a blood volume effect. Further, pVI varied across the arterial axis (see pVI_{cross section} in (b)), between arteries (see pVI_segment in (c), *p<0.02), and displayed a trend of left/right asymmetry. (Online version in colour.)

In the electronic supplementary material, we provide movies of the MRI pulse waveform in the brain (N_c=3, repeatedly displayed four times, for a total of 12 cardiac cycles displayed), in order to demonstrate specific pulsatility effects in several brain compartments such as the carotid arteries, ACA, MCA, scalp arteries, sagittal sinus, as well as CSF spaces (e.g. note that the CSF is being pushed out of the lateral ventricles into the third ventricle during the cardiac cycle).

In order to characterize the pVI, we scrutinized the origin of the MRI signal changes related to the phase of the physiological cycles, specifically the presence of possible 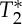effects simultaneous with the expected S₀ effects. We separated the contribution of S₀ (signal at echo-time equal to zero) and of effects by multi-echo (E1, E2) EPI. The MRI pulse waveform for four subjects computed from E1, E2, S₀ and 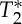is shown in figure 5: these results indicate the presence of pulsatility changes in each signal, including, interestingly, .

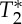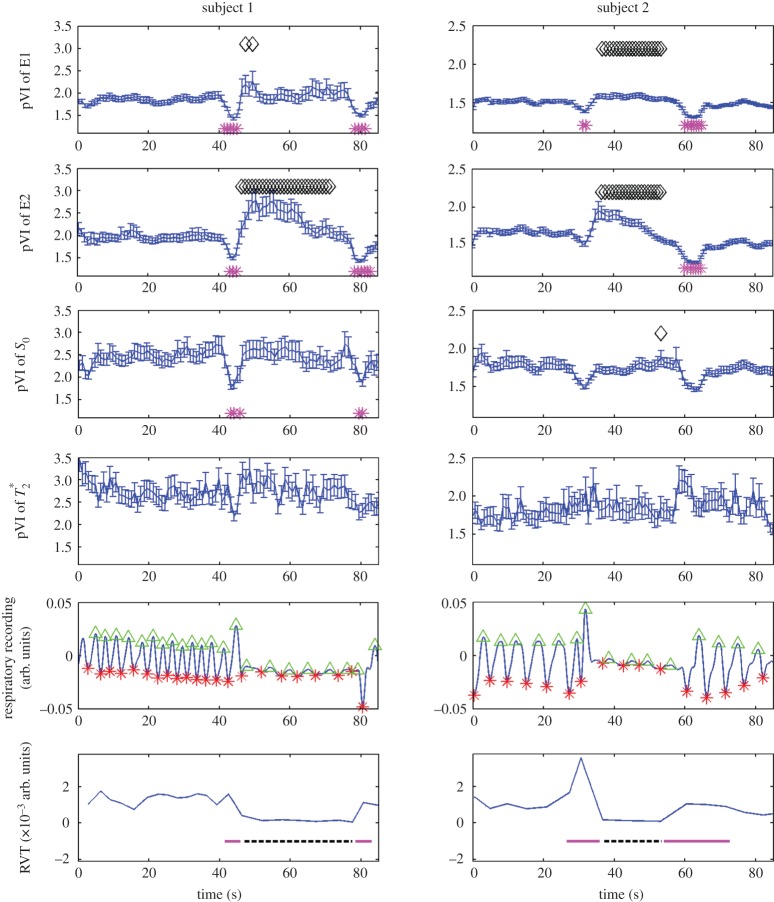
Figure 5.

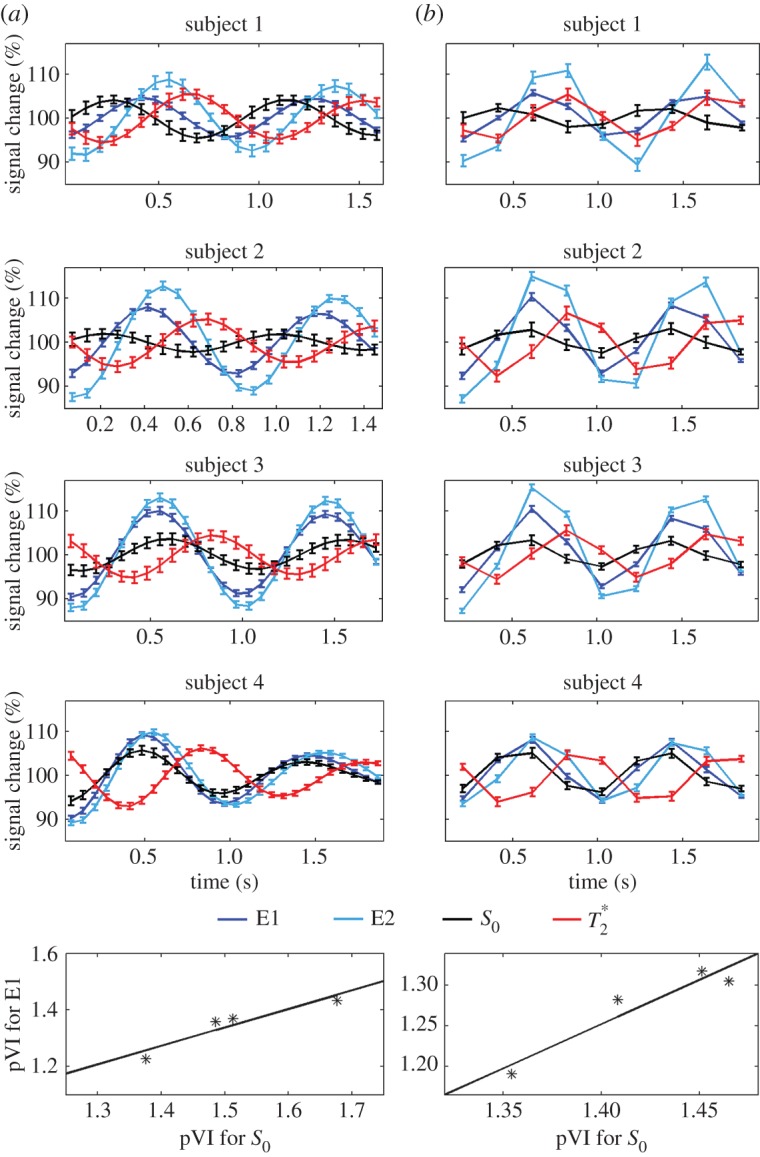
On the origin of the MRI pulse waveform, scrutinizing S₀ and possible effects owing to physiological pulse waves (experiment 3). The cardiac MRI pulse waveform in the carotid arteries for four subjects and two different TRs, (a) TR=69 ms, (b) TR=205 ms, is shown in rows 1–4, respectively, for echo 1 (E1), echo 2 (E2), S₀ and 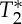signals obtained from multi-echo EPI experiments. In the bottom row, for each subject the pVI_segment of the carotid arteries computed on E1 signals versus the pVI_segment computed on S₀ signals is displayed. The MRI pulse waveform displayed changes in S₀ signals as expected from theoretical predictions in the presence of pulsatility changes in blood volume. Interestingly, 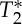changes related to the phase of the cardiac cycles were also present, and, on average (s.e.) across subjects, lagged changes in S₀ signals by 0.42±0.03 times the cardiac cycle (i.e. they were almost in anti-phase with S₀ signals). The measured 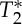changes were compatible with pulsatile blood volume effects, because a blood volume increase was expected to decrease the voxel 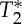signal (note that 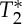is shorter in the carotid arteries than in neighbouring tissue) and at the same time increase the S₀ signal (S₀ is proportional to the total spin concentration). However, other pulsatile effects (although probably less likely, such as pulsatile fluctuations in deoxyhaemoglobin concentration) might have contributed as well to 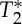changes. Therefore, we tested (bottom panel) whether 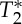effects might introduce a bias across subjects for the estimation of the pVI in experiments using single-echo signals only, rather than S₀ signals estimated from multi-echo experiments. This was not the case in our dataset, because the pVI_segment of the carotid arteries computed on S₀ signals displayed a significant correlation across subjects (r=0.95, p<0.05 for both long and short TR, see bottom panel) with the pVI_segment of the carotid arteries computed on E1 signals. (Online version in colour.)

In order to provide a preliminary validation of the pVI as a biomarker of cerebrovascular compliance, we investigated the dynamics of the pVI, underlying transient changes in cerebrovascular viscoelastic properties during a breath-holding challenge. As shown in figure 6, the pVI displayed a significant increase during breath-holding, and decreased a few seconds before and after breath-holding.

Figure 6.

ThepVI dynamics during a breath-holding challenge (experiment 4). The dynamics of pVI_segment of the carotid arteries during a breath-holding challenge are shown for two subjects and E1, E2, S₀ and 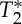signals (top four rows). We also show (fifth row) the respiratory chest recordings obtained simultaneously with the MRI acquisition (respiratory peaks and minima are indicated with green triangles and red asterisks, respectively), and the respiratory volume rate, RVT (a surrogate marker of minute ventilation, bottom row) computed from respiratory recordings. With respect to the first time-point during normocapnia, the pVI computed from E1 and E2 signals increased (black diamonds p<0.05) during breath-holding, concurrent with a decrease in RVT (black dashed line, bottom row), while it decreased (magenta asterisks p<0.05) during few seconds before and after breath-holding, concurrent with an increase in RVT (two magenta solid lines, bottom row). A trend of the same dynamics (with some time-points showing significant changes) was also present in the pVI computed from S₀ signals. The pVI computed from 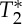signals did not change during the breath-holding challenge. These results provide a preliminary validation of the pVI as a biomarker of cerebrovascular compliance capable of detecting transient changes in the viscoelastic properties of the vessel walls in response to a breath-holding challenge. (Online version in colour.)

Finally, in the electronic supplementary material, we show the feasibility of imaging pulsatility effects in the carotid arteries at 3 Tesla, with a preliminary comparison with 7 Tesla images, obtained in the same subject and with a similar MRI acquisition scheme.

5. Discussion

Brain–heart interactions occur through several mechanisms and along several pathways, including neuronal autonomic regulation and feedback, hormonal regulation and mechanical coupling. In this work, we focused on mechanical coupling, specifically the influence of cardiac as well as respiratory activity on the mechanical and viscoelastic properties of intracranial tissue. Perturbation of these properties has been implicated in the pathophysiology underlying cerebrovascular disease (e.g. atherosclerosis, stroke and aneurysm), which is the second leading cause of mortality worldwide, and may also be involved in neurodegenerative disorders, sleep disorders, as well as in migraine. The latter is a common neurological disease, which has often been associated with neurovascular disease and increased CSF pressure [19–21], and might thus be related to the impairment of brain–heart mechanical interactions.

We designed and characterized a novel indicator of cerebrovascular and brain parenchymal compliance, the pVI, based on fast MRI of cardiac and pressure waves propagating in the brain. Here, we first discuss the benefits of the employed MRI sequence in terms of speed and sensitivity. We then discuss the spatial distribution in the brain of cardiac and respiratory effects and the possible mechanism underlying these two effects. Third, we discuss the pVI and its characterization by multi-echo imaging aimed at investigating the origin of the observed contrast, and its preliminary validation as a compliance indicator by the use of breath-holding challenges. Finally, we discuss the limitations of this work and possible future work.

(a). On the speed of the implemented echo-planar imaging sequence

The speed of the EPI sequence implemented in this work to image pulsatility effects in the brain compares favourably against commonly used gated sequences such as CINE MRI (2.5 times faster in our experiments) and phase contrast imaging (approx. 7.5 times faster, results not shown) for the following reasons: first, it does not require gating, rather it exploits the use of simultaneous physiological recording; second, it does not seek to quantify bulk-flow velocity changes (which require the use of flow-encoding gradients in three different directions), instead it provides a signal primarily dependent on blood volume changes. We expect to further boost the speed of this EPI sequence by a factor of 3 by employing simultaneous multi-slice imaging [22], and to achieve an almost full brain coverage (9 cm thick slab) with an approximately 1 mm isotropic resolution in 10 min (e.g. considering a TA of 20 s per three simultaneously acquired slices).

(b). On the use of a 90° flip angle to boost sensitivity

Our theoretical predictions and experimental results demonstrate an approximately sixfold gain in endogenous signal of fast flowing (regime 3) spins using a 90° FA compared with the Ernst angle (approx. 10° in our experiments, which instead maximizes the signal of stationary spins), as well as a concurrent significant background suppression. This work suggests that the use of exogenous contrast (e.g. gadolinium) is not needed to map cardiac and respiratory pulsatility effects for spins in regime 3 at 7 Tesla, and our preliminary results at 3 Tesla are also encouraging in this sense. For the critical speed employed in our experiments (between 2.2 and 3.6 cm s⁻¹ depending on the experiment), we expect to have spins in regime 3 for larger arteries (spin velocity>100 cm s⁻¹, e.g. carotid arteries), middle arteries (spin velocity approx. 50–100 cm s⁻¹, e.g. middle cerebral arteries), arterioles (spin velocity approx. 5–10 cm s⁻¹) and larger veins (spin velocity approx. 10 cm s⁻¹, e.g. basal vein of Rosenthal). This will not be the case for capillaries (spin velocity approx. 0.5–2 mm s⁻¹), nor the ventricular, sulcal and brain parenchymal interstitial CSF (CSF bulk flow velocity is in the range 1–4 mm s⁻¹, with the maximum bulk flow velocity of 2 cm s⁻¹ in the cerebral aqueduct [10]), whose spins will belong to regime 2.

(c). On the spatial distribution of cardiac and respiratory pulsatility effects

Cardiac and respiratory pulsatility MRI effects were mainly visible in arteries, veins and CSF spaces, as also observed in previous work [15]. Notably, in our data, we were able to observe respiratory pulsatility effects with high detail and sensitivity through the use of high spatial resolution (including the use of thin slices, which decreased the contribution of other respiratory effects, e.g. off-resonance effects in the brain owing to chest motion), an ultra-high-field scanner and optimized sequence parameters (e.g. the FA). Interestingly, the spatial distribution and amount of variance explained by cardiac pulsatility effects differed from those of respiratory effects, as the former were more visible and stronger in arteries, whereas the latter where more visible in the CSF. This might be explained in the light of the different mechanisms underlying cardiac and respiratory pulsatility. The propagation of the cardiac pressure waves occurs directly along the cerebral arterial tree. Instead, respiratory pulsatility is expected to originate mainly from the mechanical coupling of (thin-walled large neck and abdominal) veins with changes in the thoracic pressure during respiration [23,24] rather than of large (thick-walled and low compliant) arteries, as expected for cardiac pulsatility. In turn, the propagation of the respiratory pressure wave in vertebral veins might induce pulsatility mechanisms in the CSF in the spinal cord and retrogradely in CSF spaces in the brain. Therefore, in contrast to cardiac pulsatility, respiratory pulsatility might be more easily detectable in cerebral veins and the CSF than in arteries, and also might travel retrogradely in veins/spinal cord with respect to the direction of blood/CSF flow.

Previous work with Doppler ultrasound methods [25] and gated CINE MRI methods [10] mainly focuses on measuring blood/CSF velocity during the cardiac cycle only; further, to probe brain tissue elasticity, other techniques (MR elastography) employ external mechanical vibrations at high frequency (range 25–100 Hz [26,27]). The possibility, demonstrated by our results, to map the effects of two different endogenous (cardiac and respiratory) pressure waves enables one to probe brain tissue compliance at two physiological modes of vibration, hence possibly providing complementary information on cerebrovascular and brain parenchymal compliance (for instance because of different compliance mechanisms at different frequencies, namely approx. 1 Hz and approx. 0.25 Hz for cardiac and respiratory effects, respectively).

Our investigation of pulsatility effects was mainly conducted at 7 Tesla. Nevertheless, we also reported preliminary results at 3 Tesla, which demonstrate the feasibility of imaging pulsatility effects in the carotid arteries: future work will focus on optimizing the acquisition parameters (e.g. the TE) for 3 Tesla imaging, and on increasing the spatial resolution (in this paper, using a lower resolution at 3 Tesla when compared with 7 Tesla most probably caused a contrast decrease owing to partial volume effects).

(d). On the pulsatility volume index, its characterization and preliminary validation

We evaluated the proposed novel biomarker of compliance, the pVI, in response to the cardiac pressure wave, in larger cerebral arteries in a small group of subjects. Interestingly, the pVI varied across each arterial segment and across arteries, displaying a trend towards a left/right asymmetry, and a significant increase between the external and the common carotid artery. Future work is planned to confirm these findings in a larger control group cohort and possibly examine the pVI in patient populations (e.g. high blood pressure or atherosclerosis).

In addition, we sought to characterize the MRI signal changes underlying the pVI. Considering that, on the basis of our simulations (see Theory section), blood volume changes in response to pulse pressure waves were expected to produce S₀ signal changes, in the carotid arteries, we investigated the occurrence of S₀ effects related to the phase of the cardiac cycle by the use of multi-echo EPI; we also explored the possible presence (if any) of 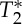effects (including BOLD effects) extracted from the same multi-echo EPI acquisition. Interestingly, we found that both S₀ and 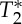displayed cardiac pulsatility effects: notably, the S₀ and 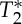signals were almost anti-correlated, a result which is compatible with the presence of a common blood volume effect underlying the two signal changes (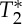-values in the carotid arteries are lower than in neighbouring tissue compartments, and thus an increase in blood volume is expected to decrease the voxel 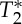simultaneous with the expected increase in S₀). Nevertheless, the lag between S₀ and 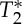signals was not exactly half of the physiological cycle: 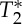minima occurred on average slightly earlier than S₀ peaks. Therefore, we cannot exclude the presence of other effects producing 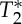signal changes with the cardiac cycle: for instance, fluctuations in the deoxyhaemoglobin concentration (although low in large arteries, e.g. only 1–3%, with the fraction of oxygenated haemoglobin being equal to 97–99% [28]) or in the density of corpuscular blood, both related to changes in spin velocity, which slightly anticipated the blood volume changes observed in S₀ signals. A dynamic interplay between deoxyhaemoglobin and blood volume changes is also usually observed in the venous compartment during functional neuronal activity (e.g. a washout of deoxyhaemoglobin lagging blood volume increases [29]), although with possible differences when compared with the systemic physiological fluctuations observed in our results (these global effects are not restricted to occur in the same blood compartment affected by responses to local neuronal events). Although further work might help to understand the presence of 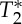effects related to the phase of the cardiac cycle in the carotid arteries, our results showed a high correlation across subjects of the pVI obtained from single-echo signals with the pVI obtained from S₀ signals. This indicated that effects did not affect the estimation of the proposed indicator of cerebrovascular compliance from single-echo EPI measures.

Finally, we employed a breath-holding task to perform a preliminary validation of the pVI, where pVI was shown to have utility as a compliance biomarker able to detect changes in cerebral vessel viscoelastic properties. In the carotid arteries, the pVI increased during breath-holding owing to the increased blood volume mediated by hypercapnia associated with breath-hold [30] (i.e. elevated CO₂, associated with a measured decrease in the RVT regressor). Interestingly, the pVI transiently decreased before and after hypercapnia, and occurred with a measured small increase in the RVT, possibly indicating a hypocapnic adjustment performed by the subject to prepare for and compensate after the breath-holding challenge. Further, by inspection of multi-echo signals, we noted that the pVI changed dynamically in single-echo signals, as well as in S₀ signals, demonstrating its positive performance as a compliance biomarker for both future single-echo and multi-echo experiments. A more marked change in pVI in second-echo rather than first-echo signals was detected, but this was not associated with significant changes in the pVI in 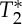signals; further work in a larger sample and possibly with higher sensitivity is thus needed to elucidate this finding. Future work might also assess whether the observed transient changes in the pVI of the carotid arteries (reflecting changes in the viscoelastic properties of the carotid artery wall) in response to a vasodilation (during the breath-hold) and a vasoconstriction (during the transients before and after the breath-hold) are related to downstream effects in the capillaries and arterioles (i.e. propagated retrogradely upstream in the carotid arteries) or to compliance changes related to the breath-holding challenge occurring directly in the carotid arteries.

(e). Limitations and future work

In this work, we have shown the feasibility of mapping the cardiac and respiratory MRI pulse waveform in several brain compartments (large and middle arteries, large veins, CSF compartments, brain parenchyma), and focused the characterization and validation of the pVI on the carotid arteries and for cardiac pulsatility only. Future work will also extend these results to other brain compartments and for respiratory pulsatility. The fast MRI of physiological pulsatility proposed here suffers from artefacts common to EPI, e.g. spatial distortion, motion and ghosting. Future work will address the impact of these artefacts on the estimation of the MRI pulse waveform and of the pVI, and on possible correction strategies (for instance, the use of field maps or images acquired with a reversed phase-encoding direction to correct for spatial distortions as is customary for fMRI). Nevertheless, we expect the pVI to be less affected by artefacts at the ROI (e.g. pVI_{cross section}, pVI_segment) than at the voxel level (e.g. pVI_voxel). Head motion will require special consideration: first, because the current two-dimensional acquisition scheme prevents a proper three-dimensional motion correction, this issue could be circumvented in the future by adopting pseudo-volumar acquisition, enabled by the use of simultaneous multi-slice imaging [22], or prospective motion correction methods; second, because the presence of local motion and deformations in high-contrast areas of the brain owing to pulsatility effects (e.g. in ‘bright’ larger arteries and CSF owing to blood volume and motion effects during the physiological cycles) are effects of interest and should not be removed by motion correction procedures.

6. Conclusion

Our work demonstrates the feasibility of imaging the cardiac and respiratory pulsatility in the brain with high sensitivity and speed by the use of a fast EPI-based MRI sequence and of optimized sequence parameters, based on the solution of the Bloch equations for non-stationary spins. Our MRI sequence might prove useful in future work for fast imaging of pulsatility effects in the brain, to investigate stiffness of walls and tissue that bound flowing/moving fluids in the brain, as well as stagnancy of cerebrovascular fluids. We expect that our MRI sequence might also be employed for fast imaging of pulsatility effects in scalp vessels (neatly visible in our data), aimed at improving models of ballistocardiogram artefacts in simultaneous EEG–fMRI studies [31]. Lastly, we foresee the possible use of the pVI, preliminarily characterized and validated in this work, in future studies of brain–heart interactions, as a more direct indicator of blood volume changes (compared with previous measures of indirect blood velocity changes) underlying cerebrovascular compliance in cerebrovascular disease (e.g. larger and smaller vessel disease), ageing and other disorders (e.g. neurodegenerative disorders, including Alzheimer's disease and multiple sclerosis, sleep disorders and migraine).

Data accessibility

Data are made available in the electronic supplementary material as movies showing pulsatility effects in the brain over time.

Author' contributions

Drs Bianciardi, Toschi, Polimeni, Evans and Keil acquired the data. Data analysis was carried out by Dr Bianciardi. All the authors substantially contributed to the conception of this work and to data interpretation, drafted the article and approved the final version to be published.

Competing interests

We have no competing interests. Dr Evans is currently an employee and stockholder of Biogen; his participation in the study and interpretation of the findings were not supported by nor have a financial interest of Biogen.

Funding

This work was supported by these sources of funding: NIH NIBIB P41-RR014075 and R01-EB000790, NIH NIMH K23MH086619, and NIH NCRR S10-RR023043 and S10-RR023401.