Numerosity representations in crows obey the Weber–Fechner law

Abstract

The ability to estimate number is widespread throughout the animal kingdom. Based on the relative close phylogenetic relationship (and thus equivalent brain structures), non-verbal numerical representations in human and non-human primates show almost identical behavioural signatures that obey the Weber–Fechner law. However, whether numerosity discriminations of vertebrates with a very different endbrain organization show the same behavioural signatures remains unknown. Therefore, we tested the numerical discrimination performance of two carrion crows (Corvus corone) to a broad range of numerosities from 1 to 30 in a delayed match-to-sample task similar to the one used previously with primates. The crows' discrimination was based on an analogue number system and showed the Weber-fraction signature (i.e. the ‘just noticeable difference’ between numerosity pairs increased in proportion to the numerical magnitudes). The detailed analysis of the performance indicates that numerosity representations in crows are scaled on a logarithmically compressed ‘number line’. Because the same psychophysical characteristics are found in primates, these findings suggest fundamentally similar number representations between primates and birds. This study helps to resolve a classical debate in psychophysics: the mental number line seems to be logarithmic rather than linear, and not just in primates, but across vertebrates.

1. Introduction

A growing body of literature suggests that the ability to judge number is widespread throughout the animal kingdom. Number discrimination has been demonstrated in such diverse taxa as insects [1,2], fish [3,4], amphibians [5,6], birds [7,8] and mammals [9–11]. Among mammals, numerical competence has been studied most intensively in primates [12–15]. Birds, however, possess similarly elaborate quantification skills [16]. In their natural habitat, birds use numerical information to counteract nest parasitism [17], to forage for food [18–20] or to communicate with conspecifics [21]. Birds can also be trained in the laboratory to distinguish stimuli based on the number of items [8,22,23]. Corvid songbirds are renowned for their flexible behaviour [24], making them ideal model organisms for the study of cognition [25,26] and high-level brain functions [27–30]. Ever since Koehler and his co-workers explored the numerical capabilities of birds [31], corvids have been known to show some level of quantity discrimination [32], and they use quantity rules to direct behaviour [33]. Jungle crows have been trained on relative numerosity discriminations to always choose the larger of two sets of (3–8) visual shapes [34]. Relative quantity judgements are also observable without training, as crows and jackdaws [20] spontaneously selected the larger of two food quantities as long as one of the sets contained fewer than five objects [19].

For non-symbolic number representations, two systems are discussed: an object file system (OFS) and/or an analogue number system (ANS). The OFS has been described for spontaneous numerosity discriminations in human infants [35,36] and rhesus monkeys [37]. It is thought that the OFS keeps track of a small number of items by assigning markers to individual set items. This system provides precise number representations, but based on the limited number of markers, it can only represent up to four items; it fails for quantities greater than four, the putative number of available markers.

As an alternative—or additional—mechanism, the ANS has been demonstrated repeatedly in animals, human infants and innumerate adults [38,39]. The ANS has no set-size limit and estimates numerosities only approximately. Numerical magnitude perception shows characteristic psychophysical effects reminiscent of sensory judgements: number discrimination improves with increasing numerical distance between two values (the numerical distance effect) and, at a given numerical distance, it worsens with increasing absolute magnitude (the numerical magnitude effect) [40–42].

Within the realm of the ANS, the scaling scheme (i.e. the relationship between stimulus magnitude and its sensation) is of special interest. If the relationship is of linear nature (linear-coding hypothesis), the internal representations are symmetric distributions on a linearly scaled number line. Such representations centred on each number would become progressively wider in proportion to increasing magnitude, and the ratio of the standard deviation to the mean (i.e. the coefficient or variation) would be constant across quantities. However, if the relationship between physical magnitude and sensation is nonlinear (nonlinear compression hypothesis), the ‘just noticeable difference’ for the discrimination of larger numbers (relative to a reference number) would be higher than for smaller numbers. This disparity would be compensated for if numerical representations would be described on a nonlinearly scaled number line, which would result in symmetric numerical representations. Here, the accuracy of the representations stays invariable with increasing size of a quantity, and the standard deviation, not the coefficient or variation, is constant across quantities. A possible nonlinear compression is the logarithmic scaling as predicted by the Weber–Fechner law [40], which states that linear increments in sensation S are proportional to the logarithm of stimulus magnitude I, such that S = k × log(I).

Previous work by Bogale et al. [19,34] and Ujfalussy et al. [20] required relative numerosity judgements. These, however, do not require animals to know anything about the precise numerical value in order to make a correct choice [43]. To explore cardinal (absolute numerosity) judgements, discriminations of variable numerosities relative to both larger and smaller adjacent numerical values are necessary. We have previously shown that carrion crows master cardinal judgements for very small (1–5) numerosities [44]. However, several important questions remained open, as follows.

First, would crows familiar with small numerosities generalize numerical judgements to much larger numerosities as a prerequisite for a conceptual grasp of cardinal number? So far, only very restricted ranges of relatively small numerosities have been applied in corvid studies. Spontaneous discriminations of the quantity of food items even suggested that they do not discriminate larger quantities [19]. Whether crows possess an ANS characterized by the absence of a set-size limit therefore remains unknown.

Second, which—and how many—representational system(s) would crows employ to assess small and large cardinal number? Work with crows spontaneously discriminating the relative quantity of food items suggested a set-size-limited OFS [19]. However, both small and large numerosities have been shown to be represented by a single ANS in non-human primates [45,46]. Only simultaneous investigation of both small and large numerosities in the same task can help to decipher the applied representational system(s).

Third, if crows possess an ANS, how would they represent cardinal numbers on the ‘number line’? Whether the mental number line for non-symbolic number is linear or rather logarithmically compressed is a classic debate in human psychophysics, but a comparative approach in different animal taxa is needed to arrive at cross-species, potentially evolutionary stable schemes of numerical representations. Suggestive evidence with small numbers indicated nonlinear compression of number representations in crows [44]. However, because discrimination for small numerosities is quite precise and only covers a very limited number range, absolute cardinality judgements to a broad range of numerosities addressing the ANS needs to be tested. This allows construction of detailed performance functions (i.e. probability density functions) that indicate subjects' behavioural representations of cardinal number. So far, numerical scaling has only been tested in two primate species: rhesus monkeys and humans [46–49].

Here, we address these issues from a comparative point of view in carrion crows, an avian vertebrate that is only distantly related with mammals and primates. To ensure direct comparability of the data, the crows performed a delayed numerosity discrimination task similar to the previously used task in rhesus monkeys and humans [42], and with the same broad range of up to 30 items. A comparative investigation of avian and mammalian species is particularly interesting, since birds lack a six-layered neocortex, which is thought to endow mammals and primates with the highest levels of cognition, and therefore also numerical competence. Instead, different parts of the avian endbrain evolved as the highest cognitive brain centre [50] after the ancestors of mammals and birds diverged 300 Ma [51]. Whether birds with an independently and distinctly evolved endbrain exhibit the same (or different) numerical representations as primates in terms of (i) the number and types of representational systems and (ii) the nature of the ‘mental number line’ is unknown.

2. Material and methods

(a). Subjects

We trained one male and one female hand-raised carrion crow (Corvus corone corone) for the experiments. For details on the birds' housing and diet, see Hoffmann et al. [52]. The crows were obtained from the institute's breeding facilities, hand raised and trained on a delayed match-to-numerosity task. The crows were maintained on a controlled feeding protocol during the sessions and earned food during and after the daily tests. Both crows were previously involved in another numerosity study [44].

(b). Apparatus

The crows sat on a wooden perch placed inside of an operant conditioning chamber in front of a touchscreen (3 M Microtouch, 15″, 60 Hz refresh rate). Viewing distance to the monitor was 14 cm. The program CORTEX (National Institute of Mental Health) presented the stimuli and stored behavioural data. An automated feeder delivered either mealworms (Tenebrio molitor larvae) or bird seed pellets upon correctly completed trials. During each trial, crows were trained to keep their head still in front of the computer display. This was controlled via a reflector foil attached to the crow's head. A trial only started when the crow moved its head into the beam of an infrared light barrier and kept its head still throughout the trial, thus ensuring stable head position. Whenever the crow made premature head movements, and thereby left the infrared light barrier with its head during an ongoing trial, the computer terminated the trial and the trial was discarded.

(c). Behavioural protocol

The two crows learned to distinguish dot displays via a delayed match-to-numerosity task (figure 1a). A crow started a trial by positioning its head in front of the monitor, thus closing an infrared light barrier and keeping the head still throughout the trial. A black screen was shown for 600 ms (pre-sample phase), followed by a display showing the sample numerosity. The sample stimulus disappeared after 800 ms and the crow had to memorize the sample for 1000 ms during the delay phase in which only the grey background circle was visible. In the following test phase, the test1 display was a ‘match’ in 50% of the cases (i.e. it contained the same number of dots as the sample stimulus). The crow had to respond to indicate a numerical match by moving its head out of the light barrier. In the other 50% of the cases, the test1 was a ‘non-match’, showing more or fewer dots than the sample display; here, the crow had to refrain from responding and wait for 800 ms until the test2 display appeared, which always displayed a match. Head movements before the test period aborted the trial automatically. Error trials led to a time-out of 3 s. Correct trials were rewarded with food via the automated feeder.

Figure 1.

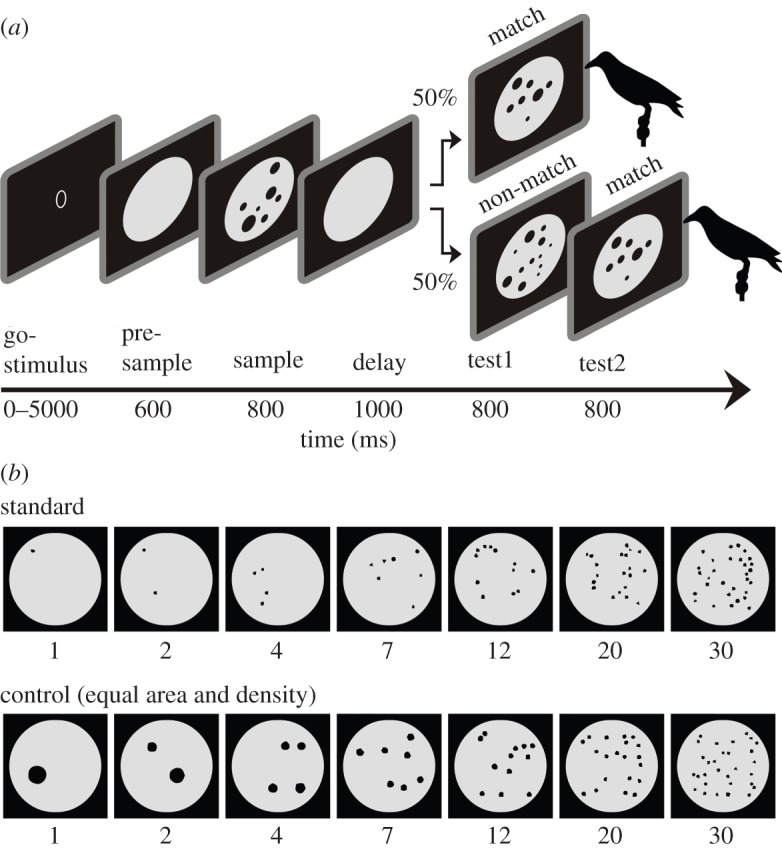
Task protocol and example stimuli. (a) Delayed match-to-numerosity task. The crow starts a trial by moving its head into the light barrier. After 600 ms, a pseudo-random sample stimulus is shown for 800 ms followed by a 1000 ms delay. Then, in 50% of the cases a ‘match’ follows, which contains the same number of dots as the sample stimulus, but differs in appearance. If a match appears, the crow has to respond by pecking at the touch screen to receive a reward. If a ‘non-match’ appears, the crow has to refrain from answering but wait for 800 ms until the non-match disappears and a match stimulus appears. (b) Example stimuli for both stimulus sets. Standard stimuli and control stimuli (equating total black area and dot density across numerosities) are shown. The number space between 1 and 30 was covered by 7 numerical values (1, 2, 4, 7, 12, 20 and 30).

(d). Stimuli

The stimuli consisted of dot displays with varying numbers of dots (figure 1b). Black dots (0.4°–2.5° of visual angle) compromising a set were drawn on a grey background circle (12.3° visual angle) shown in the centre of the screen. Seven numerosities were used: 1, 2, 4, 7, 12, 20 and 30. Each of these numerosities served as sample and test stimulus. The sample and match numerosities within one trial were always indicated by different displays, thus preventing the crows from matching visual patterns. The displays were generated using a custom-written MatLab script. The dot arrangements were pseudo-randomly generated and exchanged for new displays on a daily basis. Newly generated stimuli for each session prevented the crows from simply memorizing the visual patterns to solve the task. One stimulus batch contained 12 unique displays for each numerosity for each session (six standard and six control displays per numerosity). To further control for low-level visual features that may covary with changing numbers of dots, we showed two stimulus sets every session: the ‘standard’ trial stimuli (‘standard stimuli’) showed dots of pseudo-random size arranged randomly (but non-overlapping) on the background circle; and the ‘control’ trial stimuli (‘control stimuli’) showed dots with both equal dot area and equal dot density combined across all numerosities. ‘Dot density’ was defined as average distance between (the centres of) all dots on a numerosity display. ‘Dot area’ was defined as cumulative surface area of all dots on a numerosity display (i.e. the overall black area when individual black dots were added). Standard and control trials were randomly and unpredictably alternated.

(e). Data analysis

The percentage of correct responses for every numerosity combination was calculated and plotted on a number scale. The resulting behavioural performance functions represented the probability that the crow judged the sample and test1 numerosities as being equal. To evaluate the symmetry and the width of the performance functions (i.e. the numerosity representations), Gaussian functions were fitted (MatLab Curve Fitting Toolbox) to these behavioural performance functions plotted on four different scales: a linear scale, a power function with exponent of 0.5, a power function with exponent of 0.33 and a logarithmic (log₂) scale. The scales were chosen based on the theories of Fechner [53] and Stevens [54]: Fechner suggested that the relationship between a sensory stimulus and its sensation is of logarithmic nature, whereas Stevens claimed that the relationship is based on a power law. The more symmetrical the plotted performance functions appeared on a given scale, the better the resulting fit (r²) with the Gaussian functions. The better the fit, the better the given scale describes the relationship between the physical magnitude and its sensation. The widths of the Gaussian fits (sigma) were evaluated to test for the magnitude effect. If there is a magnitude effect, the sigmas of the linear Gaussian fits should increase when plotted against numerosity; the sigmas should be stable if the scaling is perfectly counteracting the proportional broadening of the performance functions.

The Weber fraction is a measure of how much two stimuli need to differ in order for someone to be able to detect a difference (just noticeable difference). The Weber fractions were calculated separately for the ‘smaller’ and ‘larger’ sides of the filter functions [55] (i.e. smaller and larger comparisons with respect to the sample numerosity). Weber fractions were calculated with the formulae

2.2

where n is the sample numerosity and n_S is a numerosity smaller than the sample that the crow can discriminate from the sample n in 50% of the cases. The same holds for n_L except that it is larger than the sample. The W_S-value stands for the Weber fraction for comparisons of a sample numerositiy relative to smaller (non-match) numerosities, whereas the W_L-value represents the Weber fraction for comparisons of a sample numerositiy relative to larger (non-match) numerosities. The smaller the Weber fraction, the better the crows can discriminate a numerosity from its neighbours.

3. Results

(a). General performance and reaction times

Both crows performed a delayed match-to-numerosity task that required them to distinguish numbers of up to 30 dots (figure 1a). The crows were tested over 32 (crow A) and 46 sessions (crow J), respectively. Mean performance across all sessions was 79.5 ± 0.6% for crow A and 78.9 ± 0.7% for crow J. On average, crow A completed 609 trials per session, and crow J completed 678 trials.

The reaction time was assessed from match trials only, because test2 was always a match and thus predictable if test1 happened to be a non-match. Crow A successfully completed on average 277 match trials per session, whereas crow J completed 328 match trials. The RTs differed significantly across the numerosities in both birds (p < 0.001, Friedman test). Crow A responded with a median RT of 254 ms, crow J showed a median RT of 185 ms.

(b). Numerosity discrimination performance

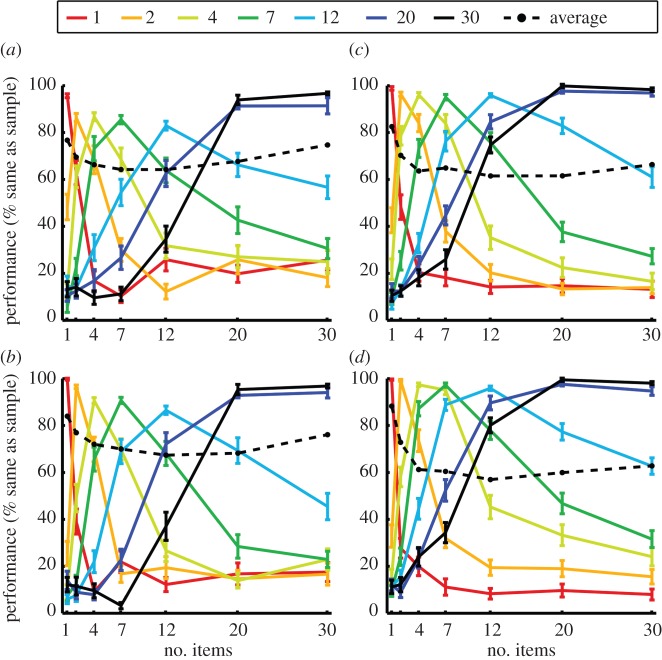
In order to ensure numerosity judgements rather than discrimination of covarying low-level visual features in the displays, we tested the crows with control stimuli in addition to the standard stimuli (figure 1b). In control stimuli, the total areas and the average density of dots was equated. Standard and control stimuli were shown equally often in a pseudo-random order. Both crows performed equally well in standard and control trials (figure 2). The behavioural performance functions indicate the probability with which the crows judged different numerosities as being equal to a specific sample numerosity. For instance, the dark green curve (figure 2a) represents trials with numerosity 7 as sample numerosity. The data point for numerosity 7 represents the proportion of correct choices (around 85% correct) when test1 showed 7 items (match trials). The data points for lower and higher numerosities signify how often the crow erroneously judged non-match numerosities being equal to the sample numerosity 7. The curve shows that the crow made many mistakes for numerosities immediately adjacent to numerosity 7, such as 4 and 12, but performed progressively better for non-match numerosities more distant from 7, such as 1 and 30. Equivalent functions are present for all tested sample numerosities in both birds, and for both standard (figure 2a,c) and control stimuli (figure 2b,d). This is a clear reflection of the ‘numerical distance effect’.

Figure 2.

Behavioural performance of both crows for standard and control stimuli. (a) Performance of crow A for standard stimuli (n = 32 sessions). (b) Performance of crow A for control stimuli (n = 32 sessions). (c) Performance of crow J for standard stimuli (n = 46 sessions). (d) Performance of crow J for control stimuli (n = 46 sessions). Colour indicates the numerosity of the sample stimulus; the x-axis shows the test1 numerosity. Performance on the y-axis represents the likelihood that a crow judges the sample and test1 numerosity as being equal (error bars ± s.e.m.). ‘Average’ indicates the performance for a given sample numerosity. (Online version in colour.)

In addition, the performance curves are quite narrow for small numerosities, such as 1 and 2, but become systematically broader with increasing sample numerosities. This reflects that the crows had more difficulties to discriminate large-value numerosities of a given distance compared with small-value numerosities. In other words, for large sample numerosities, the test1 stimulus had to be numerically more distant from the sample stimulus to be equally well discriminable compared with smaller sample stimuli. This effect is known as the ‘numerical magnitude effect’ [40–42]. Besides these well-known psychophysical effects, both crows showed comparable performance functions for standard (figure 2a,c) and control stimuli (figure 2b,d), indicating that they judged the number of items rather than low-level visual features in the displays that may covary with an increase of numerosity.

(c). Scaling of numerical representation

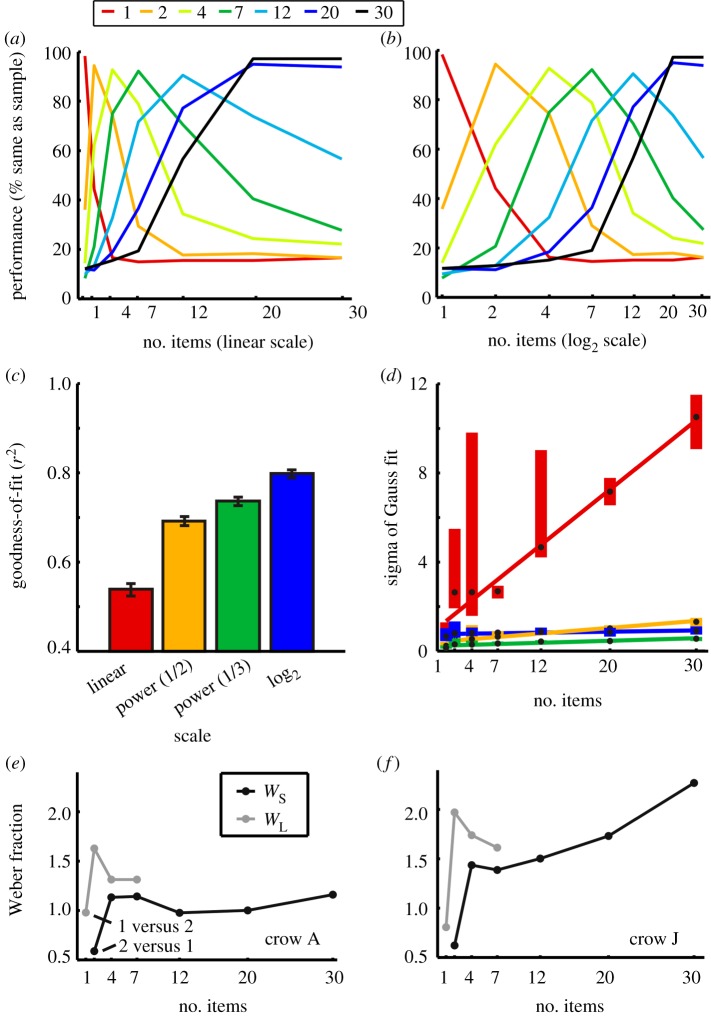
Behavioural performance functions were asymmetric when plotted on a linear number scale: the functions' slopes towards lower numerosities were steeper compared with those towards larger numerosities (figure 3a; see also individual functions in figure 2). However, plotting the same data on a logarithmically compressed number line resulted in seemingly symmetric, Gaussian peak functions (figure 3b).

Figure 3.

Characterization of performance functions. Behavioural performance functions averaged across both birds and protocols (n = 78 sessions). (a) Performance functions plotted on a linear scale. (b) Same data as in A, but plotted on a logarithmic number scale. Colour indicates the numerosity of sample stimulus; the x-axis the test1 numerosity. Performance represents the likelihood that a crow judges the sample and test1 numerosity as being equal. (c) Quantification of the suitability of different scaling schemes. Mean goodness-of-fit (r²) of the filter functions plotted on different scales to Gaussian functions (error bars ± s.e.m.). (d) Widths (sigma of fitted Gauss functions) of performance curves as a function of sample numerosity and scaling schemes. The colours indicate the scaling scheme, the edges of the boxes the 25th and 75th percentile, and the black dot inside the boxes the respective median. The coloured lines indicate linear fits to the medians. (e,f) Weber fractions of both crows calculated from the behavioural filter functions. W_S: Weber fraction for numerosities smaller than the sample; W_L: Weber fraction for numerosities larger than the sample. (Online version in colour.)

To explore and quantify the best scaling scheme for numerosity representations (i.e. the scaling that results in most symmetric curves, or probability density functions, respectively), the behavioural filter functions were plotted on different scales: a liner, a power function with exponent 0.5 (power(½)), a power function with exponent 0.33 (power(⅓)) and a logarithmic (log₂) scale. The nonlinear compression increases along this sequence. The goodness-of-fit of a Gauss function to the behavioural data was computed (figure 3c). The more symmetrical the data appeared on a given scale, the better the r² of the resulting fit with the Gauss bell. The averaged goodness-of-fits (r²) on these different scales were 0.54 ± 0.014 (linear), 0.69 ± 0.01 (power(½)), 0.74 ± 0.01 (power(⅓)) and 0.80 ± 0.01 (logarithmic). The goodness-of-fits on the four scaling schemes differed significantly from each other (p < 0.001, Friedman test, n = 78). Thus, the logarithmic scaling provided significantly better fits than the other three scales (p < 0.001, Wilcoxon test, n = 78).

Next, we analysed the widths (σ) of the Gaussian functions fitted to the performance curves. On the linear scale, the widths were increasing with increasing numerosity with a slope of 0.311 (figure 3d). The increase of the widths on the linear scaling indicates the presence of the numerical magnitude effect. The slopes of the nonlinearly compressed scales were almost even with increases of 0.032 (power(½)), 0.011 (power(⅓)) and 0.006 (logarithmic). Thus, at a logarithmic compression of the number line, the performance functions' width was constant across numerosities.

As an additional measure of quantity discriminability, the Weber fractions were computed separately for smaller (W_S) and larger (W_L) numerosity comparisons with respect to the sample numerosity. The average Weber fractions were 1.25 for W_S and 1.42 for W_L (figure 3e,f). The crows discriminated numerosity 1 from 2 and numerosity 2 from 1 with a Weber fraction of 0.75 more easily than the larger numerosities (note that the data points of W_L for number 1 and W_S for number 2 both indicate Weber fractions for numerosity 1 discriminations, namely 1 versus 2 (W_L) and 2 versus 1 (W_S), respectively).

4. Discussion

In this study, we investigated the internal representation of numerical quantity in crows. The crows were able to discriminate numerosities of up to 30, irrespective of the stimuli's appearance and low-level visual features. The applied delayed match-to-numerosity task allowed for a detailed measurement of cardinal judgements relative to both smaller and larger numerosities. The resulting peak performance functions, or probability density functions, depicted the crows' behavioural representations of numerical quantity. Performance showed clear indications of an ANS with numerical distance and magnitude effects [40–42]. Numerosity discrimination was best described by a nonlinearly compressed logarithmic scale, just as predicted by the Weber–Fechner law.

The crows robustly processed numerical information rather than low-level visual features in the displays, such as cumulated dot area and dot density, for which we controlled. Even more controls have been applied in a previous study [44], none of which distracted the crows from numerosity. Our data suggest that crows do not use number as a ‘last resort’ to discriminate quantity, as has been suggested several times (e.g. [56]). Also, previous work indicates that the number of items, and not just continuous quantity, is a salient parameter animals use to discriminate stimuli [3,8,57–59]. Neurons selectively tuned to controlled numerosity have also been reported in numerically naive monkeys that have never been trained to discriminate the number of items [60]. All these findings suggest numerical quantity as a ‘natural category’ that is spontaneously represented by different animals.

(a). Analogue number representations in crows

The crows successfully discriminated numerosity displays in a delayed match-to-numerosity task with up to 30 dots irrespective of appearance and low-level visual features. Discrimination performance showed signs of the ANS: the discriminatory precision increased with increasing numerical distance of the test stimulus from the sample quantity (numerical distance effect). Performance distributions became progressively wider for larger set sizes (numerical size effect).

Performance accuracy was largely consistent with the ANS. For numerosity 2 and higher, comparable filter functions (in terms of shape and width on a logarithmic scale) and similar average performances were observed in both experimental conditions (standard and control). No precision change between small numerosities (2 and 4) and large numerosities (7–30) were observed, as would have been expected for a transition from the OFS to the ANS, and no upper numerosity limit (characteristic for the OFS) was observed. Collectively, this argues for an ANS in crows. An equivalent pattern has been reported for trained monkeys [13,42,45], adult humans prevented from counting [42,61,62] and innumerate adult humans [63]. Whether numerical representational systems change as a function of the crows' behavioural status (conditioned versus spontaneous number discriminations) needs to be explored in more detail.

As an exception from these findings, numerosity 1 was represented much more precisely (i.e. lower Weber fraction) than all other numerosities, including small numerosities 2 and 4. This was unexpected on the background of both the OFS (which posits equal high precision for all small numerosities from 1 to 4) and the ANS (which assumes equal Weber fractions for all numerosities from 1 to 30). Numerosity 1 might indeed constitute a special set and thus be represented differently and more precisely; after all, numerosities are collections of single elements (i.e. multiples of numerosity 1). A special role of numerosity 1 is also suggested based on neuronal recordings in monkeys [60]. Moreover, the special status of one element is omnipresent in the singular–plural dichotomy (or numerosity 1 versus all other numerosities distinction) found in natural language. Our findings would support biological roots of such a singular–plural dichotomy even in a non-mammalian species.

In most previous studies with animals, discrimination accuracy has been measured based on number ratio effects (performance for smaller number/larger number), with the common finding that accuracy decreases as the ratio between the numerical values approaches 1 [45]. In this study, the crows needed more than twice the numerical distance to reach similar performance accuracy as monkeys and humans with similar dot displays [45,46,57,64,65]. This inferior discrimination performance may indicate more limited numerical capacities in crows, which was also indicated for other songbirds [66]. It could also reflect a general accuracy deficit; in teleost fish, for instance, accuracy in selecting the larger of two sets hardly exceeds 70%, no matter how easy (small) the numerical ratios are (e.g. [67]). Similar maximal accuracy levels have been reported for amphibians [6]. However, we know that crows can perform close to 100% correct [27,28,30]. Given that the tested numerical distances between match and non-match numerosities were much larger compared with previous monkey and human studies [45,46], an alternative explanation is that the crows did not exploit the full capacity of their ANS. Testing with all possible value ratios needs to resolve this question in the future. As it stands, non-human and human primates seem to show a more accurate ANS compared with fish, amphibians and birds.

(b). Precision and speed of numerosity discriminations

Except for numerosity 1, the Weber fractions characterizing the just noticeable difference between number pairs remained constant across sample numerosities. In the current study, the crows' Weber fractions of 1.12 (crow A) and 1.51 (crow J) were more than twice as large compared with values of 0.51 and 0.47 for the same two crows in our previous investigations with small numerosities from 1 to 5 [44]. The increased Weber fractions in the current report are most likely to result from much larger numerical distances of the non-match numerosities relative to the sample numerosity (i.e. the crows were not forced to discriminate as precisely as in the previous study [44] in which minimal numerical distances of one between all numerosities were applied). This indicates that the choice of the numerosities the animals have to compare has an impact on precision, and the Weber fractions we obtained for numerosities 1–5 are the more reliable and more comparable values.

The original Weber fractions of 0.51 and 0.47 for the respective crows are almost identical to the values reported for non-human primates. For instance, values of 0.51 and 0.60 were obtained for rhesus monkeys using a similar delayed match-to-numerosity task [46]. In a forced-choice delayed match-to-sample protocol, Jordan & Brannon [68] reported Weber fractions of 0.47 and 0.48 for rhesus monkeys. In this study, it was also shown that monkeys improved their precision due to training with decreasing Weber fractions from 0.58 to 0.32. This confirms our speculation that the different Weber fractions we found for our crows might be due to different task demands as a function of narrowly or broadly spaced number pairs, and it is likely to be influenced by the training stage of the animal on the specific task.

In humans tested with a delayed match-to-numerosity task, again very comparable Weber fractions of 0.55 were found for numerosities beyond 6. Cantlon & Brannon [45] found a Weber fraction of 0.26 in humans performing an ordinal number comparison task, and this value was much smaller than for monkeys performing the same ordinal task. However, the more precise performance of human subjects in this study compared with monkeys was accompanied by longer reaction times for humans (on average an additional 100 ms).

This suggests that a trade-off between speed and accuracy might be an important reason for varying Weber fractions within and between species. Interestingly, we found a similar speed–accuracy trade-off for our two crows. Crow A responded on average 96 ms faster, and crow J responded 142 ms faster in the 1–30 (this study) compared with the 1–5 protocol [44]. We suspect the crows would have shown similar discrimination behaviour for the large numerosity protocol as for the small numerosity protocol with more training, most probably at the expense of speed.

For our research goals, working with trained instead of spontaneously discriminating crows offered several advantages, including rigorous controls for non-numerical stimulus features and consistently motivated subjects that exploit their numerical competence to the best of their capacities over many trials. The latter aspect allowed us to obtain detailed and reliable performance functions that could be tested with respect to the scaling of the crows' ‘number line’. We think our data in trained crows demonstrate the numerical capacity these birds have at their disposal also in their standard ecological environment—both behaviourally and neuronally. Of course, studies on numerical competence in trained animals need to be complemented by findings in spontaneously discriminating animals to exploit the respective advantages of both approaches (discussed in [69]). For instance, why crows seem to refrain from exploiting these capacities in specific situations [19] needs further investigation. Comparative behavioural and neuronal data from monkeys indicate that the same neuronal codes and brain areas are engaged in trained and in numerically naive (untrained) animals [60]; behavioural training results in mild, but not categorically different representational enhancements in some regions of the primate brain's number network [70]. It will be interesting to know whether this neuro-ethological observation also holds for corvids.

(c). Scaling of internal numerosity representations

Our study shows that the non-symbolic representation of numerosities in crows is described best on a nonlinearly compressed, logarithmic ‘number line’. Performance distributions were asymmetric when plotted on a linear scale. By contrast, nonlinear scaling of the performance functions resulted in symmetric peak functions which were reflected in significantly higher goodness-of-fit values and constant standard deviations of the fitted Gaussian distributions. In addition, our findings indicate that the logarithmic scale (according to the Weber–Fechner law) described the data even better than power function scales (postulated by Stevens's law) because the goodness-of-fit values of the crows' performance functions were the highest for the logarithmic scaling. These findings for large numerosities are fully consistent with a previous report on small numerosities in crows [44]. More importantly, the corvid data are in agreement with findings in rhesus monkeys for small [47] and large [46] numerosities, and also for non-verbal discriminations in adult humans [46] and an Amazonian indigenous group with reduced numerical lexicon [49].

Crucially, we even have direct evidence for a logarithmic scaling of numerosities in crows (and monkeys) based on the neuronal code for numerosities. In a previous study, we recorded single-cell activity from a telencephalic association area (termed NCL) in crows, which discriminated the visual number of items [44]. NCL neurons were tuned to individual preferred numerosities, and neuronal discharges proved to be relevant for the crows' correct performance. Just like the performance functions described in the current study, the neuronal tuning functions were also best described on a logarithmic number line, arguing for a nonlinearly compressed neuronal coding of numerical information, just as predicted by the psychophysical Weber–Fechner law.

These behavioural and neuronal data showed an impressive correspondence of the codes found in the avian brain with those described earlier in the primate brain [15]. Our report helps to resolve a classical debate in psychophysics: the mental number line seems to be logarithmic rather than linear, and not just in primates, but across vertebrates. It suggests that this way of coding numerical information has evolved based on convergent evolution, because it exhibits a superior solution to a common computational problem. We believe a comparative approach is indispensable for deciphering evolutionarily stable (or newly invented) phenomena in numerical cognition.

Ethics

All experiments and procedures were realized in accordance with the NIH Guide for Care and Use of Laboratory Animals (Committee on Care and Use of Laboratory Animals, 1996) and were approved by the local ethical committee and authorized by the national authority (Regierungspräsidium).

Data accessibility

The data reported in this study are available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.rb921.

Authors' contributions

A.N. and H.M.D. designed the study, interpreted the data and wrote the manuscript. H.M.D. performed experiments and analysed the data. All authors gave final approval for publication.

Competing interests

None of the authors have competing interests.

Funding

This work was supported by DFG grant no. NI 618/3-1 to A.N.