Discovery of fairy circles in Australia supports self-organization theory

Significance

Pattern-formation theory predicts that vegetation gap patterns, such as the fairy circles of Namibia, emerge through the action of pattern-forming biomass–water feedbacks and that such patterns should be found elsewhere in water-limited systems around the world. We report here the exciting discovery of fairy-circle patterns in the remote outback of Australia. Using fieldwork, remote sensing, spatial pattern analysis, mathematical modeling, and pattern-formation theory we show that the Australian gap patterns share with their Namibian counterparts the same characteristics but are driven by a different biomass–water feedback. These observations are in line with a central universality principle of pattern-formation theory and support the applicability of this theory to wider contexts of spatial self-organization in ecology.

Abstract

Vegetation gap patterns in arid grasslands, such as the “fairy circles” of Namibia, are one of nature’s greatest mysteries and subject to a lively debate on their origin. They are characterized by small-scale hexagonal ordering of circular bare-soil gaps that persists uniformly in the landscape scale to form a homogeneous distribution. Pattern-formation theory predicts that such highly ordered gap patterns should be found also in other water-limited systems across the globe, even if the mechanisms of their formation are different. Here we report that so far unknown fairy circles with the same spatial structure exist 10,000 km away from Namibia in the remote outback of Australia. Combining fieldwork, remote sensing, spatial pattern analysis, and process-based mathematical modeling, we demonstrate that these patterns emerge by self-organization, with no correlation with termite activity; the driving mechanism is a positive biomass–water feedback associated with water runoff and biomass-dependent infiltration rates. The remarkable match between the patterns of Australian and Namibian fairy circles and model results indicate that both patterns emerge from a nonuniform stationary instability, supporting a central universality principle of pattern-formation theory. Applied to the context of dryland vegetation, this principle predicts that different systems that go through the same instability type will show similar vegetation patterns even if the feedback mechanisms and resulting soil–water distributions are different, as we indeed found by comparing the Australian and the Namibian fairy-circle ecosystems. These results suggest that biomass–water feedbacks and resultant vegetation gap patterns are likely more common in remote drylands than is currently known.

Pattern-formation theory (1) and the influence of Alan Turing’s work on understanding biological morphogenesis (2) are increasingly recognized in environmental sciences (3). Vegetation patterns resulting from self-organization occur frequently in water-limited ecosystems and, similar to Turing patterns, show pattern morphologies that change from gaps to stripes (labyrinths) to spots with decreasing plant-available moisture (4–6). The patterns may emerge on completely flat and homogeneous substrate and are induced by positive feedbacks between local vegetation growth and water transport toward the growth location. The depletion of water in the vicinity of the growing vegetation inhibits the growth there and promotes the development of large-scale patterns with a typical periodicity (5, 7–9). Spatial self-organization by scale-dependent pattern-forming feedbacks of this kind is a population-level response to water stress that complements phenotype changes at the organism level (10).

Banded or striped vegetation patterns such as tiger bush or mulga are well known from remote sensing (4, 11, 12), but landscape-scale evidence for gap patterns with circular bare-soil patches is very rare. The archetype of such a gap pattern is that of the fairy circles (FCs) of Namibia, which cover vast areas in a narrow range of climatic conditions (13, 14). However, the origin of the Namibian FCs is still unknown. Several competing hypotheses exist ranging from vegetation self-organization (13–17), termite-induced activity (18), and Euphorbia poisoning (19) to abiotic gas leakage (20). Among these, vegetation self-organization stands out as the most solid mechanism that explains the emergence of large-scale order (15, 16) and the strong dependence of fairy-circle distribution on mean annual precipitation (13). Furthermore, only self-organized biomass–water feedbacks can explain the shrinking in size and disappearance of fairy circles after above-average rainfall years and the typical enlargement and increased appearance of FCs after below-average rainfall years (21).

According to pattern-formation theory, the large-scale order that emerges from a uniform state obeys a universal pattern whose particular form is dictated by the instability that the uniform state undergoes (8, 22). The fairy-circle gap pattern observed in Namibia (15) is likely an example of a universal hexagonal pattern that, according to pattern-formation theory, is induced by a nonuniform stationary instability (3, 21–24). The mechanisms inducing the instability may differ among ecosystems, but the resulting hexagonal order of the pattern is the same. This suggests that gap patterns similar to the Namibian FCs should be observable in other water-limited landscapes, even if the mechanism of their formation is different. Also, the opponents of the self-organization hypothesis argue “if the model of self-organization were correct, it should be generic and circular bare patches should occur globally” (25).

Here, we report on the discovery and analysis of such a hexagonal gap pattern, 10,000 km away from Namibia in the remote outback of Western Australia. Using a comprehensive approach consisting of fieldwork, remote sensing, spatial pattern analysis, and process-based mathematical modeling we reveal in the following that this gap pattern is the consequence of a pattern-forming biomass–water feedback that differs from the feedback that drives the formation of FCs in Namibia.

Results and Discussion

The Australian FCs exist on flat terrain in the sparsely populated Pilbara region, encircling a radius of ∼10–20 km from east to southeast around the small mining town of Newman (Fig. 1). According to the dynamical definition of aridity (6), the Pilbara region (with an aridity index <0.2) can be classified as arid because of the bistability of bare soil and vegetation patterns implied by the coexistence of large bare-soil domains next to patterned domains (Fig. 1B). The area around Newman experiences strong long-term rainfall fluctuation (37–619 mm) around the 327-mm mean annual precipitation, and the annual evaporation is 3,200–3,400 mm (26). Monthly mean maximum air temperatures range from 22.9 °C in June to 39.2 °C in January, but daily maxima may exceed 45 °C in the summer months. Elevation of all analyzed plots in the area (fieldwork and aerial image analysis; SI Appendix, Fig. S1) ranged from 513 to 522 m. On that flat area, the FCs prevail on soils with loamy-sand to silt-loam textures being dark reddish brown in color.

Fig. 1.

The fairy circles of Australia. Aerial image of the regularly spaced gaps (A). Self-organized formation of the gap pattern within spinifex grasses under spatially variable proportions of bare soil (B). Map of Western Australia (C), where the FCs can be found to the east and south of the mining town Newman.

The Australian ecosystem is special in that it shows in a single region, with the dominant spinifex grass Triodia basedowii E. Pritz, the spectrum of vegetation states (Fig. 2) that are normally seen in different regions along the rainfall gradient. These include gaps, stripes, spots, bare soil, and transient patterns such as rings (27), suggesting an inherent multiplicity of stable states that has become visible due to local state transitions (28) induced by frequent fire disturbances (29, 30).

Fig. 2.

Different pattern morphologies in the Triodia spinifex grassland. Gaps (A), labyrinths (B), spots (C), and rings (D). Spinifex rings (D) in this habitat commonly reach 2 m and occasionally exceed 4 m in diameter and gaps (A) may exceed 6–7 m. (Scale bars in C and D, 0.5 m.)

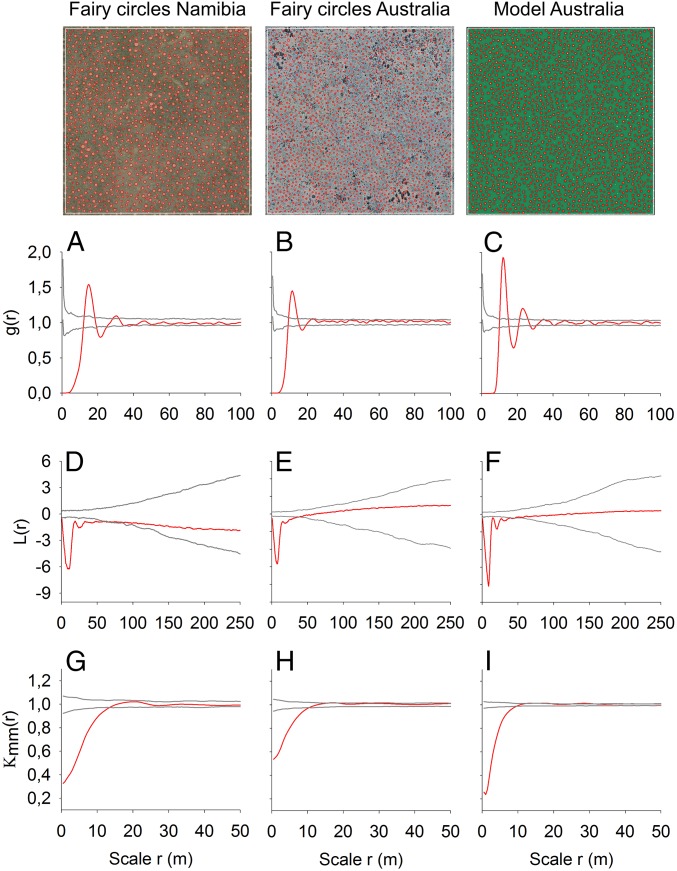
Spatial pattern analysis of aerial images (Fig. 3) demonstrates that the Australian FCs (plot C1) show nearly identical spatial characteristics to the Namibian FCs (plot G1; cf. ref. 15). They are best depicted by the pair-correlation function g(r), a neighborhood-density function that reveals strong regularity with g(r) = 0 for smallest scales, a clear peak at r ∼ 10 m radius, which is the approximate mean nearest-neighbor distance of FCs, damped oscillation of g(r) around the null model distribution of complete spatial randomness, and large-scale homogeneity of the pattern with g(r) and its cumulative counterpart, L(r), remaining inside the simulation envelopes. The first pronounced peak of g(r) with high amplitude above the upper simulation envelope of the null model indicates a hexagonal spatial arrangement where each FC has six nearest neighbors located at approximately the same distance from the focal circle. The second significant minimum of g(r) at around 17 m distance reflects the radius with “empty space” behind the first (nearest) neighbors. As shown in detail for Namibian FCs (16), these spatial characteristics lead also to two fundamental properties of the Australian FCs: a hexagonal spacing with an extraordinary degree of spatial ordering (regularity) at small scales r < 50 m and homogeneity at large scales (Fig. 3 B and E and SI Appendix, Fig. S2 and Table S1). The Australian FCs have a mean diameter of 4 m and the size of neighboring FC areas is negatively correlated up to r ∼ 9 m distance (Fig. 3H and SI Appendix, Tables S1 and S3). As also reported for Namibia (16), this below-average size of closely located FC areas is equivalent to a significant increase in the vegetation coverage, because the grasses then benefit from the higher density of the water-supplying gaps. Finally, it is remarkable that the proportion of Voronoi tiles with six corners is in all analyzed plots the largest, 46.9% on average, which is nearly identical to the 43–46% found in three different regions of Namibia. This also indicates the dominance of hexagonal FC spacing in both ecosystems (16).

Fig. 3.

Spatial pattern analysis of fairy circles. The spatial structure of the Namibian FCs (A, D, and G) agrees in all main characteristics with the Australian FCs (B, E, and H). In addition, the spatial structure of the modeled FCs (C, F, and I) based on vegetation self-organization agrees with the observed gap pattern in Australia. The size of the aerial images and the modeled map is 500 × 500 m. The spatial patterns were contrasted to null models using the pair-correlation function (A–C), L-function (D–F), and mark-correlation function (G–I). Patterns are regular and aggregated at circular neighborhood scales r if the red line of g(r) or L(r) is below the lower and above the upper gray lines of the simulation envelopes, respectively. Circle areas are negatively and positively correlated if the red line of k_mm(r) is below and above the simulation envelopes, respectively. The parameter values used in the modeled FCs are given in SI Appendix, Table S4, with P = 330 kg/(m²⋅y) (or equivalently 330 mm/y).

Our field results strongly support the existence of a pattern-forming biomass–water feedback, where water transport is in the form of overland-water flow induced by significant edaphic differences between the bare-soil gaps and the vegetation matrix. Significant differences among the three environments, gap center, gap periphery, and vegetation matrix were found for particle size distribution (clay, silt, and sand contents), hydraulic conductivity, and initial and final infiltration (SI Appendix, Table S2). Gap centers have significantly higher amounts of clay and lower infiltration rates than the vegetation matrix. A clay-rich mechanical crust is developed in the topsoil following the impact of rain drops that cause particle dispersion and a classified deposition of the fine particles on the surface. Compared with the more sandy soil textures in the vegetation matrix, this layer of the gap is compact and hard. The initial infiltration rate (I_i) of the gaps in dry soil is 0.07 mm/min, decreasing quickly to a final infiltration rate (I_f) of 0.03 mm/min. Thus, rainfall events in the arid area around Newman with rates exceeding 0.03 mm/min (26) cause excess rain to flow as runoff water over the gap surface toward the vegetation matrix. The runoff is induced by the sharp infiltration contrast between the gaps and the matrix, which makes the hardened gaps an important additional source of water for the vegetation matrix.

While supporting the grasses at the periphery and the matrix, the overland-water flow acts against seedling establishment and growth in the gaps by reducing the amount of infiltrated water there (SI Appendix, Fig. S3). Additionally, the hard soil crust in the gap causes plant death because root growth is hampered and high soil-surface temperatures, which can reach 75 °C, and the associated high evaporation rates provide a hostile microenvironment for plant survival. In contrast, the shading within the vegetation matrix and its periphery reduces surface temperatures by more than 20 °C and thus the evaporation rates, and thereby further facilitates the grass growth.

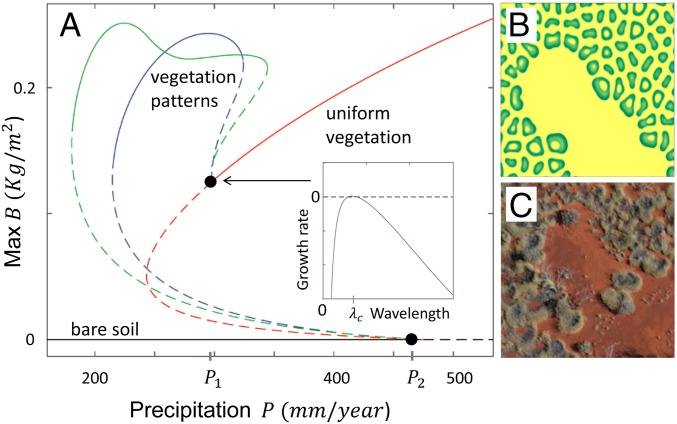
We complemented our empirical findings with numerical and mathematical analyses of a process-based model for water-limited vegetation introduced by Gilad et al. (31). The model was extended to account for the high ratio of evaporation rate to infiltration rate of surface water in bare soil and was further adapted to account for species with confined root zones such as T. basedowii (32). Model simulations produced FC patterns that agreed in all essential spatial characteristics with the observed Australian FC pattern (Fig. 3 C, F, and I). These patterns, which approach periodic hexagonal gap patterns at long times, appear as a result of a nonuniform stationary instability of the uniform vegetation state (Fig. 4A, Inset). The confined root zones of T. basedowii rule out water conduction by laterally spread root systems as a significant water-transport mechanism (22). Transport by soil–water diffusion is also unlikely due to the low infiltration rate and hydraulic conductivity in the gaps. These conclusions leave overland-water flow as the dominant mechanism (8). This is consistent with the observed infiltration contrast between vegetated and bare areas and implies in-phase spatial profiles of biomass and soil water (7) (i.e., higher water content in the vegetation matrix compared with the gaps). A direct model prediction resulting from the high ratio of evaporation rate to infiltration rate is a large stability range of the bare-soil state, even at relatively high precipitation values, as the bifurcation diagram shows (Fig. 4A). This accounts for the existence of large bare-soil patches next to vegetated areas as the model simulation and the aerial image in Fig. 4 A and C show (see also Fig. 1B). Altogether, these results strongly support the view of the Australian FCs as a self-organization phenomenon driven by a positive feedback between local vegetation growth and overland-water flow toward the growth location induced by differential infiltration (“infiltration feedback”) (8, 22).

Fig. 4.

Bifurcation diagram and related patterns. The diagram (A) shows stationary 1D solutions of SI Appendix, Eq. 1, describing uniform bare soil (black), uniform vegetation (red), and two periodic vegetation patterns (blue and green). Solid (dashed) lines represent stable (unstable) solutions. The vertical axis shows the biomass density of the uniform solutions or its maximal value for periodic solutions. (Inset) The growth rate of small sinusoidal perturbations as a function of their wavelength at P slightly below P₁. The growth of a sinusoidal perturbation of finite wavelength λ_c indicates a nonuniform instability of the uniform-vegetation solution that leads to a periodic pattern with wavelength λ_c (blue line). Additional periodic solutions exist; shown is the solution that extends to the highest P value (green line). The bare-soil solution loses stability as P exceeds the threshold P₂ given by SI Appendix, Eq. 3. Its wide stability range overlaps with those of uniform and patterned vegetation and allows for long-lived mixtures of large bare-soil patches and vegetation patches, as the model simulation in B shows. An analogous field pattern is shown in C. Parameter values for B are given in SI Appendix, Table S4, with P = 280 kg/(m²⋅y) (or 280 mm/y).

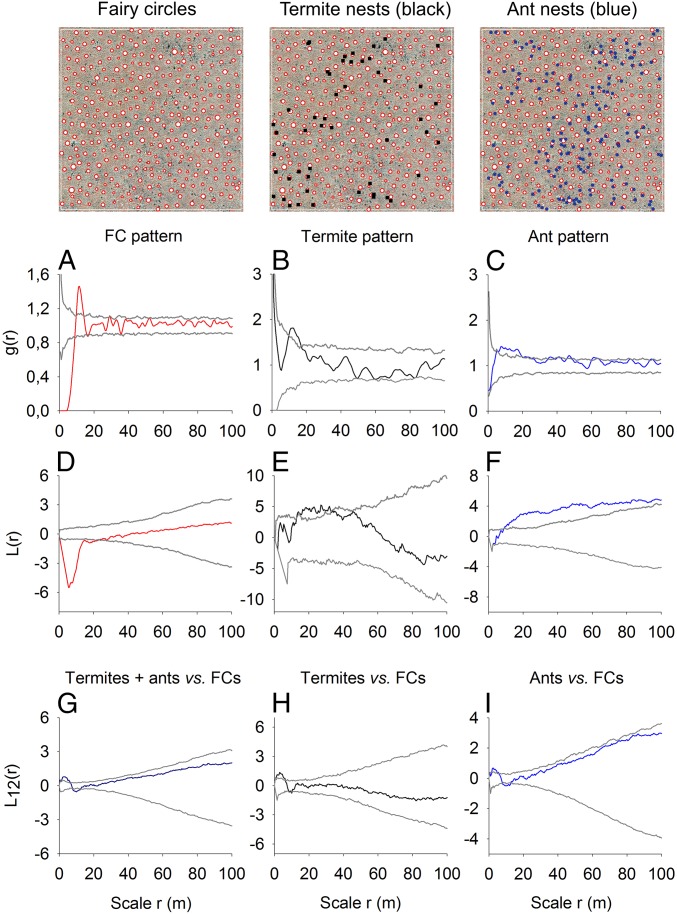
To test whether termites or ants play a role (18, 33, 34) in the formation of Australian FCs, we studied their presence in the gaps in the field. The majority of FCs lacked any signs of termite or ant activity and the proportion of gaps with termite signs (either clear mounds, low pavement mounds, or foraging holes in flat surface) were very variable, with 47%, 60%, and only 33% in the three field sites C1, L1, and L2, respectively. Furthermore, the characteristics and the number of termite signs per gap did not correlate with the size of the gaps (R² = 0.0064, P = 0.6; SI Appendix, Table S3 and Fig. S4). We also mapped the spatial distribution of all termite and ant nest locations with a GPS in the field site C2 whose vegetation was totally burnt just a few weeks before field measurements were taken. After the fire, signs of insect activity and round clay pans of fairy circles were clearly visible, making their identification easier (SI Appendix, Fig. S5 A and B). Based on an earlier orthophoto from 2014, we counted in the unburnt plot 328 fairy circles, but only 50 termite signs were found in the field. In contrast to the even spacing of fairy circles, termite or ant nests were typically aggregated and heterogeneously distributed (Fig. 5 E and F) and thus cannot explain the extremely regular FC pattern spreading homogeneously over the landscape (Fig. 5D). The spatial cross-correlation analysis with the L₁₂-function confirmed our observations from the field. If they were present, termite and ant nest locations tended to be located at the edge or partly outside of fairy circles. Because both termites and ants were similarly attracted to the gap edges (Fig. 5 G–I), we assume that these areas are favorable microenvironments for the insects, possibly because the edge interface between bare soil and vegetation matrix receives more water from runoff, and spinifex vegetation along the edge can be particularly dense and rich in shade (SI Appendix, Fig. S3). In summary, we found that neither the presence–absence data of termites and ants nor their nest position along the gap edge or their spatially variable density patterns can explain the distribution of the Australian FCs and their large diameters, which may exceed 6 to 7 m. Moreover, insect activity can also not explain the transitions of circular bare-soil patches to typical labyrinthine vegetation patterns or the large bare-soil areas that coexist together with fairy circles in the same area (Figs. 1B and 2B).

Fig. 5.

Comparison of FC patterns with insect-nest distributions. The Australian FCs (n = 328) are typically hexagonally spaced, showing strong small-scale regularity (A and D), and the pair-correlation function g(r) indicates a distinct density peak at the average distance of the six nearest neighbors at r ∼10 m (A). In contrast, the distributions of the 50 termite (black squares) and 162 ant (blue dots) nests are not regularly spaced but aggregated (B and C). Especially the cumulative L-function indicates for these insect-nest distributions aggregated spacing at small and large scales (E and F). For descriptions of functions see Fig. 3. The cross-correlation analysis with the L₁₂-function shows that the composite distribution of insects (termites + ants, dark blue line), the termite (black line), and also the ant (blue line) distributions slightly aggregate around the FCs (G–I).

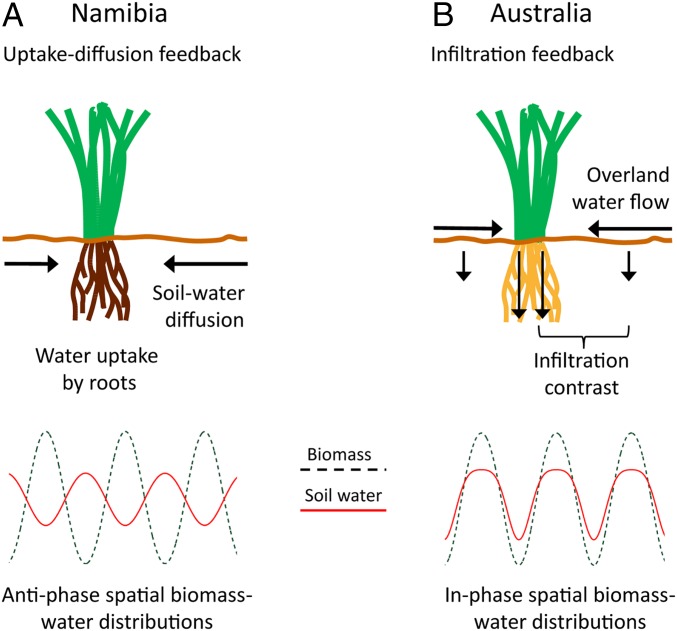
Overall, our results demonstrate a remarkable congruency in the patterns between Australian and Namibian FCs, suggesting that spatial self-organization, driven by scale-dependent biomass–water feedbacks, is the causal agent of both phenomena. However, the particular feedbacks at work in the two ecosystems are different, because the mechanisms of water transport from gaps to vegetation matrix are different (see illustration in Fig. 6). As observed in field experiments (13, 18) and predicted by model studies (21), the soil–water content in the Namibian FC gaps exceeds the content in the vegetation matrix, but the opposite is found in the Australian FCs. This is because the mechanism of water transport in the Namibian ecosystem with porous sand is soil–water diffusion, whereas in the Australian ecosystem with hard clay pans, it is overland-water flow. The sandy gaps in the Namibian ecosystem form large below-ground water reservoirs that sustain the surrounding water-consuming vegetation by soil–water diffusion (13, 15, 16). By contrast, the Australian FC gaps act as above-ground hard clay pans that produce runoff toward the surrounding vegetation matrix. As shown in model studies (7), the different mechanisms result in opposite biomass–water relationships; in-phase spatial biomass–water distributions in Australia and antiphase distributions in Namibia (Fig. 6). Antiphase distributions in Namibia have indeed been observed in field studies (13, 18). Our field results for the Australian FCs are so far less conclusive; however, our irrigation experiment and detailed soil analyses (SI Appendix, Fig. S3 H and I and Table S2), as well as field observations of reduced infiltration rates and increased runoff on crust layers in different T. basedowii regions (32), are consistent with the model prediction of in-phase spatial biomass–water distributions.

Fig. 6.

Pattern-forming feedbacks. A schematic illustration showing the different feedback mechanisms in the Namibian (A) and in the Australian (B) FC ecosystems that still lead to the same nonuniform instability characterized by the growth-rate curve shown in Fig. 4A, Inset (7). The feedbacks differ in the mechanism of water transport, soil–water diffusion in the aeolian sand of Namibia, induced by local water uptake vs. overland-water flow on the hard soil layer in Australia, induced by differential infiltration. The different mechanisms lead to different soil–water distributions, antiphase with the biomass distribution (Namibia) and in-phase with it (Australia), as illustrated in the bottom part of the figure.

An open question is to what extent hybrid states and hybrid-state transitions, manifested as birth and death of FCs and observed in the Namibian ecosystem (21), exist also in the Australian ecosystem. Hybrid states have not been identified in the model-parameter range used in this study and have not been studied yet in the field. This may suggest a significant difference between the responses of the two ecosystems to rainfall variability (21, 28), which is more stochastic in Namibia, but further model and empirical studies are needed to clarify this point. Upcoming research on the Australian vegetation patterns should also investigate the time scales over which FCs emerge, expand, and die, and how edaphic factors influence the transitional pattern morphologies from gaps to labyrinths and large bare-soil areas. Recurrent fire disturbances play a key role in these spinifex systems (30), and their potential effect on revealing the inherent multiplicity of stable vegetation states and on inducing transient patterns such as spinifex rings needs to be studied in future.

Conclusion

The results reported here showcase a central universality principle of pattern-formation theory. The principle classifies self-organized patterns into universal classes that are determined by the nature of the instabilities that induce the patterns and predicts that different systems that go through the same instability type will show similar patterns (1, 8). For the Namibian and Australian ecosystems we have shown that the different water-transport mechanisms induce a Turing-like nonuniform stationary instability that leads to the monotonic growth of a spatially structured mode (7) (Fig. 4A, Inset). In 2D systems, such an instability leads to periodic hexagonal patterns (1, 8). Thus, the appearance of nearly hexagonal FC patterns in both the Namibian and the Australian ecosystems, despite the different mechanisms that drive them, is in accord with the universality principle of pattern-formation theory and highlights the significance of this theory to the understanding of spatial ecological processes.

Materials and Methods

Field Survey.

In December 2014, we undertook a field survey in a radius of ∼10–20 km east to southeast around the mining town of Newman, Western Australia (Fig. 1). We selected three field sites with FCs for taking soil samples and for recording gap sizes, signs of termite and ant activity, soil-surface temperatures, and water infiltration. These sites were dominated either by purely gapped FC patterns (plot C1, Fig. 3) or partly interspersed with labyrinthine vegetation patterns (plots L1 and L2; see SI Appendix, Fig. S1), with the latter type resulting in a proportion of bare soil >10%. In each of the three study sites, 15 neighboring gaps were chosen in a random walk and their diameters were measured at the larger two sides (90° displacement). The surrounding spinifex vegetation was identified as being dominated by T. basedowii E. Pritz.

Termites are important litter feeders (34, 35). In each gap, we carefully recorded any visible sign of termite and ant presence. Termite signs included up to ∼40-cm-high mounds, as are typical for the species Tumulitermes hastilis, and pavement-like mounds that are up to ∼20 cm high or that have thick mound caps that may be even level with the surrounding soil surface, as being typical for Drepanotermes rubriceps and Drepanotermes perniger (36–38). Signs of termite activity also included foraging holes in the flat soil surface of the gaps, as are typical for the harvester termite Schedorhinotermes actuosus (39). In those few cases when the thick mechanical soil crusts resulting from weathering could not be visually distinguished from the thick caps of pavement-like mounds, the crusts were opened with a hammer to verify the presence of termite galleries or holes below the hardened soil crusts. Signs of ant activity were similarly recorded either as clearly visible round nest entrances with a central hole or as elevated cone-like mounds (40) (SI Appendix, Fig. S5 B and C). In addition, the spatial positions of all termite and ant signs were mapped with a GPS device in a recently burnt 210- × 210-m plot, named C2, to enable the comparison of their spatial patterns with the typical distribution of FCs (Fig. 5).

Soil samples were taken in the three field plots C1, L1, and L2 and at each plot from five FCs (n = 15). For each FC, samples were taken at 0- to 5-cm depth at the gap center, gap periphery, and matrix vegetation. The soil samples were analyzed in the laboratory for physical and chemical properties such as particle size distribution, mineralogy, major elements, and hydrology, including also scanning electron microscopy (see SI Appendix for detailed methods and SI Appendix, Fig. S4 and Table S2 for soil results).

Aerial Image and Spatial Statistical Analysis.

To assess the spatial patterns of the gaps in Australia, we used the same approach as was undertaken for the Namibian FCs (15). The aerial image (RGB orthophoto with 0.5 m per pixel resolution) was acquired on April 12, 2014, and is part of the BHP Billiton Iron Ore master orthophotography mosaic imagery dataset. From this image, we selected seven sample plots that were dominated by fairy circles (C1–C7) and five plots where gaps were partly interspersed with labyrinthine vegetation patterns (L1–L5; SI Appendix, Fig. S1). However, only the seven plots with pure gap patterns were analyzed with spatial statistics.

C1 was a representative 500- × 500-m plot for direct comparison with the previously analyzed G1 plot from Namibia (15) (Fig. 3). C2 represents the field plot (in a vegetation condition before burning) where signs of termite and ant activity were mapped with a GPS (Fig. 5). C3–C7 were five randomly chosen sample plots that span from southwest to northeast over a maximal distance of 12 km in the area (SI Appendix, Figs. S1 and S2). All gaps within the plots were delineated to create shapefiles (a geospatial vector format digitized with ArcGIS-10.3 software). Hence, for each gap we created one shapefile with geo-referenced information on the circle’s x,y coordinate, area, and perimeter.

Similar to the Namibian FCs (15), these spatially explicit data were analyzed with point pattern statistics (41–44). We used g(r), the pair-correlation function (PCF), which is the expected density of points at a given distance r of the typical point, divided by the intensity λ of the pattern (44). This noncumulative neighborhood-density function is particularly suitable to reveal critical scales and the strength of small-scale order in the pattern (41, 43). Under conditions of complete spatial randomness (CSR) the function g(r) = 1. Thus, if g(r) is for large scales within the simulation envelopes of CSR, the patterns can be described as homogeneous. Values of g(r) = 0 mean that the PCF did not detect any vegetation gap at this neighborhood radius (typical for smallest scales), g(r) < 1 indicates regularity (overdispersion), and g(r) > 1 indicates aggregation. If g(r) strongly fluctuates at smaller distances r around the value of g(r) = 1, this indicates an extremely ordered pattern with a distinct density peak at the radius where the first six, approximately equally spaced, nearest neighbors occur.

Additionally, the L-transformation of Ripley’s K-function, $L\left(r\right)=\sqrt{K\left(r\right)/\pi }-r$, was used to better assess departures from CSR at larger distances (41, 44). Under CSR, L(r) = 0 and values of L(r) < 0 indicate regularity, whereas values of L(r) > 0 indicate aggregation. To assess the spatial association of insects around FCs we used the bivariate cross K₁₂-function, K₁₂(r), which is defined as the expected number of type-2 points (insects) within distance r of the typical type-1 point (fairy circles), divided by the intensity λ₂ of pattern 2, and the corresponding square-root transformation $L_{12}\left(r\right)=\sqrt{K_{12}\left(r\right)/\pi }-r$. Under independence of insect and FC patterns we expect L₁₂(r) = 0, whereas positive values of L₁₂(r) indicate attraction and negative deviations segregation (41, 44).

In a third analysis, we tested whether the sizes (the continuous variable “gap area” of bare soil) of two nearby vegetation gaps indicated spatial correlations that depended on their distance r. This was analyzed with the mark-correlation function, k_mm(r), which is the mean value of the test function t₁(m_i,m_j) = m_im_j of the marks (areas) m_i and m_j of two gaps i and j that are separated by distance r, normalized by the mean value of the test function taken over all i–j pairs regardless of their distance (42, 44). We find k_mm(r) = 1 if the gap areas show no spatial correlations, k_mm(r) < 1 if there is negative correlation between the FC sizes at scale r, and k_mm(r) > 1 if there is a positive correlation. Negative correlation of the mark gap area is equivalent to a significant increase of the vegetation coverage (15) up to the neighborhood distance where k_mm(r) = 1.

The spatial correlation functions g(r) and L(r) were tested against the homogeneous Poisson process (CSR) using the fifth-lowest and fifth-highest values of 199 Monte Carlo simulations for constructing ∼95% simulation envelopes (44). Similarly, we used the bivariate L₁₂-function and the toroidal shift null model to test for independence between the insect and FC patterns. The k_mm(r) was assessed against the independent marking null model by randomly shuffling the mark gap area.

Finally, we computed Voronoi tessellations for the gap patterns (15, 42). Voronoi tiles determine for a given center of a gap the surrounding area that is closer to the gap center than to any other gap center of the spatial pattern. The number of corners provides information on the strength of ordering (or regularity) of the pattern, because the higher the proportion of tiles with six corners, the more regular the pattern. However, it should be noted that true honeycomb patterns with 100% hexagons will hardly be attained in vegetation patterns due to inherent stochastic influences and noise (16). In this Voronoi analysis, edge tiles with corners touching the plot borders were removed. All analyses were carried out using R-software (package Spatstat; www.R-project.org/).

Model Description and Analysis.

The model used in this study is an adaptation of the vegetation model introduced by Gilad et al. (31) in accordance with the particular characteristics of the ecosystem under consideration. The Gilad et al. (31) model consists of a set of integro-partial differential equations for the coupled dynamics of three spatial densities: vegetation biomass (B), soil water (W), and surface water (H), all having units of kilograms per square meter. One adaptation of this model was based on the confined root zones of T. basedowii (32), which allows the replacement of the root integrals by algebraic forms (8, 28). Another adaptation was based on the high evaporation rate of surface water, relative to the infiltration rate, that is typical of this particular ecosystem. This condition implies that the evaporation term in the surface-water equation cannot be neglected here, as was done in earlier studies (9, 24), assuming most of the evaporation is soil water. As we see in SI Appendix, this term has an important effect on the stability of the bare-soil state, extending its stability to the precipitation range where uniform vegetation is stable. This is unlike most earlier model studies where no overlap between the stability ranges of the two uniform states has been found. The model equations, in dimensional and dimensionless forms, are given by SI Appendix, Eqs. 1 and 2. We integrated SI Appendix, Eq. 2 numerically in 2D to obtain the model patterns in Fig. 3 and Fig. 4B and used numerical continuation in 1D to obtain the bifurcation diagram in Fig. 4A. The stability threshold of the bare-soil state, given by SI Appendix, Eq. 3, was calculated using linear stability analysis.