Hierarchy and extremes in selections from pools of randomized proteins

Significance

Evolution by natural selection requires populations to be sufficiently diverse, but merely counting the number of different individuals provides a poor indication of the potential of a population to satisfy a new selective constraint. To achieve a more relevant characterization of this selective potential, we performed in vitro experiments of selection with populations of partially randomized proteins and analyzed the results quantitatively by high-throughput sequencing. We find that selective potentials in these populations follow simple statistical laws, which can be interpreted with extreme value theory (the mathematical theory of extreme events—here, the rare finding of a protein meeting the selective constraints). Our results provide an approach to quantitatively measure the selective potential of a population.

Abstract

Variation and selection are the core principles of Darwinian evolution, but quantitatively relating the diversity of a population to its capacity to respond to selection is challenging. Here, we examine this problem at a molecular level in the context of populations of partially randomized proteins selected for binding to well-defined targets. We built several minimal protein libraries, screened them in vitro by phage display, and analyzed their response to selection by high-throughput sequencing. A statistical analysis of the results reveals two main findings. First, libraries with the same sequence diversity but built around different “frameworks” typically have vastly different responses; second, the distribution of responses of the best binders in a library follows a simple scaling law. We show how an elementary probabilistic model based on extreme value theory rationalizes the latter finding. Our results have implications for designing synthetic protein libraries, estimating the density of functional biomolecules in sequence space, characterizing diversity in natural populations, and experimentally investigating evolvability (i.e., the potential for future evolution).

Diversity is the fuel of evolution by natural selection, but translating this concept into quantitative measurements is not straightforward (1). A simple count of the number of different individuals in a population, for instance, fails to account for the very different responses to selection that two populations with the same number of different individuals may elicit. The problem is even acute at the molecular scale, where it also takes a very practical form: libraries of diverse proteins are routinely screened as a way to identify biomolecules of interest (binders, catalysts, etc.), and a proper “diversity” is critical for success (2, 3). However, beyond a general agreement that maximizing the number of different elements is desirable, there is no general rule for engineering and comparing diversity in these libraries.

A common design of many protein libraries is to concentrate variations at one or a few variable parts located around a fixed “framework,” which is shared by all members of the library (2, 3). The natural design of antibody repertoires, the pools of immune proteins with potential to recognize nearly every molecular target, follows this pattern. Most of the sequence variations in antibodies are, indeed, concentrated at a few loops extending from a common structural scaffold (4). This architecture has inspired the conception of artificial protein libraries built on frameworks other than the Ig fold (5).

Here, we present an approach to quantitatively characterize the selective potential of molecular libraries. To develop this approach, we designed and screened 24 synthetic protein libraries with identical sequence variations but different frameworks and analyzed their response to well-defined selective pressures by high-throughput sequencing. Between libraries, we find that selective potentials vary widely and define a hierarchy of frameworks. Within libraries, we find that selective potentials exhibit a simple scaling law, characterized by few parameters. The essence of these results is captured by an elementary probabilistic model based on extreme value theory (EVT).

Previous work has quantified the functional potential of totally or partially random biomolecules by counting the number of positive hits resulting from successive rounds of selections and amplifications of a large sample of these biomolecules (6–11). Our results lead us to propose a different approach to characterize the selective potential of a population. Compared with previous analyses, this approach does not depend strongly on the sensitivity of the experimental assay or the number of copies in which each distinct biomolecule is present in the initial population.

Experimental Approach

Library Design.

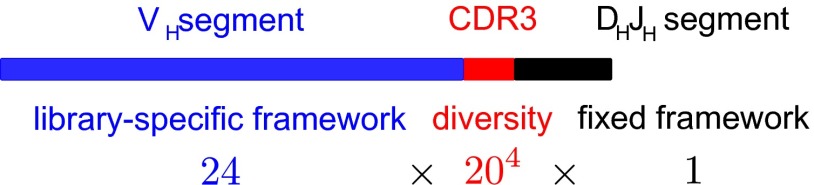
We built 24 minimal libraries with different frameworks but identical sequence diversity (Materials and Methods, Fig. 1, SI Appendix, Fig. S1, and Dataset S1). Twenty frameworks consist of single-domain antibodies taken from natural heavy-chain genes of diverse origins ($V_H$ fragments), typically sharing $40\text{\%}$ of their amino acids (SI Appendix, Fig. S2); they originate from maturated antibodies, which are mutated relative to their germ-line form, except for the S1 framework that comes from a germ-line (naïve) antibody. Three additional frameworks are more closely related and correspond to the germ-line and two maturated forms of the same human antibody, with the maturated frameworks sharing 65% and 85% sequence identity with the germ line. Finally, one framework consists exclusively of glycines to serve as a control. Diversity is limited to four consecutive amino acids at the complementarity determining region 3 (CDR3), the part of antibody sequences most critical for specificity (12). Structurally, the CDR3 forms one of three loops that define the binding pocket of a $V_H$ domain (4); in our design, the two other loops (CDR1 and CDR2) are, thus, part of the framework. Our libraries are minimal on two accounts: the framework consists of a single domain of $\sim 100$ amino acids, and the total diversity is ${20}^4=1.6\times {10}^5$—all combinations of 20 natural amino acids at the four varied sites. For comparison, the most commonly used antibody libraries consist of two domains ($V_H$ and $V_L$) and have $>{10}^8$ variants, with variation introduced at different CDRs (13). Libraries based on $V_H$ only are, however, known to be effective (14). “Minimalist libraries” have also been built by restricting the alphabet of amino acids at the variables sites but contained $>{10}^{10}$ variants (8–10). One of the simplest libraries shown so far, built on a synthetic scaffold, still contained $>{10}^6$ variants randomly sampled from a much larger pool of potential sequences (11).

Fig. 1.

Library design. We designed a total of 24 libraries with distinct frameworks and identical sequence diversity consisting of all ${20}^4=1.6\times {10}^5$ combinations of 20 natural amino acids at four consecutive positions. The design follows the natural design of the variable (V) region of the heavy chain (H) of antibodies, which is assembled by joining three gene segments: the variable ($V_H$), diversity ($D_H$), and joining ($J_H$) segments. The library-specific parts of the frameworks (blue) are from natural $V_H$, and diversity is introduced at CDR3 (red) at the junction between $V_H$ and $D_H{J}_H$, a part of the sequence critical for specific binding to antigens; the $D_H$ and $J_H$ segments (black) are common to all libraries.

Selection.

We screened our libraries by phage display for binding to one of two targets: a neutral synthetic polymer, polyvinylpyrrolidone (PVP), and a short DNA loop of 9 nt (Materials and Methods). Two previous studies established the capacity of antibody phage display to select binders for these targets (15, 16). Phage display is a standard high-throughput screening technique (17). It is based on the fusion of each antibody sequence to the sequence of the pIII surface protein of the filamentous bacteriophage M13, a natural virus of the bacterium Escherichia coli with the shape of a 1-μm-long and 10-nm-wide cylinder (17). The engineered phage encapsulates the DNA sequence of an antibody and displays the corresponding polypeptide at its surface. Populations of up to ${10}^{14}$ phages displaying a total diversity of up to ${10}^{10}$ different antibodies can, thus, be manipulated. A round of selection consists of retrieving the phages bound to either the bottom of a plate, where the PVP target is attached, or magnetic beads, where the DNA target is coated. It is followed by a round of amplification achieved by infecting bacteria with the selected phages. We performed experiments where each sequence is initially present in at least ${10}^4$ copies and where targets are provided in at least a 100-fold excess. Starting either from a single library (single framework) or a mixture of different libraries, three rounds of selection/amplification were performed. Although the enrichment of some of the sequences is intended to reflect binding to the specified targets, other factors may contribute, such as sequence-specific differences in amplification. In our experiments, such nontarget-specific selective factors can be detected but are nondominant (SI Appendix). Our analysis and its interpretation, however, do not rely on the precise nature of the selective pressure.

High-Throughput Sequencing.

We sequenced samples of ${10}^6-{10}^7$ sequences at different rounds of selection by Illumina Miseq paired-end high-throughput sequencing (18). The results give us an estimation of the relative frequencies $f_i^t$ of each sequence i in the population at each round $t=0\text{,\hspace{0.17em}}1\text{,\hspace{0.17em}}2\text{,\hspace{0.17em}or\hspace{0.17em}}3$. In estimating these frequencies, we take into account both sequencing and sampling errors (Materials and Methods).

Provided that a sequence i is present in many copies $n_i^{t-1}$ and $n_i^t$ before and after selection, its probability to be selected can be estimated as $s_i^0=n_i^t/n_i^{t-1}$. Practically, because only the relative frequencies $f_i^{t-1}=n_i^{t-1}/{\displaystyle {\sum }_j{n}_j^{t-1}}$ and $f_i^t=n_i^t/{\displaystyle {\sum }_j{n}_j^t}$ are experimentally accessible, $s_i^0$ can be inferred up to a multiplicative factor from the ratio $f_i^t/f_i^{t-1}$ (19). We, thus, define the selectivity to a target of each sequence i as

$$s_i=a\hspace{0.17em}\frac{f_i^t}{f_i^{t-1}},$$ [1]

where we fix a so that ${\displaystyle {\sum }_i{s}_i=1}$. This choice is arbitrary but ensures that $s_i$ values are defined independently of the round t of selection; we explain below how our conclusions depend on this choice. We compare the frequencies between rounds $t=3$ and $t-1=2$, where sequences with highest selectivities are best represented.

Previous studies have applied next generation sequencing to the outcome of phage display screens as a way to identify a large number of binders (20, 21) or infer sequence–function relationships (19) but have not investigated the statistical properties of the distribution of the relative selectivities of these binders.

Reproducibility and Specificity.

Several observations based on the frequencies and amino acid patterns of the sequences in populations under selection validate our experimental approach. (i) Screening the same library against the same target in separate experiments yields reproducible frequencies $f_i^t$ at the last round $t=3$ (SI Appendix, Fig. S3). (ii) Screening the same library against different targets yields target-specific amino acid patterns (SI Appendix, Fig. S4). (iii) Screening two libraries against the same target yields library-specific amino acid patterns (SI Appendix, Fig. S4). Taken together, these results show that enrichment of some of the sequences is reproducible and that it arises from selection for specific binding to the targets.

We note that one feature of our experiments is critical for reproducibility: the initial populations have a large degeneracy (the number of copies of each sequence) and not just a large diversity (the number of distinct sequences). For a sequence i with probability $s_i^0$ to pass a round of selection to be reproducibly selected, its number $n_i^0$ of copies in the initial population must, indeed, be large compared with $1/s_i^0$; if instead, $n_i^0\sim 1/s_i^0$, the sequence will be lost in $\sim 1/3$ of the experiments. The initial degeneracy, thus, controls the range of selectivities that we can reliably infer.

Results

Hierarchy Between Libraries.

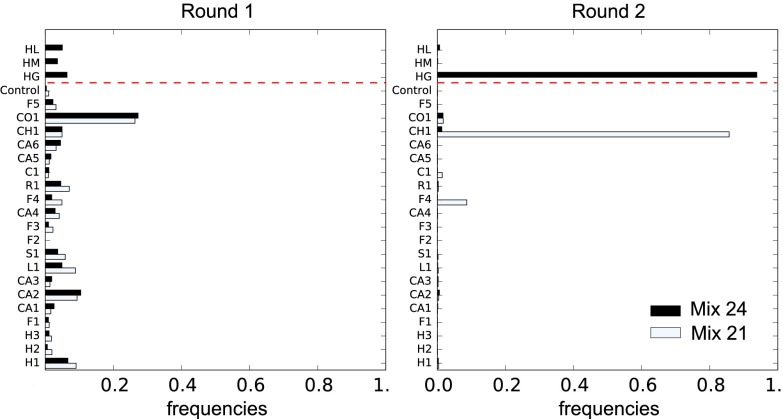
To compare the selective potentials of libraries built around different frameworks, we performed experiments in which the initial population of sequences consists of a mixture of libraries with distinct frameworks—a metalibrary. The results of these experiments reveal a striking hierarchy. Diverse members of the same library (i.e., sequences sharing a common framework) typically dominate. When repeating the experiment with an initial mixture of libraries that excludes the dominating library, another library dominates (Fig. 2). Libraries not selected when mixed with other libraries, nevertheless, do contain sequences with detectable selectivities as shown by screening them in isolation (SI Appendix, Fig. S4). These results are not explained by uneven representations of the libraries in the initial population (because the distribution of frequencies at round 2 is remarkably different from the distribution at round 1) or framework-specific differences during amplification (SI Appendix, Fig. S5).

Fig. 2.

Hierarchy between libraries. Frequencies of the different libraries, mixed together, in two successive rounds of selection against the DNA target (here, we represent frequencies and not selectivities, because the selectivity of a population of diverse sequences is ill-defined: it varies from round to round as the composition of the population varies). Black bars report selection of all 24 libraries, and white bars show selection of a subset of 21 libraries, excluding 3 libraries above the red dotted line. The labels HL, HM, etc. refer to the different frameworks (SI Appendix, Fig. S17). (Right) At the second round, the population is enriched in sequences from one particular library, the HG library, in contrast to what is observed (Left) at the first round. The subset of 21 libraries excludes the library dominating the mixture of all 24 libraries, which leads another library, the CH1 library, to dominate. Within the two libraries, several different CDR3s are selected (Fig. 3 B and D). Enrichment from the other libraries can also be observed when they are screened in isolation (SI Appendix).

Differences in frameworks are, thus, generally more significant than differences between variable parts, although these parts are clearly under selection for binding (different CDR3s have different selectivities) (Fig. 3 B and D). This result may not be surprising for very dissimilar frameworks, but our frameworks are all expected to share the same structural fold, and some frameworks have few sequence differences. In particular, the dominating framework when selecting the mixture of all 24 libraries against the DNA target (Fig. 2) is a germ-line human $V_H$ framework, which dominates two libraries built on frameworks derived from it by affinity maturations that share 65% and 85% of their amino acids. The observed hierarchy is target-dependent: different frameworks dominate when screening the metalibrary against different targets. Remarkably, when screening 24 libraries against the PVP target (SI Appendix, Fig. S6), the dominating framework is the only other germ-line framework of the mixture (the S1 framework). As noted previously, differences between frameworks also appear in the patterns of amino acids that are selected at the level of CDR3s (SI Appendix, Fig. S4 C–E).

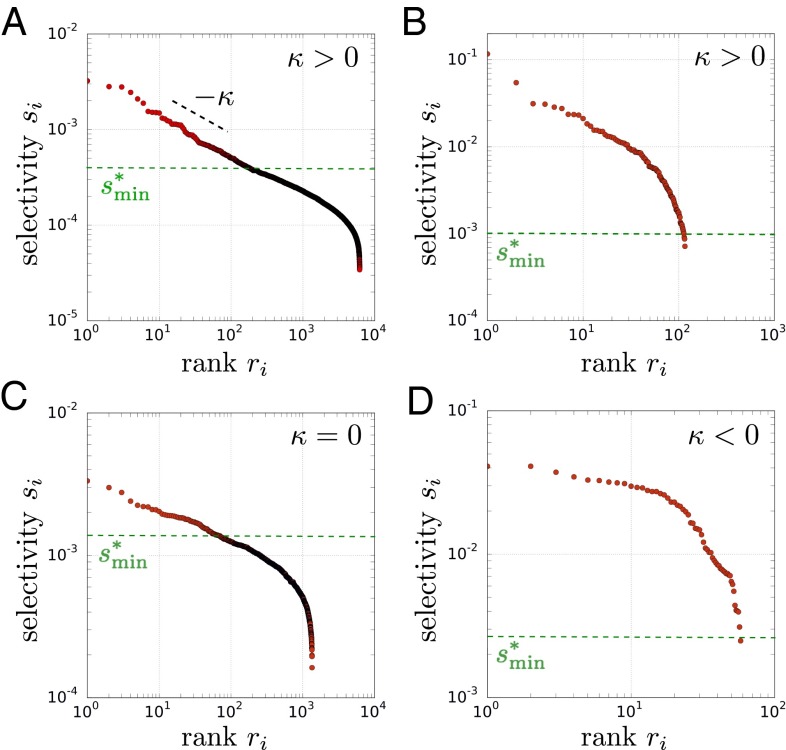
Fig. 3.

Scaling relations within libraries. The selectivities $s_i$ of the sequences are represented vs. their ranks $r_i$ for four experiments differing by the input library and the choice of the target against which it is selected. (A) S1 library against the PVP target. (B) HG library against the DNA target. (C) F3 library against the PVP target. (D) CH1 library against the DNA target. In A, the distribution of the top $\sim \mathrm{1,000}$ sequences follows a power law with exponent $\kappa \simeq 0.5$. This behavior is consistent with the prediction of EVT when the shape parameter is positive: $\kappa >0$ (Fig. 4 shows the analysis that justifies this conclusion). Although not obvious from this representation, the data in B are also consistent with EVT when $\kappa >0$, whereas the data in C and D are consistent with EVT when $\kappa =0$ and $\kappa >0$, respectively. The green dotted line indicates $s_{\text{min}}^{*}$, a value of s above which the data are well-fitted by the model from EVT (Fig. 4); in B and D, the fit, thus, extends far beyond the range of selectivities that may be described by a power law (SI Appendix, Fig. S19).

Scaling Within Libraries.

To compare the selectivities of sequences sharing a common framework and therefore, differing by, at most, four amino acids (Fig. 1), we rank these sequences in decreasing order of their selectivity $s_i$ and plot these selectivities vs. the ranks on a double logarithmic scale—a representation of the cumulative distribution of selectivities within a library. For several experiments, this representation reveals a power law: if $s\left(r\right)$ is the selectivity of the sequence of rank r, then for the sequences with top ranks,

$$s\left(r\right)\sim r^{-\kappa }.$$ [2]

Fig. 3A shows an example where the exponent is $\kappa \simeq 0.5$. Although this power law is observed for several libraries (different frameworks) and selective pressures (different targets), it is not systematic: deviations are often observed for the very top sequences (Fig. 3B), and for several experiments, a power law cannot be justified (Fig. 3D).

Both the power law and its various deviations can, however, be rationalized under an elementary mathematical model. This model rests on two assumptions. First, it assumes that the selectivity of each sequence in a library is drawn independently at random from a common probability density $\rho \left(s\right)$, which may depend on the framework and the target. Second, it assumes that the sequences with top selectivities are in the tail of this probability density.

The model is, thus, probabilistic, although—barring experimental noise—the experiments have no inherent stochastic element. To the extent that selectivity reflects binding at thermodynamic equilibrium, the selectivity $s_i$ of antibody i is, indeed, determined by its binding free energy $\mathrm{\Delta }{G}_i$ to the target: $s_i\propto e^{-\mathrm{\Delta }{G}_i/k_{B}T}$, where T represents the temperature, and $k_B$ is the Boltzmann constant. The binding free energy $\mathrm{\Delta }{G}_i$ is a physical quantity that, in principle, is fully determined by the sequence of amino acids. In the spirit of applications of random matrix theory to nuclear physics (22), it may, nevertheless, be advantageous to discard this microscopic description in favor of a coarser probabilistic description, which treats the selectivity $s_i$ as an instance of random variables independently drawn from a common probability density $\rho \left(s\right)$. In contrast to nuclear physics, no symmetry constrains $\rho \left(s\right)$ a priori, but if concerned only with the largest $s_i$, results from EVT, the branch of probability theory dealing with extrema of random variables (23), do constrain the form of the tail of $\rho \left(s\right)$ from which they originate, thus allowing for nontrivial predictions.

EVT, indeed, indicates that random variables s independently drawn from the tail of a common probability density have themselves a probability density of the form (24)

$$f_{\kappa ,\tau ,s^{\ast }}\left(s\right)=f_{\kappa }\left(\frac{s-s^{\ast }}{\tau }\right),$$ [3]

with $f_{\kappa }$ necessarily belonging to the generalized Pareto family:

$$f_{\kappa }\left(x\right)=\{\begin{array}{ll}{\left(1+\kappa x\right)}^{-\frac{\kappa +1}{\kappa }}\hfill & \text{if}\hspace{0.17em}\kappa \ne 0\hfill \\ e^{-x}\hfill & \text{if}\hspace{0.17em}\kappa =0\hfill \end{array},$$ [4]

where the exponential for $\kappa =0$ is just the continuous limit of $f_{\kappa }\left(x\right)$ when $\kappa \to 0$. Here, $s^{\ast }$ represents a threshold above which the tail of $\rho \left(s\right)$ is defined, τ is a scaling factor (that absorbs the factor a introduced in Eq. 1), and $\kappa \ge -1$ is the so-called shape factor (independent of a), which defines the universality class to which the distribution of selectivities belongs: the probability densities $\rho \left(s\right)$ may differ, but if they are associated with the same κ, events drawn from their tails will share similar statistical properties. The value of κ depends on the nature of the tail of the distribution. Distributions with a light tail and unbounded support, such as the exponential, normal, and log-normal distributions, thus belong to the same class with $\kappa =0$. However, distributions with a heavy tail, such as the Cauchy or Lévy distributions, are associated with $\kappa >0$, and distributions with bounded support, such as the uniform distribution in an interval, are associated with $\kappa <0$ (illustrations are in SI Appendix, Fig. S18).

As suggested by the notations, when $\kappa >0$ but only when $\kappa >0$, this model predicts that the top-ranked sequences follow a power law with exponent κ as described by expression 2. Mathematically, when considering a large number N of samples, the rank $r\left(s\right)$ is, indeed, related to the cumulative distribution of selectivities by

$$r\left(s\right)\sim N{\displaystyle \underset{s}{\overset{\infty }{\int }}\rho \left(x\right)dx}.$$ [5]

If $\rho \left(s\right)\sim s^{-(\kappa +1)/\kappa }$ for large s as predicted by Eq. 4, for $\kappa >0$, we must then have ${\displaystyle {\int }_s^{\infty }\rho \left(x\right)dx}\sim s^{-1/\kappa }$, and therefore, $r\left(s\right)\sim s^{-1/\kappa }$, which is equivalent to expression 2. In other words, the power law seen in Fig. 3A corresponds to the expected relationship between the rank and the values of random variables drawn from the tail of a probability density when this density belongs to a class associated with $\kappa >0$.

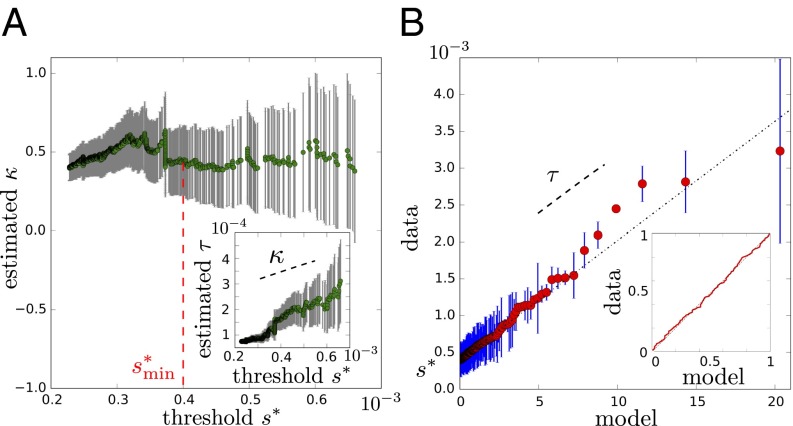
To precisely assess the ability of our model to describe all of the different cases, we followed the point over threshold approach, a standard method in applications of EVT to empirical data (24). This approach consists of fitting the data $s_i$ satisfying $s_i>s^{\ast }$ by a function of the form $f_{\kappa ,\tau ,s^{\ast }}\left(s\right)$ for different values of the threshold $s^{\ast }$ and then, estimating whether a threshold $s_{\text{min}}^{\ast }$ exists, such that, for $s^{\ast }>s_{\text{min}}^{\ast }$, the inferred parameter $\widehat{\kappa }\left(s^{\ast }\right)$ is nearly independent of $s^{\ast }$. To apply this method, we inferred the parameters $\widehat{\kappa }\left(s^{\ast }\right)$ and $\widehat{\tau }\left(s^{\ast }\right)$ by maximum likelihood from the data $s_i>s^{\ast }$ for every value of $s^{\ast }$. For the data presented in Fig. 3A, an illustration is provided in Fig. 4A, with error bars indicating 95% confidence intervals (SI Appendix discusses the analyses of other experiments). In this example, we observe that $\widehat{\kappa }\left(s^{\ast }\right)$ becomes nearly constant (of the order of 0.5) for $s^{\ast }>s_{\text{min}}^{\ast }\simeq 4\times {10}^{-4}$ (a smaller value of $s_{\text{min}}^{\ast }$ could also work in this case). The determination of $s_{\text{min}}^{\ast }$ is performed by visual inspection, but any choice of $s^{\ast }>s_{\text{min}}^{\ast }$ should give equivalent results.

Fig. 4.

Extreme value analysis by the point over threshold approach. (A) Values of the inferred parameter $\widehat{\kappa }\left(s^{*}\right)$ from selectivity $s_i>s^{*}$ as a function of the threshold $s^{*}$. The inference is made by maximum likelihood, and the error bars indicate 95% confidence intervals. (A, Inset) Similarly for $\widehat{\tau }\left(s^{*}\right)$, the second parameter of the model, which is estimated jointly to $\kappa \left(s^{*}\right)$. For sufficiently large $s^{*}$, $s^{*}>s_{\text{min}}^{*}$, $\kappa \left(s^{*}\right)$ should be constant, and $\widehat{\tau }\left(s^{*}\right)$ should increase linearly with slope $\kappa \left(s^{*}\right)$. These relations are observed here for $s_{\text{min}}^{*}\simeq 4\times {10}^{-4}$ (red dotted line) with $\kappa =0.45\pm 0.22$ and $\tau =1.6\times {10}^{-4}\pm {10}^{-5}$; $\kappa =0$ can be excluded by likelihood ratio test with a P value $<{10}^{-4}$. (B) Q-Q plot representing the data $s_i$ against predictions from the model based on the inferred value of κ only. A straight line is expected for a good fit with a slope and the y intercept given by the two other parameters τ and $s^{*}$. (B, Inset) The P-P plot comparing the empirical cumulative distributions from the data with the cumulative distribution from the inferred model, showing an excellent agreement. The data come from the selection of the S1 library against the PVP target as in Fig. 3A (SI Appendix, Figs. S8–S10 shows similar analyses of the data shown in Fig. 3 B–D).

Given $s^{\ast }>s_{\text{min}}^{\ast }$ and the associated values of $\kappa =\widehat{\kappa }\left(s^{\ast }\right)$ and $\tau =\widehat{\tau }\left(s^{\ast }\right)$ inferred from maximum likelihood, the next step is to estimate whether this best fit is, indeed, a good fit. The diagnosis is commonly performed visually using probability–probability (P-P) and quantile–quantile (Q-Q) plots (24). The P-P plot compares the empirical and modeled cumulative distributions by representing the quantile function $q\left(s\right)=r\left(s\right)/N$ (the fraction of the data above s) against the cumulative $F_{\widehat{\kappa },\widehat{\tau },s^{\ast }}\left(s\right)={\displaystyle {\int }_0^s{f}_{\widehat{\kappa },\widehat{\tau },s^{\ast }}\left(x\right)dx}$. As indicated by expression 5, a straight line $y=x$ is expected if the fit is perfect, which Fig. 4B, Inset shows to be nearly the case in this example. The Q-Q plot makes a similar comparison but by representing s against $F_{\widehat{\kappa },\mathrm{0,0}}^{-1}\left(q^{-1}\left(s\right)\right)$, where $q^{-1}\left(x\right)$ represents the value of s above which a fraction x of the data is located. This representation has two advantages over the P-P plot: it relies only on the estimation of κ, and it displays more clearly the contribution of the most extreme values. A straight line is expected if the fit is perfect but this time, with a slope τ and a y-intercept $s^{\ast }$. Fig. 4B indicates, again, a very good fit in the illustrated case.

Performing the same analysis on results of selections of various libraries against various targets, we find that the model is able to describe all of the experiments (SI Appendix, Figs. S8–S12). Different values of κ are obtained with differences that are statistically significant (SI Appendix, Table S1). In particular, the three cases, $\kappa >0$, $\kappa =0$, and $\kappa <0$, are each represented.

Although many models can lead to a power law (25), our probabilistic model has the merit of explaining the various deviations from this behavior that the data exhibit. First, when $\kappa >0$, EVT predicts a power law with exponent κ for the top-ranked sequences but accounts for deviations for both the very top-ranked sequences, which under the model may vary widely (SI Appendix, Fig. S7), and sequences of smaller selectivities, where $f_{\kappa }$ in Eq. 4 can provide an excellent fit well beyond the point where the power law applies ($s_{\text{min}}^{\ast }$ in Fig. 3 B and D and SI Appendix, Fig. S19). Second, EVT predicts behaviors differing from a power law if the probability density $\rho \left(s\right)$ belongs to a universality class associated with $\kappa \le 0$, consistent with the results of some of the experiments (Fig. 3D and SI Appendix, Fig. S10).

Discussion

We presented a quantitative analysis of in vitro selections of multiple libraries of partially randomized proteins with variations limited to four consecutive amino acids. The distribution of selectivities of the top-ranked sequences is described by few parameters, with an interpretation provided by an elementary probabilistic model based on EVT.

Within a library with members that share a common framework, this distribution is characterized by a shape parameter κ, which may be positive, negative, or zero. This parameter is independent of the factor a in Eq. 1 and has several interpretations. For instance, it controls the relative spacing between selectivities: ranking the sequences from best to worst, the expected difference of selectivity between sequences at rank r and $r+1$, ${\mathrm{\Delta }}_r=\mathbb{E}\left[s_r-s_{r+1}\right]$, satisfies ${\mathrm{\Delta }}_r/{\mathrm{\Delta }}_1\sim r^{-\left(\kappa +1\right)}$ (i.e., the larger the κ, the wider the spread between phenotypes in the library) (SI Appendix). The shape parameter also provides a statistical answer to the following question: if sampling N sequences yields a top-ranked sequence of selectivity $s_1$, what best selectivity $s_1\prime$ may we expect from sampling $N\prime >N$ sequences? The difference $\mathbb{E}\left[s_1\prime -s_1\right]$ is a sharply increasing function of κ (SI Appendix, Fig. S13); as a consequence, multiplying by a factor of 1,000 the number of sequences when $\kappa =0$ is expected to have the same effect as multiplying it by a factor of 2 when $\kappa =0.2$ if starting with $N={10}^5$ sequences.

Other than the shape parameter κ, the other parameters are the scaling parameter τ, the threshold of selectivities parameter $s^{\ast }$ that defines where the tails starts, and the fraction ϕ of the data above this threshold (there is some freedom in the choice of $s^{\ast }$, on which both τ and ϕ depend, as shown in SI Appendix). Within our experimental setup, where the selectivities are determined only up to a multiplicative factor (Eq. 1), the values of $s^{\ast }$, ϕ, and τ obtained from different experiments cannot be directly compared, but our selections with mixtures of libraries suggest that $s^{\ast }$ varies from library to library on a scale larger than the scale of the differences of selectivity within libraries. All of the parameters of the model are found to be both framework- and target-dependent (SI Appendix, Table S1).

Based on these results, we propose these parameters as general descriptors of the selective potential of a population of random variants facing a given selective constraint. In particular, these descriptors could be applied to revisit the fundamental problem of estimating the density of functional proteins or RNA in sequence space. Previous studies have estimated this density by counting the number of different sequences enriched in in vitro selections (6, 7). The results of such experiments depend on experimental noise, which sets a lower limit $s_{\text{noise}}$ on detectable selectivities. In turn, our approach is dependent only on the library content and the selective pressure provided $s^{\ast }>s_{\text{noise}}$.

Power laws are seemingly ubiquitous in distributions of protein features (26, 27). Most closely related to our work, the distribution of abundances of distinct antibody sequences in zebrafish has been shown to follow a power law with exponent $\alpha \simeq 1$ (28, 29). Only instantaneous frequencies, not selectivities, are accessible in such a case, but assuming a homogeneous initial distribution of sequences, frequencies and selectivities have the same distribution, and $\alpha =\kappa$ if $\kappa >0$. However, repeating n times the same selection leads to $\alpha =n\kappa$, which does not account for a stable exponent $\alpha >0$ that may arise in natural repertoires from fluctuating selective pressures (30). One possible extension of our approach could be to explore this scenario by changing the target between successive rounds of selection.

Although many models can be consistent with a power law, our model based on EVT covers without additional assumption the deviations from a power law observed in the data; in particular, it can fit the data over a wider range of selectivities and account for nonpower law behaviors. Our work is, however, not the first application of EVT to the description of biological variation: Gillespie (31, 32) first introduced it in models of evolutionary dynamics as a way to constrain the distribution of beneficial effects obtained when mutating a wild-type individual. Gillespie (31, 32) assumed $\kappa =0$, arguing that this class includes all “well-behaved” distributions, among which are the exponential, normal, log-normal, and gamma distributions. Mathematical models for the distribution of affinities in combinatorial molecular libraries have also proposed that it should have universal features but only considered distributions in the exponential class $\kappa =0$ (33, 34).

Several experimental studies have recently investigated the value of κ applicable to the distribution of beneficial effects in viral or bacterial populations (35, 36). The sample sizes available in these studies are, however, insufficient to conclusively validate or invalidate the EVT hypothesis. In these experiments, the number of mutants found in the tail has, indeed, been so far very low (of the order of a dozen); estimating the sign of the shape parameter κ can be attempted (37), but assessing the validity of the fit using Q-Q plots as in Fig. 4 is not possible with such limited data. Our rich dataset provides a thorough test of the applicability of EVT to the analysis of biological diversity.

Comparable datasets are now being increasingly produced. In particular, several groups have characterized the phenotype of every single-point mutant of a protein (38). Our model may be viewed as a mathematical formalization of the concept of a random library, from which single-point mutants may deviate. We note, however, that selectivities from nonrandom subsets of one of our libraries do follow the same model as the full library (SI Appendix, Fig. S14). In any case, significant deviations will have to be quantified against our null model.

Beyond protein libraries, the model is relevant to the screening of synthetic chemical libraries, including the combinatorial libraries of small molecules developed in the pharmaceutical industry for drug discovery (39, 40). In this context, one previous study was performed with enough data points to possibly discriminate between different universality classes but considered only the exponential case $\kappa =0$ (41).

Finally, our work raises a question for future studies: if the selective potential of a partially randomized library is captured by few parameters and if these parameters can vary from library to library, what controls them? More simply, what features of the framework define a universality class? For instance, how does extending the variable parts to other sites change κ? The patterns of amino acids forming the sequences, which we have analyzed here only to confirm the reproducibility of the experimental results and their specificity with respect to the targets and libraries, may provide valuable insights (29).

The question may also be asked at another level: can we or natural evolution control these parameters to optimize the selective potential of a population? This question relates to the debated “evolution of evolvability” (42, 43), cast here into a concrete conceptual and experimental setting. Antibodies potentially define an excellent model system to experimentally study this question, because they are subject to selection and maturation toward a diversity of targets as part of their natural function. The approach and concepts introduced in this work provide the means to address the problem with quantitative experiments.

Materials and Methods

Phage Display.

PVP plates were prepared as described in ref. 15. The DNA target was prepared by self-assembly of a hairpin DNA, labeled with biotin at its 5′ end (5′-biotin: AAAAGACCCCATAGCGGTCTGCGT), and purchased from Eurogentec. E. coli TG1-competent cells were purchased from Lucigen Lt. Phage production, phage display screens based on the pIT2 phagemid vector, and helper phage KO7 production were performed following the standard protocol from Source BioScience (lifesciences.sourcebioscience.com/media/143421/tomlinsonij.pdf) and our own previous work (15, 44), with some modifications as specified in SI Appendix.

Sequencing Data.

Library phagemids were purified from E. coli stocks after each selection round using Midiprep Kits from Macherey-Nagel. v3 Illumina MiSeq sequencing was performed by Eurofins Genomics. The MiSeq paired-end technology was used. Frameworks were recovered on the forward read, and only the reads having all of the expected restriction sites and less than four errors on 126 base pairs were kept. The CDR3s were accessible on the reverse read, and only the reads having all of the expected restriction sites and an average value of quality read Q > 30 on 12 base pairs defining the CDR3 were kept (SI Appendix, Table S2 has an estimation of sequencing errors). Datasets (Datasets S2–S19) are provided, with the identity of the framework in the column 1, the CDR3 sequence in column 2, and the count in column 3.

Computational Analysis.

We infer the selectivity $s_i$ of an amino acid sequence i by Eq. 1 with $t=3$ (third round of selection). The frequencies are simply given by $f_i^t=n_i^t/{\displaystyle {\sum }_j{n}_j^t}$, where $n_i^t$ is the number of sequences i present in the sample. Given sampling errors, estimated as $\mathrm{\Delta }{s}_i/s_i=1/\sqrt{n_i^2}+1/\sqrt{n_i^3}$, and given sequencing errors, estimated at ∼5% over 12 base pairs of the CDR3 (SI Appendix, Table S2), the estimation of $s_i$ is meaningful only for sequences that are sufficiently present at each round: $n_i^{t-1}>n_0$ and $n_i^t>n_0$. We took $n_0=10$ and verified that the results are not sensitive to this exact value (SI Appendix, Table S3). With $n_0=10$, relative sampling errors are, in the worst case, as high as $2/\sqrt{n_0}\sim 60\text{\%}$, but assuming that sampling errors are uncorrelated, this uncertainty has no major incidence on the estimation of aggregated properties of the distribution of the largest $s_i$, which involves several hundreds of different sequences i.

Extreme Value Statistics.

We followed the standard approach for modeling threshold excesses (24). The parameters κ and τ were estimated by maximum likelihood, and the 95% confidence intervals shown in Fig. 4A were obtained under the hypothesis of normality by calculating the inverse of Fisher’s information. To ensure that the data allow us to discriminate between $\kappa =0$ and $\kappa \ne 0$, a P value was calculated by a likelihood ratio test, whose distribution was estimated by numerical simulations. Maximum likelihood estimations are calculated on at least 50 data points. Codes in the format of an ipython notebook are provided in SI Appendix to facilitate similar analyses with other datasets.