Abstract
Background
Heart failure is characterised by recurrent hospitalisations, but often only the first event is considered in clinical trial reports. In chronic diseases, such as heart failure, analysing all events gives a more complete picture of treatment benefit. We describe methods of analysing repeat hospitalisations, and illustrate their value in one major trial.
Methods and Results
The Candesartan in Heart failure Assessment of Reduction in Mortality and morbidity (CHARM)-Preserved study compared candesartan with placebo in 3023 patients with heart failure and preserved systolic function. The heart failure hospitalisation rates were 12.5 and 8.9 per 100 patient years in the placebo and candesartan groups respectively. The repeat hospitalisations were analysed using the Andersen-Gill, Poisson and Negative Binomial methods. Death was incorporated into analyses by treating it as an additional event. The win ratio method and a method that jointly models hospitalisations and mortality were also considered. Using repeat events gave larger treatment benefits than time to first event analysis. The Negative Binomial method for the composite of recurrent heart failure hospitalisations and cardiovascular death gave a rate ratio of 0.75 (95% CI 0.62-0.91, P=0.003), and the hazard ratio for time to first heart failure hospitalisation or cardiovascular death was 0.86 (95% CI 0.74-1.00, P=0.050).
Conclusions
In patients with preserved ejection fraction, candesartan reduces the rate of admissions for worsening heart failure, to a greater extent than from analysing only first hospitalisations. Recurrent events should be routinely incorporated into the analysis of future clinical trials in heart failure.
Introduction
Composite outcomes are frequently adopted as primary endpoints in clinical trials as they take account of both the fatal and non-fatal consequences of the disease under study, thereby providing more comprehensive information about the impact of the treatments compared, and lead to higher event rates and power, thus requiring smaller sample sizes, shorter follow-up or both.[1] Most commonly in trials of chronic heart failure trials, the composite outcome is death (or cardiovascular death) or first hospitalisation for heart failure, and the time to first event is analysed using a proportional-hazards model.
However, such analyses of time to first event are suboptimal for a chronic disease such as heart failure, as relevant information on recurrent hospitalisations is ignored. Recurrent hospitalisations are distressing for patients, a marker of disease progression with adverse prognostic implications, and expensive.[2,3] The effect of treatment on these non-fatal, recurrent events is important to quantify, but there is controversy as to which statistical methods of analysis are the most appropriate.
A simple measure of the number of admissions to hospital for worsening heart failure is the event rate. The Poisson distribution is commonly used to determine if rates of an event differ between treatment groups, but ignores the heterogeneity (differing frailty) amongst patients within treatment groups.[4] The Andersen-Gill model is a survival based approach to analysing recurrent events that examines the inter-event times and is a generalisation of the Cox proportional-hazards model.[5] A more appropriate alternative approach that allows for different individual tendencies (frailties) for repeat heart failure hospitalisations, and has previously been used, retrospectively, to analyse repeat hospitalisations in the Eplerenone in Mild Patients Hospitalization and SurvIval Study in Heart Failure trial (EMPHASIS-HF), uses the Negative Binomial distribution.[6] The Ghosh and Lin method offers a non-parametric estimate of the cumulative number of recurrent events through time which incorporates death as a competing risk.[7]
The conventional analysis of composite endpoints treats all contributory outcomes as of equal importance, and only acknowledges the first outcome. The win ratio method accounts for clinical hierarchies in composite outcomes, that is, cardiovascular deaths are given higher priority than heart failure hospitalisations.[8]
Our aim here is to illustrate and compare these various methods of analysing data on repeat hospitalisations, using data from the CHARM-Preserved trial.[9] In addition to describing each method and its estimated treatment effect and statistical significance, we investigate the statistical power using bootstrapping techniques.
Study Design and Patients
The design and primary results of the CHARM-Preserved trial have been published previously.[9] In brief, the ‘Candesartan in Heart failure Assessment of Reduction in Mortality and morbidity’ (CHARM) programme was made up of three parallel, independent, randomised, double-blind, placebo-controlled trials.[10] Patients with symptomatic heart failure were randomised to receive candesartan or placebo in addition to recommended therapy. The three component parts of CHARM were CHARM-Added, CHARM-Alternative, and CHARM-Preserved.[11,12,9] CHARM-Preserved enrolled patients with LVEF greater than 40%. Patients with a LVEF less than or equal to 40% were enrolled in CHARM-Alternative (patients not receiving angiotensin-converting-enzyme (ACE) inhibitors) or CHARM-Added (patients taking an ACE inhibitor). The primary outcome of the overall programme was all-cause mortality, and for the component trials was a composite of cardiovascular death or hospitalisation for heart failure. Median follow-up was 37 months. The times to event were analysed using a Cox proportional-hazards model.
Methods
Exploratory Analyses
A bar plot for the distribution of the number of heart failure hospitalisations per patient, by treatment group was created to give a preliminary descriptive display of potential treatment differences. However, these crude plots ignore differences in patient follow-up times.
Cumulative incidence of heart failure hospitalisations over time were calculated for the two treatment groups. Such plots can be confounded by the competing risk of death, so the Ghosh and Lin non-parametric analysis of the cumulative hospitalisation rates was also adopted to assess the impact of death on results.
Estimation of Treatment Effects
Composite of Heart Failure Hospitalisation or Cardiovascular Death, analysed as time to first event
The composite of heart failure hospitalisation or cardiovascular death, analysed as time to first event was the pre-defined primary outcome for CHARM-Preserved. All first heart failure hospitalisations were adjudicated, whereas recurrent heart failure hospitalisations within individuals were not. For this reason, the primary outcome is analysed in two ways: using the adjudicated heart failure hospitalisations and using the investigator-reported hospitalisations. The latter ensures the validity of comparisons made with methods for recurrent hospitalisations.
Analysing Recurrent Heart Failure Hospitalisations
The crude rate of heart failure hospitalisations per 100 patient-years of follow-up was calculated by dividing the total number of heart failure hospitalisations by the total follow-up duration of all patients in each group. The consequent rate ratio (95% confidence interval (CI) and P-value) for this simple analysis is based on the Poisson distribution.[4]
The Negative Binomial model was used to modify such an estimated rate ratio by recognising the heterogeneity (differing frailties) of patients with respect to their risks of repeat hospitalisations.[13] It assumes that each patient’s hospitalisations follow an individual-specific Poisson rate, and that these rates vary according to a Gamma distribution. The Gamma distribution is mathematically convenient, and has statistical flexibility.[14] The Negative Binomial provides more valid mean rates of heart failure per group, and a more reliable estimate of the rate ratio allowing for different patient risks, e.g. a few patients that have many hospitalisations are less influential in analysis and the 95% CI will tend to be wider than for the naive Poisson method.
Recurrent heart failure hospitalisations were also analysed using the Andersen-Gill approach, a generalisation of the Cox proportional-hazards model which considers each repeat hospitalisation (event) as a separate term in the partial likelihood. However, events were assumed to be independent when in fact they may not be. For standard errors in the Andersen-Gill model, a robust variance estimator that allows for heterogeneity in hospitalisation rates between patients was used.[15]
Analysing the Composite of Recurrent Heart Failure Hospitalisations and Cardiovascular Death
The above methods were extended for the composite of recurrent heart failure hospitalisations and cardiovascular death, by counting each cardiovascular death as an additional event. The consequent rate ratio is for the effect of candesartan on the composite of recurrent heart failure hospitalisations and cardiovascular death. Note, if a patient died during a heart failure hospitalisation, this counted as one event.
Jointly Modelling Recurrent Heart Failure Hospitalisations and Cardiovascular Death
We used a parametric joint frailty model to analyse the recurrent heart failure hospitalisations and time to cardiovascular death simultaneously. The aim was to analyse repeat hospitalisation data, whilst accounting for their associated mortality risk.[16] The joint model specifies distributions for recurrent hospitalisations and for time to cardiovascular death, with a common frailty term inducing an association between the two processes. This frailty term can be thought of as an unmeasured indication of the severity of illness which affects both hospitalisation rate and hazard for cardiovascular death. We assumed Poisson and Log-logistic distributions for the heart failure hospitalisations and time to cardiovascular death respectively, conditional on the frailty terms, with individual frailties assumed to follow a Gamma distribution. Thus, heart failure hospitalisation rates follow a Negative Binomial distribution and times to cardiovascular death follow a Lomax distribution.
The Win Ratio
The win ratio method analyses the composite of recurrent heart failure hospitalisations and death, by allowing for clinical hierarchies.[8] Firstly, patients in the two treatment groups are formed into matched pairs based on their risk profiles. For each pair, the new treatment is a ‘winner’ or ‘loser’ according to who had a cardiovascular death first. If that is unknown, then whether they are labelled a ‘winner’ or ‘loser’ depends on who had more heart failure hospitalisations over their common follow-up time. Otherwise, they are considered tied. The ‘win ratio’ is the number of winners divided by the total number of losers.
An alternative ‘unmatched’ approach compares every patient on candesartan with every patient on placebo, noting ‘winner’, ‘loser’ or ‘tied’ for each comparison. For both matched pairs and unmatched win ratios, a 95% CI and P-value can be obtained, though for the latter, calculations are somewhat more complex.[17]
Simulation Study of Power
A power comparison was carried out for the conventional composite of first hospitalisation or cardiovascular death, the Negative Binomial analysis of the repeat hospitalisations and the Negative Binomial analysis of the composite of repeat hospitalisations and cardiovascular death. In these power calculations, the null and alternative distributions of each test statistic were approximated using bootstrap methods. For each sample size, data were drawn from the CHARM-Preserved dataset with replacement. Each bootstrap sample was analysed using the chosen methods, and the test statistic calculated. There were 5000 realisations under the null and the alternative, which were used to calculate the statistical power of each method for two-sided α=0.05. Throughout the manuscript, nominal P-values are presented without adjustment.
Results
Incidence of Hospital Admissions
The frequency of hospital admissions of different types are presented in Table 1. Of the 3023 patients randomised, 481 (16%) died and 1832 (61%) had at least one hospital admission, of whom 1290 (70%) had at least one admission for a cardiovascular cause and 508 (28%) had at least one admission for worsening heart failure. There were 4947 hospital admissions in total (including repeats), of which 2738 (55%) were cardiovascular, with 939 (19%) due to heart failure.
Table 1. Number of patients hospitalised and number of hospital admissions in CHARM-Preserved.
| Placebo | Candesartan | |
|---|---|---|
| Number of patients | 1509 | 1514 |
| Total follow-up years | 4374.03 | 4424.62 |
| Number of deaths | 237 | 244 |
| Number of CV deaths | 170 | 170 |
|
| ||
| All-cause hospitalisation | ||
| • patients with ≥ 1 admission | 920 | 912 |
| • patients with ≥ 2 admissions | 552 | 556 |
| • total admissions | 2484 | 2463 |
|
| ||
| Cardiovascular hospitalisation | ||
| • patients with ≥ 1 admission | 659 | 631 |
| • patients with ≥ 2 admissions | 339 | 311 |
| • total admissions | 1434 | 1304 |
|
| ||
| Heart failure hospitalisation | ||
| • patients with (no. of hospitalisations) | ||
| 1 | 164 | 135 |
| 2 | 55 | 56 |
| 3 | 25 | 23 |
| 4 | 13 | 9 |
| 5 | 9 | 4 |
| 6 | 4 | 1 |
| 7 | 2 | 2 |
| 8 | 2 | 0 |
| 9 | 2 | 0 |
| 13 | 1 | 0 |
| 16 | 1 | 0 |
| • patients with ≥ 1 admission | 278 | 230 |
| • patients with ≥ 2 admissions | 114 | 95 |
| • total admissions | 547 | 392 |
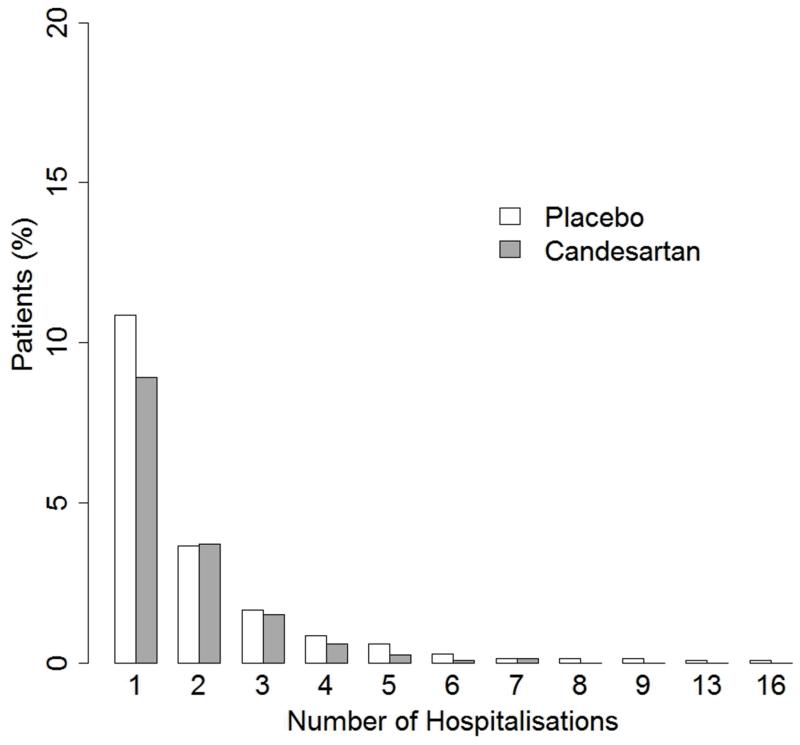
There were 278 patients with at least one heart failure hospitalisation in the placebo group, compared with 230 patients in the candesartan group. This represents an 18% relative risk reduction (95% CI 3%-30%, P=0.018). Non-significant reductions were observed in cardiovascular hospitalisations (5% relative risk reduction [95% CI −4%-12%, P=0.268]) and all-cause hospitalisations (1% relative risk reduction [95% CI −5%-7%, P=0.681]), indicating that the effect of candesartan on admissions is confined to those due to heart failure only. All subsequent analyses are confined to heart failure hospitalisation only, and their bar plot distribution is shown in Figure 1.
Figure 1. Distributions of the number of heart failure hospitalisations per patient.
Cumulative Incidence of Heart Failure Hospitalisations
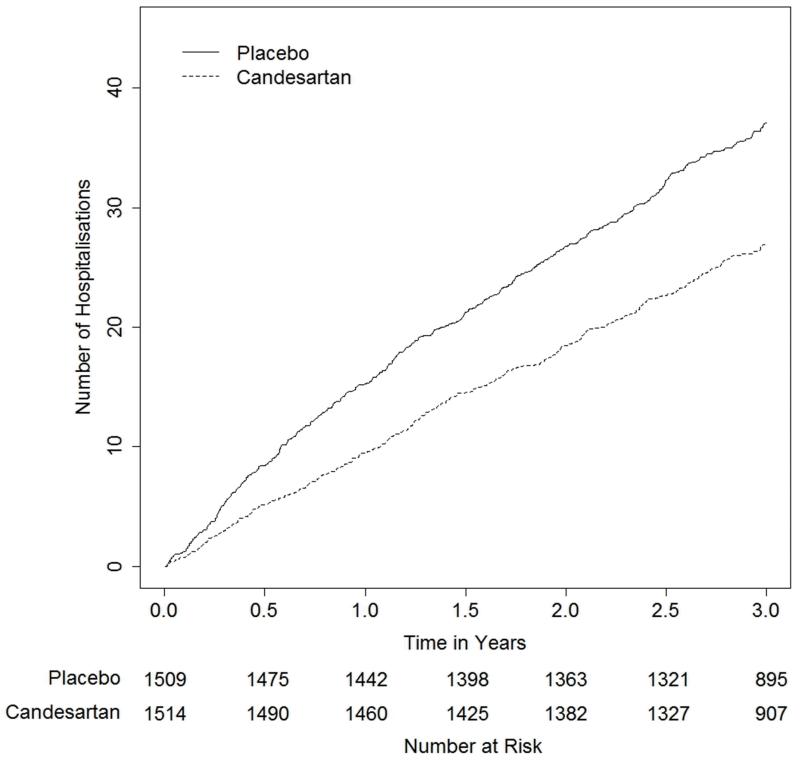
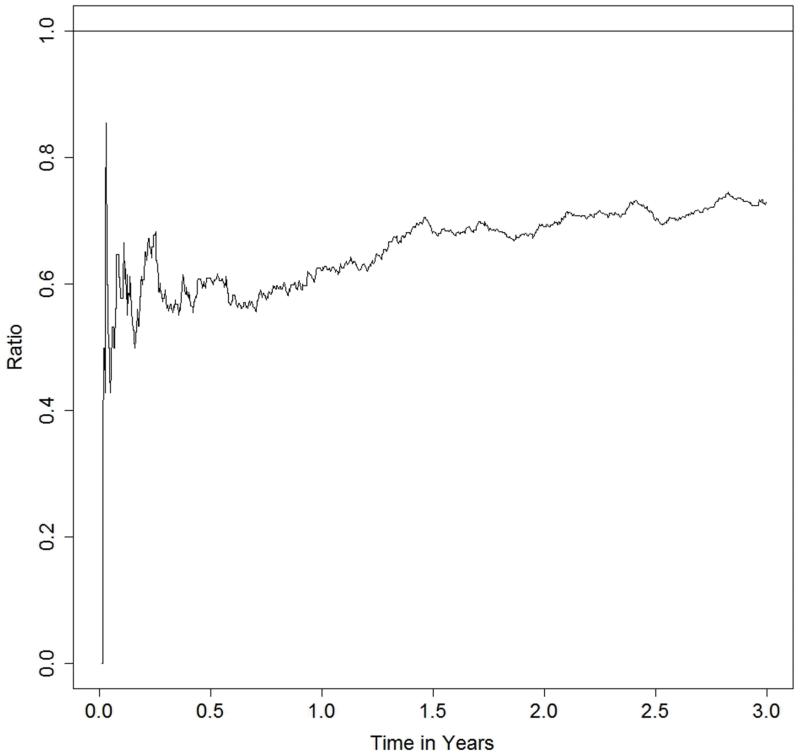
Figure 2 shows the cumulative number of admissions for heart failure hospitalisation per 100 patients in the two treatment groups, with early and continuing separation of the event curves for each treatment. This plot allows us to make descriptive, exploratory observations of the recurrent heart failure hospitalisations. By one year, the cumulative number of heart failure hospitalisations per 100 hundred patients is 15.23 on placebo, compared to 9.46 on candesartan, a treatment difference of 5.76 per 100 patients. Beyond one year, this difference continues to increase (8.27 at two years and 10.08 at three years). Figure 3 shows the ratio of the cumulative numbers of heart failure hospitalisations between candesartan and placebo groups. This ratio is around 0.6 for the first year, and attenuates slightly to 0.7 by 18 months, after which it then appears to remain constant.
Figure 2. Estimated cumulative rate of heart failure hospitalisations per 100 people, over time, stratified by treatment.
Figure 3. Risk ratio (candesartan versus placebo) of the cumulative incidence of heart failure hospitalisations over time.
To assess the impact of death on hospitalisation rates, estimates of the cumulative number of heart failure hospitalisations were also calculated using methods that allow for mortality as a competing risk (Ghosh and Lin, 2000). Such estimates were slightly lower than those that ignored mortality, although this made negligible difference to the treatment comparison.
Estimation of Treatment Effects
Table 2 presents the estimated treatment effect, with the associated confidence intervals and P-values for each of the methods considered.
Table 2. Comparison of treatment effects for the composite endpoints and recurrent events, with 95% CI and P-value.
| Treatment Effect | 95% CI | P-Value | |
|---|---|---|---|
| Hazard Ratios for Composite of First Heart Failure Hospitalisation and Cardiovascular Death | |||
| Adjudicated composite | 0.89 | (0.77,1.03) | 0.118 |
| Unadjudicated composite | 0.86 | (0.74,1.00) | 0.050 |
|
| |||
| Rate Ratios for Recurrent Heart Failure Hospitalisations | |||
| Poisson | 0.71 | (0.62,0.81) | <0.001 |
| Negative Binomial | 0.68 | (0.54,0.85) | <0.001 |
| Andersen-Gill (robust SE) | 0.71 | (0.57,0.88) | 0.002 |
|
| |||
| Rate Ratios for Composite of Recurrent Heart Failure Hospitalisations and Cardiovascular Death | |||
| Poisson | 0.78 | (0.69,0.87) | <0.001 |
| Negative Binomial | 0.75 | (0.62,0.91) | 0.003 |
| Andersen-Gill (robust SE) | 0.78 | (0.65,0.93) | 0.006 |
|
| |||
| Joint Frailty Model | |||
| Rate ratio | 0.69 | (0.55,0.85) | <0.001 |
| Hazard ratio | 0.96 | (0.73,1.26) | 0.769 |
|
| |||
| Win ratio | |||
| Matched pairs approach | 1.18 | (1.00,1.40) | 0.049 |
| Unmatched approach | 1.16 | (1.00,1.35) | 0.062 |
Composite of Heart Failure Hospitalisation or Cardiovascular Death, analysed as time to first event
As previously reported, the hazard ratio for candesartan compared with placebo was 0.89 (95% CI 0.77-1.03, P=0.118)[9]. When the same analysis was done for investigator reported hospitalisations, the hazard ratio was 0.86 (95% CI 0.74-1.00, P=0.050).
Analysing the Recurrent Heart Failure Hospitalisations
In the placebo and candesartan groups there were 547 and 392 heart failure hospitalisations over 4374.03 years and 4424.62 years of follow-up respectively. Thus, heart failure hospitalisations rates, per 100 person years, are 12.5 in the placebo group and 8.9 in the candesartan group, a rate ratio of 0.71 (95% CI 0.62-0.81, P<0.001). This simple analysis of heart failure hospitalisations (including repeats) was based on the Poisson distribution. The Negative Binomial regression model gave a rate ratio for the candesartan group, as compared with the placebo group, of 0.68 (95% CI 0.54-0.85, P<0.001). The Andersen-Gill approach using robust standard errors gave an estimated hazard ratio of 0.71 (95% CI 0.57-0.88, P=0.002).
Separate analyses were conducted for the first hospitalisation only and for repeat hospitalisations (after the first). In the placebo and candesartan groups there were 278 and 230 first heart failure hospitalisations, respectively, giving corresponding rates of 16.1 and 12.5 per 100 patient-years and a Poisson rate ratio of 0.82 (95% CI, 0.69–0.97; P=0.025). Note the Poisson distribution is fine here since there is at most one hospitalisation per individual. A Negative Binomial regression model was used to analyse repeat heart failure hospitalisations (excluding the first). This gave a rate ratio for the candesartan group, in comparison with placebo, of 0.58 (95% CI, 0.39–0.87; P=0.009).
Analysing the Composite of Recurrent Heart Failure Hospitalisations and Cardiovascular Death
To account for mortality, cardiovascular death (except if occurring during a heart failure hospitalisation) was counted as an additional event and the subsequent event rates are analysed using the Poisson, Negative Binomial and Andersen-Gill models. This approach yielded 705 events in the placebo group and 554 events in the candesartan group.
The Poisson model gave a rate ratio for the composite of recurrent heart failure hospitalisations or cardiovascular death of 0.78 (95% CI 0.69-0.87, P<0.001). The Negative Binomial model yielded an estimated rate ratio of 0.75 (95% CI 0.62-0.91, P=0.003). The Andersen-Gill model with robust standard errors gave an estimated hazard ratio of 0.78 (95% CI 0.65-0.93, P=0.006).
Jointly Modelling the Recurrent Heart Failure Hospitalisations and Cardiovascular Death
The joint model gave an estimate for the recurrent heart failure hospitalisation rate ratio which takes into account death as informative censoring, and an estimate for the hazard ratio for cardiovascular death which accounts for effect of hospitalisations on death. The estimated rate ratio for heart failure hospitalisations in the candesartan group, as compared with the placebo was 0.69 (94% CI 0.55-0.85, P<0.001). The estimated hazard ratio for cardiovascular death in the candesartan group, as compared with placebo was 0.96 (95% CI 0.73-1.26, P=0.769).
The Win ratio
The win ratio, using the matched pairs approach, for the composite of recurrent heart failure hospitalisations or cardiovascular death was 1.19 (95% CI 1.00-1.40, P=0.049). The unmatched win ratio was slightly smaller: 1.16 (95% CI 1.00-1.35, P=0.062).
CHARM-Added and CHARM-Alternative
As further illustration of the key methods, data from the CHARM-Added and CHARM-Alternative trials were also analysed using the Cox proportional-hazards model for the composite of heart failure hospitalisations or cardiovascular death and the Negative Binomial method for the composite of recurrent heart failure hospitalisations and cardiovascular death. For CHARM-Added, analysing time to the first heart failure hospitalisation or cardiovascular death, gave a hazard ratio for candesartan versus placebo, of 0.83 (95% CI 0.74-0.94, P=0.003). The Negative Binomial model for the repeat hospitalisations and cardiovascular death yielded a rate ratio of 0.75 (95% CI 0.62-0.91, P=0.003). For CHARM-Alternative, the hazard ratio for time to first event was 0.77 (95% CI 0.67-0.89, P<0.001), whereas the rate ratio under the Negative Binomial was 0.65 (95% CI 0.51-0.82, P<0.001).
Simulation Study of Power
Power calculations were carried out for the two composite analyses of first hospitalisation or cardiovascular death, the Negative Binomial analysis of the repeat hospitalisations and the Negative Binomial analysis of the composite of repeat hospitalisations and cardiovascular death (Table 3). There was a substantial increase in statistical power with the methods that incorporate all heart failure hospitalisations, compared with the analyses using only first events. For example, with a sample size of 3500, the analysis of heart failure hospitalisation or cardiovascular death using the Negative Binomial, yielded statistical power of over 80%, compared with 57% for the same composite outcome analysed as time to first event.
Table 3. Results from the power simulations.
| Number of Events | Sample Size | ||||
|---|---|---|---|---|---|
| 2000 | 2500 | 3000 | 3500 | ||
| Adjudicated composite | 699 | 30.5% | 39.8% | 46.1% | 53.6% |
| Unadjudicated composite | 704 | 34.2% | 43.3% | 48.5% | 55.7% |
| Negative Binomial for Recurrent Heart Failure Hospitalisations | 939 | 75.3% | 84.4% | 91.3% | 94.2% |
| Negative Binomial for Recurrent Heart Failure Hospitalisations and Cardiovascular Death | 1257 | 58.7% | 71.0% | 77.9% | 84.4% |
Discussion
Our analyses of CHARM-Preserved show that methods that take account of repeat hospital admissions can demonstrate a larger treatment benefit than the conventional time to first event analysis, even when accounting for death. Inclusion of recurrent events also leads to a considerable gain in statistical power compared to the time to first event even approach.
The motivation for considering these alternative approaches to analysis of clinical outcomes is that many cardiovascular diseases are chronic illnesses characterised by a relatively long period before death during which multiple non-fatal events occur, often leading to hospital admission. Heart failure and preserved ejection fraction (HF-PEF) is a typical example of this, contrasting with heart failure and reduced ejection fraction (HF-REF) which has a much higher rate of death due to cardiovascular causes; HF-PEF has a lower mortality rate and a larger proportion of deaths are non-cardiovascular. In our view, an analysis that takes account of all of the disease-related cardiovascular events that occur as a result of a condition, rather than just the first event, gives a better description of the true burden of the disease and is also the real target for treatment both from a patient perspective and provider (i.e. economic) and societal perspective. Statistically, the challenge is to determine the best way (or ways) of conducting such analyses.
These analyses of CHARM-Preserved show that candesartan not only reduces the risk of first admissions to hospital for worsening heart failure, but decreases the incidence of repeat admissions. For instance, in the placebo and candesartan groups there were 114 and 95 patients who had second or subsequent hospital admissions for heart failure. These patients presented with an additional 269 hospitalisations in the placebo group and 162 in the candesartan group. Crucially, these hospitalisations would be ignored in a time to first event analysis. In other words, only 508 (54%) of the total of 939 heart failure hospitalisations would be accounted for in a conventional analysis. Furthermore, the effect of candesartan on the rate of these repeat heart failure hospitalisations, as compared with placebo, appears greater than the effect of treatment on the rate of first admissions.
The greatest treatment effect of candesartan in CHARM-Preserved was obtained using the Negative Binomial analysis of the recurrent heart failure hospitalisations. The estimated treatment effects under the Poisson and Andersen-Gill are the same, but the confidence intervals are wider under both the Negative Binomial and the Andersen-Gill. This is not surprising since the Gamma frailty distribution in the Negative Binomial and robust standard errors in the Andersen-Gill both account for heterogeneity, whilst the Poisson analysis naively assumes independence of repeat events.
We observe slight attenuation of the estimated treatment effects once cardiovascular death is included as an additional recurrent event. This is to be expected given that the numbers of patients experiencing cardiovascular deaths were the same in the two treatment groups. Note, however, that all of the estimated rate ratios for the composite of recurrent heart failure hospitalisations and cardiovascular death remain highly statistically significant.
In CHARM-Preserved, the win ratio methods appeared a less powerful tool than the Negative Binomial methods for repeat events. This is because there was no treatment difference in cardiovascular deaths, and their greater priority in the win ratio method diluted the impact on the frequency of heart failure hospitalisations which feature second in the hierarchy of events. Thus, win ratio methods are more suitable for trials in which our hypotheses that any treatment benefit will manifest itself in both reduced incidence of cardiovascular death and heart failure hospitalisations.
For each of the methods described here, we have also undertaken covariate adjusted analyses based on the same pre-defined set of baseline covariates as in the original CHARM publications.[9-12] In every case, such covariate adjustment led to the same conclusions regarding the relative merits of the different methods, with only very slight changes to the estimated hazard ratios and rate ratios.
The sample size assumption for CHARM-Preserved was an annual event rate of 11%, so that a planned sample size of 2900 patients would provide a power of 80% to detect a relative risk reduction of 18% at an α level of 0.05.[9] What we actually observed, was a relative risk reduction of 11% with consequent lack of statistical power, while the Negative Binomial analysis of the recurrent heart failure hospitalisations has statistical power of over 80%.
The gains in terms of statistical power of analysing all heart failure hospitalisations are clearly demonstrated. We have observed that analysing all the heart failure hospitalisations in CHARM-Preserved gives both more events to analyse and also an apparently greater treatment effect than when analysing time to first event, so an increase in power is unsurprising. This increase in treatment effect was also observed when the recurrent hospitalisations in CHARM-Added and CHARM-Alternative were analysed using the Negative Binomial method.
An increase in treatment effect was also observed in the Eplerenone in Mild Patients Hospitalization and SurvIval Study in Heart Failure trial (EMPHASIS-HF) trial data, when the recurrent hospitalisations were analysed using the Negative Binomial, as compared to an analysis that just considers time to first event.[6]
One cannot predict what would happen in future heart failure trials that use repeat event analyses but, based on these case studies, it seems plausible that treatment benefit would not be confined to first heart failure hospitalisations only, so that substantial gains in statistical power are likely to occur.
The joint frailty model estimated a rate ratio for the heart failure hospitalisations, whilst incorporating the competing risk of death and a hazard ratio for cardiovascular death that allowed for the heart failure hospitalisations. Models of this kind are appealing as they allow distinct treatment effects to be estimated for the two processes, whilst taking into account the association between the two. A limitation of the joint model in its current form is that the individual-specific frailties are assumed to affect the rate of heart failure hospitalisations and the hazard for cardiovascular death in the same way. This assumption may not be appropriate in practice.
There are several limitations to note. CHARM-Preserved is a specific case study, so perhaps some caution is needed in discussing generalisable conclusions regarding the benefits of incorporating repeat hospitalisations into future heart failure trials’ primary analyses. However, supportive findings from the other two CHARM trials, EMPHASIS-HF, SHIFT and PLATO trials add weight of evidence to the claim that we are missing a valuable opportunity for both greater insight and increased statistical power if we continue to ignore events in our primary trial conclusions.[6,18,19]
One specific limitation of the CHARM trials was that only first heart failure hospitalisation was adjudicated, and hence we would encourage future trials to undertake central adjudication of all potential heart failure hospitalisations to enhance data quality. However, we do acknowledge that there is an ongoing debate as to whether centralised event adjudication is necessary at all in double blind placebo-controlled clinical trials.
Future heart failure trialists face the dilemma of deciding which is to be their primary method of analysis for repeat heart failure hospitalisations. This choice is particularly important regarding what methods are deemed acceptable by regulators, e.g. the Food and Drug Administration and European Medicines Agency. There is an ongoing debate amongst sponsors, statisticians, clinicians and regulators in this regard, and we hope that our findings are a valuable contribution to this.
We advocate the use of the joint frailty model, as this method allows estimation of a treatment effect for recurrent events, whilst accounting for death as informative censoring. Where death rates are low, the Negative Binomial distribution could be used, as this is a more simple method of analysis. Our perspective is that the choice of any one specific primary analyses (whether that be Negative Binomial, joint frailty model, or whatever) should bear in mind a balance between clarity for non-statisticians and statistical robustness. In this latter regard, it is important that trialists undertake various sensitivity analyses to demonstrate that any apparent treatment benefit is not dependent on the chosen statistical technique.
It is important to stress that our analyses were undertaken after publication of the European Society of Cardiology/Heart Failure Association 2012 guidelines which state “no treatment has yet been shown convincingly to reduce morbidity and mortality in patients with HF-PEF”.[20] While our new analyses might challenge that interpretation, we recognise that guideline writing committees (and regulators) must give most credence to the pre-specified primary analysis of trials and be cautious about retrospective analyses. What is needed, as stated above, are new trials where analysis of repeat events is the pre-specified primary analysis and such a trial has now been designed in patients with HF-PEF using the agiotensin receptor neprilysisn inhibitor (ARNi) LCZ696[21,22] – the Prospective comparison of ARni with Arb Global Outcomes in heart failure with preserved ejectioN fraction (PARAGON-HF).
In conclusion, we intend that the methods and results presented here indicate a way forward whereby future trials in heart failure can make the most of incorporating all heart failure hospitalisations (not just the first) into their primary conclusions regarding treatment benefits. We encourage both further case studies and collective agreement on which methods to employ, so that in due course repeat event analyses become a routinely accepted key component in the reporting of heart failure trials. What matters is that heart failure trials stop giving priority to inefficient methods (time to first heart failure hospitalisation) and make better use of the totality of evidence as captured by all heart failure hospitalisations and mortality.
Acknowledgments
Funding Sources
The CHARM programme was sponsored by AstraZeneca.
References
- 1.Freemantle N, Calvert M, Wood J, Eastaugh J, Griffin C. Composite outcomes in randomized trials: greater precision but with greater uncertainty? JAMA. 2003;289(19):2554–2559. doi: 10.1001/jama.289.19.2554. [DOI] [PubMed] [Google Scholar]
- 2.Conard MW, Heidenreich P, Rumsfeld JS, Weintraub WS, Spertus J, Cardiovascular Outcomes Research Consortium Patient-reported economic burden and the health status of heart failure patients. J Card Fail. 2006;12:369–374. doi: 10.1016/j.cardfail.2006.03.004. [DOI] [PubMed] [Google Scholar]
- 3.Stewart S, Jenkins A, Buchan S, McGuire A, Capewell S, McMurray JJ. The current cost of heart failure to the National Health Service in the UK. Eur J Heart Fail. 2002;4:361–371. doi: 10.1016/s1388-9842(01)00198-2. [DOI] [PubMed] [Google Scholar]
- 4.Glynn RJ, Buring JE. Ways of measuring rates of recurrent events. BMJ. 1996;312:364–367. doi: 10.1136/bmj.312.7027.364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Andersen PK, Gill RD. Cox’s regression model for counting processes: a large sample study. The Annals of Statistics. 1982;10(4):1100–1120. [Google Scholar]
- 6.Rogers JK, McMurray JJV, Pocock SJ, Zannad F, Krum H, Veldhuisen DJ, Swedberg K, Shi H, Vincent J, Pitt B. Eplerenone in Patients With Systolic Heart Failure and Mild Symptoms: Analysis of Repeat Hospitalizations. Circulation. 2012;126:2317–2323. doi: 10.1161/CIRCULATIONAHA.112.110536. [DOI] [PubMed] [Google Scholar]
- 7.Ghosh D, Lin DY. Nonparametric analysis of recurrent events and death. Biometrics. 2000;56:554–562. doi: 10.1111/j.0006-341x.2000.00554.x. [DOI] [PubMed] [Google Scholar]
- 8.Pocock SJ, Ariti CA, Collier TJ, Wang D. The win ratio: a new approach to the analysis of composite endpoints in clinical trials based on clinical priorities. European Heart Journal. 2012;33(2):176–182. doi: 10.1093/eurheartj/ehr352. [DOI] [PubMed] [Google Scholar]
- 9.Yusuf S, Pfeffer MA, Swedberg K, Granger CB, Held P, McMurray JJV, Michelson EL, Olofsson B, Östergren J. Effects of candesartan in patients with chronic heart failure and preserved left-ventricular ejection fraction: the CHARM-Preserved Trial. The Lancet. 2003;362:777–781. doi: 10.1016/S0140-6736(03)14285-7. [DOI] [PubMed] [Google Scholar]
- 10.Pfeffer MA, Swedberg K, Granger CB, Held P, McMurray JJV, Michelson EL, Olofsson B, Östergren J, Yusuf S. Effects of candesartan on mortality and morbidity in patients with chronic heart failure: the CHARM-Overall programme. The Lancet. 2003;362:759–766. doi: 10.1016/s0140-6736(03)14282-1. [DOI] [PubMed] [Google Scholar]
- 11.McMurray JJV, Östergren J, Swedberg K, Granger CB, Held P, Michelson EL, Olofsson B, Yusuf S, Pfeffer MA. Effects of candesartan in patients with chronic heart failure and reduced left-ventricular systolic taking angiotensin-converting-enzyme inhibitors: the CHARM-Added trial. The Lancet. 2003;362:767–771. doi: 10.1016/S0140-6736(03)14283-3. [DOI] [PubMed] [Google Scholar]
- 12.Granger CB, McMurray JJV, Yusuf S, Held P, Michelson EL, Olofsson B, Östergren J, Pfeffer MA, Swedberg K. Effects of candesartan in patients with chronic heart failure and reduced left-ventricular systolic function intolerant to angiotensin-converting-enzyme inhibitors: the CHARM-Alternative trial. The Lancet. 2003;362:772–776. doi: 10.1016/S0140-6736(03)14284-5. [DOI] [PubMed] [Google Scholar]
- 13.Greenwood M, Yule GU. An inquiry into the nature of frequency distributions representative of multiple happenings with particular reference to the occurrence of multiple attacks of disease or of repeated accidents. Journal of the Royal Statistical Society. 1920;83(2):255–279. [Google Scholar]
- 14.Hsu L, Gorfine M, Malone K. On robustness of marginal regression coefficient estimates and hazard functions in multivariate survival analysis of family data when the frailty distribution is mis-specified. Statistics in Medicine. 2007;26:4657–4678. doi: 10.1002/sim.2870. [DOI] [PubMed] [Google Scholar]
- 15.Lin DY, Wei LJ. The Robust Inference for the Cox Proportional-hazards Model. Journal of the American Statistical Association. 1989;84:1074–1078. [Google Scholar]
- 16.Liu L, Huang X. The use of Gaussian quadrature for estimation in frailty proportional-hazards models. Statistics in Medicine. 2008;27:2665–2683. doi: 10.1002/sim.3077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Finkelstein DM, Schoenfeld DA. Combining mortality and longitudinal measure in clinical trials. Statistics in Medicine. 1999;18:1341–1354. doi: 10.1002/(sici)1097-0258(19990615)18:11<1341::aid-sim129>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- 18.Borer JS, Böhm M, Ford I, Komajda M, Tavazzi L, Sendon JL, Alings M, Lopez-de-Sa E, Swedberg K. Effect of ivabradine of recurrent hospitalization for worsening heart failure: the SHIFT Study. European Heart Journal. 2012;33(22):2813–2820. doi: 10.1093/eurheartj/ehs259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kohli P, Wallentin L, Reyes E, Horrow J, Husted S, Angiolillo DJ, Ardissino D, Maurer G, Morais J, Nicolau JC, Oto A, Storey RF, James SK, Cannon CP. Reduction in First and Recurrent Cardiovascular Events With Ticagrelor Compared With Clopidogrel in the PLATO Study. Circulation. 2013;127(6):673–680. doi: 10.1161/CIRCULATIONAHA.112.124248. [DOI] [PubMed] [Google Scholar]
- 20.McMurray JJV, Adamopoulos S, Anker SD, Auricchio A, Böhn M, Dickstein K, Falk V, Filippatos G, Fonseca C, Gomez-Sanchez MA, Jaarsma T, Køber L, Lip GYH, Maggioni AP, Parkhomenko A, Pieske BM, Popescu BA, Rønnevik PK, Rutten FH, Schwitter J, Seferovic P, Stepinska J, Trindade PT, Voors AA, Zannad F, Zeiher A. ESC Guidelines for the diagnosis and treatment of acute and chronic heart failure 2012. European Journal of Heart Failure. 2012;14:803–869. doi: 10.1093/eurjhf/hfs105. [DOI] [PubMed] [Google Scholar]
- 21.Solomon SD, Zile M, Pieske B, Voors A, Shah A, Kraigher-Krainer E, Shi V, Bransford T, Takeuchi M, Gong J, Lefkowitz M, Packer M, McMurray JJ. Prospective comparison of ARNI with ARB on Management Of heart failUre with preserved ejectioN fracTion (PARAMOUNT) Investigators. The angiotensin receptor neprilysin inhibitor LCZ696 in heart failure with preserved ejection fraction: a phase 2 double-blind randomised controlled trial. Lancet. 2012;380:1387–95. doi: 10.1016/S0140-6736(12)61227-6. [DOI] [PubMed] [Google Scholar]
- 22.McMurray JJ, Packer M, Desai AS, Gong J, Lefkowitz MP, Rizkala AR, Rouleau J, Shi VC, Solomon SD, Swedberg K, Zile MR, on behalf of the PARADIGM-HF Committees and Investigators Dual angiotensin receptor and neprilysin inhibition as an alternative to angiotensin-converting enzyme inhibition in patients with chronic systolic heart failure: rationale for and design of the Prospective comparison of ARNI with ACEI to Determine Impact on Global Mortality and morbidity in Heart Failure trial (PARADIGM-HF) Eur J Heart Fail. 2013 Apr 18; [Epub ahead of print] PubMed PMID: 23563576. [Google Scholar]