Conditionally Increased Acoustic Pressures in Nonfetal Diagnostic Ultrasound Examinations Without Contrast Agents: A Preliminary Assessment

Abstract

The mechanical index (MI) has been used by the US Food and Drug Administration (FDA) since 1992 for regulatory decisions regarding the acoustic output of diagnostic ultrasound equipment. Its formula is based on predictions of acoustic cavitation under specific conditions. Since its implementation over 2 decades ago, new imaging modes have been developed that employ unique beam sequences exploiting higher-order acoustic phenomena, and, concurrently, studies of the bioeffects of ultrasound under a range of imaging scenarios have been conducted. In 2012, the American Institute of Ultrasound in Medicine Technical Standards Committee convened a working group of its Output Standards Subcommittee to examine and report on the potential risks and benefits of the use of conditionally increased acoustic pressures (CIP) under specific diagnostic imaging scenarios. The term “conditionally” is included to indicate that CIP would be considered on a per-patient basis for the duration required to obtain the necessary diagnostic information. This document is a result of that effort. In summary, a fundamental assumption in the MI calculation is the presence of a preexisting gas body. For tissues not known to contain preexisting gas bodies, based on theoretical predications and experimentally reported cavitation thresholds, we find this assumption to be invalid. We thus conclude that exceeding the recommended maximum MI level given in the FDA guidance could be warranted without concern for increased risk of cavitation in these tissues. However, there is limited literature assessing the potential clinical benefit of exceeding the MI guidelines in these tissues. The report proposes a 3-tiered approach for CIP that follows the model for employing elevated output in magnetic resonance imaging and concludes with summary recommendations to facilitate Institutional Review Board (IRB)-monitored clinical studies investigating CIP in specific tissues.

1 Introduction

The acoustic output levels used in diagnostic ultrasonic imaging in the United States have been subject to a de facto limitation by guidelines established by the US Food and Drug Administration (FDA) in response to the Medical Device Amendments of 1976. These original guidelines were determined based on existing output levels at that time, for which no known bioeffects had been reported (ie, preexisting levels). As such, they were not, and indeed could not have been, based on scientific evidence related to the induction of specific bioeffects by diagnostic ultrasound.¹ In 1992, in response to the suggestion that image quality could be enhanced for some applications if higher acoustic outputs were allowed, new metrics were developed and implemented: the mechanical index (MI) and the thermal index (TI).² These metrics were derived through an effort to relate output guidelines to potential bioeffects, with the MI addressing the potential risks of nonthermal mechanical effects during diagnostic ultrasound exams, such as inertial cavitation, ie, bubble motion characterized by a large expansion followed by a rapid, violent collapse. While under development, there was debate as to whether maximum upper levels should be specified or, alternatively, whether output should be determined via risk-benefit analysis on a case-by-case basis³ through the ALARA (as low as reasonably achievable) principle.⁴ Experts in the ultrasonic imaging and bioeffects communities were on both sides of this issue. The 1992 track 3 FDA guidelines represent a compromise in that they relaxed the maximum recommended output levels for some applications but still linked overall thresholds to the preexisting levels from 1976 through the derating process described below.⁵ Acoustic output levels have subsequently increased within the context of the newer guidelines.⁶ Concurrently, new imaging technologies have been developed that employ unique beam sequences (ie, harmonic imaging⁷ and acoustic radiation force impulse–based elasticity imaging methods⁸) or require the injection of stabilized microbubbles as ultrasound contrast agents. None of these new modalities were well developed when the current regulatory scheme was implemented, so neither the MI nor the TI takes them into account in an optimal manner. In 2008, the American Institute of Ultrasound in Medicine (AIUM) issued a consensus report on potential bioeffects of diagnostic ultrasound.¹ This report recommended that the AIUM take the lead to encourage the FDA to develop an open, scientifically valid process for assessing the benefits and risks of relaxing the current regulatory guidelines for specified imaging conditions. In 2011, the AIUM Output Standards Subcommittee issued a report reviewing the TI.⁹ In 2012, the AIUM Technical Standards Committee convened a working group of its Output Standards Subcommittee to examine and report on the potential risks and benefits of conditionally increasing acoustic pressure levels for specific clinical imaging scenarios where there is strong expectation of a relatively high benefit-to-risk ratio. This report is the result of that effort. Production of a companion paper exploring the evidence for potentially reducing the MI under certain conditions, eg, when using ultrasound contrast agents or imaging lung, is in its initial stages.

In the following sections, we review the history of, and the scientific basis for, the MI, define an acoustic output regime, and specify clinical applications under consideration for conditionally increased pressures (CIP), review the potential risks of CIP in this regime based on existing scientific evidence, and summarize the evidence for the potential clinical benefits of CIP. Finally, we provide summary recommendations.

2 The Mechanical Index

2.1 US FDA Acoustic Output Guidelines

US FDA regulations designate most diagnostic ultrasound imaging and Doppler devices as Class 2, which means that before a new device can be legally marketed in the United States, a “510(k)” (named for a section of the 1976 FDA Medical Device Amendments) premarket notification must be cleared by the FDA. In this notification, a device sponsor or applicant must demonstrate that the device is substantially equivalent in terms of safety and effectiveness to either a device legally marketed before May 28, 1976, the date of enactment of the FDA Medical Device Amendments, or to a device that has been legally marketed as a Class 2 device since that date. To evaluate equivalent safety, the FDA uses acoustic output quantities, including the MI, to compare maximum output levels. The definition for the MI used by the FDA can be found in IEC 62359¹⁰:

$$MI=p_{r,0.3}\left(z_{\text{MI}}\right)f_{\text{awf}}^{-1/2},$$ (1)

where p_r,0.3(z_MI) is the attenuated (ie, derated) peak-rarefactional acoustic pressure at the depth z_MI (assuming an attenuation coefficient [α] of 0.3 dB cm⁻¹ MHz⁻¹); z_MI is depth on the beam axis from the transducer to the plane of maximum attenuated pulse-intensity integral (pii_0.3); and f_awf is the acoustic-working frequency.

In a survey conducted by the FDA and others of diagnostic ultrasound devices on the market prior to May 28, 1976, the highest MI was found to be 1.9, which was based on a system with an f_awf = 2 MHz.¹¹ The FDA uses this value in its regulatory decisions for all applications except ophthalmic, in which case an MI of 0.23 (the highest value found for an ophthalmic diagnostic ultrasound device prior to May 28, 1976) is used.

2.2 Scientific Rationale for MI

The MI was developed in the late 1980s from theoretical calculations and experimental observations. In their theoretical development, Apfel and Holland¹² determined the approximate acoustic pressure amplitude required to cause an optimally sized bubble (ie, the bubble size having the lowest threshold) to undergo inertial cavitation, ie, a large expansion followed by a rapid, violent collapse. Such a collapse can radiate shock waves and cause the gas within the bubble to attain a very high temperature (5000 K), thereby producing large numbers of highly reactive free radicals. Inertial cavitation can also lead to mechanical tissue disruption due to micro-streaming and jetting, which has been associated with petechial hemorrhage. The threshold pressures were predicted under the following assumptions: (1) bubble present of optimal diameter¹²; (2) water/blood around bubble¹²; (3) a pulse duration of only 1 period¹²; and (4) the use of a single derating factor for all imaging scenarios.¹³. Applying their findings, they proposed a threshold of 0.7 for their ”mechanical energy index.”¹². It is interesting to note that this is below the pre-1976 established levels (ie, MI = 1.9). In the following sections, the assumptions employed during the original development of the MI have been extended to include more realistic, yet also more complex parameters.

Viscoelasticity

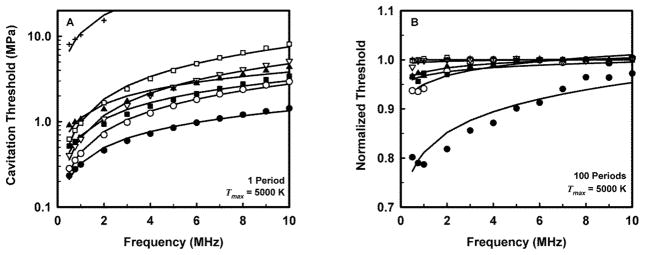
The MI was developed based on an assumption of preexisting bubbles in liquids (water and blood); however, most soft tissues are viscoelastic materials. As shown in Figure 1A, the theoretical threshold for inertial cavitation increases by a factor of 2 or more at all frequencies when comparing that for water with corresponding thresholds in soft tissues.^14,15

Figure 1.

Theoretical thresholds for inertial cavitation of optimally sized air bubbles in materials with various viscoelastic properties for a threshold criterion of T_max = 5000 K. A, Thresholds calculated assuming pressure durations of 1 acoustic period. B, Normalized (by data from 1 acoustic period in A) thresholds for inertial cavitation in each material at a pulse length of 100 acoustic periods. Curves are the best fits of P_t = Bf_cⁿ to the numerical data for water (●) blood (○), heart (□), kidney (■), liver (▽), skeletal muscle (▲), and skin (+). The average value for n (the power of frequency) for the combined curves was 0.75.¹⁵

Pulse Duration

An assumption of a single acoustic period was made during the development of the MI. While this is applicable to many ultrasonic imaging modes available on diagnostic scanners, including harmonic imaging modes, some Doppler modes employ pulse durations of between 10 and 20 acoustic periods, and acoustic radiation force impulse (ARFI) pulses are typically several hundred acoustic periods. The effect of increasing pulse length from 1 to tens of acoustic periods is to reduce the cavitation threshold for most bubbles. However, increasing pulse lengths above about 100 periods does not further reduce the threshold.^15,16 Figure 1B portrays thresholds for cavitation determined assuming 100 acoustic periods of insonation that have been normalized by their corresponding values shown in Figure 1A for 1 acoustic period.¹⁵ The impact is more significant in water and blood, whereas in soft tissues, the thresholds remain within 95% of those at 1 period.

Frequency

The MI currently employs a frequency power-law dependence of f^0.5, which was derived assuming propagation through water or blood. Theoretical studies in viscoelastic materials indicate that the frequency dependence of the threshold for inertial cavitation is better modeled by a factor of f^0.75.15 Further, experimental evidence of cavitation-mediated capillary damage in the presence of contrast agents suggests that an exponent of 1.0, rather than 0.5, more accurately predicts a threshold for this bioeffect.¹⁷

Single Derating Factor for All Imaging Scenarios

One of the significant challenges in the development of acoustic output guidelines is estimating in vivo acoustic exposure due to the widely variable level of signal loss encountered along the propagation path during imaging. The FDA guidance specifies that acoustic output measurements be made in water, and derated by a factor (α) of 0.3 dB cm⁻¹ MHz⁻¹ to account for frequency-dependent attenuation in tissue when comparing new and pre-1976 device output levels.⁵ The selection of a single derating factor of 0.3 dB cm⁻¹ MHz⁻¹ was a compromise when the MI and TI were developed.¹³ Several other models were considered, including the use of a factor of 0.5 dB cm⁻¹ MHz⁻¹ for a known soft tissue propagation path. However, with the goal of maintaining simplicity of implementation, the use of a single, conservative model was selected. In practice, a wide range of energy levels occurs in vivo for a given system output due to differences in imaging location and patient-to-patient variability in attenuation. For example, in all human transthoracic or transabdominal examinations of internal organs, the ultrasound must pass through the body wall. For both the intercostal space of the human thorax¹⁸ and the abdominal wall,^19,20 the attenuation at the body wall is about 1.3 dB cm⁻¹ MHz⁻¹, which arises both from absorption and scattering. However, the attenuation is highly variable, with about 30% variation.²¹ In addition, the thickness of the body wall varies significantly among patients. As a result, a wide range of energy levels occurs in vivo for a given system output, and the current derating approach likely overestimates actual in situ acoustic energy levels in many cases, particularly for patients with larger body habitus.

3 Challenges With Estimation of In Situ Pressures

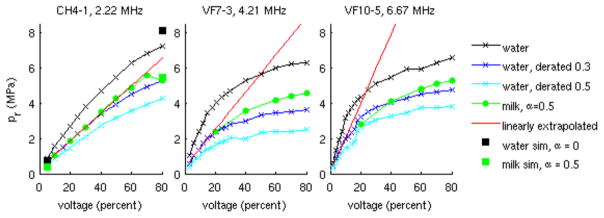
Because of differences in tissue acoustic attenuation, sound speed, and nonlinearity, the wide range of energy levels that occur cannot be easily predicted from water-based measurements. There are many clinical imaging scenarios in which the current derating scheme overestimates in situ exposures, given that α = 0.3 dB cm⁻¹ MHz⁻¹ represents a conservative estimate for the reported attenuation of many soft tissues.²² The value of 0.3 dB cm⁻¹ MHz⁻¹ was a compromise between lower amniotic fluid values and an average value of 0.5 dB cm⁻¹ MHz⁻¹ for soft tissues. The use of either higher average derating factors or layered derating schemes to account for the increased energy loss in the body wall has been considered. However, in some imaging scenarios, due in large part to saturation effects in water, the current derating scheme can also lead to underestimation of in situ exposures, particularly for the cases of higher-frequency and f-number focal configurations^23,24 (Figure 2). It is also possible, although rare, that an ultrasound beam would be focused substantially more sharply in inhomogeneous tissues than the beams assumed in the calculations of the MI and TI, resulting in higher pressures and intensities in situ than would otherwise be expected. For example, reflection from the concave surface of the pleura/lung interface or transmission through a convex, symmetric fat lobule might focus a beam at a shorter depth than intended. The accurate estimation of in situ exposure remains a significant challenge in ultrasonic imaging, without a clear solution. Some proposed approaches are described below.

Figure 2.

Peak rarefactional pressure (p_r) values measured in water (x) and derated by: 0.3 dB cm⁻¹ MHz⁻¹ (x), and 0.5 dB cm⁻¹ MHz⁻¹ (x); p_r derated water measurements linearly extrapolated from small signal values ((−), see appendix A); p_r estimated using a grid of source pressure measurements in water and modeling nonlinear propagation using the 3D KZK model with numerical solution methods described previously⁴⁴ (CH4-1 only) assuming propagation through water (■) and milk (■); as well as in situ p_r measurements made in an evaporated milk solution ((●), measured attenuation = 0.5 dB cm⁻¹ MHz⁻¹). Note that derating water values by 0.3 dB cm⁻¹ MHz⁻¹ provides reasonable agreement with the milk measurements (to within 20% for all transducers); however, derating water values by the actual measured attenuation of the milk (0.5 dB cm⁻¹ MHz⁻¹) leads to considerable underestimation of the milk measurements. Additionally, the linear extrapolation approach considerably overestimates the milk measurements for the higher frequency transducers, whereas the source pressure + nonlinear simulation approach (black squares and green squares, left plot) is in good agreement with the milk measurements. Each array transducer was focused with an F/2 lateral focal configuration concurrent with its fixed elevation focus.

Effective Mechanical Index

In many research articles, investigators report an effective mechanical index (MIE^25–27) in addition to or instead of the MI. This concept represents an attempt to accurately characterize in situ acoustic pressures. The MIE approach employs the estimated in situ p_r in the numerator of Equation 1, rather than using a derating factor of 0.3 dB cm⁻¹ MHz⁻¹ as specified by the FDA guidance and the International Electrotechnical Commission (IEC).¹⁰ The MIE is useful because it provides a more calibrated reference for comparison of the actual in situ values of p_r associated with cavitation-mediated bioeffects in different experimental protocols, for which the prefocal losses are often not accurately modeled by an attenuation factor of 0.3 dB cm⁻¹ MHz⁻¹. The MIE is thus more indicative of absolute safety thresholds, in contrast to the MI, which currently enables comparison with pre-1976 output levels.

There is not, however, a current consensus on a method to quantify MIE. In Church et al,²⁸ the following method was recommended for estimation of MIE when the MI is provided. Given an MI value, the water value of p_r is estimated by correcting for frequency-dependent derating utilizing the focal length F (cm) and transducer center frequency f_c (MHz) as follows: $p_r=e^{0.115\alpha f_{c}F}\sqrt{f_c}MI$. Then, to estimate a derated p_r at another location, this back-calculated water value is derated by the attenuation along the new path length and divided by $\sqrt{f_c}$ to estimate an approximate derated MIE_a at a site, $p_{\mathrm{r},\mathrm{a}}/\sqrt{f_{\mathrm{c}}}$. This estimate can be easily implemented from the selected focal depth and knowledge of the attenuation along the tissue path. Note that this is a simplification; the more accurate way of calculating MIE would be to derate the original measured water value p_r(z) for the attenuation along the tissue path α(f, z) and find the maximum value as $\mathit{MIE}=\mathit{maximum}[p_r(z)e^{-0.155\alpha (f_c,z)}/\sqrt{f_c}]$. In general, α(f, z) = α₀|f|^y z for each tissue path segment along z, α₀ is in dB cm⁻¹ MHz^−y, where y is an exponent appropriate to the selected tissue, and z is the distance from the source. While this approach enables MIE estimation for tissues with different attenuation values, it does not address challenges in acoustic output characterization introduced by nonlinear propagation in water.

Nonlinear Propagation and Output Characterization

Figure 2 provides examples of several investigative approaches that have been employed to account for nonlinearity and saturation effects in the estimation of MIE for a range of imaging configurations. One approach is to perform measurements in lossy media to more closely match in vivo imaging.^29,30 This approach was used to obtain the green lines in Figure 2, using a modified attenuating fluid recipe (evaporated milk and water). Challenges of this approach include establishing a standard medium with specific acoustic properties, calibrating and maintaining the hydrophone in the new medium, and satisfying the need for ease of maintenance and repeatability (as water does), which would be required for commercial implementation.

A second approach is to develop an approximate multiplier to convert waves measured in water to those generated in tissue.^31–33 A specific example in IEC Technical Specification IEC TS 61949³⁴ (see Appendix A) specifies extrapolating measurements from the “quasilinear” region in water to the nonlinear region, so that linear tissue attenuation models can be more accurately applied. While this approach reduces the likelihood of underestimation, it can lead to considerable overestimation of actual in situ values, since it ignores nonlinear losses that occur in lossy media (Figure 2, red lines). A twist on this approach useful to both shocked and unshocked waves, but only for focused sources where it can be assumed nonlinear effects are concentrated in a small portion of the tissue pathway, is to empirically develop a lookup table between input values and focal waveforms in water and then use the standard attenuation times focal distance loss, e^−0.115_αz, to derate the input source value and look up the corresponding focal waveform.³⁵ The input value may be pressure, voltage, power, etc, at the source. From the waveform, relevant acoustic parameters, MIE, intensity, etc, are obtained.

A third approach, described in greater detail in Appendix B, is to attempt to make the simplest, most robust, and reproducible measurement in water and then use that information with a numerical model to calculate the acoustic waveform in a specific tissue pathway in a 3-dimensional (3D) volume^36–42 (Figure 2, left plot, black and green squares). The specific method described in IEC Technical Specification IEC TS 62556, Appendices E–G,⁴³ describes one measurement in a plane and acoustic holography for simulation using a numerical model of the 3D nonlinear acoustic field in situ. The technique is a straightforward single measurement in water at a low output level under quasilinear conditions (as determined by a “quasilinear” criterion described in IEC TS 61949³⁴) and numerical calculation with well-established models. The challenges are details of the measurement to collect magnitude and phase, time to collect a raster-scanned surface of data, and validation of the specific numerical tools. Details on adequate sampling and the numerical calculations and checkpoints are provided in IEC TS 62556.⁴³ The advantages of this approach include a minimum number of measurements to characterize the entire acoustic field, a capability to simulate propagation in homogeneous absorbing tissue layers, and the faithful simulation of propagation from imperfect, flawed, or asymmetric transducers. The same data can be used for linear simulation³⁴ or nonlinear simulation,⁴² as summarized in Appendix B.

Figure 2 portrays measurements obtained with 3 typical diagnostic transducers over a range of transmit voltages processed using several of the methods described above to estimate in situ exposure. For these examples, derating the water measurements by 0.3 dB cm⁻¹ MHz⁻¹ provided a reasonable approximation to the p_r measured in the milk solution, whereas using an attenuation of 0.5 dB cm⁻¹ MHz⁻¹ (ie, the measured attenuation of the milk solution) for derating the water measurements considerably underestimates the milk measurements. This is due to excess energy loss in water in the prefocal region arising from nonlinear propagation in the water. Figure 2 also portrays the linearly extrapolated water-derated values (as described in Appendix A), indicating that extrapolation works reasonably well at lower frequencies to approximate the milk measurements; however, it can significantly overestimate the values in milk for the higher frequency transducers (VF7-3 and VF10-5) at the higher transmit voltages. This is because nonlinear losses in the milk increase with increasing frequency, and these losses are not modeled by the linear extrapolation approach described in Appendix A. Most tissues have a frequency exponent greater than the value 1 used for derating here, and a nonlinear parameter B/A greater than that of water¹⁹; therefore, larger disagreement between data and derating schemes for tissue can be expected. Furthermore, water is a highly nonlinear medium with negligible absorption; therefore, measured pressure waveforms in water are usually highly distorted before derating.³³ A more accurate method for simulating highly nonlinear propagation in absorbing media and water combines hydrophone measurements to create an effective source field distribution, which is then used as an input to a full nonlinear propagation simulation model capable of calculating the 3D in situ field as described in Appendix B. This approach has been used to simulate accurately the fields of a therapeutic array for pressures up to 100 MPa.⁴² The black and green squares in the leftmost plot of Figure 2 were computed using a measured grid of hydrophone data at a plane near the transducer surface, which was used as input to a full, 3D nonlinear KZK forward propagation simulation (with numerical solution methods described by Pinton⁴⁴) to provide focal pressure estimates which were in good agreement with the milk solution measurements. A simpler alternative is to combine average pressure waveforms over the source (or at the focal point) at low drive levels and knowledge of the effective focusing geometry with a nonlinear field simulator.⁴⁵ In summary, combined measurement/simulation methods that facilitate accurate in situ MIE estimates including nonlinear effects are now becoming available.

4 Experimental Evidence of Bioeffects for Relevant CIP Levels in Nonfetal Tissues Not Known to Contain Gas Bodies

A fundamental assumption used to derive the MI is the presence of a bubble of optimal diameter to serve as a cavitation nucleus. In most mammalian tissues, endogenous cavitation nuclei (ie, bubbles) are rare,⁴⁶ which invalidates that assumption. More significantly for this report, if the insonification beam path excludes bubbles, then cavitation will not occur at the acoustic pressures contemplated for CIP exposures. However, under some extraordinary conditions a bubble may be spontaneously nucleated.⁴⁷ This occurs when gas comes out of solution, a process that takes place more readily at lower static pressures; this is the reason the boiling temperature of water decreases with increasing elevation. The acoustic pressure threshold for spontaneous nucleation of a bubble in water is predicted to be quite high (30–100 MPa), while the threshold in other materials depends on the interfacial tension. In certain unusual cases, the nucleation threshold can approach the threshold value for cavitation of a preexisting bubble, or, more usually, it can be more than twice this threshold.⁴⁷ In all cases studied, the nucleation threshold is essentially independent of frequency while the threshold for inertial cavitation is predicted to increase with frequency.⁴⁷

In 2005, the AIUM convened a bioeffects conference, in which leading experts came together to review and discuss bioeffects associated with diagnostic ultrasound. An excerpt from the summary of their analysis in the context of the risk of non-thermal bioeffects follows¹:

“One of the primary mechanisms for nonthermal bioeffects is the interaction of ultrasound fields with very small pockets of gas, referred to as gas bodies. There are locations within the body that naturally harbor gas bodies, the most obvious being the lungs and intestines. In addition, decompression sickness shows the possibility for generation of gas bodies in soft tissue. As discussed by Church et al,⁴⁸ biological tissue is generally free of gas bodies, making the likelihood of their interaction with ultrasound fields quite small; the potential of a clinically significant biological effect from such interactions is smaller still. Additionally, for effects such as the rapid growth and collapse of gas bodies, referred to as inertial cavitation, the fluid motion induced by the gas bodies and other effects due to the ultrasound interactions are confined to a small region immediately surrounding the gas bodies. Although a strategically placed gas body could have a deleterious effect, this is statistically highly improbable. In experiments conducted in tissues that are not known to contain well-defined gas bodies, the requisite amplitude of the ultrasound field for inducing bioeffects is relatively high; for example, 10-microsecond pulses of 1-MHz ultrasound up to a peak rarefactional acoustic pressure of 4 MPa would not produce such an effect. This is a rather low frequency and long pulse even for Doppler ultrasound, and to provide some reference, the corresponding MI would be 4.”

The likelihood of such an effect associated with these parameters was estimated to be 1 in 10,000,000,000.⁴⁸ In this document, the general term “gas bodies” is used to remain consistent with previous statements, reports, and publications from the AIUM; however, we also use the term “bubbles” to mean pockets of gas on the order of micrometers or less.

As described in the following review, literature on this subject continues to support the conclusion that in tissues without known gas bodies, ultrasound interactions with MIE values up to 4 would not be expected to cause adverse cavitation-mediated bioeffects. It should be noted that it is implicitly assumed that any cavitation-mediated bioeffect will be undesirable due to the very large concentration of energy such events involve⁴⁹; this is not true for other mechanisms. Although it is conceivable that other nonthermal mechanisms may induce adverse bioeffects, none have been demonstrated to date, and this possibility has not been as well studied. Radiation force was the subject of a recent review,⁵⁰ and little cause for concern was expressed, except possibly for embryonic tissue. Recently, the safety committee of the Japanese Society of Ultrasonics in Medicine started to investigate bioeffects induced by ARFI ultrasound. They investigated temperature rise in tissue^51–53 and are planning to investigate other potential bioeffects, including nonthermal effects. Some research suggests that some types of exposures to specific tissues may be cause for concern^54–56 which is included in the discussion below.

4.1 Ultrasonic Stimulation of Bone Growth

Stimulation of bone growth is one of the earliest known bioeffects of ultrasound relevant to this topic. In 1954, Bender et al⁵⁷ reported osteogenesis within the marrow cavity of dog femurs exposed to relatively high powers (varying from 5 to 20 W, intensity not reported), 4 weeks after the exposure; the osteogenesis seemed to “grow” from osteotomies in the cortical bone. Later, Dyson and Brookes⁵⁸ reported healing effects in rats with fibular fractures exposed for 5 minutes on 4 consecutive days to pulsed wave ultrasound (2 milliseconds on, 8 milliseconds off) with spatial-average intensity of 0.5 W/cm² operated at either 1.5 or 3.0 MHz. The threshold for stimulation of the healing of fractures is much lower. Duarte⁵⁹ demonstrated that daily application of ultrasound (5-microsecond bursts of ultrasound at either 1.65 or 4.93 MHz and a pulse repetition frequency [PRF] of 1.0 kHz for 20 minutes, 50–60 mW/cm² spatial-average temporal-average intensity [I_SATA]) in rabbits with midshaft fibular osteotomies accelerated the healing process by a factor of 1.7. Significantly, Reher et al⁶⁰ found that while 3-MHz ultrasound pulsed with a duty factor of 20% (2 milliseconds on, 8 milliseconds off) and an intensity of 100 mW/cm² I_SATA caused bone growth acceleration in 5-day-old mouse calvaria, higher intensities did not. There is a commercially available therapeutic ultrasonic system (Exogen, Bioventus, LLC ), that employs 200-microsecond bursts at 1.5 MHz, I_SATA = 30 mW/cm², and duty factor = 0.2 applied for 20 minutes, which has been reported to accelerate bone healing by up to 40%.⁶¹ While the mechanism for these effects remains unresolved, none seem to be adverse.

4.2 Human Sensing of Ultrasonic Radiation Force

Ultrasound can affect both the central nervous system (CNS) and the peripheral nervous system (PNS). Gavrilov and Tsirulnikov⁶² identified 3 main PNS responses to ultrasound: tactile, thermal, and pain. It has been demonstrated in a variety of studies that human beings are capable of sensing exposure to ultrasound. Carefully designed experiments^62,63 identified acoustic radiation force as the main mechanism in tactile sensation of ultrasound. For example, subjects were able to perceive 10- to 100-millisecond pulses of 2-MHz ultrasound emitted at approximately 20 W by a 1-cm transducer coupled to the forearm⁶⁴; the total radiation force was about 13 mN. Subjects were also able to detect 2.2-MHz ultrasound administered to the fingertip in a single burst of 10 to 100 milliseconds above a threshold force of 3 mN (power ≈ 2.3 W) or administered repetitively in 2.5-millisecond bursts at a PRF of 200 Hz above a threshold radiation force of 0.5 mN (power ≈ 0.4 W). The ear can detect higher frequencies and shorter pulses than the finger. For example, the threshold for detection of sinusoidally modulated megahertz ultrasound by the ear varies with the frequency of modulation in a way similar to that in which it responds to audible airborne sound, with a broad minimum (indicating a maximum sensitivity) of about 1 W/cm² in the range from 200 to 4000 Hz. This corresponds to a radiation pressure of about 7 Pa, and since this is much greater than the threshold for hearing airborne sound (about 20 μPa), the ear was apparently detecting the audio-frequency radiation force generated by the transmitted ultrasound rather than the 2.5-MHz carrier wave. Fetuses have also responded to this kind of modulation.⁶³ Although these and other reports^62,65 provide interesting examples of reversible biological effects of acoustic radiation force, there appears to be little cause for concern from such mechanisms, except possibly in embryonic tissue, which lacks the structural strength that develops in later fetal and adult life. since the intercellular matrix has yet to develop.⁵⁰

4.3 Ultrasonic Brain Stimulation

The CNS can be affected by ultrasound through the mechanisms of neurostimulation and neuromodulation.^62,65–67 Recent experiments indicate that finely focused ultrasound excites neural responses in the retina, the most accessible part of the CNS.⁶⁸ A 43-MHz transducer focused on a salamander retina did not directly activate retinal ganglion cells but instead stimulated the interneurons beyond the photoreceptors. Low-intensity transcranial pulsed ultrasound (one 100-millisecond pulse at 320 kHz, derated pressure estimated at 0.35 MPa, spatial-peak temporal-average intensity [I_SPTA] 13.5 mW/cm²) focused in the frontal eye field of the brain in awake monkeys caused a significant increase in the latency period of antisaccade eye movements.⁶⁹ The investigation indicated that focused ultrasound can modulate behavior in the waking brain of nonhuman primates.⁶⁹ In related experiments, a mouse brain was modulated transcranially with both pulsed and continuous-wave (CW) unfocused 500-kHz ultrasound (spatial-peak pulse-average intensity [I_SPPA] = 0.01–79.02 W/cm²) delivered near the top of the head.⁷⁰ Somatomotor twitches of all legs at once triggered by the ultrasound stimulation appeared to be of the all-or-nothing type; ie, stronger stimulus intensities and durations increased the probability of a motor response without affecting the duration or strength of the response. Others have also succeeded in affecting the brain transcranially with ultrasound.⁷¹ While higher intensities have shown clear effects on nerves with no observed histological changes,⁷² lower intensities are also being studied. A recent review⁷³ specifically summarizes efforts using low-intensity focused ultrasound for neuromodulation and brain stimulation. Recent human studies have shown effects ranging from mood improvements (GE LOGIQe system with an 12L-RS probe, 8 MHz, MI = 0.7)⁷⁴ to changes in electroencephalographic activity (0.5-MHz pulsed ultrasound, I_SPPA = 23.87 W/cm², peak rarefactional pressure = 0.8 MPa).⁷⁵ The neuromodulatory effect is confirmed to be mediated through mechanical interaction with the tissue,^76,77 with evidence that the observed effects are proportional to the cumulative radiation force.

4.4 Cavitation-Related Bioeffects

Almost every adverse nonthermal biological effect of diagnostically relevant ultrasound that has been identified has been related to bubble activity of some kind. However, micrometer-sized bubbles are extremely rare in normal mammalian blood and tissues. Blood seems to be essentially free of bubbles. For example, Gross et al⁷⁸ used a resonance-bubble detector but did not detect cavitation bubbles in the abdominal aortas of dogs during exposure of heart or aortic blood to 0.5- to 1.6-MHz CW ultrasound up to 16 W/cm² (0.7 MPa). Using a similar detector, they were also unsuccessful in attempts to identify cavitation from left ventricular blood in dogs exposed to 0.75- and 1.45-MHz ultrasound up to 1 kW/cm² (5.5 MPa),⁷⁹ as reported by Williams et al.⁸⁰ Hwang et al⁸¹ detected an increase in endothelial damage in the auricular veins of rabbits exposed to 500-cycle, 5-Hz-PRF pulses of 1.13-MHz ultrasound at a peak rarefactional pressure of 6.5 MPa but no increase at a p_r of 3.3 MPa; damage of endothelial cells is correlated with inertial cavitation⁸² Similar results were obtained in a replicate experiment using 500-cycle pulses of 1.17-MHz ultrasound at a PRF of 1 Hz.⁸³

Most cavitation-related bioeffects that have been experimentally observed in tissues not known to contain gas bodies are associated with lower frequencies and longer durations than would be employed in CIP in either harmonic imaging or ARFI imaging. For example, Frizzell et al⁸⁴ investigated hind limb paralysis in mouse neonates exposed to 1-MHz ultrasound with a 10-microsecond pulse duration and a 2.4-second exposure duration at 10°C, finding that the threshold p_r for cavitational involvement in the paralysis was greater than 5.1 MPa for a 5-kHz PRF; the threshold decreased as the PRF increased. The sudden onset of subharmonic emissions, scattering, attenuation, and the rate of heating during hyperthermia procedures in dog thigh muscle was used by Hynynen⁸⁵ to estimate the threshold for inertial cavitation as about 3.8 MPa at 0.6 MHz, 5.9 MPa at 1 MHz, and 9.5 MPa at 1.7 MHz; the pulse length was 1 second in all cases. Vykhodtseva et al⁸⁶ used the onset of subharmonic emissions to determine the cavitation threshold in rabbit brain as 10.4 MPa at 0.94 MHz and 13.6 MPa at 1.72 MHz Cavitation-related cardiomyocyte death using a pulsing regime of 1.55 MHz, 2-millisecond duration, and a p_r of 8 MPa (measured in water) has been reported by Miller et al.⁵⁴ Recently, Gateau et al have reported the direct observation by ultra-high-speed ultrasound imaging of the nucleation of large bubbles (ie, those able to persist for at least 100 microseconds) by 2-cycle pulses of 0.66-MHz focused ultrasound in ex vivo thigh muscle⁸⁷ and in vivo brain⁸⁸ of sheep. The threshold p_r’s were 6.4 MPa in the former case and 12.7 MPa in the latter. The summary of these data given in Table 1 reveals a wide range of actual threshold values, which could be attributed to differences in animal model, cavitation detection methods, and tissue type. The lowest threshold, 1.8 MPa, occurs at a frequency of 0.25 MHz, or MIE = 3.8; this is below the usual diagnostic frequency range. The lowest value in the diagnostic range, 5.0 MPa, is found at 1.0 MHz. This corresponds to an MIE of about 5.0, or more than 2½ times the current maximum MI in the guidance on substantial equivalence from the US FDA. The fact that the experimental cavitation thresholds and the corresponding values of MIE are both much higher than their equivalent theoretical values suggests that these tissues do not contain pre-existing gas bubbles.

Table 1.

Summary of Experimentally Determined Cavitation Thresholds in Tissue

Frequency	Pulse Length	No. of Pulses	pr	Derating Factor	pr (In Situ)	MIE $\left(\frac{p_{\mathrm{r},\mathrm{a}}}{\sqrt{f_{\mathrm{c}}}}\right)$	Tissue	Source
MHz	μs	–	MPa	dB	MPa	–	–	–
0.17	58.8	12000	4.9	0.3	4.7	11.5	Pig kidney	92
0.25	1000000	1*	1.8	0.0	1.9	3.8	Dog muscle	85
0.56	1000000	1*	3.8	0.0	3.6	4.8	Dog muscle	85
0.66	3.0	1–2	6.4	0.5	6.0	7.4	Sheep muscle	87
0.66	3.0	1–2	12.7	0.5	12.0	14.8	Sheep brain	88
0.94	1000	1	10.4	0.0	10.4	10.7	Rabbit brain	86
1.0	10	12000	5.1	0.1	5.0	5.0	Mouse neonate	84
1.0	1000000	1*	5.9	0.0	5.9	5.9	Dog muscle	85
1.13	442.5	60	6.5	0.1	6.4	6.0	Rabbit blood	81
1.17	427.35	120	6.5	0.1	6.4	5.9	Rabbit blood	83
1.5	20	1	8.0	1.2	7.0	5.7	Rat heart	54
1.5	2000	1	8.0	1.2	7.0	5.7	Rat heart	54
1.68	1000000	1*	9.5	0.0	9.5	7.3	Dog muscle	85
1.72	1000	1	13.6	0.0	13.6	10.4	Rabbit brain	86

It is important to note that while the ratio $p_{\mathrm{r},\mathrm{a}}/\sqrt{f_{\mathrm{c}}}$ has the same form as the MI, for many of these studies the propagation path includes both water and tissue, and estimates were made to determine an accurate value of the attenuated p_r, in situ. This approach represents an estimate of the MIE, thus differing from the definition of the MI, which specifies derating by 0.3 dB cm⁻¹ MHz⁻¹.

^*CW exposure.

In cardiac imaging, premature ventricular contractions (PVCs) have been reported as a bioeffect that can be associated with ultrasonic insonation, primarily in the presence of ultrasonic contrast agents and with the use of elevated acoustic output levels.^54,89,90 In one study, in the absence of contrast agents, for 5-millisecond pulses at 1.2 MHz, a minimum threshold of 1.5 MPa p_r was required to induce PVCs in mice (MIE = 1.3). For shorter pulses (1 millisecond), the threshold p_r was 3.0 MPa (MIE = 2.6), and these were less effective at inducing PVCs than even lower-pressure, longer-duration pulses.⁸⁹ An earlier study of PVC induction in frogs produced similar results.⁵⁶ These MIE thresholds are much lower than those reported in Table 1, when direct evidence of cavitation was quantified. Given this discrepancy, one might hypothesize that cardiac tissue is more susceptible to bioeffects than other tissues, and/or that the PVCs in these studies were mediated not by cavitation but by radiation force, which would be more likely in mice than humans, since the entire murine heart was encompassed by the focused beam in these studies. This is suggested by the threshold intensity versus pulse duration relationship for PVCs and also by the strong evidence for radiation force as the mechanism for reduced aortic pressure in frogs.⁹¹

Perhaps the most thorough examination of the effects of pulsed ultrasound on biological tissues was that conducted over a period of many years at the University of Illinois. In the early 1970s, several studies were performed related to the safety of ultrasound, and thresholds for tissue damage were evaluated for a variety of acoustic parameters in exposed feline brain. The values of the acoustic parameters spanned the range from diagnostic to therapeutic output levels and frequencies. The researchers divided the lesions that were generated into 3 categories (thermal, cavitation, and a “combination” of effects, likely mechanical).^93.94 Through these studies, the authors found that the threshold for lesion formation was related to in situ pulse intensity (I), exposure duration (t), and frequency (f) by $I\sqrt{t}=c(f)$, where c(f) was an empirically derived threshold with a moderate frequency dependence.⁹⁵ The acoustic intensities were quantified using linear extrapolation of small signal values (in a manner similar to that discussed in Appendix A) to avoid saturation artifacts in the measurements, which, as shown in Figure 2, can overestimate the actual in situ values, particularly for higher frequencies.

Based on these studies, Dunn and Fry⁹³ reported that subthreshold pulses did not sum to produce a suprathreshold functional effect unless the duty cycle was nearly one-half and the pulse duration was 10 milliseconds. In addition, they reported that:

“1100 cats have been irradiated in the laboratory under procedures yielding 10,000 individual exposures producing lesions in the adult cat brain in the ‘focal region’ of the dosage curve. All animals were examined histologically in the focal region of the sound beam and in intervening tissue between the focal region and the port of entry of the sound into the brain. It is pointed out here that the intervening tissue received multiple doses ranging from just below threshold values, near the beam focus, to much lesser values, at the cortex. Animal survival was allowed to range from a few minutes to five years, with more than half being sacrificed between one and two years after exposure. From all these data no evidence emerges suggesting tissue abnormalities produced by the passage of sound through intervening tissue.”⁹³

Although it is tempting to make use of these data for the purposes of this report, this would be difficult to support scientifically. The research was not expressly aimed at studying cavitation in tissue, at least not the type of cavitation the MI was designed to predict. That is, there were no measurements of acoustic emissions specific to inertial cavitation; there was no search for the microlesions expected to be produced by inertial cavitation at threshold exposures; the $I\sqrt{t}$ dependence is puzzling (and is still not understood, except possibly in the context of a thermal dose analysis⁹⁶); the frequency dependence was not that expected for cavitation; and the cavitation resulting from these exposures was not necessarily at the focus. Further, the acoustic field measurements are difficult to compare to equivalent measurements made using modern techniques. These difficulties make it challenging to place this work in the context of the modern MI and TI scheme.

However, the work done at the University of Illinois is not without value for the subject herein. For example, the data suggest that the duration of excitation has a significant impact on the cavitation threshold. From a mechanistic point of view, the experimental results shown in Table 1 and from the University of Illinois^93–95 suggest that the probability that exposure to diagnostic ultrasound (emitted by devices cleared under current track 3 guidelines) will induce cavitation in tissue not containing preexisting gas bodies is essentially zero. Further, given the apparently large safety margin provided by the current FDA diagnostic ultrasound guidance⁹⁷ (under the assumption that the MI accurately reflects in situ levels), it seems reasonable to suggest that exceeding the recommended maximum level given in the guidance could be warranted if a significant increase in diagnostic information could be obtained thereby.

The question of the extent to which the current recommended maximum should be exceeded is best addressed by considering the data in Table 1. A plot of the in situ cavitation threshold rarefactional pressures as a function of frequency is given in Figure 3. The values for all tissues other than brain are shown as circles, while the three values for brain are the triangles. The physical characteristics of brain seem to be different from those of the other tissues, thus leading to higher thresholds, but the nature of the differences is not clear. The solid black curve labeled MI = 1.9 gives the in situ rarefactional pressure at the upper end of the range in the guidance for track 3 devices: $p_r=1.9\sqrt{f/1\text{MHz}}\text{MPa}$. The solid red curve labeled MIE = 4.0 gives the proposed upper limit on p_r for use during the exploratory phase of the CIP process described below. Note that this curve passes through the lowest datum at 0.25 MHz (within experimental error). This is the lowest experimentally determined in situ threshold value for rarefactional pressure at any frequency, which justifies its use as a limit at this time. In addition, the value of rarefactional pressure at 1 MHz is 4.0 MPa, which provides a safety margin of 1.0 MPa over the lowest datum at that frequency; 1.0 MHz is sometimes cited as being at the lower end of typical diagnostic frequencies. The MIE retains the frequency response of the MI, so the safety margin can be expected to increase further as the acoustic frequency increases.

Figure 3.

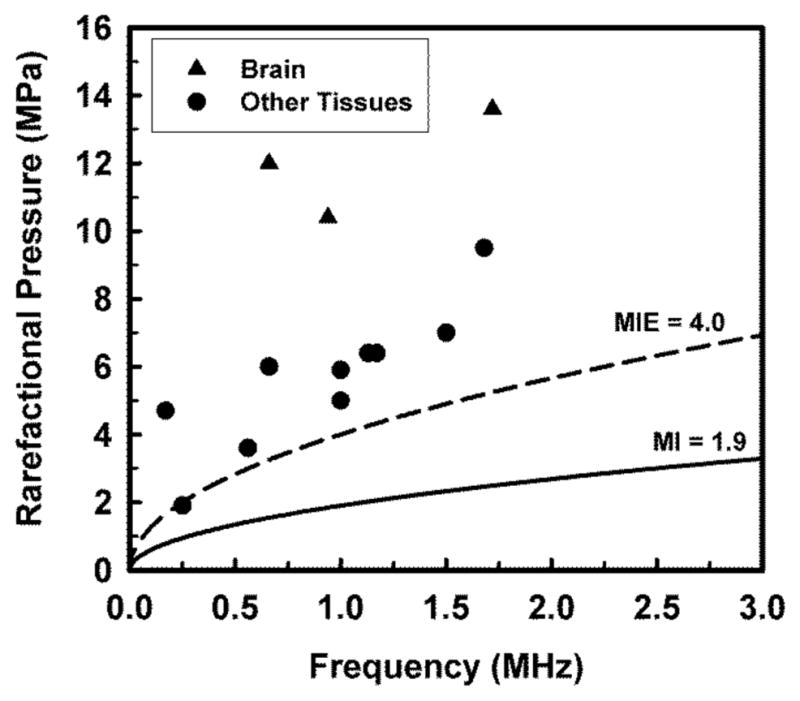
Best estimates of in situ rarefactional pressure shown in Table 1. Triangles and circles indicate values for brain and all other tissues, respectively. Curves delineate pressures calculated for the maximum value of the MI in the FDA’s guidance for track 3 devices (solid curve, labeled MI = 1.9) and an effective mechanical index of 4.0 (dashed curve, labeled MIE = 4.0).

5 Imaging Scenarios Excluded From Consideration for CIP

5.1 Tissues Known to Contain Gas Bodies

Evidence from in vivo animal research shows that mechanical bioeffects can occur in tissues containing gas bodies at outputs associated with in situ exposure levels well below an MI of 1.9. Two situations of concern have begun to be elucidated. First, the lung is susceptible to pulmonary hemorrhage induced by diagnostic ultrasound⁵⁵ or laboratory pulsed-ultrasound exposure approximating diagnostic ultrasound.²⁸ This effect is thought to be due to the interaction of the pulses with the alveolar gas. Similar effects are seen near bowel gas, which are discussed in the fetal imaging section below. Second, microbubbles in ultrasound contrast agents can nucleate ultrasonic cavitation during contrast-enhanced diagnostic ultrasound, leading to injury of tissue capillaries.⁹⁸ Both of these effects appear to have threshold output levels for a given set of imaging conditions. Below the threshold, the risk appears to be negligible, while the extent and severity of the effects increase rapidly with increasing output above the threshold.

Lung Thresholds

Ultrasound induction of pulmonary hemorrhage may be characterized by threshold output pressure amplitudes for various clinical ultrasound frequencies and other ultrasound parameters. Thresholds for different animals and exposure conditions are similar and appear to increase with ultrasound frequency. Average in situ thresholds range from about 0.54 MPa at 1 MHz (MI = 0.54) to about 1.3 MPa at 4 MHz (MI = 0.63).⁹⁹ However, some studies in mice and pigs using laboratory exposure systems indicated thresholds equivalent to MI = 0.3–0.4.¹⁰⁰ A recent study in rats found a threshold of about MI = 0.44 for diagnostic ultrasound at 7.6 MHz.⁵⁵ These empirical data have a considerably different relationship between the threshold for damage and the MI, suggesting that the development of a lung-specific MI would be appropriate.

Ultrasonic Contrast Agent Thresholds

The induction of capillary hemorrhage by contrast-enhanced diagnostic ultrasound may be variable depending on the specific tissue, contrast agent, and ultrasound mode. Little information is available to provide specific thresholds for all situations. However, testing with presently available agents seems to show comparable bioeffects risks for different agents and tissues. Studies of muscle tissue have shown thresholds of about MI = 0.4 for low diagnostic ultrasound frequencies,⁹⁸ including rat spinotrapezius muscle at 2.3 MHz¹⁰¹ and rat heart at 1.7 MHz using the highest output level tested without capillary hemorrhage, 0.54 MPa, as the threshold.¹⁰² One study of glomerular capillary hemorrhage in rat kidney indicated that thresholds were approximately proportional to 0.5 MPa times frequency from 1.5–7.4 MHz.¹⁷ This frequency dependence is stronger than that incorporated into the MI by an additional square-root of the frequency. The World Federation for Ultrasound in Medicine and biology (WFUMB) and European Federation of Societies for Ultrasound in Medicine and Biology (EFSUMB), in coordination with the AIUM, recently issued a consensus statement on the use of contrast enhanced diagnostic ultrasound, which addresses both recommended output levels and the use of the ALARA principle in this setting.¹⁰³

Given the reported potential for bioeffects in tissues known to contain gas bodies described above, and the continuing efforts of the bioeffects community to address these concerns, these tissues have been excluded from consideration for CIP as discussed herein.

5.2 Fetal Imaging

There are reports of increased fetal activity during diagnostic ultrasound imaging, which have been attributed to radiation forces on the fetal head or auditory structures at PRFs within the auditory frequency range.¹⁰⁴ Although this phenomenon has not been considered deleterious,¹⁰⁴ the radiation forces generated by ARFI pulses are applied using pulse durations 1–2 orders of magnitude longer than those associated with conventional B-mode/Doppler imaging. The impact of these longer-duration pulses on fetal activity is currently unknown.

In addition, while there is a body of literature indicating that ultrasound exposure of air-filled lung and intestine at diagnostic output levels can be associated with localized hemorrhage, fetal tissues do not contain preexisting cavitation nuclei. There are no confirmed experimental studies with laboratory animals showing a direct association between an adverse fetal biological effect and nonthermal mechanisms from exposure to diagnostic ultrasound output levels.¹⁰⁴ Further, in studies of pregnant mice, Hartmann et al¹⁰⁵ applied 10 lithotripter pulses at a peak positive pressure amplitude of 20 MPa, far exceeding diagnostic levels, resulting in extensive hemorrhage in the air-filled maternal lungs, but there was no observable gross hemorrhage in the fluid-filled fetal lungs. Similar findings were reported for murine fetal intestine,¹⁰⁶ suggesting that CIP as discussed herein, specifically in the context of the lack of preexisting cavitation nuclei in fetal imaging, would not be associated with elevated risk due to cavitation.

However, there are reports of vascular damage in murine fetuses near developing bone for acoustic output exceeding diagnostic levels but within the range of CIP proposed herein, albeit for a longer imaging duration. In lithotripter fields with amplitudes less than 1 MPa, hemorrhages were reported near developing bone in the head, limbs, lung, and ribs; no vascular damage was observed in murine fetuses exposed at a gestation stage prior to bone formation.¹⁰⁷ In pulsed ultrasound, fetal hemorrhagic damage near bone interfaces in late-gestation mice was reported for 3-minute exposures to 1 MHz, 10-microsecond, 100-Hz PRF beams with a threshold p_r of 2.5 MPa, which corresponds to an MIE of 2.5.¹⁰⁸ Recently, several additional reports have suggested cause for concern regarding fetal imaging. Exposure of chick brain to pulsed Doppler ultrasound (MI = 0.48, I_SPTA = 576 W cm⁻²) for 4 or 5 minutes at day 19 of incubation was reported to impair memory in chicks at day 2 following hatching.¹⁰⁹ Rat fetuses exposed to standard 2-dimensional imaging (13 MHz, MI = 0.71, I_SPPA = 222.4 W cm⁻²) for from 1 to 4 sessions of 45 to 55 seconds each on different days of gestation exhibited changes in the expression of some genes, most notably those implicated in developmental signaling pathways.¹¹⁰ Prenatal exposure of rat fetuses to B-mode ultrasound (2.89 MHz, MI = 1.1, spatial-average pulse-average intensity [I_SAPA] = 157 mW cm⁻²) for 1 or 2 hours per day for 9 days reportedly increased the permeability of the blood-brain barrier on postnatal day 10 but not later.¹¹¹ The acoustic mechanism responsible for these bioeffects is not yet understood.

Taken together, these findings suggest that fetal imaging should be excluded from consideration for CIP until further data are available.

6 Potential Clinical Benefit of CIP in Nonfetal Tissues Not Known to Contain Gas Bodies

Among the new imaging techniques that often approach the maximum recommended acoustic output levels are harmonic imaging modes¹¹² and ARFI-based elasticity imaging modes.^113,114 In a subset of patients, the diagnostic information obtained with these modalities can be limited by poor image quality. The causes can be wide ranging, including decreased signal strength due to intervening tissue attenuation and increased noise generally attributed to clutter/reverberation and phase aberration. Many creative approaches that operate within existing output guidelines have been developed to address poor image quality, including, eg, synthetic aperture imaging, compounding, and tissue harmonic imaging (see below). However, because of concerns regarding FDA clearance, systems have not been engineered to exceed the established guidelines, and there are limited data available exploring the potential benefits of imaging in this output regime. Initial discussion and findings for 2 imaging modes that have the potential to benefit from elevated output are discussed below.

6.1 B-Mode/Tissue Harmonic Imaging

Tissue harmonic imaging (THI) involves acoustic transmission at one frequency and image formation at the second harmonic (twice the transmission frequency).¹¹⁵ The advantages of THI are based on improvements in image quality in the presence of phase aberration and clutter, and since its introduction in the late 1990s, this imaging mode has become ubiquitous in clinical imaging. However, due to the relatively weak signal as compared to the fundamental frequency (typically −20 dB), THI modes often have limited depth penetration in many imaging scenarios.

For both conventional B-mode and harmonic imaging, higher transmit power will increase the scattered signal level, thus increasing the signal-to-noise ratio (SNR) and concurrently increasing the depth of penetration. For conventional B-mode imaging, however, the predicted gains are not significant: in one analysis, only a 6% increase in depth of penetration is estimated for a 40% increase in transmit intensity.¹¹⁶ For harmonic imaging, the improvement with increased transmit power can be appreciable, since the production of harmonics is proportional to the square of the pressure at the fundamental frequency of the transmit wave.¹¹⁵ Thus, a 3-dB increase in the fundamental will result in a 6-dB increase in harmonic intensity.

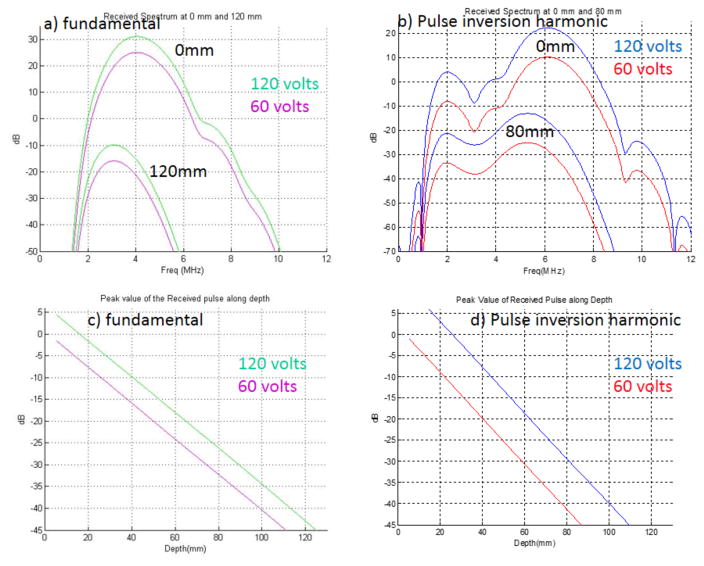
The amount of harmonic that is produced and eventually received by the transducer is dependent on the transmit power, the focal zone location, the distance the wave travels inside the tissue, the transducer bandwidth, system signal processing, and the tissue properties. Figure 4 provides a comparison of simulations run for a typical curvilinear abdominal imaging array, operating in fundamental (a and c) and pulse-inversion harmonic modes (b and d).

Figure 4.

a (fundamental) and b (THI pulse inversion), The two sets of curves represent the simulated (full-wave propagation) spectral content from a typical curvilinear array [center frequency = 3.8 MHz (a), 3.0 MHz (b)] at 0 mm (top set) and then at 12 (or 8) cm of depth (bottom set) after propagating through an attenuating medium (0.5 dB cm⁻¹ MHz⁻¹, plus 1.3 dB cm⁻¹ MHz⁻¹ at skin line). For each set, the green (blue) line is the received signal spectra with 120-V transmit, and the pink (red) line is the received signal spectrum with 60-V transmit. The bandwidth difference between the depths is about 0.25 MHz for the fundamental and 1 MHz for the harmonic sequence. c and d, Corresponding peak value of the received pulse as a function of depth for the fundamental (c) and THI (d) cases. Assuming signals below −45 dB will not be detected, these images indicate that a 100% increase in transmit voltage leads to a 1.25-cm (12%, fundamental) and 2.25-cm (25%, THI) increase in depth of penetration. Data provided by Fujifilm SonoSite.

Increasing the transmit voltage causes more waveform distortion at any given depth, leading to more harmonic generation. Figure 4 shows that with a 6-dB increase in transmit voltage, there is a 6-dB increase in the fundamental and a 12-dB increase in THI signal at all depths. In addition, assuming −45 dB as the minimum detection level, the corresponding increases in depth of penetration are 12% (fundamental) and 25% (THI), with the increased depth of penetration for THI approaching that obtained with the lower transmit voltage in the fundamental mode. It was previously concluded that for B-mode imaging, a 6-dB increase in transmit voltage would not produce a dramatic improvement in either penetration or image quality.¹¹⁶ In contrast, for THI, a 6-dB increase in the transmit voltage may generate a detectable improvement in depth of penetration and image quality. It should be noted that these analyses did not consider phase aberration issues, which are more detrimental for fundamental imaging than THI; thus, it may be that increased transmit voltage will have additional benefit for THI. This finding supports the hypothesis that increased acoustic output in the context of harmonic imaging could have significant clinical benefit. However, controlled studies are needed to determine the magnitude of the improvement.

6.2 Acoustic Radiation Force–Based Imaging

Recently, ARFI-based elasticity imaging methods developed in research laboratories have become commercially available. These tools employ focused “pushing pulses” that generate acoustic radiation force in the tissue and monitor the resulting tissue dynamic displacement response with conventional ultrasonic motion-tracking methods. The tissue displacement magnitude is on the order of microns. Both the displacement magnitude and the speed of the shear wave propagation away from the pushing location are related to the viscoelastic tissue properties; thus, these modalities provide an additional contrast mechanism that is adjunctive to the information provided by B-mode imaging.⁸ Initial studies from early adopters have reported promising findings for a wide variety of clinical applications, including, for example, noninvasively staging liver fibrosis (Virtual Touch [Siemens],¹¹⁷ SWE [SuperSonic Imagine,¹¹⁸ ElastPQ [Philips]), and breast lesion characterization (SWE,¹¹⁹ Virtual Touch¹²⁰).

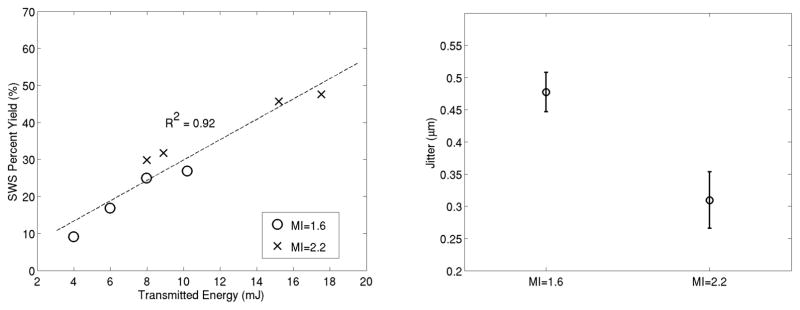
However, these tools have been developed within the current guidelines for MI and TI, and limitations are being identified that might be alleviated with the use of CIP. Studies routinely report depth penetration limitations and exclude patients with hepatic lesions deeper than 6–8 cm¹²¹; technical failure and unreliable measurement rates for liver stiffness have been reported to increase both with an elevated patient body mass index (BMI, a measure of obesity)^122,123 and in the presence of significant hepatic fibrosis.^118,122 Further, most protocols report median values from 10–12 successful replicate measurements,¹²⁴ leading to increased time and repeated measurements when technical failures occur. While studies are required to determine the causes of the failures in these different scenarios, a leading hypothesis is that limited tissue displacement magnitude is a major contributing factor, which might be alleviated with CIP. Preliminary results from an ongoing study exploring this issue suggest that the number of technically successful measurements increases, and the displacement estimation jitter (noise) decreases, when using CIP (Figure 5).

Figure 5.

Left, Percentage of successful shear wave speed measurements (8 attempts/patient/energy level) as a function of transmit energy level (E = transmit voltage²/element impedance) from 22 patients with a range of liver fibrosis stages and BMIs (E = 4 mJ is typical for current commercial systems). Right, Shear wave displacement estimation noise level (jitter) in these sequences obtained using harmonic imaging as a function of MI level. Note the increased yield and decreased jitter levels associated with CIP in these data. Data provided from an ongoing IRB-approved study at Duke University.¹²⁵

While noninvasive liver stiffness measurement systems are available that do not employ acoustic radiation force, these systems are also challenged by the obese population. The FibroScan system, which noninvasively measures liver stiffness using 1-dimensional ultrasound and an external vibration source, suffers from measurement failure and unreliable estimates in obese subjects.¹²⁶ Another alternative is magnetic resonance elastography (MRE).¹²⁷ However, MRE generally requires a separate clinic visit and considerable cost as compared to ultrasonically based shear wave methods, and it is not uncommon for morbidly obese patients to be excluded from MRE when they cannot fit inside the imaging apparatus. The development of ARFI-based methods that successfully characterize hepatic disease in the obese patient population thus remains a worthy goal, which these initial data suggest would be fostered by the use of CIP.

7 Discussion

The scientific rationale for the assumptions employed during the development of the MI is discussed in section 2.2. It is shown that if more accurate assumptions were employed, the following changes would be appropriate. First, in most soft tissues, any bubble that is present will likely be surrounded by viscoelastic material rather than water, and in this case, the threshold for inertial cavitation increases by a factor of 2 or more at all frequencies. Second, in contrast to the assumed single-cycle pulse duration, pulses of several hundred acoustic periods are typically employed by ARFI methods, and in soft tissues, although longer pulse durations are associated with decreased thresholds for inertial cavitation, they remain within 95% of those at one period. Taken together, these findings suggest that ignoring the effects of pulse duration remains reasonable under the assumption of the presence of a preexisting bubble, while the predicted threshold (if determined by safety, rather than preexisting levels from 1976) might be doubled. Third, the frequency dependence of the threshold for inertial cavitation in viscoelastic materials is theoretically shown to be better modeled by a power of 0.75, and experimental evidence of cavitation-based capillary damage in the presence of contrast agents suggests that a power of 1.0, rather than 0.5, more accurately predicts a threshold for this bioeffect. Thus, changing the frequency dependence in Equation 1 could be justified.

However, while modifying Equation 1 per the above findings (specifically increasing the power of the frequency dependence and development of a more accurate derating scheme) could potentially provide more accurate predictions of in situ parameters, the FDA guidelines are based on calculating a threshold within preexisting maximum recommended levels. Any modifications to the governing equation would necessarily involve recalculating the preexisting levels as well.

One strength of the MI, as currently implemented, is that it provides a valuable design parameter to which existing ultrasound systems have been optimized. However, there is a large safety margin between the guidelines based on preexisting levels determined using the MI formulation and the threshold values that are reported in the literature for cavitation-mediated bioeffects in tissues not known to contain gas bodies. From an absolute safety standpoint, the literature summarized in section 4 clearly supports the use of CIP in these tissues, within the limits of Table 1. This raises the question: Why is the disparity between absolute safety thresholds and the regulatory guidelines so large? First, the regulatory reference to preexisting levels is based on the absence of reported bioeffects prior to 1976, rather than observation of bioeffects at these preexisting levels. Second, Equation 1 presupposes the existence of cavitation nuclei; in tissues not known to contain gas bodies, this model appears to be invalid. It is noteworthy that the likelihood of detection of spontaneously nucleated bubbles increases with increasing numbers of acoustic periods at acoustic pressures near threshold values for a given tissue. The apparent disparity between the findings that pulse duration has a negligible effect on cavitation thresholds in soft tissues (Figure 1B) and the empirically reported dependence of cavitation in soft tissues on pulse duration (Table 1) likely arises from the fact that pr-existing cavitation nuclei of optimal diameter were not present in the experiments. Thus, we conclude that the observed thresholds in Table 1 must be related to either the presence of very small bubbles (R ≈ 10 nm) or the pressures required for spontaneous nucleation of bubbles, rather than cavitation of preexisting bubbles of optimal size.

Given the large safety margin provided by the current guidance, it seems reasonable to suggest that increasing the maximum recommended level given in the guidance would be warranted if a significant increase in diagnostic information could be obtained thereby. This might also be warranted if the recommended level could be related to the MIE, rather than the MI. However, only limited data are available to evaluate the potential clinical benefit, in large part because commercial systems are designed to the existing guidelines and thus do not enable such studies. In the context of harmonic imaging, while the predicted 25% improvement in depth penetration for this imaging mode (Figure 4) combined with additional possible improvements due to the benefits of harmonic imaging in overcoming phase aberration artifacts¹²⁸ could be significant, clinical studies are required to determine the impact of this improvement. In the context of ARFI/shear wave imaging, as shown in Figure 5, the use of CIP would lead to improved measurement success in difficult-to-image patients.¹²⁵ However, further studies are required to quantify the magnitude of the potential benefit. To facilitate this analysis, manufacturers would need to produce machines that would allow the needed clinical data to be gathered under investigational device exemption (IDE) with IRB approval, and studies would need to be designed implementing ALARA on an application-specific basis, including risk analyses in the unlikely event that cavitation might occur.

There is precedence for using elevated output levels in “difficult-to-image” scenarios in the diagnostic imaging community. A multitiered scheme regarding safety levels has been employed for magnetic resonance imaging as described in IEC 60601-2-33 and summarized below. The 3-tiered scheme is based on a specific absorption rate (SAR), which is related to radiofrequency power absorbed per unit of mass (W/kg):

Operating Mode	Whole-Body SAR, W/kg	Partial-Body SAR, W/kg	Head SAR, W/kg
Normal	2	2–10	3.2
First-level controlled	4	4–10	3.2
Second-level controlled	>4	>(4–10)	>3.2

The partial-body SAR limits scale dynamically with the ratio “exposed patient mass/patient mass.” In the first-level controlled mode, medical supervision is required. In the second-level controlled mode, explicit ethical approval from the IRB is required.¹²⁹ Note that the first 2 modes are presumably widely employed as needed, without specific IRB approval.

In the context of ultrasonic imaging, if clinical benefit is demonstrated using CIP for specific clinical applications under IDE with IRB approval, a similar 3-tier approach might be pursued. The normal operating mode would include any output up to the current guideline, MI = 1.9. In the first-level controlled tier, the MIE would be estimated in addition to the MI, and the MIE would remain below the MIE threshold values for cavitation reported in Table 1. This tier would require imaging be performed under medical supervision by a qualified practitioner. One possible implementation approach would be that CIP could be initiated by a button or foot pedal on the user interface. The CIP mode would be active only with positive action by the operator and restricted to some predetermined time limit, which would be related to the time required to obtain the required diagnostic information as dictated by the suggested IRB/IDE-governed studies. The CIP images would be stored for immediate or later analysis. The CIP mode acoustic output level could be varied, or could be fixed, but it could not exceed a value based on an MIE safety analysis. The need for and use of a real-time display of the MIE would need to be discussed.

If clinical benefit were demonstrated under tier 2, a third tier could be introduced, which would permit the thresholds in Table 1 to be approached but would also require imaging be performed under medical supervision by a qualified practitioner and IRB oversight. A method for identifying the boundary between levels 2 and 3, however, is not obvious. Manufacturers typically employ a self-imposed margin of 15%–30% below FDA-recommended guidelines when establishing the output for diagnostic scanners (thus, most systems do not currently employ outputs exceeding MI = 1.6). This allows for probe variability, system variability, and measurement uncertainty. Choosing a lower target value might also be done by a manufacturer to facilitate lower sample rates for acoustic testing. If we arbitrarily select a safety margin of 20% with respect to the minimum MIE in Table 1 for the MHz range (5.0), this leads to an MIE of 4 for the threshold between the two investigational output levels. In addition, one could consider including pulse duration or duty cycle dependencies for the third tier. For all of the proposed tiers shown in the table below, an additional constraint would be that the TI values would need to be within current guidelines.

Operating mode	MI
Normal	MI ≤1.9
First-level controlled	MIE ≤4
Second-Level controlled	MIE >4

It is important to note that while these recommendations are based on all of the evidence available, the extent of that evidence is rather limited. There is a need for information on several parameters affecting cavitation thresholds in tissue. First and foremost among these is the value of the threshold itself in each of several frequently scanned tissues not known to contain gas bodies. These include heart, liver, kidney, and brain. Most of the information currently available has been obtained in the range of 0.66–1.72 MHz (see Table 1), so extending this range to higher frequencies is paramount. Second, the pulse durations shown in Table 1 vary widely, and there is an obvious need for more uniformity among the results. Third, there is also significant variation in the pulse repetition frequency and the total number of pulses among the exposures used in the studies compiled for Table 1. Greater consistency in the exposure conditions used by various laboratories would allow more thoughtful extrapolation to other conditions that have yet to be investigated or that cannot be studied at all. Fourth, there is also a need to standardize the definition of threshold and the technique used in its determination. The range of the technical details to be addressed in even the simplest approach can be so broad that ensuring comparability across laboratories can become a daunting task. Finally, whatever technique is adopted, it must be sufficiently simple as to allow the greatest number of researchers to participate in the acquisition of the desired data. With this information in hand, the creation of a rigorous, science-based safety index for cavitation-induced adverse biological effects would be possible.

Based on established guidelines and historical experience, there is a widely held perception that diagnostic ultrasound is safe. Although implementation of the ALARA principle is recommended for all ultrasonic imaging examinations, the presumed safety of the modality can lead to laxity among the clinical community in consideration of risk. If methods are introduced enabling CIP for specific applications, it would be possible that the uninformed user might employ CIP in an inappropriate setting (eg, in the presence of contrast agents). As with all diagnostic imaging scenarios, this risk would need to be balanced against the potential benefit of providing access to the imaging studies using CIP for their intended purpose (ie, to obtain diagnostic information that could not otherwise be obtained in difficult-to-image patients).

Taking into consideration the paucity of data on which these recommendations are based, it is deemed prudent to exclude certain classes of patients and certain structures in potential patients during the period of exploratory investigations. While this may deny potentially beneficial medical imaging to some, this represents a straightforward application of the age-old dictum, “First, do no harm.” Among the obvious classes of patients to avoid are embryos, fetuses, and neonates and also any subject who has been given a microbubble contrast agent within the preceding 24 hours. Structures that are potentially sensitive to CIP are lung, intestine, and any other tissue suspected of harboring undissolved gas, eg, tissues having active infections. Additionally, because no data are available with respect to ophthalmic imaging with MI values above 0.23, further studies would be required to assess the potential sensitivity of the eye. The precise manner by which to avoid scanning such tissues is best left to the skilled user, but there is a significant need for education and understanding of the safety issues involved with CIP before its use can be contemplated. Although the guidelines recommended above are considered to encompass a robust safety margin, this is an investigational procedure that may involve a level of risk that is greater than is usually the case for diagnostic ultrasound. Therefore, there is a very real need for assessing the risk-to-benefit ratio on a clinical application-specific basis, assessing the MIE as well as the MI, and for taking the application of the ALARA principle seriously.

Given the lack of an accepted standard for determination of MIE and the existing challenges for the various investigational methods, at this time, it seems prudent to recommend that studies should be designed to report both the MI and an estimate of MIE. Ideally the MIE would be estimated consistently between reports.

The safety of CIP exposures may be assessed in terms of 2 primary mechanisms, mechanical and thermal. Mechanical effects can be divided further into cavitational and noncavitational (eg, radiation force, radiation torque, and acoustic streaming). Some studies have posited that noncavitational effects are a source of stimulation in tissues with apparently elevated sensitivity (ie, brain and cardiac tissue), although these effects are generally reversible. A device’s ability to induce damage by a cavitation mechanism is determined almost entirely by the frequency and maximum rarefactional pressure amplitude in vivo. This is because cavitation is a threshold phenomenon, and if the output level of any device never exceeds the threshold, then the risk from exposure at any level below the threshold is negligible. With regard to thermal mechanisms, safety can be assessed as is done currently for any other imaging mode, ie, by use of the maximum time-average intensity and the TI, where the FDA guidance requires that an explanation be provided for a TI value greater than 6.0.⁵ If deemed necessary for particular exposure conditions for elastography, these metrics may be augmented with an analysis of the transient temperature rise associated with ARFI bursts, which would be particularly important where bone and air interfaces are involved, as reported by Liu et al.¹³⁰

8 Summary/Consensus Statements

In this article, we summarized the current formulation of the MI and presented evidence supporting modifications of some assumptions under the current formulation. Further, we summarized the existing experimental evidence for cavitation thresholds in the literature in nonfetal tissues not known to contain preexisting gas bodies. We discussed the need for and challenges associated with accurate estimation of in situ exposures and the use of the MIE as a metric to quantify such estimates. In addition, we discussed 2 imaging methods that might benefit from CIP and the lack of data available to enable evaluation of potential clinical benefits. Through this analysis, we conclude the following:

1. From a mechanistic point of view, the probability that exposure to diagnostic ultrasound (emitted by devices cleared under current track 3 guidelines) will induce cavitation in tissue not known to contain gas bodies is essentially zero, except in very unusual cases of long fluid paths or specific inhomogeneous media as discussed in section 3.

2. Given the generally large safety margin provided by the current guidance for tissues not known to contain gas bodies, it seems reasonable to suggest that exceeding the maximum MI level given in the guidance⁵ could be warranted without concern for increased risk of cavitation in these tissues, if p_r.3 is approximately equal to the actual value of p_r in situ, ie, when the MI is approximately equal to the MIE.

3. At this time, there is a paucity of data/studies investigating the potential increase in diagnostic information that might be afforded by the use of CIP.

4. Professional societies, manufacturers, academics, and other interested parties should cooperate and work to enable studies of investigational use of CIP when there is reasonable expectation of substantial clinical benefit.

5. Studies investigating CIP should report both the MI and an estimate of the MIE.

6. A standard method for MIE estimation is needed that accounts for acoustic nonlinearity and attenuation.

7. The maximum MIE for investigational CIP studies should be determined by a risk-benefit analysis on an application-specific basis.

8. In keeping with the recommendations of IEC 60601-2-37 regarding risk-benefit analyses, and the current knowledge pertaining to nonfetal tissues in the absence of known gas bodies (eg, Table 1), we recommend investigation of MIE levels up to 4.0 for initial studies evaluating CIP in these tissues when there is reasonable expectation of substantial clinical benefit.

9. Based on: (1) increased risk of cavitation, (2) increased potential sensitivity to CIP, (3) risk of harm if cavitation were to occur, or (4) lack of sufficient data to assess risk, the following specific human tissues require further study and justification before applying the above recommendations on CIP for diagnostic imaging:

   1. Tissues known to contain gas bodies (eg, lung, intestine, and regions with infection);

   2. Tissues that contain ultrasound contrast agents;

   3. Fetal tissues;

   4. Ophthalmic tissues; and

   5. Tissues known to be sensitive to ultrasonic stimulation, such as the CNS and cardiac tissues.

Appendix A: Summary of IEC TS 61949

Uncertainties in the estimation and control of in situ ultrasonic output values are exacerbated as output pressures increase due to effects associated with nonlinear acoustic propagation in water, the standard medium used for diagnostic medical ultrasound acoustic output measurements due to its ready availability and maintainability, and the repeatability of measurements made using it (IEC 62359, IEC 62127, and AIUM/NEMA measurement standards).

These nonlinear effects include harmonic generation, with subsequent increased frequency-dependent absorption, and waveform saturation and distortion, with accompanying asymmetry of the compression and rarefaction pressure half-cycles.²⁴

These effects also occur in tissue and are made use of in ultrasound systems’ tissue harmonic modes. In fact, the nonlinearity parameter, β, for many tissues is higher than β for water (= 5.2). However, the overall effects are less severe in tissue than in water, being more quickly balanced by the increased attenuation in tissues. A measure of this balance is the Goldberg number (a nondimensional number proportional to the ratio of the nonlinearity parameter to the attenuation coefficient), which has much higher values for water than tissue.³³

With increasing pressure amplitude and spectral range, measurement uncertainty increases due to measurement equipment bandwidth and response uniformity limitations and due to migration toward the transducer of the apparent positions of maximum pressure and intensity. As saturation and nonlinear absorption losses increase, the accuracy of traditional fixed-attenuation mathematical tissue models declines.

IEC TS 61949³⁴ is a technical specification providing a standard scheme for quantifying a threshold for the onset of nonlinear distortion and loss. It specifies a method for scaling up measurements from the “quasilinear” region in water to the nonlinear region so that tissue attenuation models can provide more accurate results. The scaling up is accomplished by multiplying quasilinear values, measured at the point of interest (eg, the focal point), by the ratio of mean source-pressure values, $\frac{p_{\mathrm{s},\text{high}}}{p_{\mathrm{s},\text{quasi-linear}}}$, measured close to the transducer radiating surface, where effects of nonlinear propagation have not yet been generated.

The local distortion parameter, σ_q, defined and used by IEC TS 61949, is expressed as:

$${\sigma }_{\mathrm{q}}=zp\frac{2\pi f_{\mathit{awf}}\beta }{\rho c^3}\frac{1}{\sqrt{F_a}}.$$

The units of the constituent parameters are arranged to make σ_q nondimensional: z is distance; p is acoustic pressure; f_awf is acoustic center frequency; β is the nonlinearity parameter; ρ is density; c is the acoustic propagation speed; and F_a is the “local area factor”:

$$F_a=\sqrt{\frac{0,69A_{\mathit{SAeff}}}{A_{b,-6dB}}},$$

where A_SAeff and A_{b, −6dB} are, respectively, the effective area of the transmitting aperture and the −6-dB area of the ultrasound beam at depth, z.

σ_q is a simplification of the acoustic propagation parameter, σ_m, introduced by Bacon,¹³¹ and clearly shows nonlinear distortion increasing with depth, frequency, pressure, and β and decreasing with density, sound speed, and focusing gain.

Measurements following a protocol such as listed in IEC TS 61949 may require additional time or effort and may create overestimates of actual tissue values. However, such measurement results may be more reproducible from lab to lab and between measurement equipment. Finally, in the present version (2007) of 61949, a σ_q value of 0.5 is designated the quasilinear threshold, above which scaled-up values are recommended. Proposed improvements to future versions of IEC TS 61949 include raising the σ_q value threshold to 1.0, to increase the SNR of estimates.

Appendix B: Summary of IEC TS 62556 Appendices E and F

Hybrid measurement/simulation approaches rely on a combination of low-amplitude hydrophone measurements in the linear propagation regime in conjunction with linear or nonlinear modeling. The hydrophone measurements, linear simulation models, and calibration methods are described in detail in Appendices E and F in IEC TS 62556.⁴³ Use of the same data in combination with nonlinear simulation can be found in Kreider et al.⁴² Details of these approaches can be summarized as follows:

1. Acoustic holography measurements in the linear propagation regime are made in water. For a source operating in CW mode, these measurements entail the scanning of a calibrated hydrophone over a planar region in front of the source to determine pressure magnitude and phase at many discrete points. For the more general case of a source generating a transient output, the relevant measurement at each point comprises the full pressure waveform rather than just magnitude and phase. In both CW and transient regimes, the source must be repeatedly triggered for each measurement to produce the same focal geometry for which the MIE estimate is desired. Holography measurements can then be used to define a hologram of the full 3D sound field (ie, the “measured hologram”) and can be used to mathematically reconstruct the pattern of vibrations on the surface of the source (ie, the “source hologram”). Backward projection methods for reconstructing the source hologram include the Rayleigh integral⁴⁰ and the angular spectrum or Fourier method.⁴¹ The main use of this method is to employ the hologram for forward projection or the simulation of the forward-propagating field in water or an in situ configuration of tissues.

2. The source hologram can be used as a boundary condition for a forward projection model that accounts for nonlinear propagation and realistic tissue properties to calculate the acoustic field in situ. However, the source hologram was determined based on linear measurements made at a single output power level. To provide suitable boundary conditions for the forward projection model at the desired output level, the pattern of vibrations represented by the source hologram should be scaled. To determine this scaling factor, the linear pressure magnitude at a near-source location can be measured at both the output level used for holography measurements and the output level at which the MIE is desired. The measurement location ideally should be near a local pressure maximum, while also being close to the source to minimize nonlinear propagation effects. Pressures measured at this near-source location are presumed to be proportional to the actual pressure generated at the source’s surface, thus providing a suitable metric for scaling the linear source hologram from step 1.

3. Using the scaled source hologram as a boundary condition, the nonlinear acoustic field in an arbitrary medium with known properties can be calculated. Even nonlinear modeling of the full 3D field generated by an array transducer is possible, though computationally challenging.^128,132 Several models of nonlinear acoustic propagation have been validated in medical applications.^{41,45,133–135} These are most often based on the KZK¹³⁶ or Westervelt equations.¹³⁷

4. Experimental conditions of focusing in situ can be very different in terms of propagation path and acoustic parameters of tissue, and full 3D nonlinear simulations for each situation can be challenging. A nonlinear derating method^35,138,139 can be applied to predict nonlinear HIFU fields in situ for planning exposure protocols based on the results of holography measurements and nonlinear modeling in water. The method relies on scaling the source outputs to compensate for attenuation in tissue and the difference in nonlinearity of tissue and water. The method has been shown to provide accurate results for strongly or moderately focused transducers.