A feasibility study of singlet oxygen explicit dosmietry (SOED) of PDT by intercomparison with a singlet oxygen luminescence dosimetry (SOLD) system

Abstract

An explicit dosimetry model has been developed to calculate the apparent reacted ¹O₂ concentration ([¹O₂]_rx) in an in-vivo model. In the model, a macroscopic quantity, g, is introduced to account for oxygen perfusion to the medium during PDT. In this study, the SOED model is extended for PDT treatment in phantom conditions where vasculature is not present; the oxygen perfusion is achieved through the air-phantom interface instead. The solution of the SOED model is obtained by solving the coupled photochemical rate equations incorporating oxygen perfusion through the air-liquid interface. Experiments were performed for two photosensitizers (PS), Rose Bengal (RB) and Photofrin (PH), in solution, using SOED and SOLD measurements to determine both the instantaneous [¹O₂] as well as cumulative [¹O₂]_rx concentrations, where [¹O₂]_rx = (1/τ_Δ) · ∫[¹O₂]dt. The PS concentrations varied between 10 and 100 mM for RB and ~200 mM for Photofrin. The resulting magnitudes of [¹O₂] were compared between SOED and SOLD.

1. INTRODUCTION

Improving dosimetry for photodynamic therapy (PDT) is an ongoing goal for use in the treatment of cancer and other localized diseases. PDT is a multi-faceted, dynamic process that involves the interactions of light, photosensitizer, and ground state oxygen (³O₂), that create reactive singlet oxygen (¹O₂) in a type II process or other reactive oxygen species (such as O₂^−•) in a type I process [1]. A macroscopic singlet oxygen explicit dosimetry (SOED) model has been previously developed and studied for various sensitizers [2–12]. The use of SOED can be advantageous due to the difficulty of measuring the singlet oxygen luminescence signal in vivo due to its short lifetime of 30–180 ns [13, 14]. Furthermore, PDT dose alone is not sufficient as a dosimetric quantity, particularly in hypoxic environments that are created with high fluence rate treatments. SOED was compared to a direct dosimetry method, singlet oxygen luminescence dosimetry (SOLD) in photosensitizer solution.

2. MATERIALS AND METHODS

2.1 SOED Model in Phantoms

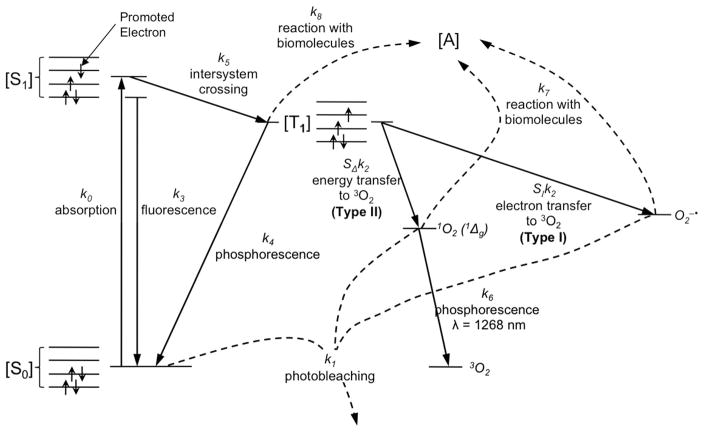
Singlet oxygen produced during illumination was calculated using an explicit dosimetry model. Based on both type I and type II processes modeled in figure 1, a set of coupled differential equations have been established for the photochemical reactions [11, 12, 15–17]:

$$\frac{d[S_0]}{dt}=-k_0[S_0]-k_{12}[{{}^{1}O}_2]([S_0]+\delta )-k_{11}[O_2^{-•}]([S_0]+\delta )+k_2[T_1][{{}^{3}O}_2]+k_3[S_1]+k_4[T_1]$$ (1)

$$\frac{d[S_1]}{dt}=-(k_3+k_5)[S_1]+k_0[S_0]$$ (2)

$$\frac{d[T_1]}{dt}=-k_2[T_1][{{}^{3}O}_2]-k_4[T_1]+k_5[S_1]-k_8[T_1][A]$$ (3)

$$\frac{d[{{}^{3}O}_2]}{dt}=-S_{\mathrm{\Delta }}{k}_2[T_1][{{}^{3}O}_2]-S_I{k}_2[T_1][{{}^{3}O}_2]+k_6[{{}^{1}O}_2]$$ (4)

$$\frac{d[{{}^{1}O}_2]}{dt}=-k_{12}[{{}^{1}O}_2]([S_0]+\delta )+S_{\mathrm{\Delta }}{k}_2[T_1][{{}^{3}O}_2]-k_6[{{}^{1}O}_2]-k_{72}[A][{{}^{1}O}_2]$$ (5)

$$\frac{d[O_2^{-•}]}{dt}=-k_{11}[O_2^{-•}]([S_0]+\delta )+S_I{k}_2[T_1][{{}^{3}O}_2]-k_{71}[A][O_2^{-•}]$$ (6)

$$\frac{d[A]}{dt}=-k_{72}[A][{{}^{1}O}_2]-k_{71}[A][O_2^{-•}]-k_8[T_1][A]$$ (7)

Figure 1.

Jablonski diagram for PDT. In type I reactions, the triplet photosensitizer will transfer an electron to ³O₂ react with molecular targets to produce radical species, or alternatively interact directly with the acceptor, [A], without oxygen mediation. In type II reaction, the energy is transferred from the triplet photosensitizer to ground state molecular oxygen (³O₂), creating reactive singlet oxygen (¹O₂).

With a focus on only the dynamic process of PDT in the time scale of a few seconds to hours, the time derivatives on the right hand sides of the equations for the excited singlet state photosensitizer, the triplet state photosensitizer, singlet oxygen, and superoxide anion (Eqs. (2), (3), (5), (6)) can be set to zero because these processes are known to be very fast (~μs or less). These can then be simplified to [11, 17]

$$[S_1]={\tau }_f\frac{\epsilon }{h\nu }\varphi [S_0],$$ (8)

$$[T]=\frac{{\mathrm{\Phi }}_t}{[{{}^{3}O}_2]+\beta }\frac{1}{k_2}\frac{\epsilon }{h\nu }\varphi [S_0],$$ (9)

$$[{{}^{1}O}_2]={\xi }_{II}{\tau }_{\mathrm{\Delta }}\frac{[{{}^{3}O}_2]}{[{{}^{3}O}_2]+\beta }\varphi [S_0],$$ (10)

$$[O_2^{-•}]={\xi }_I{\tau }_S\frac{[{{}^{3}O}_2]}{[{{}^{3}O}_2]+\beta }\varphi [S_0],$$ (11)

$$\frac{d[S_0]}{dt}=-\frac{[{{}^{3}O}_2]}{[{{}^{3}O}_2]+\beta }\varphi [S_0]([S0]+\delta ))({\xi }_{II}{\sigma }_{II}+{\xi }_I{\sigma }_I)-\eta \frac{1}{[{{}^{3}O}_2]+\beta }\varphi [S_0],$$ (12)

$$\frac{d[{{}^{3}O}_2]}{dt}=-\frac{[{{}^{3}O}_2]}{[{{}^{3}O}_2]+\beta }\varphi [S_0]({\xi }_{II}({\sigma }_{II}\left([S_0]+\delta \right)+k_{72}[A]{\tau }_{\mathrm{\Delta }})+{\xi }_I),$$ (13)

$$\frac{d[A]}{dt}=-\frac{[{{}^{3}O}_2]}{[{{}^{3}O}_2]+\beta }\varphi [S_0]({\xi }_{II}{k}_{72}[A]{\tau }_{\mathrm{\Delta }}+{\xi }_I)-\eta \frac{1}{[{{}^{3}O}_2]+\beta }\varphi [S_0],$$ (14)

where σ_II = k₁₂τ_Δ, σ_I = k₁₁ τ_S, τ_Δ = 1/(k₆+k₇₂[A]), τ_S = 1/k₇₁[A], τ_f = 1/(k₃+k₅), ${\xi }_{II}={\mathrm{\Phi }}_{\mathrm{\Delta }}\frac{\epsilon }{h\nu },{\xi }_I=S_I{\mathrm{\Phi }}_t\frac{\epsilon }{h\nu },\eta ={\mathrm{\Phi }}_t\frac{\epsilon }{h\nu }\frac{k_8[A]}{k_2}$, Φ_t=k₅/(k₃+k₅), and β = k₄+k₈[A]/k₂. It was assumed that σ_II([S₀]+δ) ≪ 1 and σ_I ([S₀]+δ) ≪ 1, which is true for this case. Here, Φ_Δ = S_ΔΦ_t is the singlet oxygen quantum yield in the solvent used (methanol for Photofrin phantoms and water for Rose Bengal phantoms), ε is the extinction coefficient at 523 nm, and h is Planck’s constant. The parameters used for the calculation in each phantom are summarized in Table 1. This model has been used in in vivo systems previously where k₇[A] ≫ k₆ [2–12]. In phantoms, the substitute for biological substrate ([A]) to interact with the reactive singlet oxygen generated in the photodynamic process is sodium azide (NaN₃), a well known singlet oxygen quencher. In the experiments performed without NaN₃, [A] = 0.

Table 1.

Summary of photophysical and photochemical parameters for Photofrin (PH) and Rose Bengal (RB) in vitro

Parameter	Definition	Photofrin	Rose Bengal
ε (cm−1 μM−1)	Photosensitizer extinction coefficient	0.0089 @523nm	0.059 @523nm
k0, ka @100mW/cm2 (s−1)	Photon absorption rate of photosensitizer as a function of photosensitizer concentration (in mM), k0 = εϕ/hν, for ϕ = 100 mW/cm2.	3.89 [1]	25.69 [1]
k12, kos (μM−1s−1)	Bimolecular rate for 1O2 reactions with ground-state photosensitizer	2.1×10−1 [2]	6.6×10−2 [2]
k2, kot (μM−1s−1)	Bimolecular rate of triplet photosensitizer quenching by 3O2	1.278×103 [3]	1.2×103 (1.2 – 1.6)×103 [20, 21]
k3, kf (s−1)	Fluorescence rate of first excited singlet state photosensitizer to ground state photosensitizer	2.9×107 [22]	2.12×108 [4]
k4, kp (s−1)	Phosphorescence rate of monomolecular decay of the photosensitizer triplet state	1.52×105 [5]	1.43×104 [5]
k5, kisc (s−1)	Intersystem crossing (ISC) rate from first excited photosensitizer to triplet state photosensitizer	4.94×107 [6]	6.36×108 [6]
k6, kd (s−1)	Spontaneous phosphorescence rate of 1O2 to 3O2	1.1×105 [7]	2.6×105 [7]
k72, koa (μM−1s−1)	Bimolecular rate of reaction of type II 1O2 with biological substrate [A]	2.35×102 [7]	2.58×101 [7]
β (μM)	Oxygen quenching threshold concentration $\frac{k_4}{k_2}$	11.9 [23]	11.9 [9]
δ (μM)	Low concentration correction	33 (33 – 150) [24]	33 [8]
ξII (cm2mW−1s−1)	Specific oxygen consumption rate ${\xi }_{II}={\mathrm{\Phi }}_{\mathrm{\Delta }}\frac{\epsilon }{h\nu }$	24.9×10−3 @ 523 nm	195.2×10−3 @ 523 nm
σII (μM−1)	Specific photobleaching ratio where σII = k12τΔ	1.0×10−6 [9]	2.5×10−7 [9]
g (mM/s)	Macroscopic maximum oxygen supply rate	0 [10]	0 [10]
Φt	Triplet quantum yield $\frac{k_5}{k_3+k_5}$	0.91 [25] (0.63 – 0.93) [17, 25–27]	0.75 in water [20, 28]
ΦΔ	Singlet oxygen quantum yield $S_{\mathrm{\Delta }}\frac{k_5}{k_3+k_5}$	0.25 in MeOH [29, 30] (0.12–0.56) [26, 31] [32] [29,30]	0.76 in vitro [33]
Φf	Fluorescence quantum yield $\frac{k_3}{k_3+k_5}\frac{A_{10}}{k_3}$, where A10 is spontaneous transition rate between S1 and S0.	0.16 [20]	0.08 [33]
τΔ (s)	Singlet oxygen lifetime $\frac{1}{k_6+k_7[A]}$, [A] = 0.	(9.4±0.2)×10−6 [11]	(3.8±0.3)×10−6 [11]
τf (s)	Fluorescence decay time $\frac{1}{k_3+k_5}$	(5.5±1.2)×10−9 [34]	1.18×10−10 [35]
τt (s)	Triplet state lifetime $\frac{1}{k_4+k_2[{{}^{3}O}_2]}$	(0.43±0.03)×10−6 [11]	(2.1±0.2)×10−6 [11]

^[1]Calculated based on value of ε and ϕ = 100 mW/cm²: k₀ = εϕ/(hν))

Photofrin: k₀ = (0.0089 μM⁻¹cm⁻¹) / (6.022×10¹⁴ cm²μM⁻¹) × (100 mW/cm²) / (3.80 ×10⁻¹⁶ mW s) = 3.89 s⁻¹

Rose Bengal: k₀ = (0.059 μM⁻¹cm⁻¹) / (6.022×10¹⁴ cm²μM⁻¹) × (100 mW/cm²) / (3.80 ×10⁻¹⁶ mW s) = 25.69 s⁻¹

^[2]Calculated based on value of σ that was fit to data (see Fig. 3 and 4) and measured τ_Δ: k₁ =σ/τ_Δ

Photofrin: k₁ = (2×10⁻⁶ μM⁻¹) / (9.4×10⁻⁶ s) = (2.1 ×10⁻¹ μM⁻¹s⁻¹)

Rose Bengal: k₁ = (2.5×10⁻⁷ μM⁻¹) / (3.8×10⁻⁶ s) = (6.6 ×10⁻² μM⁻¹s⁻¹)

^[3]Calculated based on measured value of τ_t: $k_{\mathit{2}}=({\tau }_t^{-\mathit{1}}-k_{\mathit{4}})/[{{}^{\mathit{3}}O}_{\mathit{2}}]$

Photofrin: k₂ = ((0.43×10⁻⁶ s⁻¹) − (1.52×10⁵ s⁻¹))/(170 μM) = 1.278×10³ μM⁻¹s⁻¹

^[4]Calculated based on the value of Φ_t and τ_f: k₃ = (1 − Φ_t)/τ_f

Rose Bengal: k₃ = (1 − 0.75) / (1.18×10⁻¹⁰ s) = 2.12×10⁹ s⁻¹

^[5]Calcualted based on assumed value of β: k₄ = β×k₂

Photofrin: k₄ = (11.9 μM) × (1.278×10³ μM⁻¹s⁻¹) = 1.52×10⁵ s⁻¹

Rose Bengal: k₄ = (11.9 μM) × (1.278×10³ μM⁻¹s⁻¹) = 1.43×10⁴ s⁻¹

^[6]Calculated based on value of k₃ and Φ_t: k₅ = Φ_t k₃/(1 − Φ_t)

Photofrin: k₅ = (0.63) × 2.9×10⁷ s⁻¹ / (1 − 0.63) = 4.94×10⁷ s⁻¹

Rose Bengal: k₅ = (0.75) × (2.12×10⁹ s⁻¹) / (1 − 0.75) = 6.36×10⁹ s⁻¹

^[7]Calculated based on fit to data in figure 5.

^[8]Assumed to be the same as that of Photofrin

^[9]Based on fit to the [³O₂] data when [A] = 0 (Figs. 3 and 4)

^[10]Due to absence of blood flow and reoxygenation in phantoms

^[11]Measured values from SOLD experiment when [A] = 0, i.e., without NaN₃.

For the type II photosensitizers (PH and RB) used in this study, η = 0 since there is no direct triplet interaction. [³O₂](t) and [S₀](t) can be solved by the coupled differential Eqs. (12) and (13). Assuming that [³O₂]₀ ≫ β and there is minimal photobleaching of the photosensitizer, i.e., σ_I ≈ σ_II ≈ 0, thus [S₀] = [S₀]₀ from Eq. (12), then Eq. (13) can be solved as

$$[{{}^{3}O}_2](t)={[{{}^{3}O}_2]}_0-\varphi [S_0]({\xi }_{II}({\sigma }_{II}({[S_0]}_0+\delta )+k_7[A]{\tau }_{\mathrm{\Delta }})+{\xi }_I)t={[{{}^{3}O}_2]}_0-\gamma \varphi [S_0]t$$ (15)

where γ = ξ_II (σ_II ([S₀]₀ + δ) + k₇[A]τ_Δ) + ξ_I = ξ_IIσ_II ([S₀] + δ) + ξ_I (when [A] = 0), is the PDT oxygen consumption rate per PDT dose rate and is 2.1×10⁻⁶ μM/s/(μMmW/cm²) for Photofrin and 4.1×10⁻⁶ μM/s/(μMmW/cm²) for RB for [S₀] = 50 μM. The expression of the photosensitizer([S₀]) can be solved by combining Eqs. (10), (11) and (12), regarless of the value of σ, to be

$$\frac{d[S_0]}{dt}=-\frac{{\sigma }_{II}}{{\tau }_{\mathrm{\Delta }}}\left([S_0]+\delta \right)[{{}^{1}O}_2]-\frac{{\sigma }_I}{{\tau }_I}\left([S_0]+\delta \right)[O_2^{-•}].$$ (16)

Thus the solution:

$$[S_0](t)=\left({[S_0]}_0+\delta \right)e^{-{\sigma }_{II}{[{{}^{1}O}_2]}_{rx}+{\sigma }_I{[O_2^{-•}]}_{rx}}-\delta \approx {[S_0]}_0-{\sigma }_{II}({[S_0]}_0+\delta ){[{{}^{1}O}_2]}_{rx}-{\sigma }_I({[S_0]}_0+\delta ){[O_2^{-•}]}_{rx},$$ (17)

where

$${[{{}^{1}O}_2]}_{rx}\equiv \frac{1}{{\tau }_{\mathrm{\Delta }}}{\int }_0^t[{{}^{1}O}_2]dt={\int }_0^t\frac{[{{}^{3}O}_2]}{[{{}^{3}O}_2]+\beta }\phi [S_0]dt$$ (18)

and

$${[O_2^{-•}]}_{rx}\equiv \frac{1}{{\tau }_S}{\int }_0^t[O_2^{-•}]dt={\int }_0^t\frac{[{{}^{3}O}_2]}{[{{}^{3}O}_2]+\beta }\phi [S_0]dt.$$ (19)

Oxygen measurements were compared with the modeled values of oxygen using both the full coupled differential equations (Eqs. (12)–(13)) as well as the simplified verion stated above (Eqs. (15) and (17)). In all our model, we have made the assumption that type I interaction is negligible, i.e., σ_I = 0 and ξ_I = 0.

Fluorescence spectra as well as absoroption spectra were used to determine the experimentally measured values of [S₀] and absorption properties to compare with expected calculated values.

2.2 SOLD Instrumentation

Singlet oxygen luminescence dosimetry was performed using a compact, fiber optic probe-based singlet oxygen luminescence detection system [18]. The near-infrared luminescence probe was coupled to a compact InGaAs/InP single photon avalanche diode (SPAD) detector. Samples were irradiated with a 523 nm wavelength pulsed-laser source coupled into the delivery fiber via a collimation package. Patterned time gating was used to limit the unwanted dark counts and eliminate the strong photosensitizer luminescence background. The luminescence signal of singlet oxygen at 1270 nm was confirmed through spectral filtering and lifetime fitting for Rose Bengal and Photofrin.

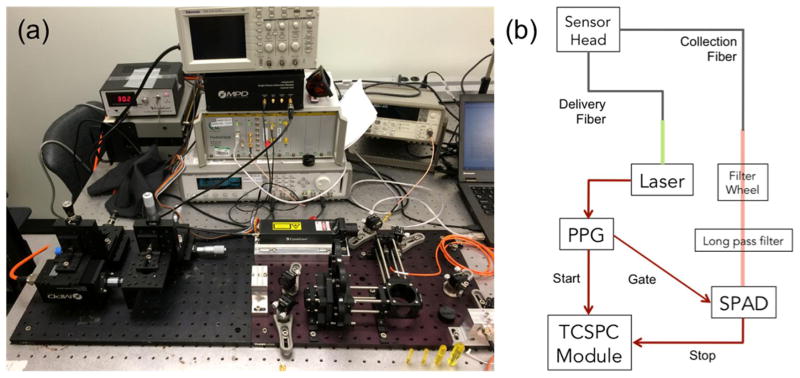
Figure 2 shows a photo and schematic of the experimental setup. A pulsed 523 nm wavelength laser with 10 ns pulses at a repetition rate of 18.2 kHz was coupled into the delivery fiber with a collimation package. The laser outputs an electrical signal that is sent to a programmable Pulse Pattern Generator (PPG). Each pulse generates outputs on two separate channels, each with pulse shape designed to match the intended input The first output is a single pulse sent to the ‘start’ channel of the time-correlated single-photon counter (TCSPC), while the second is a pattern of pulses sent to the SPAD control module. The SPAD is turned on for a pre-assigned time, only when the control module receives a pulse from the PPG.

Figure 2.

SOLD instrumentation setup (a) on an optical bench and (b) schematic diagram of the experimental arrangement. The 523 nm laser source is coupled into the delivery fiber with a collimation package. The laser outputs a synchronous signal that is sent to a programmable Pulse Pattern Generator (PPG). Light from the collection fiber is coupled out through another collimation package, directed through a filter wheel (FW) for the bandpass filter selection, and then a long pass filter. The fiber core is imaged onto the face of the SPAD detector.

2.3 Comparison Study

Liquid phantoms were created using the appropriate solvent (methanol (MeOH) for Photofrin and water (H₂O) for Rose Bengal) in cuvettes. Rose Bengal is a commonly used, well-characterized model compound of a single molecular species that was used for verification of the singlet oxygen signal. Photofrin is a clinically-active photosensitizer that is FDA approved and currently in use for many clinical trials. Phantoms were made with various concentrations of each sensitizer in cuvettes.

Ground state oxygen measurements were performed with an Oxford Optronix OxyLite system (Oxford Optronix Ltd., Oxford, United Kingdom). Illumination light was briefly turned off during these measurements, and multiple values were recorded for a single phantom. Oxygen partial pressure was measured in mmHg and converted to μM by using a factor of α = 1.3 [9, 19].

3. RESULTS

Singlet oxygen explicit dosimetry modeling was validated in two methods: ground state oxygen (³O₂) modeling and singlet oxygen (¹O₂) modeling. ³O₂ was modeled for a phantom system with no external oxygen perfusion. This is due to the illumination of the phantom happneing at a depth of at least 1 cm below the water-air surface. Diffusion of oxygen in standard conditions could not supply oxygen to the illumination area with the set-up.

Singlet oxygen luminescence counts were compared to singlet oxygen concentrations calculated with equation (10). The parameters used for each sensitizer are summarized in table 1. The values are for in vitro conditions using their respective solvents.

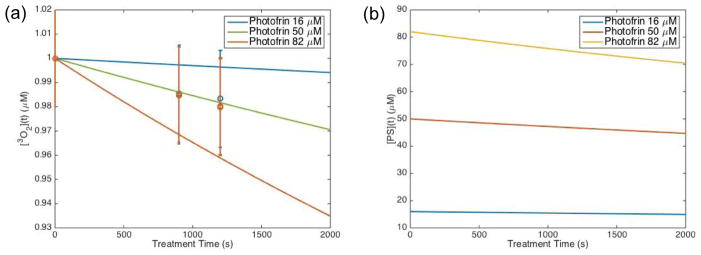
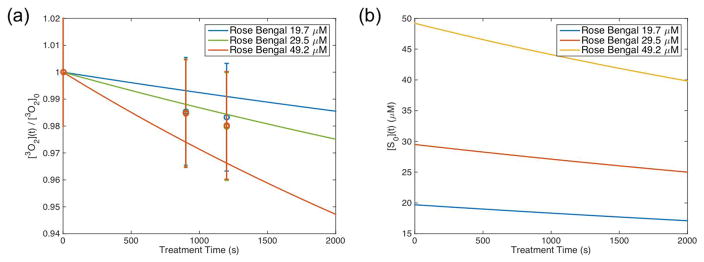
Figures 3(a) and 4(a) show a comparison between the measured oxygenation versus the explicit model-calculated values of oxygen for Photofrin and Rose Bengal, respectively. Data was plotted relative to the measured initial oxygen concentration, which is around 170 μM (2% uncertainties). The measured values had large standard deviations; however, the model was able to look at the reduction of oxygen in the phatom with the treatment conditions outlined. Further studies can be done with more measurements at the initial drop off as well as with different light dose and sensitizer concentrations to validate the model in more detail.

Figure 3.

Explicit model calculation of (a) relative ground state oxygen ([³O₂]) and gound state sensitizer ([S₀]) plotted for Photofrin using the parameters summarized in Table 1. Open circles represent oxygen measurements performed in phantoms after illumination with 523nm light for 15 minutes and then another 5 minutes. Ground state oxygen is plotted relative to the initial oxygen concentration ([³O₂]₀) that was measured at ~ 170 μM.

Figure 4.

Explicit model calculation of (a) relative ground state oxygen ([³O₂]) and gound state sensitizer ([S₀]) plotted for Rose Bengal using the parameters summarized in Table 1. Open circles represent oxygen measurements performed in phantoms after illumination with 523nm light for 15 minutes and then another 5 minutes. Ground state oxygen is plotted relative to the initial oxygen concentration ([³O₂]₀) that was measured at ~ 170 μM.

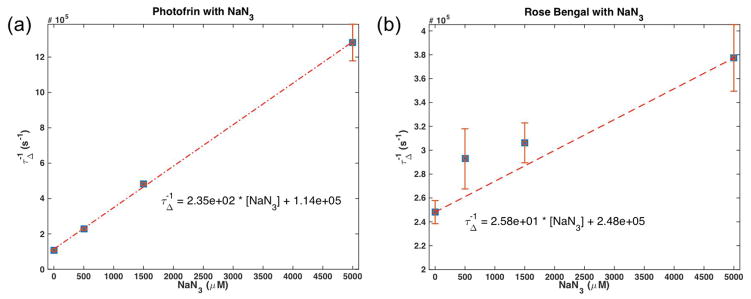
Using a NaN₃, a singlet oxygen quencher, singlet oxygen lifetimes could be used to determine parameters k₆ and k₇, the spontaneous phosphorescence rate of ¹O₂ to ³O₂ and the bimolecular rate of reaction for ¹O₂ with a substrate ([A]), respectively. By plotting the inverse of singlet oxygen lifetime against the concentration of singlet oxygen quencher, the following equation can be fit with a line

$${\tau }_{\mathrm{\Delta }}^{-1}=k_6+k_7[A]$$ (14)

The values obtained are summarized in table 1 and are consistent with values obtained for k₆ without any quencher. Figure 5 shows the plot of τ_Δ⁻¹ versus [A].

Figure 5.

Inverse of singlet oxygen lifetime versus singlet oxygen quencher concentration for (a) Photofrin and (b) Rose Bengal. Values for parameters k₆ and k₇ are given by the fits to data according to equation (9).

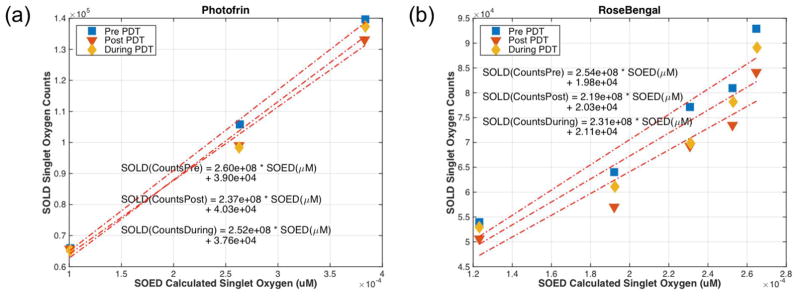
Figure 6 shows the comparison of SOLD singlet oxygen counts versus SOED model calculated singlet oxygen. With two different sensitizers in two different solvents, there were differences in photochemical parameters. Using the values summarized, the comparison shows that the SOLD system and SOED system are consistent even with two very different type II photosensitizers. The calculation of instantaneous singlet oxygen was done using Eq. 8. The slope between SOLD and SOED calculated singlet oxygen is the same regardless photosensitizers used, (2.5 ± 0.1) × 10⁸ for Photofrin and (2.3 ± 0.2) × 10⁸ for RB.

Figure 6.

SOLD system singlet oxygen counts plotted against SOED calculated singlet oxygen for (a) Photofrin and (b) Rose Bengal. The plots show that the two systems are comparible with two different sensitizers.

4. CONCLUSION

Singlet oxygen luminescence detection (SOLD) technology was compared with singlet oxygen explicit dosimetry (SOED) calculations for phantoms using Photofrin and Rose Bengal. Oxygen measurements were used to validate one aspect of SOED, while SOLD photon counts of singelt oxygen signal at 1270 nm were compared to SOED-calculated singlet oxygen to validate their correspondence using two different sensitizers and their solvents. SOED system validation is performed in vitro.