The potential and electric field in the cochlear outer hair cell membrane

Abstract

Outer hair cell electromechanics, critically important to mammalian active hearing, is driven by the cell membrane potential. The membrane protein prestin is a crucial component of the active outer hair cell’s motor. The focus of the paper is the analysis of the local membrane potential and electric field resulting from the interaction of electric charges involved. Here the relevant charges are the ions inside and outside the cell, lipid bilayer charges, and prestin-associated charges (mobile-transferred by the protein under the action of the applied field and stationary-relatively unmoved by the field). The electric potentials across and along the membrane are computed for the case of an applied DC-field. The local amplitudes and phases of the potential under different frequencies are analyzed for the case of a DC+AC-field. We found that the effect of the system of charges alters the electric potential and internal field, which deviate significantly from their traditional linear and constant distributions. Under DC+AC conditions, the strong frequency dependence of the prestin mobile charge has a relatively small effect on the amplitude and phase of the resulting potential. The obtained results can help in a better understanding and experimental verification of the mechanism of prestin performance.

1 Introduction

Electric charges located inside and near the cell membrane play a crucial role in the membrane function. Because of these charges, an applied electric field results in changes in the membrane geometry [30], continuity [7], phase transition [14] and deformation [21]. Conversely, the movement and interaction among the membrane charges generate an electric field [30, 13]. The outer hair cell membrane containing an array of prestin proteins is the site of physiologically important interaction between the membrane charges and local electric field.

Cochlear outer hair cells are critical to sound amplification and the sharp frequency selectivity of the mammalian ear [6, 37] (for review). They are a key part of the process called the cochlear amplifier that works via two interrelated mechanisms, somatic electromotility and an active hair bundle [3] (for review). Outer hair cell electromotility is driven by changes in the cell membrane electric potential resulting from modulation of the current passing through mechanotransduction (MT)-channels in the cell hair bundle [5], [1], [32]. The outer hair cell generates an electromechanical force of almost constant amplitude and phase up to 80 kHz [11]. The outer hair cell force provides the active power necessary to overcome frequency-dependent losses in the cochlea.

The membrane protein, prestin, is crucial to outer hair cell electromotility [41], [20], [8]. It is believed that changes in the membrane electric potential cause transfer of an electric charge inside the membrane resulting in conformational changes of the protein. This charge transfer driven by the electric field is a critical component of prestin-associated electromechanics. It is usually assumed that the electric potential varies linearly and the corresponding electric field is a constant inside the membrane. Such an approach, however, does not take into account the effects of various charges and their interactions involved in prestin-associated charge transfer. These effects can significantly modify the local potential and electric field. It has also been shown in other cells (e.g., in axons of neurons) that the membrane and near-membrane charges can alter the transmembrane electric potential [39, 40].

At present, the physical nature of the charge transferred by prestin is not fully clear. In older models, it was assumed that the prestin mobile charge was an internal protein charge (e.g., [2]). It was later found that chloride ions inside the cell are involved in prestin-associated charge transfer and the corresponding model with three states of the chloride ion, unbound, bound, and transferred, was proposed [27]. Further experiments showed that this model does not fully explain the dependence of cell nonlinear capacitance on chloride concentration [31] and a concept that internal chloride binds prestin and allosterically triggers transfer of internal protein charges was proposed [35]. Another model, that explains the experimentally observed dependence of nonlinear capacitance on the chloride concentration, treats prestin as a chloride/sulfate exchanger with mobile internal protein charges [24]. There was a long discussion whether prestin is a full transporter/exchanger, as other members of SLC26 family [24], [4], or it has a special mechanism developed in mammals by the evolution [27], [33]. Recently, Gorbunov et al. [12] showed that mammalian prestin features a site (central cavity) of binding of external ions accessible to the intracellular ions only while the other members of SLC26 family, probably, experience exposure of such cavity to the extracellular space as well. Based on the analysis of the mechanism of ion binding Gorbunov et al. [12] have developed a 3-D structural model of prestin. While the transferred charge was traditionally associated with nonlinear capacitance implying no-phase shift between the transferred charge and applied voltage, recent experiments [31], [10], [26] showed that such a phase shift exists. Further modeling analysis has shown that this phase shift becomes significant for high-frequency regimes [38]. In addition, the amplitude of the transferred charge also depends on frequency and decreases under high-frequency conditions.

Here, the electric potential and the corresponding electric field inside and near the outer hair cell membrane are obtained computationally by solving the 2-D (axisymmetric) nonlinear Poisson-Boltzmann equation. The outer hair cell wall is a tri-laminar structure, including the subsurface cisternae, the cortical lattice, and the outermost plasma membrane [6]. It has been previously demonstrated [13, 25] that the subsurface cisternae and space between it and the plasma membrane (extracisternal space) might affect the distribution of the electric potential along the cell plasma membrane, especially under high-frequency conditions. This analysis, however, did not consider the electric potential and field distributions across the membrane. Here we focus on the electric field affecting the protein prestin critical to this cell’s active properties. Because prestin is the membrane protein, we concentrate our analysis on the electric charges, potential, and field inside and near the plasma membrane. The membrane electrical characteristics are determined by a system of charges, including the ions in the solutions inside and outside the membrane, the charges associated with the membrane phospholipids groups, and prestin-related charges. The prestin charges are split into two categories, stationary charges of immobile protein residues and mobile charges moved by the applied electric field. We found that the electric potential and internal field can deviate significantly from their traditional linear and constant distributions. Under DC+AC conditions, the strong frequency dependence of the prestin mobile charge has a relatively small effect on the amplitude and phase of the resulting electric potential. The voltage sensitive dyes have previously been applied to and revealed features of the outer hair cell membrane potential, such as its frequency-dependent phase [25]. While those earlier data cannot be directly used the present case, a more recent development of the voltage sensitive dye technique based the microbial rhodopsin protein [18, 19] can potentially provide a highly-sensitive tool to verify across-the-membrane potentials and electric fields computed in this paper. The obtained results can help in a better understanding of the mechanism of charge transfer by prestin and the performance of the outer hair cell motor critical to the cochlear amplification

2 Methods

The electric potential inside and near the outer hair cell plasma membrane is determined by the externally applied electric field and the quantity and position of a system of the membrane-associated charges. Some of these charges are considered to be fixed in space while others are regarded as mobile, i.e. may change position in response to an applied electric field. In addition to charges usual to a plasma membrane such as ions outside and inside the membrane as well as the molecular charges of the phospholipids, the outer hair cell membrane includes the protein prestin whose molecules are distributed along the cell’s lateral surface. Under the action of a transmembrane electric field, prestin transfers a charge through a part of (or the whole) membrane. The nature of this charge is probably a combination of an internal protein charge and an external chloride ion. We previously proposed a Fokker-Planck equation to describe the probability of prestin-associated charge being at a certain position inside the outer hair cell membrane (within prestin) at a certain moment of time. To find the outer hair cell membrane electric potential, we use this probability and estimate the statistical average of the charge position. Note that our model of the mobile component of the prestin-associated charge is not based on any particular secondary structure of the protein and is adjusted by using the direct experimental data on the transferred charge and nonlinear capacitance. In addition to the mobile charge, we consider prestin stationary structural charges introduced according to the recently proposed [9, 26] two models (called here models 1 and 2) that differ in terms of the number of transmembrane domains and locations of the charged residues (see these models presented back to back in Figs. 5a and 5b in [4]). Such structural differences result in the corresponding changes in the membrane distribution of the electric potential (see below). We use a 2-D (axisymmetric) analysis where all characteristics involved are functions of the radius, r, along the membrane surface and the vertical position, z, across the membrane. A structural model of prestin based on the data on intracellular ion binding to the protein has just become available [12]. While not providing information on the charge transferred by the prestin, this model is the first 3-D model of the protein. The incorporation of the structural charges based on this model requires essentially 3-D analysis, which is beyond the scope of the current paper (see also the Conclusions section).

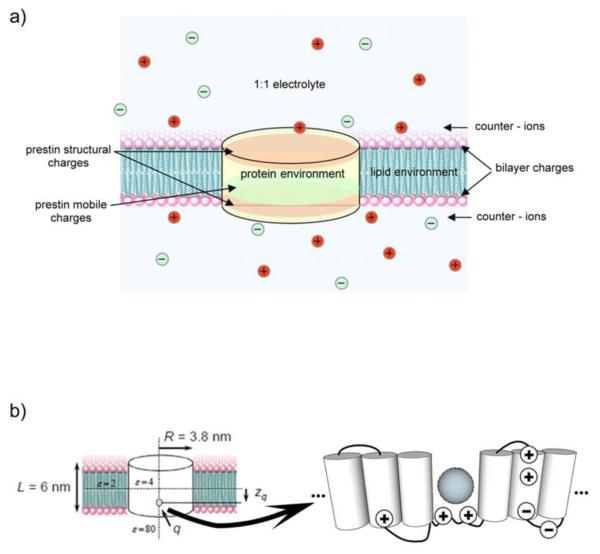
Fig. 1a introduces the major charges involved in the generation of the local potential and electric field. For our model shown in Fig. 1b, we choose prestin to occupy a cylinder of 3.8-nm radius and 6-nm height [23]. The electrical properties of the domains, prestin, membrane space outside of prestin, and the liquid space outside of the membrane area characterized by their electric permittivity, ε. As a result of changes in the applied voltage, prestin transfer a charge, q, whose vertical position is z_q (Fig. 1b, left panel). A sketch of a hypothetical environment with several transmembrane domains is shown in the right panel of Fig. 1b. The charge transferred by prestin is presented as a sphere.

Fig. 1.

A) The system of charges inside and near outer hair cell membrane affecting the local potential and electric and b) The left panel shows the cylindrical domain occupied by prestin, typical electrical permittivities of three regions under consideration, inside prestin, inside the membrane and outside prestin, and outside the membrane, the total mobile charge, q, and its average position, z_q. The right panel sketches a conceptual structure of prestin, including several transmembrane domains, charged residues, and mobile charge shown as a sphere.

The inner- and near- outer hair cell membrane electric potential, ψ, is described by Poisson’s equation (see also [13])

$$\nabla \cdot \left[\epsilon \right(r,z)\nabla \psi (r,z\left)\right]=-\rho (r,z)$$ (1)

Here ▽· and ▽ are respectively the divergence and gradient operators in the r,z-coordinates, ε is the electric permittivity of the region under consideration, and ρ is the volume density of the charges involved. Eq. 1 is solved with the boundary conditions

$$\psi =\{\begin{array}{cc}0\text{if}\hfill & \mathrm{z}\to \infty \hfill \\ V\text{if}\hfill & \mathrm{z}\to -\infty \hfill \end{array}\phantom{\}}$$ (2)

where V is the voltage applied to the membrane.

The electrical permittivity is determined by three different values associated with three different sub-regions involved, the areas near the membrane (inside the cell/in the extracisternal space and outside the cell), inside the prestin volume, and inside the membrane but outside of prestin. For computational purposes, we use smoothing functions between the neighboring sub-regions to provide the continuity and smoothness of the permittivity in the whole area of consideration. Thus the electrical permittivity is given by the following equation of

$$\epsilon =\{\begin{array}{cc}2{\epsilon }_0+f_{\mathrm{sm}}^1(r,z)\text{inside the membraneand outside prestin}\hfill & \hfill \\ 4{\epsilon }_0+f_{\mathit{sm}}^2(r,z)\text{inside prestin}\hfill & \hfill \\ 80{\epsilon }_0+f_{\mathit{sm}}^3(r,z)\text{outside the membrane}\hfill & \hfill \end{array}\phantom{\}}$$ (3)

where ε₀ is the vacuum electrical permittivity and $f_{\mathit{sm}}^i(\mathrm{i}=1-3)$ are smoothing functions in the corresponding sub-domains.

The charge densities, ρ, in the right-hand side on Eq. 1 are determined by typical charges in the corresponding sub-regions. Assuming 1:1 mixture of positive and negative ions in the near-membrane areas inside the cell-in the extracisternal space and outside the cell, we use the Gouy-Chapman model (e.g., [16]), for the distribution of the charge density

$$\rho (r,z)=-2n_0\sinh \left[e\right(\psi (r,z)-V)∕\mathit{kT}]$$ (4)

where n₀ is the charge density in the bulk solution, and e is the electronic charge. The electric potential in the near-membrane area is obtained by substituting the charge density from Eq. 4 into the right-hand side of Eq.1. The resulting Poisson-Boltzmann equation takes into account the electrostatic and thermal forces in the near-membrane layer. Additional forces, such as Van der Waals forces, can result in a specific sub-layer of adsorbed ions at the membrane surface (Stern layer, e.g., [34]). Note that the further solution of the Poisson-Boltzmann equation deals with the exact nonlinear terms in Eq. 4 without any small-potential approximation.

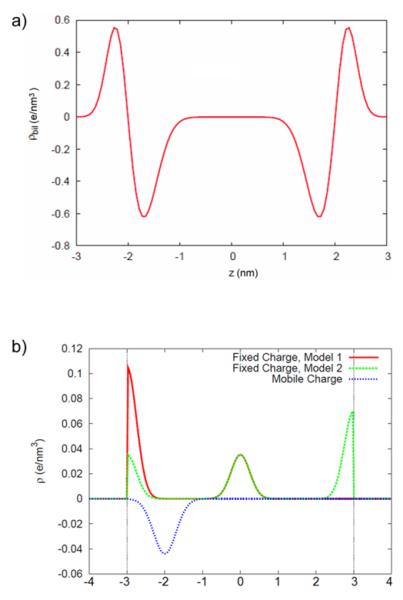
We now consider the densities of charges associated with phospholipid molecules. For each leaflet, we assume positive charges on the outer side and negative charges on the inner side. The latter density is assumed to be larger to give an overall negative resultant. For both positive and negative bilayer charges, we assume that the corresponding densities are Gaussian in terms of the transmembrane coordinate z and uniform in terms of the in-plane coordinate r (Fig. 2a). We use a model bilayer which is imagined to be mixture of anionic phospholipids (e.g., phosphatidylserine) with a zwitterionic ion (e.g., phosphatidylcholine). These charges are spread according to the time averaged distribution of the location of these charges. These distributions are taken from simulation studies on model bilayers (e.g., [22],[28], [29]) and are Gaussian in shape in the transmembrane coordinate, z, and uniform in the in-plane coordinate, r (Fig. 2a). This model bilayer has a net negative charge density of −0.02 e/nm^3 associated with a charge which is neutralized by positive ions just outside the membrane surface. Other factors (in addition to the phospholipid groups) may also contribute to the membrane charges included in our model.

Fig. 2.

A) Charge density of the phospholipids charges as a function of the transmembrane coordinate z based on molecular dynamic simulations (-z towards the inside of the cell) and b) Density of prestin-associated charges, including the mobile (dark dashed line) and stationary charges based on models 1 (solid line) and 2 (light dashed line). Notice that two models have the same central charge (the corresponding lines overlap) and they differ toward the inner and outer boundaries of the membrane. The density representing the mobile charge has a central position at −2nm closer to the inner boundary of the membrane corresponding to the case of application of a depolarizing electric field.

Finally, we describe the densities of prestin-associated charges. We assume that the density of the mobile charge is distributed around a central point located at the axis of symmetry (z-axis). The coordinate of this central point is determined by the solution of the Fokker-Planck equation for a given voltage V. Then the density of the mobile charge is described by a Gaussian distribution in terms of the z-coordinate (dark dotted line in Fig. 2b that corresponds to a certain position of the mobile charge inside the membrane) and a uniform distribution in terms of the radius, r. To introduce the density of the structural charges of prestin, we consider the available charged residues across the membrane. We divide the prestin space into three domains, bottom, central and top, with the bottom and top domains being close to the interface with the solution inside and outside the membrane. Knowing the charge of each residue, we sum them up and represent each domain with the resulting charge. In the central domain, the density of the resulting charge is assumed to be Gaussian in terms of the z-coordinate and uniform in terms of the radial coordinate. In the top and bottom domains, the densities of the representative charges are assumed to be “half-Gaussian.” Fig. 2b shows the z-distributions of all considered prestin charges, including the mobile and stationary charges. The densities of the stationary charges resulting from the corresponding distributions of prestin’s charged residues are presented for two models (see above on models 1 and 2) used in our analysis (solid and light dotted lines for models 1 and 2, respectively).

From a computational standpoint, the solvent charges (Eq. 4) make the problem nonlinear. Here we used the computational package COMSOL Multiphysics to solve Eq. 1 with boundary conditions (2) (imposed at z = ±5 nm) and compute the electric potential, ψ, and electric field, E ( E = −▽ψ ), inside and near the outer hair cell membrane; For a more accurate presentation of the features of the potential and electric field, we start with a solution on a cruder mesh and then use mesh refinements. Note that the steady state limit of the average position of the mobile charge can be obtained analytically from the Fokker-Planck equation resulting in the following equation

$$<z>=L(\frac{e^{\beta L}}{e^{\beta L}-1}-\frac{1}{\beta L})$$ (5)

where β = q(ψ–ψ*)/kTL, q= −1.5e, and ψ*=−30 mV. These parameters were previously adjusted [38] based on fitting the data on the voltage dependence of the prestin-associated charge with typical experimental chloride concentrations of about 140mM [36]. We use Eq. 5 to control our computational results.

3 Results

3.1 Stationary case of a DC- field

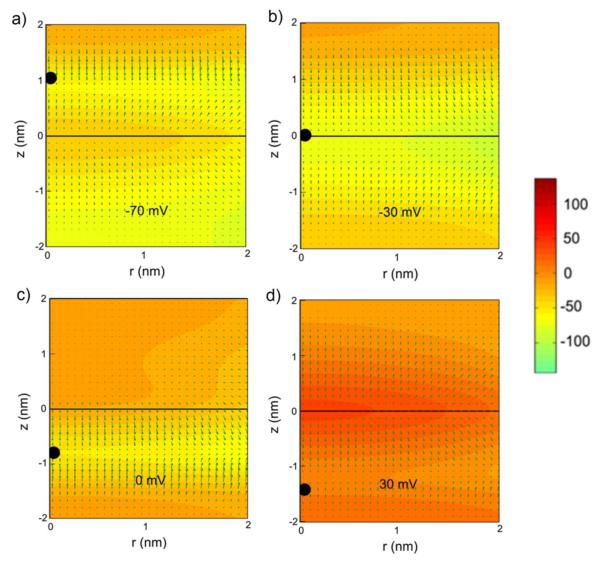
First we consider the local potentials and electric fields associated DC-potentials applied across the membrane, and Fig. 3 presents the cases of −30, −70, 0, and 30 mV of the applied voltage. Its first value is equal to the membrane resting potential in vitro, and the range between the first and second values covers the available estimates of the outer hair cell resting potential in vivo [17]. In the experiment, the electromotile outer hair cells are stimulated by an external electric field to observe the tendency in the voltage dependence of cellular characteristics. For the same reason, we consider here two additional values of the DC-potential equal to 0 and 30 mV. In Fig. 3, the results are grouped together to show the effect of the DC-voltage. The a-d-panels presents 2-D (rz) plots of the electric potential inside prestin and the associated membrane area with arrows showing the direction and magnitude of the local electric field. The correspondence between the 2-D plotted potentials and their values is shown via the representative bar in Fig. 3. The 2D computations are limited to the prestin stationary charges extracted from prestin model 1 because the results for two models, 1 and 2 (Fig 2b here and Figs 5a and 5b in [4]), are quite close (demonstrated in the e-h-panels in Fig. 3). The black bullets on the z-axes show the average position on the mobile charge transferred by prestin. In e, g, f, and h-panels, we present the distributions of the electric potential along the central (z) axis of the system that correspond to the DC voltage of −70,−30, 0, and 30 mV, respectively. In these panels, we show the contribution to the resulting electric potential of each component of the system of charges under consideration. In light solid lines, we show the potentials resulting from the external field and membrane charges with no prestin-associated charges taken into account. The dark dotted lines correspond to the case when the external field, membrane charges, and prestin mobile charge are considered but no prestin stationary charges are included. Finally, the solid and thin dashed lines correspond to the cases when all system charges are taken into account and prestin stationary charges are treated according to models 1 and 2 (see Figs 5a and 5b in [4]), respectively.

Fig. 3.

Electric potential and electric field inside and near prestin in the case of the applied DC-field. A-D) Two-dimensional (rz) plots of the potential in a central inside-prestin area of the membrane. The correspondence between the 2-D plotted potentials and their values are shown via the representative bar. The arrows show the direction and magnitude of the local electric field. The black bullet represents the average position of the mobile charge. DC-voltage is −70 (a), −30 (b), 0 (c), and 30 mV (d) and d. E-H) one-dimensional (along the central z-axis) distributions of the electric potential. The light solid line, dark dotted line, solid line, and thin dashed line correspond, respectively, to applied voltage and membrane charges with no prestin charges, mobile prestin charges included, all charges considered with prestin stationary charges determined according to model 1, and all charges considered with prestin stationary charges determined according to model 2. DC-voltage is −70, −30, 0, and 30 mV, respectively, in e, f, g, and h.

3.2 Dynamic DC+AC-case. Frequency dependence

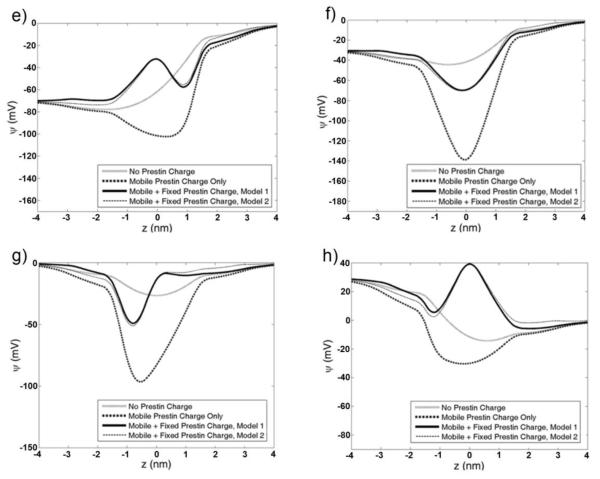
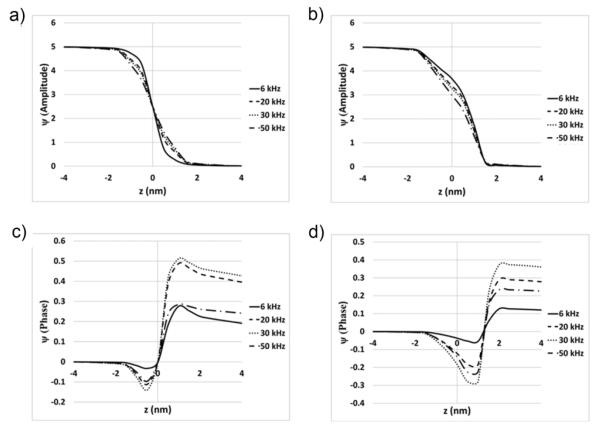
We now consider in Fig. 4 the case when a DC-voltage is superimposed by an AC-component with the varying frequency (6, 20, 30. and 50kHz) and fixed amplitude (5mV) to analyze the effect of frequency on the resulting potential and electric field. Such an effect is associated with the frequency dependence of the amplitude and phase of the prestin mobile charge. Here, we consider the most physiologically relevant values (−30 and −70mV) of the DC-voltage. The results for other voltages (0 and 30mV) are obtained also but not graphically shown. We compute the resulting local electric potential along the z-axis and show its amplitude (a- and b-panels for DC-potentials of −70 and −30 mv, respectively) and phase with respect to the externally applied field (c- and d-panels for DC-potentials of −70 and −30 mV, respectively). In all panels, the solid, dashed, dotted, and dashed-dotted lines correspond to the frequency of 6, 20, 30, and 50 kH, respectively. The dynamic potentials in Fig.4 are computed as follows. First, the midpoint, amplitude, and phase are determined for the average position of the mobile charge by the solution of the Fokker-Planck equation. This solution has a short transient interval following by stationary oscillations. The data for the oscillatory regime are fitted with sinusoidal functions that have amplitude and phase determined by the DC-component and frequency of the AC-component of the voltage. After the position of the mobile charge is fully characterized, these data are introduced in the solution of the Poisson-Boltzmann equation via the corresponding charge density. For each z along the axis of symmetry, the electric potential is computed by considering a sequence of moments of time corresponding to several cycles of the potential change.

Fig. 4.

Electric potential along the axis of membrane (prestin) symmetry (z-axis) for four different frequencies, 6, 20, 30, and 50 kHz and two DC-voltages. The prestin stationary charges are computed by using model 1. A and b) Amplitude of the potential for DC-voltage of −70 (a) and −30 mV (b). C and d) Phase of the potential (in radians) with respect to the applied voltage for DC-voltage of −70 (c) and −30 mV (d).

4 Discussion

4.1 Application of a DC-field

The average position of the mobile charge varies with the DC-component of the voltage moving up (Fig. 3a) and down (Figs. 3c and 3d) in the cases of the membrane hyperpolarization and depolarization, respectively. The voltage of −30 mV corresponds to a special case of symmetry when the average position is in middle of the membrane (z=0, Fig, 3b). These results on the position of the mobile charge are electrostatically-consistent with our treatment of prestin-associated charge as being negative. The sign of the mobile (transferred) charge can be explained by the contribution of chloride ions binding prestin from the inside of the cell. The 3e-3h-panels results in Figs. 3 can be interpreted in terms of interaction among the components of the charge system (see above). The standard approach considers a constant electric field (linear potential) across the membrane. Our results in the cases when prestin charges are not taken into account (light solid lines) have a linear range away from the membrane boundaries (Figs 3e, 3f and 3h) affected by the electrical double-layers closer to the boundaries. The negative prestin-associated mobile charge results in a significant dip in the potential curve whose position depends on the DC-component of the applied voltage. The inner-membrane structural charges in the models used (Fig. 2b) are positive, and they balance the negative mobile charge The obtained data mean that the internal structural charges make a more significant contribution to the local potential compared to the structural charges at the membrane boundaries (Fig. 2b). Note that the maximum of the charge density associated with the internal structural charge is smaller than that related to the prestin mobile charge. Thus, dips in the curves of the potential remain. This effect is especially clearly seen in Fig. 3f (for the DC-component of −30mV) where the maxima of the internal structural and prestin mobile charges are at the position of z=0. It is also important that the resulting potential is not very sensitive to the structural model used.

Thus, the electric potential distribution in a realistic outer hair cell membrane with typical near-membrane, membrane, and prestin charges deviates significantly from the linear one determined by the applied electric field (Figs. 3a-h). The potential gradients (electric field) determine the local forces acting on the electric charges associated with charge transfer and conformational changes of prestin. Without the charge effect considered here the electric field would be constant along and across membrane. Figs. 3a-d show that the electric field varies both in terms of magnitude and direction inside the membrane. In particular, the areas of the greatest variation of the electric field are the strips along the membrane at z-coordinates corresponding to the extrema of the electric potential which mainly determined by the average position of the of the mobile charge and that of the central structural charge. For example, in the case of −70 mV (Fig. 3a), the electric field changes its direction along the lines z=1 (average position of the mobile charge) and z=0 (position of the central structural charge in both models of the prestin secondary structure). Thus, the observed effect is two-fold, first the local charges change the DC-component of the electric potential that drives OHC electromotility and, second, they affect prestin-associated charge transfer and the related conformational changes and active force production.

4.2 Dynamic DC+AC case

Under the dynamic conditions, the amplitude and phase of the prestin mobile charge change significantly with frequency, e.g., the phase of this charge reaches about 60° at 50 kHz and about 75° at 75 kHz [38]. Thus, we investigate this effect on the resulting potential and electric field and, ultimately on the strategically important phase of the active force produced by the outer hair cell.

Without the effect of frequency on the electric potential, the amplitude of the potential would be close to a linear function of z between 5 and 0 mV (see the potential for a low frequency of 6 kHz in Figs. 4a and 4b). With the full consideration of the mobile charge effect, the amplitude of the potential deviates from the quazi-linear distribution being smaller or greater than that in the low-frequency case, depending on the position of the mobile charge for a given DC-voltage (Figs. 4a and 4b). This deviation increases monotonically with frequency. Similar trends can be observed in the results for cases of DC-voltage equal to 0 and 30 mV (not shown). Nevertheless, such frequency effect on the amplitude of the dynamic potential is relatively small throughout the whole membrane.

We now discuss the phase of the electric potential relative to that of the applied AC-voltage. The results in Figs. 4c and 4d show that the computed potential has a frequency-dependent phase shift. In contrast to the amplitude, the phase of the dynamic potential is not monotonic with frequency but it is greatest at 30 kHz. In terms of its position along the z-axis, the phase shift is maximal at some point whose coordinate depends on the value of the DC-voltage (Fig. 4c and 4d). The same conclusions are valid for two other values of the DC-voltage, 0 and 30 mV. Overall, the phase shift of the electric potential does not exceed 30°, which probably does not have a significant effect on the force acting on the charge transferring through prestin and ultimately the active force produced by the cell. Thus, the effect of the large phase shift in the mobile prestin charge is diminished by the other charges of the system resulting in a relatively small phase shift of the electric potential.

5 Conclusions and future directions

Traditionally, it is assumed that the electric potential changes linearly and the electric field is constant across the outer hair cell membrane. Here, we develop a computational model and show that these electric characteristics are significantly affected by the system of prestin and near-membrane charges. Thus, the local electric field can significantly deviate from constant, which can make implications for the forces acting on the charge transferred by prestin and the overall force produced by the outer hair cell. Under conditions of a DC+AC applied voltage, the strong frequency dependence of the prestin mobile charge has a relatively small effect on the amplitude and phase of the resulting electric potential, resulting in a quazi-linear amplitude and a small phase across the membrane. The obtained across-the-membrane distributions of the electric potential can potentially be verified by using recently developed voltage sensitive dyes. Further, the model can include a finer representation of the electric bilayer to take into account the ion interaction beyond the electrostatic and thermal forces. Finally, the developed model can be extended to a 3-D one which will incorporate the new developments in revealing the 3-D structure of prestin and provide in a more accurate representation of the protein-associated charges.