Collective Motion of Mammalian Cell Cohorts in 3D

Abstract

Collective cell migration is ubiquitous in biology, from development to cancer; it occurs in complex systems comprised of heterogeneous cell types, signals and matrices, and requires large scale regulation in space and time. Understanding how cells achieve organized collective motility is crucial to addressing cellular and tissue function and disease progression. While current two-dimensional model systems recapitulate the dynamic properties of collective cell migration, quantitative three-dimensional equivalent model systems have proved elusive. To establish such a model system, we study cell collectives by tracking individuals within cell cohorts embedded in three dimensional collagen scaffolding. We develop a custom algorithm to quantify the temporal and spatial heterogeneity of motion in cell cohorts during motility events. In the absence of external driving agents, we show that these cohorts rotate in short bursts, <2 hours, and translate for up to 6 hours. We observe, track, and analyze three dimensional motion of cell cohorts composed of 3–31 cells, and pave a path toward understanding cell collectives in 3D as a complex emergent system.

Introduction

From early development to morphogenesis, wound healing, and even in cancer pathologies, biological function hinges on collective cell migration. Currently, studies of the inter-cellular dynamics of collective cell motion are primarily conducted via two dimensional (2D) monolayer experiments. Here we present a 3-dimensional study of cell collectives.

Cells must coordinate adherence and motility to maintain organized coherent motion¹; extensive work continues to probe how cells establish such communication and organization^2,3. Cells migrate collectively to build and vascularize tissues, heal wounds, and occasionally in tumor metastases. A comprehensive review of collective cell motility establishes the many modes of migration available to cell collectives as well as the forces that drive motility⁴. A broad classification for 3D collective migration modes can comprise of two categories— in the first, cells never dissociate from their original tissue, as in the case of branching morphogenesis, angiogenesis, and multicellular strand invasion of cancers; and in the second, a detached cluster moves through ECM and other non-motile cells as observed in cancer metastases and drosophila border cells^5,6.

From a mechanical and physical standpoint, time-lapse imaging and immunohistochemistry reveal relevant characteristics of collective cell migration (CCM) ^1,7,8. For example, in Drosophila, E-cadherin is essential for collective direction sensing⁹, and tissue rotation is essential for building an extracellular-matrix (ECM) to control egg shape¹⁰. In a 3D example, human mammary cells embedded in 3D gels reveal that rotation is essential to the formation of breast acini- it does not occur for cancerous breast cells, and when disrupted within normal cells, acini do not form¹¹. Tracking assays on monolayers reveal density-dependent phase transitions¹², substrate dependence¹³, and the forces driving CCM^14,15. A comprehensive study of the mechanical properties of epithelial monolayers identified E-cadherin and P-cadherin as key proteins contributing to intercellular forces¹⁶. Heterogeneity emerges within groups of cells exhibiting collective behavior- functionally distinct populations of cells are termed leader and follower cells⁴. Leader cells are located at the front of a moving collective; they are responsible for receiving cues and directing the collective. Well-defined leader cells are found in cases of sprouting morphogenesis and angiogenesis¹⁷. In sheet migration, key molecules are upregulated to form leader cells at the leading edge; removal of these leader cells disrupts migration¹⁸.

Cancer pathologies are not amenable to direct observations of coherent translation due to diagnostic limitations; however, indirect evidence from in vivo measurements demonstrates that cancer metastases can migrate through tissue layers as collective masses^5,6,19. Clinically, patients with epithelial-originating cancers or carcinomas present with circulating tumor microemboli, or clusters of circulating tumor cells up to 8 cells large^20,21. Typical 3D studies of cell collectives involve immunohistochemistry assays and invasion assays of immortalized cancerous and non-cancerous cell lines. Immunohistochemistry has elucidated biochemical markers crucial to the emergence of leader-follower heterogeneity²² in cancer cell lines. Invasion assays involve seeding a large spheroid (>200 μm in diameter) of cancerous or non-cancerous cells into a 3D matrix; the subsequent invasion of the spheroid into the matrix can take the form of single cell invasion or multicellular strand invasion. Time-lapse microscopy conducted on invasion assays highlights cell dynamics, leader-cell formation²³, and cell jamming²⁴; together these data suggest that cancer cells have inherent plasticity of migration modes and the ability to transition between these modes²⁵.

The dynamics of collective cell motility are essential to understanding collective processes and function. In 2D environments, epithelial cells and fish keratocytes²⁶ have been used as model systems to study the dynamic aspects of collective cell migration. Here, we present a model system for quantifying 3D collective migration using mammalian cell cohorts comprised of three to thirty-one cells. This can serve as a tool for understanding the motility of detached cellular clusters that have been observed in cancer metastases in vitro and found as circulating tumor microemboli in vivo. We track individual cells within cohorts embedded in a 3D scaffold and identify events of emergent collective behavior in the absence of external driving agents. Our system serves as a 3D experimental model for collective motility of cells that is able to analyze each cell cohort as an individual entity. It is a first step toward a physical understanding of collective cell motility in 3D, including cancer cell invasion and the critical conditions that lead toward collective metastasis.

Materials and Methods

Cell Culture

MDCK Type II epithelial cells are propagated in monolayers at 37°C, 5% CO₂, and ~ 70% humidity; monolayers are cultured in DMEM media supplemented with 10% fetal bovine serum and 1% penicillin/streptomycin. Cells are stably transfected to express Nuclear Localization Signal (NLS) bound to Green Fluorescent Protein (GFP). Transfection is accomplished by a GFP-NLS plasmid (Clontech, Takara Bio, Japan) of Lipofectamine 2000 (Invitrogen, Life Technologies, Grand Island, NY). To maintain fluorescence 0.5 mg/ml G418 is added to the media; Fluorescence Activated Cell Sorting (FACS) selects for the brightest 1% of cells. Identical procedures are followed on MDCK GFP-Ecad cell lines²⁷.

3D Cluster protocol

Single cell suspensions are formed by immersing cells in media after trypsinization; cells are passed through a 40 μm cell strainer (BD Biosciences, San Jose, CA); cells are then seeded onto a 10 cm diameter Ultra Low Attachment Dish (Corning, Corning NY) with 10 ml media. After 48 hours, clusters are extracted by passing the solution through a 100 μm cell strainer followed by a 40 μm cell strainer, retaining clusters of 10–20 cells. These are resuspended and centrifuged at 800 rcf, and then immersed in a collagen solution for 3D culture and imaging.

A 2 mg/ml collagen dilution is obtained by mixing equal volumes of collagen Type 1 stock (BD Biosciences, San Jose, CA) solution and neutralizing buffer (100mM Hepes in 2x PBS, pH 7.3) with PBS. Cell clusters are added to the 2 mg/ml collagen solution; this cluster-collagen suspension is seeded onto several wells of a 24-well plate or 96 well-plate (MatTek, Ashland MA). The plates are incubated at 37°C, 5% CO₂ and ~ 70% humidity for 2 hours until the collagen has polymerized, after which ~1–2 ml of growth media is added to each well. FluoSpheres® Carboxylate-Modified Microspheres in 1.0 μm (Invitrogen) with red fluorescence (580/605) are diluted to ~ 10⁸ beads/ml collagen when used.

Imaging and Tracking

Images are acquired with a DMI600B Microscope (Leica, Solms, Germany) and ImagEM EM-CCD Camera (Hamamatsu Photonics, Hamamatsu, Japan) using a Spinning Disk Confocal setup (Yokogawa, Tokyo, Japan). Micro-Manager 1.4 Software (http://www.micro-manager.org) employs a 10× 0.3 NA objective lens to image ~560 × 560 × 100 μm³ fields of view. 3D stacks are acquired in the XY plane with a Z-step of 4 μm, every 10 minutes, for ~48 hours over a 100–200 μm depth. For the experiment with GFP-Ecad a 20× 0.4 NA objective lens was used with a Z-step of 2 μm over a 42 μm depth. Cells can sense the substrate beneath the 3D matrix from inside the collagen gel²⁸, and cells that are closer to the glass bottom show very high proliferation along with sheet-like dynamics. Since the scope of this work pertains to 3D cell morphology, acquisition and analysis is restricted to cells clusters located >100 μm from the glass bottom. 3D morphology is further verified before tracking and analysis.

ImageJ (NIH) is used to estimate the average nuclear diameter (~8 μm). This diameter is input into a Matlab (MathWorks, Natick, MA) spot-tracking algorithm designed by the Kilfoil group²⁹; the algorithm is modified for 3D nucleus detection and tracking. Parameters such as nucleus diameter, mask, minimum track time, and maximum displacement between consecutive time points, are optimized until varying each parameter independently has a minimal effect on the output. This metric is optimized until on average, 93% of all nuclei identified are assigned to a track. New cell identifiers are assigned when tracking is lost after 3 consecutive time points or after cell division. For a single track, if a cell is missing for up to two time points, its position is interpolated by assuming a straight path. A de-drifting algorithm designed by the Kilfoil group³⁰ eliminates net motion that is common to all cells in the 3-dimensional field of view to account for stage drift, which is ~25–40 μm every 24 hours.

Clustering Algorithm

A custom hierarchical clustering algorithm is written in Matlab to sort cells into cohorts, or groups of cells that are physically attached to each other. The algorithm is agglomerative- each cell is initially assigned a unique cluster identifier. For the first cell considered, all cells positioned within 35 μm are assigned to its cluster; all cells positioned within 35 μm of those cells are then assigned the same cluster. The process repeats until there are no cells that could be grouped into the same cluster; then the next cell with a unique cluster ID is considered. For these cells, a cutoff distance of 35 μm is empirically determined to be ~1.5 3D cell lengths; thus minimizing the likelihood of skipping an adherent neighbor. Cutoff distances ranging between 25–45 μm do not affect the output data. A custom function auto-correlates cluster IDs between consecutive time-points to ensure that each cluster has a unique ID for the duration of the experiment. A cluster is reassigned the same ID if it retains a majority of cell IDs from the previous time point, such that if two cohorts merge, the new cluster is labeled as the larger of the two.

Displacement Squared Quartiles and Order

Displacements of each cell in a cohort between time t+ 0.5*T_int and t-(0.5*T_int + ΔT) are calculated across the entire timespan of the experiment, where T_int = 1 h and ΔT = 10 min (gap between consecutive time points). This results in a distribution with as many values as number of cells in the cohort at each time point. Displacements are squared, and the median, upper-quartiles, and lower-quartiles of this distribution are evaluated for all time points of the experiment. To calculate order parameter³¹, a smoothing function is run on XYZ position data between consecutive time points according to Equation 1 where x represents position and t represents time; the interval between consecutive data points is 10 minutes.

$${\stackrel{\rightharpoonup }{x}}_t=\frac{{\stackrel{\rightharpoonup }{x}}_{t-\mathrm{\Delta }T}+{\stackrel{\rightharpoonup }{x}}_t+{\stackrel{\rightharpoonup }{x}}_{t+\mathrm{\Delta }T}}{3}$$ (1)

The T_int order parameter is calculated for the cohort between time t+ 0.5*T_int and t-(0.5*T_int + ΔT) as shown in Equation 2 where v is velocity and N is the number of cells in the cohort.

$$\phi (t)=\frac{\left|{\sum }_{i=1}^N{\overrightarrow{v}}_{i{T}_{\mathit{int}}}\right|}{{\sum }_{i=1}^N\left|{\overrightarrow{v}}_{i{T}_{\mathit{int}}}\right|}$$ (2)

T_int is selected by studying Mean Squared Displacement (MSD) vs. time interval plots (data not shown) for all cells in the experiment. MSD plots suggest that the cells in these experiments have high heterogeneity of behavior over intervals as low as 30 minutes. In order to account for bias induced by tracking, de-drifting, and noise, we doubled this number to set T_int = 1 h.

Automated Event Selection

To analyze individual cohorts, a custom algorithm is written in Matlab to detect motility events from median displacement squared data. Initially, Matlab’s built-in peak finding algorithm is used to find all peaks in the data. Peaks are merged if the valley between them > 0.5*P_min and the time gap between them <1.5*T_int. Then peaks with width < T_int or height >P_min are eliminated. P_min, or the minimum peak height for a motility event, is conservatively set at 60 μm², in order to track motion of ~1 3D nucleus diameter and minimize the loss of relevant information.

Pairwise Correlations

Once an event is identified, smoothed positions of cells for that event inform correlation functions between all possible cell pairs within a cohort. This correlation function is represented by Equation 3 where i and j are the cell pair, τ is time difference, t is time, and v is the velocity³².

$$C_{i,j}(\tau )=\langle {\left(\frac{{\overrightarrow{v}}_i}{\mid \overrightarrow{v_i}\mid }\right)}_t·{\left(\frac{{\overrightarrow{v}}_j}{\mid \overrightarrow{v_j}\mid }\right)}_{t+\tau }\rangle$$ (3)

This correlation function reaches a maximum peak value at a lag time τ_c; when a peak has a height > 0.5, a correlation is considered significant and τ_c is retained. For positive τ_c, cell i lags cell j with duration τ_c; conversely, for negative τ_c, cell j lags cell i with duration τ_c.

Results

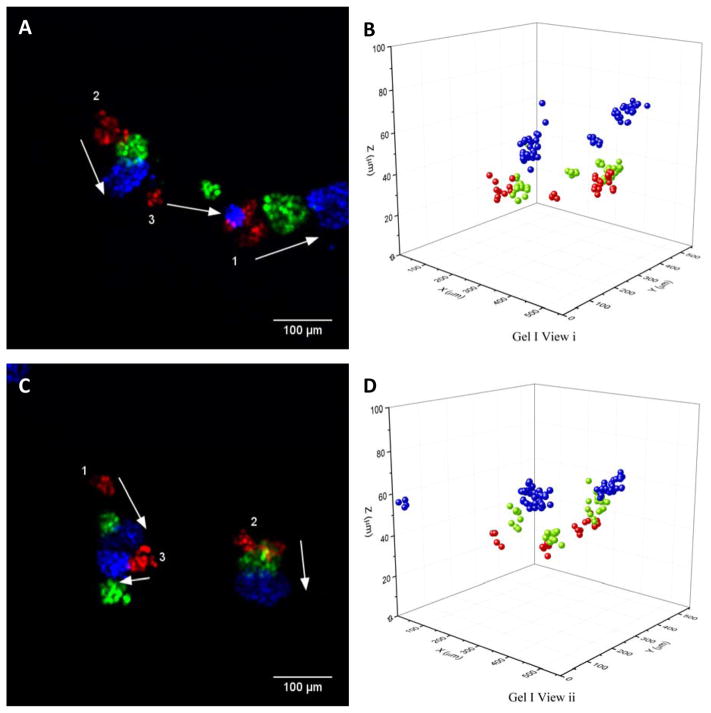
To investigate long term behavior and heterogeneity of motion in time, 3D cell tracking is performed on representative cell cohorts comprising 3–31 cells every 10 minutes over a duration of 48 hours. Positions, cell IDs, and cluster IDs for twelve cell cohorts are obtained from two different 2mg/ml collagen gels and five independent fields of view. Cohorts are dynamic and exhibit spatial and temporal heterogeneity; behavior may include seemingly random movement, collective rotation, or collective translation. Planar projections and renderings of nuclear tracking at 0 h, 24 h and 48 h are represented in red, green and blue, respectively, in Figure 1. Two of the cohorts merge between 24 and 48 h, as visible in Figure 1 C and D. For this merging event, one cohort changes direction of motion in the second half of the experiment. Data for the other 3 fields of view is represented in Supplementary Figure 1; planar projection time-lapse videos and renderings of nuclear tracking are presented in Supplementary Videos 1–5. The videos qualitatively demonstrate rotation and translation of individual cohorts at various time-points; individual cohorts within a field of view may or may not be correlated to each other. To verify that motion is not caused by external ECM deformation, an experiment is performed using 1 μm fluorescent beads embedded alongside the cells in the collagen matrix (Supplementary Video 6). This video suggested that the matrix is relatively stable except for perturbations caused in the vicinity of cohorts, likely due to pulling of the gel. GFP-Ecad planar projections are in Supplementary Video 7, illustrating that E-cadherin is membrane bound in the cohorts.

Figure 1.

Panels A and C show Z-projections of 2 fields of view from the same 3D collagen gel with MDCK GFP-NLS cell cohorts at 0 h (red), 24 h (green) and 48 h (blue). The numbers in white indicate cohort number as determined by a clustering algorithm. Panels B and D are 3D renderings of nuclear tracking corresponding to Panel A and C respectively.

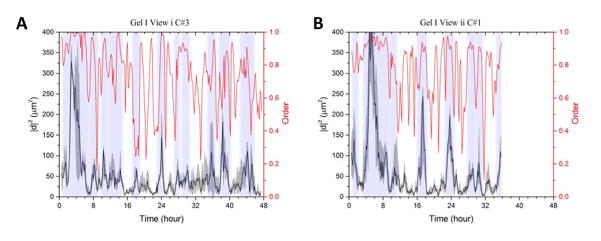
The heterogeneity of cohorts in time is determined by studying the individual cell displacements for each cohort. For the 48 hour experiment, 1-hour displacements for all cells in a cohort are calculated; these displacements are squared (|d²|), and the median of the resulting distribution is plotted corresponding to the left y-axis of Figure 2. The upper and lower quartiles for the same distributions are plotted in the gray regions around the lines representing the median. The motility events isolated are depicted in shaded vertical strips in Figure 2. Upon isolating motility events for each individual cohort, we find evidence of coherent rotation and translation within intervals ranging from 1 to 6 hours. For these 12 cohorts, a total of 61 motility events are obtained; five cohorts have 1–3 events, whereas those depicted in Figure 2 are motile for almost the entire duration of the experiment. Displacements and events for ten other cohorts are displayed in Supplementary Figure 2.

Figure 2.

Panel A has temporal analysis for Gel I View i Cohort #3, and Panel B has the same for Gel I View ii Cohort #1. The left y-axis corresponds to the 1h squared displacement distribution: black line is the median, grey shaded regions are upper and lower quartiles. Vertical shaded regions represent motility events. The right y-axis and the red line correspond to 1h order parameter of the cohort.

Order parameters provide a quantitative metric to measure the collectivity of systems. Establishing an order parameter for this system identifies the presence of translation, and also distinguishes between rotation and translation. For cells translating collectively, the order parameter is ~1, and for cells rotating collectively this parameter is low, between 0 – 0.5. For a cohort rotating about an axis in the center of the cohort, the order parameter is 0. For cohorts rotating about an off-center or external axis the order parameter is higher. This is because when the axis of rotation is in the middle of the cohort there is an average velocity of 0 within the cohort.

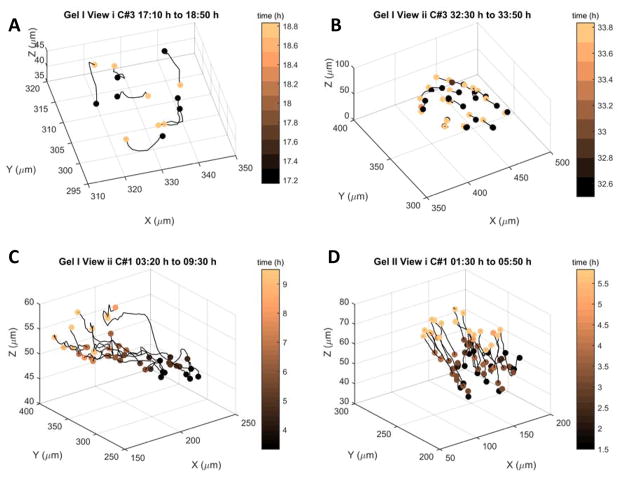
For the 48 h experiment, 1-hour order parameters are plotted corresponding to the right y-axis in Figure 2. All motility events are identified via peaks in displacement; translation events are accompanied by peaks in the order parameter; rotation events are accompanied by fluctuations or valleys in the order parameter (Figures 2 and Table 1). While translation occurs over durations of 1 to 6 hours, rotation only occurs in bursts of 1 to 2 hours (Figure 2, Table 1 and Figure 3). For selected motility events, metrics such as total displacement of the cohort, average order, and average number of cells are depicted in Table 1; metrics for all 61 events are in Supplementary Tables.

Table 1.

Parameters of four motility events. C is Cohort ID, Ti is the initial time, Tf is the final time, |d| is the displacement of the cohort, <φ> is the average order, and Nc is the average number of cells in the cohort

Gel	View	C	Ti (h)	Tf (h)	|d| (μm)	<φ>	Nc
I	i	3	17:10	18:50	3.35	0.39	7
I	ii	1	3:20	9:30	89.06	0.92	10
II	i	1	1:30	5:50	53.09	0.84	19
I	ii	3	32:30	33:50	6.33	0.72	23

Figure 3.

Cell trajectories extracted from raw data for four different events and cohorts. Each cell track is represented by a single black line. Colors of spots mark initial and final time for each track. Panels A and B depict rotation, panels C and D depict translation.

The highest observed translation event has a duration of 6 hours and measures ~90 μm, corresponding to ~8 3D cell diameters. To visualize a few motility events, cell trajectories derived from raw data with events from four different cohorts are mapped in Figure 3. Panels A and B show rotation, Panels C and D show translation. Spots are colored to indicate the initial and final time point of cell tracks within the event.

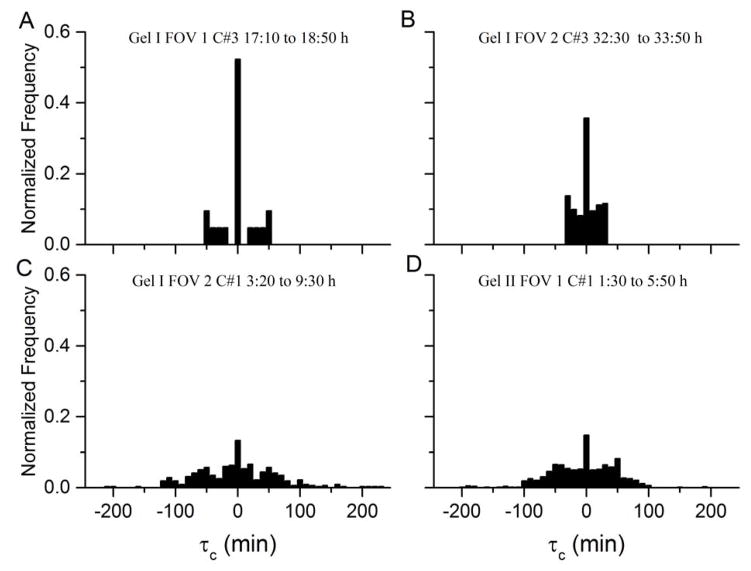
Directional correlation functions, defined in Equation 3, probe the inter-cellular dynamics within each cohort during a motility event. For the four representative events depicted in Figure 3, leading and lagging times are calculated using pairwise correlation functions; normalized occurrence frequencies of these times are displayed in Figure 4. For all cohorts in motility events, most cell pairs have 0 time lag between trajectories. For the two translating events in panels C and D, some cell-pairs have lags up to 200 minutes. For the shorter rotating events, the range of lag times is relatively smaller. There is no clear correlation between the magnitude of this time lag and the distance between cells.

Figure 4.

For four events, these histograms show the normalized occurrence frequency of leading and lagging times τc. τc is obtained from pair-wise correlation functions, and it represents the time lag at which the function has a peak above 0.5, indicating the delay between cell trajectories.

Discussion and Conclusion

Conventional cell tracking research assumes that the behavior of cells in 2D and 3D is homogenous in time; information from all time points is averaged to deduce the timescales for various cellular behavior³³. This is typically achieved by fitting cell trajectories to a stochastic random walk model³⁴ to evaluate speed and persistence of cells in 2D or 3D; however the basic assumptions of a persistent random walk fail in a system of cell collectives. Simplified versions of this analysis have been used on cell collectives in 3D to evaluate diffusion coefficients and angular velocity of human mammary cells¹¹, however these techniques are inapplicable to data presented here, since the first assumption to evaluating Mean Squared Displacement vs. time-lag is temporal homogeneity. As evident in Figure 2 and Supplementary Figure 2, for cell cohorts in this study, temporal heterogeneity is observable in patterns of motion. These systems are not correlated within a single field of view over the duration of observation— there are intervals in which clusters move away (Supplementary Video 1, 4–7 s) and intervals in which the same clusters move toward each other and merge (Supplementary Video 1, 33–40 s). Not all cohorts are alike; some exhibit higher translation, rotation, and fluctuation than others. For example, Gel I View i Cohort #3 has fourteen high motility events of both translation and rotation, while Gel II View ii Cohort #1 has only one motility event of translation (Figure 2, and Supplementary Tables). Cells in 3D are smaller than their 2D counterparts- our average cohort diameter is on the order of 2D single cell lengths³⁵, but in 3D, it spans ~6 –15 cells (Figure 1, and Supplementary Figure 1). Thus, displacements on the order of tens of microns, which would not be relevant for 2D studies, mark coherent collective motility in these 3D studies (Figure 1 and 2).

Cell collective studies of epithelial monolayers typically calculate the velocity correlation length^13,36,37 of monolayers. This correlation length is the length at which a radius-dependent velocity-correlation function equals zero on average for the monolayer. These analyses are effective at characterizing properties and differences between 2D cellular systems; however the underlying assumption is constant cellular density. Constant density is neither feasible nor interesting for 3D-collectives, since it does not pertain to any known 3D collective motility modes and cannot account for the ECM. Therefore analysis techniques from the field of collective motion³¹ are adapted here, specifically order parameters¹ and directional correlation functions, which have successfully been used to characterize heterogeneity in pigeon flocks³². Order parameters are easily adapted for this study— instead of calculating the order for the entire field of view, order parameters can be calculated on a cohort-by-cohort basis. The larger trajectory lags between cell-pairs that occur within a translating cohort as observed in our system may represent information transfer and polarity along the cohort. The order parameter of cohorts is seldom lower than 0.2, and the quartiles follow the same trends as the median (Figure 2); thus there is a tendency for cells to stay within cohorts instead of splitting apart and invading the matrix. These results imply that cell-cell junctions contribute largely to cohort integrity and function. Indeed, GFP E-cadherin MDCK cell cohort experiments displayed E-cadherin localized at cell boundaries in 3D (Supplementary Video 6).

Many modes of collective cell motility have been observed in the presence of an external driving agent⁴. The results presented here suggest that the system of cell-matrix interactions is complicated and diverse enough to drive collective motion. Emergent motility events arise in the absence of external or forced driving agents, and are stochastic, as in the case of the two clusters that merged (Figure 1C and D). There are examples of other similarly sized clusters that do not merge and in fact move in opposite directions (Supplementary Figure 1E and F). The transient nature of these events suggests that this system displays stochasticity and plasticity, both suspected to occur in cancer pathologies.³⁸ Our setup provides a model system that allows for characterization of inter-cohort and intra-cohort dynamics as well as identification and analysis of emergent motility events. The techniques presented here could be applied to cancer explants, which are known to show coordinated collective motion in vitro^5,6. As opposed to visually searching for motility, our work presents quantitative algorithms to isolate, observe, and characterize it. Since the methods operate on a cohort-by-cohort basis, they can be applied to a large amount of data and automated to extract motility events and compare different cellular cohorts.

Considering the balance of adherence and motility required for collective motion, translation over a few cell lengths in the absence of an external agent provides a promising model for the study of emergent phenomena and collective dynamics. Our results suggest that in the absence of external driving agents, interactions between cohorts and a collagen matrix are sufficient to drive collective cell motility. We show, for the first time, that cells spontaneously rotate in short bursts and translate for several hours; our analyses lay the foundation for quantitatively identifying supracellular polarity. The short bursts of rotation and comparatively larger spans of translation suggest that an internal stimulus arises within the dynamic cell-matrix system that attempts to drive collective translation. This work presents a quantitative approach to 3D cell collectives that have dynamic spatiotemporal heterogeneity– each cellular cohort is unique, and the algorithm finds motility events on a cohort-by-cohort basis. We built our custom algorithm using empirical data; however, it can be used for other cell types and experimental set-ups in order to probe questions of 3D collective mechanics, function, and efficiency. Our approaches can be expanded to study a range of phenomena in 3D, including collective cancer migration, density-dependent phase transitions, cell jamming, and emergent systems.