Abstract
We propose a method for the design of branched macromolecules that are capable of building up high tension (~nN) in their covalent bonds without applying an external force. The tension is self-generated due to repulsion between branches and depends on the molecular architecture leading to amplification and focusing of tension in specific bonds. The simplest architecture is a pom-pom composed of a linear spacer and two z-arm stars at its ends resulting in z-fold tension amplification. Adsorption of those macromolecules on a substrate results in further increase in tension as compared to molecules in solution.
Material properties, such as conductivity, color, and chemical reactivity change whenever molecules are under tension. Particularly strong effects are observed when the bond tension approaches the nano-Newton (nN) range, where covalent bonds typically rupture. This phenomenon is the subject of mechanochemistry [1] and mechanical biology [2–4]. Tension can be delivered to individual molecules using various micromanipulation techniques, such as atomic force microscopy, optical tweezers, and extensional flow [5–10]. However, controlling weak forces in single molecules is very challenging. Alternatively, molecules can be stretched by applying stress to bulk materials, such as polymer solutions, networks, and fibers [11–13]. In this case, the stress is distributed in a nonuniform way between many molecules. We propose a new method, which allows delivering high tension (~nN) to a large number of molecules in a controllable way without applying an external force. This method is based on intelligent molecular design which allows amplification of bond-tension from the pN to nN range. Recently, we have shown that nN tension is developed in brushlike macromolecules upon their adsorption to substrate [14]. In these experiments, the tension amplification is achieved due to adsorption-induced crowding of side chains. However, in solution, molecular brushes experience much lower tension (~10 pN), which is experimentally undetectable. Here we show how to achieve nN bond tension in solution, which can be detected by available spectroscopic techniques and, thus, expands the range of practical applications of the designed molecules as sensors, drug delivery, and catalysts.
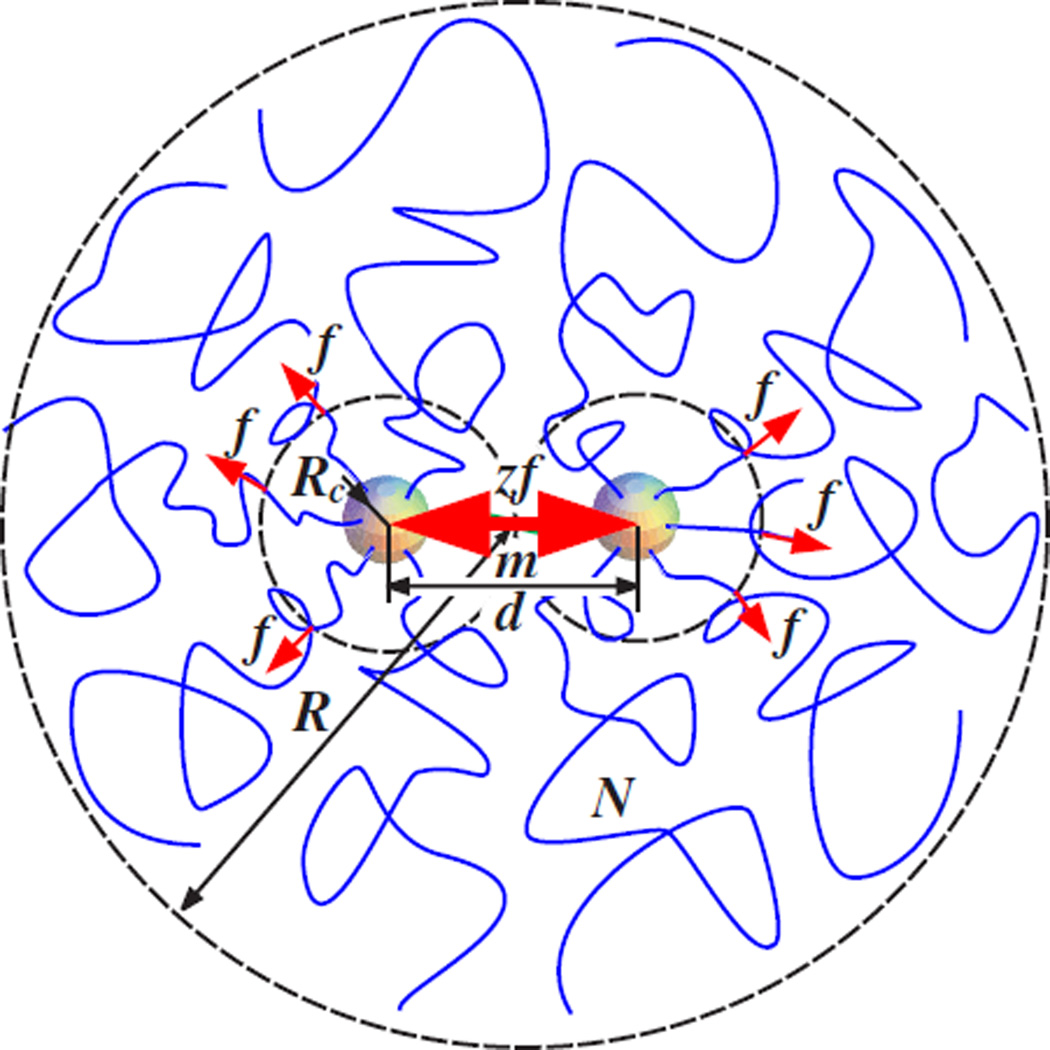
Two components are required for the construction of molecular tension amplifiers. The first component is a brushlike block that has intrinsic tension in its branches. The second component is a linear spacer which links the blocks in a particular way to focus the branch tension to the spacer. Figure 1 shows one of the simplest examples of the tension amplifier, a pom-pom macromolecule with two z-arm starlike brushes connected with a linear spacer. The tension in the brush arms is typically below 1 pN. By linking molecular stars, the individual tensions from z arms get focused to the single spacer leading to z-fold amplification of the spacer tension.
FIG. 1.
(color online). Architecture of a pom-pom macromolecule including a dense (solid) branching core of radius Rc, a region (Rc < r < d) of unperturbed star arms, and the corona of 2z arms whose conformation is perturbed by linking (pushing) together two z-arm stars.
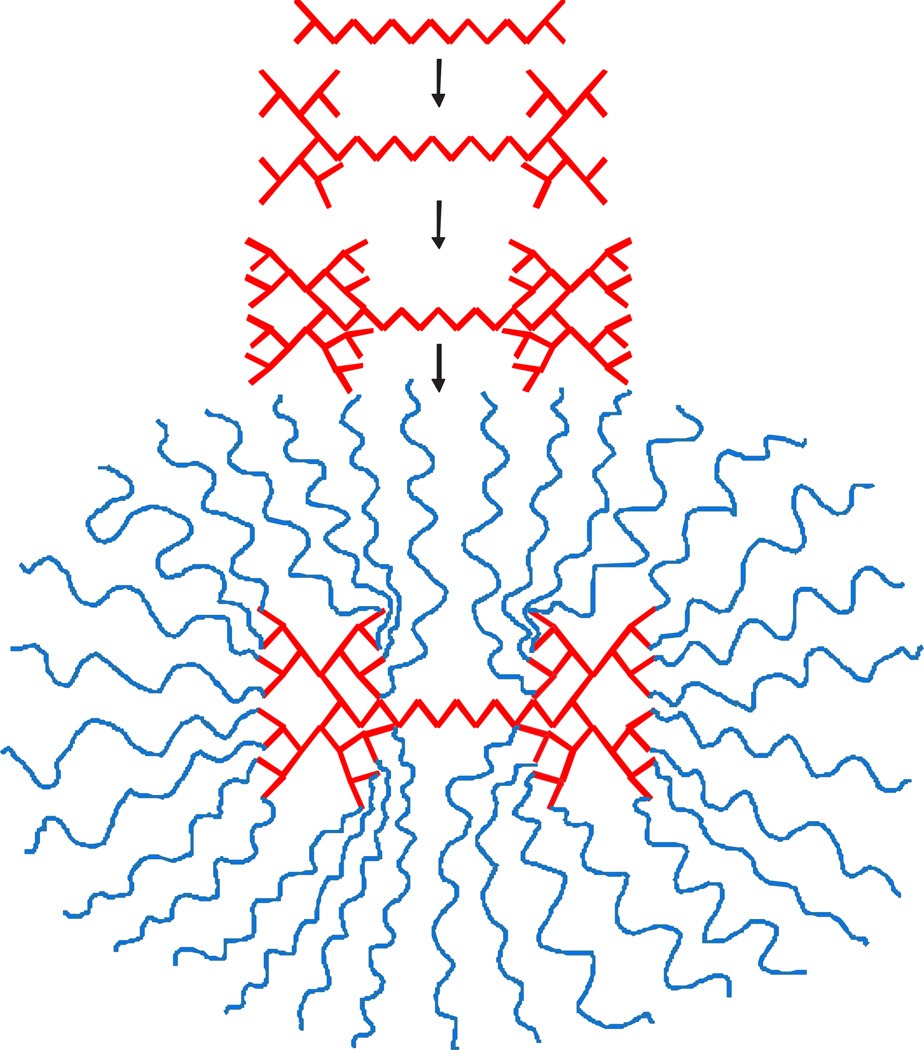
Such pom-poms can be synthesized starting from a linear precursor consisting of m Kuhn segments of length b each and two branching centers ABp−1 at its ends (Fig. 2). This is followed by reacting ABp−1 monomers to each of p − 1 reacting groups B (diverging polymerization [15,16]). This step is repeated a − 1 times, resulting in a dual-core dendrimer with 2(p − 1)a end groups. Finally, z = (p − 1)a linear arms are grown from each dendritic core. Since the tension in the arms decreases with distance from the branching centers, these arms should grow without significant steric hindrance, as long as the spacer length is larger than the diameter of the dendrimer. The grown arms repel each other and stretch the spacer. Using scaling approach, we will show that pom-pom architecture enables amplification of tension from the pN range in its arms to nN forces in the spacer.
FIG. 2.
(color online). Strategy for synthesizing pom-pom macromolecules which includes three major steps: (i) synthesizing a linear linker endcapped with branching functionalities, (ii) introducing z branches with reactive end groups, and (iii) growing z arms from these groups.
Star
Linear chains in a z-arm polymer star are under tension. In good and θ solvents, this tension is determined by osmotic repulsion between extended arms [17]. At θ temperature, the second virial coefficient is zero; however, the net interaction is repulsive due to the positive third virial coefficient [18]. The average distance between monomers of neighboring arms (correlation length ξ) linearly increases with distance r from the center of the star as
| (1) |
We drop numerical coefficients on the order of unity keeping our discussion on the scaling level. The osmotic repulsion leads to local tension in each arm as
| (2) |
where Rc is the smallest radius of the dendrimer core for a star with z arms. The highest tension in the arms is achieved at the surface of the core (r = Rc) as
| (3) |
which is ≃ 4 pN for a typical Kuhn monomer length b ≃ 1 nm.
It is less evident that the densely grafted arms are also stretched in poor solvents and even in a melt state, where the arms can overlap [19–21]. In this case, their extension is caused by constrained packing of z arms into a small volume. For a “dry” star (melt), the arm tension changes with r as
| (4) |
Note that the maximum tension f0 ≃ kT/b ≃ 4 pN is the same as in the case of a “wet” star [Eq. (3)].
Pom-Pom
Here we use the scaling model of star polymers to demonstrate the basic principles of bond-tension amplification by focusing the tension from individual branches to a particular polymer strand within a branched macromolecule. If two z-arm stars are pushed together, there is a repulsive force due to steric crowding of the arms. This repulsion is balanced by linking the stars with a spacer of length d. The tension in the spacer can be calculated from the difference between the free energies of 2z-arm star and two z-arm stars. For example, the energy difference in solution can be written as , where Rz (and R2z) is the radius of a z-arm (and 2z-arm) star and r is the radius of the unperturbed regions of each star [17]. This gives the spacer tension f = −∂(ΔF)/r|r≃d ≃ f0z3/2b/d, which can be interpreted as a sum of tensions in z individual arms measured at a distance r ≃ d. Using Eqs. (2) and (4), one calculates the tension as
| (5a) |
| (5b) |
A short spacer becomes fully stretched (d = bm) if its tension fsp > f0 [Eq. (3)]. In this case, the tension is given by Eq. (5):
| (6a) |
| (6b) |
Here, the lower limit for m is given by the radius of the dendrimer cores (Fig. 1), i.e., , while the upper limit of m is given by the lower limit of the spacer tension (fsp ≃ f0) at its full extension. For short spacers (m ≃ z1/2), the tension is on the order of zf0. For example, 7th-generation dendrimers with a branching functionality p = 3 and z = 512 arms [15,16] induce tension in the spacer of about 512 × 4 pN ≃ 2 nN, which is close to the strength of covalent bonds [1]. Note that the dendrimer radius should be 6.5 nm to accommodate 512 arms at a grafting density of 1 chain/nm2 [22,23], which is consistent with the radius of a typical 7th generation dendrimers. The tension of longer spacers with m > z1/2 is lower; however, it can be fine-tuned by adjusting the quality of the solvent between the two limits, defined in Eq. (6). Here, the melt state corresponds to the limiting poor solvent condition, called nonsolvent.
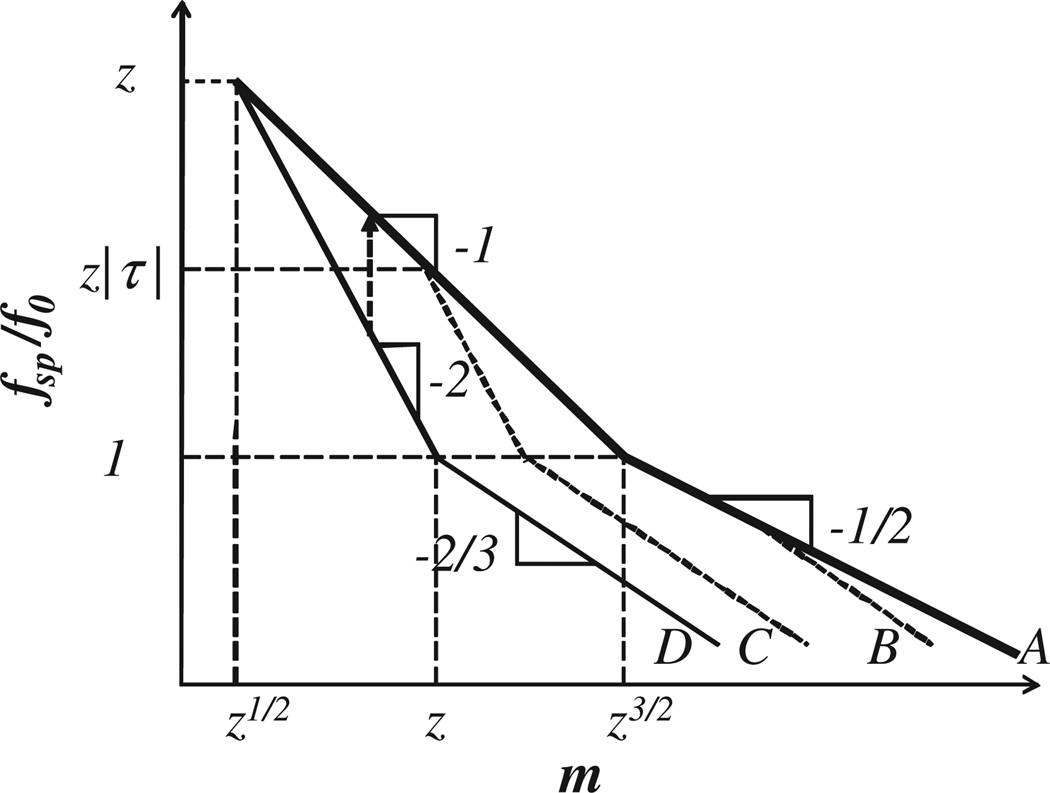
Figure 3 shows the equilibrium tension fsp as a function of the spacer length in different solvents. In the high tension range (fsp > f0), the bond tension in the fully extended spacer (d = bm) is given by Eq. (6). The equilibrium size of a longer spacer (which is not fully extended) is obtained by balancing the tensile force [Eq. (5)] by the chain elasticity fel = kTd/(b2m) = f0d/(bm) as
The corresponding tension can be written as
| (7a) |
| (7b) |
The crossover between the two limiting solvent conditions in Eqs. (6) and (7) can be described by introducing the excluded volume parameter υ, on the order of −b3 in a nonsolvent (melt) and υ = 0 in a θ-solvent [18]. For intermediate values of υ = b3τ (−1 < τ < 1), the tension in the spacer follows the θ behavior until the correlation length in the star at r = d [Eq. (1)] becomes larger than the size of the thermal blob b/|τ| [18]. In longer spacers, the tension follows the nonsolvent (melt) behavior and depends on the parameter of the solvent quality τ (middle lines in Fig. 3).
FIG. 3.
Log-log plot of tension fsp in a spacer with m Kuhn segments for pom-pom in different solvents. Upper curve— θ-solvent, middle curves—poor solvent; lower curve—melt condition.
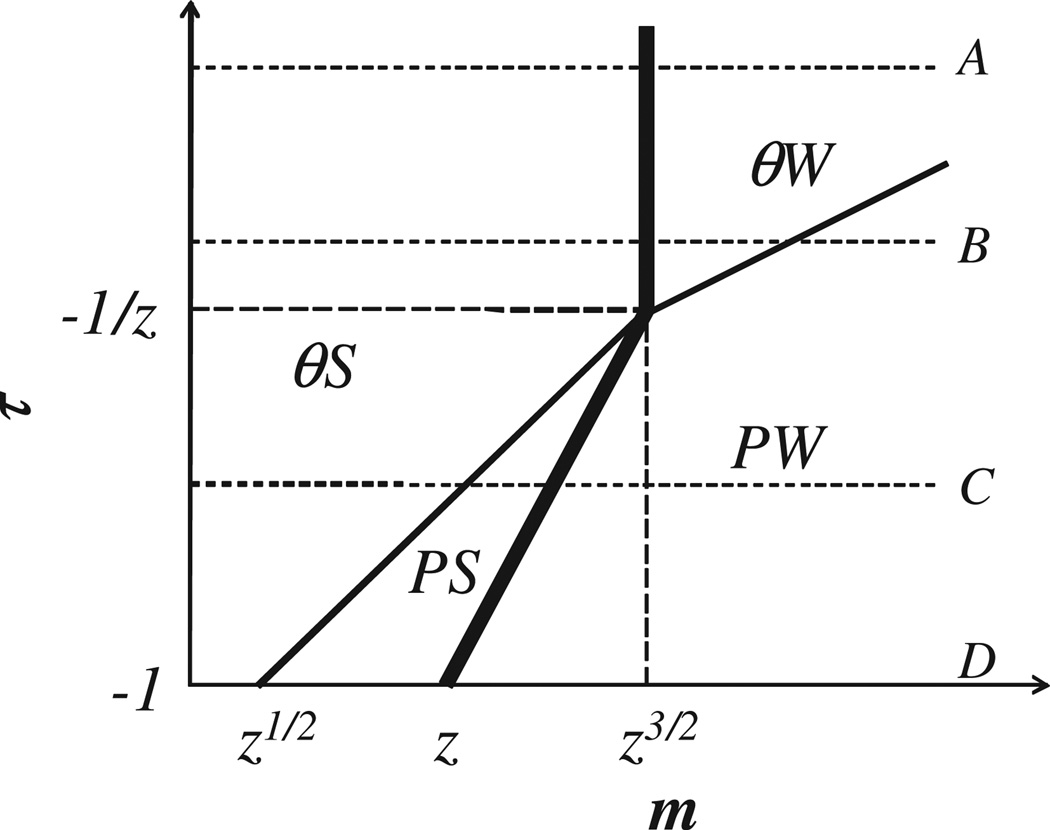
Different regimes of tension amplification in solvents of different quality are presented in Fig. 4. Part of the diagram to the left of the thick solid line corresponds to a fully extended spacer (regimes θS and PS) with fsp > f0, while the right part of this diagram corresponds to a weakly extended spacer (regimes θW and PW). Along the thin line in Fig. 4, the size of the thermal blob b/|τ| is on the order of correlation length at the length scale of the spacer [Eq. (1)]. This line separates θ-solvent regimes (θS and θW) from poor solvent regimes (PS and PW). The upper part of the diagram (regimes θS and θW) corresponds to θ solvent with the spacer tension given by Eqs. (6a) and (7a), see line A in Fig. 3. The nonsolvent (τ = −1) regime corresponds to the bottom boundary of the diagram, where the tension is given by Eqs. (6b) and (7b), see the lowest line (thin solid line D) in Fig. 3.
FIG. 4.
Diagram of states of a pom-pom in a poor and theta (θ) solvents. The four regimes depicted in the diagram are θ solvent for arms with strongly (θS) and weakly (θW) stretched spacer as well as poor solvent for arms with strongly (PS) and weakly (PW) stretched spacer. The boundary between strongly and weakly stretched spacer (thick line in the diagram) is given by the fully extended chain (d ≃ bN). The logarithmic axes are ln(m) and −ln|τ|.
In moderately poor solvent with −1 < τ < −z−1, the crossover between θ-like (regime θS) and poor-solvent-like (regime PS) behavior occurs in the lower part of the diagram in Fig. 4 (e.g., along the dotted line C). The tension along line C is
| (8a) |
| (8b) |
| (8c) |
as shown by the dashed curve C in Fig. 3. Closer to the θ point with −z−1 < τ < 0 (dashed line B in Fig. 4) the tension shows the θ-like behavior [Eq. (6a)] for a strongly stretched spacer (regime θS) with z1/2 < m < z3/2 and continues into the Gaussian zone for a weakly stretched spacer (regime θW), following Eq. (7a) for z3/2 < m < z−1/2|τ|−2. The tension of longer spacers (regime PW) is given by the poor solvent expression [Eq. (8c)] for z−1/2|τ|−2 < m < N/z, see the dashed line B in Fig. 3.
One of the important findings of this work is that the tension in a spacer can be fine-tuned by adjusting the quality of the solvent. For example, one can start with the spacer, consisting of z1/2 < m < z Kuhn segments in a nonsolvent (melt) state with the tension in the spacer given by Eq. (6b). As the solvent quality improves (arrow in Fig. 3) the tension in the spacer increases as |τ|−1 [Eq. (8b)] and saturates at the θ-solvent value of fsp [Eq. (8a)] for solvents with |τ| ≲ z1/2/m. The maximum solvent-induced change in tension by a factor of z1/2 is predicted for a spacer with m = z. In the case of 7th-generation dendrimer (considered above), the spacer tension increases from f0 ≃ 4 pN (in a melt with τ ≃ −1) to (at nearly θ temperature with |τ| ≲ 0.03).
Surprisingly, improving the solvent quality above the θ point (τ > 0) does not increase the tension in the spacer. For a fully extended spacer (z1/2 < m < z3/2), the correlation length ξ at the fixed distance r = bm from the branching center is determined by the number of monomers, m, in the spacer [Eq. (1)] independent on solvent quality. In the case of longer spacers (m > z−1/2τ−2), the behavior is even more surprising since the tension decreases with the solvent quality as
| (9) |
This softening is due to the partial swelling of the spacer and the resulting change of spacer elasticity from the Gaussian to nonlinear regime.
Another important result is that the tension amplification is independent of the number of monomers N in the arms and their polydispersity at N > m3/z for fully extended spacers with m < z and at N > mz for m > z. This underscores the origin of the tension due to local crowding of the 2z star-arms at a distance r ≃ mb. At r < mb, the arms maintain unperturbed conformation of single stars. At larger distances (r > mb), the steric repulsion rapidly decays due to the spherical shape of the stars resulting in logarithmic distance dependence of the energy.
In this Letter, we demonstrate that one can design a macromolecule which generates high bond tension (on the order of nN) in solution without applying an external force. The design strategy is based on linking multiple branches in such a way that weak (pN) tension in individual branches is focused and amplified to the nN range where covalent bonds fundamentally change their electronic structure and may eventually break. In addition to pom-poms, there are other types of branched architectures that allow tension amplification. For example, in cylindrically shaped molecular brushes, the tension from densely grafted side chains is focused to the backbone leading to significant tension increase which depends on the grafting density and the solvent quality [24]. The tension in the backbone is minimal in a nonsolvent with τ = −1 (melt), fsp ≃ f0, and increases with solvent quality, reaching the value f0N1/3 in a θ-solvent (τ = 0) and f0N3/8 in an athermal solvent (τ = 1). Unlike pom-poms, the tension in the brush backbone depends on the side-chain length N.
Acknowledgments
We would like to acknowledge financial support of National Science Foundation under Grants No. CHE-0616925 (M. R.), No. DMR-0606086 (S. S. S.), and No. CBET-0609087 (M. R. & S. S. S.), National Institutes of Health under Grant No. 1-R01-HL0775486A (M. R.), and Petroleum Research Fund under Grant No. 46204-AC7 (S. S. S.). We are grateful to E. B. Zhulina for very stimulating discussions.
Contributor Information
Sergey V. Panyukov, P. N. Lebedev Physics Institute, Russian Academy of Sciences, Moscow 117924, Russia
Sergei S. Sheiko, Department of Chemistry, University of North Carolina, Chapel Hill, North Carolina 27599-3290, USA
Michael Rubinstein, Department of Chemistry, University of North Carolina, Chapel Hill, North Carolina 27599-3290, USA.
References
- 1.Beyer MK, Clausen-Shaumann M. Chem. Rev. 2005;105:2921. doi: 10.1021/cr030697h. [DOI] [PubMed] [Google Scholar]
- 2.Discher DE, Janmey P, Wang Y-L. Science. 2005;310:1139. doi: 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
- 3.Evans EA, Calderwood DA. Science. 2007;316:1148. doi: 10.1126/science.1137592. [DOI] [PubMed] [Google Scholar]
- 4.Wiita AP, Ainavarapu SRK, Huang HH, Fernandez JM. Proc. Natl. Acad. Sci. U.S.A. 2006;103:7222. doi: 10.1073/pnas.0511035103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mehta AD, Rief M, Spudich JA, Smith DA, Simmons RM. Science. 1999;283:1689. doi: 10.1126/science.283.5408.1689. [DOI] [PubMed] [Google Scholar]
- 6.Janshoff A, Neitzert M, Oberdorfer Y, Fuchs H. Angew. Chem., Int. Ed. 2000;39:3212. doi: 10.1002/1521-3773(20000915)39:18<3212::aid-anie3212>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
- 7.Bustamante C, Keller D, Oster G. Acc. Chem. Res. 2001;34:412. doi: 10.1021/ar0001719. [DOI] [PubMed] [Google Scholar]
- 8.Grandbois M, Beyer M, Rief M, Clausen-Schaumann H, Gaub HE. Science. 1999;283:1727. doi: 10.1126/science.283.5408.1727. [DOI] [PubMed] [Google Scholar]
- 9.Harrington RE, Zimm BH. J. Phys. Chem. 1965;69:161. [Google Scholar]
- 10.Odell JA, Muller AJ, Narh KA, Keller A. Macromolecules. 1990;23:3092. [Google Scholar]
- 11.Watson WF. Makromol. Chem. 1959;34:240. [Google Scholar]
- 12.Zhurkov SN, Korsukov VE. J. Polym. Sci., Polym. Phys. Ed. 1974;12:385. [Google Scholar]
- 13.Hickenboth CR, Moore JS, White SR, Scottos NR, Baudry J, Wilson SR. Nature (London) 2007;446:423. doi: 10.1038/nature05681. [DOI] [PubMed] [Google Scholar]
- 14.Sheiko SS, et al. Nature (London) 2006;440:191. doi: 10.1038/nature04576. [DOI] [PubMed] [Google Scholar]
- 15.Tomalia DA, Naylor AM, Goddard WA. Angew. Chem., Int. Ed. Engl. 1990;29:138. [Google Scholar]
- 16.de Brabander-van den Berg EMM, Meijer EW. Angew. Chem., Int. Ed. Engl. 1993;32:1308. [Google Scholar]
- 17.Daoud M, Cotton JP. J. Phys. (Paris) 1982;43:531. [Google Scholar]
- 18.Rubinstein M, Colby RH. Polymer Physics. Oxford, UK: Oxford University Press; 2003. [Google Scholar]
- 19.Zhulina EB, Birshtein TM. Polym. Sci. USSR. 1985;27:570. [Google Scholar]
- 20.Birshtein TM, Zhulina EB. Polymer. 1989;30:170. [Google Scholar]
- 21.Semenov AN. Sov. Phys. JETP. 1985;61:733. [Google Scholar]
- 22.Tsujii Y, Ohno K, Yamamoto S, Goto A, Fukuda T. Advances in Polymer Science. Vol. 197. Berlin: Springer; 2006. Surface-Initiated Polymerization I; p. 1. [Google Scholar]
- 23.Brittain WJ, Minko S. J. Polym. Sci. A. 2007;45:3505. [Google Scholar]
- 24.Panyukov S, Zhulina EB, Sheiko SS, Randal G, Brock J, Rubinstein M. J. Phys. Chem. B. 2009;113:3750. doi: 10.1021/jp807671b. [DOI] [PMC free article] [PubMed] [Google Scholar]