Abstract
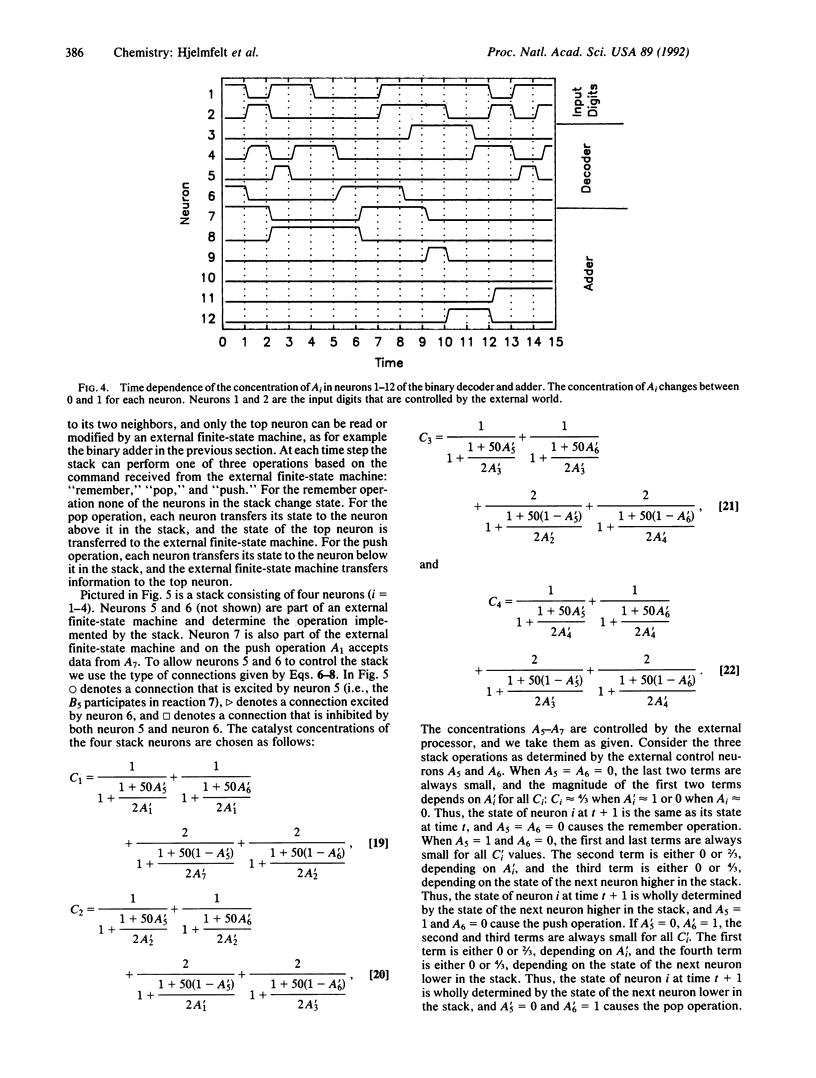
With methods developed in a prior article on the chemical kinetic implementation of a McCulloch-Pitts neuron, connections among neurons, logic gates, and a clocking mechanism, we construct examples of clocked finite-state machines. These machines include a binary decoder, a binary adder, and a stack memory. An example of the operation of the binary adder is given, and the chemical concentrations corresponding to the state of each chemical neuron are followed in time. Using these methods, we can, in principle, construct a universal Turing machine, and these chemical networks inherit the halting problem
Full text
PDF



Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Hjelmfelt A., Weinberger E. D., Ross J. Chemical implementation of neural networks and Turing machines. Proc Natl Acad Sci U S A. 1991 Dec 15;88(24):10983–10987. doi: 10.1073/pnas.88.24.10983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore C. Unpredictability and undecidability in dynamical systems. Phys Rev Lett. 1990 May 14;64(20):2354–2357. doi: 10.1103/PhysRevLett.64.2354. [DOI] [PubMed] [Google Scholar]
- Okamoto M., Hayashi K. Dynamic behavior of cyclic enzyme systems. J Theor Biol. 1983 Oct 21;104(4):591–598. doi: 10.1016/0022-5193(83)90247-3. [DOI] [PubMed] [Google Scholar]
- Okamoto M., Sakai T., Hayashi K. Switching mechanism of a cyclic enzyme system: role as a "chemical diode". Biosystems. 1987;21(1):1–11. doi: 10.1016/0303-2647(87)90002-5. [DOI] [PubMed] [Google Scholar]
- Wolfram S. Undecidability and intractability in theoretical physics. Phys Rev Lett. 1985 Feb 25;54(8):735–738. doi: 10.1103/PhysRevLett.54.735. [DOI] [PubMed] [Google Scholar]


