Skip to main content
NCBI home page
Nucleic Acids Research logoLink to Nucleic Acids Research
. 2016 Mar 1;44(6):2528–2537. doi: 10.1093/nar/gkw137

Quantitative assessment of ribosome drop-off in E. coli

Celine Sin 1,†, Davide Chiarugi 1,†, Angelo Valleriani 1,*
PMCID: PMC4824120  PMID: 26935582

Abstract

Premature ribosome drop-off is one of the major errors in translation of mRNA by ribosomes. However, repeated analyses of Ribo-seq data failed to quantify its strength in E. coli. Relying on a novel highly sensitive data analysis method we show that a significant rate of ribosome drop-off is measurable and can be quantified also when cells are cultured under non-stressing conditions. Moreover, we find that the drop-off rate is highly variable, depending on multiple factors. In particular, under environmental stress such as amino acid starvation or ethanol intoxication, the drop-off rate markedly increases.

INTRODUCTION

Translating messenger RNA (mRNA) into proteins is a complex polymerization process that lies at the heart of protein synthesis. Ribosomes play a pivotal role in this process, decoding of the genetic information contained in the mRNA into amino acid sequences (1).

Given their crucial role, ribosomes are designed to be accurate and robust processive machines. Nevertheless, inherent to all biological processes, errors can occur during protein synthesis. One of the possible errors is premature termination of the translation process; here the ribosome fails to complete the synthesis of a full-length protein.

Various mechanisms are known to mediate translation abortion. Some of them are believed to be relevant mainly when the cell faces stressing conditions that hamper mRNA translation, e.g. amino acid starvation. In bacteria, at least four abortion-mediating factors, namely the tmRNA-SmpB complex (2,3), RF3 (4), ArfA (5) and ArfB (6) are known to help rescue stalling ribosomes through processes that eventually lead to premature termination of protein synthesis. More surprisingly, translation abandonment can be also part of a proof reading mechanism that interrupts the synthesis of miscoded polypeptides (7). Besides these factor-mediated pathways, unspecific events, often referred to as nonsense errors (8) or processivity errors (9–12) can interrupt the elongation of the nascent peptide. Some examples of these errors include premature termination due to a false stop codon resulting from frameshift and accidental peptidyl tRNA dissociation from the translation complex (13,14). Also, local depletion of ternary complexes can provoke longer pausing events, which may trigger the drop-off of the ribosome (15). Both factor-mediated translation abandonment and processivity errors prevent the ribosome from reaching the final stop codon. Hence, irrespectively of the mechanism involved, we will use the term ‘ribosome drop-off’' to denote all the events that entail the premature detachment of the ribosomes from the mRNA template.

Ribosome drop-off is not limited to stress conditions; it occurs even when the cell is in a non stressing environment (9,10,12,16–18). In these conditions, the frequency of drop-off events in not affected by external stress and, thus, it is expected to assume a ‘basal’ value. In addition to the seminal works of Kurland et al. – reviewed in (12) – other proposals have explored the magnitude of the ribosome drop-off ‘basal rate’ or the dynamics of the phenomenon. In (10,17,18) ribosome drop-off was clearly detected and estimated for the β-galactosidase gene through different in vitro approaches. In (16), an in vivo experiment estimated the drop-off rate for E. coli to be 4  ×  10−4 events per codon. In (19), theoretical arguments demonstrate that the presence of a basal drop-off rate leads necessarily to an exponential distribution of ribosomes along the mRNA, while in (8), a model-based approach elucidates the impact of ribosome drop-off on protein synthesis. Thus, a well assessed quantitative estimate of the rate of ribosome drop-off could have a strong impact on modeling of ribosomal traffic and protein synthesis (20,21) as well as provide further hints to understand the relationship between gene length and protein abundance (22,23). In spite of these well-assessed findings, so far the analysis of data from Ribosome-profiling (Ribo-seq) experiments failed to find the existence of measurable ribosome drop-off frequency in non stressing conditions (24–26).

The ribosome profiling technique (27) begins with drug-mediated interruption of the cellular translation process, followed by the hydrolysis of the mRNA regions that are not covered (protected) by the ribosomes. The residual mRNA oligomers (known as ribosome protected fragments, RPF, because they are the mRNA fragments that were protected by the ribosome) are deep sequenced. Then, the positions of the ribosomes are determined by mapping the sequences to the reference genome.

In this setting, the relative abundance of RPFs that map to different parts of the single genes, usually evaluated in terms of ribosome density (RD) and measured in number of RPFs per codon, is typically used to estimate the protein synthesis rate for each gene. The distribution of RPFs along the genes can also provide information about the possible presence of ribosome drop-off: an average decrease of the RD from the 5’ end to the 3’ end of each open reading frame (ORF) reveals that a significant number of ribosomes fail to reach the 3’ end.

In this work, we reevaluate the analysis of Ribo-seq data with the goal of quantifying weak signals of ribosome drop-off. The methods used so far were not able to detect any ribosome drop-off in these data, despite experimental evidence of the phenomena. Through a new way of analyzing the same Ribo-seq data we will show that we find significant evidence of ribosome drop-off and that its rate of occurrence can be determined quantitatively and it is consistent with earlier experimental estimates.

MATERIALS AND METHODS

To compute the ribosome drop-off rate in E. coli, we analyzed all the related datasets present up to now in the GEO database (28) in which both the Ribo-seq data and the corresponding RNA-seq data were submitted. The GEO coordinates for these datasets are reported in Table 1. The experimental datasets analyzed here provide both ribo-seq and RNA-seq data for E. coli grown under different normal and stressed conditions. Datasets 1 and 2 refer to E. coli grown in LB medium (dataset 1) and then subject to acute heat stress at 47° C (dataset 2). Datasets 3 and 4 refer to E. coli grown in minimal medium (dataset 3) and then subject to acute osmotic stress (dataset 4). Dataset 5 refers to a strain of E. coli unable to synthesize Leucine when grown in a medium with Leucine. Dataset 5 will be compared with dataset 6, where the growth medium has no Leucine. Dataset 7 refers to a strain of E. coli unable to synthesize Serine when grown in a medium that provides Serine. Dataset 7 will be compared with dataset 8, where the growth medium has no Serine. Datasets 9, 11, 13 refer to E. coli grown in LB medium, subject to acute ethanol stress, and subject to chronic ethanol stress, respectively. Datasets 10, 12, 14 are replicas thereof. In datasets 15 and 16, E. coli is grown under normal conditions (dataset 15) and then subject to induced high expression of the sigma factor σE. Finally, dataset 17 reports on E. coli grown under normal conditions (LB medium).

Table 1. Coordinates of the datasets analyzed in this paper.

Dataset Series Organism Samples Ref.
# (GSE ID) (E. coli) (GSM ID)
1 68762 MC4100 1680885–1680884 (29)
2 MC4100 1680887–1680886
3 MC4100 1680889–1680888
4 MC4100 1680891–1680890
5 51052 MG1655 1399615–1399616 (30)
6 MG1655 1399610–1399611
7 BW25113 1399617–1399618
8 BW25113 1399612–1399613
9 56372 MG1655 1360042–1360030 (31)
10 MG1655 1360043–1360031
11 MG1655 1360044–1360032
12 MG1655 1360045–1360033
13 MG1655 1360046–1360034
14 MG1655 1360045–1360035
15 58637 MG1655 1415871–1415869 (38)
16 MG1655 1415872–1415870
17 53767 MG1655 1300279–300282 (24)
Open in a new tab

Column 1: Samples ID (referenced throughout the paper); Column 2: GEO Series ID; Column 3: Organisms used for the sequencing; Column 4: GEO Samples ID (left: Ribo-seq sample; right: RNA-seq sample). Column 4: Publication of reference. The entries reported in italic are the technical replicates of the entries reported above them.

In each case, we started our study from the ‘raw data’ consisting of FASTQ files (32). These files contain both the sequence of the oligonucleotides (reads) coming from the deep sequencing process (without any a posteriori data manipulation) and information about the quality of each read, i.e., the probability that of each nucleotide being correctly sequenced.

Our analysis protocol consists of two subsequent steps. In the ‘upstream phase’, we use existing software tools pipelined together to obtain a reliable mapping of the reads on the reference genome. In the ‘downstream phase’, we performed statistical analysis of the outputs from the upstream step using in-house scripts written in the ‘R environment’ (33).

Upstream analysis

For the upstream analysis of both the Ribo-seq and the related RNA-seq data, we applied the following procedure. The raw data was filtered using CUTADAPT (34) (release 1.8.3) such that only high quality reads were kept (Q-score ≥ 40, which corresponds to a sequencing error probability of 0.0001%). This refinement of the read sequences allowed us to reduce the probability of errors in the subsequent mapping phase; the presence of mis-sequenced nucleotides introduces artifacts that can increase the similarities between the query sequences and wrong mapping positions in the reference genome, thus increasing the probability of incorrect mapping. CUTADAPT was then used again to trim the adaptor sequences from the remaining reads.

We then filtered out all the reads that were shorter than 15 nucleotides to reduce the prevalence of multi-mapping errors. Shorter reads have a much higher chance of mapping to multiple places in the reference genome, simply due to combinatorics; thus with short reads, we cannot be confident that the part of the genome that the read mapped to actually reflects the origin of the read.

Afterward, we mapped the resulting reads against the rRNA sequences of E. coli to filter out the reads coming from the sequencing of rRNAs. We used the Bowtie2 aligner (35) (release 2.2.5) setting the running parameters in order to allow a successful mapping only when a high degree of similarity between the query read and the reference sequence occurs. In particular, we set the seed length to 15 (the minimum reads length) and we allowed no mapping mistakes in the seed. In this way, we maximized the probability of ruling out only the rRNA reads.

Finally, the remaining reads were mapped against the whole set of protein coding ORFs in E. coli, taken from the EnsemblBacteria database (36). Among the reads that mapped on the reference ORFs we selected the ones that mapped with the highest score possible for Bowtie2 (MAPQ = 42).

Ultimately, in the upstream phase we aim to minimize the bias that could arise either from the non-optimal quality of the sequenced reads or from the mapping process. For each sample analyzed (Table 1, fourth column), we obtained two set of reads (one coming from the raw Ribo-seq data and the other from the corresponding raw RNA-seq data) mapping on the same set of ORFs. These ‘refined’ datasets are used in the subsequent phase of our analysis.

Downstream analysis

In this step of our analysis lies the core of our method. All the procedures described hereafter were implemented through a custom script in the ‘R environment’. For the sake of readability we report all the details of the downstream analysis in the Supplementary Materials, Section 1.

Computing the average number of RPFs per ORF: a novel binning strategy

For each dataset reported in Table 1, we divided each ORF in bins of ℓ nucleotides and we counted the number of RPFs that mapped in each bin. This results in the RPF matrix composed by cells (i, j) reporting the number of RPFs that, for any given ORFi map in the corresponding bin j (see Supplementary Figure S1).

To normalize the amount of RPFs with the abundance of the corresponding RNA-seq reads, we divided the value in each cell of the RPF matrix by the quantity RNA(i, j) given by

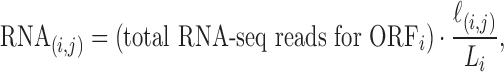graphic file with name M5.gif (1)

where ℓ(i, j) is the number of nucleotides of the ORFi in cell (i, j) and Li is the length of the ORFi in number of nucleotides. In this way, we obtain the matrix NRPF that reports the normalized Number of RPFs per bin in each cell:

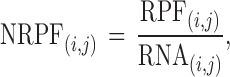graphic file with name M6.gif (2)

which is equivalent to assume a uniform coverage of each ORF by the RNA-seq reads mapping on it.

Finally, we computed the average over each column j of the NRPF matrix, obtaining a vector Y that contains the average normalized number of RPFs per bin for the whole set of ORFs. This averaging procedure ensures that sequence-specific features are also averaged out. We then use the vector Y to compute the drop-off rate r as detailed in the next paragraph. Supplementary Figure S1 reports a schematic representation of the binning strategy described above.

Estimation of the drop-off rate and its associated error

To obtain an estimate of the drop-off rate r per codon, we investigated the relationship between the average number of RPFs per bin Y and the bin number X. Inspired by theoretical considerations (19), we studied the dependence of Y from X in the form of the exponential decay

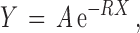graphic file with name M7.gif (3)

where X = 1, 2, … is the bin number and A is the intercept, which is of no interest here. The value of R can be referred to as the drop-off rate per bin and, widely speaking, indicates the probability per bin that a ribosome prematurely detaches from the mRNA template. The corresponding drop-off rate per codon r can be exactly related to R considering that drop-off events can occur anywhere inside each bin. Indeed, if r is the drop-off rate per codon, then the probability that the ribosome does not drop-off within a bin of ℓc codons is 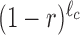Inline graphic. 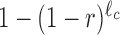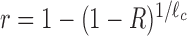Consequently, the probability R that any ribosome drops-off anywhere within the bin is Inline graphic and the drop-off per codon is Inline graphic.

To obtain a precise estimate of R and its associated error, we relied on a bootstrapping procedure, applied to each column of the NRPF matrix. In this way, for each dataset, we produced 105 Y vectors that are independent but statistically equivalent to each other. For each Y vector of any given dataset, we estimated one value of R through the (weighted) linear regression of ln Y versus X, thus exploiting the relationship described by Equation (3). From this procedure we obtained a normal distribution of the possible values of R for each original dataset (Supplementary Figure S2). The average and the variance of that distribution provide a first estimate of the true value of R and its associated variance. We call RBS the estimate of the drop-off rate per bin from the bootstrap. Its standard deviation is called SBS. Both RBS and SBS are specific to each single dataset (Supplementary Table S1).

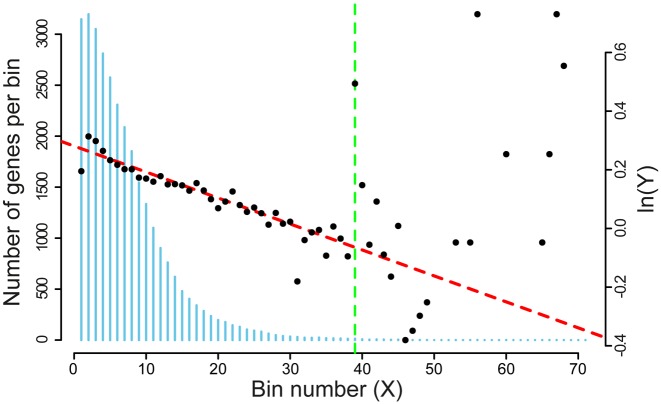
We further evaluated our estimate of R for possible systematic errors resulting from the choice of the bin size and the number of bins considered for the regression. The bin size affects the sensitivity of the regression to the drop-off rate. Larger bin sizes result in smoother curves, but lose information to averaging. Furthermore, the number of bins considered in the regression also affects the reliability of the estimation of R. In E. coli, the length of ORFs in genes is not uniformly distributed – there are significantly fewer genes with very long ORFs (Figure 1). Thus, statistics for later bins are sparse, and the bin average becomes a bad estimator of vector Y.

Figure 1.

Figure 1.

Open in a new tab

Number of elements in each column of the NRPF and BS matrices. The histogram (blue vertical bars) gives the number of genes contributing in each bin (scale on the left vertical axes). This number decreases from left to right. The plot superimposed to the vertical bars (resulting from the analysis of dataset 17, right vertical axes) shows that the scattering of the plotted values increases with the bin number, indicating an increase of the variance associated to the estimation of average normalized RPF's per bin, Y. The dashed vertical line (green) represents the cut-off (39 bins of 100 nucleotides) that we chose to obtain the best estimate of the drop-off rate.

To evaluate possible systematic errors, for each one of the analyzed datasets we created several simulated datasets. The simulated datasets replicated the original counterparts both in the ORDs lengths and in the number of reads mapping in each ORF. The position of the RPFs, instead, was redistributed along the ORFs according to a nominal drop-off rate. Our aim was to repeat the boostrapping procedure as we did for the real datasets and to measure the systematic deviations from the nominal drop-off rate used to generate the artificial profiles. For each dataset, we repeated the bootstrap process for various combinations of bin sizes and number of bins considered in the regression, looking for the combination that resulted in an R closest to the nominal drop-off rate. From this analysis we found that using a bin size of 100 nucleotides and the first 39 bins for the regression yields an estimate of R which is closest to the nominal value used for all datasets. With these settings, the estimated R was offset from the nominal value by a datasets-specific Δ and an associated standard deviation SΔ. The results obtained are reported in detail in Supplementary Table S1. Thus, for each experimental dataset, the best estimate of the drop-off rate R and its associated standard deviation per bins of 100 nucleotides is given by

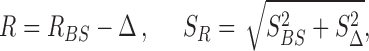graphic file with name M11.gif (4)

from which we obtain the drop-off rate and standard deviation per codon as r = 1 − (1 − R)3/100 and Sr = 1 − (1 − SR)3/100, respectively.

Summing up, our procedure to evaluate R consists of two steps: first, our bootstrap approach allows us to produce a set of ‘simulated technical replicas’. From this, we obtain a provisional estimate of the drop-off rate RBS and its associated standard deviation SBS. Next, we correct for the systematic effects of binning by subtracting the offset Δ while taking its variance 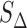Inline graphic into account.

RESULTS

For each experimental dataset reported in Table 1 we applied the analysis protocol described in Materials & Methods. The values we obtained for the drop-off rate per codon, r, are reported in Table 2 together with the respective standard deviations, Sr, and the 99% confidence intervals (Supplementary Materials, section 2).

Table 2. Drop off rates detected in the analyzed datasets.

Dataset r (10−4) Sr (10−4) CI (10−4)
1 2.9 0.3 r ± 0.8
2 2.2 0.4 r ± 1.0
3 2.4 0.2 r ± 0.5
4 1.9 0.3 r ± 0.8
5 0.7 0.3 r ± 0.8
6 n.a. n.a. n.a.
7 1.9 0.2 r ± 0.5
8 n.a. n.a. n.a.
9 2.4 0.5 r ± 1.3
10 2.2 0.7 r ± 1.8
11 5.1 0.4 r ± 1.0
12 5.6 0.3 r ± 0.8
13 2.3 0.3 r ± 0.8
14 2.3 0.3 r ± 0.8
15 3.0 0.3 r ± 0.8
16 0.0 0.4 r ± 1.0
17 1.4 0.2 r ± 0.5
Open in a new tab

Column 1: Datasets ID (see Table 1 for the respective GEO coordinates). Column 2: Drop-off rate per codon. Column 3: Standard deviation associated to r. Column 4: 99% Confidence Interval associated to r.

To check whether the values we obtained for r are significantly different from 0, we performed a Z-test for the mean for each of the r with a significance level of 0.01 (Supplementary Table S2). The results of our tests revealed that in 14 out of 17 cases we measured a drop-off rate significantly larger than 0. In the two datasets 6 and 8, instead, the relationship between X and Y is more complex than the single exponential decay described by Equation 3 and, thus, r cannot be evaluated through our method. The corresponding entries in Table 2 are, then, labeled with n.a.

Further analysis, based on the ANOVA test revealed significant differences among some values of r (see section 2.3 in Supplementary Materials for details). Given that the ANOVA test does not tell us which of the tested values are significantly different or equal to each other, we performed a series of coupled post hoc tests to investigate the sources of the detected variability. In particular, we compared the values we obtained for r within each GEO series. The outcomes of this analysis are reported in the next paragraphs.

Comparing the Drop-off rates in normal and stressing conditions

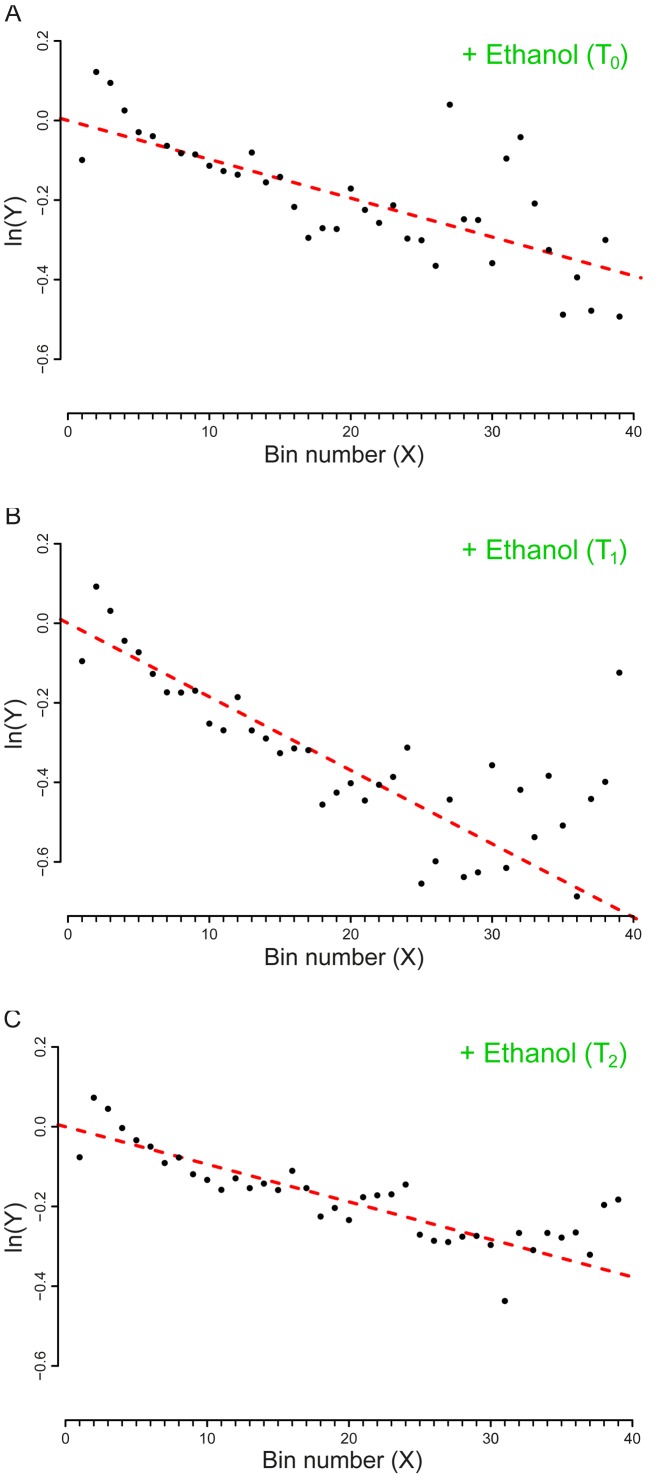
Datasets 9, 11 and 13: Ethanol-induced stress

This series refers to a set of experiments performed to elucidate the effect of ethanol intoxication on the translation machinery of E. coli MG1655. To this aim, the bacterial cells, first cultured in a minimal medium (M9 minimal medium, supplemented with MgSO4 1 mM, CaCl2 0.1 mM, and glucose 10 g/l) were exposed at T0  =  0 to a toxic concentration of ethanol (40 g/l) and sampled after T1 = 10 min and T2 = 70 min.

Through the Z-test, we compared the drop-off rate that we measured at each time point and, as shown in Table 3, it resulted that at T1 there was a significant increase in the drop-off rate. At T2, instead, the frequency of drop-off events restored to values similar to the basal rate that we measured at T0.

Table 3. Results of the Z-tests to compare the drop-off rates of Datasets 9, 11 and 13.
Compared samples Exp. conditions Z score Sig. level ZB
(Dataset ID) ( ± Z0.0025 )
9 M9 Minimal Medium
vs. vs. 4.19 ±2.81 ±3.14
11 Ethanol stress - T1
9 M9 Minimal Medium
vs vs. 0.17 ±2.81 ±3.14
13 Ethanol stress - T2
13 Ethanol stress - T2
vs vs. 6.08 ±2.81 ±3.14
11 Ethanol stress - T1
Open in a new tab

Column 1: Dataset ID (see Table 1 for the respective GEO Coordinates). Column 2: Experimental conditions. Column 3: Z-score computed from the comparison of the Drop-off rates. Column 4: Percentiles of the standard normal distribution corresponding to a total rejection area of 0.005. Column 5: Percentiles of the standard normal distribution corresponding to a total rejection area of 0.005, corrected according to the Bonferroni method (40). This test shows that the drop-off rate under acute ethanol stress is significantly different form the drop-off rate under normal conditions and chronic stress.

The results of our analysis agree with the findings that ethanol alters the structure of ribosomes, inducing an increase of translational errors and stalling events that in turn trigger cellular responses leading to premature translation termination (3). Figure 2, reporting the plots we obtained from our analysis, provides a graphical view of our findings.

Figure 2.

Figure 2.

Open in a new tab

Plot of the vector Y vs. the number of bins (X). The slopes of the dashed lines correspond to the drop-off rate r reported in Table 2. (A) Dataset 9 – Control (T0). (B) Dataset 11 – T1, after 10 minutes of ethanol stress. (C) Dataset 13 – T2, after 70 minutes of ethanol stress. The plots includes only the first 39 bins that we considered in our analysis. To facilitate the comparison with the similar graphs present in the paper we shifted the plots for a distance equal to the intercept of the regression line. The complete plots are reported in Supplementary Figure S6.

Hence, our approach reveals the existence of a basal drop-off rate that can be affected by environmental stress. Moreover, performing our analysis at different time points, we were able to provide some insights on the timing of the stress response: the reliability of the translation process is affected by ethanol only for a limited amount of time.

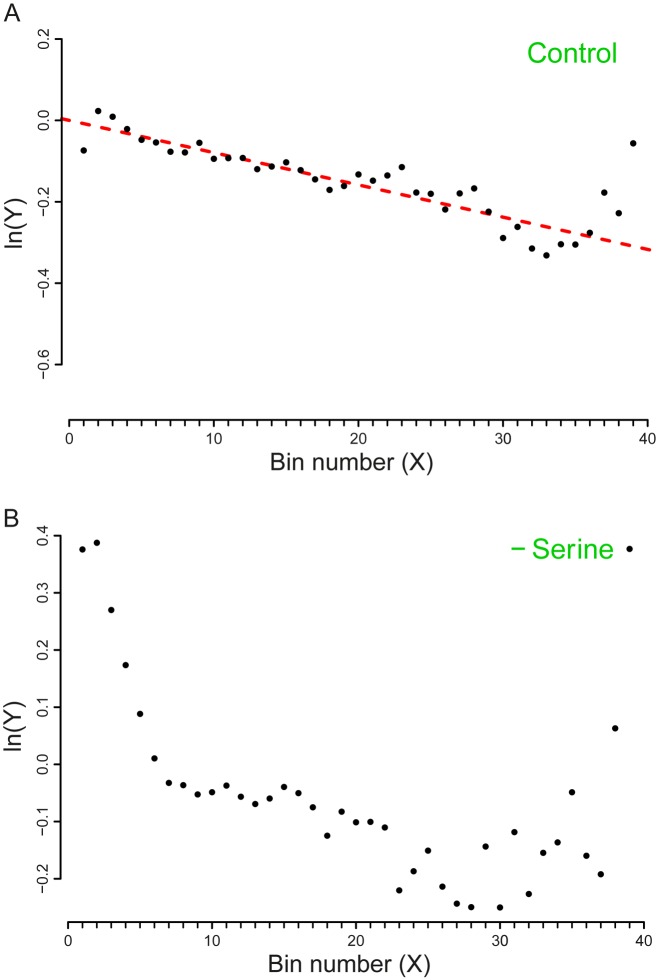
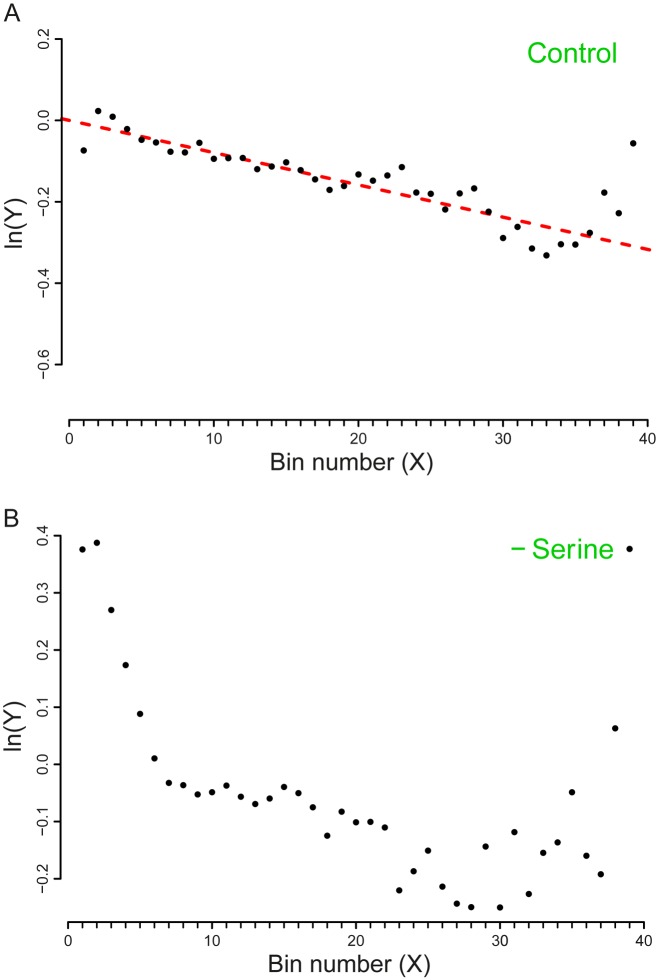
Datasets 5, 6, 7, 8: amino acids starvation

The experiments related to this series report the analysis of E. coli MG1655 and E. coli BW25113 cells that exhibit auxotrophic phenotypes respectively for the amino acids Serine and Leucine. The auxotrophic strains were grown either in a complete medium containing also the essential amino acids (rich medium – MOPS) or in conditions of starvation of the essential amino acid. Through our analysis, we succeeded in evaluating the basal drop-off rates related to the control experiments (growth in rich medium). More interestingly, the effect of premature ribosomal drop-off in the starvation conditions resulted to be qualitatively different from the normal conditions (Figures 3 and 4). This finding is consistent with the findings in (30) where an increase in the drop-off events upon amino-acid starvation was detected. Noticeably, the method used in (30) did not allow the detection of drop-off events in the control conditions. A possible explanation for this discrepancy is that in (30) a sliding window approach was used to average the ribosome profiles. In our method, the averages are computed in bins of fixed length. Even though the sliding window technique usually enhances the signal to noise ratio, it is also less sensitive to the signal detection with respect to our strategy. Therefore, it is possible that in (30) low frequencies of drop-off events are not detected because the sensitivity is compromised for the noise dampening. Another likely possibility is that a drop-off rate of 10−4 is hardly visible at the scale used in the plots of (30).

Figure 3.

Figure 3.

Open in a new tab

Plot of the vector Y vs. the number of bins (X). The slope of the dashed line corresponds to the drop-off rate r reported in Table 2. (A) Dataset 5 – Control (MOPS - Rich medium). (B) Dataset 6 – Leucine starvation. In this case, due to the poor fit with a single exponential model, we could not compute r. Thus, the regression line is not represented here.The plots include only the first 39 bins that we considered in our analysis. To facilitate the comparison with the similar graphs present in the paper we shifted the plot for a distance equal to the intercept of the regression line. The complete plots are reported in the Supplementary Figure S7.

Figure 4.

Figure 4.

Open in a new tab

Plot of the vector Y vs. the number of bins (X). The slope of the dashed line corresponds to the drop-off rate r reported in Table 2. (A) Dataset 7 – Control (MOPS – Rich medium). (B) Dataset 8 - Serine starvation. In this case, due to the poor fit with a single exponential model, we could not compute r. Thus, the regression line is not represented here. The plots include only the first 39 bins that we considered in our analysis. To facilitate the comparison with the similar graphs present in the paper we shifted the plot for a distance equal to the intercept of the regression line. The complete plots are reported in the Supplementary Figure S8.

Inspecting the plots, the decay of the density profile Y under both starvation conditions seem as it could be better desribed by a two-exponential decay model in which a steeper exponential curve is followed by a less steep one. Thus, the poor fit with a single exponential decay prevents a computation of r. This finding suggests that a more complex dynamics of the drop-off events is likely to come into play in conditions of heavy cellular stress such as amino acid starvation.

Summing up, our method allowed us to gain preliminary insights on the dynamics of drop-off events measured in different experimental settings. The global increase in the drop-off rate during amino-acid starvation is consistent with the idea that the starvation-induced increase of ribosome stalling events enhances the triggering of the rescue pathways (3) that, eventually, lead to a higher frequency of translation abortions.

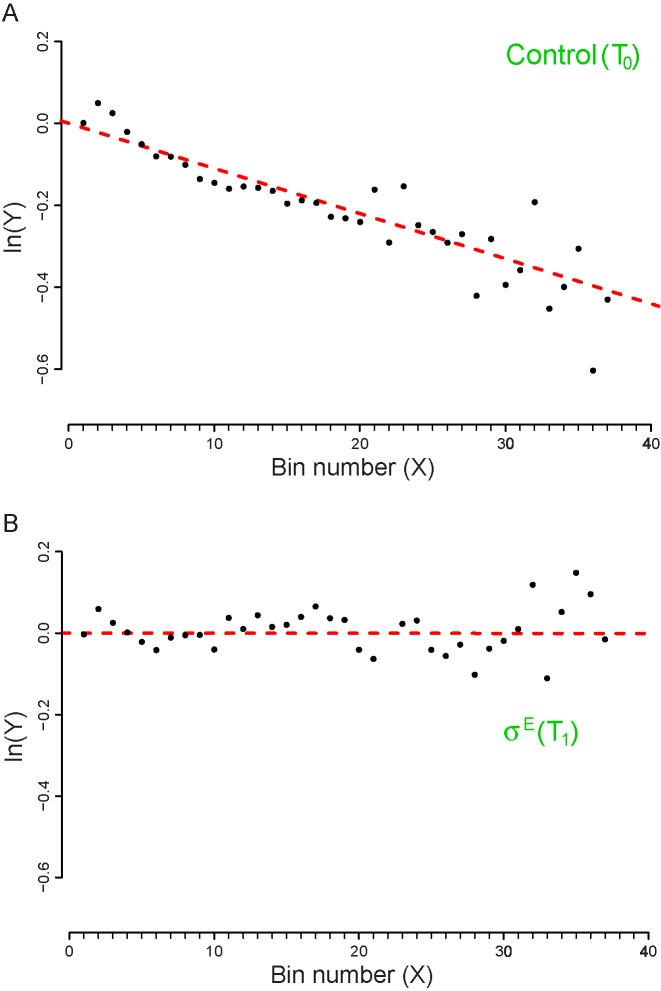
Datasets 15 and 16: A novel 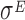Inline graphic-induced sRNA

The set of experiments related to this dataset were performed to find putative novel targets for the 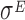Inline graphic transcription factor, which is known to play a pivotal role in regulating the homeostasis of the outer membrane (39). In one of the experiments, 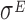Inline graphic was ectopically overexpressed, inducing the overespression plasmid pRpoE through 1mM of IPTG. Two samples were, then, harvested at T0  =  0 and T1  =  20 min and analyzed through Ribo-seq and the corresponding RNA-seq.

We analyzed the outcomes of these experiments and measured the drop-off rates at the two time points. Our Z-test reveals a clear difference in the two drop-off rates (see Table 4) which is evident also by inspecting the plots reported in Figure 5.

Table 4. Results of the Z-tests to compare the drop-off rates of samples coming from the GEO Series GSE58637.
Compared samples Exp. conditions Z score Sig. level ZB
(Dataset ID) ( ± Z0.0025 )
15 Control - T0
vs. vs. 6.07 ±2.81 n.a.
16 High level 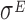Inline graphic - T1
Open in a new tab

Column 1: Dataset ID (see Table 1 for the corresponding GEO coordinates). Column 2: Experimental conditions. Column 3: Z-score computed from the comparison of the drop-off rates. Column 4: Percentiles of the standard normal distribution corresponding to a total rejection area of 0.005. Column 5: Percentiles of the standard normal distribution corresponding to a total rejection area of 0.005, corrected according to the Bonferroni method (40). The result of the Z-test confirms a significant difference between the drop-off rates at time T = 0 and at time T = 20 min.

Figure 5.

Figure 5.

Open in a new tab

Plot of the vector Y vs. the number of bins (X). The slope of the dashed lines correspond to the drop-off rates r reported in Table 2. (A) Dataset 15 – Control (T0). (B) Dataset 16 – T1, after 20 minutes of 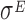Inline graphic over expression induction. The plots include only the first 39 bins that we considered in our analysis. To facilitate the comparison with the similar graphs present in the paper we shifted the plot for a distance equal to the intercept of the regression line. The complete plots are reported in the Supplementary Figure S9.

In particular, the sample collected at T1 exhibits a drop-off rate approximately equal to zero, which is the only case we obtained in our analysis. The biological interpretation of this finding is not easy to achieve, due to the scarcity of information regarding the role of 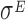Inline graphic in the regulation of the translation process. Indeed, the transcription factor 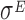Inline graphic is mainly known as a pleiotropic gene expression inducer that promotes the transcription of about 100 genes and three small regulatory RNAs. Our results point towards possible additional roles of 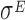Inline graphic in increasing the reliability of the translation process, at least when it is highly expressed.

Datasets 1, 2, 3 and 4: heat and osmotic stress

The data reported in (29) refer to the analysis of E. coli MC4100 cells cultured in the LB medium or in a minimal medium (12.8 g/l Na2HPO4·7H2O, 3 g/l KH2PO4, 1 g/l NH4Cl, 2 mM MgSO4, 0.1 mM CaCl2, 0.4% glucose) and subjected, respectively, to acute heat stress (47°C for 7 min) and to acute osmotic stress (NaCl 0.3M for 20 min 37°C). Through our analysis we succeeded in measuring a ‘basal’ rate of drop-off events (see Supplementary Figures S10 and S11) but we detected no significant differences in the drop-off rates between the control and stress condition. Table 5 reports the results of our Z-tests for the mean, showing that the obtained Z-scores (column 3) are in the boundaries of the acceptance area, thus supporting the null hypothesis of equal means.

Table 5. Results of the Z-tests to compare the drop-off rates of samples coming from the GEO Series GSE68762.
Compared samples Exp. conditions Z-score Sig. level ZB
(Dataset ID) (± Z0.0025 )
1 LB Medium
vs. vs. 1.61 ±2.81 ±3.02
2 Heat Stress
3 Minimal Medium
vs. vs. 1.21 ±2.81 ±3.02
4 Osmotic Stress
Open in a new tab

Column 1: Dataset ID (see Table 1 for the corresponding GEO coordinates). Column 2: Experimental conditions. Column 3: Z-score computed from the comparison of the drop-off rates. Column 4: Percentiles of the standard normal distribution corresponding to a total rejection area of 0.005. Column 5: Percentiles of the standard normal distribution corresponding to a total rejection area of 0.005, corrected according to the Bonferroni method (40). The results of the tests (all the Z scores falls into the acceptance area) show that the drop-off rates measured in normal and stressed conditions do not differ significantly.

These results could imply either that the cell-scale translation reprogramming events that are expected to occur in stressing conditions are not strong enough to be detected by our method or that the time scales chosen for harvesting the cells subjected to the stressing conditions were large enough to allow the translation dynamics to be restored to the initial levels. Unfortunately, our method does not allow to discriminate between these two hypotheses.

DISCUSSION AND CONCLUSIONS

Despite clear experimental evidence of ribosome drop-off, past attempts to detect ribosome drop-off in Ribo-Seq data were unsuccessful. In this paper we present a simple data analysis method that is sensitive enough to detect the weak decay of ribosome density over the ORF, which allows us to measure the cell-wide ribosome drop-off rate. With this method, we can even measure the basal rate of ribosome drop-off for cells in non-stressed conditions.

The other analytical approaches reported in literature so far were unsuccessful because the proposed binning strategy was not sensitive enough. These approaches typically divide each ORF into two halves and compare the number of reads that map on each half (see (24) and section 1.3 of Supplementary Materials). A significant reduction of reads in the second half would reveal that a certain number of ribosomes have not successfully completed translation. These results are typically illustrated by means of scatterplots where the ribosome density in the first half are plotted against the ribosome density in the second half (Supplementary Figures S3 and S5). When there is no significant difference between the densities in the two halves, the plotted points will cluster around a straight line with slope =1. For an ORF where the density of the second half is significantly lower than the first half, the corresponding point would fall below the straight line. At least in principle, this method is mathematically sound. However, it has a major drawback: the sensitivity of this approach depends critically on the ORF length. When the frequency of drop-off events is not large enough with respect to length of the ORFs, the difference in ribosome density between the two halves of the ORF is too small to be detected in a log-log scatterplot. As a consequence, if the genome of interest prevalently contains short genes, the scatterplot-method is not sensitive enough to detect the drop-off. This would lead to the wrong conclusion that, at the genome scale, the ribosome drop-off rate is not measurable.

Fortunately, our analysis technique is not affected by the length of the ORFs. We used our method to analyze various datasets referring to the bacterium E. coli cultured in different experimental conditions. The values we obtained for the drop-off rate ranged from a minimum of 1.4 × 10−4 to a maximum of 5.6 × 10−4 events per codon. These values make ribosome drop-off not negligible at the cellular level. Indeed, if we consider a drop-off rate of 4 × 10−4 per codon and an ORF length of 300 codons (approximately the average ORF length for E. coli), it turns out that on average, 10 out of every 100 ribosomes will fail to complete the translation of the messenger. Furthermore, taking into account the speed of ribosomes and the number of ribosomes actively involved in translation (37), and assuming a drop-off rate of 4 × 10−4 per codon in all growth conditions, the number of premature ribosome drop-off ranges from 1400 per minute per cell at slow growth conditions to 29 000 per minute per cell at fast growth conditions. Even considering the lifetime of a cell (37), the total number of drop-off events in a slowly growing population is about 14 × 104 events per cell cycle at slow growth (doubling time 100 min) and 75 × 104 at fast growth conditions (doubling time 25 min).

Furthermore, we come to a more general result relating drop-off rate and the length of genes. We found that, for a given drop-off rate, there is a limiting gene length above which the translation process becomes ineffective due to the high number of expected drop-off events. In the case of low drop-off rate, this threshold length is usually higher than the maximum gene length of E. coli. However, in those cases where ribosomes drop off with a higher frequency, the completion of translation is only reliable for shorter mRNAs. This suggests that when living organisms face conditions leading to increased drop-off rate (e.g. amino acids starvation) only a subset of genes can be effectively expressed. Since the probability of a ribosome to complete translation decreases exponentially with the ORF length, the magnitude of ribosome drop-off becomes an important evolutionary constraint of ORF length. If the genome of an organism is composed of ORFs that are too long relative to the drop-off rate, the reliability of translation may not support cell viability.

Our result is related also to the ongoing discussion concerning the existence of a high density of reads at the beginning of the ORF, a phenomenon sometimes referred to as the ‘ramp’ (41). With the exception of the data referring to the acute amino acids starvation, the analysis of our density profiles shows that in the samples considered here there is no phenomenological cross-over between the beginning of the ORF and the more downstream bins. Qualitatively, this means that our results would not change after eliminating the two first upstream bins. This indicates that in E. coli there is only one mechanism, namely ribosome drop-off, responsible for the decrease of the reads density in the whole ORF.

Contrary to previous Ribo-seq analysis results, we have shown that the magnitude of ribosome drop-off is highly variable and dependent on case-specific factors, including experimental conditions and the protocol used to collect Ribo-Seq data. Since the estimation of translation rates from Ribo-seq data assumes negligible ribosome drop-off, these estimations should be reevaluated to correct for possible biases due to drop-off events. In fact, we speculate that ribosome drop-off could be a possible explanation for the ubiquitous negative correlation between gene length and protein synthesis rate.

Supplementary Material

SUPPLEMENTARY DATA
supp_44_6_2528__index.html (748B, html)

Acknowledgments

The authors would like to thank Z. Ignatova, A. Bartholomaeus, L. Calviello for useful discussions and help at an early stage of this work.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Funding for open access charge: Home Institute's funding. This research work was supported by a grant of the European Union (ITN NICHE).

Conflict of interest statement. None declared.

REFERENCES

  • 1.Ramakrishnan V. Ribosome structure and the mechanism of translation. Cell. 2002;108:557–572. doi: 10.1016/s0092-8674(02)00619-0. [DOI] [PubMed] [Google Scholar]
  • 2.Keiler K.C., Waller P.R., Sauer R.T. Role of a peptide tagging system in degradation of proteins synthesised from damaged messenger RNA. Science. 1996;271:990–993. doi: 10.1126/science.271.5251.990. [DOI] [PubMed] [Google Scholar]
  • 3.Keiler K.C. Mechanisms of ribosome rescue in bacteria. Nat. Rev. Microbiol. 2015;13:285–297. doi: 10.1038/nrmicro3438. [DOI] [PubMed] [Google Scholar]
  • 4.Zaher H.S., Green R. A primary role for elastase factor 3 in quality control during translation elongation in Escherichia coli. Cell. 2011;147:396–408. doi: 10.1016/j.cell.2011.08.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Chadani Y., Ono K., Ozawa S., Takahashy Y., Takay K., Nanamiya H., Tozawa Y., Kutsukake K., Abo T. Ribosome rescue by Escherichia Coli Arf-A (YhdL) in the absence of trans-translation systems. Mol. Microbiol. 2010;78:796–808. doi: 10.1111/j.1365-2958.2010.07375.x. [DOI] [PubMed] [Google Scholar]
  • 6.Chadani Y., Ono K., Kutsukake K., Abo T. Escherichia Coli YaeJ protein mediates a novel ribosome-rescue pathway distinct from SsrA- and Arf-A mediated pathways. Mol. Microbiol. 2010;80:772–785. doi: 10.1111/j.1365-2958.2011.07607.x. [DOI] [PubMed] [Google Scholar]
  • 7.Zaher S.A., Green R. Quality control by the ribosome following peptide bond formation. Nature. 2009;457:161–166. doi: 10.1038/nature07582. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Gilchrist M.A., Wagner A. A model of protein translation including codon bias, nonsense errors and ribosome recycling. J. Theor. Biol. 2006;239:417–434. doi: 10.1016/j.jtbi.2005.08.007. [DOI] [PubMed] [Google Scholar]
  • 9.Kurland C.G. Translational Accuracy and the Fitness of Bacteria. Ann. Rev. Genet. 1992;26:29–50. doi: 10.1146/annurev.ge.26.120192.000333. [DOI] [PubMed] [Google Scholar]
  • 10.Jorgensen F., Kurland C.G. Processivity errors of gene expression in Escherichia coli. J. Mol. Biol. 1990;215:511–521. doi: 10.1016/S0022-2836(05)80164-0. [DOI] [PubMed] [Google Scholar]
  • 11.Hooper S. D., Berg O.G. Gradients in nucleotide and codon usage along Escherichia coli genes. Nucleic Acids Res. 2000;28:3517–3523. doi: 10.1093/nar/28.18.3517. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Kurland C.G., Mikkola R. The impact of nutritional state on the microevolution of ribosomes. In: Kjelleberg S, editor. Starvation in Bacteria. NY: Plenum Press; 1993. pp. 225–238. [Google Scholar]
  • 13.Baranov P.V., Atkins J.F., Yordanova M.M. Augmented genetic decoding: global, local and temporal alterations of decoding processes and codon meaning. Nature Rev. Genet. 2015;16:517–529. doi: 10.1038/nrg3963. [DOI] [PubMed] [Google Scholar]
  • 14.Gurvich O.L., Baranov P.V., Zhou J, Hammer A.W., Gesteland R.F., Atkins J.F. Sequences that direct significant levels of frameshifting are frequent in coding regions of Escherichia coli. EMBO J. 2002;22:5941–5950. doi: 10.1093/emboj/cdg561. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Zhang G., Fedyunin I., Miekley O., Valleriani A., Moura A., Ignatova Z. Global and local depletion of ternary complex limits translational elongation. Nucleic Acids Res. 2010;38:4778–4787. doi: 10.1093/nar/gkq196. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Menninger J.R. Peptidyl transfer RNA dissociates during protein synthesis from ribosomes of Escherichia coli. J. Biol. Chem. 1976;251:3392–3398. [PubMed] [Google Scholar]
  • 17.Manley J.L. Synthesis and degradation of termination and premature-termination fragments of beta-galactosidase in vitro and in vivo. J. Mol. Biol. 1978;125:407–432. doi: 10.1016/0022-2836(78)90308-x. [DOI] [PubMed] [Google Scholar]
  • 18.Tsung K., Inouye S., Inouye M. Factors affecting the efficiency of protein synthesis in Escherichia coli: production of a polypeptide of 6000 amino acid residues. J. Biol. Chem. 1989;264:4428–4433. [PubMed] [Google Scholar]
  • 19.Valleriani A., Ignatova Z., Nagar A., Lipowsky R. Turnover of messenger RNA: polysome statistics beyond the steady state. EPL. 2010;89:58003. [Google Scholar]
  • 20.Ciandrini L., Stansfield I., Romano M.C. Ribosome traffic on mRNAs maps to gene ontology: genome-wide quantification of translation initiation rates and polysome size regulation. PLOS Comp. Biol. 2013;9:e1002866. doi: 10.1371/journal.pcbi.1002866. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Reuveni S., Meilijson I., Kupiec M., Rupin E., Tuller T. Genome-scale analysis of translation elongation with a ribosome flow model. PLOS Comp. Biol. 2011;7:e1002127. doi: 10.1371/journal.pcbi.1002127. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Lu P., Vogel C., Wang R., Yao X., Marcotte E.M. Absolute protein expression profiling estimates the relative contributions of transcriptional and translational regulation. Nature Biotech. 2007;25:117–124. doi: 10.1038/nbt1270. [DOI] [PubMed] [Google Scholar]
  • 23.Valleriani A., Zhang G., Nagar A., Ignatova Z., Lipowsky R. Length-dependent translation of messenger RNA by ribosomes. Phys. Rev. E. 2011;83:042903. doi: 10.1103/PhysRevE.83.042903. [DOI] [PubMed] [Google Scholar]
  • 24.Li G.W., Burkhardt D., Gross C., Weissman J.S. Quantifying absolute protein synthesis rates reveals principles underlying allocation of cellular resources. Cell. 2014;157:624–634. doi: 10.1016/j.cell.2014.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Li G.W., Oh E., Weissman J.S. The anti-Shine-Dalgarno sequence drives translational pausing and codon choice in bacteria. Nature. 2012;484:538–541. doi: 10.1038/nature10965. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Oh E., Becker A.H., Sandikci A., Huber D., Chaba R., Gloge F., Nichols R.J., Typas A., Gross A.A., Kamer G., Weissman J.S., Bukau B. Selective ribosome profiling reveals the cotranslational chaperone action of trigger factor in vivo. Cell. 2011;147:1295–1308. doi: 10.1016/j.cell.2011.10.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Ingolia N.T. Ribosome profiling: new views of translation, from single codons to genome scale. Nat. Rev. Genet. 2014;15:205–213. doi: 10.1038/nrg3645. [DOI] [PubMed] [Google Scholar]
  • 28.Edgar R., Domrachev M., Lash A.E. Gene Expression Omnibus: NCBI gene expression and hybridization array data repository. Nucleic Acids Res. 2002;30:207–210. doi: 10.1093/nar/30.1.207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Bartholomaeus A., Fedyunin I., Feist P., Sin C., Zhang G., Valleriani A., Ignatova Z. Bacteria differently regulate mRNA abundance to specifically respond to various stresses. Phil. Trans. R. Soc. A. 2016;374:20150069. doi: 10.1098/rsta.2015.0069. [DOI] [PubMed] [Google Scholar]
  • 30.Subramaniam A.R., Zid B.M., O'Shea E.K. An integrated approach reveals regulatory controls on bacterial translation elongation. Cell. 2014;159:1200–1211. doi: 10.1016/j.cell.2014.10.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Haft R.J., Keating D. H., Schwaegler T., Schwalbach M. S., Vinokur J., Tremaine M., Peters J.M., Kotajic M.V., Pohlmann E. L., Ong I. M., et al. Correcting direct effects of ethanol on translation and transcription machinery confers ethanol tolerance in bacteria. PNAS. 2014;111:E2576–E2585. doi: 10.1073/pnas.1401853111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Cock P.J.A., Fields C.J., Heuer M.L., Rice P.M. The Sanger FASTQ file format for sequences with quality scores, and the Solexa/Illumina FASTQ variants. Nucleic Acids Res. 2010;38:1767–1771. doi: 10.1093/nar/gkp1137. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.R Development Core Team. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing; 2008. [Google Scholar]
  • 34.Martin M. CUTADAPT removes adapter sequences from high-throughput sequencing reads. EMBnet.journal. 2011;17:10–12. [Google Scholar]
  • 35.Langmead B., Salzberg S. Fast gapped-read alignment with Bowtie 2. Nat. Methods. 2012;9:357–359. doi: 10.1038/nmeth.1923. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Kersey P. J., Allen J.E., Christensen M., Davis P., Falin L.J., Grabmueller C., Hughes D.S., Humphrey J., Kerhornou A., Khobova J., et al. The Ensembl Genomes 2013: scaling up access to genome-wide data. Nucleic Acids Res. 2014;42:D546–D552. doi: 10.1093/nar/gkt979. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Bremer H., Dennis P.P. Modulation of chemical composition and other parameters of the cell by growth rate. In: Neidhardt FC, editor. Escherichia coli and Salmonella. 2nd edn. Washington, DC: ASM Press; 1996. pp. 1553–1569. [Google Scholar]
  • 38.Guo M.S., Updegrove T.B., Gogol E.B., Shabalina S.A., Gross C.A., Storz G. MicL, a new σE-dependent sRNA, combats envelope stress by repressing synthesis of Lpp, the major outer membrane lipoprotein. Genes Dev. 2014;14:1620–1634. doi: 10.1101/gad.243485.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Barchinger S.E., Ades S.E. Regulated proteolysis: control of the Escherichia coli σE-dependent cell envelope stress response. Subcell. Biochem. 2013;66:129–160. doi: 10.1007/978-94-007-5940-4_6. [DOI] [PubMed] [Google Scholar]
  • 40.Dunn O.J. Multiple comparisons among means. Am. Statist. Assoc. 1961;56:52–64. [Google Scholar]
  • 41.Tuller T., Carmi A., Vestsigian K., Navon S., Dorfan Y., Zaborske J., Pan T., Dahan O., Furman I., Pilpel Y. An evolutionarily conserved mechanism for controlling the efficiency of protein translation. Cell. 2010;141:344–354. doi: 10.1016/j.cell.2010.03.031. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

SUPPLEMENTARY DATA
supp_44_6_2528__index.html (748B, html)
supp_gkw137_nar-03629-f-2015-File019.pdf (1.1MB, pdf)

Articles from Nucleic Acids Research are provided here courtesy of Oxford University Press

RESOURCES