Reference Correlation of the Thermal Conductivity of Carbon Dioxide from the Triple Point to 1100 K and up to 200 MPa

Abstract

This paper contains new, representative reference equations for the thermal conductivity of carbon dioxide. The equations are based in part upon a body of experimental data that has been critically assessed for internal consistency and for agreement with theory whenever possible. In the case of the dilute-gas thermal conductivity, we incorporated recent theoretical calculations to extend the temperature range of the experimental data. Moreover, in the critical region, the experimentally observed enhancement of the thermal conductivity is well represented by theoretically based equations containing just one adjustable parameter. The correlations are applicable for the temperature range from the triple point to 1100 K and pressures up to 200 MPa. The overall uncertainty (at the 95% confidence level) of the proposed correlation varies depending on the state point from a low of 1% at very low pressures below 0.1 MPa between 300 K and 700 K, to 5% at the higher pressures of the range of validity.

1. Introduction

Carbon dioxide is a widely used industrial fluid with many applications including as a solvent for supercritical extraction¹, as a refrigerant², to aid in enhanced oil recovery³ and most recently as a potential working fluid in supercritical Brayton cycles that may be used in solar, geothermal, or other power cycle applications⁴. It is therefore important to have available accurate formulations for the thermodynamic and transport properties of this fluid.

In 1990, Vesovic et al.⁵ published a reference correlation for the thermal conductivity surface of carbon dioxide valid over the temperature range from 200 K to 1000 K and up to 100 MPa. In 2006, Scalabrin et al.⁶ developed a new correlation that extended the upper pressure limit to 200 MPa. The uncertainty of both of these formulations, however, is limited due to the data available at the time. Recently, new measurements have been made⁷ that will allow improvements in the uncertainty of a CO₂ thermal conductivity correlation, especially in the liquid phase. In addition, there have been recent improvements in the potential energy surface that provide values for the thermal conductivity in the dilute-gas limit⁸ that can be used to guide the behavior of the dilute gas, especially at low and high temperatures where quality data are scarce or unavailable. The present work aims to incorporate both new data and theory to provide an improved wide-ranging correlation for the thermal conductivity of carbon dioxide that is valid over gas, liquid, and supercritical states.

In a series of recent papers, reference correlations for the thermal conductivity of normal and parahydrogen,⁹ SF₆,¹⁰ toluene,¹¹ benzene,¹² xylenes and ethylbenzene,¹³ n-hexane,¹⁴ n-heptane,¹⁵ methanol,¹⁶ ethanol,¹⁷ and water,¹⁸ as well as a series of reference correlations for the viscosity of fluids,^19–22 covering a wide range of conditions of temperature and pressure, were reported. In this paper, the work is extended to the thermal conductivity of carbon dioxide.

2. Methodology

The thermal conductivity λ is expressed as the sum of three independent contributions, as

$$\lambda (\rho ,T)={\lambda }_{\mathrm{o}}(T)+\mathrm{\Delta }\lambda (\rho ,T)+\mathrm{\Delta }{\lambda }_{\mathrm{c}}(\rho ,T)$$ (1)

where ρ is the density, T is the temperature, and the first term, λ_ο(T) = λ(0,T), is the contribution to the thermal conductivity in the dilute-gas limit, where only two-body molecular interactions occur. The final term, Δλ_c(ρ,T), the critical enhancement, arises from the long-range density fluctuations that occur in a fluid near its critical point, which contribute to divergence of the thermal conductivity at the critical point. Finally, the term Δλ(ρ,T), the residual property, represents the contribution of all other effects to the thermal conductivity of the fluid at elevated densities including many-body collisions, molecular-velocity correlations, and collisional transfer.

The identification of these three separate contributions to the thermal conductivity and to transport properties in general is useful because it is possible, to some extent, to treat both λ_ο(T) and Δλ_c(ρ,T) theoretically. In addition, it is possible to derive information about λ_ο(T) from experiment. In contrast, there is almost no theoretical guidance concerning the residual contribution, Δλ(ρ,T), so that its evaluation is based entirely on experimentally obtained data.

The analysis described above should be applied to the best available experimental data for the thermal conductivity. Thus, a prerequisite to the analysis is a critical assessment of the experimental data. For this purpose, two categories of experimental data are defined: primary data employed in the development of the correlation, and secondary data used simply for comparison purposes. According to the recommendation adopted by the Subcommittee on Transport Properties (now known as The International Association for Transport Properties) of the International Union of Pure and Applied Chemistry, the primary data are identified by a well-established set of criteria.²³ These criteria have been successfully employed to establish standard reference values for the viscosity and thermal conductivity of fluids over wide ranges of conditions, with uncertainties in the range of 1%. However, in many cases, such a narrow definition unacceptably limits the range of the data representation. Consequently, within the primary data set, it is also necessary to include results that extend over a wide range of conditions, albeit with a poorer accuracy, provided they are consistent with other more accurate data or with theory. In all cases, the accuracy claimed for the final recommended data must reflect the estimated uncertainty in the primary information.

3. The Correlation

Table 1 summarizes, to the best of our knowledge, the experimental measurements^7,24–112 of the thermal conductivity of carbon dioxide reported in the literature. Eighty nine sets are included in the table. From these sets, 21 were considered as primary data. We started with the same data sets that were considered as primary in the work of Vesovic et al.⁵ in Tables 2 and 7 of that work. This includes the work of Millat et al.,²⁵ Johns et al.,²⁶ Clifford et al.,²⁹ Scott et al.,²⁸ Bakulin et al.,³³ Keyes,⁴¹ Lenoir and Comings,⁴² Johnston and Grilly,⁴³ Dickins,⁴⁴ Snel et al.,³⁰ and LeNeindre et al.^35–38 Initially we considered the single point of Franck⁸⁹ at 197 K that was considered primary in Vesovic et al.⁵, but it was later not used as discussed in the dilute-gas section. For Millat et al.,²⁵ following Vesovic et al.⁵, we also did not select any data from the 425 K isotherm. We included all points of Johns et al.²⁶ (except for one at a nominal temperature of 430 K and 20.4 MPa which is anomalously lower than others at that isotherm). All points from Clifford et al.,²⁹ Dickins,⁴⁴ Johnston and Grilly,⁴³ and Snel et al.³⁰ were included in the primary set. Following Vesovic, we also excluded the 316 K isotherm from Scott et al.²⁸ from the primary set. Initially all points in Keyes⁴¹ were included in the primary set but two points at the highest pressures at 273 K were later excluded. In addition, we added to the primary set the data from Keyes⁴⁰ as they extended down to 207 K. From Lenoir and Comings,⁴² we included only the points at atmospheric pressure as the density dependence of the other data in this set were inconsistent with other data. All points from the data of Bakulin et al.,³³ made with a steady-state hot-wire apparatus, were included in the primary set. In addition, we added another set of Bakulin’s measurements³² to the primary set, but excluded data above 1000 K, as we rely on the theoretical calculations of Hellmann⁸ in this region as will be discussed below. We also included the data of LeNeindre et al.^35–38 in the primary data set. All data from LeNeindre’s work were included, including the highest temperature data extending to 951 K, with the exception of several points that appeared to have typographical errors or that were clearly inconsistent with other data. This included one point from the Ref.(37) at 298 K, 30 MPa, and 3 points at 366 K and 70.3 MPa, at 372.45 K and 41.6 MPa, and 529 K, 35.2 MPa, from Ref. (35).

TABLE 1.

Thermal conductivity measurements of carbon dioxide

1st author	Year Publ.	Technique employeda	Purity (%)	Uncertainty (%)	No. of data	Temperature range (K)	Pressure range (MPa)
Primary data
Perkins7,b	2016	THW,SSHW	99.994	0.5–3	4824	218–757	0.1–68.7
Li24	1994	THW	99.999	1.6	14	324	0.19–2.1
Millat25,b	1987	THW	99.995	1	91	305–425	0.68–6.7
Johns26	1986	THW	99.995	1	46	380–474	1.83–30.6
Imaishi27	1984	THW	99.9	0.5	23	300–301	0.62–3.9
Scott28,b	1983	THW	99.995	1	92	301–349	0.3–24.6
Clifford29	1979	THW	99.999	0.5	22	301–304	0.6–5.9
Snel30	1979	HW	99.99	1	133	298–323	0.004–5.5
Tarzimanov31,b	1978	SSHW,CC	99.9	3	94	292–678	0.1–196
Bakulin32,b	1976	HF	na	5	10	400–1300	0.015
Bakulin33	1975	HF	na	5	28	225–316	0.1–2
Haarman34	1973	THW	na	1	8	328–468	0.1
Le Neindre35, 36	1973	CC	na	2–5	536	293–961	0.1–128
LeNeindre37,b	1972	CC	na	2–5	194	298–951	0.1–120
Le Neindre38,b	1968	CC	na	2–5	31	294–309	0.1–104
Michels39,b	1962	PP	na	2	253	298–322	0.1–18
Keyes40	1955	CC	na	5	2	207–273	0.1
Keyes41	1951	CC	na	5	9	273–423	0.1–6
Lenoir42,b	1951	CC	99.5	2	32	314–340	0.1–20.7
Johnston43,b	1946	HW	99.999	1–5	14	186–379	0.001
Dickins44	1934	HW	na	1	6	285	0.0001–0.001
Secondary data
Tomida45	2010	THW	na	3	19	273–294	4–15
Patek46	2005	THW	99.98	1.2	77	298–428	0.5–15
Heinemann47	2000	THW	na	5	3	323–420	0.1
Chen48	1999	TM	na	2	66	304–316	1.5–13
Dohrn49	1999	THW	na	5	7	300–420	0.1
Zheng50	1984	CC	99.5	3	13	298	0.10–5.4
Yorizane51	1983	CC	99.0	3	15	303–323	0.1–4.5
Becker52,c	1978	HolInt	99.994	3–5	216	298–308	3–49
Ulybin53	1977	HW	na	5	14	225–312	0.112–1.01
Chen54	1975	TEM	99.995	5	34	350–2000	0.1
Salmanov55	1973	SSHW	99.9	3	19	222–282	2–9
Shashkov56	1973	SSHW	na	4	9	315–403	0.1
Dijkema57	1972	CC	na	na	2	298–333	0.1
Gupta58	1970	HW	na	5	11	373–1348	0.07
Maczek59	1970	SSHW	na	3	1	323	0.1
Murthy60	1970	PP	99.99	3	53	305–310	7.5–8.3
Murthy61	1970	PP	99.99	3	3	305–307	0.1–8.2
Tarzimanov62	1970	SSHW	99.9	3	52	299–678	0.1–98.1
Golubev63	1969	CC	na	1.5–3	733	180–1400	0.1–51.0
Rosenbaum64	1969	CC	na	3	50	335–434	3–69
Barua65	1968	HW	99.5	1	5	283–473	0.1
Shingarev66	1968	SSHW	na	na	23	231–326	1–19.6
van Dael67	1968	HW	99.95	0.5	1	296	0.1
Freud68	1967	TEM	99.9	10	42	298	0.48–56
Mukhopadhyay69	1967	HW	na	1	7	258–473	0.1
Mukhopadhyay70	1967	HW	na	2	5	273–473	0.1
Baker71	1964	HW	na	na	1	478	0.1
Senftleben72	1964	na	na	4	8	273–673	0.1
Amirkhanov73	1963	PP	99.96	1	20	293–304	5.7–7.2
Cheung74	1962	CC	na	5	2	376–593	0.1
Guildner75	1962	CC	99.5	5	39	277–348	0.21–30
Westenberg76	1962	TWHW	na	3	3	299–500	0.1
Geier77	1961	CC	na	2	23	273–1273	0.1
Vines78	1960	CC	na	1	4	543–1174	0.1
Chaikin79	1958	HW	na	10	5	293–503	0.1
Guildner80	1958	CC	99.99	5	22	304–348	0.2–30.4
Waelbroeck81	1958	HW	na	na	1	313	0.1
Salceanu82	1956	HW	na	na	1	303	0.05
Kulakov83	1955	HW	na	na	2	338, 603	0.1
Rothman84	1955	CC	99.5	1	2	651–842	0.099–0.100
Filippov85	1954	HW	na	3	6	288–363	0.1
Thomas86	1954	SSHW	na	0.04–0.2	4	313–337	0
Davidson87	1953	CC	na	5	1	273	0.1
Rothman88	1953	CC	99.5	7.5	25	631–1047	0.1
Franck89	1951	HW	na	na	7	197–598	0.02–0.04
Kannuiluik90	1950	HW	na	0.3	9	275	0.001–0.11
Stolyarov91	1950	HW	99	3	17	280–475	0.1–30
Borovik92	1949	HW	na	na	18	283–313	5.1–9.1
Keyes93	1949	CC	na	5	8	223–623	0.1
Stops94	1949	HW	na	na	1	273	0.1
Timrot95	1949	HW	99.0	4	160	293–473	0.1–29
Kannuiluik96	1947	HW	na	5	26	196–373	0.1
Vargaftik97	1946	HW	na	na	13	325–881	0.1
Eucken98	1940	HW	na	na	6	195–598	0.1
Koch99	1940	na	na	5	71	283–313	0.1–9
Sherratt100	1939	HW	na	na	10	339–565	0.1
Archer101	1935	HW	na	0.4	11	285–591	0.1
Kannuiluik102	1934	HW	na	2	1	273	0.1
Kardos103	1934	na	na	na	6	273–308	5.9–8.8
Sellschopp104	1934	HW	na	2.5	50	284–323	0.10–9.15
Trautz105	1933	HW	na	1	19	273	0.24–1.19
Kornfeld106	1931	HW	na	na	1	298	0.1
Gregory107	1927	HW	99.82	na	6	278–286	0.1
Weber 108	1927	HW	na	1	1	273	0.1
Weber109	1917	HW	na	na	1	273	0.1
Schleiermacher110	1888	HW	na	na	1	298	0.1
Graetz111	1881	HW	na	na	1	273	0.1
Winkelmann112	1880	HW	na	na	1	298	0.1

^aCC, coaxial cylinder; HF, hot filament; HolInt, Heated plate observed by holographic interferometry; HW, hot wire; na, not available; PP, parallel plate; SSHW, steady-state hot wire; TEM, Thermoelectric method; THW, transient hot wire; TWHW, Thermal wake following hot wire heating.

^bonly selected points considered primary

^cthermal diffusivity

TABLE 2.

Primary data considered for dilute-gas analysis

1st author	No. of Data	Uncertainty (%)	T range (K)	Density (kg m−3)
Perkins7	1129	2–3	218–751	0.8–47.8
Li24	14	1.6	324	3–38
Millat25	4	1	308–426	0
Johns26	3	1	380–470	0
Imaishi27	1	0.5	301	0
Scott28	19	1	301–349	5–48
Clifford29	1	0.5	301	0
Snel30	3	1	293–323	0
Bakulin32	7	5	400–1000	0.1–0.2
Bakulin33	28	5	225–316	2–49
Haarman34	8	1	328–468	1.1–1.6
Le Neindre35, 36	78	2–3	296–961	0.7–50
Le Neindre37	37	2–3	298–951	0.6–1.8
Le Neindre38	7	2–3	296–309	1.7–46
Michels39	20	1	298–348	1.6–49
Keyes40	2	5	207–273	2.0–2.5
Keyes41	6	5	273–423	1.3–38
Lenoir42	5	2	314–340	1.7–40
Keyes93	5	5	223–473	23–48
Johnston43	14	1–5	186–380	0.02–0.04
Dickins44	6	1	285	0.03–0.2

TABLE 7.

Sample points for computer verification of the correlating equations.

T (K)	ρ (kg m−3)	λ (mW m−1 K−1)
250.0	0.0	12.99
250.0	2.0	13.05
250.0	1058.0	140.00
310.0	400.0	73.04a
310.0	400.0	72.28b
310.0	400.0	76.05c
310.0	400.0	39.92d

^aComputed with modified Olchowy–Sengers critical enhancement; the viscosity at this point for use in Eq. (5) was taken as η = 28.048 μPa s from Ref. ¹²⁶ (see Section 3.3.1). Thermodynamic properties required for the enhancement term Eq. (5)–(8) are from Span and Wagner¹¹⁴

^bComputed with modified Olchowy–Sengers critical enhancement; the viscosity at this point for use in Eq. (5) was taken as η = 28.706 μPa s from Ref. ¹²⁴. Thermodynamic properties required for the enhancement term Eq. (5)–(8) are from Span and Wagner¹¹⁴

^cComputed with empirical critical enhancement Eq. (10).

^dComputed without any critical enhancement term.

Although not considered as primary measurements in Vesovic’s⁵ analysis, we included all measurements of Haarman³⁴ and those of Imaishi et al.²⁷ as primary data. Haarman’s measurements³⁴ were made in a transient hot-wire apparatus and cover 328 K to 468 K at atmospheric pressure. Imaishi et al.²⁷ were also transient hot-wire measurements, but cover a very small temperature region around 301 K at pressures to 4 MPa. Finally, sources of primary data that focus on the critical region (Michels et al.,³⁹) were included although in the development of the background equation points within 1 K of critical were not used. Michels et al.³⁹ measured the thermal conductivity in the critical region with a parallel plate apparatus, and in addition to points within 1 K of critical we also excluded some points near the coexistence line (298 K, 6.4249 MPa; 298 K, 6.4208–6.4338 MPa; 303 K, 7.202–7.209 MPa), and any points that were marked with an asterisk in their tables. The thermal diffusivity data of Becker and Grigull⁵² were only used for analysis and validation of the critical region and were not used in the development of the background function, and will be discussed further in the critical enhancement discussion in Sec. 3.3.

Surprisingly, since Vesovic et al.⁵ made their correlation more than twenty years ago, in 1990, very few new measurements have been made.^{7, 24, 45–49} The only new measurements suitable as primary are those of Li et al.²⁴ and the most recent work of Perkins.⁷ Li’s work was done with a transient hot-wire instrument with an estimated uncertainty of 1.6%, but is limited to one isotherm at 324 K; all of these points were included in the primary data set. The measurements of Perkins⁷ were obtained with two hot-wire instruments; a low-temperature apparatus (218 K to 340 K), and a high-temperature apparatus (300 K to 750 K) at pressures up to 70 MPa. Both steady state and transient hot wire measurements were made, with uncertainties ranging from a low of 0.5 % for the liquid, increasing to 3 % for gas below 1 MPa, for temperatures above 500 K, and in the critical region. The data set of Perkins⁷ is large compared to the others, and not all points from Perkins were used as primary data. We included in the primary set the data measured with double platinum hot wires, but only points measured with a single platinum wire where the temperature ranges did not overlap since the double-wire data were considered of lower uncertainty and were preferred for primary data. We also did not include transient data from Perkins⁷ for low-density gas at temperatures above 505 K in the primary set, since for transient hot-wire measurements, the correction for the finite outer boundary containing the gas becomes increasingly large, due to the increasing thermal diffusivity of the gas, as the pressure of the gas decreases. This correction becomes even more significant as the temperature increases and for outer boundaries less than 1 cm diameter, and is why we do not include in the primary data the low-density (< 50 kg m⁻³) measurements made above 505 K. Steady-state hot-wire measurements of the dilute gas require much smaller corrections and have lower uncertainty than such transient hot-wire measurements with relatively large corrections for the finite outer boundary, and all steady-state low-density measurements made with double wires were included in the primary set, and single-wire steady-state measurements above 655 K. We also excluded from primary several point in the liquid phase where the equation of state calculated densities in the wrong phase for the given experimental temperature and pressure.

Finally, to extend the range of the measurements to high pressures, we added 11 points from Tarzimanov and Arslanov³¹ that are in the liquid phase to the primary data, and also 15 high-temperature (>550 K) high-pressure ( >98 MPa) supercritical points. These measurements reported in Table 1 in Tarzimanov and Arslanov³¹ were made with a coaxial cylinder apparatus, and those in Table 2 are from a steady-state hot-wire apparatus; we have assigned an uncertainty of 3% to both sets.

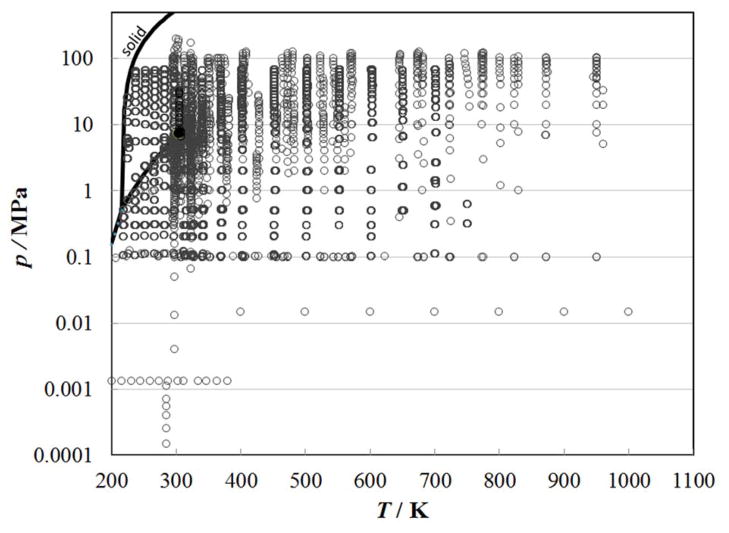
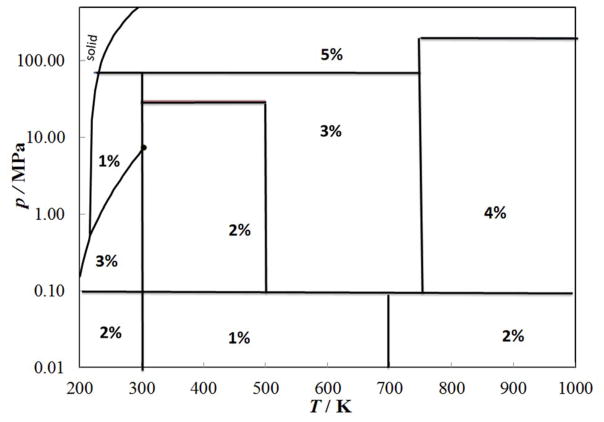
Figure 1 shows the temperature and pressure range of the primary measurements outlined in Table 1 considered for use as primary data. The critical point, solid-liquid, solid-vapor, and vapor-liquid lines are also indicated. With the inclusion of the recent data of Perkins,⁷ there is now good coverage of the liquid-phase region up to 70 MPa. Temperatures for all data were converted to the ITS-90 temperature scale.¹¹³ The development of the correlation requires densities; Span and Wagner¹¹⁴ in 1996 reviewed the thermodynamic properties of carbon dioxide and developed an accurate, wide-ranging equation of state valid for the fluid region from the triple point to 1100 K at pressures up to 800 MPa. The estimated uncertainty in density ranges from 0.03% to 0.05% in the density at pressures up to 30 MPa and temperatures to 523 K. Special interest was given to the description of the critical region, and the extrapolation behavior of the equation. We also adopt the values for the critical point and triple point from this equation of state; the critical temperature, T_c, and the critical density, ρ_c, were taken to be equal to 304.1282 K and 467.6 kg m⁻³, respectively, and the triple-point temperature is 216.592 K.¹¹⁴ We also adopt Span and Wagner’s correlation¹¹⁴ for the isobaric ideal-gas heat capacity, used in the theoretical model for the critical enhancement.

Figure 1.

Temperature and pressure ranges of the primary experimental thermal conductivity data for carbon dioxide.

3.1. The dilute-gas limit

To develop the zero-density correlation, we follow the procedure used in the development of a standard reference formulation for the thermal conductivity of water,¹⁸ which uses the concept of Key Comparison Reference Values¹¹⁵ to consider the uncertainties from different data sources. We first incorporated data sources^{25, 26, 28, 29, 33, 40, 42–44, 89} used in Table 2 of the 1990 Vesovic correlation,⁵ with the uncertainty estimates as given in Table 1. As mentioned above, we retained only data at densities less than 50 kg m⁻³. To those points, we added the zero-density point of Imaishi et al.²⁷ obtained by analysis of an isotherm at 301 K at a range of densities in a transient hot-wire instrument, and three zero-density points presented in Snell et al.³⁰ that resulted from their analysis of a range of densities for three isotherms obtained in a hot-wire apparatus. One additional publication by Keyes⁴¹ was included, considering only points at densities under 50 kg m⁻³. We also considered all points at densities below our cutoff from the work of Haarman,³⁴ LeNeindre et al.,^{35, 37, 38} Li et al.,²⁴ Michels et al.,³⁹ and Bakulin et al. ³² In addition, for Bakulin et al.,³² we considered only points at or below 1000 K. Finally, we included all double-wire measurements from the recent work of Perkins⁷ that were below the cutoff density except the transient data from Perkins⁷ for temperatures above 505 K as discussed earlier.

All low-density, primary data points were then arranged into bins encompassing a range of 8 K or less, with at least 4 data points in each bin. The average bin size was less than 3 K. Points that were already at zero-density ^{25–27, 29, 30} were not put into bins and were treated as separate isotherms. It was not possible to bin all points, since some exceeded the 8 K limit or failed to have at least 4 points. For example, it was not possible to include in a bin the data point of Franck at 197 K, so this point was not included in the primary data. This resulted in a total of 1328 points from 22 sources, obtained with a variety of experimental techniques and with a range of uncertainties.

The nominal temperature of an isotherm “bin” was computed as the average temperature of all points in a bin. The thermal conductivity of each point was then corrected to the nominal temperature, T_nom, by use of the following equation:

$${\lambda }_{\text{corr}}(T_{\text{nom}},\rho )={\lambda }_{\text{exp}}(T_{exp},\rho )+{[\lambda (T_{\text{nom}},\rho )-\lambda (T_{exp},\rho )]}_{\text{calc}},$$ (2)

where the calculated values were obtained from the Vesovic et al.⁵ thermal conductivity formulation.

Weighted linear regression was then used to extrapolate the nominal isotherms in order to obtain the value at zero density, λ₀. The difference between the zero-density thermal conductivity and the value at a density of 50 kg m⁻³ is small enough so that a linear expression can be used to extrapolate to zero density, but needs to be taken into account; for example, at 500 K the difference is about 5 %. Points were weighted with a factor equal to the inverse of the square of the estimated relative uncertainty. Confidence intervals of 95% were constructed from the regression statistics. Isotherms with large inconsistencies in the underlying data were rejected from further consideration. The resulting set of zero-density isotherms contained 47 points from 219 K to 751 K.

In order to supplement the experimental data set at very low and at high temperatures where data are unavailable or sparse, we incorporated selected theoretical data points from the recent work of Hellmann et al.⁸ The theoretical calculations were made with a new four-dimensional rigid-rotor potential energy surface, and the classical-trajectory method. We first adjusted the theoretical values by increasing their magnitude by a factor of 1.011 and ascribed to the theoretical values an uncertainty as recommended by Hellmann,⁸ namely 1% for points between 300 K and 700 K, increasing to 2% at 150 K and 2000 K. The adjustment of 1.011 was recommended by Hellmann based on comparisons with the best available experimental data and accounts for uncertainties in the intermolecular potential. We included 8 points from 150 K to 215 K, and 14 points from 760 K to 2000 K, so that the final set of zero-density values range from 150 K to 2000 K.

The zero-density values were fit using the orthogonal distance regression package ODRPACK¹¹⁶ to the same form of equation used in the water formulation¹⁸ for the dimensionless thermal conductivity in the limit of zero density,

$${\lambda }_{\mathrm{o}}(T_{\mathrm{r}})=\frac{\sqrt{T_{\mathrm{r}}}}{{\displaystyle \sum _{k=0}^J}\frac{L_k}{{T_{\mathrm{r}}}^k}},$$ (3)

where T_r= T/T_c is a reduced temperature, and λ_o is in mW m⁻¹ K⁻¹. We used the critical temperature from the Span and Wagner equation of state,¹¹⁴ T_c=304.1282 K.

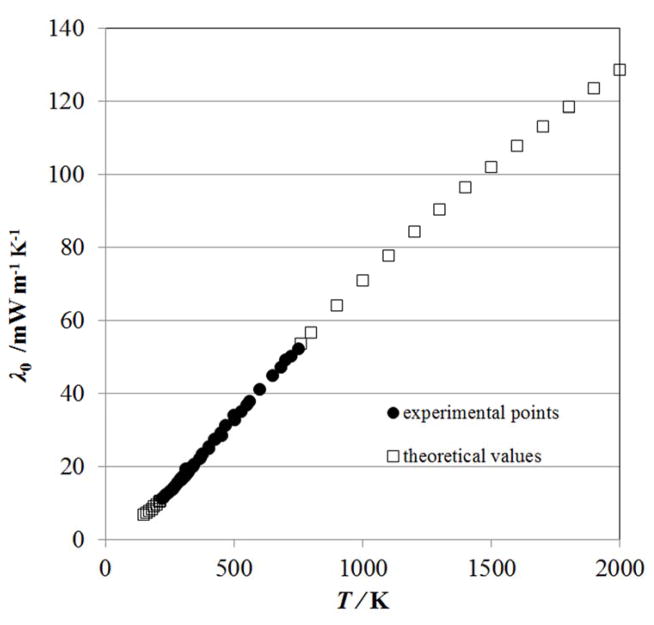
The final set of λ_o values contained 69 data points from 150 K to 2000 K and is shown in Fig. 2. The coefficients obtained from the regression are given in Table 3; we found a total of four terms were necessary. The initial weights were equal to the inverse of the square of the estimated uncertainty.

Figure 2.

Dataset for λ_o used in the regression.

Table 3.

Coefficients in Eq. (3) for λ_o

k	Lk
0	1.518 743 07×10−2
1	2.806 740 40×10−2
2	2.285 641 90×10−2
3	−7.416 242 10×10−3

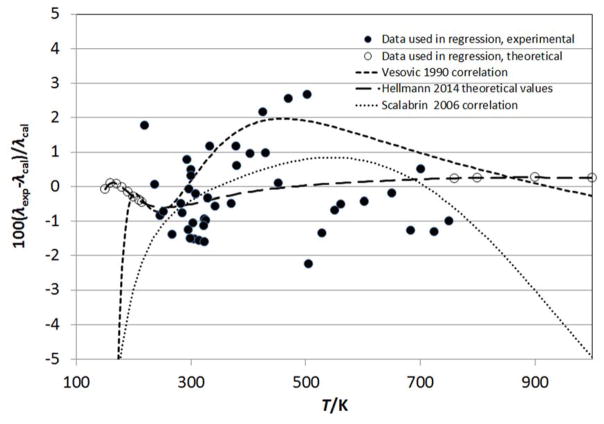
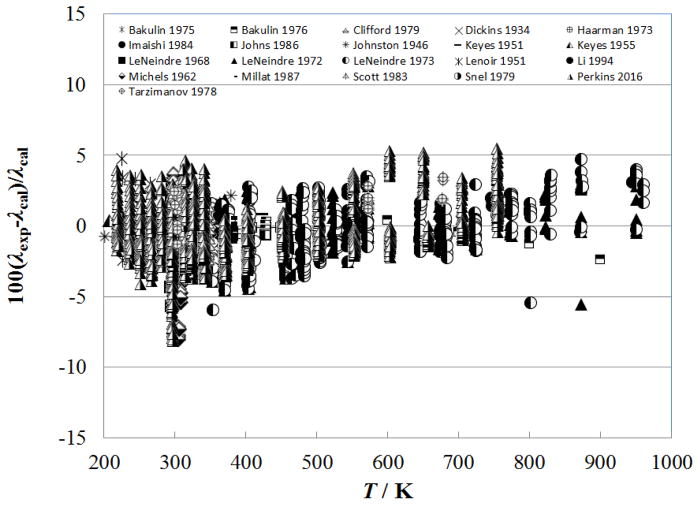
Figure 3 displays the percent deviation (100·(λ_o,_exp–λ_o,_cal)/λ_o,_cal) between the λ_o data and Eq.(3). Also shown are deviations with respect to the correlations of Vesovic et al.⁵ and Scalabrin et al.,⁶ and also with the theoretical calculations of Hellmann.⁸ The values of Hellmann⁸ have been scaled upward by a factor of 1.011 as mentioned earlier. The correlations of Vesovic et al.⁵ and Scalabrin et al.⁶ were valid only over the range 200 K to 1000 K, and it is obvious that at low temperatures both do not extrapolate well. At high temperatures, the Vesovic et al.⁵ correlation extrapolates much better than Scalabrin et al.⁶ since Vesovic included theoretical considerations in the high-temperature behavior. The present work uses the theoretical calculations of Hellmann⁸ to guide both the low (150 < T /K < 215) and high temperature (760 < T /K< 2000) behavior of the correlation, outside of the range of the best experimental data. Equation (3) may be extrapolated safely to 2000 K, the limit of the theoretical data included in the fit, although it does not take into account partial dissociation of CO₂ at high temperatures.¹¹⁷ The correlation of Vesovic et al.⁵ relied heavily on the works Millat et al.²⁵ and Johns et al.²⁶ particularly in the region 330 K to 470 K, while this work considered additional data (primarily Perkins⁷) that tended to be lower than of Millat et al.²⁵ and Johns et al.²⁶ and that are in closer agreement with Hellmann.⁸ Since there is considerable scatter in the experimental points, with many of the underlying data not in agreement within their stated uncertainties, we consider the comparisons with the scaled theoretical values of Hellmann⁸ to assess the uncertainty of the dilute-gas correlation. The theoretical values have an estimated uncertainty of 1 % between 300 K and 700 K, increasing to 2 % at both 150 K and 2000 K, and we adopt those values for our uncertainty estimate for Eq. (3).

Figure 3.

Comparison of λ_o correlations with the theoretical and experimental data.

3.2. The residual thermal conductivity

The thermal conductivities of pure fluids exhibit an enhancement over a large range of densities and temperatures around the critical point and become infinite at the critical point. This behavior can be described by models that produce a smooth crossover from the singular behavior of the thermal conductivity asymptotically close to the critical point to the residual values far away from the critical point.^118–120 The density-dependent terms for thermal conductivity can be grouped according to Eq. (1) as [Δλ(ρ,T) + Δλ_c(ρ,T)]. To assess the critical enhancement either theoretically or empirically, we need to evaluate, in addition to the dilute-gas thermal conductivity, the residual thermal-conductivity contribution. The procedure adopted during this analysis used ODRPACK (Ref. ¹¹⁶) to fit the primary data to determine the coefficients B_ij of the background thermal conductivity, Eq. (4), while maintaining the values of the dilute-gas thermal-conductivity data obtained by Eq. (3) and calculating the critical enhancement with the model discussed in the next section. The density values employed were obtained by the equation of state of Span and Wagner.¹¹⁴ The residual thermal conductivity was represented with a polynomial in temperature and density:

$$\mathrm{\Delta }\lambda (\rho ,T)=\sum _{i=1}^6\left(B_{1,i}+B_{2,i}(T/T_c)\right){(\rho /{\rho }_c)}^i.$$ (4)

During the regression process, it was found that the residual contribution as given by Eq. (4) does not require the temperature-dependent coefficients B_2,i for representation of supercritical and vapor-phase data. This also was pointed out by Vesovic et al.⁵ However, we found that allowing for temperature dependence of the residual contribution improved the representation of the liquid-phase data at high pressures (especially above 70 MPa), and we have included temperature coefficients B_2,i in our correlation. The coefficients B_1,i and B_2,i are shown in Table 4.

TABLE 4.

Coefficients of Eq. (4) for the residual thermal conductivity of carbon dioxide.

i	B1,i (W m−1 K−1)	B2,i (W m−1 K−1)
1	1.001 28 × 10−2	4.308 29 × 10−3
2	5.604 88 × 10−2	−3.585 63 × 10−2
3	−8.116 20 × 10−2	6.714 80 × 10−2
4	6.243 37 × 10−2	−5.228 55 × 10−2
5	−2.063 36 × 10−2	1.745 71 × 10−2
6	2.532 48 × 10−3	−1.964 14 × 10−3

3.3. The critical enhancement

The thermal conductivity and viscosity of a pure fluid diverge at the critical point.^{121, 122} The thermal diffusivity, a = λ/ρC_p, approaches zero at the critical point since the isobaric specific heat, C_p, diverges more rapidly than the thermal conductivity.¹²² Data for thermal diffusivity can be converted to thermal conductivity data when accurate values for the density and isobaric specific heat are available or can be calculated at the measurement conditions with an equation of state. Thermal conductivity data obtained from thermal diffusivity data have additional uncertainty associated with the ρ and C_p values that must be considered. Thus, it was decided to base the correlation on direct determinations of the thermal conductivity.

Thermal diffusivity data from light scattering are available much closer to the critical point and have the advantage in the critical region of not requiring a macroscopic temperature gradient, with a corresponding density gradient that can drive convection during thermal conductivity measurements. It was further decided to validate the critical enhancement model with the thermal diffusivity data very close to the critical point where thermal conductivity data are not available.

3.3.1. Simplified crossover model

The theoretically based crossover model proposed by Olchowy and Sengers^118–120 is complex and requires solution of a quartic system of equations in terms of complex variables. A simplified crossover model has also been proposed by Olchowy and Sengers.¹²³ The critical enhancement of the thermal conductivity from this simplified model is given by

$$\mathrm{\Delta }{\lambda }_{\mathrm{c}}=\frac{\rho C_p{R}_{\mathrm{D}}{k}_{\mathrm{B}}T}{6\mathrm{\pi }\overline{\eta }\xi }(\overline{\mathit{\Omega }}-{\overline{\mathit{\Omega }}}_0),$$ (5)

with

$$\overline{\mathit{\Omega }}=\frac{2}{\mathrm{\pi }}\left[\left(\frac{C_p-C_v}{C_p}\right)arctan({\overline{q}}_{\mathrm{D}}\xi )+\frac{C_v}{C_p}{\overline{q}}_{\mathrm{D}}\xi \right]$$ (6)

and

$${\overline{\mathit{\Omega }}}_0=\frac{2}{\mathrm{\pi }}\left[1-exp\left(-\frac{1}{{({\overline{q}}_{\mathrm{D}}\xi )}^{-1}+{({\overline{q}}_{\mathrm{D}}\xi {\rho }_{\mathrm{c}}/\rho )}^2/3}\right)\right].$$ (7)

In Eqs. (5) – (7), k_B is Boltzmann’s constant, η̄ is the viscosity, and C_p and C_v are the isobaric and isochoric specific heat. All thermodynamic properties were obtained from the equation of state of Span and Wagner.¹¹⁴ To estimate the viscosity, one can use either the correlation of Fenghour¹²⁴ or a new correlation just developed.¹²⁶ Both are implemented in the REFPROP (Ref. 125) program, the results reported here use the new formulation.¹²⁶ The correlation length ξ is given by

$$\xi ={\xi }_0{\left(\frac{p_{\mathrm{c}}\rho }{\mathrm{\Gamma }{\rho }_{\mathrm{c}}^2}\right)}^{\nu /\gamma }{\left[{\frac{\partial \rho (T,\rho )}{\partial p}|}_T-{\left(\frac{T_{\text{ref}}}{T}\right)\frac{\partial \rho (T_{\text{ref}},\rho )}{\partial p}|}_T\right]}^{\nu /\gamma }.$$ (8)

This crossover model requires the universal constants¹²¹ R_D = 1.02, ν = 0.63, and γ = 1.239, and system-dependent amplitudes Γ and ξ₀. For this work, as was done previously by Vesovic et al.,⁵ we adopted the values Γ = 0.052 and ξ₀ = 1.50×10⁻¹⁰ m, determined specifically for carbon dioxide¹²⁷ instead of using the general-method presented by Perkins et al.¹²¹ The reference temperature T_ref, far above the critical temperature where the critical enhancement is negligible, was calculated by T_ref = (³/₂) T_c,¹²¹ which for carbon dioxide is 456.19 K. The only critical-region parameter that needs to be determined is q̄_D. We used the effective cutoff wavelength ${\overline{q}}_{\mathrm{D}}^{-1}$ found in Vesovic et al.,⁵ 4.0 ×10⁻¹⁰ m. The equation of state of Span and Wagner¹¹⁴ displays some non-physical behavior at temperatures very close to the critical point that affects the heat capacity and the derivative of density with respect to pressure, so all data within 1 K of the critical point were excluded from the regression, and the set of B_1,i coefficients were obtained. The scaled equation of state of Albright et al.¹²⁷ was then used to validate this value of q̄_D and the background coefficients of Eq. (4), with both thermal conductivity and thermal diffusivity data within 1 K of critical as discussed in Sec. 3.3.2.

Table 5 summarizes comparisons of the primary data with the correlation. We have defined the percent deviation as PCTDEV = 100·(λ_exp–λ_cal)/λ_cal, where λ_exp is the experimental value of the thermal conductivity and λ_cal is the value calculated from the correlation. Thus, the average absolute percent deviation (AAD) is found with the expression AAD = (Σ|PCTDEV|)/n, where the summation is over all n points, the bias percent is found with the expression BIAS = (ΣPCTDEV)/n. Table 6 summarizes the deviations over all data sets.

TABLE 5.

Evaluation of the carbon dioxide thermal-conductivity correlation for the primary data.^a

1st author	Year Publ.	Nο. of Data	AAD (%)	BIAS (%)
Perkins7	2016	4095	1.42	−0.63
Li24	1994	14	0.39	0.12
Millat25	1987	78	0.80	−0.70
Johns26	1986	46	0.40	−0.04
Imaishi27	1984	23	0.56	−0.27
Scott28	1983	47	1.23	−0.96
Clifford29	1979	20	0.49	−0.23
Snel30	1979	93	1.63	−1.63
Tarzimanov31	1978	26	1.92	1.80
Bakulin32	1976	7	1.31	−1.05
Bakulin33	1975	28	1.33	0.08
Haarman34	1973	8	0.37	−0.35
Le Neindre35, 36	1973	528	1.57	−0.28
LeNeindre37	1972	193	1.47	0.27
Le Neindre38	1968	27	2.14	0.64
Michels39,a	1962	162	2.79	−1.69
Keyes40	1955	2	0.98	−0.55
Keyes41	1951	7	0.95	0.18
Lenoir42	1951	3	0.70	0.70
Johnston43	1946	14	0.82	−0.05
Dickins44	1934	6	0.81	−0.81
Entire data set		5427	1.5	−0.6

^aData within +/− 1 K of the critical temperature excluded

TABLE 6.

Evaluation of the carbon dioxide thermal-conductivity correlation for all data sets.

1st author	Year Publ.	No. of data	AAD (%)	BIAS (%)
Perkins7	2016	4824	4.1	2.2
Tomida45	2010	19	1.3	−0.6
Patek46	2005	77	0.7	−0.4
Heinemann47	2000	3	4.7	4.7
Chen48	1999	66	38.6	35.7
Dohrn49	1999	7	4.3	4.3
Li24	1994	14	0.4	0.1
Millat25	1987	91	0.8	−0.4
Johns26	1986	47	0.5	−0.2
Imaishi27	1984	23	0.6	−0.3
Zheng50	1984	13	0.5	−0.2
Scott28	1983	92	2.1	0.6
Yorizane51	1983	15	1.2	0.3
Clifford29	1979	22	0.5	−0.2
Snel30	1979	133	1.4	−1.4
Becker52	1978	217	7.7	−1.0
Tarzimanov31	1978	94	2.8	2.5
Ulybin53	1977	14	2.0	0.6
Bakulin32	1976	10	2.7	−2.6
Bakulin33	1975	28	1.3	0.1
Chen54	1975	34	4.6	−4.6
Haarman34	1973	8	0.4	−0.4
LeNeindre35, 36	1973	536	1.6	−0.2
Salmanov55	1973	19	3.3	3.3
Shashkov56	1973	9	1.4	−1.0
Dijkema57	1972	2	4.0	−4.0
LeNeindre37	1972	194	1.5	0.2
Gupta58	1970	11	5.2	−5.2
Maczek59	1970	1	1.9	−1.9
Murthy60	1970	3	1.3	0.9
Murthy61	1970	53	33.3	29.4
Tarzimanov62	1970	52	50.3	49.1
Golubev63	1969	733	9.9	9.1
Rosenbaum64	1969	50	2.8	0.3
Barua65	1968	5	2.2	−2.1
LeNeindre38	1968	31	2.2	0.8
Shingarev66	1968	23	3.8	−0.8
van Dael67	1968	1	1.5	−1.5
Freud68	1967	42	6.0	1.6
Mukhopadhyay69	1967	7	1.7	−0.9
Mukhopadhyay70	1967	5	2.2	−2.1
Baker71	1964	1	1.9	−1.9
Senftleben72	1964	8	2.3	0.9
Amirkhanov73	1963	20	22.6	−22.2
Michels39	1962	253	11.8	6.4
Cheung74	1962	2	1.1	−1.1
Guildner75	1962	39	10.3	8.0
Westenberg76	1962	3	1.5	−1.5
Geier77	1961	23	9.6	−8.9
Vines78	1960	4	1.2	0.5
Chaikin79	1958	5	5.4	−5.4
Guildner80	1958	22	15.6	13.5
Waelbroeck81	1958	1	1.0	−1.0
Salceanu82	1956	1	6.2	−6.2
Keyes40	1955	2	1.0	−0.6
Kulakov83	1955	2	64.9	−64.9
Rothman84	1955	2	4.9	−4.9
Filippov85	1954	6	13.1	4.3
Thomas86	1954	4	1.5	−1.5
Davidson87	1953	1	3.8	−3.8
Rothman88	1953	25	3.6	−2.2
Franck89	1951	7	4.8	−4.8
Keyes41	1951	9	1.6	1.0
Lenoir42	1951	32	4.4	4.4
Kannuiluik90	1950	9	2.7	−2.7
Stolyarov91	1950	17	8.0	3.1
Borovik92	1949	18	7.0	−6.8
Keyes93	1949	8	4.6	−4.5
Stops94	1949	1	1.3	1.3
Timrot95	1949	160	11.8	−0.7
Kannuiluik96	1947	15	1.6	1.5
Johnston43	1946	14	0.8	0.0
Vargaftik97	1946	13	2.7	−2.7
Eucken98	1940	6	5.3	−4.8
Koch99	1940	54	5.2	−4.8
Sherratt100	1939	10	2.0	1.8
Archer101	1935	11	6.4	−6.4
Dickins44	1934	6	0.8	−0.8
Kannuiluik102	1934	1	2.3	−2.3
Kardos103	1934	6	150.2	150.2
Sellschopp104	1934	50	7.7	0.6
Trautz105	1933	19	29.2	22.6
Kornfeld106	1931	1	2.6	2.6
Gregory107	1927	6	0.6	0.2
Weber 108	1927	1	2.6	−2.6
Weber109	1917	1	3.7	−3.7
Schleiermacher110	1888	1	2.0	2.0
Graetz111	1881	1	11.1	−11.1
Winkelmann112	1880	1	13.5	−13.5

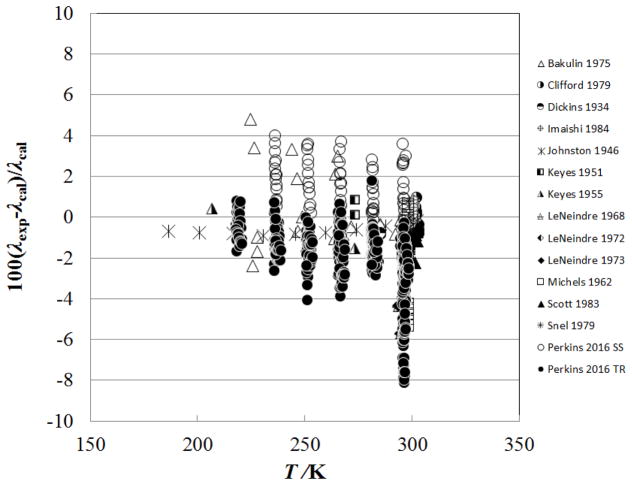
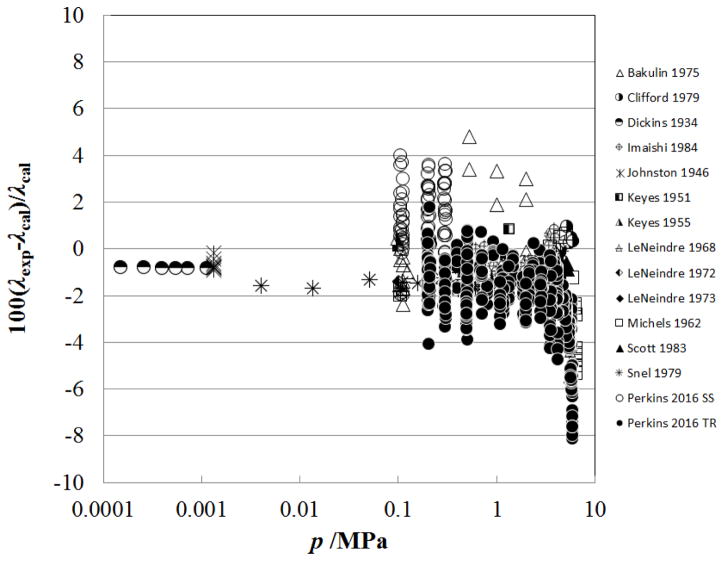
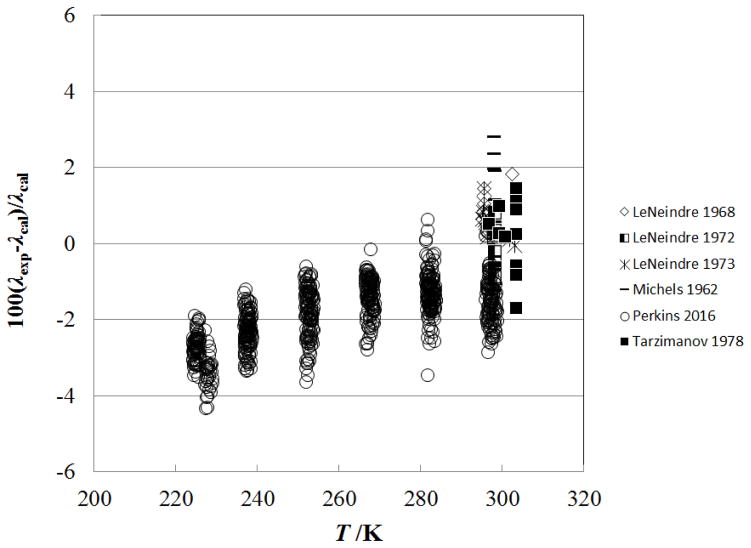
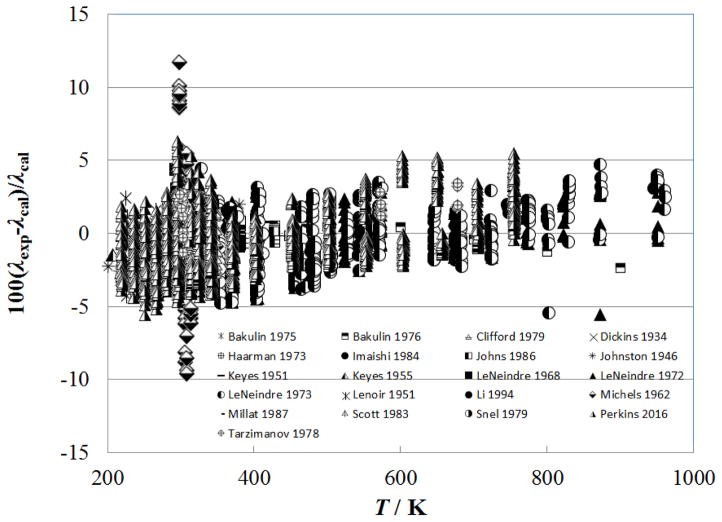
Figure 4 shows the percentage deviation of the primary data for the sub-critical vapor region (densities from 0.02–341.81 kg m⁻³, pressures from 0.0001 MPa to 7.2 MPa) as a function of temperature, while Fig. 5 shows the deviations as a function of pressure. The data sets with the lowest uncertainties cover only the region very close to 300 K (298 K – 304 K) and are Imaishi et al.,²⁷ Clifford et al.,²⁹ and Snel et al.³⁰ There is a systematic offset for Snel et al.³⁰ due to the dilute-gas correlation, but all three of these data sets are represented to within 1%. The measurements of Perkins⁷ cover the broader range of temperatures from 218 K to 299 K, at pressures from 0.1 MPa to 5.5 MPa. The steady-state measurements of Perkins with the low-temperature apparatus are systematically higher than the transient results, but still generally within the estimated uncertainty of ±3 %. This is likely due to increased uncertainty in the temperature rise measurement; the low-temperature instrument only has three leads within the pressure vessel so the potential across each hot–wire is measured with wires that also carry the measurement current. As the critical temperature and pressure are approached, the Michels et al.³⁹ data show larger deviations; data within 1 K of critical have been excluded from the plot.

Figure 4.

Percentage deviations of primary experimental data of carbon dioxide from the values calculated by the present model as a function of temperature, for the vapor region.

Figure 5.

Percentage deviations of primary experimental data of carbon dioxide from the values calculated by the present model as a function of pressure, for the vapor region.

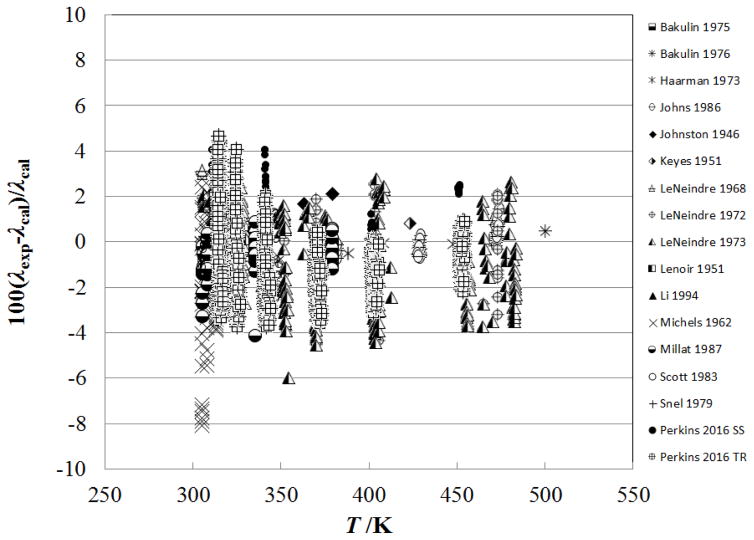
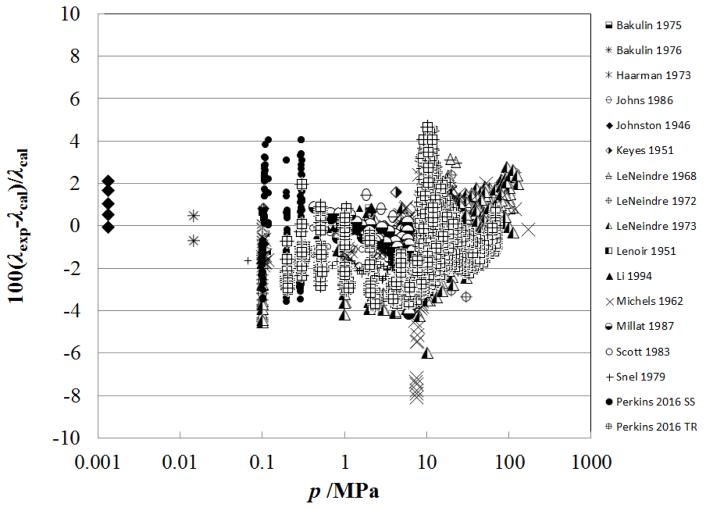
Figure 6 shows the percentage deviation of the primary data for the supercritical region at temperatures up to 500 K (densities from 0.02–341.81 kg m⁻³, pressures from 0.0001 MPa to 7.2 MPa) as a function of temperature, while Fig. 7 shows the deviations as a function of pressure. In this region, the measurements of Haarman³⁴ and Snel et al.³⁰ are represented to within 1%, although there is a systematic offset for Snel et al.³⁰ due to the dilute-gas correlation. The steady-state hot-wire measurements of Perkins range up to 70 MPa and are represented to within their experimental uncertainty of 2%. The other measurements (transient method) of Perkins in the temperature region from the critical temperature to 500 K, have a slightly higher uncertainty, 3% and are also represented to within 2%.

Figure 6.

Percentage deviations of primary experimental data of carbon dioxide from the values calculated by the present model as a function of temperature, for the supercritical region at temperatures to 500 K.

Figure 7.

Percentage deviations of primary experimental data of carbon dioxide from the values calculated by the present model as a function of pressure, for the supercritical region at temperatures to 500 K.

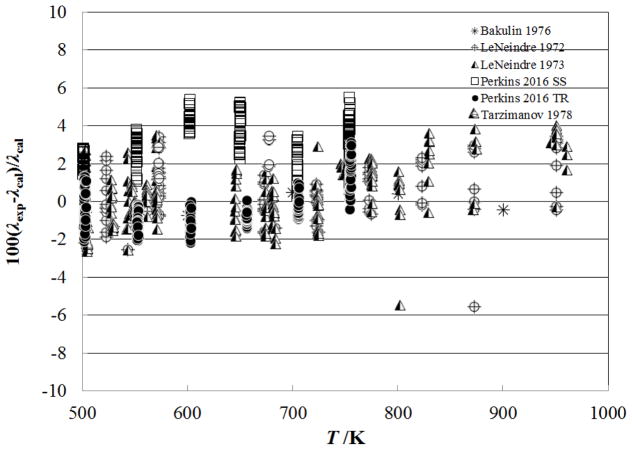
Figure 8 shows the percentage deviation of the primary data for temperatures above 500 K as a function of temperature, while Fig. 9 shows the deviations as a function of pressure. The measurements of Perkins⁷, extending to 70 MPa, are represented to within their estimated uncertainty, 3%. The measurements of LeNeindre et al.,^{35, 37} Bakulin et al.,³² and Tarzimanov and Arslanov³¹ also fall within 3%.

Figure 8.

Percentage deviations of primary experimental data of carbon dioxide from the values calculated by the present model as a function of temperature, for the supercritical region at temperatures above 500 K.

Figure 9.

Percentage deviations of primary experimental data of carbon dioxide from the values calculated by the present model as a function of pressure, for the supercritical region at temperatures above 500 K.

Figure 10 shows the percentage deviations of the primary data in the liquid phase as a function of temperature, and Fig. 11 shows the same as a function of pressure, excluding data within 1 K of critical. The measurements of Perkins in this region have an estimated uncertainty of 0.5%, and the correlation represents the data to within 1%. Comparisons with the data of Tarzimanov and Arslanov³¹ show deviations lower than 3% at pressures to 196 MPa. As the critical region is approached, the deviations become larger. One of the motivations for this work was to incorporate the new liquid-phase measurements of Perkins⁷ to allow improvement in the representation of the liquid phase. Figures 12 and 13 show the percentage deviations of the primary data in the liquid phase as a function of temperature for the previous correlations, that of Vesovic et al.⁵ (Fig. 12) and Scalabrin et al.⁶ (Fig. 13). Upon comparing these two figures with Fig. 10, the improvement in the representation of the liquid phase is shown.

Figure 10.

Percentage deviations of primary experimental data of carbon dioxide from the values calculated by the present model as a function of temperature, for the liquid phase.

Figure 11.

Percentage deviations of primary experimental data of carbon dioxide from the values calculated by the present model as a function of pressure, for the liquid phase.

Figure 12.

Percentage deviations of primary experimental data of carbon dioxide from the values calculated by the Vesovic et al.⁵ model as a function of temperature, for the liquid phase.

Figure 13.

Percentage deviations of primary experimental data of carbon dioxide from the values calculated by the Scalabrin et al.⁶ model as a function of temperature, for the liquid phase.

3.3.2. Thermal diffusivity validation

The thermal conductivity model described above is based entirely on reliable thermal conductivity data that were measured at temperatures where the equation of state of Span and Wagner¹¹⁴ is accurate. The scaled equation of state of Albright et al.¹²⁷ provides better values for the thermodynamic properties in the temperature region (303.1282 ≤ T / K ≤ 305.1282) with densities (350 ≤ ρ / kg m⁻³ ≤ 530). The Albright et al.¹²⁷ equation of state was also used in the 1990 correlation of Vesovic et al.⁵ where it was required over a larger temperature region (301.15 ≤ T / K ≤ 323) K and density region (290 ≤ ρ/ kg m⁻³ ≤ 595). The Albright et al.¹²⁷ scaled equation of state was based on the IPTS–68 temperature scale so we have used it here with the ITS–90 values for the critical point of CO₂ from the equation of state of Span and Wagner¹¹⁴ to effectively convert it to the ITS–90 temperature scale.

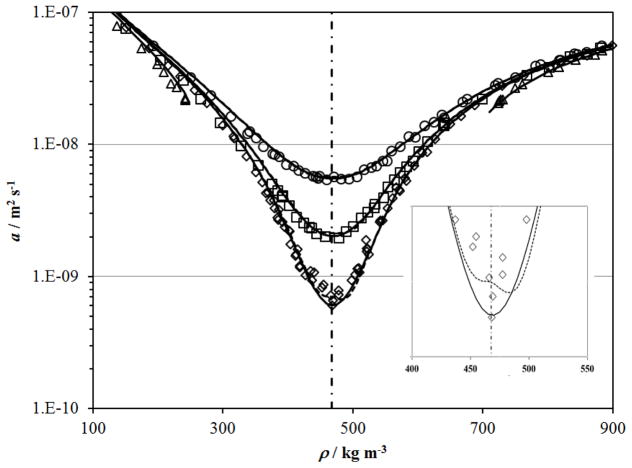
The thermal diffusivity of CO₂ was measured with transient interferometry of the fluid below a horizontal heated surface near its critical point by Becker and Grigull.⁵² These measurements were reported along one liquid isotherm at 298.147 K and three supercritical isotherms at 304.362 K, 305.228 K and 307.958 K (converted to ITS-90), and are shown in Figure 14 along with curves calculated with the correlation described above and thermodynamic properties from the Albright et al.¹²⁷ scaled equation of state. Only the isotherm at 304.362 K requires the scaled equation of state¹²⁷ but it is valid at all of these temperatures. Non–physical behavior is visible in the values calculated with the Span and Wagner¹¹⁴ equation of state, dashed line, at 304.362 K, seen more easily in the inset in Figure 14.

Figure 14.

Thermal diffusivity of CO₂ measured with a interferometry of the fluid sample below a transient heated plate by Becker and Grigull⁵² along isotherms near the critical point. The isotherms are designated by symbols: △, 298.147 K; ◇, 304.362 K; □, 305.228 K, ○, 307.958 K. The dashed lines show the calculated thermal diffusivity with the present correlation with the Span and Wagner¹¹⁴ equation of state and the solid lines show the calculated thermal diffusivity with the present correlation with the Albright et al. ¹²⁷ scaled equation of state. The critical density is shown with the dot–dashed line.

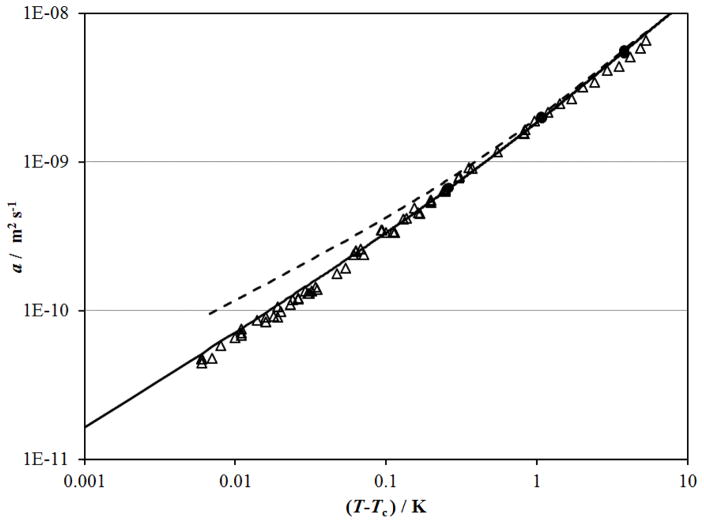
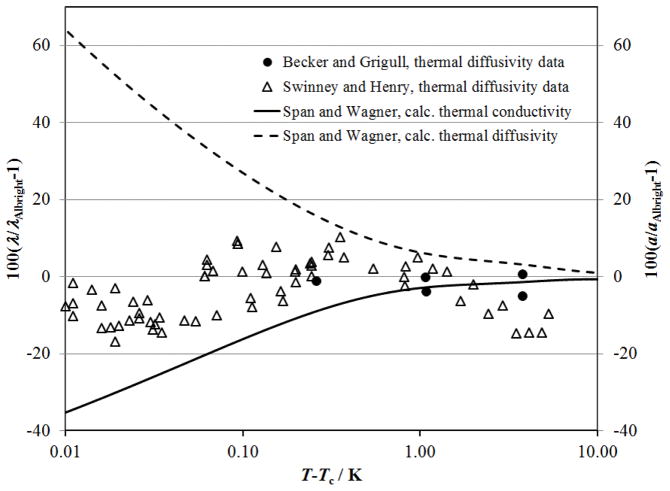
The thermal diffusivity of CO₂ was also determined from light–scattering measurements of the width of the Rayleigh line.^128–131 Here we will focus on the measurements of Swinney and Henry¹²⁸ where tabular results were given. The other light–scattering measurements are consistent with these results. Swinney and Henry¹²⁸ provide the Rayleigh line width, Γ, and the magnitude of the scattering vector, q, as a function of (T–T_c) along the critical isochore. The thermal diffusivity can be obtained from these values with the expression

$$a=\frac{\mathrm{\Gamma }}{\left(\frac{3}{4{\xi }^2}\right)\left[1+q^2{\xi }^2+\left(q^3{\xi }^3-\frac{1}{q\xi }\right)arctan(q\xi )\right]}$$ (9)

as shown by Kawasaki¹³² and applied by Henry et al.¹³³ Equation (9) requires values for the correlation length, ξ, that were calculated with the Albright et al.¹²⁷ scaled equation of state. Alternatively, along the critical isochore ξ= ξ₀ [(T–T_c)/T_c]^−ν with ξ₀ and ν given in Sec. 3.3.1. Values of the thermal diffusivity, a, calculated from the light-scattering data of Swinney and Henry¹²⁸ with Eq. (9) are shown in Fig. 15. The correlation for thermal conductivity developed here is consistent with the thermal diffusivity from light scattering to within (T–T_c)=0.006 K when used with the Albright et al. ¹²⁷ scaled equation of state. The equation of state of Span and Wagner¹¹⁴ exhibits increasing errors near the critical point as indicated by the dashed line.

Figure 15.

Thermal diffusivity of CO₂ along the critical isochore close to the critical temperature from the Rayleigh scattering line width from Swinney and Henry¹²⁸ (△) and the transient interferometry measurements of Becker and Grigull⁵² (●). Solid curve is from the correlation for thermal conductivity described here with thermodynamic properties from the Albright et al. ¹²⁷ equation of state. Dashed curve is based on properties from the Span and Wagner¹¹⁴ equation of state.

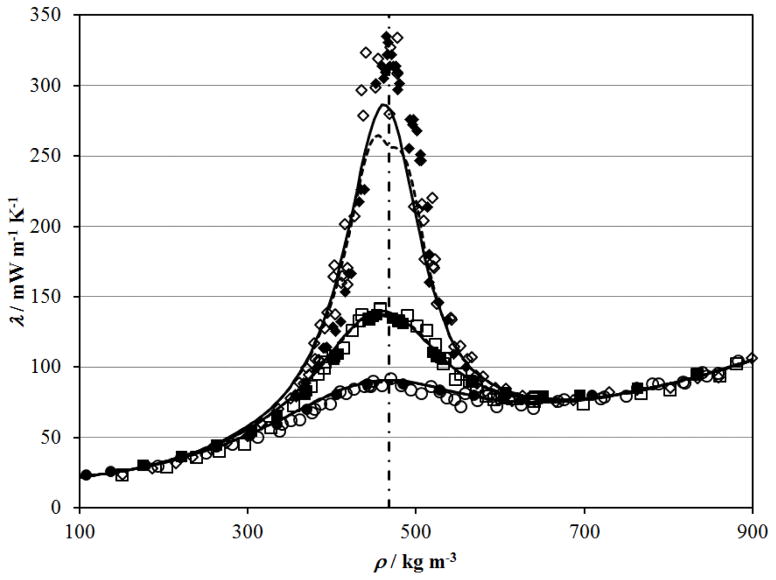
Finally, the thermal diffusivity data of Becker and Grigull⁵² are converted to thermal conductivity values for comparison with the direct thermal conductivity measurements of Michels et al.³⁹ made with a steady–state parallel plate apparatus in the critical region. The thermal conductivity isotherms are shown in Fig. 16. Good agreement is found between the thermal conductivity data of Michels et al.³⁹ and the thermal conductivity obtained from the thermal diffusivity data of Becker and Grigull.⁵² As in Fig. 14, the values calculated for thermal conductivity at 304.36 K exhibit non–physical behavior for the Span and Wagner¹¹⁴ equation of state (dashed line).

Figure 16.

Thermal conductivity along isotherms near the critical point measured directly by Michels et al. ³⁹ and calculated from the thermal diffusivity data of Becker and Grigull⁵² with ρ and C_p from the Albright et al. equation of state. ¹²⁷ Michels et al.³⁹ thermal conductivity isotherms are designated by symbols; ◆, 304.357 K; ■,305.271 K; ●, 307.848 K. Becker and Grigull⁵² isotherms are designated by symbols: ◇, 304.362 K; □, 305.228 K, ○, 307.958 K. The dashed lines show the calculated thermal conductivity with the present correlation with the Span and Wagner¹¹⁴ equation of state and the solid lines show the calculated thermal conductivity with the present correlation with the Albright et al. ¹²⁷ scaled equation of state. The critical density is shown with the dot–dashed line.

3.3.3. Empirical critical enhancement

For engineering applications at state points that are more than 10 K from the critical point, the critical enhancement in mW m⁻¹ K⁻¹ is represented to within about 5% by the following empirical expression:

$$\mathrm{\Delta }{\lambda }_c(\rho ,T)=\frac{-17.47-44.88\mathrm{\Delta }{T}_{\mathrm{c}}}{0.8563-exp[8.865\mathrm{\Delta }{T}_{\mathrm{c}}+4.16\mathrm{\Delta }{\rho }_{\mathrm{c}}^2+2.302\mathrm{\Delta }{T}_{\mathrm{c}}\mathrm{\Delta }{\rho }_{\mathrm{c}}-\mathrm{\Delta }{\rho }_{\mathrm{c}}^3]-0.4503\mathrm{\Delta }{\rho }_{\mathrm{c}}-7.197\mathrm{\Delta }{T}_{\mathrm{c}}}$$ (10)

where ΔT_c = (T/T_c) – 1 and Δρ_c = (ρ/ρ_c) – 1. This equation does not require accurate information on the compressibility, specific heat, and viscosity of carbon dioxide in the critical region, as does the theory of Olchowy and Sengers.⁶⁹ However, it has no theoretical basis at all, and does not go to the theoretical limit at the critical point. It was obtained by using a symbolic regression program¹³⁴ to fit the primary data with the background (Eqs. (3) and (4) ) coefficients fixed. This is an unusual function with poles, but they occur well within the two phase region and do not affect the calculation of the enhancement. Simpler empirical enhancement terms such as those used in previous publications were investigated, ^11–17 but Eq. (10) gave superior results. Figure 17 shows the percentage deviations between all primary data (excluding values within 1 K of critical) and the values calculated by Eqs. (1), (3), (4) and (5–8), as a function of the temperature, while Fig. 18 shows the same calculated instead with Eqs. (1), (3), (4) and (10). By comparing these two figures, it can be seen that employing Eq. (10) is an adequate empirical representation of the thermal conductivity surface excluding the region within 10 K of the critical temperature.

Figure 17.

Percentage deviations of all primary experimental data of carbon dioxide from the values calculated by the full model Eq. (1), (3), (4) and (5)–(8) as a function of temperature.

Figure 18.

Percentage deviations of all primary experimental data of carbon dioxide from the values calculated by the empirical critical enhancement model Eq. (1), (3), (4) and (10) as a function of temperature.

4.0 Uncertainty assessments

4.1 Uncertainty outside of the critical region

Figure 19 shows the estimated uncertainty of the correlation at a 95% confidence level. As indicated in the figure, for the vapor region below critical at pressures from 0.1 MPa to slightly below the critical pressure (~7 MPa) the estimated uncertainty is 3%. This is an improvement over the previous correlation of Vesovic et al.⁵ which had an uncertainty of 5% in this region. The improvement is due to the availability of the new data of Perkins.⁷ The liquid region, at temperatures from 224 K to 299 K at pressures to 70 MPa, is another region where the availability of new data has enabled improvements in the surface. Previously, the correlation of Vesovic et al.⁵ had an uncertainty estimate of 5% in this region; the present correlation has 1% uncertainty. Similarly, the availability of the new data of Perkins at temperatures to 750 K and pressures to 70 MPa made it possible to lower the uncertainty to 3% for this supercritical region. At very low pressures below 0.1 MPa, the correlation has an estimated uncertainty of uncertainty of 1% between 300 K and 700 K, increasing to 2% at both 150 K and 2000 K. Additional future measurements in the remaining areas of the pressure-temperature space at high temperatures and high pressures are desirable to allow further reductions in uncertainty for the thermal conductivity surface.

Figure 19.

Estimated uncertainty for the correlation excluding the critical region.

4.2 Uncertainty in the critical region

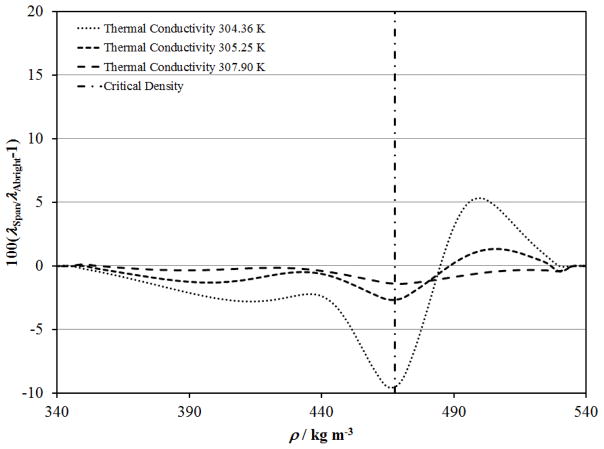
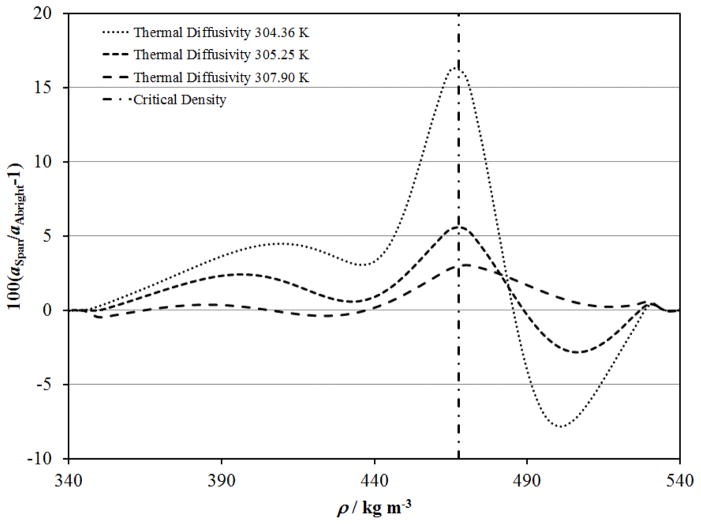
Figures 14 to 16 show that the critical enhancement calculated with ξ and C_p from the Albright et al. ¹²⁷ scaled equation of state better represents the data in the critical region due to the limitations of the Span and Wagner¹¹⁴ equation of state. Figures 20 and 21 show differences between λ and a respectively, calculated with each of these equations of state along the isotherms near 304.36 K, 305.25 K and 307.90 K where reliable thermal conductivity and thermal diffusivity data are available. The data at 304.36 K are within 0.2 K of the critical temperature and were not included in the primary data set, while the thermal conductivity data of Michels et al. ³⁹ near 305.25 K and 307.90 K were used with ξ and C_p from the Span and Wagner¹¹⁴ equation of state. Errors in λ and a due to non–physical behavior of the Span and Wagner¹¹⁴ equation of state in the critical region are less than 3% and 5% respectively near 305.25 K and 2% and 3% respectively near 307.90 K. The largest errors are near the critical density with systematic deviations in terms of density. The systematic errors in the Span and Wagner¹¹⁴ equation of state contribute to increased deviations for the Michels et al. ³⁹ data at 305.25 K and 307.9 K in Figs. 6 and 7 on the supercritical isotherms, and similarly for the near-critical liquid and vapor in Figs. 10 and 11, and Figs. 4 and 5, respectively.

Figure 20.

Deviations in λ for the present correlation with thermodynamic properties calculated with the equation of state of Span and Wagner¹¹⁴ relative to the Albright et al.^{. 127} scaled equation of state in the critical region.

Figure 21.

Deviations in a for the present correlation with thermodynamic properties calculated with the equation of state of Span and Wagner¹¹⁴ relative to the Albright et al.^{. 127} scaled equation of state in the critical region.

Figure 22 shows the deviations between the correlation developed here when the equation of state of Span and Wagner¹¹⁴ is used along the critical isochore relative to the same correlation with the scaled equation of state of Albright et al. ¹²⁷ These deviations represent the maximum deviation observed at any given temperature in the critical region and increase dramatically as the critical temperature is approached. The thermal diffusivity is overestimated by about 65 % with (T–T_c)=0.01 K, while the thermal conductivity is underestimated by about 35 % when the Span and Wagner¹¹⁴ equation of state is used. Deviations between the available thermal diffusivity data and the correlation with thermodynamic properties from the scaled equation of state of Albright et al. ¹²⁷ are also shown for reference. Clearly, the scaled equation of state of Albright et al. ¹²⁷ should be used at temperatures very close to the critical temperature, when |(T–T_c)| < 1 K.

Figure 22.

Deviations in λ and a for the present correlation with thermodynamic properties calculated with the equation of state of Span and Wagner¹¹⁴ relative to the Albright et al. ¹²⁷ scaled equation of state near the critical temperature, along the critical isochore. The solid line show deviations for thermal conductivity and the dashed line show deviations for thermal diffusivity. Deviations for measured thermal diffusivity data are shown with symbols: △, Swinney and Henry¹²⁸ ; ●, Becker and Grigull.⁵²

5. Computer–Program Verification and Recommended Values

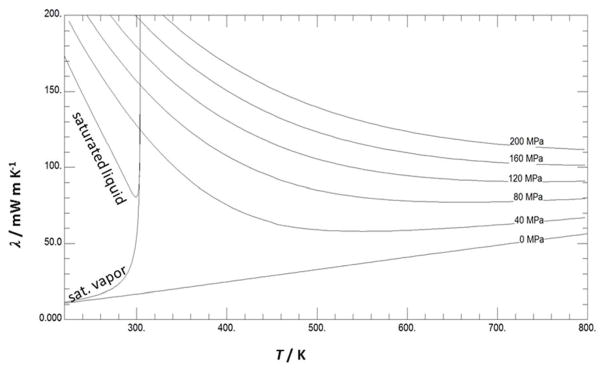
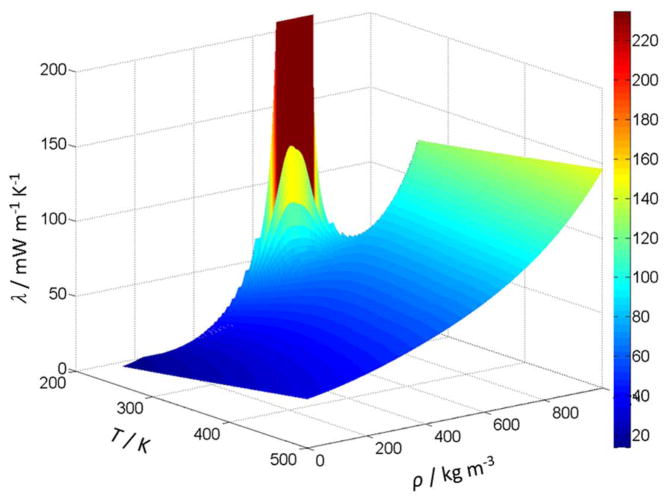
Table 7 is provided to assist the user in computer–program verification. The thermal–conductivity calculations are based on the tabulated temperatures and densities. Note that the point at 310 K has a very significant contribution from the enhancement term–approximately half of the thermal conductivity is the result of the enhancement term. Table 8 provides some recommended values over the thermal conductivity surface. Finally, Fig. 23 shows the thermal conductivity of CO₂ as a function of temperature for different pressures calculated with the full model, Eq. (1), (3), (4) and (5)–(8), while Fig. 24 shows a portion of the 3-dimensional thermal conductivity surface, including the critical enhancement, which theoretically approaches infinity at the critical point and has been truncated at 240 mW m⁻¹ K⁻¹in this figure.

TABLE 8.

Recommended values of CO₂ thermal conductivity (mW m⁻¹ K⁻¹)

Pressure (MPa)	Temperature (K)
	240	300	400	500	600	700	800	900	1000	1100
0	12.28	16.72	24.67	32.84	40.93	48.80	56.41	63.72	70.75	77.51
0.1	12.34	16.77	24.72	32.88	40.96	48.83	56.44	63.75	70.78	77.53
20	165.5	106.0	47.40	43.17	48.04	54.31	60.97	67.67	74.28	80.74
40	180.2	127.4	75.10	58.84	57.97	61.23	66.04	71.50	77.23	83.05
60	193.1	143.3	92.68	72.94	68.47	69.29	72.34	76.47	81.18	86.17
80	204.7	156.8	106.5	84.55	77.80	77.02	78.85	81.97	85.81	90.06
100	215.5	168.8	118.5	94.66	86.01	84.00	84.96	87.38	90.60	94.27
120	225.7	179.9	129.5	103.9	93.50	90.33	90.56	92.45	95.22	98.49
140		190.3	139.8	112.6	100.5	96.20	95.70	97.12	99.55	102.5
160		200.1	149.5	121.0	107.3	101.8	100.5	101.5	103.6	106.3
180		209.5	158.8	129.2	114.0	107.2	105.1	105.5	107.3	109.8
200		218.7	167.9	137.2	120.6	112.6	109.6	109.5	110.9	113.1

Figure 23.

Thermal conductivity of CO₂ as a function of temperature for different pressures.

Figure 24.

Thermal conductivity surface of CO₂.

6. Conclusion

New wide-ranging correlations for the thermal conductivity of carbon dioxide were developed based on critically evaluated experimental data. The correlations are valid from the triple point to 1100 K, and at pressures up to 200 MPa. The correlations are expressed in terms of temperature and density, and the densities were obtained from the equation of state of Span and Wagner.¹¹⁴ The range of validity of this equation of state is 1100 K and 800 MPa. We recommend the use of the present thermal conductivity correlation only to 200 MPa, as there were no data available for validation at pressures above 200 MPa. The new formulation incorporates new experimental data of Perkins⁷ in the liquid phase, and recent theoretical calculations Hellmann⁸ for the dilute gas region. The overall uncertainty (at the 95% confidence level) of the proposed correlation varies depending on the state point from a low of 1% at very low pressures below 0.1 MPa between 300 K and 700 K, to 5% at the higher pressures of the range of validity. Representation of data very near the critical point is adversely affected by some anomalous behavior of the equation of state; future improvements in the equation of state would permit improvements in the critical region. In addition, there is room for improvement in the high pressure region (100 MPa-200 MPa) due to limited data in this region.