Real-time Adaptive EEG Source Separation using Online Recursive Independent Component Analysis

Abstract

Independent Component Analysis (ICA) has been widely applied to electroencephalographic (EEG) biosignal processing and brain-computer interfaces. The practical use of ICA, however, is limited by its computational complexity, data requirements for convergence, and assumption of data stationarity, especially for high-density data. Here we study and validate an optimized online recursive ICA algorithm (ORICA) with online recursive least squares (RLS) whitening for blind source separation of high-density EEG data, which offers instantaneous incremental convergence upon presentation of new data. Empirical results of this study demonstrate the algorithm's: (a) suitability for accurate and efficient source identification in high-density (64-channel) realistically-simulated EEG data; (b) capability to detect and adapt to non-stationarity in 64-ch simulated EEG data; and (c) utility for rapidly extracting principal brain and artifact sources in real 61-channel EEG data recorded by a dry and wearable EEG system in a cognitive experiment. ORICA was implemented as functions in BCILAB and EEGLAB and was integrated in an open-source Real-time EEG Source-mapping Toolbox (REST), supporting applications in ICA-based online artifact rejection, feature extraction for real-time biosignal monitoring in clinical environments, and adaptable classifications in brain-computer interfaces.

I. Introduction

Independent Component Analysis (ICA), as a means for blind source separation (BSS), has enjoyed great success in telecommunications and biomedical signal processing [1]. In biomedical applications, such as scalp electroencephalography (EEG), ICA methods have been widely used to separate artifacts such as eye blinks and muscle activities [2] and to study brain activities [3]. For example, ICA can extract fetal electrocardiography (ECG) from maternal abdomen electrode recordings [4], and it can also isolate pathological activities associated with disease states of epilepsy [5]. In addition, applying ICA to remove task-irrelevant activities and reduce dimensionality of data can improve the performance of Brain-Computer Interfaces (BCI) [6].

The application of ICA to EEG data is justified by a reasonable assumption that multi-channel scalp EEG signals arise as a mixture of weakly dependent latent non-Gaussian sources [7]. Although several ICA algorithms have been developed [1] to learn these sources from channel mixtures, most of the algorithms require access to large amount of training data and are only suitable for offline applications. Furthermore, the offline ICA algorithms commonly assume spatiotemporal stationarity of the data, as in the widely used Infomax ICA [8] and FastICA [9] algorithms. For a few ICA methods that allow non-stationarity such as Adaptive Mixture ICA [10], they are computationally expensive. In many real-world applications, including real-time functional neuroimaging [11], artifact rejection and adaptive BCI [6], online (sequential) source separation methods are needed. Desirable properties of an online method include fast convergence, real-time computational performance, and adaptivity to non-stationary data.

Many existing online ICA methods are listed in Table I. Two major learning rules are least-mean-squares (LMS) and recursive-least-squares (RLS) methods. LMS-type algorithms use stochastic gradient descent approaches and are computationally simple, but they require careful selection of an appropriate learning rate for stable convergence. Examples include Equivariant Adaptive Separation via Independence (EASI) [12] and Natural Gradient (NG) [13] methods. RLS-type algorithms accumulate past data in an exponentially decaying fashion and use Sherman-Morrison matrix inversion to achieve higher convergence rate and better tracking capability, yet require complex computation [14], [15]. This category includes the RLS approach of Nonlinear PCA (RLS-NPCA) [16], Iterative Inversion [17], and Natural Gradient-based RLS (NG-RLS) [18]. Alternatively, Online Recursive ICA (ORICA) [19] gives an RLS-type recursive rule by solving a fixed-point approximation and has been shown to exhibit fast convergence and low computational complexity [20]. Readers can refer to [15], [17] and [21] for theoretical relationships and comparisons between the above methods.

TABLE I.

Comparison of online ICA methods.

Name	Author	Year	Learning rule and optimization method	Pre-whitening
EASI	Cardoso et al. [12]	1996	Relative gradient-based (LMS) that max. kurtosis	LMS
NG	Amari et al. [13]	1996	Natural gradient-based (LMS) that min. mutual information	no
RLS-NPCA	Karhunen et al. [16]	1997	RLS that min. LSE of NPCA criterion	PCA
Iterative Inversion	Cruces-Alvarez et al. [17]	2000	Quasi-Newton method with iterative inversion that decorrelates high order statistics	no
NG-RLS	Zhu et al. [18]	2004	RLS with natural gradient that min. LSE of NPCA criterion	RLS
ORICA	Akhtar et al. [19]	2012	Recursive rule with iterative invesrion from fixed-point solution of Infomax with natural gradient	no

The aforementioned papers focused on theoretical derivations and proofs of convergence and only demonstrated applications of the methods to low-density data (fewer than 10 channels) and simulated “toy” examples such as sinusoidal and square waves. When the number of channels and sources increases, many existing algorithms exhibited slow convergence and poor real-time performance [9]. In a recent study, a real-time online ICA method for high-density EEG was proposed [20]. The method was compared with other offline ICA methods, and its stability and steady-state performance were analyzed in [22].

Additionally, an important advantage of online ICA methods is their ability to adapt to spatiotemporal non-stationary data, a common occurrence in real-world applications. For instance, spatial non-stationarity in the ICA (un)mixing matrix can arise as a consequence of location shifts in either sensors or sources, or changes in electrode impedances. However, few of the online ICA methods have been carefully studied under non-stationary conditions. Further investigation is needed to characterize algorithmic performance and optimal parameter selection using non-stationary simulated and real EEG data.

In this study, we extend ORICA as formulated in [19] and [20], and the contributions are three-fold. Firstly, we demonstrate ORICA's suitability for accurate and efficient source identification in a realistic simulation of stationary 64-channel EEG data. Specifically, we include a serial orthogonalization step of the unmixing matrix in the ORICA algorithm, and we systematically examine the impact of parameters such as the forgetting factor and block sizes for pre-whitening and ORICA on algorithmic performance. Secondly, we examine ORICA's capability to adaptively decompose spatially non-stationary 64-channel EEG data corresponding to abrupt displacements of electrodes, a common source of spatial non-stationarity in real-world mobile applications. We introduce a non-stationarity index and an adaptation approach for non-stationarity detection and online adaptation. Thirdly, we evaluate ORICA's real-world applicability for rapidly extracting principal brain and artifact sources using 61-channel real EEG data recorded from a subject performing an Eriksen flanker task [23]. We demonstrate that ORICA and offline Infomax ICA [24] obtain comparable results in terms of extracting informative independent components (ICs) and their single trial and averaged event-related potentials (ERPs), yet ORICA can learn the ICs online with less than half of the data. Finally, the proposed ORICA pipeline is made freely available as functions supported in BCILAB [25] and EEGLAB [26], and it is also integrated in an open-source Real-time EEG Source-mapping Toolbox (REST) [27].

II. Methods

Standard ICA assumes a linear generative model x = As, where x represents scalp EEG observations, s contains unknown sources, and A is an unknown square mixing matrix. The objective is to learn an unmixing matrix B = A⁻¹ such that the sources are recovered exactly, up to an unknown permutation and scaling matrix, by y = Bx, where y represent the recovered source activations. A column of B⁻¹ represents the spatial distribution of a source over all channels, often referred to as a “component map.”

It is desirable to optimize the ICA contrast function, a measurement of the degree of independence between sources such as kurtosis or mutual information, under the decorrelation constraint R_y = E[yy^T] = I. Hence the separating process can be factored into two stages as B = W M, where M is the whitening matrix that decorrelates the data and W is the weight (preferably orthogonal) matrix that optimizes the ICA contrast function [12], [18]. Serial update rules of M and W and detailed features are presented in the following subsections.

A. Online recursive-least-squares (RLS) pre-whitening

Pre-whitening (decorrelating) the data reduces the number of independent parameters an ICA update must learn, and can improve convergence [1]. Pre-whitening may be efficiently carried out in an online RLS-type learning rule [18]:

$${\mathit{M}}_{n+1}={\mathit{M}}_n+\frac{{\lambda }_n}{1-{\lambda }_n}\left[\mathit{I}-\frac{{\mathit{v}}_n\cdot {\mathit{v}}_n^T}{1+{\lambda }_n({\mathit{v}}_n^T\cdot {\mathit{v}}_n-1)}\right]{\mathit{M}}_n,$$ (1)

where n is the number of iterations, M_n is the whitening matrix, v_n = M _nx_n is the decorrelated data, λ_n is a forgetting factor, and I is the identity matrix. A non-overlapping block of data x_n with a block size L_white is used at each iteration to reduce the computational load and to increase the robustness of the estimated correlation matrix ${\mathbf{v}}_n{\mathbf{v}}_n^T$. This RLS-type whitening rule exhibits faster convergence than LMS whitening methods [18].

B. Online recursive ICA (ORICA)

The ORICA algorithm can be derived from an incremental update form of the natural gradient learning rule of Infomax ICA [28]:

$${\mathit{W}}_{n+1}={\mathit{W}}_n+\eta [\mathit{I}-\mathit{f}\left({\mathit{y}}_n\right)\cdot {\mathit{y}}_n^T]{\mathit{W}}_n$$ (2)

where y_n = W _nv_n, η is a learning rate, and f(·) is a nonlinear activation function. In the limit of a small η and assuming a fixed f(·), the convergence criterion 〈f (y) · y^T〉 = I leads to a fixed-point solution in an iterative inversion form [19]:

$${\mathit{W}}_{n+1}^{+}=(1-{\lambda }_n){\mathit{W}}_n^{+}+{\lambda }_n{\mathit{v}}_n\cdot {\mathit{f}}^T\left({\mathit{y}}_n\right)$$ (3)

where ${\mathit{W}}_n^{+}$ is the Moore-Penrose pseudoinverse of W_n and λ_n is a forgetting factor for an exponentially weighted series of updates. It should be noted that λ_n differs from η, which is the step size for stochastic gradient optimization.

Following [19], applying the Sherman-Morrison matrix inversion formula to Eq. 3, the final online recursive learning rule becomes:

$${\mathit{W}}_{n+1}={\mathit{W}}_n+\frac{{\lambda }_n}{1-{\lambda }_n}\left[\mathit{I}-\frac{{\mathit{y}}_n\cdot {\mathit{f}}^T\left({\mathit{y}}_n\right)}{1+{\lambda }_n({\mathit{f}}^T\left({\mathit{y}}_n\right)\cdot {\mathit{y}}_n-1)}\right]{\mathit{W}}_n$$ (4)

The near-identical forms of Eq. 4 and Eq. 1 allow us to understand ORICA as a nonlinear (or kernel) form of the RLS whitening filter: ORICA's use of non-linearity f(·) allows for independence of sources for moments above second order.

Following the Eq. 4, the orthogonality of the weight W is not guaranteed. To preserve the decorrelation property of recovered source activities y = WMx and maintain learning stability, we apply an orthogonal transformation to W after each ICA update:

$${\mathit{W}}_{n+1}\leftarrow \left({VD}^{-1∕2}{\mathit{V}}^{-1}\right){\mathit{W}}_{n+1},$$ (5)

where D and V contain, respectively, the eigenvalues and eigenvectors of ${\mathit{W}}_{n+1}{\mathit{W}}_{n+1}^T$. Note that this orthogonalization step is costly compared to the ORICA update. A possible alternative would be to reformulate the ORICA update rule under the orthogonal constraint or combine the serial whitening and weight updates into a single update rule [12].

1) Block-update rule

The typical single measurement vector approach [29] requires application of the update rule (Eq. 4) for each data sample, which can be computationally expensive, particularly for the commonly-used MATLAB (The Mathworks, Natick, MA) runtime environment. To reduce the computational load and ensure consistent real-time performance, we may adopt an multiple measurement vector approach [29] and perform updates on short blocks of samples. To achieve this without loss of accuracy, we solve Eq. 4 for time index l = n to l = n+L–1, assuming y_l is approximated as W_nv_l and λ_l is small. This leads to a block-update rule [20]:

$${\mathit{W}}_{n+L}\approx \left({\prod }_{l=n}^{n+L-1}\frac{1}{1-{\lambda }_l}\right)\cdot \left[\mathit{I}-{\sum }_{l=n}^{n+L-1}\frac{{\mathit{y}}_l\cdot {\mathit{f}}^T\left({\mathit{y}}_l\right)}{\frac{1-{\lambda }_l}{{\lambda }_l}+{\mathit{f}}^T\left({\mathit{y}}_l\right)\cdot {\mathit{y}}_l}\right]{\mathit{W}}_n$$ (6)

In this form, the sequence of updates can be vectorized for fast computation. Note that Eq. 6 appropriately accounts for the decaying forgetting factor at each time point. This keeps the approximation error to a minimum.

2) Forgetting factor

The forgetting factor λ determines an effective length of a time window wherein data are aggregated. A large value of λ corresponds to a short window length. In this case, much heavier weights are applied to new data than past data, yielding fast adaptation and convergence yet large errors and variability. As a general rule, a large λ is preferred during initial learning to promote fast convergence; a small λ is suggested at convergence to minimize variance. To this end, we adopt the forgetting factor with time-varying annealing defined in [19]:

$${\lambda }_n=\frac{{\lambda }_0}{n^{\gamma }}$$ (7)

where λ₀ is a fixed initial forgetting factor and γ determines the rate of exponential decay of λ towards zero as a function of time. The same forgetting factor is applied to the RLS whitening filter, although theoretically it can be different.

3) Nonlinear function

The choice of non-linearity f(·) depends on the probability distribution of the sources. Lee et al. [28] proposed an extended Infomax ICA algorithm that adopts distinct activation functions to separate subgaussian and supergaussian sources based on an estimate of source kurtosis. Here we follow [1], [19] and choose the component-wise nonlinearity f(y) = −2 tanh(y) for supergaussian sources and f(y) = tanh(y) −y for subgaussian sources.

4) Number of sub- and super-gaussian sources

While approaches for adaptively selecting f(y) within ORICA have been proposed [19], these are heuristic and presently lack convergence proofs. In practice, we found that both convergence speed and run-time performance were improved by pre-assuming a fixed number of sub- and super-Gaussian sources. The detail of selecting an appropriate number was discussed in Section V and the effect of inaccurate assumptions was explored in Section IV.

C. Non-stationarity detection

In this study, the non-stationarity refers to any changes in the ICA model x = As, including spatial non-stationarity of the mixing process between sources and the measurements A and temporal non-stationarity of probability distributions of source activities s. Hence the non-stationarity might arise from switching of active brain sources, transient muscle activities, sensor displacement, or impedance changes. Our goal is to propose a generic approach to detect and adapt to the non-stationarity in EEG data.

1) Non-stationarity index

As previously described, ORICA is derived from a fixed point solution to the convergence criterion 〈y · f(y)^T〉 = I, reflecting independence of sources moments above second order. Violation of this criterion once an algorithm reaches steady-state can be interpreted as a change in the latent source or mixture distribution, which leads us to define the following heuristic non-stationarity index:

$${\delta }_{ns}={\Vert {\mathit{y}}_n{\mathit{f}}^T\left({\mathit{y}}_n\right)-\mathit{I}\Vert }_F$$ (8)

where ∥ · ∥_F represents the Frobenius norm and n is the current sample point. After ICA decomposition converges, δ_ns would remain small when data are stationary, while δ_ns would increase and fluctuate when data are non-stationary.

2) Adaptation of the forgetting factor

If the non-stationarity index δ_ns increases above a threshold, we may interpret this as evidence of a change in the latent mixing matrix and increase the RLS forgetting factor allowing ORICA to more rapidly adapt to the new mixing matrix. In this study, the threshold value was heuristically chosen to be a percentage (e.g. 1-10%) of initial δ_ns, which was several standard deviations above the mean of δ_ns at convergence in the simulated stationary data. Once δ_ns reached the threshold, we increased the forgetting factor to its initial value.

III. Materials

A. Data collection

The performance of ORICA was evaluated under simulated and real-world conditions. Previous works of online ICA mostly used “toy” simulations with artificially constructed sources (sinusoids, i.i.d. random data, etc), stationary mixing matrices, and relatively small numbers of channels and sources. Here we generated high-density EEG (64 channels and 64 sources) under more realistic conditions, including use of auto-correlated stochastic sources, realistic source locations and mixing matrices derived from Boundary Element Method (BEM) modeling, and spatial non-stationarity. Simulated data were generated using the EEG simulation module in Source Information Flow Toolbox (SIFT) [30], using an approach similar to [31].

1) Simulated spatially stationary EEG data

To test ORICA's performance in separating stationary EEG sources, we generated 64 supergaussian independent source time-series from stationary and random-coefficient order-3 autoregressive (AR-3) models (300Hz sampling rate, 10-min), assigned each source a random cortical dipole location, and projected these through a zero-noise 3-layer BEM forward model (MNI “Colin27”) with standard 10-20 electrode locations matching the 64-channel Cognionics montage used subsequently for real-world ORICA evaluation. This yielded 64-channel EEG data.

2) Simulated spatially non-stationary EEG data

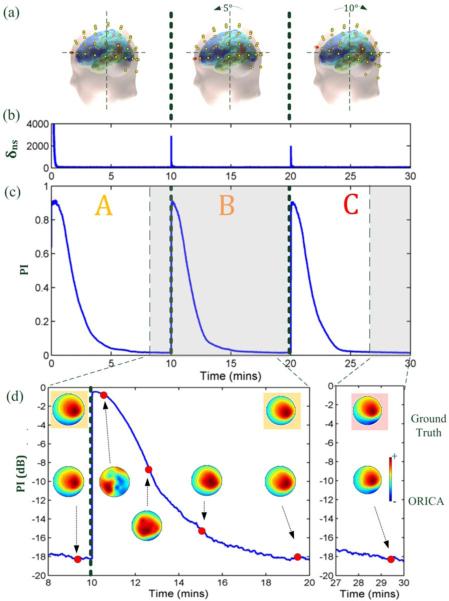
To evaluate ORICA's capability to adapt to spatial non-stationarity, we simulated abrupt shifts of the electrode montage during continuous recording. We first generated 30 minutes of temporally stationary AR-3 source data, as described above. The data was partitioned into thirds. For each 10 minute segment, 64 channel EEG data was generated using a unique BEM forward (mixing) matrix, corresponding respectively to (a) the standard electrode montage, (b) a 5 degree anterior cap rotation, and (c) a subsequent 10 degree posterior cap rotation (5 degree posterior rotation from standard position). The procedure is illustrated in Figure 5a.

Fig. 5.

Application of ORICA to 64-ch simulated non-stationary EEG data consisting of three concatenated 10-minute sessions which simulate a 5-deg forward EEG cap rotation followed by a 10-deg backward cap rotation. (a) Electrode locations for each session. (b) non-stationarity index δ_ns = ∥yf^T – I∥F detects the abrupt change between sessions. (c) The PI convergence curve shows the adaptation behavior. (d) Zoomed-in plots of log-scaled convergence curve with ground truth component maps (top row) and reconstructed IC at different time points.

3) Real EEG data

One session of high-density EEG data was collected from a 24 year-old right-handed male subject using a 64-channel wearable and wireless EEG headset with dry electrodes (Cognionics, Inc) [32]. In the 20 minutes session, the subject performed a modified Eriksen flanker task [23] with a 133 ms delay between flanker and target presentation. The subject was asked to press buttons according to the target stimuli as quickly as possible. Flanker tasks are known to produce robust error-related negativity (ERN, Ne) at frontal-central electrode sites. The goal here is to extract these event-related potential (ERP) components from high-density EEG data in a real-world setting using the proposed ORICA pipeline.

B. The ORICA pipeline

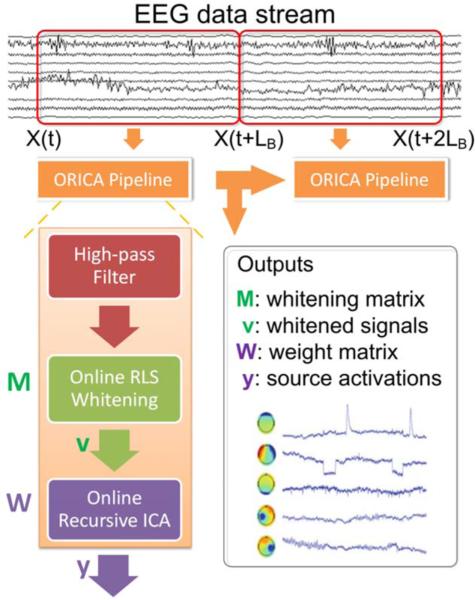
As shown in Figure 1, the ORICA pipeline continuously fetched the streamed data with variable size L_B in the online buffer and processed the data with the three filters in sequence: a Butterworth IIR high-pass filter, an online RLS whitening filter, and an ORICA filter. The high-pass filter removed the trend and low-frequency drift, ensuring the zero-mean criterion for ICA was satisfied. For each update, the pipeline computed and output the whitening matrix M and the weight matrix W according to Eq. 1 and Eq. 6. The next non-overlapping data chunk was then used for the subsequent update.

Fig. 1.

The ORICA pipeline for online EEG data processing. X(t) is the input data vector at time t and L_B is the size of data in the online buffer.

The pipeline was implemented and analyzed in a simulated online environment using BCILAB, an open source MATLAB toolbox designed for BCI research [11], [25]. It was initialized with the first second of data segment from the dataset. For the simulated 64-ch stationary data, we investigated the effect of the parameters on empirical convergence, and we used block sizes L_white = L_ICA = 16 as an example to show the decomposed components since the block sizes returned satisfactory results in the shortest computational time. For the simulated 64-ch non-stationary data and real 61-ch data, we used L_white = 8 and L_ICA = 1, which were found to be optimal for the simulated stationary data. Table II summarizes the parameters of the three filters.

TABLE II.

List of parameters for the ORICA pipeline: IIR high-pass filter (IIR), online RLS whitening filter (RLS), and online recursive ICA filter (ICA).

Filters	Parameters	Values	Description
IIR	BW	0.2–2 Hz	Transition bandwidth
RLS	Lwhite	1~16	Block-average size
RLS	λ 0	0.995	Initial forgetting factor
ICA	γ	0.60	Decay rate of forgetting factor
ICA	LICA	1~16	Block-update size
	nsub	0	Number of subgaussian sources

C. Data processing and analysis

We applied additional procedures to process and analyze the recorded EEG data from the subject. Firstly, an automatic removal of bad (e.g. flatlined or abnormally correlated) channels was applied prior to the ORICA pipeline using BCILAB routines, which removed 3 out of 64 channels. Secondly, following application of the ORICA pipeline, the source activities were epoched in a −400 to 600 msec window time locked to subject's responses (button press), yielding 693 epochs (104 error and 589 correct trials). The epochs were averaged to produce ERPs and were analyzed offline in EEGLAB [26].

D. Performance evaluation

1) Performance index

If the ground truth (N-by-N) mixing matrix A is known, a performance index PI for assessing quality of source separation can be defined as [33]:

$$PI=\frac{1}{N-1}\left[N-\frac{1}{2}\sum _{i=1}^N\left(\frac{\underset{1\le j\le m}{\max }{\mid {\mathit{C}}_{ij}\left(n\right)\mid }^2}{{\sum }_{j=1}^N{\mid {\mathit{C}}_{ij}\left(n\right)\mid }^2}+\frac{\underset{1\le j\le m}{\max }{\mid {\mathit{C}}_{ji}\left(n\right)\mid }^2}{{\sum }_{j=1}^N{\mid {\mathit{C}}_{ji}\left(n\right)\mid }^2}\right)\right]$$ (9)

where C(n) = W _nM _nA. This measures a normalized total cross-talk error of the estimated whitening matrix M and weight matrix W, accounting for scale and permutation ambiguities. For perfect separation at convergence, PI approaches zero.

2) Best-matched correlation coefficients and Hungarian algorithm

PI reflects ORICA's global performance across all components. However, it is also useful to evaluate convergence of individual independent components (ICs), i.e. rows of W. One metric is the Pearson correlation between an estimated IC and its counterpart in a “ground truth” weight matrix, W*. Due to permutation ambiguities, a matching algorithm is required for optimal pairing of rows of W and W*. This study used the Hungarian method [34] to maximize the sum of absolute pairwise correlations. We used Niclas Borlin's implementation in EEGLAB's matcorr(·) function.

IV. Results

A. Simulated 64-ch stationary EEG data

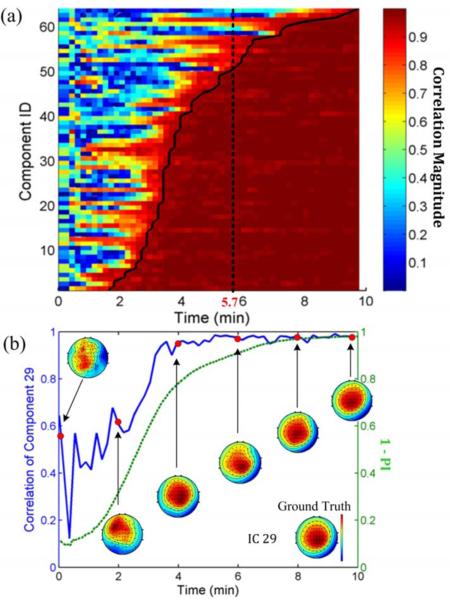
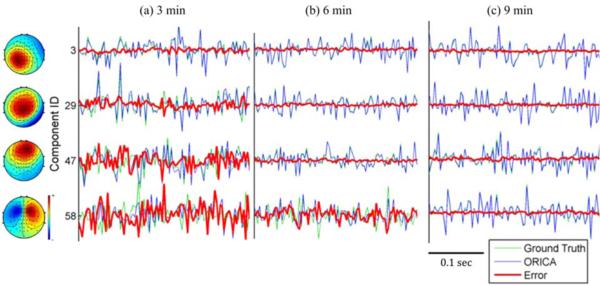
1) Evaluation of the decomposed components: Figure 2a plots the correlation magnitudes between ORICA components and their ground-truth counterparts. The components were sorted such that smaller component ID represented faster convergence. We observed that all components coverged, i.e. correlation magnitudes approached 1, by the end of the 10-minute session. A common empirical heuristic for the number of training samples required for separating N stable ICA sources using Infomax ICA was kN², where k > 25 [24]. For 64 channels, the heuristic time required for convergence amounted to 64² × 25 = 102400 samples = 5.7 minutes with a 300 Hz sample rate. By 5.7 minutes, 77% (91%) of ICs reached a correlation magnitude of 0.95 (0.8); by 3.5 minutes, more than half of the ICs reached a correlation magnitude of 0.95. Figure 2b shows the evolution of the component maps of a randomly selected IC #29 and its correlation magnitudes with ground truth. This IC converged to a steady-state correlation magnitude of 0.95 under 4 minutes. The superimposed global performance index (1 – PI, in green) exhibited a similar convergence trajectory. Figure 3 shows 300-msec time-series of four representative ICs reconstructed by ORICA at 3, 6, and 9 minutes. At 9 minutes, ORICA correctly reconstructed all the source dynamics with the errors approached 0. At the heuristic time 5.7 minutes, only ID #58 had not converged. Interestingly, components such as IC #3 converged within 3 minutes. Both decomposed component maps and recovered source dynamics demonstrated ORICA's suitability for accurate and efficient decomposition of high-density (64-channel) data, albeit with systematic variation in convergence speed.

Fig. 2.

(a) Evolution of component-wise correlation magnitudes between ORICA-decomposed ICs and ground truth on simulated stationary 64-ch EEG data [20]. ICs sorted with respect to time required to reach a correlation magnitude of 0.95 (solid curve). The dotted line is the heuristic time for separating 64 stable ICs. (b) Evolution of correlation magnitudes (blue) and component maps of a randomly selected IC #29. One minus the performance index (green) is superimposed.

Fig. 3.

Source dynamics and the corresponding component maps of four representative components reconstructedby ORICA at (a) 3 min, (b) 6 min, or (c) 9 min of simulated mixed 64-channel stationary EEG data. Reconstructed source dynamic (blue) is superimposed on ground truth (green) with error, i.e. difference, (red). The oscillatory (autocorrelated) and burst-like source dynamics, as well as homogeneous component maps of the four depicted ICs, are characteristic of real EEG source dynamics.

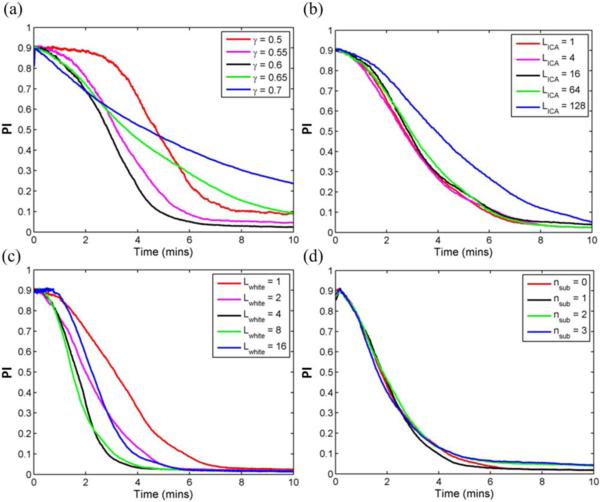
2) Effect of ORICA parameters

As shown in Figure 4, we systematically evaluated the effects of four ORICA parameters on convergence. The decay rate of forgetting factor γ had a significant impact on convergence speed, with the fastest convergence for γ = 0.6 (Figure 4a). A sigmoidal profile for the convergence trajectory was observed for γ ≤ 0.6, while an exponential decay profile was observed for γ > 0.6. The ORICA block size L_ICA had negligible effect on the convergence for L_ICA ≤ 64 (Figure 4b). This demonstrated the approximation error of the block update rule (Eq. 6) was negligible for small to moderate block sizes. The block size of online whitening L_white significantly affected the ICA convergence (Figure 4c). L_white between 4 and 8 samples achieved the best performance. Interestingly, L_white = 1 was not the optimal value, mainly due to the effect of variable time scale of adjustments in the whitening matrix on the convergence of the subsequent ORICA. The pre-assumed number of subgaussian sources n_sub had little effect on the convergence, within the range of n_sub = 0 ~ 3, with the true number n_sub = 0. The performance of ORICA was rather insensitive to assumptions on the kurtosis of the sources. For the above results, we set γ = 0.6, L_ICA = 1, L_white = 1, and n_sub = 0 unless otherwise noted.

Fig. 4.

Effect of ORICA pipeline parameters on convergence trajectory, i.e. performance index over time, applied to 64-ch simulated stationary EEG data. (a) Decay rate γ of forgetting factor, (b) block size L_ICA of ORICA, (c) block size L_white of the online whitening, and (d) pre-assumed number n_sub of subgaussian sources.

3) Quantification of computational load

Table III shows the average execution time required to apply the ORICA pipeline to 1-second of data, computed by averaging the processing rates (data size divided by time) of the incoming data chunks for 1 minute. Runtime was uniformly less than one second, illustrating the 64-ch data were processed faster than accumulated in the input buffer, and thus the pipeline was capable of real-time operation. The online whitening filter ran 3 to 9 times faster than ORICA did and the runtime monotonically decreased as the block size increased. The execution time of the ORICA filter was nearly halved as block size doubled when L ≤ 8, with diminishing returns for L ≥ 16. This allows us to balance the tradeoff between runtime of the pipeline and accuracy of the block-update rule.

TABLE III.

Averaged execution time (ms) for 1 sec (300 samples) 64-channel data using online RLS whitening and ORICA with different block sizes L_white and L_ICA.

Time (ms)	Block Size
Algorithm	1	2	4	8	16	32	64	128
RLS	35.2±5.2	23.8 ±7.9	13.5±6.0	8.6±4.3	5.3±1.5	4.1±4.5	3.0±4.2	2.5±4.9
ORICA	332±29	174±37	79.5±14.5	36.3±11.8	21.0±5.2	15.1±7.2	10.6±9.4	6.6±2.6

Run in MATLAB 2012a on a dual-core 2.50GHz Intel Core i5-3210M CPU with 8GB RAM.

B. Simulated 64-ch non-stationary EEG data

Figure 5 plots ORICA's peformance in tracking spatial non-stationarity in simulated 64-channel EEG data, with the simulated abrupt shifts of the EEG cap (Figure 5a). Figure 5b plots the non-stationarity index δ_ns as a function of time. The index robustly identified changes in the mixing matrix due to cap displacements. Figure 5c plots the performance index of ORICA's decomposition as a function of time. Following the detection of non-stationarity, ORICA's forgetting factor was reset to its initial value, and ORICA smoothly adapted to the new mixing matrix. Figure 5d plots the ground truth and the estimated component maps for a representative IC at different time-points, superimposed on a plot of log-transformed PI. For this IC, suitable convergence was obtained within 15 minutes, and improved further over time. The effect of cap rotation was captured by the concomitant shift of the component maps, indicating ORICA's capability to detect and adapt to the spatial abrupt non-stationarity.

C. Real 61-ch EEG data from the flanker task

Since the ground truth was unknown for real EEG data, we adopted the offline Extended Infomax ICA algorithm [28], as implemented in the EEGLAB [26] function RUNICA, as a “gold standard”. The robustness and stability of the algorithm on high-density EEG data had been shown to outperform most blind source separation algorithms [7].

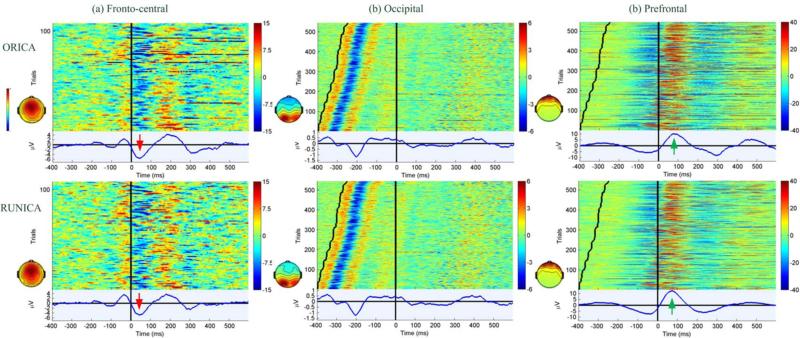
To confirm whether ORICA yielded a comparable solution at convergence (average over the last minute) as RUNICA, we investigated event-related activities of three sets of components with stereotypical fronto-central, occipital, and prefrontal spatial topographies. Figure 6a revealed that the ORICA- and RUNICA-decomposed fronto-central ICs and their characteristic ERN were comparable and consistent with the results from previous studies [11], [35]. Figure 6b shows that averaged occipital visual-evoked potentials (VEP) elicited by flanker (0-50 msec window after the onset of stimulus) and target (100-150 msec window after) presentation were clearly observed using both methods. Figure 6c shows eye blinks time-locked to response (click of button), as previously described in [35]. The ERN and VEP shown in Figure 6 were representative, with comparable results obtained from all subjects, indicating the reproducibility of the ORICA pipeline. In summary, the empirical results demonstrated comparable performance of ORICA to RUNICA in separating informative ICs and resolving single trial and averaged ERPs. Furthermore, ORICA required significantly less computation time than RUNICA.

Fig. 6.

Color-coded event-related potential (ERP) images (trials by time) of (a) fronto-central, (b) occipital, and (c) prefrontal components reconstructed by ORICA (top row) and RUNICA (bottom row) on real 61-ch EEG data from the flanker task, time-locked to the response at time 0 (vertical straight line). Averaged ERP traces are shown in bottom panel. Only error trials are included in (a) such that error-related negativity (ERN) can be observed as red arrows indicate. In (b) and (c), all trials are sorted based on reaction time, i.e. onset of flanker stimulus (sawtooth line) to response. A visually evoked potential (VEP) is clearly observed in (b). Green arrows in (c) indicate to eye blinks.

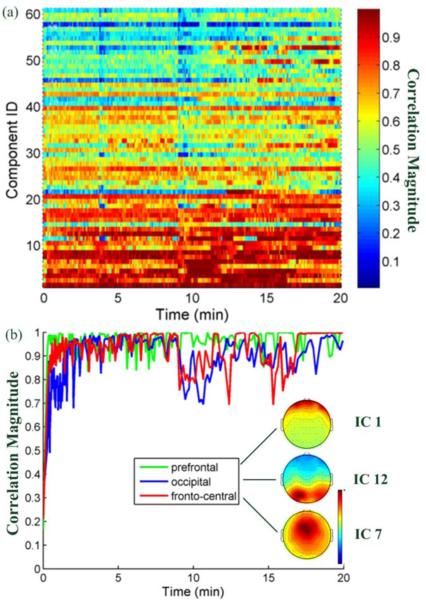
Adopting a procedure similar to Figure 2, Figure 7a plots the correlation magnitudes between all ICs learned by ORICA and their best-matched RUNICA counterparts. Firstly, only 10% (26%) of the ORICA components reached a correlation magnitude of 0.9 (0.8) at the end of the session (average over the last minute). Secondly, 8% (21%) of the components reached a correlation magnitude of 0.9 (0.8) within 3-4 minutes, only half of the empirical heuristic time suggested by [24].

Fig. 7.

(a) Evolution of component-wise correlation magnitudes between ORICA- and RUNICA-decomposed ICs on real 61-ch EEG data from the flankerTask. (b) Evolution of correlation magnitudes and spatial filters of three rapidly converged ICs: prefrontal (eye-blinks), occipital (VEP), and fronto-central (ERN) components.

Among those ICs with the highest correlation magnitudes (larger than 0.95), we found a number of ICs with stereotypical and plausible component maps. Figure 7b plots the convergence profile (evolution of correlation magnitudes) for three such informative ICs: prefrontal (IC 1, accounting for eye-blink), occipital (IC 12, accounting for VEP), and fronto-central (IC 7, accounting for ERN) components. These ICs converged to their RUNICA counterparts within 3-4 minutes. The correlation magnitude curves of both the occipital and fronto-central components fluctuated across time and eventually reached a steady-state. In contrast, the correlation magnitude time series of the prefrontal component was relatively stable across the whole session.

Figure 2a and Figure 7a exhibit significant performance differences in decomposing simulated versus real EEG data, which can be attributed to the differences in the quality of the gold standard. Those ICs producing poor correlation corresponded to non-dipolar sources in the gold standard, i.e., sources with high residual variance in dipole fitting, such as mixtures of sources or noise [7]. This phenomenon is commonly observed and reported when applying ICA methods to real EEG data that are inevitably noisy and likely non-stationary [1], [6].

V. Discussion

A. Fast Convergence Speed

The ORICA pipeline was capable of accurately decomposing 64-channel simulated EEG data within the required heuristic convergence time (kN²) [24]. The fast convergence could be attributed to three important factors: (a) combining online RLS pre-whitening and ORICA, (b) choosing an optimal forgetting factor profile and parameters, and (c) fixing the numbers of modeled sub- and super-gaussian sources.

Simulation results showed that faster convergence of the whitening matrix facilitated ICA convergence. This was consistent with the findings in previous studies [1], [18], which suggested pre-whitening could significantly improve the ICA convergence by reducing the dimensionality of the parameter space. For online whitening, a local block-average approach could provide a more robust estimate than a stochastic (single sample) update approach. Besides RLS whitening, online LMS whitening method [12] can also be considered, which has lower computational complexity, but slower convergence [18].

The forgetting factor, especially its decay rate γ, had a significant effect on ORICA's convergence. For highly non-stationary data, a large γ and thus a shorter effective window size were preferred. Factors including data dimension (number of channels) and underlying stationarity of the data affected the choice of optimal parameters. Alternative approaches for adapting the forgetting factor were suggested in [17] and [36].

Fixing the numbers of sub- and super-gaussian sources increased both the stability and the speed of convergence, especially for high-density data. The experiments with synthetic data showed that the choice was not critical, and a model mismatch in these numbers could be tolerated. This study further examined the kurtosis of the real 61-ch EEG data and found that all sources were supergaussian distributed, which was consistent with previous studies [2], [26] that EEG signals from most brain activities and non-brain artifacts were primarily supergaussian. For greater accuracy under general conditions, online kurtosis estimation as described in [19] and [37] can be incorporated into the ORICA pipeline. This may lead to better steady-state performance but potentially decreased stability of convergence.

Several approaches not yet implemented in this study can further improve the convergence speed of ORICA. For example, dimensionality reduction methods such as PCA, or selecting a subset of channels prior to ORICA decomposition, can reduce the empirical convergence time. Another promising approach is to pre-process the data using artifact reduction methods such as Artifact Subspace Reconstruction [11] to mitigate sensitivity to transient artifacts in noisy high dimensional EEG data.

B. Real-time processing

ORICA was implemented as a BCILAB function with block-update vectorization, and could easily perform real-time processing with a user-defined block-size for 64-channel EEG on a standard laptop. The block update rule, while approximate, incurred negligible loss in accuracy up to L_ICA = 64 for 64-channel simulated data. Even without the block-update (L_white = L_ICA = 1), the ORICA pipeline still ran in real-time. The block update may be most valuable when computational resources are constrained; for instance, when applying multiple data processing operations in serial or operating on a low-power mobile device.

C. Application to real EEG data

Empirical results on the 61-channel EEG data collected in the flanker task experiment demonstrated that ORICA could decompose brain sources and artifact ICs that resembled results from standard RUNICA. We observed that the most informative ICs, such as VEP and ERN brain sources and eye-blink artifacts, had the highest correlation magnitudes among all ICs and converged much quicker than the heuristic convergence time—a fortunate circumstance for real-time applications in mobile EEG BCI. We speculate that those components exhibit robust and frequently occurring statistical patterns which facilitate ICA separation. These observed phenomena support applications of ORICA for rapid decomposition of high-density data as much less time is required to decompose brain and artifact components.

The ORICA pipeline also revealed non-stationarity in the experimental data, captured by the dynamics of component maps and the non-stationarity index. One challenge for ORICA and RUNICA is the order switching of ICs, especially for non-stationary real EEG data. This hinders the identification of informative ICs over time, i.e. tracking the same set of components regardless of the weight matrix permutations. One solution to the problem is to sort the current weight matrix W (t) based on the correlation matching with the previous weight matrix W (t–1) using the Hungarian method described in section III-D to keep track of the same components. This is useful for online identifying and separating artifact components from noisy EEG recordings.

D. Non-stationarity detection and adaptation

This study proposed using the Frobenius norm of ICA error matrix, ∥yf(y)^T – I∥_F, for the ORICA pipeline as an index to non-stationarity events in the data, identified as abrupt changes in the mixing matrix. This non-stationarity index measurement captured the fitness of the ICA model to the current data, i.e. the degree to which nonlinear decorrelation was achieved. Alternative forms for the non-stationarity index can be used depending on applications, for instance mutual information reduction (MIR) in windowed data provides a measure of statistical independence between sources [7] and thus can capture the changes in data statistics as MIR varies.

This study also presented a method of non-stationary adaptation by increasing the forgetting factor when the non-stationarity index exceeds a hard threshold, e.g. 1-10% of the initial value when ICA had not converged. However, this method required prior knowledge of the hard threshold and did not address continuous variation in degree of non-stationarity. For selection of the threshold, it is possible to design an adaptive threshold that depends on the online estimated mean and standard deviation of δ_ns. For adaption of the forgetting factor, one possible solution is to adopt the strategy similar to the adaptive learning rate proposed by Murata et al. [38] for a gradient-based algorithm in an online environment. An adaptive forgetting factor for ORICA, as an RLS-like recursive online algorithm, is crucial for its ability to track non-stationarity, calling for further investigation.

E. Applications and future directions

The proposed online ICA method for real-time processing of high-density EEG opens up new opportunities for the following potential applications: (1) ICA-based real-time artifact removal (especially for sporadic muscle activities), (2) ICA-based brain activity monitoring (e.g. epilepsy, etc) for clinical practice, and (3) adaptable ICA-based features for brain state (e.g. cognitive functions, fatigue level, etc) classification in real-time brain-computer interfaces.

A significant next step is to leverage ORICA for real-time source localization, for instance using anatomically constrained low resolution electrical tomographic analysis (LORETA) [39]. A recent study [27] attempted to combine online ICA and source localization, yet further validation of sources’ reliability were needed. Knowledge of the source locations in the brain can be used to assess the reliability of the sources (e.g. validate consistency of the source locations over time and with anatomical expectations), to provide biological interpretation of the decomposed sources, and to integrate with other real-time source-level methods such as connectivity analysis in SIFT [11], [30].

VI. Conclusion

This study proposed and demonstrated an efficient computational pipeline for real-time, adaptive blind source separation of EEG data using Online Recursive ICA. The efficacy of the proposed pipeline was demonstrated on three datasets: a simulated 64-channel stationary dataset, a simulated 64-channel non-stationary dataset, and a real 61-channel EEG dataset collected under an Eriksen flanker task. Through application of ORICA to simulated stationary data we (a) systematically evaluated the effects of key parameters on convergence; (b) characterized the convergence speed, steady state performance, and computational load of the algorithm; and (c) quantitatively compared the proposed ORICA method with a standard offline Infomax ICA algorithm. Our analysis of a simulated non-stationary 64-channel EEG dataset demonstrated ORICA's ability to adaptively track changes in the mixing matrix due to electrode displacements.

Applied to 61-channel experimental EEG data, we demonstrated ORICA's ability to decompose brain and artifact subspaces online, with comparable performance to offline Infomax ICA. Furthermore, we found that subspaces of biologically plausible ICs (e.g. eye, occipital and frontal midline sources) could be reliably learned in much less time than required by the kN² empirical heuristic for ICA convergence. To serve the EEG and BCI communities, the proposed pipeline has been implemented as BCILAB [25] and EEGLAB compatible functions, it has also been integrated into an open-source Real-time EEG Source-mapping Toolbox (REST) [27]. Future work will focus on further validation of this promising method as well as application to artifact rejection, clinical monitoring, and brain-computer interfaces [11].

Biography

Sheng-Hsiou Hsu (S'14) received the B.S. degree in electrical engineering from the National Taiwan University, Taipei, Taiwan, in 2011. He was a sole recipient of the scholarship of government sponsorship for overseas study in Biomedical Engineering in 2012. He is currently a Ph.D. student in bioengineering at University of California at San Diego, La Jolla CA, working with the Swartz Center for Computational Neuroscience and Institute for Neural Computation. His major research interests include brain-computer interfaces, machine learning, and signal processing with respect to functional imaging of brain dynamics.

Tim R. Mullen (S'13-M'14) received dual B.A. degrees in Computer Science (high honors) and Cognitive Neuroscience (highest honors) in 2008 from the University of California, Berkeley. He received M.S. (2011) and Ph.D (2014) degrees in Cognitive Sciences from University of California, San Diego while at the Swartz Center for Computational Neuroscience. Graduate awards included Glushko, Swartz, and San Diego fellowships; best paper awards; and the 2014-15 UCSD Chancellor's Dissertation Medal. His research has focused on modeling neural dynamics and interactions from human electrophysiological recordings, with applications to clinical and cognitive neuroscience and neural interfaces. He is co-founder and CEO at San Diego neurotechnology company Syntrogi Inc (aka Qusp) and Research Director of its R&D division Syntrogi Labs.

Tzyy-Ping Jung (F15) received the B.S. degree in electronics engineering from National Chiao Tung University, Hsinchu, Taiwan, in 1984, and the M.S. and Ph.D. degrees in electrical engineering from The Ohio State University, Columbus, OH, USA, in 1989 and 1993, respectively. He is currently a Research Scientist and the Co-Director of the Center for Advanced Neurological Engineering, Institute of Engineering in Medicine, University of California-San Diego (UCSD), La Jolla, CA, USA. He is also an Associate Director of the Swartz Center for Computational Neuroscience, Institute for Neural Computation, and an Adjunct Professor of Bioengineering at UCSD. In addition, he is an Adjunct Professor of Computer Science, National Chiao Tung University, Hsinchu, Taiwan. His research interests are in the areas of biomedical signal processing, cognitive neuroscience, machine learning, time-frequency analysis of human EEG, functional neuroimaging, and braincomputer interfaces and interactions. He is currently an Associate Editor of IEEE Transactions on Biomedical Circuits and Systems.

Gert Cauwenberghs (S'89-M'94-SM'04-F'11) is Professor of Bioengineering and Co-Director of the Institute for Neural Computation at UC San Diego, La Jolla CA. He received the Ph.D. degree in Electrical Engineering from California Institute of Technology, Pasadena in 1994, and was previously Professor of Electrical and Computer Engineering at Johns Hopkins University, Baltimore, MD, and Visiting Professor of Brain and Cognitive Science at Massachusetts Institute of Technology, Cambridge. He co-founded Cognionics Inc. and chairs its Scientific Advisory Board. His research focuses on micropower biomedical instrumentation, neuron-silicon and brain-machine interfaces, neuromorphic engineering, and adaptive intelligent systems. He received the NSF Career Award in 1997, ONR Young Investigator Award in 1999, and Presidential Early Career Award for Scientists and Engineers in 2000. He serves IEEE in a variety of roles including as General Chair of the IEEE Biomedical Circuits and Systems Conference (BioCAS 2011, San Diego), as Program Chair of the IEEE Engineering in Medicine and Biology Conference (EMBC 2012, San Diego), and as Editor-in-Chief of the IEEE Transactions on Biomedical Circuits and Systems.