Real-time Data Acquisition and Maximum-Likelihood Estimation for Gamma Cameras

Abstract

We have developed modular gamma-ray cameras for biomedical imaging that acquire data with a raw list-mode acquisition architecture. All observations associated with a gamma-ray event, such as photomultiplier (PMT) signals and time, are assembled into an event packet and added to an ordered list of event entries that comprise the acquired data. In this work we present the design of the data-acquisition system, and discuss algorithms for a specialized computing engine to reside in the data path between the front and back ends of each camera and carry out maximum-likelihood position and energy estimations in real time while data was being acquired..

I. Introduction

We have developed and applied modular gamma-ray cameras that acquire data with a raw list-mode acquisition architecture. We divide the data acquisition task into a front-end that performs digital event detection and list-mode entry generation, and a back-end that buffers data. All observations associated with a gamma-ray event, such as photomultiplier (PMT) signals and time, are assembled into an event packet and added to an ordered list of event entries that comprise the acquired data. The raw observations are recorded with the full acquired precision in order that position and energy estimation algorithms of arbitrary complexity can be applied to the analysis of the original data. It is a particular benefit that carefully collected calibration data can be incorporated into the estimation process to account for minor manufacturing variations present in the cameras..

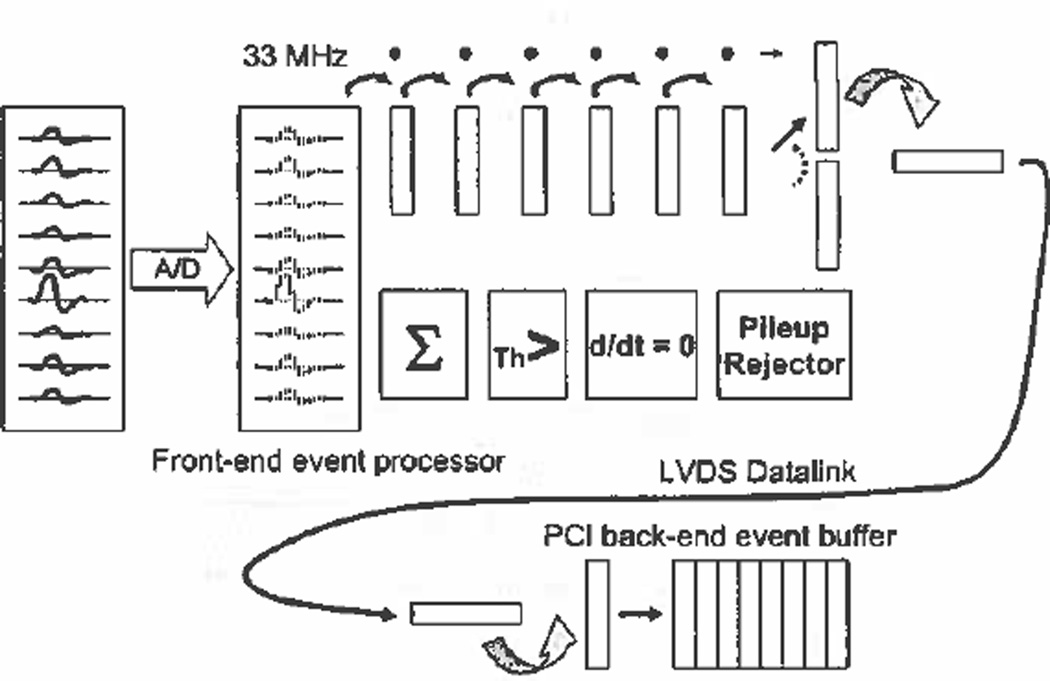
The event processor is realized in FPGA firmware. The event-detection algorithm is fully pipelined with an algorithm diagrammed in Fig. 1. A continuous entering stream of nine 12-bit data words every 30 nanoseconds are summed, analyzed for an event maximum by a combination threshold trigger and first-derivative zero-crossing detector, and packaged into an event packet in six stages driven by a 33 MHz clock. A pile-up rejector is implemented as a state-machine that holds a detected event long enough to ensure that no second trigger occurs within the support of the analog shaping amplifiers. Each processor digests 3.5 gigabits of raw data per second.

Fig. 1.

Block diagram representation of the operation of the modular gamma cameras list-mode data acquisition system. Signals from PMT anodes are shaped with analog filters, digitized with free-running ADCs, and then scanned for events by the event detection pipeline. Observations associated with events are assembled into data packets and transmitted via LVDS to back-end buffers.

Since our imaging systems typically have many cameras (16–24) operating in parallel [1], the post-acquisition computing required to perform maximum-likelihood position and energy estimation on an event by event basis is considerable. In this work we are investigating the design of a specialized computing engine that could reside in the data path between the front and back ends of each camera and perform the estimation computations in real time while data are being acquired. The result, an x and y position, can be concatenated onto the original data packet such that the original intent of information conservation is still accomplished.

II. Data Acquisition Hardware

A. Front-end Event Processors

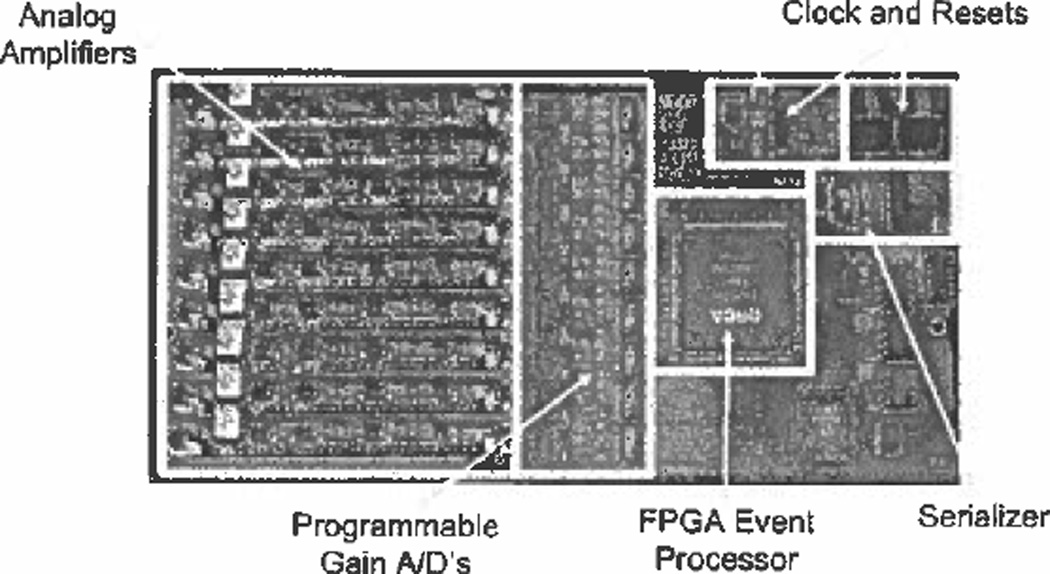
The front end board is designed to be mounted in proximity to the modular gamma-ray camera it serves. The board is roughly divided as analog on the left side and digital on the right, with the A/D converters straddling the boundary. The analog filters are modular and mounted in 30-pin SIMM sockets to allow for easy exchange of filter function. The processor board with its array of analog amplifiers is shown in the photo of Fig. 2. A single FPGA forms the core of the list-mode engine.

Fig. 2.

Front-end list-mode event processor board with key features identified. Each processor may be driven by its own on-board clock, or accept an external distributed clock when synchronization with other acquisition boards is required.

Data transmission and control lines are connected to the back end with a single, standard cat-5 twisted-pair cable.

B. Back-end Buffers

The back-end board in Fig. 3 conforms to the 66 MHz 64-bit PCI form factor and utilizes a field programmable system chip (FPSC) that combines a general purpose gate array with an ASIC core dedicated to the implementation of the PCI interface. Substantial socketed buffer memory is provided on this board that permits the accumulation of lengthy lists of data before a transfer must be made to disk. Two channels of data are accommodated on each back-end buffer card. A kernel-level driver memory maps the data buffers and about a dozen control registers into the user’s virtual address space.

Fig. 3.

Back-end list-mode event buffer with key features identified. Each board can support two modular cameras with completely parallel and independent data channels.

III. List-Mode Data

The advantages of List-mode data collection, the recording of the full set of observations associated with a data event as an entry in an ordered list, have been demonstrated in prior work [2–3]. In brief, statistical methods applied to estimate individual photon properties such as energy and position, or the fluence function, or even the tomographically reconstructed source object always have access to the data observations at their full collected precision.

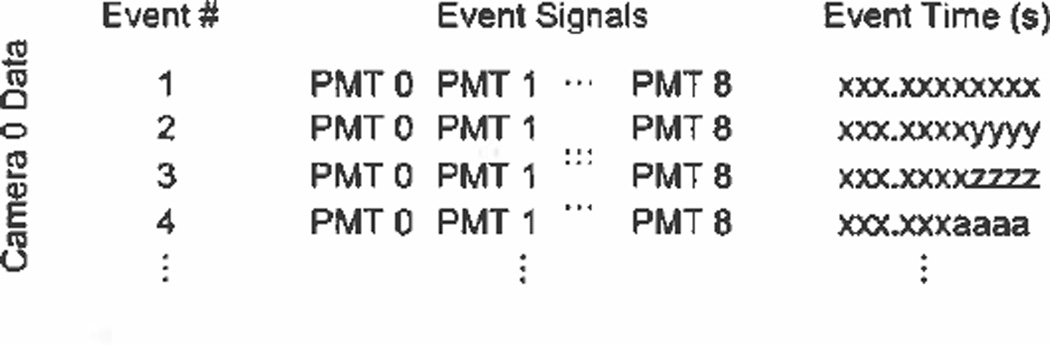
For the modular scintillation camera, the data comprises the peak amplitudes of the shaped PMT signals and the time when the event occurred, as shown in Fig. 4. Scans with collimated sources can be used to acquire calibration data.

Fig. 4.

Contents of list-mode data buffer after acquisition with modular gamma camera.

IV. Position Estimation

The output signal at each PMT anode in a modular scintillation camera is proportional to number of primary photoelectrons produced at the photocathode. The number of primary photoelectrons generated obeys Poisson statistics, and the signals in different PMTs are independent [4]. Thus we can write the probability of generating a particular data vector from an event at a particular location in terms of the mean signals in each of the PMTs resulting from events at that location:

$$\text{Pr}(\mathbf{g}|\mathbf{ḡ})=\prod _{i=1}^9\frac{e^{-{ḡ}_i}{ḡ}_i^{g_i}}{g_i!}.$$ (1)

To invert a given data vector with maximum-likelihood estimation, we seek the location r that has the maximum probability of generating the observed data. If we work with log likelihood for convenience, the problem can be stated as

$$\hat{\mathbf{r}}=\underset{\mathbf{r}}{\text{arg max}}\text{ln Pr}(\mathbf{g}|\mathbf{ḡ}(\mathbf{r}))=\underset{\mathbf{r}}{\text{arg max}}\sum _{n=1}^9[g_n\text{ln}{ḡ}_n(\mathbf{r})-{ḡ}_n(\mathbf{r})-\text{ln}{g}_n!]=\underset{\mathbf{r}}{\text{arg max}}\sum _{n=1}^9[g_n\text{ln}{ḡ}_n(\mathbf{r})+(-{ḡ}_n(\mathbf{r}))].$$ (2)

One method for rapid maximum likelihood estimation is to pre-compute an estimated position for every possible input vector, and use look-up tables that treat the vector as an address. However, when vectors get large, in this case 108 bits, this is not a feasible approach. It is instead necessary to carry out a search. We have found a convenient algorithm for carrying out ML position estimation that is suitable for implementation in a gate array pipeline that can be described as follows:

1. Zero pad the region around the detector to the nearest dimension that is a power of two

2. Pre-compute both terms in equation 2 that depend only on calibration data and scale appropriately to permit use of integer multiplications and sums

3. For i = 1 to 6 (for a 128 by 128 “pixel” detector)

   1. Compute the log likelihood at 16 test locations defined as the centers of 16 squares that cover the detector region under test
   2. Select the location with the highest log likelihood as the center of the next iteration’s region of interest
   3. Decrease the region of interest by a factor of 2 in both dimensions

The operation of the algorithm is graphically illustrated in Fig. 5.

Fig. 5.

Log-likelihood map (zero-pad region in blue; red is region of highest likelihood) and progress of the search algorithm through the six iteration stages for a sample data vector (1 event). The algorithm is operating on real data from a real camera, but in integer-only software for demonstration purposes.

V. Discussion

A maximum-likelihood search with a Poisson model (eq. 1) is at first glance an unlikely candidate for realization as a pipelined function in a gate array. There is a need for exponentials, factorials, multiplications, divisions, and sums with floating point precision, and the search algorithm may take an unknown number of steps to converge. In the prior section we show, however, that restating the problem in terms of log likelihood and using look-up tables containing means and log means multiplied by scaling factors (65536 is adequate for the sample in Fig. 5) permits the computations to be carried out with a small number of integer multiplications and sums. The factorial term has no position dependence and can be ignored for position estimation, though it needs to be reintroduced in a post-processing step for a final likelihood evaluation if likelihood thresholding is desired.

The search itself is carried out very efficiently by the suggested algorithm. There are several features that make the method very suitable for synthesis in a gate array. In each step, exactly sixteen trial locations need to be evaluated and they can be computed in parallel. For a given detector size, in units of pixels or resolvable elements, die search will require the same number of stages each time. Each stage is a natural pipeline step. The zero-padded perimeter is a key feature that allows the algorithm to work smoothly out to the edges of the detector without any special hard-to-synthesize conditional processing.

The algorithm has shown some robustness to noise in that even if the result of the first step of the iteration is not the point closest to the log likelihood map maximum, the region of interest shrinks slowly enough that the algorithm can recover and re-center in the correct area in time for the final iteration.

The algorithm is fast in software, and we are already employing it for near real-time viewing of projection data on an experimental SPECT imager with four cameras.

VI. Conclusion

The advantage of raw-signal list-mode acquisition is that there is no information loss or binning in the acquisition electronics. But raw signals don’t form images until they have been inverted into gamma-ray interaction location. Moving position estimation out of the acquisition computer and towards the camera will make it possible to immediately visualize projections for the purpose of making decisions about experimental parameters such as whether the tissue of interest is in the center of the field of view.

The maximum-likelihood (ML) search algorithm proposed is independent of the probability model, which in this case was Poisson, and may find application in other estimation problems where real-time processing is desirable. Therefore, the pipelined ML estimation engine we are designing in VHDL will have a general purpose structure that can be adapted to other instrumentation projects.