Robust time-shifted spoke pulse design in the presence of large B0 variations with simultaneous mitigation for through-plane dephasing, B1+ effects and the specific absorption rate using parallel transmission

Abstract

Purpose

We design parallel transmission (pTx) spokes pulses with time-shifted sub-pulse profiles for joint mitigation of intensity variations due to B1+ effects, signal loss due to through-plane dephasing and the specific absorption rate (SAR) at 7 Tesla.

Methods

We derive a slice-averaged small tip-angle (SA-STA) approximation of the magnetization signal at echo time that depends on the B1+ transmit profiles, the through-plane B0 gradient and the amplitude and time-shifts of the spoke waveforms. We minimize a magnitude least-squares (MLS) objective based on this signal equation using a fast interior-point approach with analytical expressions of the Jacobian and Hessian.

Results

Our algorithm runs in less than three minutes for the design of 2-spoke pulses subject to hundreds of local SAR constraints (single CPU, Matlab implementation). On a B0/B1+ head phantom, joint optimization of the channel-dependent time-shifts and spoke amplitudes allowed signal recovery in high-B0 regions at no increase of SAR. Although the method creates uniform magnetization profiles (i.e., uniform intensity), the flip-angle varies across the image which makes it ill-suited to T1-weighted applications.

Conclusions

The SA-STA approach presented in this work is best suited to T2*-weighted applications with long echo times that require signal recovery around B0 “hotspots”.

Introduction

Ultra-high field imaging offers the promise of greater sensitivity and resolution, but its widespread use is hampered by the non-uniformity of transmit fields, increased specific absorption rate (SAR) as well as signal losses and image distortions due to the increased susceptibility differences between air and biological tissues. Advanced multi-coil shimming strategies have been proposed recently that allow higher order B0 corrections than the traditional 2^nd order spherical harmonic approach implemented in most scanners (1–3). Work done in our group indicates that using as many as 32 independent shim channels allows significant reduction of B0-induced image distortions in fast echo-planar imaging at 3 T (3). However, even with this strategy, gradient recalled echo (GRE) images still suffer from significant signal losses in regions with large through-plane dephasing (e.g., frontal and temporal lobes). Some authors have proposed using post-processing corrections of B0-induced signal losses based on the knowledge of the through-plane B0 gradient (4–6), but it is doubtful that these corrections can actually recover contrast in regions with large B0 since the signal may have completely disappeared by the time when the correction is applied. The use of thin slices and/or spin echoes can solve the through-plane dephasing problem (7), but these strategies are not always applicable.

The “z-shim” technique initially proposed by Frahm et al. (8) consists in acquiring several images per slice while under- or over-refocusing the slice-selection gradient so as to create a linear variation of the phase across the slice. This phase ramp can be used to pre-phase the spins, which, when properly calibrated, can exactly cancel through-plane susceptibly variations at echo time (TE) (9–11). Variants of these techniques have been developed for 3D (12), spiral (13) and echo-planar imaging (EPI) (14,15). These improved z-shim technique are faster than the original approach by Frahm et al., but still require acquisition of additional data compared to the equivalent uncompensated protocol. Single shot z-shim techniques have been developed that rely on RF pre-phasing (instead of gradient pre-phasing like in the original z-shim technique) using 3DRF pulses. This allows applying different amounts of through-plane pre-phasing in different parts of the image, but leads to unacceptably long excitation pulses (>50 ms) (16). Stenger et al. proposed a multi-shot variant of the 3DRF technique to overcome the long duration of their 3DRF pulse (50 ms), but this segmented strategy requires acquisitions of additional data compared to the uncompensated protocol (17). Recently, Zheng et al. used parallel transmission (pTx) to accelerate 3DRF pulses and showed signal recovery in EPI images using an 8-channel pTx system at 7 T (18). Another single shot z-shim technique is the spatio-spectral approach of Yip et al. (single channel version) (19) and Yang et al. (pTx version) (20), which assumes that there is a fixed relationship between the local B0 offset and its through-plane B0 gradient. These approaches work well but yield long RF pulses (>12 ms) which makes them sensitive to errors in the B0 mapping process.

Using the insight that it is equivalent to under- or over-refocus the slice-select gradient waveform and to use a perfectly refocused slice-select waveform but to shift the RF pulse in time, Deng et al. proposed a method that consists in time-shifting the RF waveforms played on the different channels of a pTx system. This can be used to create different amounts of signal pre-phasing in different parts of the image (21). This technique does not assume a fixed relationship between the in-plane B0 offset and the through-plane B0 gradient, results in short RF pulses (duration comparable to traditional spoke pTx pulses) and yields rectangular slice-profiles (a sinc pulse can be used). Recently, Schneider et al. extended this pTx z-shim technique to correct for both in-plane B1+ inhomogeneity and through-plane signal drop-out for head imaging at 3 T (22). Although more sophisticated than the manual approach used in the work of Deng et al., the tuning of channel-dependent time-shifts by Schneider et al. is somewhat ad-hoc and needs to be tuned carefully. Because this method is not based on an optimization algorithm, it is not clear how it would perform at ultra-high field (e.g., 7 T) where transmit field non-uniformities and B0 variations are more pronounced than at 3 T where the method was evaluated.

In this work, we propose a fully optimized pTx pulse design tailored to ultra-high field applications that optimally balances the competing requirements of mitigation of B1+ effects, recovery of signal losses due to through-plane dephasing as well as reduction of SAR. As in the work of Deng et al and Schneider et al, our approach is based on pTx spokes RF waveforms which we shift in time in order to achieve simultaneous correction for in-plane B1+ and through-slice B0 dephasing effects (consistent with this previous work, we call these pulses “time-shifted spoke pulses” since they are based on the same gradient trajectory as traditional spoke pulses and use the same typical sinc envelop profile, only shifted with respect to the center of the slice select gradient lobe). We developed, tested and characterized our approach at 7 T using a 3D-printed head phantom with four compartments (bone, brain, muscle and internal air cavities) and realistic B1+ and B0 field distributions. The specific contributions of this work include:

• Derivation of a new signal equation, which we call the slice-averaged small tip-angle (SA-STA) approximation, incorporating the effects of slice averaging in the presence of linear through-plane B0 variations and time-shifting of the spoke sub-pulses played on a pTx system.

• Analysis of the SAR of time-shifted composite pTx pulses (theory and simulations).

• A fast, SAR-constrained magnitude least-squares (MLS) spoke pulse design algorithm with joint optimization of spoke amplitudes and channel- and spoke-dependent time shifts. We provide compact analytical expressions of the Jacobian (vector of first derivatives) and the Hessian (matrix of second derivatives) of the MLS objective function and the power and SAR constraints for faster convergence.

• Design and creation of a 3D-printed head phantom with four compartments (bone, brain, bone, muscles and internal air cavities) with realistic B1+ and B0 field distributions.

• Demonstrations of the ability of our SA-STA algorithm to optimally balance the three competing requirements of image intensity uniformization, intra-voxel dephasing signal recovery and SAR reduction in simulations and phantom experiments at 7 T.

• Free distribution of the Matlab code, which can be found at http://martinos.org/~guerin/.

Methods

Slice-averaged small tip-angle approximation

In the small tip-angle (STA) approximation, the expression of the complex transverse magnetization M_T for a multi-channel transmit device at time TE is (23):

$$M_T\left(\mathbf{r},TE\right)=j\gamma M_0\sum _c{B}_{1+,c}\left(\mathbf{r}\right)\underset{0}{\overset{T}{\int }}{rf}_c\left(t\right){\mathrm{e}}^{j\left[\mathbf{k}\left(t\right)·\mathbf{r}-\gamma \mathrm{\Delta }{B}_0\left(\mathbf{r}\right)\left(TE-t\right)\right]}dt,$$ [1]

Where r = (x, y, z) is the 3D vector of spatial coordinates, γ is the gyromagnetic ratio, T is the RF pulse duration, B_1+c(r) is the transmit sensitivity profile of channel c, rf_c(t) is the RF waveform played on channel c, $\mathbf{k}\left(t\right)=\gamma {\int }_t^T\mathbf{G}\left(u\right)du$ is the transmit k-space trajectory (24) and ΔB₀(r) is the spatially-varying in-plane B0 offset. For a time-shifted spoke pulse with sub-pulse profile u(t), we have rf_c,s(t) = b_c,s u(t−T_s−Δt_c,s) where s is the spoke index, T_s is the time at which spoke s crosses the kz=0 plane (corresponds to the center of the slice-select plateau when the gradient waveform is refocused, which we assume in this work) and b_c,s and Δt_c,s are the amplitude and time shift of spoke s played on channel c (b_cs has units of Volts and u (t) has no units). By further assuming that RF is played only during the constant slice-select gradient plateau G_z, Eq. [1] becomes:

$$M_T\left(\mathbf{r},TE\right)=j\gamma M_0\sum _{c,s}{B}_{1+,c}{b}_{c,s}{e}^{j{\mathbf{k}}_s·{\mathbf{r}}_T}{e}^{-j\gamma \mathrm{\Delta }{B}_0\left(TE-\mathrm{\Delta }{t}_{c,s}\right)}{e}^{-j\gamma {\left(-1\right)}^s{G}_{z}z\mathrm{\Delta }{t}_{c,s}}\underset{T_s-T^{\prime }/2}{\overset{T_s+T^{\prime }/2}{\int }}u\left(t-T_s\right)e^{-j\gamma \left[{\left(-1\right)}^s{G}_{z}z-\mathrm{\Delta }{B}_0\right]t}dt$$ [2]

Where k_s = (k_s,x, k_s,y) is the location of spoke s in transverse transmit k-space, r_T = (x, y) is the position on the transverse plane defined by the slice and T′ is the sub-pulse duration (we have removed the explicit dependence of the field maps with the spatial location r for clarity; i.e., it is understood that these quantities depend on the spatial location r). The term (−1)^s indicate the alternating polarity of the G_z gradient from one spoke to the other (this term disappears if all spokes traverse kz in the same direction, i.e. monopolar slice-select Gz gradients). Note that we have assumed that the slice-select plateau is long enough for all time-shifted sub-pulses to be played without being cropped in time, which is crucial for maintain the quality of the slice-selection profile.

Assuming now a sinc shape for the sub-pulse profile, u(t)= sinc(ωt), the time integral in Eq. [2] becomes:

$$\underset{T_s-T^{\prime }/2}{\overset{T_s+T^{\prime }/2}{\int }}u\left(t-T_s\right)e^{-j\gamma \left[{\left(-1\right)}^s{G}_{z}z-\mathrm{\Delta }{B}_0\right]t}dt=\frac{e^{j\gamma \mathrm{\Delta }{B}_0{T}_s}}{\mid \omega \mid }P\left(\frac{\gamma \left[{\left(-1\right)}^s{G}_{z}z-\mathrm{\Delta }{B}_0\right]}{2\pi \omega }\right),$$ [3]

Where ω is the modulation frequency of the sinc spoke sub-pulse for excitation of a slice with thickness Z (see definition of ω after Eq. [4] below) and P(z) is the slice-profile, which is more or less a RECT function depending on the characteristics of the sinc sub-pulse such as number of zero-crossings and the smoothing filter used. In this work we use sinc pulses with 7 lobes (8 zero crossings) windowed using a Hanning filter. Expanding ΔB₀(r) up to the first order in space and assuming that the intra-voxel B0 variation is only significant in the slice-select direction, we have:

$$\mathrm{\Delta }{B}_0\left(\mathbf{r}\right)\approx \underset{\mathrm{\Delta }{B}_0\left({\mathbf{r}}_T\right)}{\underbrace{\mathrm{\Delta }{B}_0\left(x,y,z=0\right)}}+z\underset{g\left({\mathbf{r}}_T\right)}{\underbrace{{\frac{\partial \mathrm{\Delta }{B}_0}{\partial z}|}_{x,y,z=0}}}.$$ [4]

Usually, for excitation of a slice of thickness Z, the sinc modulation frequency is chosen as ω= γG_zZ/2π. The term g(r_T) in Eq. [4] represents the gradient of B0 in the slice direction which has been shown to be the main cause of signal loss in high-B0 regions (19,25). If ΔB₀(r)≠0, Eq. [3] and Eq. [4] show that this results in selection of slice that is offset with respect to its ideal position and is thicker or thinner than the ideal thickness depending on whether or not the background B0 gradient is collinear with G_z (this is the “potato chip” effect described in Ref. (26)). Incorporation of the linear ΔB₀ approximation of Eq. [4] and the sinc modulation frequency equation given above into the slice profile expression of Eq. [3] yields the following expressions for the spatially-varying slice offset (Z₀) and thickness (Z_eff):

$$Z_0\left({\mathbf{r}}_T\right)=\frac{\mathrm{\Delta }{B}_0\left({\mathbf{r}}_T\right)}{{\left(-1\right)}^s{G}_z-g\left({\mathbf{r}}_T\right)}{Z}_{\mathit{eff}}\left({\mathbf{r}}_T\right)=Z\frac{G_z}{{\left(-1\right)}^s{G}_z-g\left({\mathbf{r}}_T\right)}.$$ [5]

Since the sub-pulse time-shifts Δt_c,s do not appear in these expressions, it is not possible to correct for the potato chip effect by shifting in time the sub-pulse profiles of a pTx RF spoke pulse. Instead, time-shifting of the spoke sub-pulses can only help recover signal loss in regions with high ΔB₀ but cannot correct for ΔB₀-induced slice deformations.

Inserting Eq. [3] in Eq. [2] yields, after some re-organization:

$$M_T\left(\mathbf{r},TE\right)=j\frac{2\pi M_0}{G_{z}Z}\sum _{c,s}P\left(\frac{z-Z_0}{Z_{\mathit{eff}}}\right)B_{1+,c}{b}_{c,s}{e}^{j{\mathbf{k}}_s·{\mathbf{r}}_T}{e}^{-j\gamma z\left[{\left(-1\right)}^s{G}_z\mathrm{\Delta }{t}_{c,s}+g\left({\mathbf{r}}_T\right)\left(TE-\mathrm{\Delta }{t}_{c,s}-T_s\right)\right]}{e}^{-j\gamma \mathrm{\Delta }{B}_0\left({\mathbf{r}}_T\right)\left(TE-\mathrm{\Delta }{t}_{c,s}-T_s\right)}.$$ [6]

Finally, averaging this expression across the slice-direction (z) gives:

$$\begin{array}{l}{M}_T\left({\mathbf{r}}_T,TE\right)=\frac{1}{Z_{\mathit{eff}}}\underset{Z_0-Z_{\mathit{eff}}/2}{\overset{Z_0+Z_{\mathit{eff}}/2}{\int }}{M}_T\left(\mathbf{r},TE\right)dz\\ =j\frac{2\pi M_0}{G_{z}Z}\sum _{c,s}{B}_{1+,c}{e}^{-j\gamma \mathrm{\Delta }{B}_0\left({\mathbf{r}}_T\right)\left(TE-\mathrm{\Delta }{t}_{c,s}-T_s\right)}{b}_{c,s}{e}^{j{\mathbf{k}}_s·{\mathbf{r}}_T}\left\{\frac{1}{Z_{\mathit{eff}}}\underset{Z_0-Z_{\mathit{eff}}/2}{\overset{Z_0+Z_{\mathit{eff}}/2}{\int }}P\left(\frac{z-Z_0}{Z_{\mathit{eff}}}\right)e^{-j\gamma z\left[{(-1)}^s{G}_z\mathrm{\Delta }{t}_{c,s}+g\left({\mathbf{r}}_T\right)\left(TE-\mathrm{\Delta }{t}_{c,s}-T_s\right)\right]}dz\right\}\\ =j\frac{2\pi M_0}{G_{z}Z}\sum _{c,s}{B}_{1+,c}{b}_{c,s}{e}^{j\left[{\mathbf{k}}_s·{\mathbf{r}}_T-\frac{\gamma \mathrm{\Delta }{B}_0\left({\mathbf{r}}_T\right){\left(-1\right)}^s{G}_z\left(TE-T_s\right)}{{\left(-1\right)}^s{G}_z-g\left({\mathbf{r}}_T\right)}\right]}\text{sinc}\left\{\frac{\gamma G_{z}Z}{2\pi }\left(\mathrm{\Delta }{t}_{c,s}+\frac{g\left({\mathbf{r}}_T\right)\left(TE-T_s\right)}{{\left(-1\right)}^s{G}_z-g\left({\mathbf{r}}_T\right)}\right)\right\},\end{array}$$ [7]

Where the last equality was obtained by assuming that the slice profile is an ideal RECT function. We call this equation the slice-averaged small tip-angle (SA-STA) approximation at TE. From now on we use the notation α = γG_zZ/2π and β_c,s = αg(r_T)(TE−T_s)/[(−1)^s G_z − g (r_T)].

Impact of time-shifts on SAR

The SAR of a time-shifted pTx composite pulse is:

$$\begin{array}{ll}\mathit{SAR}=\frac{\sigma }{2\rho }\frac{1}{T}\underset{0}{\overset{T}{\int }}{\mid \mathbf{E}\left(t\right)\mid }^{2}dt\hfill & =\frac{\sigma }{2\rho }\frac{1}{T}\underset{0}{\overset{T}{\int }}\left[\sum _{c_1,c_2}{rf}_{c_1}\left(t\right)r{f}_{c_2}^{\ast }\left(t\right){\mathbf{E}}_{c_1}{\mathbf{E}}_{c_2}^{\ast }\right]dt\hfill \\ \hfill & =\frac{1}{S}\sum _s\sum _{c_1,c_2}{b}_{c_1,s}{b}_{c_2,s}^{\ast }\underset{{\left[\mathbf{Q}\right]}_{c_1{c}_2}}{\underbrace{{\mathbf{E}}_{c_1}{\mathbf{E}}_{c_2}^{\ast }\frac{\sigma }{2\rho }}}\underset{{\left[\mathbf{C}\left(\mathbf{\Delta }{\mathbf{t}}_s\right)\right]}_{c_1{c}_2}}{\underbrace{\frac{1}{T^{\prime }}\underset{0}{\overset{T^{\prime }}{\int }}\left[u\left(t^{\prime }-\mathrm{\Delta }{t}_{c_1,s}\right)u^{\ast }\left(t^{\prime }-\mathrm{\Delta }{t}_{c_2,s}\right)\right]d{t}^{\prime }}}\hfill \\ \hfill & =\frac{1}{S}\sum _s{\mathbf{b}}_s^H\left[\mathbf{Q}\circ \mathbf{C}\left(\mathbf{\Delta }{\mathbf{t}}_s\right)\right]{\mathbf{b}}_s\hfill \end{array},$$ [8]

Where σ and ρ are the conductivity and density, respectively, E_c is the electric field created by Tx channel c in response to a 1 V excitation and s is the spoke index. The symbols ∘ and ^H denotes the term-by-term matrix multiplication and the complex-transpose operator, respectively. Eq. [8] shows that the SAR created by a time-shifted composite pulse has the standard quadratic form, only its kernel is the SAR matrix multiplied (term-by-term) by the correlation matrix of the time-shifted sub-pulses profiles.

The diagonal values of the correlation matrix C(Δt_s) do not depend on the time shifts and are all equal to the time average of the square of the sub-pulse. However, the off-diagonal elements depend on the time shifts. In the extreme case where two sub-pulses are shifted by T′ (the total length of the sub-pulse); these do not overlap in time and have a correlation factor equal to zero. This, of course, reflects the fact that the SAR of two RF pulses transmitted serially (as opposed to in parallel) is simply the average of the SAR of the two pulses. In other words, time-shifting of spokes can reduce SAR.

Joint optimization of spoke amplitudes and time shifts with SAR constraints

The SA-STA approximation (Eq. [7]) provides the basic building block for our pulse design approach. We jointly optimize the spoke amplitudes and time shifts by solving the following magnitude least-squares (MLS) problem:

$$\begin{array}{ll}\hfill & \underset{\mathbf{\Delta }\mathbf{t},\mathbf{b}}{min}\mathrm{\Psi }={\Vert \left|{\mathbf{M}}_T\left(\mathbf{\Delta }\mathbf{t},\mathbf{b}\right)\right|-\left|{\mathbf{M}}_{T,\text{target}}\right|\Vert }_2^2\hfill \\ \hfill \mathrm{s}.\mathrm{t}.\mathrm{a})& \frac{1}{S}\sum _s{\mathbf{b}}_s^H\left[{\mathbf{Q}}_i\circ \mathbf{C}\left(\mathbf{\Delta }{\mathbf{t}}_s\right)\right]{\mathbf{b}}_s\le \mathit{lSAR}\forall i\hfill \\ \hfill \mathrm{b})& \frac{1}{S}\sum _s{\mathbf{b}}_s^H\left[\langle \mathbf{Q}\rangle \circ \mathbf{C}\left(\mathbf{\Delta }{\mathbf{t}}_s\right)\right]{\mathbf{b}}_s\le \mathit{gSAR}\hfill \\ \hfill \mathrm{c})& \frac{{\left|b_{c,s}\right|}^2}{8Z_0}\le P_{\text{peak}}\forall c,\forall s\hfill \\ \hfill \mathrm{d})& \left|\mathrm{\Delta }{t}_{c,s}\right|\le \mathrm{\Delta }{t}_{max}\forall c,\forall s\hfill \end{array},$$ [9]

where M_T(Δt,b) is given by Eq. [7] and M_T,target is a flat target magnetization pattern (only its magnitude is relevant). The constraints a) through d) constrain local SAR, global SAR, peak power and the maximum time shifts, in this order (lSAR, gSAR, P_peak and Δt_max are the maximum local SAR, maximum global SAR, maximum peak power and maximum time shift, respectively). As in Ref. (27), we constrain local SAR using a compressed set of SAR matrices obtained using the virtual observation points (VOPs) algorithm (28). The MLS objective function in Eq. [9] is required since the use of long TEs in the presence of large B0 offsets create rapid phase variations that are not possible to cancel using only a few spokes. Since the MLS term in Eq. [9] is computed using the SA-STA approximation, this minimization problem jointly minimizes image non-uniformities due to B1+ variations and signal loss due to through-plane dephasing.

To solve Eq. [9] over spoke amplitudes and time-shifts, we directly minimize the MLS cost function (as opposed to using the phase adoption approach of Setsompop et al. (29)). To speed-up convergence, we provide analytical formulas for the Jacobian (vector of first derivatives, see Appendix) and the Hessian (matrix of second derivatives, see supporting material) of the MLS objective function as well as the SAR and power constraint functions. Using these expressions, the Jacobian and Hessian blocks can be evaluated quickly using fast vector-vector, vector-matrix and matrix-matrix multiplications such as implemented in Matlab. We solve Eq. [9] using the interior-point optimizer as implemented in Matlab (function fmincon, Matlab 8, Mathworks, Natick MA).

B0-robustness

To improve the robustness of our pulse design in the presence of large B0 offsets, we impose realization of the target magnetization pattern over a frequency range (spatio-spectral design) as in Ref. (30). For our 7 T experiments, we enforced good performance of the pulse design algorithm at −50 Hz, 0 Hz (Larmor) and + 50 Hz. We also investigated the impact of using monopolar slice-select gradients (Gz has the same polarity of all spokes) in multi-spoke pulses.

Experiments using a 3D-printed head phantom at 7 T

To develop and validate our approach, we 3D-printed a realistic head phantom with four compartments (bone, brain, muscle and internal air cavities). Three-dimensional printing was performed using the Dimension SST 1200 ES printer with ABS plastic as the printed material. The phantom was based on the 3 T MRI scan of a healthy volunteer segmented into six tissue classes: Air, white matter (WM), grey matter (GM), cerebro-spinal fluid (CSF), skull and “everything else” (31,32). The brain compartment was obtained by combining the WM, GMN and CSF tissue classes. The skull was printed as solid plastic with a hole to allow filling of the brain cavity (plastic has a low conductivity which mimics the properties of bone). The internal air cavities of the model (mainly the sinuses) were simplified, embedded in the skull compartment and sealed to prevent agar gel to seep in when filling the phantom. Filling holes, plastic groves and sliders were added to the original surfaces to facilitate assembly and sealing of the phantom (Fig. 1a). All plastic parts were water-proofed before filling using a rubber coating spray. The brain compartment was filled with a gel made of 0.12% NaCl and 3% agar (σ=0.5 S/m, ε=80 @ 297 MHz as measured using an 85070E Agilent dielectric probe, Agilent, Santa Clara CA). The muscle compartment was filled with a gel mixture of 0.26% NaCl and 3% agar (σ=0.7 S/m, ε=80 @ 297 MHz). Small amounts of Gadolinium (0.1%) and NaN3 (0.05%) were added to decrease T1 and prevent bacterial proliferation, respectively (all concentrations are given in weight).

Fig. 1.

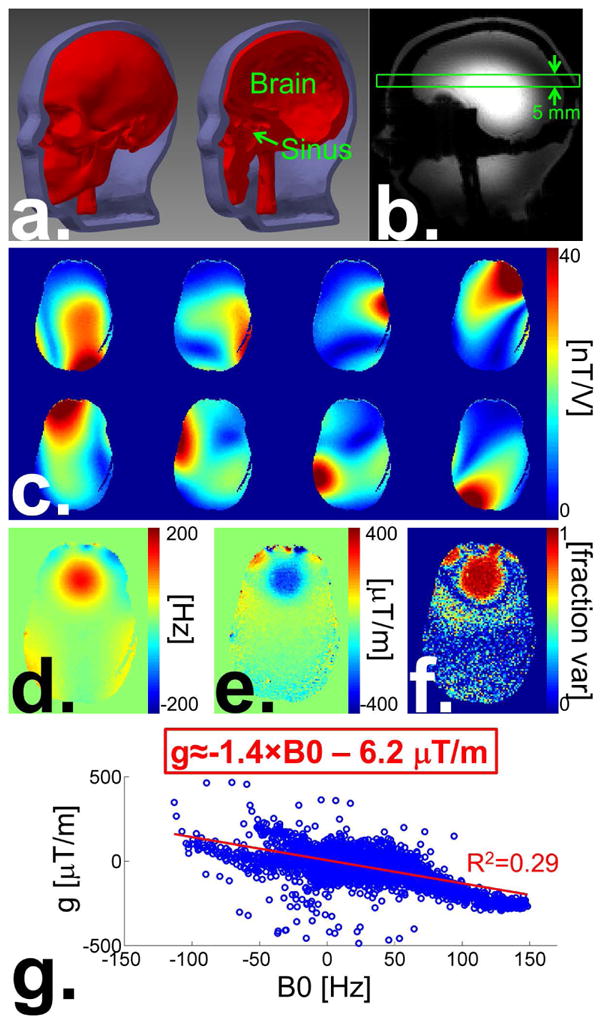
a: CAD model of the 3D-printed B1+/B0 phantom showing the bone (i.e., skull), brain and sinus compartments. The space between the bone and the outer layer of the phantom is filled with agar gel with electrical properties similar to muscle tissues. b: GRE image of the phantom in the sagittal orientation obtained using the birdcage mode of the pTx array. The green rectangle shows the slice position corresponding to c–g. c: B1+ maps (magnitude) of our pTx system’ 8 channels. d: B0 map. e: Map of the through-plane B0 gradient. f: Map of the fraction of variance of the through-plane B0 variation explained by first-order linear fit. g: Scatter plot of the through-plane B0 gradient and the in-plane B0 within the brain mask. The red line shows the best linear fit through the scatter data.

Experiments were run on our receive/transmit 8-channel 7 T pTx system (“step 2”, Magnetom 7 T, Siemens Healthcare, Erlangen Germany). B1+ and B0 maps were acquired using the saturated TFL technique (33) and the GRE field mapping Siemens product sequences, respectively. The phantom was shimmed up to second order spherical harmonics terms using the scanner’ automated procedure. The through-plane B0 gradient was estimated on a pixel-by-pixel basis using a 3D B0 map (estimated from two 3D GRE acquisitions with ΔTE=2 ms) with 5 mm-slab thickness (0.5 mm z resolution) and linear fit of B0 variations in the z direction. Spoke pulses were designed so as to create a uniform magnetization distribution with M_T/M0=0.17 with minimal through-plane dephasing (this target magnetization value was chosen because it corresponds to a 10° flip-angle and therefore guarantees that the transverse magnetization signal is within the range of validity of the small tip-angle approximation). When playing two spokes, the first spoke was always placed at (k_x,k_y)=(0;0) and the second spoke at (k_x,k_y)=(5;5) in units of m⁻¹. The 1-spoke and 2-spoke results presented in this work were obtained on the same slice of the B1+/B0 phantom using the same acquisition parameters (e.g., TE, TR etc…). GRE images were corrected for the receive sensitivity profiles using the SENSE algorithm without acceleration (R=1). The receive profiles of the transmit/receive loop channels were estimated by division of the individual channel GRE images obtained at short TE (6 ms) by the transmit profiles obtained by Bloch simulation for a simple pseudo birdcage mode (pBC) excitation (the pBC mode excitation was obtained by exciting all channels with the same amplitude but phases equal to the opposite of their B1+ phases at the center of the image). Division of the individual coil images by the Bloch-simulated transmit profile of the pulse was necessary to isolate the receive sensitivity profiles from the total image (which is, for each coil, a combination of the image contrast, the receive profile and the flip-angle distribution). This somewhat convoluted process was used as it is not possible to acquire a reference image with uniform receive sensitivity on our 7 T scanner. Therefore, unlike at 3 T where a body birdcage coil with highly uniform receive sensitivity profile in the head is usually available; we could not obtained the coil sensitivity maps by division of images acquired with these coils with an image acquired with the body coil using the same sequence parameters (e.g., TE, TR etc…).

We characterize our algorithm performance using the magnetization error, which is simply the root mean square error of the magnetization distribution computed with respect to the target magnetization. We also use the fraction of signal retained (FSR), which is computed as FSR(x, y) = |∫_z exp{iϕ(x, y, z)}dz|/Z, where φ(x,y,z) is the phase at location (x,y,z) and Z is the slice thickness. FSR values of 0 and 1 indicate complete loss of signal due to through-plane dephasing and complete signal recovery, respectively.

SAR simulation

We simulated the electric fields inside the 3D head-phantom using a co-simulation strategy based on the field simulator HFSS (Ansys, Canonsburg PA) and the circuit simulator ADS (Agilent, Santa Clara CA) that we and others have previously used and validated extensively (27,34–36). The coil was tuned (@ 297 MHz) and matched (better than −20 dB for all channels) in the circuit simulator as explained in Ref. (36). As in the actual coil, individual loops were shielded which resulted in low coupling of the transmit channels (less than −12 dB for all pairs). Electric fields and the conductivity and density maps were exported on a 2 mm isotropic voxel grid. The original 370,085 SAR matrices of the model were compressed into 544 virtual observation points or VOPs (maximum SAR overestimation factor of 5% of the maximum possible SAR) (28).

Results

A strong B0 hotspot around 200 Hz in the frontal lobe (Fig. 1d) as well as the dielectric resonance intensity weighting (Fig. 1b) that are typical of 7 T brain imaging are clearly visible on the phantom field maps. The fraction of the total B0 variance along the slice direction explained by the linear fit (Fig. 1f, this quantity is also referred to as R² in statistics) is close to unity in the frontal lobe hotspot, showing that the linear component of the total B0 through-plane variation in that region captures most of the dephasing effects for this slice (there is little B0 variations across the slice at other locations, which results in small values of the fraction of variance explained by the linear fit). Plotting the through-plane B0 gradient as a function of the in-plane B0 offset reveals a roughly linear dependence (R²=0.29) of the two quantities with a proportionality constant equal to −1.4 μT/m/Hz (Fig. 1g), which is consistent with previously published results (19,25).

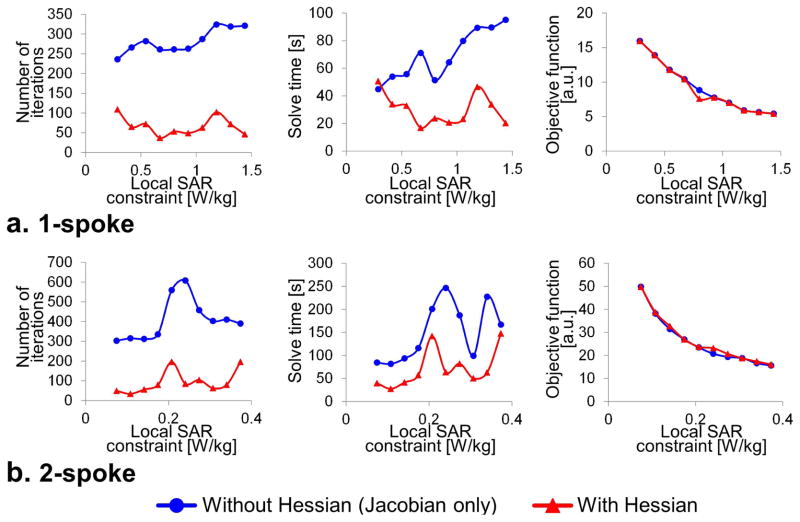
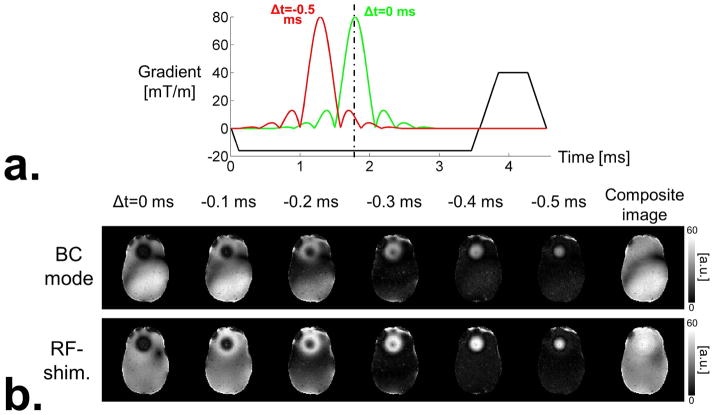
Fig. 2 shows the performance of the slice-averaged small tip-angle (SA-STA) algorithm with and without incorporation of the analytical Hessian information in the optimization process. Use of the Hessian information significantly improved the convergence of the spoke design algorithm, resulting in computation time faster than 1 min. and 3 min. for 1-spoke and 2-spoke pulses, respectively, subject to 544 VOPs SAR constraints and computed in Matlab on a single CPU (2.8 GHz Intel Core i7). Such rapid optimization makes the technique highly amenable to multi-slice imaging where each slice is excited using a pulse specifically optimized for that slice. In Fig. 3, we show the results of global z-shims adapted to pTx by using the same time-shifts for all Tx channels. For each set of z-shim steps (one step correspond to one value of the time-shifts), a composite image is computed as the maximum of the pixel intensities across all z-shim steps. This composite image, as shown originally by Frahm et al. (8), shows excellent signal recovery in the frontal lobe. Fig. 3 also shows that a global z-shim strategy can be used in conjunction with 1-spoke pulses, thus yielding a composite image with uniform intensity across the field-of-view.

Fig. 2.

a: Convergence performance of our slice-averaged small tip-angle (SA-STA) design algorithm for 1-spoke pulses with (red) and without (blue) analytical computation of the Hessian matrix. The number of iterations, solve time and final objective function value are shown for various values of the maximum local SAR constraint. Local SAR was constrained using the virtual observation point compression of SAR matrices (544 VOPs). The duty-cycle was 100% for all pulses (i.e., TR is equal to the RF pulse duration in these results. Results for different TRs are simply obtained by scaling local SAR constraints by the duty-cycle) and the target magnetization was MT/M0=0.17. Spokes amplitudes and time-shifts were optimized jointly. No B0 robustness was enforced in the design of these 1-spoke pulses. These results show that providing the analytical expression of the Hessian matrix to the optimizer significantly reduces the number of iterations and computation time. Moreover, this acceleration comes at no cost in term of design quality since the objective function values achieved by both methods (with and without analytical Hessian) are almost identical (this is not trivial as the magnitude least-squares SA-STA optimization problem of Eq. [9] is non-convex, therefore convergence to the global optimum is not guaranteed). b: Same convergence performance metrics of the SA-STA design algorithm for 2-spoke pulses. B0 robustness was enforced in the design of these 2-spoke pulses using ±50 Hz as the off-resonance frequencies.

Fig. 3.

a: Radio-frequency (RF) and slice-selection gradient waveforms superimposed on the same graph (RF waveforms are scaled to arbitrary units). RF waveforms are Hanning-windowed sinc pulses with 7 lobes (8 zero-crossings). The green RF pulse is perfectly centered with respect to the slice-selection gradient lobe. As a result, it creates a perfectly refocused slice profile with no through-plane phase variation. The red RF pulse however is shifted by 500 us and is therefore not completely refocused by the refocusing lobe of the gradient waveform. As a result, this pulse creates a slice profile with a linear phase variation in the slice direction. Note that the duration of the slice selection gradient is long enough to allow playing the time-shifted pulse without cropping it, which is crucial for maintaining the quality of the slice profile across time-shifts. b: Global z-shims obtained by time-shifting the RF waveforms played on different transmit channels by the same amount. Two RF drives are considered: Birdcage mode and RF-shimming (equivalent to 1-spoke). In both cases, the RF amplitudes and phases are kept constant for all the “steps” of the z-shim process (one step corresponds to one time-shift). The right-most images of the BC mode and RF-shimming image rows are composite images obtained by taking the maximum intensity of all z-shim steps for each pixel.

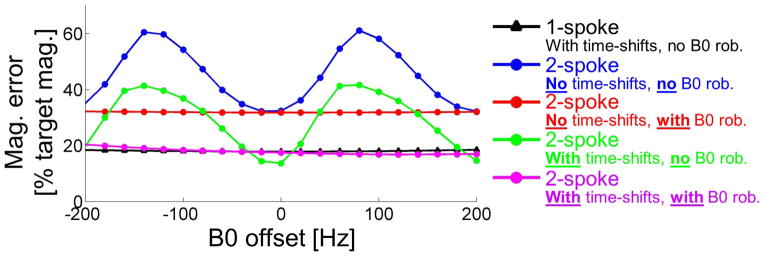
Fig. 4 shows performance plots of various RF pulses (1-spoke and 2-spoke, with and without optimization of the time-shifts) as a function of the offset frequency (relative to the Larmor frequency). Although 1-spoke pulses were designed without B0 robustness constraints, they show remarkable robustness in the face of off-resonance effects with a root mean square error of the magnetization profile essentially constant over 400 Hz (black triangles). In contrast, 2-spoke pulses designed without B0 robustness constraints are very sensitive to off-resonance effects in this frequency range (blue and green circles). Incorporation of B0 robustness constraints at −50 Hz and +50 Hz largely resolved this problem (red and purple circles), however at a small cost of flip-angle homogeneity performance at the Larmor frequency.

Fig. 4.

Plot of the magnetization error (computed using a 3D Bloch simulation) as a function of the frequency offset around the Larmor frequency for five design strategies: 1-spoke with optimization of the time-shifts and 2-spoke with/without optimization of the time-shifts and with/without B0 robustness constraint in the pulse design.

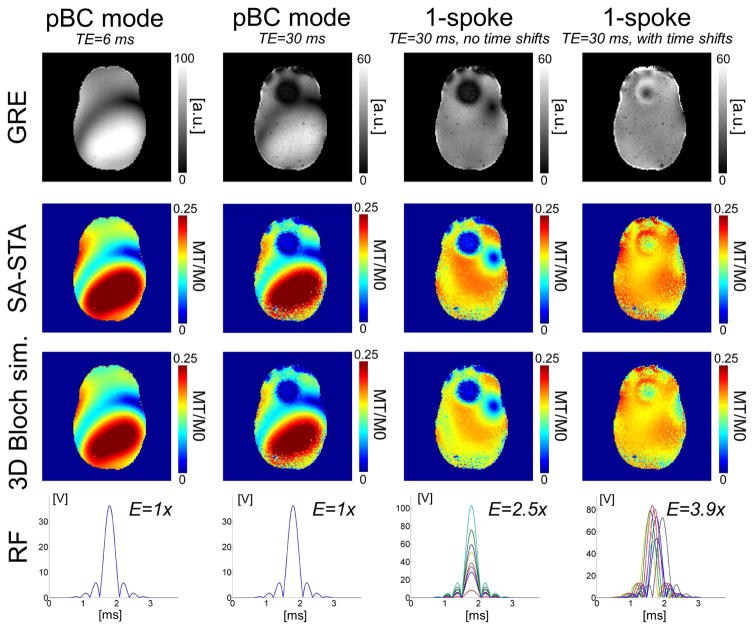
Fig. 5 shows GRE images (after removal of receive sensitivity profiles) acquired on our 8-channel pTx system as well as magnetization maps (SA-STA signal equation and 3D Bloch simulation). In the absence of correction for through-plane dephasing (i.e., no time-shifts), the GRE signal in the frontal lobe area was completely destroyed by through-slice dephasing. This signal was almost completely recovered using the SA-STA approach with optimization of time-shifts (time-shifts were limited to ±500 μs). In addition, the SA-STA excitation was able to create a uniform magnetization distribution across the slice. In this phantom with no tissue contrast variations (uniform agar gel), the GRE images closely reflect the magnetization maps predicted by the 3D Bloch simulation and the SA-STA signal equation. The good agreement between these GRE images, the 3D Bloch simulation and the SA-STA maps is a direct validation of Eq. [7].

Fig. 5.

Gradient recall echo (GRE) image, slice-averaged magnetization maps and radio-frequency (RF) waveforms for four single-spoke excitation strategies: Pseudo birdcage (pBC) mode at short (TE=6 ms) and long TE (TE=30 ms) and 1-spoke with/without optimization of the sub-pulse time shifts (maximum time shift is ±500 us). The target magnetization was MT/M0=0.17 and the slice-thickness was 5 mm. Magnetization maps obtained using the slice-averaged small tip-angle (SA-STA) approximation and using a 3D Bloch simulation (i.e., in-plane and across the slice) show excellent agreement, thus validating Eq. 7 (small differences remain between the Bloch simulation and SA-STA due to the fact that an ideal rectangular slice-profile is assumed in our derivation Eq. 7). GRE images are shown after removal of the receive sensitivity profile and are in very good agreement with magnetization maps in this phantom with little PD/T1/T2 contrast (uniform agar gel). The time-shift optimized 1-spoke strategy was able to recover most of the signal lost in the frontal lobe area due to through-plane dephasing while creating a much more uniform excitation than the birdcage mode. Next to each RF waveform, we show the total pulse energy (integral of the square of the RF pulse) as a fraction of the pBC mode RF pulse’ energy.

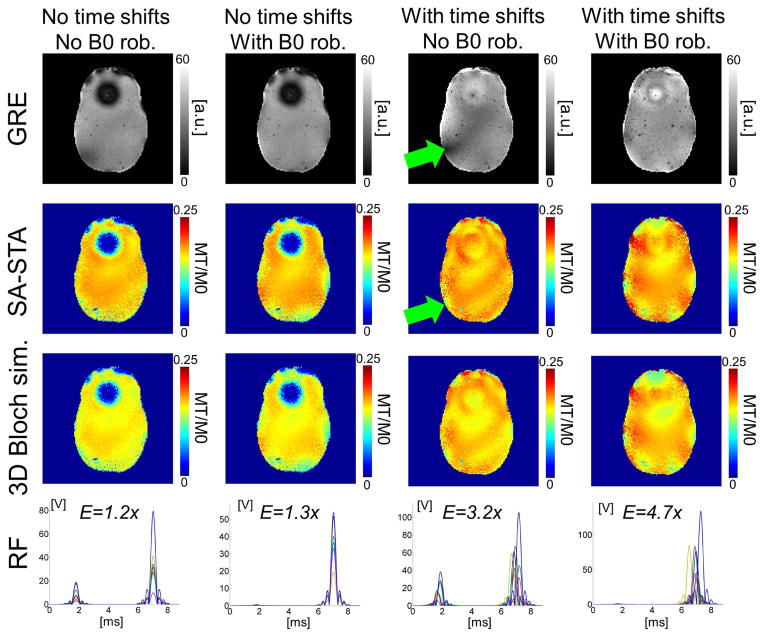
The performance of 2-spoke pulses optimized with and without incorporation of B0 robustness constraints is shown in Fig. 6 (monopolar slice-selection spoke gradients for all pulses in this figure). GRE images show a better correlation with the 3D Bloch simulation results when enforcing B0-robustness constraints in the pulse design process. This is especially true when optimizing both the spokes amplitudes and the time-shifts (green arrows). It is evident from this figure that enforcing B0-robustness constraints causes the pulse design algorithm to use only one of the two spokes. As a consequence, the performance of B0-robust 2-spoke pulses in term of uniformity of the magnetization distribution and through-plane signal recovery is essentially the same than that of our 1-spoke pulses (Fig. 5, this is also visible on Fig. 4). We point out that the time-shifted 1-spoke and 2-spoke pulses shown in Figs. 5 & 6 consume more energy (as measured by the integrated sum of squares of the RF waveforms) than their counterparts without time-shifts.

Fig. 6.

Gradient recall echo (GRE) image, slice-averaged magnetization maps and radio-frequency (RF) waveforms for four 2-spoke excitation strategies combining optimization of the sub-pulse time-shifts and incorporation of B0 robustness constraints in the pulse design. The maximum time-shift was ±500 us. The TE was 30 ms for all images. The target magnetization was MT/M0=0.17 and the slice-thickness was 5 mm. Like in Fig. 5, agreement between the slice-averaged small tip-angle (SA-STA) approximation and the 3D Bloch simulation is excellent for all designs. GRE images are shown after removal of the receive sensitivity profile. When using non-zero sub-pulse time-shifts for recovery of the through-plane signal drop-out, the agreement between 3D Bloch simulations and GRE images was better when imposing B0 robustness constraints in the design (green arrows). The time-shift-optimized 2-spoke strategy with B0 robustness constraint was able to create a highly uniform excitation across the slice while recovering most of the through-slice signal drop-out. When incorporating B0 constraints in the presence of strong B0 variation, as it is the case for this slice, the 2-spoke pulse solution utilizes only a single of the two spoke (columns 2 & 4). Next to each RF waveform we show the total pulse energy (integral of the square of the RF pulse) as a fraction of the pseudo birdcage mode RF pulse’ energy.

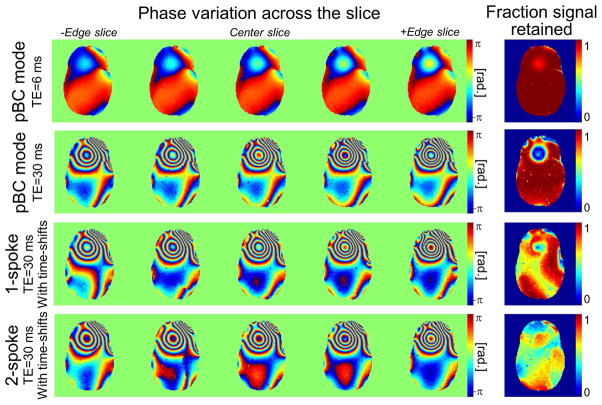
Fig. 7 shows measured 3D GRE phase maps at several depths inside the 5 mm-thick slice for pseudo-CP mode and SA-STA excitations. Pseudo-CP mode phase maps acquired at TE=30 ms display the expected rapid phase evolution in high-B0 regions (black arrows) causing important dephasing. In contrast, the SA-STA pulses display more stable phase variations in this region. As indicated by maps of the fraction of signal retained (FSR) metric, the price to pay for improved phase stabilization in regions with large B0 with SA-STA comes in the form of significant signal losses in other regions. To create a uniform magnetization profile integrated across the slice despite this, the SA-STA algorithm over-flips spins in these regions. This explains why time-shifted pulses have greater power demands than traditional pulses without time-shifts (Figs. 5 & 6). Because of this over-flipping effect, SA-STA excitations create uniform magnetization distributions with non-uniform flip-angle weighting across the image (this is not a contradiction as both the flip-angle and through-plane dephasing contribute to the net magnetization).

Fig. 7.

Phase variation across the slice and fraction of signal retained for pseudo birdcage mode (pBC), 1-spoke and 2-spoke SA-STA pulses (SA-STA pulses were optimized for magnetization uniformization and through-plane signal recovery, but not the pBC mode pulses). These through-slice phase profiles show that optimization of the sub-pulse time-shifts (1-spoke and 2-spoke results in rows 3 & 4) results in a phase pattern that varies more slowly at locations with strong through-plane B0 gradient compared to the birdcage mode excitation (row 2). The fraction of signal retained reveals that, in order to create uniform magnetization profiles, the SA-STA algorithm creates through-plane signal losses in low-B0 regions and then increases the signal in these regions by “over-flipping” the spins. As a consequence, SA-STA excitations create uniform magnetization (which is a combination of the flip-angle and spin dephasing) profiles but non-uniform flip-angle weighting.

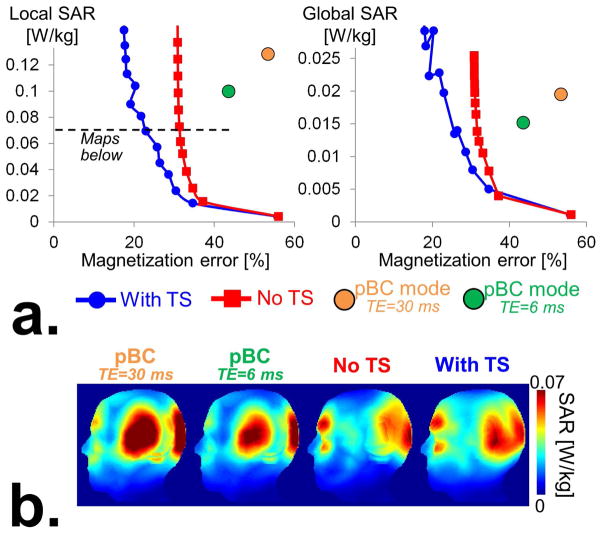
Fig. 8 shows that, despite their increased power consumption, of SA-STA pulses do not create more SAR than traditional pTx pulses (not time-shifted). Indeed, as explained in the Methods section, partially overlapping spoke sub-pulses create less SAR than fully overlapped ones. Our implementation of the SAR constraints in Eq. [9] incorporates this phenomenon, which is modeled mathematically by multiplying the SAR (or VOP) matrices by the correlation matrix of the time-shifted sub-pulses (Eq. [8]). Because of this, the SA-STA design algorithm is able to find the optimal tradeoff between magnetization uniformization and through-plane dephasing signal recovery without penalty in term of local and global SAR.

Fig. 8.

a: L-curves showing the tradeoff between local SAR and the magnetization error (expressed in percent of the target magnetization) for 1-spoke pulses computed with (“With TS”) and without optimization of the sub-pulse time-shifts (“Without TS”). Also shown are data points corresponding to pseudo-birdcage mode excitations (“pBC mode”) obtained with TE=30 ms and TE=6 ms. Note that the SAR of the pBC mode data points obtained for TE=6 ms and TE=30 ms are slightly different because the RF amplitudes are scaled so as to reach the average magnetization target. Since the pBC mode image for TE=30 ms has a large signal drop-out region in the frontal lobe, this scaling factor is greater for the TE=30 ms image than for the TE=6 ms image, which results in greater SAR. b: Maximum intensity projections of SAR maps of the “With TS”, “No TS” and birdcage mode excitation strategies. These results show that joint optimization of the spokes amplitudes and sub-pulse time-shifts (“With TS”) yields pulses with significantly better excitation profiles (see Fig. 5) than excitations only optimized for spoke amplitudes (“No TS”) for the same local SAR.

Discussion

We have described a pTx spoke pulse design approach that mitigates intensity variations due to B1+ and B0 effects as well as SAR in a unified and fast algorithm. The method is based on a new small tip-angle signal equation that we call the slice-averaged small tip-angle (SA-STA) approximation and that accounts for the non-uniformity of the B1+ transmit profiles, linear through-plane B0 variations as well as time-shifting of the spoke sub-pulse profiles. We validated the accuracy of the SA-STA signal equation by comparison with 3D Bloch simulations and GRE images acquired on a 7 T 8-channel pTx system. Our pulse design fully optimizes both channel- and spoke-dependent time-shifts as well as spokes amplitudes and does not require any manual intervention or tuning. It is straightforward to use and runs in less than three minutes for up to two spokes subject to B0 robustness constraints as well as peak power, local and global SAR constraints on a single CPU (2.8 GHz Intel Core i7) and a Matlab implementation. In addition to B0 and B1+ field maps that need to be acquired as with most pTx pulse design optimization techniques, the proposed approach requires knowledge of the through-slice B0 gradient which can be deduced from a 3D GRE acquisition (1–2 minutes per slice) or estimated from the in-plane B0 field map using the linear relationship of Fig. 1g (no additional data to be acquired). This method is highly amenable to multi-slice imaging (one pulse per slice) as well as non-standard pTx coil geometries for which manual setting of the time-shifts may not be straightforward. We have shown (Figs. 3, 5 and 6) that the SA-STA approach yields excitations with comparable quality than those obtained with the global z-shim approach originally proposed by Frahm et al (8). However, SA-STA, unlike global z-shim approaches, does not require acquisition of multiple datasets and is therefore more efficient from a sampling perspective.

In the presence of large ΔB₀ variations, we have shown that B0-robustness constraints need to be incorporated in the 2-spoke design problem. Otherwise, significant deviations between the predicted and achieved magnetization profiles may be present that degrade the quality of the B1+ and through-slice dephasing corrections (Fig. 6). In contrast, 1-spoke pulses (i.e., only one spoke played at (k_x;k_y)=(0;0)) proved extremely robust to off-resonance effects even when not enforcing this as a design constraint. An interesting finding of this study is that when designing 2-spoke pulses with B0-robustness constraints, the design algorithm returned pulses that only used one of two spoke (Fig. 6). In other words, our design algorithm enforced robustness constraints in the 2-spoke design problem by removing one of the spoke, thus converting the pulse into a 1-spoke solution. This means that the only multiple-spoke solution intrinsically robust to off-resonance effect is the 1-spoke solution. We point out that this result is likely due to the extreme ΔB₀ variations studied in this work (|ΔB₀|>150 Hz). In fact, we did not observe this behavior in slices with more moderate ΔB₀ variations (in these cases the B0-robust 2-spoke solutions did use both spokes).

A limitation of the SA-STA approach presented here is that it creates excitations with uniform magnetization profiles but non-uniform flip-angle weighting. As shown in Fig. 7, this is because the algorithm is able to stabilize the phase in regions with large through-plane B0 variations albeit at the cost of severe dephasing in other regions. To compensate for this, the algorithm over-flips spins in regions with large signal loss due to time-shifting of the channel-dependent RF waveforms. The net result of this effect is the creation of excitations with uniform magnetization distributions but non-uniform flip-angle maps. Although counter-intuitive, this is simply due to the fact that the magnetization is a metric that depends both on the flip-angle and through-slice dephasing. Non-uniform flip-angle weighting of the SA-STA excitations is a significant drawback compared to other through-plane dephasing correction approaches such as the spectral method of Yip et al (19). However, the benefit of recovering signal that is otherwise lost in regions with large B0 variations using short RF pulses may outweigh this downside for some applications (our SA-STA pulses are less than 5 ms long, compared to more than 14 ms for the spectral pulses of Yip et al (19) and Yang et al (20)). As a consequence, we expect the SA-STA approach to be of interest for T2*-weighted imaging, but not for T1-weighting application in which contrast is strongly affected by flip-angle. The long TEs often used in T2*-weighted imaging accentuate the problem of signal loss due to spin dephasing, so we expect SA-STA pulses to have most impact in these cases anyway. We also point out that dephasing of the through-slice signal in low B0 regions with our methods in a direct consequence of the fact that we attempt to correct for both B1+ and B0 effect across the entire slice despite having only a limited number of transmit degrees-of-freedom (we use 8 transmit channels in this work). If one were to focus the optimization algorithm to the region containing the B0 hotspot (this is easily done by adjusting the optimization mask to this region), one may achieve even better signal recovery in this region. We also point out that different tradeoffs between flip-angle non-uniformity across the slice and correction for through-slice dephasing in high B0 regions can be achieved by attempting to create a lower target magnetization value at the B0 hotspot than at other locations in the slice (this is simply implemented by using a spatially-varying target magnetization map in Eq. [9]). Such strategy could be useful to create some level of signal recovery in the high B0 region while limiting through-slice dephasing in low B0 regions (we expect this to hold both for 1-spoke and 2-spoke pulses). Moreover, using a pTx coil with more than 8 transmit channels would improve the algorithm ability to pre-phase the spins in the high B0 regions where they need to be pre-phased while leaving them alone in low B0 regions. In other words, by using a pTx coil with a large number of transmit channels, one may be able to cancel exactly the through-slice phase in region with high B0 variation while creating zero through-slice phase variation in low B0 regions. This would create excitations with uniform magnetization and uniform flip-angle distributions across the entire slice.

It is widely recognized that the small tip-angle approximation (without time shifts) scales very favorably to large flip-angles up to 90° (37). In other words, a reasonable solution for designing 90° pTx excitation pulses consists in designing first a small tip-angle pulse (e.g., 10°) and then scaling it to achieve a mean flip-angle of 90°. Unfortunately, in our experience this solution fails with the SA-STA technique described here. This is due to two reasons. First, as pointed out in the Results section (Figs. 5 & 6), time-shifted spoke pulses consume more energy than traditional spoke pulses and are more peak power-limited. Scaling them to larger flip-angles may therefore result in pulse clipping issues, although these could be potentially mitigated by using less “peaky” sub-pulse profiles obtained, for example, using the VERSE algorithm (38). A second limitation of the use of our time-shifted spokes to excite large flip-angles is that, as discussed in the previous paragraph, it over-flips spins in order to achieve the target flip-angle despite severe dephasing in low B0 regions. This method obviously fails for 90° pulses since, by definition, spins cannot be over-flipped beyond 90°. The SA-STA technique presented here is therefore strictly a small tip-angle technique that does not scale favorably at greater flip-angles.

At long TEs and in the presence of strong B0 variations, the phase of the excitation profile varies rapidly (there are typically multiple phase wraps across the image, see Fig. 6). It is therefore imperative to use a magnitude least-squares (MLS) objective function since spoke pulses do not have the required degrees-of-freedom to compensate for such rapidly varying phase variations. In this work, we directly minimized the MLS objective function using analytical expressions of its Jacobian (vector of first derivatives, expressions in the Appendix) and Hessian (matrix of second derivatives, expression available in supporting material). In agreement with Ref. (39), we found this technique to be faster and to yield better pulses than the phase adoption approach proposed by Setsompop et al. (29), which converged very slowly in the presence of such rapid phase variations. Because of the non-convexity of the MLS design problem and the non-linearity of the SA-STA signal equation (the signal strength depends on the time-shifts via a sinc term), the solutions found by our algorithm are not guaranteed to correspond to the global optimum. Despite this caveat, we found the performance of the local pulse solutions studied in this work to be excellent. One potential issue with the direct MLS minimization approach is the creation of “holes” in the flip-angle map. These are caused by rapid variation of the image phase which look like “phase swirls” on the complex flip-angle phase map. Although problematic, these phase swirls actually correspond to the true MLS minimum. Indeed, when they occur, the poor performance of the algorithm in these regions (the flip-angle target is not met) allows the design algorithm to create excellent flip-angle match in other regions thus reducing the overall the MLS error. Ironically, the slower convergence of the phase adoption method of Setsompop et al can be an advantage in these situations because it often stops before convergence to the true MLS minimum that contains these holes. Another advantage of the phase adoption method is that it allows straightforward regularization of the phase map by smoothing it between MLS iterations (regularization of the phase map is also possible in the direct MLS minimization approach, but is more complex to implement as it requires addition of a phase roughness penalty to the MLS objective). We found that the creation of holes in the flip-angle map using our direct MLS minimization algorithm only occurred when using noisy, low quality B1+ and B0 maps with artefacts as phase swirls would generally occur around small image artifacts or large speckles of noise. Such phase swirls did not affect the 1-spoke and 2-spoke results obtained in this work using the high quality, low noise field maps shown in Fig. 1. In summary, we recommend using the direct MLS minimization approach in conjunction with high quality field maps. If holes occur in the flip-angle maps, a simple solution is to switch the minimization procedure to the phase adoption approach.

In order to implement and characterize our approach, we found it useful to use a realistic 3D-printed phantom of a human head mimicking the B1+ and B0 field distributions of in-vivo imaging at ultra-high field. This phantom, which is based on an MRI scan of a volunteer, has four compartments (bone, brain, muscle and internal air cavities), is easy to chain-produce using a 3D-printer. We are now using such phantoms routinely at our center for development and testing of many sequences, which is a time-consuming task and is therefore exceedingly expensive when performed on human subjects. In this work, we mapped the through-plane B0 gradient on a pixel-by-pixel basis using a 3D GRE B0 field map with a 5 mm-slab thickness. Using this technique, we verified that the through-plane B0 gradient is roughly proportional to the in-plane B0 offset with a proportionality constant equal to −1.4 μT/m/Hz (R²=0.29), which is in agreement with previously published results (19,25). Using electromagnetic simulation of the electric fields inside the phantom, we showed that SA-STA pulses, despite having greater power consumption than traditional spoke pulses with no time-shifts (as explained above, this is because SA-STA pulses over-flip spins in some regions), create no more local SAR and global SAR than traditional spoke pulses. This is due to the fact that composite time-shifted pulses tend to produce less SAR (global and local) than pTx pulses with synchronous sub-pulse profiles. Indeed, in the extreme case where the RF waveforms played on different channels are played sequentially (this occurs if the time-shifts are greater than the half duration of the sub-pulse), there are no interactions between the electric fields created by each channels and SAR decreases dramatically. Mathematically, we have shown that this is modeled by multiplying the SAR matrices (or VOPs) by the correlation matrix of the time-shifted sub-pulses played on every channels. As a result SA-STA pulses excite slices with uniform magnetization profiles and with recovery for signal loss due to through-plane dephasing at no additional local and global SAR than traditional spoke pulses with no time-shifts.

Appendix

In this appendix we provide compact analytical expressions of the Jacobian (vector of first derivatives) of the objective and constraints functions of the optimization problem in Eq. [9]. Compact expressions of the Hessian terms can be found in the supporting material (all expressions were verified by comparison with numerical differentiation).

Jacobian of the MLS objective

The Jacobian of the MLS objective with respect to the spoke amplitudes is:

$$\frac{\partial \mathrm{\Psi }}{\partial Re\left(b_j\right)}=\sum _i\frac{\partial }{\partial Re\left(b_j\right)}{\left({\left|\mathbf{Ab}\right|}_i-{\left|{\mathbf{M}}_{T,\text{target}}\right|}_i\right)}^2=\sum _{i}2\underset{y_i}{\underbrace{\left({\left|\mathbf{Ab}\right|}_i-{\left|{\mathbf{M}}_{T,\text{target}}\right|}_i\right)}}\frac{\partial {\left|\mathbf{Ab}\right|}_i}{\partial Re\left(b_j\right)},$$ [10]

Where:

$${\left[\mathbf{A}\right]}_{i,\left(cs\right)}=\frac{2\pi M_0}{G_{z}Z}{B}_{1+,c}\left({\mathbf{r}}_i\right)e^{j\left[{\mathbf{k}}_s·\mathbf{x}-\frac{\gamma \mathrm{\Delta }{B}_0\left({\mathbf{r}}_i\right){\left(-1\right)}^s{G}_z\left(TE-T_s\right)}{{\left(-1\right)}^s{G}_z-g\left({\mathbf{r}}_i\right)}\right]}\text{sinc}\left\{\alpha \mathrm{\Delta }{t}_{c,s}+\beta \left({\mathbf{r}}_i,TE\right)\right\},$$ [11]

As per Eq. [7]. Using:

$$\frac{\partial {\left|\mathbf{Ab}\right|}_i}{\partial Re\left(b_j\right)}=\frac{\partial \sqrt{{\left|\mathbf{Ab}\right|}_i^2}}{\partial Re\left(b_j\right)}=Re\left\{{\left[\mathbf{A}\right]}_{ij}^{\ast }{e}^{j\angle {[\mathbf{Ab}]}_i}\right\},$$ [12]

Eq. [10] simplifies to:

$$\frac{\partial \mathrm{\Psi }}{\partial Re\left(b_j\right)}=2Re\left\{{\left[{\mathbf{A}}^H\left(\mathbf{y}\circ e^{j\angle \mathbf{Ab}}\right)\right]}_j\right\}.$$ [13]

Where the symbol ∘ represent the term-by-term matrix multiplication. Similarly:

$$\frac{\partial \mathrm{\Psi }}{\partial Im\left(b_j\right)}=2Im\left\{{\left[{\mathbf{A}}^H\left(\mathbf{y}\circ e^{j\angle \mathbf{Ab}}\right)\right]}_j\right\}.$$ [14]

The relationship between the slice-averaged transverse magnetization and the time shifts is not linear. We have:

$$\begin{array}{l}\frac{\partial \mathrm{\Psi }}{\partial \mathrm{\Delta }{t}_{c,s}}=\frac{\partial }{\partial \mathrm{\Delta }{t}_{c,s}}\sum _i{\left(\left|{\left[{\mathbf{M}}_T\left(\mathbf{b},\mathbf{\Delta }\mathbf{t}\right)\right]}_i\right|-\left|{\left[{\mathbf{M}}_{T,\text{target}}\right]}_i\right|\right)}^2\\ =2\sum _i{y}_i\frac{\partial \left|{\left[{\mathbf{M}}_T\left(\mathbf{b},\mathbf{\Delta }\mathbf{t}\right)\right]}_i\right|}{\partial \mathrm{\Delta }{t}_{c,s}}\\ =2Re\left\{\sum _i{y}_i{e}^{j\angle {\left[{\mathbf{M}}_T\left(\mathbf{b},\mathbf{\Delta }\mathbf{t}\right)\right]}_i}\frac{\partial {\left[{\mathbf{M}}_T\left(\mathbf{b},\mathbf{\Delta }\mathbf{t}\right)\right]}_i^{\ast }}{\partial \mathrm{\Delta }{t}_{c,s}}\right\},\end{array}$$ [15]

Where y_i has the same meaning as in Eq. [10]. The derivatives of the transverse magnetization with respect to the time shifts are stored in a matrix dM_T(b,Δt) of size N×(C×S) where N is the number of pixels in the optimization ROI and C×S is the number of channels multiplied by the number of spokes:

$$\begin{array}{l}\frac{\partial {\left[{\mathbf{M}}_T\left(\mathbf{b},\mathbf{\Delta }\mathbf{t}\right)\right]}_i}{\partial \mathrm{\Delta }{t}_{c,s}}={\left[{\mathbf{dM}}_T\left(\mathbf{b},\mathbf{\Delta }\mathbf{t}\right)\right]}_{i,\left(cs\right)}\\ =\underset{K_{\mathit{isc}}}{\underbrace{j\frac{2\pi M_0}{G_{z}Z}{B}_{1+,c}\left({\mathbf{r}}_i\right)b_{c,s}{e}^{j\left[{\mathbf{k}}_s·\mathbf{x}-\frac{\gamma \mathrm{\Delta }{B}_0\left({\mathbf{r}}_i\right){\left(-1\right)}^s{G}_z\left(TE-T_s\right)}{{\left(-1\right)}^s{G}_z-g\left({\mathbf{r}}_i\right)}\right]}}}\frac{\partial }{\partial \mathrm{\Delta }{t}_{c,s}}\text{sinc}\underset{x}{\underbrace{\left\{\alpha \mathrm{\Delta }{t}_{c,s}+{\beta }_s\left({\mathbf{r}}_i,TE\right)\right\}}}\\ =K_{i,\left(sc\right)}\alpha \pi \left\{\frac{cos\left(\pi x\right)}{\pi x}-\frac{sin\left(\pi x\right)}{{\left(\pi x\right)}^2}\right\}.\end{array}$$ [16]

Therefore in compact notations:

$$\frac{\partial \mathrm{\Psi }}{\partial \mathrm{\Delta }{t}_{c,s}}=2Re\left\{{\left[{\mathbf{dM}}_T{\left(\mathbf{b},\mathbf{\Delta }\mathbf{t}\right)}^H\left(\mathbf{y}\circ e^{j\angle {\mathbf{M}}_{\mathbf{T}}\left(\mathbf{b},\mathbf{\Delta }\mathbf{t}\right)}\right)\right]}_{c,s}\right\}.$$ [17]

Jacobian of the SAR constraints

A SAR constraint is a quadratic form of the spoke amplitudes. Therefore we easily show that:

$$\begin{array}{l}\frac{\partial \mathit{SAR}}{\partial Re\left(b_{s_1,c_1}\right)}=\frac{2}{S}Re\left\{{\left[\left[\mathbf{Q}\circ \mathbf{C}\left(\mathbf{\Delta }{\mathbf{t}}_{s_1}\right)\right]{\mathbf{b}}_{s_1}\right]}_{c_1}\right\}\\ \frac{\partial \mathit{SAR}}{\partial Im\left(b_{s_1,c_1}\right)}=\frac{-2}{S}Im\left\{{\left[\left[\mathbf{Q}\circ \mathbf{C}\left(\mathbf{\Delta }{\mathbf{t}}_{s_1}\right)\right]{\mathbf{b}}_{s_1}\right]}_{c_1}\right\}.\end{array}$$ [18]

The Jacobian of the SAR constraints with respect to the time shifts is more complex. Using the notations of Eq. [8]:

$$\frac{\partial \mathit{SAR}}{\partial \mathrm{\Delta }{t}_{c,s}}=\frac{1}{S}\sum _s\sum _{c_1,c_2}{b}_{c_1,s}{b}_{c_2,s}^{\ast }{\left[\mathbf{Q}\right]}_{c_2,c_1}\frac{\partial {\left[\mathbf{C}\left(\mathbf{\Delta }{\mathbf{t}}_s\right)\right]}_{c_2,c_1}}{\partial \mathrm{\Delta }{t}_{c,s}}.$$ [19]

The derivatives of the time-shifted sub-pulse correlation matrix are given by:

$$\frac{\partial {\left[\mathbf{C}\left(\mathbf{\Delta }{\mathbf{t}}_s\right)\right]}_{c_2,c_1}}{\partial \mathrm{\Delta }{t}_{c_1,s}}={\left[\mathbf{DC}\left(\mathbf{\Delta }{\mathbf{t}}_s\right)\right]}_{c_2,c_1}=\frac{-1}{T^{\prime }}\underset{0}{\overset{T^{\prime }}{\int }}{u\left(t-\mathrm{\Delta }{t}_{c_2,s}\right)\frac{\partial u}{\partial t}|}_{t-\mathrm{\Delta }{t}_{c_1,s}}dt,$$ [20]

And are stored in the matrix DC(Δt_s) of size C×C, where C is the number of Tx channelsl. Eq. [20] can be computed very quickly using the analytical expression of the derivative of the sub-pulse profile. Using this notation, Eq. [19] simplifies to:

$$\begin{array}{l}\frac{\partial \mathit{SAR}}{\partial \mathrm{\Delta }{t}_{c,s}}=\frac{1}{S}\sum _{c_1,c_2}{b}_{c_1,s}{b}_{c_2,s}^{\ast }{\left[\mathbf{Q}\right]}_{c_2,c_1}\left\{{\delta }_{c,c_1}{\left[\mathbf{DC}\left(\mathbf{\Delta }{\mathbf{t}}_s\right)\right]}_{c_2,c_1}+{\delta }_{c,c_2}{\left[\mathbf{DC}\left(\mathbf{\Delta }{\mathbf{t}}_s\right)\right]}_{c_1,c_2}\right\}\\ =\frac{1}{S}\left\{\sum _{c_2}{b}_{c,s}{b}_{c_2,s}^{\ast }{\left[\mathbf{Q}\right]}_{c_2,c}{\left[\mathbf{DC}\left(\mathbf{\Delta }{\mathbf{t}}_s\right)\right]}_{c_2,c}+\sum _{c_1}{b}_{c_1,s}{b}_{c,s}^{\ast }{\left[\mathbf{Q}\right]}_{c,c_1}{\left[\mathbf{DC}\left(\mathbf{\Delta }{\mathbf{t}}_s\right)\right]}_{c_1,c}\right\}\\ =\frac{2}{S}Re\left\{b_{c,s}\sum _i{b}_{i,s}^{\ast }{\left[\mathbf{Q}\right]}_{i,c}{\left[\mathbf{DC}\left(\mathbf{\Delta }{\mathbf{t}}_s\right)\right]}_{i,c}\right\}\\ =\frac{2}{S}Re\left\{{\left[{\mathbf{b}}_s\ast {\left({\mathbf{b}}_s^H\left[\mathbf{Q}\circ \mathbf{DC}\left(\mathbf{\Delta }{\mathbf{t}}_s\right)\right]\right)}^T\right]}_c\right\}.\end{array}$$ [21]