A Bayesian Model for Highly Accelerated Phase-Contrast MRI

Abstract

Purpose

Phase-contrast magnetic resonance imaging (PC-MRI) is a noninvasive tool to assess cardiovascular disease by quantifying blood flow; however, low data acquisition efficiency limits the spatial and temporal resolutions, real-time application, and extensions to 4D flow imaging in clinical settings. We propose a new data processing approach called Reconstructing Velocity Encoded MRI with Approximate message passing aLgorithms (ReVEAL) that accelerates the acquisition by exploiting data structure unique to PC-MRI.

Theory and Methods

ReVEAL models physical correlations across space, time, and velocity encodings. The proposed Bayesian approach exploits the relationships in both magnitude and phase among velocity encodings. A fast iterative recovery algorithm is introduced based on message passing. For validation, prospectively undersampled data are processed from a pulsatile flow phantom and five healthy volunteers.

Results

ReVEAL is in good agreement, quantified by peak velocity and stroke volume (SV), with reference data for acceleration rates R ≤ 10. For SV, Pearson r ≥ 0.996 for phantom imaging (n = 24) and r ≥ 0.956 for prospectively accelerated in vivo imaging (n = 10) for R ≤ 10.

Conclusion

ReVEAL enables accurate quantification of blood flow from highly undersampled data. The technique is extensible to 4D flow imaging, where higher acceleration may be possible due to additional redundancy.

Introduction

Phase-contrast magnetic resonance imaging (PC-MRI) is a noninvasive technique capable of quantifying hemodynamics in the heart and great vessels (1). Because spin moving through a spatially varying magnetic field accumulates phase compared to static spin, velocity information in PC-MRI is encoded into the phase of the complex-valued image. This information is then retrieved by measuring the phase differences between images collected under different values of the velocity-encoding gradients. Cardiovascular applications of PC-MRI include quantification of cardiac function (2), evaluation of stenosis (3, 4), assessment of congenital heart disease (5), and evaluation of aortic atherosclerosis (6).

Clinical application of PC-MRI to 4D flow imaging and to real-time through-plane velocity imaging has been precluded by long scan times and low acquisition efficiency (7). Several methodological improvements have been proposed to reduce acquisition time of flow imaging via PC-MRI: parallel MRI (pMRI) (8), fast sampling strategies (9, 10, 11, 12), and iterative image recovery inspired by compressive sensing (CS) concepts (13, 14). For 2D PC-MRI, Kim et al. (15) proposed k-t SPARSE-SENSE and reported a six-fold acceleration for liver imaging with electrocardiogram triggering; k-t SPARSE-SENSE combines randomized Cartesian sampling, pMRI, and sparsity via temporal principal components analysis (PCA). More recently, Giese et al. individually processed principal components from multiple spatial compartments in the image series to capture the spatially varying dynamic behavior (16). Kwak et al. (17) recovered five-fold accelerated 2D PC-MRI by enforcing total variation (TV) minimization of both encoded and compensated images as well as exploiting the sparsity of the complex difference image. Most 2D PC-MRI reconstruction methods can be extended for 4D flow where even higher acceleration is possible due to additional redundancy. Knobloch et al. (18) proposed a method that utilizes both temporal PCA and the complex difference of velocity-encoded and velocity-compensated images to report an eight-fold acceleration for 4D flow. Despite these proposed processing methods, the challenge remains to achieve 4D flow imaging in clinically relevant acquisition times.

In this work, we propose a novel technique for accelerated PC-MRI. The technique is based on Bayesian inference yet admits fast computation via an approximate message passing algorithm (19). The Bayesian formulation allows us to model and exploit the statistical relationships across space, time, and encodings in order to achieve reproducible estimation of flow from highly undersampled data. Six characteristics distinguish the approach from prior art.

1. Data are jointly processed across all coils, frames, and encodings.

2. We employ overcomplete (non-decimated) wavelets for transform-based compression jointly across both space and time.

3. An optimized sampling strategy provides a distinct variable density sampling pattern for each encoding; the sampling also facilitates estimation of coil sensitivity maps.

4. We employ a mixture density model to capture the strong redundancy between the background and velocity-encoded images; the approach captures not only the similarity in magnitudes between background and velocity-encoded images but also the phase similarity in velocity-free regions. From the mixture density, the algorithm implicitly learns a probabilistic segmentation of image frames into velocity-containing and velocity-free regions.

5. Approximate message passing provides a fast computational framework to enable minimum mean squared error (MMSE) estimation while jointly processing the large corpus of spatiotemporal data.

6. An expectation-maximization procedure within the empirical Bayes framework provides automatic parameter tuning.

Together, these six characteristics yield a principled estimation approach that enables accelerated PCMRI. We coin our technique ReVEAL for Reconstructing Velocity EncodedMRI with Approximate Message passing aLgorithms. For time-resolved, planar imaging with one velocity encoded direction (through-plane), we demonstrate prospectively undersampled acquisition achieving an acceleration factor of 10 using both phantom and in vivo data. We conjecture that the technique will yield higher acceleration with the increased number of correlated encodings present in 4D flow imaging.

Theory

Parallel MRI signal model

We first describe the received signal model for 2D dynamic MRI with multiple receiver coils. The measured data ${\mathit{y}}_i^t$ from the i^th coil at time index, or frame, t is

$${\mathit{y}}_i^t={\mathit{D}}^t\mathit{F}{\mathit{S}}_i^t{\mathit{x}}^t+{\mathit{\varphi }}_i^t$$ [1]

where D^t is a k-space sample selection operator at time t, F is the 2D Fourier operator, and ${\mathit{S}}_i^t$ is a diagonal matrix which represents the i^th coil sensitivity map. Here, x^t ∈ C^N is a vectorization of the two-dimensional image to be recovered, ${\mathit{y}}_i^t\in {\mathrm{C}}^M$ is the subsampled Fourier measurements, and ${\varphi }_i^t\in {\mathrm{C}}^N$ is additive noise.

We can rewrite [1] in block notation for C coils as follows.

$$\underset{{\mathit{y}}^t}{\underbrace{\left[\begin{array}{c}{\mathit{y}}_1^t\\ {\mathit{y}}_2^t\\ ⋮\\ {\mathit{y}}_C^t\end{array}\right]}}=\underset{{\mathit{A}}^t}{\underbrace{\left[\begin{array}{c}{\mathit{D}}^t\mathit{F}{\mathit{S}}_1^t\\ {\mathit{D}}^t\mathit{F}{\mathit{S}}_2^t\\ ⋮\\ {\mathit{D}}^t\mathit{F}{\mathit{S}}_C^t\end{array}\right]}}{\mathit{x}}^t+\underset{{\mathit{\varphi }}^t}{\underbrace{\left[\begin{array}{c}{\mathit{\varphi }}_1^t\\ {\mathit{\varphi }}_2^t\\ ⋮\\ {\mathit{\varphi }}_C^t\end{array}\right]}}.$$ [2]

The 2D signal model given in [2] can be viewed as a single time instance in a dynamic image sequence. The signal model for the dynamic sequence of P frames is given by

$$\underset{\mathit{y}}{\underbrace{\left[\begin{array}{c}{\mathit{y}}^1\\ {\mathit{y}}^2\\ ⋮\\ {\mathit{y}}^P\end{array}\right]}}=\underset{\mathit{A}}{\underbrace{\left[\begin{array}{cccc}{\mathit{A}}^1& 0& \cdots & 0\\ 0& {\mathit{A}}^2& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\mathit{A}}^P\end{array}\right]}}\underset{\mathit{x}}{\underbrace{\left[\begin{array}{c}{\mathit{x}}^1\\ {\mathit{x}}^2\\ ⋮\\ {\mathit{x}}^P\end{array}\right]}}+\underset{\mathit{\varphi }}{\underbrace{\left[\begin{array}{c}{\mathit{\varphi }}^1\\ {\mathit{\varphi }}^2\\ ⋮\\ {\mathit{\varphi }}^P\end{array}\right]}},$$ [3]

where A^t represents the measurement matrix at time t with possibly time-dependent downsampling and coil sensitivities D^t and ${\mathit{S}}_i^t$, respectively. We compactly write [3] as y = Ax + ϕ.

For the k-space sampling pattern described by D^t, t = 1, …, P, we employ variable density incoherent sampling patterns as reported in (20). The design results in sampling patterns that differ across frames as well as across the velocity encodings. The sampling design optimizes a constrained energy potential to produce a pseudo-random pattern that promotes incoherence of the operator A, limits eddy currents, and provides a fully sampled k-space when time-averaged across all frames. The last of these constraints facilitates estimation of coil sensitivities without calibration data. A representative VISTA sampling pattern for PC-MRI is given in Fig. 1. In Fig. 1(a-b), two independent VISTA sampling patterns are plotted for encoded and compensated measurements. The interleaved acquisition strategy for PC-MRI data is given in Fig. 1(c), where the sampling patterns are incoherent across encodings.

Figure 1.

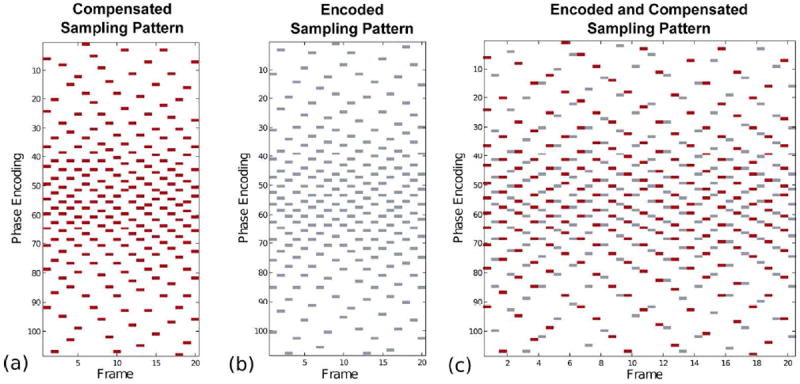
A representative set of VISTA sampling patterns for ReVEAL at an acceleration rate of R = 10 with 108 phase encode lines and 20 frames. (a) The VISTA sampling pattern for the compensated data. (b) The VISTA sampling pattern for the encoded measurements. (c) The interleaved encoded and compensated sampling patterns.

Bayesian representation of data dependencies

In phase-contrast imaging, velocity is encoded into the phase of the complex-valued MR images (21). Due to off-resonance effects and magnetic field inhomogeneities, the MR images have phase, referred to here as background phase, which does not contain velocity information. To compensate for background phase, two measurements are made. The first, denoted by y_b, is the velocity-compensated measurement. The corresponding image x_b = me^jθ_b only contains the background phase, θ_b; the multiplication and exponentiation are to be interpreted pixel-wise. The second, denoted by y_υ, is the velocity-encoded measurement. The corresponding image x_υ = me^{j(θ_b+θ_υ)} contains both the background phase, θ_b, and the velocity-encoded phase, θ_υ. The relationship between the two images is assumed to be

$${\mathit{x}}_{\upsilon }=\mathit{m}{e}^{j({\mathit{\theta }}_b+{\mathit{\theta }}_{\upsilon })}={\mathit{x}}_b{e}^{j{\mathit{\theta }}_{\upsilon }}.$$ [4]

The signals x_b and x_υ are measured under the model in [3], which we denote as

$${\mathit{y}}_b={\mathit{A}}_b{\mathit{x}}_b+{\mathit{\varphi }}_b$$ [5]

$${\mathit{y}}_{\upsilon }={\mathit{A}}_{\upsilon }{\mathit{x}}_{\upsilon }+{\mathit{\varphi }}_{\upsilon },$$ [6]

where ϕ_b and ϕ_υ are additive measurement noise. The measurement matrices, A_b and A_υ, may differ, thereby allowing for different sampling patterns for each of the two measurements.

To capture the physical behavior suggested in [4], we model x_b, x_υ, and θ_υ as random variables. The key object of interest, the phase difference θ_υ, explicitly appears in the model as a parameter to be inferred from the noisy data. In addition, we introduce a “hidden” Bernoulli random variable, denoted as υ, to indicate the inferred locations in x_υ that contain non-zero velocity. By application of Bayes’ theorem and the chain rule for conditional probability densities, the posterior distribution on these unknown variables, given the observed noisy measurements, can be written

$$p({\mathit{x}}_b,{\mathit{x}}_{\upsilon },{\mathit{\theta }}_{\upsilon },\mathit{\upsilon }\mid {\mathit{y}}_b,{\mathit{y}}_{\upsilon })\propto p({\mathit{x}}_b)\prod _{m=1}^{M}p\left(y_{\mathit{bm}}\mid x_b\right)p\left(y_{\mathit{\upsilon m}}\mid x_{\upsilon }\right)\prod _{n=1}^{N}p(x_{\mathit{\upsilon n}}\mid x_{\mathit{bn}},{\theta }_{\mathit{\upsilon n}},{\upsilon }_n)p({\theta }_{\mathit{\upsilon n}})p({\upsilon }_n).$$ [7]

Here, ∝ denotes proportionality; the double subscripts y_bm and x_bn denote the m^th measurement sample and n^th image pixel, respectively, for the background encoding. Further, N and M denote the total number of pixels and measurements, respectively. Three independence assumptions are invoked. The model in [7] assumes that θ_υ and x_b are independent, i.e. p(θ_υ∣x_b) = p(θ_υ). Likewise, we assume υ to be independent of both θ_υ and x_b, i.e. p(υ∣x_b, θ_υ) = p(υ). A third independence assumption, p(θ_υ∣υ) = p(θ_υ) is chosen for convenience, similar to indicator variable modeling adopted in other applications (22, 23, 24). These independence assumptions are a conservative choice to bypass potential regularizing structure in favor of modeling and computational simplicity; more prominent signal structure is exploited in the remaining factors discussed below.

Motivated by the idealized relationship in [4], we adopt a mixture density to capture the redundancy between a velocity-encoded pixel, x_υn, and the corresponding velocity-compensated (background) pixel, x_bn. The conditional distribution is given by

$$p(x_{\mathit{\upsilon n}}\mid x_{\mathit{bn}},{\theta }_{\mathit{\upsilon n}},{\upsilon }_n)=(1-{\upsilon }_n)\mathit{CN}(x_{\mathit{\upsilon n}};x_{\mathit{bn}},{\sigma }^2)+{\upsilon }_n\mathit{CN}(x_{\mathit{\upsilon n}};x_{\mathit{bn}}{e}^{j{\theta }_{\mathit{\upsilon n}}},{\sigma }^2).$$ [8]

The notation CN (x; μ, σ²) denotes a circularly symmetric complex-valued Gaussian density on x with mean μ and variance σ². The distribution is conditioned on the hidden indicator variable, υ_n, which serves as probabilistic segmentation of the image into velocity-containing and velocity-free regions, with υ_n = 1 denoting velocity at pixel n. The first term of [8], (1 – υ_n)CN (x_υn; x_bn, σ²), represents the relationship between x_υ and x_b for zero-velocity regions. This term models x_υn as a Gaussian perturbed version of x_bn. The variance, σ², serves to model physical departures of noiseless images from the idealized assumption in [4]; in contrast, the effects of measurement noise are modeled by the likelihood function given below. The conditional distribution of x_υn given both x_bn and υ_n = 0 is depicted in Fig. 2(a), where the black arrow denotes the complex-value x_bn. The second term of [8], υ_nCN (x_υn; x_bne^jθυn, σ²), describes the relationship for regions that contain velocity-encoded phase. The non-Gaussian conditional distribution of x_υn given x_bn and υ_n = 1 (i.e., velocity-containing pixels) is depicted in Fig. 2(b), where the phase is non-informative and the magnitude is Rician centered at |x_bn|. The functional form of this conditional distribution is (25, 26),

$$\begin{array}{lll}p(x_{\mathit{\upsilon n}}\mid x_{\mathit{bn}},{\upsilon }_n=1)& =& \frac{1}{2\pi }{\mathit{\int }}_0^{2\pi }\mathit{CN}(x_{\mathit{\upsilon n}};x_{\mathit{bn}}{e}^{j{\theta }_{\mathit{\upsilon n}}},{\sigma }^2)d{\theta }_{\mathit{\upsilon n}}\\ & =& \frac{|x_{\mathit{\upsilon n}}|}{\pi {\sigma }^2}\exp \left(-\frac{{|x_{\mathit{\upsilon n}}|}^2+{|x_{\mathit{bn}}|}^2}{{\sigma }^2}\right)I_0\left(\frac{2|x_{\mathit{\upsilon n}}||x_{\mathit{bn}}|}{{\sigma }^2}\right),\end{array}$$ [9]

where I₀(x) denotes a zeroth-ordered Bessel function of the first kind.

Figure 2.

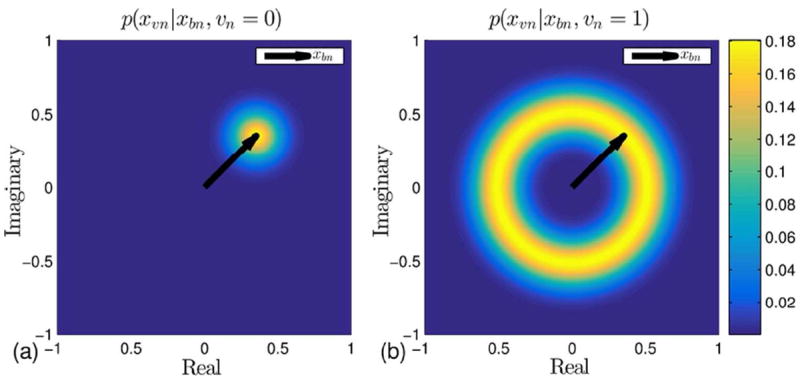
The conditional prior distributions used by ReVEAL. (a) The conditional distribution for a velocity-encoded, complex-valued pixel given the corresponding velocity-compensated pixel for velocity-free regions. In this case, the magnitude and phase are constrained. (b) The conditional distribution for a velocity-encoded, complex-valued pixel given the corresponding compensated pixel for velocity-containing regions. Here, only the magnitude is constrained.

Four more modeling choices remain in [7]. First, we assume the k-space measurements y_b and y_υ are corrupted by additive, circularly symmetric complex Gaussian noise. This choice yields the likelihood models

$$p(y_{\mathit{bn}}\mid {\mathit{x}}_b)=\mathit{CN}(y_{\mathit{bn}};{[{\mathit{A}}_b{\mathit{x}}_b]}_n,{\omega }^2)$$ [10]

$$p(y_{\mathit{\upsilon n}}\mid {\mathit{x}}_{\upsilon })=\mathit{CN}(y_{\mathit{\upsilon n}};{[{\mathit{A}}_{\upsilon }{\mathit{x}}_{\upsilon }]}_n,{\omega }^2),$$ [11]

where ω² is the noise variance, and the mean, [Ax]_n, is the n^th element of the matrix vector product Ax. Second, for the prior on the phase, p (θ_υn), we adopt the non-informative prior of equal probability on the interval [0, 2π). Third, we define the hidden variable υ ∈ {0, 1}^N as a Bernoulli indicator with p (υ_n = 1) = γ. Thus, γ is the prior probability that any pixel contains non-zero velocity, and 1 − γ is the prior probability that a pixel contains no velocity.

Finally, we address the prior p(x_b). We experimentally observe that a three-dimensional non-decimated wavelet transform, Ψ, applied to x_b and x_υ across both space and time results in multiple sparse representations. Rather than postulate a prior density to model this behavior, we instead make the convenient and effective choice of augmenting the likelihood, as in (27). To this end, we form M̃ -by-N matrices Ã_b and Ã_υ, appending Ψ as additional rows to the matrices A_b and A_υ; then, we adopt a zero-mean Laplace likelihood for p([Ψx_b]_m∣x_b) and p([Ψ x_υ]_m∣x_υ). The Laplace density for a complex-valued random variable x and scaling parameter λ is

$$p(x)=\frac{1}{2\pi {\lambda }^2}\exp \left\{\frac{-|x|}{\lambda }\right\}.$$ [12]

The Laplace prior in [12] can be related to the ℓ₁ norm by the maximum a posteriori (MAP) estimate. The MAP solution maximizes the posterior distribution. To see the relation, maximize the log posterior under Gaussian likelihood and Laplace prior given as

$$x_{\mathit{MAP}}=\arg \underset{x}{\max }p(x\mid y)=\arg \underset{x}{\max }p(y\mid x)p(x)$$ [13]

$$=\arg \underset{x}{\max }\log (p(y\mid x))+\log (p(x))$$ [14]

$$=\arg \underset{x}{\min }\frac{1}{{\sigma }^2}{\Vert y-\mathit{Ax}\Vert }_2^2+\frac{1}{\lambda }{\Vert x\Vert }_1.$$ [15]

However, in this work, we seek to approximate the minimum mean squared error (MMSE) estimate, given by the mean of the posterior distribution, via sum-product message passing. The cost function for MMSE minimization, within an approximate message passing algorithm, is described by the Bethe Free Energy (28, 29).

Approximate message passing

The data model in [7] can be visualized as a factor graph. Factors and random variables are represented by nodes in the graph, with squares denoting factors and circles denoting variables. Edges on the graph represent the dependence of a given factor on a variable. The factor graph of the posterior distribution for the proposed model is given in Fig. 3. By expressing the posterior probability distribution of [7] as a factor graph, we can apply the sum-product algorithm to compute approximate marginal posterior distributions of x_b, x_υ, θ_υ, and υ through the use of message passing techniques (30). From the marginal posterior distribution of a variable, the mean value provides the MMSE estimate. As depicted in Fig. 3, messages are passed along edges in the graph and convey nodes’ “beliefs” about the states of their neighboring variable nodes. The interested reader is referred to (31) and (32) for an introduction to sum-product message passing. Importantly, on the dense, loopy portion of the graph, the message passing computation can be greatly simplified by adopting generalized approximate message passing (GAMP) (33), which invokes the central limit theorem and Taylor series approximations to dramatically reduce computational complexity. We employ the GAMP toolbox¹ for message passing on this portion of the graph. We note that message evaluation requires a first order computation involving the matrix A, the conjugate transpose, A^H, and the wavelet transforms Ψ and Ψ^H; therefore, fast transforms or parallel hardware for the implementation of A, A^H, Ψ, and Ψ^H enable computation in seconds, not hours.

Figure 3.

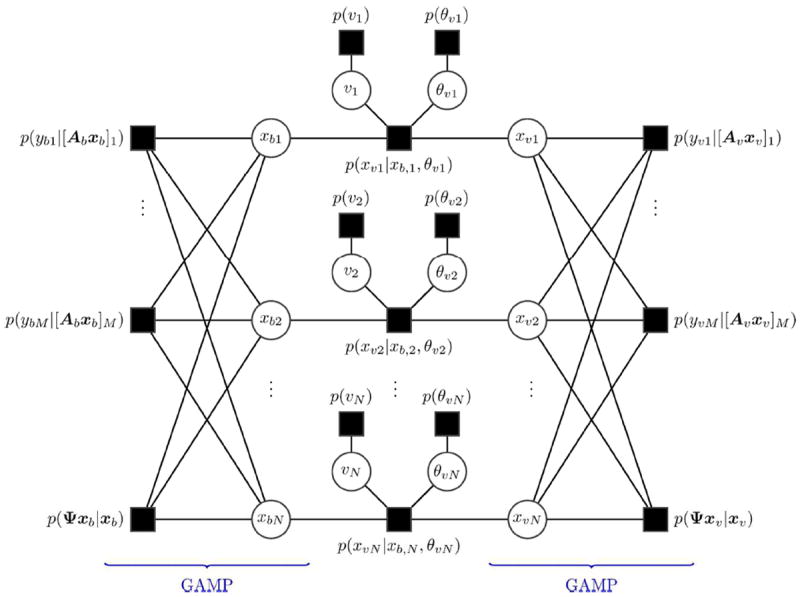
The factor graph representation of the joint posterior of PC-MRI data for the proposed model. Message passing on the graph, also known as belief propagation, is a metaphor for an iterative algorithm. By applying the sum-product rule, the update rules for the algorithm can be derived. Computation on the left and right loopy portions are accelerated via GAMP. The center potion of the graph is updated using standard belief propagation.

Methods

Retrospectively accelerated in vivo cardiac data acquisition

A healthy volunteer was imaged on a 1.5 T (Avanto, Siemens Healthcare, Erlangen, Germany) scanner using an 18-channel coil array. The imaging plane was perpendicular to the ascending aorta and captured crosssections from both ascending and descending aorta. Fully sampled data were acquired and retrospectively downsampled to obtain acceleration factors R = 2, 4, 6, 8, 10, 12, 14, and 16 using VISTA. The data were collected using a gradient-echo pulse sequence, with TE = 3.21 ms, TR = 5.63 ms. This in vivo dataset was collected in a single breath-hold using segmented acquisition with prospective EKG triggering. The VENC was set at 180 cm/s and the segment size (k-space lines/segment) was set at 3, resulting in a temporal resolution of 33.8 ms and acquisition time of 36 heartbeats. The matrix size and field of view were 192 × 108 and 360 × 248 mm², respectively.

Prospectively accelerated flow phantom data acquisition

For experimental validation, we used a CardioFlow 5000 MR flow pump (Shelley Medical Imaging Technologies, Toronto, Ontario, Canada). This programmable pump generates periodic, reproducible flow profiles and is capable of generating a volumetric flow rate of 300 ml/s. The phantom included a water bottle and flexible pipe. The pipe was bent into a u-shape such that two sections of the pipe were aligned in parallel beneath the bottle. The imaging plane was perpendicular to the parallel pipe sections such that in-flow and return-flow to the pump were measured simultaneously. For flow quantification, the two cross-sections of the pipe in each image sequence were treated as separate measurements. We note that the volume passing through each cross section must be the same, but their velocity-time profile may differ. CardioFlow 5000 MR comes with two pre-programmed physiological waveforms: one waveform that mimics femoral flow and the other that mimics carotid flow. To generate additional data, these two waveforms were modified by changing the vertical scaling, horizontal scaling, and duty cycle. In total, twelve different waveforms were generated for n = 24 unique measurements per acceleration factor. Data were collected on the 1.5 T Siemens scanner with a 32-channel coil array. The prospectively downsampled data were collected using VISTA for seven different acceleration rates, i.e., R = 1, 2, 4, 5, 8, 10, and 16.

All data were collected using a gradient-echo pulse sequence, with TE = 2.94 ms, TR = 4.92 ms, and VENC = 150 cm/s. The datasets were collected using prospectively triggered segmented acquisition, with pseudo-EKG trigger signal generated by the flow pump. The segment size was set at 4, resulting in a temporal resolution of 39.4 ms that was fixed across all datasets. The matrix size and field of view were 160 × 160 and 300 × 300 mm², respectively. The acquisition time was 40/R pseudo-heartbeats.

Prospectively accelerated in vivo cardiac data acquisition

Five healthy volunteers were imaged on the 1.5 T Siemens scanner using an 18-channel coil array. Two imaging planes were selected above the left atrium, one perpendicular to the ascending aorta and one perpendicular to the descending aorta. The prospectively downsampled data were collected using VISTA sampling for six different acceleration rates, i.e., R = 2, 4, 5, 8, 10, and 16. As a comparative reference, two additional datasets were collected with uniform rate-2 undersampling and fully sampled central k-space for a net acceleration of R = 1.74. Each dataset was collected in a separate breath-hold. The reference datasets were collected before and after the six VISTA accelerated acquisitions and were reconstructed using GRAPPA (34). The flow information from the GRAPPA-reconstructed images was extracted by following the procedure reported by Bernstein et al. (35). Together, these five volunteers, and two cross-sections of aorta, generated ten independent measurements for flow quantification, i.e., n = 10.

The data were collected using a gradient-echo pulse sequence, with TE = 3.10 ms and TR=5.17 ms. Each in vivo dataset was collected in a single breath-hold using segmented acquisition with prospective EKG triggering. For these data, the VENC was set at 150 cm/s and the segment size was set at 4, resulting in a temporal resolution of 41.3 ms and acquisition time of 40/R heartbeats. The matrix size and field of view were 160 × 160 and 300 × 300 mm², respectively.

Image reconstruction

The ReVEAL reconstruction was computed off-line using customized Matlab software (Mathworks, Natick, MA) running on Red Hat Enterprise Linux with an Intel Core™9/2/2015 i7-2600 at 3.4 GHz CPU and 8 GB of RAM. Coil sensitivity maps, for all methods, were self-calibrated by averaging undersampled k-space data over all time frames and applying the adaptive array combination method (36). Maxwell correction was applied to all the datasets by incorporating the correction map into the data model given in [8].

The noise variance, ω², was automatically estimated from the periphery of k-space for each acquisition, after SVD-based compression from 32 (phantom) or 18 (in vivo) coils to 12 virtual coils (37). The prior probability of flow, γ, at each pixel and frame is learned directly from the data using the expectation-maximization procedure (38, 39, 40). The parameter σ² characterizes the variability between encodings and was set to ${\omega }^2/\sqrt{C}$. The relative values of λ across the 8 wavelet sub-bands were λ₀ × {0.01, 1, 1, 2, 1.2, 2.4, 2.4, 3.6}; these relative values were determined by application of an automated procedure (41) to a separate in vivo data set and were held fixed across all acceleration rates and for both phantom and in vivo data. The single algorithm parameter requiring ad hoc tuning was λ₀, which sets a global scaling of the wavelet regularization. We employed λ₀ = 0.7 for all in vivo data and λ₀ = 4 for the flow phantom data. Daubechies db1 wavelets were used in the spatial dimensions and db3 wavelets in the temporal dimension. Codes to perform 1-4 dimensional non-decimated wavelet transforms are provided by the authors on GitHub².

ReVEAL is compared with k-t SPARSE-SENSE (15) as well as ReVEAL with the mixture density omitted, termed “ReVEAL no mixture.” Although the ReVEAL no mixture reconstruction relies on overcomplete spatio-temporal wavelets, a squared-error penalty for data fidelity, optimized VISTA sampling patterns, and message passing computation, it does not assume any relationship between encodings. Comparison between ReVEAL and ReVEAL no mixture is intended to highlight the benefit from the regularizing effect of the proposed statistical model between encodings in [8]. A code to implement k-t SPARSE-SENSE was provided by Daniel Kim, Li Feng, and Hassan Haji-Valizadeh. We utilized the same VISTA sampling patterns for k-t SPARSE-SENSE as used for ReVEAL and ReVEAL no mixture; thus, we forfeit any potential gain for ReVEAL and ReVEAL no mixture from using the interleaved VISTA pattern when compared to k-t SPARSE-SENSE with the pattern used by Kim et al. in (15). The regularization parameter for k-t SPARSE-SENSE was set in concordance with (15). Reconstruction times for the prospectively downsampled in vivo dataset at R = 10 were approximately 6.5 minutes, 3.5 minutes, and 7 minutes, for ReVEAL, ReVEAL no mixture, and k-t SPARSE-SENSE, respectively.

Data analysis

Peak velocity (PV) and stroke volume (SV) were used as quantitative measures of fidelity. The PV is defined as the maximum velocity across all pixels and frames within a region of interest (ROI). The SV is defined as the volume of blood or fluid passing through an ROI for one heartbeat or pump cycle. ROIs were identified for each image series by manually segmenting the pipes or blood vessels from the magnitude images. To capture the motion of the aorta during the heartbeat, each ROI was manually shifted from frame-to-frame. The size of the ROI was held constant across different acceleration rates and frames to limit variation in PV and SV due to ROI selection.

For phantom imaging and retrospectively downsampled in vivo data, the reconstructions corresponding to R = 1 (fully sampled) data were used as reference. Results from R = 1 were calculated using the adaptive array combination method (36). For the prospectively accelerated in vivo data, data reconstructed at R = 1.74 with GRAPPA (34) were used as reference. Bland-Altman plots–one for each acceleration rate–were used to display PV and SV. To quantify variations due to physiological changes, an additional Bland-Altman plot was created comparing the two R = 1.74 GRAPPA reconstructions.

The retrospectively downsampled in vivo dataset, collected from a single volunteer, does not mimic a clinical acquisition process but is included because it does not suffer from physiological variations present in the prospectively sampled datasets. In the retrospectively accelerated case, the reference is know precisely up to measurement noise, and we are guaranteed the same velocity-time profile for each acceleration. A Bland-Altman plot was not constructed for the retrospectively downsampled in vivo data due to the small sample size. However, normalized mean squared error (NMSE) and the structural similarity index (SSIM) (42) for the velocity map were calculated for each acceleration rate. NMSE is defined as

$$\mathit{NMSE}=10{\log }_{10}\left(\frac{{\Vert {\mathit{x}}_{\mathit{ref}}-\widehat{{\mathit{x}}_r}\Vert }_2^2}{{\Vert {\mathit{x}}_{\mathit{ref}}\mathit{\Vert }}_2^2}\right),$$ [16]

where x_ref is the noisy reference from fully sampled data and x̂_r the reconstructed image from acceleration rate r. x_ref and x̂_r were formed from the compensated image magnitude and velocity encoded phase, i.e. |x_b|e^jθ_υ.

Results

Retrospectively accelerated in vivo data

The retrospectively downsampled image sequences were reconstructed using ReVEAL, ReVEAL no mixture, and k-t SPARSE-SENSEs; results are shown in Fig. 4. The PV and SV were calculated inside the ascending aorta and plotted versus acceleration rate R. Results from R = 1 were calculated using the adaptive array combination method and are given as a reference. As shown in Fig. 4(a-b), quantitative fidelity of SV and PV was preserved to an acceleration factor of R = 12. For R ≤ 12, the PV and SV were within 6.5% and 2.5% of the reference, respectively. Additionally, ReVEAL showed the lowest NMSE for R ≥ 6 and highest velocity SSIM for R ≥ 4. Images from fully sample data and R = 12 data for ReVEAL, ReVEAL no mixutre, and k-t SPARSE-SENSE are given in Fig. 5. As evident in Fig. 5(c-d) ReVEAL greatly reduced aliasing artifacts and showed increased accuracy of velocities in the ascending aorta. The spatial regularization used in ReVEAL and ReVEAL no mixture greatly reduced background noise in the magnitude image at the cost of spatial blurring, as shown in Fig. 5(a-b). For R = 10, the velocity-time profiles for mean and peak velocities are shown in Fig. 6(a-b). See Movie S1 in the supporting material for images reconstructed at R = 12.

Figure 4.

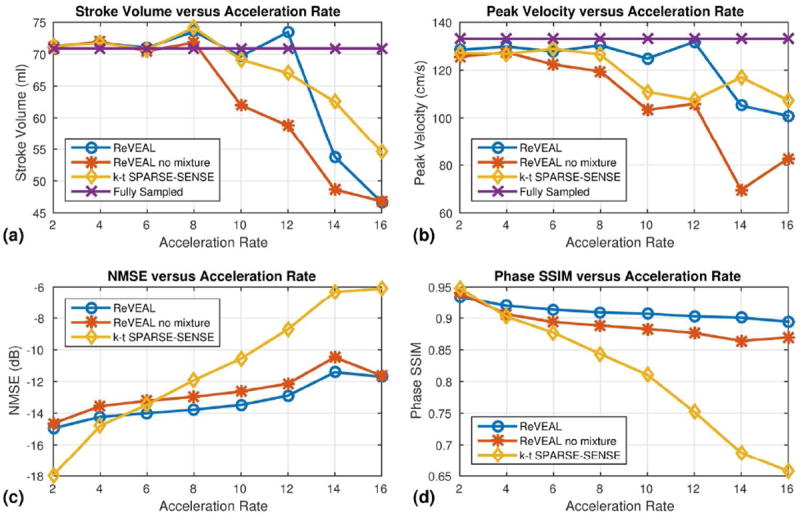
A summary of retrospectively accelerated in vivo data quality metrics. A fully sampled through-plane image of the ascending aorta was acquired and retrospectively accelerated for rates R = 2, 4, 6, 8, 10, 12, 14, and 16. ReVEAL, ReVEAL no mixture, and k-t SPARSE-SENSE are compared to fully sampled data. (a) The stroke volume in the ascending aorta versus acceleration rate. (b) The peak velocity in the ascending aorta versus acceleration rate. (c) The normalized mean squared error (NMSE) in dB versus acceleration rate. The images used to calculate NMSE were obtained by forming a complex number with magnitude equal to the compensated image magnitude, i.e. |x_b|, and phase equal to the velocity encoded phase, i.e. θ_υ. (d) The structural similarity index (SSIM) (42) for the velocity encoded phase image versus acceleration rate. The phase SSIM measurement was performed only on pixels within the top 95% of magnitude value in the reference image.

Figure 5.

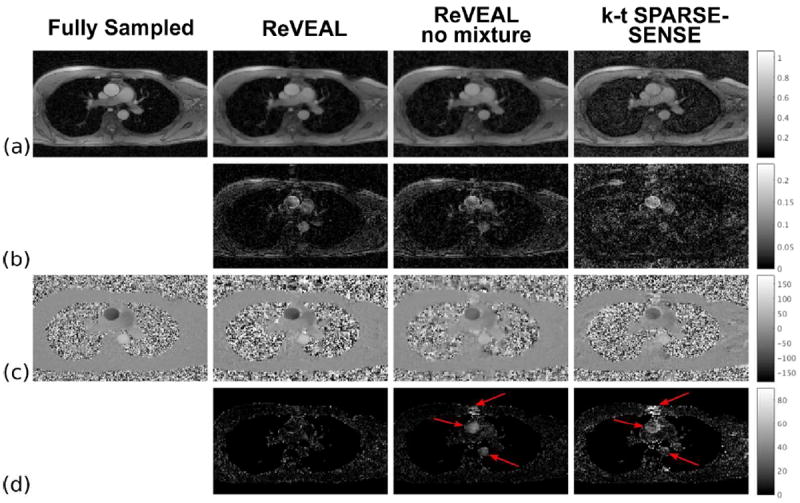
Retrospectively accelerated in vivo data reconstructed at R = 12. ReVEAL, ReVEAL no mixture, and k-t SPARSE-SENSE are compared to the fully sampled data for one representative frame. The first column was reconstructed from fully sampled data using the adaptive array combination method (36). The remaining columns were reconstructed from R = 12 accelerated data with ReVEAL, ReVEAL no mixture, and k-t SPARSE-SENSE. (a) The reconstructed, normalized magnitude images. (b) The absolute difference in magnitude between the accelerated images and the fully sampled image. (c) The velocity maps in cm/s. (d) The absolute difference between the fully sampled velocity map and the velocity map recovered from accelerated data. The difference was taken for pixels within the top 90% of magnitude in the reference image to avoid large differences due to low magnitude phase noise.

Figure 6.

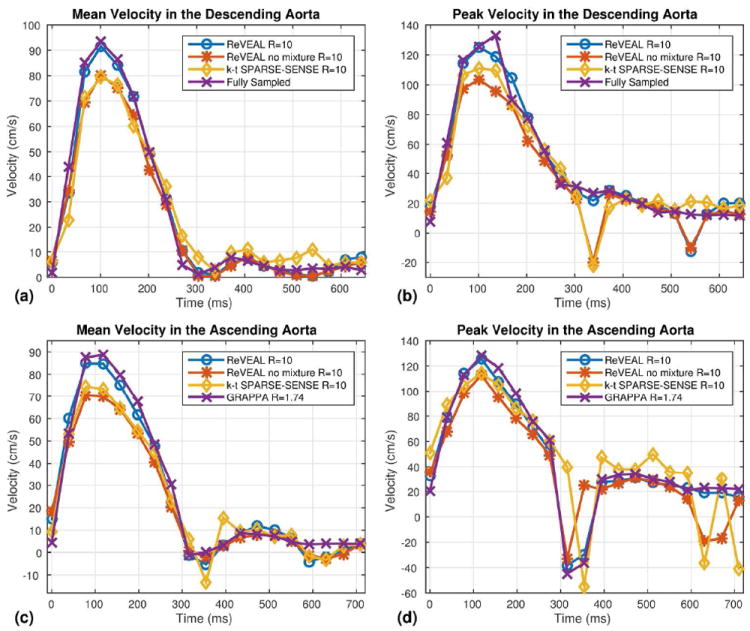
Representative velocity-time profiles from in vivo data. (a) The mean velocity in an ROI versus time in the descending aorta from retrospectively accelerated in vivo data at R = 10. ReVEAL, ReVEAL no mixture, and k-t SPARSE-SENSE are compared to fully sampled data. (b) The peak velocity in an ROI versus time in the descending aorta from retrospectively accelerated in vivo data. (c) The mean velocity in an ROI versus time in the ascending aorta from prospectively accelerated in vivo data at R = 10. ReVEAL, ReVEAL no mixture, and k-t SPARSE-SENSE are compared to GRAPPA at R = 1.74. (d) The peak velocity in an ROI versus time in the ascending aorta from prospectively accelerated in vivo data.

To examine the modeling choice in [8], histograms were constructed from fully sampled data, as shown in supporting Fig. S2. Panel (a) shows the real part of the complex difference between the encoded images, x_υ − x_b, for a zero-velocity region; a chi-square goodness-of-fit accepts the hypothesis of a Gaussian distribution with a 5% significance level. Additionally, for pixels taken from a region inside the descending aortic arch, panel (b) shows the histogram of the ratio of the magnitudes; a chi-square goodness-of-fit accepts the hypothesis of a Rician distribution with a 5% significance level.

Prospectively accelerated phantom data

The phantom data were reconstructed using ReVEAL, ReVEAL no mixture, and k-t SPARSE-SENSE; the fully sampled data, reconstructed with the adaptive array combination array combination method, were used as reference. The resulting Bland-Altman analyses and Pearson correlation coefficients are tabulated in Table 1. The corresponding Bland-Altman plots are provided in the supporting material Figures S2-S4.

Table 1.

Tabulated values from Bland-Altman and Pearson correlation analyses for prospectively accelerated flow phantom data. Here, μ_d is the mean difference, σ_d is the standard deviation of the difference, and r is the Pearson correlation coefficient. ReVEAL, ReVEAL no mixture, and k-t SPARSE-SENSE are compared to fully sampled data. The lowest absolute mean difference, lowest standard deviation, and highest Pearson correlation coefficient for each acceleration rate is in bold font.

Prospectively Accelerated Phantom Compared to Fully Sampled Data
		R = 2			R = 4			R = 5			R = 8			R = 10			R = 16
		μd	σd	r	μd	σd	r	μd	σd	r	μd	σd	r	μd	σd	r	μd	σd	r
ReVEAL	SV (ml)	-0.11	0.95	0.99	-0.11	0.47	0.99	0.44	0.87	0.99	0.35	0.75	0.99	-0.11	0.87	0.99	-0.08	2.39	0.98
ReVEAL no mixture	SV (ml)	-0.40	1.24	0.99	-0.36	1.02	0.99	0.25	0.79	0.99	-2.28	2.59	0.99	-2.38	1.26	0.99	-0.53	4.55	0.89
k-t SPARSE-SENSE	SV (ml)	-0.18	0.96	0.99	-0.25	0.49	0.99	0.21	0.82	0.99	-0.13	2.03	0.98	-0.57	1.18	0.99	-0.84	5.74	0.83
		μd	σd	R	μd	σd	R	μd	σd	R	μd	σd	R	μd	σd	R	μd	σd	R
ReVEAL	PV (cm/s)	0.72	2.81	0.99	0.83	2.30	0.99	0.95	2.61	0.99	0.87	2.72	0.99	-0.62	3.89	0.99	-2.10	6.30	0.97
ReVEAL no mixture	PV (cm/s)	-0.52	2.60	0.99	-0.13	2.54	0.99	-0.12	2.72	0.99	-11.53	17.93	0.79	-7.67	6.33	0.97	-2.78	8.27	0.95
k-t SPARSE-SENSE	PV (cm/s)	0.25	2.72	0.99	0.59	2.39	0.99	0.43	2.80	0.99	4.04	11.37	0.90	0.72	3.46	0.99	13.76	26.70	-0.55

The variability of ReVEAL is low up to R = 10, increasing only moderately compared to R = 2. The fidelity of reconstruction is therefore preserved to an acceleration factor R = 10. Fidelity of PV and SV is, however, lost at R = 16 as seen in the negative bias and increased variance. In comparison, ReVEAL no mixture compares favorably to ReVEAL at low acceleration rates but degrades significantly beyond R = 5, and k-t SPARSE-SENSE exhibits large variances. Also, the Pearson correlation coefficients for ReVEAL are consistently higher than those of ReVEAL no mixture and k-t SPARSE-SENSE.

Prospectively accelerated in vivo data

The prospectively sampled in vivo data were reconstructed using ReVEAL, ReVEAL no mixture, and k-t SPARSE-SENSE. The GRAPPA reconstructions at R = 1.74 were used as reference. The resulting Bland-Altman analyses and Pearson correlation coefficients are tabulated in Table 2. The corresponding Bland-Altman plots are provided in the supporting material Figures S5-S7. To quantify physiological changes in prospectively accelerated data, Bland-Altman analysis between two GRAPPA acquisitions was performed. The values for two GRAPPA aquisitions for SV are μ_d = −1.28 ml, ${\sigma }_d^2=2.59\mathrm{ml}$, and r = 0.99 and for PV μ_d = 0.66 cm/s, ${\sigma }_d^2=9.72\mathrm{cm}/\mathrm{s}$, and r = 0.81.

Table 2.

Tabulated values from Bland-Altman and Pearson correlation analyses for prospectively accelerated in vivo data. Here, μ_d is the mean difference, σ_d is the standard deviation of the difference, and r is the Pearson correlation coefficient. ReVEAL, ReVEAL no mixture, and k-t SPARSE-SENSE are compared to GRAPPA at R = 1.74. The lowest absolute mean difference, lowest standard deviation, and highest Pearson correlation coefficient for each acceleration rate is in bold font.

Prospectively Accelerated in vivo Compared to GRAPPA R=1.74
		R = 2			R = 4			R = 5			R = 8			R = 10			R = 16
		μd	σd	r	μd	σd	r	μd	σd	r	μd	σd	r	μd	σd	r	μd	σd	r
ReVEAL	SV (ml)	2.49	3.92	0.98	-0.97	4.92	0.97	-2.76	4.07	0.98	-2.90	5.51	0.96	-2.08	3.95	0.98	-13.91	10.17	0.85
ReVEAL no mixture	SV (ml)	2.05	3.76	0.98	-1.55	4.46	0.97	-3.04	3.71	0.98	-6.00	8.10	0.91	-6.87	6.45	0.94	-36.87	18.70	0.17
k-t SPARSE-SENSE	SV (ml)	-2.73	10.24	0.93	-5.28	9.62	0.94	-7.31	7.54	0.94	-8.47	7.68	0.93	-10.58	10.32	0.90	-14.71	17.43	0.55
		μd	σd	r	μd	σd	r	μd	σd	r	μd	σd	r	μd	σd	r	μd	σd	r
ReVEAL	PV (cm/s)	5.55	10.79	0.80	3.70	13.42	0.67	-0.54	10.98	0.81	-5.87	11.31	0.73	-7.57	11.74	0.82	-16.31	10.07	0.82
ReVEAL no mixture	PV (cm/s)	4.32	10.15	0.83	0.04	14.18	0.61	-2.56	11.18	0.80	-13.06	12.60	0.70	-18.27	13.85	0.82	-73.52	15.95	0.79
k-t SPARSE-SENSE	PV (cm/s)	6.24	13.99	0.85	8.34	12.55	0.83	3.32	13.99	0.81	3.89	16.48	0.82	2.12	21.21	0.79	8.01	22.39	0.55

As evident from Table 2, the variability of ReVEAL, for R ≤ 10, compares favorably to both ReVEAL at R = 2 and GRAPPA at R = 1.74. As was the case for phantom imaging, fidelity of PV and SV is lost at R = 16 as reflected in the relatively large bias and variance. In comparison, the performances of ReVEAL no mixture and k-t SPARSE-SENSE degrade rapidly beyond R = 5. For R = 10, representative velocity-time profiles for mean and peak velocities are shown in Fig. 6(c-d). As evident from the figure, the profiles generated from ReVEAL closely follow the reference, while the profiles from ReVEAL no mixture show excessive bias and the profiles from k-t SPARSE-SENSE show both excessive bias and variance. An example of images reconstructed at R = 10 using the three methods is provided in Fig. 7. The bottom row in Fig. 7 shows the posterior probability of the velocity indicator variable, υ. This posterior probability map is an estimate produced by ReVEAL of the likely locations of velocity (shown in white) on a per pixel basis; it is a direct consequence of the mixture density model used in ReVEAL. See Movie S2 in the supporting material for images reconstructed at R = 10.

Figure 7.

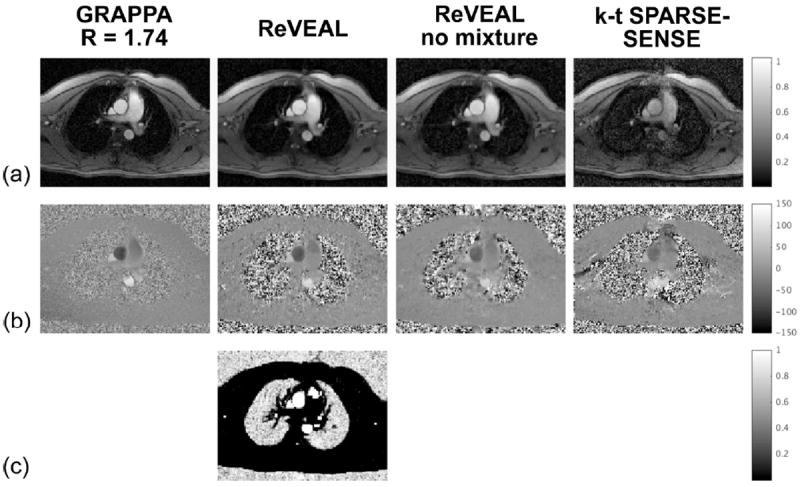
Prospectively accelerated in vivo data reconstructed at R = 10 and GRAPPA at R = 1.74. ReVEAL, ReVEAL no mixture, and k-t SPARSE-SENSE are compared for one representative frame. (a) The normalized magnitude image. (b) The velocity (phase) map in cm/s. (c) The posterior probability of velocity present in a voxel, in grayscale from 0 (black) to 1 (white). Only ReVEAL provides this time-resolved posterior estimate of velocity locations.

Discussion

The proposed ReVEAL approach for PC-MRI yields an empirical Bayes reconstruction with fast message passing computation that jointly processes the entire data set across space, time, coils, and encodings. Estimation of stroke volume and peak velocity using prospective in vivo acquisition at R = 10 showed variance and Pearson correlation coefficient similar to R = 1.74 GRAPPA (n = 10); the accelerated measurement comprised four heart-beats in a single breath-hold, segmented acquisition. The posterior means computed by the algorithm provide MMSE estimates of image magnitude and velocity-encoded phase, and posterior variances provide, if desired and with no additional computation, confidence labels for the estimated quantities produced by the nonlinear reconstruction. Further, these posterior probabilities enable automated tuning of algorithm parameters via expectation-maximization, demonstrated here for selection of the prior probability of flow parameter, γ. The wavelet regularization in ReVEAL provides spatio-temporal regularization, while k-t SPARSE-SENSE, for example, captures only temporal regularization. Further, the signal structure present between encodings is exploited in ReVEAL using a non-Gaussian mixture density, which significantly reduced both bias and variance in SV and PV for R > 5. The mixture density implicitly results in an automated segmentation of pixels via the posterior probability of the velocity indicator variable, υ; the action of this velocity indicator, υ, is particularly visible, for example, at the brachial arteries seen in Fig. 7.

The proposed Bayesian data model includes the independence assumption, p(θ_υ∣υ) = p(θ_υ). This choice to impose no additional statistical dependence is adopted for computational convenience; that is, potential regularization gain from additional physically-motivated structure is conservatively bypassed in favor of computational simplicity. Yet, additional structure across space, time and encodings may indeed be incorporated in the Bayesian model presented here and is a topic of continuing investigation. Examples include Markov random fields (23) and Markov trees (24). We believe that the Bayesian approach of ReVEAL enables both a flexible modeling framework and a fast computational engine for exploiting signal structure not readily captured in traditional regularized inversion methods.

The ReVEAL approach, as presented here, required one user-defined parameter, λ₀, that scaled the wavelet regularization; and, the ratios of regularization parameters for the eight wavelet subbands were set using a separate in vivo scan not otherwise included in the study. We believe that the automated expectationmaximization procedure used here for selection of the prior probability of velocity, γ, could be employed for fully-automated tuning of all parameters.

The acceleration provided by ReVEAL may be traded for improved spatial or temporal resolution. For example, enhanced temporal resolution can allow flow imaging for pediatric and stress imaging applications where higher heart rates are encountered or for vessels, e.g. carotid or femoral arteries, with rapidly changing velocity-time profiles. Alternatively, the acceleration may enable real-time, free-breathing acquisition for 2D PC-MRI. We conjecture that acceleration beyond the R = 10 demonstrated here for through-plane flow imaging can be achieved in 4D flow imaging due to the added redundancy from the two additional encodings and one additional spatial dimension. The computational complexity of the approximate message passing algorithm scales only linearly in the number of encodings, receive coils, frames, and number of k-space samples per coil; therefore, we expect ReVEAL to remain computationally tractable for larger image series and for 4D flow imaging.

Conclusion

We have presented ReVEAL as a novel technique for recovery of accelerated PC-MRI data; the approach includes Bayesian modeling of PC-MRI data, a VISTA sampling strategy, and fast message passing computation. Quantitative results were presented for in vivo and flow phantom data for 2D through plane flow measurements; further, ReVEAL is extensible to applications such as 4D flow, real-time 2D flow, and DENSE (43).

Supplementary Material

Supp FigureS1-S5

Figure S1: Evaluation of ReVEAL modeling choices using images from fully sampled in vivo data. (a) The histogram of the real portion of the complex difference between velocity-encoded and velocity-compensated images in a velocity-free region. The data were fit with a Gaussian distribution. The Gaussian fit was confirmed using a χ² test with 5% significance level (p = 0.15, χ² = 9.37, and 6 degrees of freedom). Similar goodness of fit was observed for the imaginary portion of the compex difference (data not shown). Therefore, the Gaussian model in [8] and the in vivo data are in agreement. (b) A histogram of the ratio of magnitudes for velocity-encoded and velocity-compensated images and a Rician fit. The Rician fit was confirmed using a χ² test with 5% significance level (p = 0.40, χ² = 7.27, and 7 degrees of freedom). Therefore, the Rician magnitude model in [9] and in vivo data are in agreement.

Figure S2: Bland-Altman analyses for prospectively accelerated phantom data reconstructed with ReVEAL. Each column in the figure represents a different acceleration rate R. The top row contains results for peak velocity (PV); the bottom row contains results for stroke volume (SV). The solid line represents the mean difference, and dashed lines represent the 95% confidence intervals (mean ±1.96×standard deviation).

Figure S3: Bland-Altman analyses for prospectively accelerated phantom data reconstructed with ReVEAL no mixture. Each column in the figure represents a different acceleration rate R. The top row contains results for peak velocity (PV); the bottom row contains results for stroke volume (SV). The solid line represents the mean difference, and dashed lines represent the 95% confidence intervals (mean ±1.96×standard deviation).

Figure S4: Bland-Altman analyses for prospectively accelerated phantom data reconstructed with k-t SPARSE-SENSE. Each column in the figure represents a different acceleration rate R. The top row contains results for peak velocity (PV); the bottom row contains results for stroke volume (SV). The solid line represents the mean difference, and dashed lines represent the 95% confidence intervals (mean ±1.96×standard deviation).

Figure S5: Bland-Altman analyses for prospectively accelerated in vivo data reconstructed with ReVEAL. In the first column, the variation between two R = 1.74 GRAPPA reconstructions is quantified. The remaining columns compare R = 1.74 GRAPPA and ReVEAL at R = 2, 4, 5, 8, 10, and 16. Each column in the figure represents a different acceleration rate R. The top row contains results for peak velocity (PV); the bottom row contains results for stroke volume (SV). The solid line represents the mean difference, and dashed lines represent the 95% confidence intervals (mean ±1.96×standard deviation).

Figure S6: Bland-Altman analyses for prospectively accelerated in vivo data reconstructed with ReVEAL no mixture. In the first column, the variation between two R = 1.74 GRAPPA reconstructions is quantified. The remaining columns compare R = 1.74 GRAPPA and ReVEAL at R = 2, 4, 5, 8, 10, and 16. Each column in the figure represents a different acceleration rate R. The top row contains results for peak velocity (PV); the bottom row contains results for stroke volume (SV). The solid line represents the mean difference, and dashed lines represent the 95% confidence intervals (mean ±1.96×standard deviation).

Figure S7: Bland-Altman analyses for prospectively accelerated in vivo data reconstructed with k-t SPARSESENSE. In the first column, the variation between two R = 1.74 GRAPPA reconstructions is quantified. The remaining columns compare R = 1.74 GRAPPA and ReVEAL at R = 2, 4, 5, 8, 10, and 16. Each column in the figure represents a different acceleration rate R. The top row contains results for peak velocity (PV); the bottom row contains results for stroke volume (SV). The solid line represents the mean difference, and dashed lines represent the 95% confidence intervals (mean ±1.96×standard deviation).

Supp MovieS1

Movie S1: Retrospectively accelerated in vivo data reconstructed at R = 12. ReVEAL, ReVEAL no mixture, and k-t SPARSE-SENSE are compared to the fully sampled data. The first column was reconstructed from fully sampled data using the adaptive array combination method (36). The remaining columns were reconstructed from R = 12 accelerated data with ReVEAL, ReVEAL no mixture, and k-t SPARSE-SENSE. (a) The reconstructed, normalized magnitude images. (b) The absolute difference in magnitude between the accelerated images and the fully sampled image. (c) The velocity maps in cm/s. (d) The absolute difference between the fully sampled velocity map and the velocity map recovered from accelerated data. The difference was taken for pixels within the top 90% of magnitude in the reference image to avoid large differences due to low magnitude phase noise.

Supp MovieS2

Movie S2: Prospectively accelerated in vivo data reconstructed at R = 10 and GRAPPA at R = 1.74. ReVEAL, ReVEAL no mixture, and k-t SPARSE-SENSE are compared. (a) The normalized magnitude image. (b) The velocity (phase) map in cm/s. (c) The posterior probability of velocity present in a voxel, in grayscale from 0 (black) to 1 (white). Only ReVEAL provides this posterior estimate of velocity locations.