Abstract
Speech separation systems usually operate on the short-time Fourier transform (STFT) of noisy speech, and enhance only the magnitude spectrum while leaving the phase spectrum unchanged. This is done because there was a belief that the phase spectrum is unimportant for speech enhancement. Recent studies, however, suggest that phase is important for perceptual quality, leading some researchers to consider magnitude and phase spectrum enhancements. We present a supervised monaural speech separation approach that simultaneously enhances the magnitude and phase spectra by operating in the complex domain. Our approach uses a deep neural network to estimate the real and imaginary components of the ideal ratio mask defined in the complex domain. We report separation results for the proposed method and compare them to related systems. The proposed approach improves over other methods when evaluated with several objective metrics, including the perceptual evaluation of speech quality (PESQ), and a listening test where subjects prefer the proposed approach with at least a 69% rate.
Index Terms: Deep neural networks, speech separation, speech quality, complex ideal ratio mask
I. Introduction
THERE are many speech applications where the signal of interest is corrupted by additive background noise. Removing the noise from these mixtures is considered one of the most challenging research topics in the area of speech processing. The problem becomes even more challenging in the monaural case where only a single microphone captures the signal. Although there have been many improvements to monaural speech separation, there is still a strong need to produce high quality separated speech.
Typical speech separation systems operate in the time-frequency (T-F) domain by enhancing the magnitude response and leaving the phase response unaltered, in part due to the findings in [1], [2]. In [1], a series of experiments are performed to determine the relative importance of the phase and magnitude components in terms of speech quality. Wang and Lim compute the Fourier transform magnitude response from noisy speech at a certain signal-to-noise ratio (SNR), and then reconstruct a test signal by combining it with the Fourier transform phase response that is generated at another SNR. Listeners then compare each reconstructed signal to unprocessed noisy speech of known SNR, and indicate which signal sounds best. The relative importance of the phase and magnitude spectra is quantified with the equivalent SNR, which is the SNR where the reconstructed speech and noisy speech are each selected at a 50% rate. The results show that a significant improvement in equivalent SNR is not obtained when a much higher SNR is used to reconstruct the phase response than the magnitude response. These results were consistent with the results of a previous study [3]. Ephraim and Malah [2] separate speech from noise using the minimum mean-square error (MMSE) to estimate the clean spectrum, which consists of MMSE estimates for the magnitude response and the complex exponential of the phase response. They show that the complex exponential of the noisy phase is the MMSE estimate of the complex exponential of the clean phase. The MMSE estimate of the clean spectrum is then the product of the MMSE estimate of the clean magnitude spectrum and the complex exponential of the noisy phase, meaning that the phase is unaltered for signal reconstruction.
A recent study, however, by Paliwal et al. [4] shows that perceptual quality improvements are possible when only the phase spectrum is enhanced and the noisy magnitude spectrum is left unchanged. Paliwal et al. combine the noisy magnitude response with the oracle (i.e. clean) phase, non-oracle (i.e. noisy) phase, and enhanced phase where mismatched short-time Fourier transform (STFT) analysis windows are used to extract the magnitude and phase spectra. Both objective and subjective (i.e. a listening study) speech quality measurements are used to assess improvement. The listening evaluation involves a preference selection between a pair of signals. The results reveal that significant speech quality improvements are attainable when the oracle phase spectrum is applied to the noisy magnitude spectrum, while modest improvements are obtained when the non-oracle phase is used. Results are similar when an MMSE estimate of the clean magnitude spectrum is combined with oracle and non-oracle phase responses. In addition, high preference scores are achieved when the MMSE estimate of the clean magnitude spectrum is combined with an enhanced phase response.
The work by Paliwal et al. has led some researchers to develop phase enhancement algorithms for speech separation [5], [6], [7]. The system presented in [5] uses multiple input spectrogram inversions (MISI) to iteratively estimate the time-domain source signals in a mixture given the corresponding estimated STFT magnitude responses. Spectrogram inversion estimates signals by iteratively recovering the missing phase information, while constraining the magnitude response. MISI uses the average total error between the mixture and the sum of the estimated sources to update the source estimates at each iteration. In [6], Mowlaee et al. perform MMSE phase estimation where the phases of two sources in a mixture are estimated by minimizing the square error. This minimization results in several phase candidates, but ultimately the pair of phases with the lowest group delay is chosen. The sources are then reconstructed with their magnitude responses and estimated phases. Krawczyk and Gerkmann [7] enhance the phase of voiced-speech frames by reconstructing the phase between harmonic components across frequency and time, given an estimate of the fundamental frequency. Unvoiced frames are left unchanged. The approaches in [5], [6], [7] all show objective quality improvements when the phase is enhanced. However, they do not address the magnitude response.
Another factor that motivates us to examine phase estimation is that supervised mask estimation has recently been shown to improve human speech intelligibility in very noisy conditions [8], [9]. With negative SNRs, the phase of noisy speech reflects more the phase of background noise than that of target speech. As a result, using the phase of noisy speech in the reconstruction of enhanced speech becomes more problematic than at higher SNR conditions [10]. So in a way, the success of magnitude estimation at very low SNRs heightens the need for phase estimation at these SNR levels.
Recently, a deep neural network (DNN) that estimates the ideal ratio mask (IRM) has been shown to improve objective speech quality in addition to predicted speech intelligibility [11]. The IRM enhances the magnitude response of noisy speech, but uses the unprocessed noisy phase for reconstruction. Based on phase enhancement research, ratio masking results should further improve if both the magnitude and phase responses are enhanced. In fact, recent methods have shown that incorporating some phase information is beneficial [12], [13]. In [12], the cosine of the phase difference between clean and noisy speech is applied to IRM estimation. Wang and Wang [13] estimate the clean time-domain signal by combining a subnet for T-F masking with another subnet that performs the inverse fast Fourier transform (IFFT).
In this paper, we define the complex ideal ratio mask (cIRM) and train a DNN to jointly estimate real and imaginary components. By operating in the complex domain, the cIRM is able to simultaneously enhance both the magnitude and phase responses of noisy speech. The objective results and the preference scores from a listening study show that cIRM estimation produces higher quality speech than related methods.
The rest of the paper is organized as follows. In the next section, we reveal the structure within the real and imaginary components of the STFT. Section III describes the cIRM. The experimental results are shown in Section IV. We conclude with a discussion in Section V.
II. Structure within Short-time Fourier Transform
Polar coordinates (i.e. magnitude and phase) are commonly used when enhancing the STFT of noisy speech, as defined in
| (1) |
where |St,f| represents the magnitude response and θSt,f represents the phase response of the STFT at time t and frequency f. Each T-F unit in the STFT representation is a complex number with real and imaginary components. The magnitude and phase responses are computed directly from the real and imaginary components, as given below respectively.
| (2) |
| (3) |
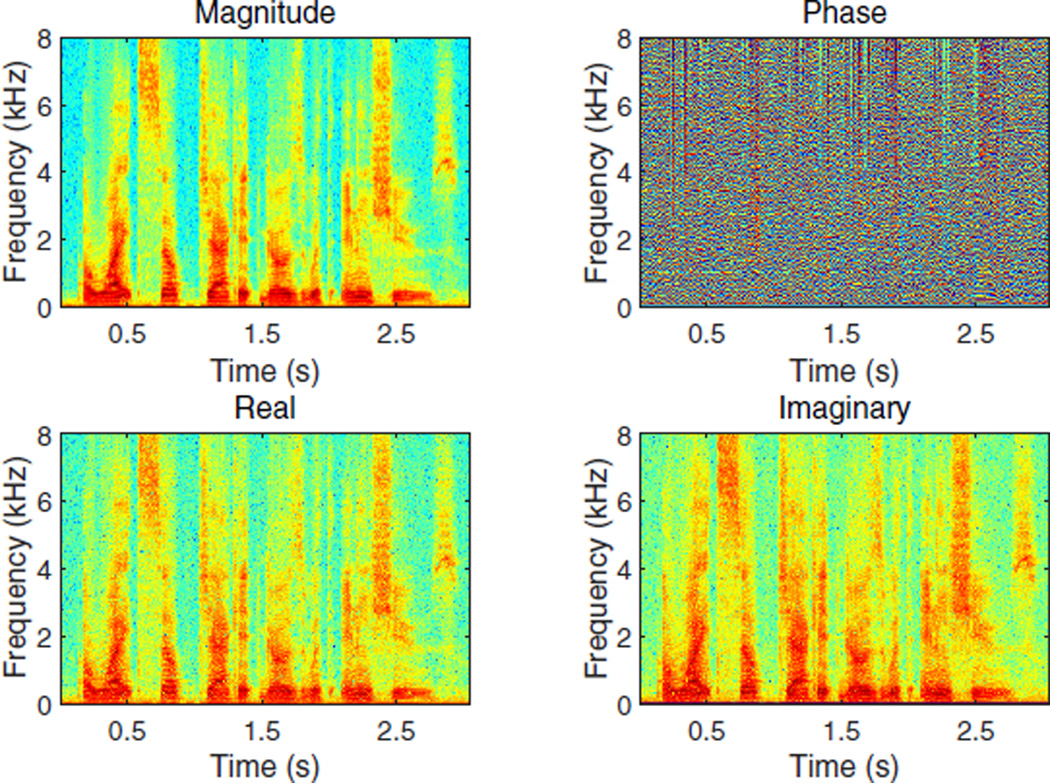
An example of the magnitude (top-left) and phase (top-right) responses for a clean speech signal is shown in Fig. 1. The magnitude response exhibits clear temporal and spectral structure, while the phase response looks rather random. This is often attributed to the wrapping of phase values into the range of [−π, π]. When a learning algorithm is used to map features to a training target, it is important that there is structure in the mapping function. Fig. 1 shows that using DNNs to predict the clean phase response directly is unlikely effective, despite the success of DNNs in learning clean magnitude spectrum from noisy magnitude spectrum. Indeed, we have tried extensively to train DNNs to estimate clean phase from noisy speech, but with no success.
Fig. 1.
(Color online) Example magnitude (top-left) and phase (top-right) spectrograms, and real (bottom-left) and imaginary (bottom-right) spectrograms, for a clean speech signal. The real and imaginary spectrograms show temporal and spectral structure and are similar to the magnitude spectrogram. Little structure is exhibited in the phase spectrogram.
As an alternative to using polar coordinates, the definition of the STFT in (1) can be expressed in Cartesian coordinates, using the expansion of the complex exponential. This leads to the following definitions for the real and imaginary components of the STFT:
| (4) |
| (5) |
| (6) |
The lower part of Fig. 1 shows the log compressed, absolute value of the real (bottom-left) and imaginary (bottom-right) spectra of clean speech. Both real and imaginary components show clear structure, similar to magnitude spectrum, and are thus amenable to supervised learning. These spectrograms look almost the same because of the trigonometric co-function identity: the sine function is identical to the cosine function with a phase shift of π/2 radians. Equations (2) and (3) show that the magnitude and phase responses can be computed directly from the real and imaginary components of the STFT, so enhancing the real and imaginary components leads to enhanced magnitude and phase spectra.
Based on this structure, a straightforward idea is to use DNNs to predict the complex components of the STFT. However, our recent study shows that directly predicting the magnitude spectrum may not be as good as predicting an ideal T-F mask [11]. Therefore, we propose to predict the real and imaginary components of the complex ideal ratio mask, which is described in the next section.
III. Complex Ideal Ratio Mask and Its Estimation
A. Mathematical derivation
The traditional ideal ratio mask is defined in the magnitude domain, and in this section we define the ideal ratio mask in the complex domain. Our goal is to derive a complex ratio mask that, when applied to the STFT of noisy speech, produces the STFT of clean speech. In other words, given the complex spectrum of noisy speech, Yt,f, we get the complex spectrum of clean speech, St,f, as follows:
| (7) |
where ‘*’ indicates complex multiplication and Mt,f is the cIRM. Note that Yt,f, St,f and Mt,f are complex numbers, and can be written in rectangular form as:
| (8) |
| (9) |
| (10) |
where the subscripts r and i indicate the real and imaginary components, respectively. The subscripts for time and frequency are not shown for convenience, but the definitions are given for each T-F unit. Based on these definitions, Eq. (7) can be extended:
| (11) |
From here we can conclude that the real and imaginary components of clean speech are given as
| (12) |
| (13) |
Using Eqs. (12) and (13), the real and imaginary components of M are defined as
| (14) |
| (15) |
resulting in the definition for the complex ideal ratio mask
| (16) |
Notice that this definition of the complex ideal ratio mask is closely related to the Wiener filter, which is the complex ratio of the cross-power spectrum of the clean and noisy speech to the power spectrum of the noisy speech [14].
It is important to mention that Sr, Si, Yr, and Yi ∈ ℝ, meaning that Mr and Mi ∈ ℝ. With this, the complex mask may have large real and imaginary components with values in the range (−∞, ∞). Recall that the IRM takes on values in the range [0, 1], which can be conducive for supervised learning with DNNs. The large value range may complicate cIRM estimation. Therefore, we compress the cIRM with the following hyperbolic tangent
| (17) |
where x is r or i, denoting the real and imaginary components. This compression produces mask values within [-K,K] and C controls its steepness. Several values for K and C are evaluated, and K = 10 and C = 0.1 perform best empirically and are used to train the DNN. During testing we recover an estimate of the uncompressed mask using the following inverse function on the DNN output, Ox:
| (18) |
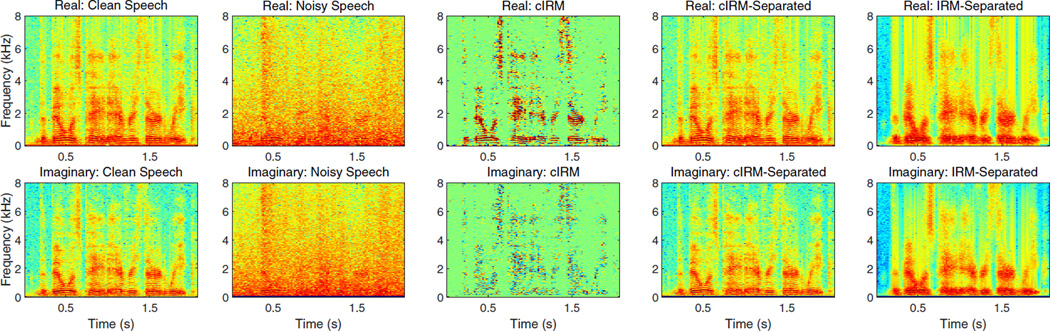
An example of the cIRM, along with the spectrograms of the clean, noisy, cIRM-separated and IRM-separated speech are shown in Fig. 2. The real portion of the complex STFT of each signal is shown in the top, and the imaginary portion is in the bottom of the figure. The noisy speech is generated by combining the clean speech signal with Factory noise at 0 dB SNR. For this example, the cIRM is generated with K = 1 in (17). The denoised speech signal is computed by taking the product of the cIRM and noisy speech. Notice that the denoised signal is effectively reconstructed as compared to the clean speech signal. On the other hand, the IRM-separated speech removes much of the noise, but it does not reconstruct the real and imaginary components of the clean speech signal as well as the cIRM-separated speech.
Fig. 2.
(Color online) Spectrogram plots of the real (top) and imaginary (bottom) STFT components of clean speech, noisy speech, the complex ideal ratio mask, and speech separated with the complex ideal ratio mask and the ideal ratio mask.
B. DNN based cIRM estimation
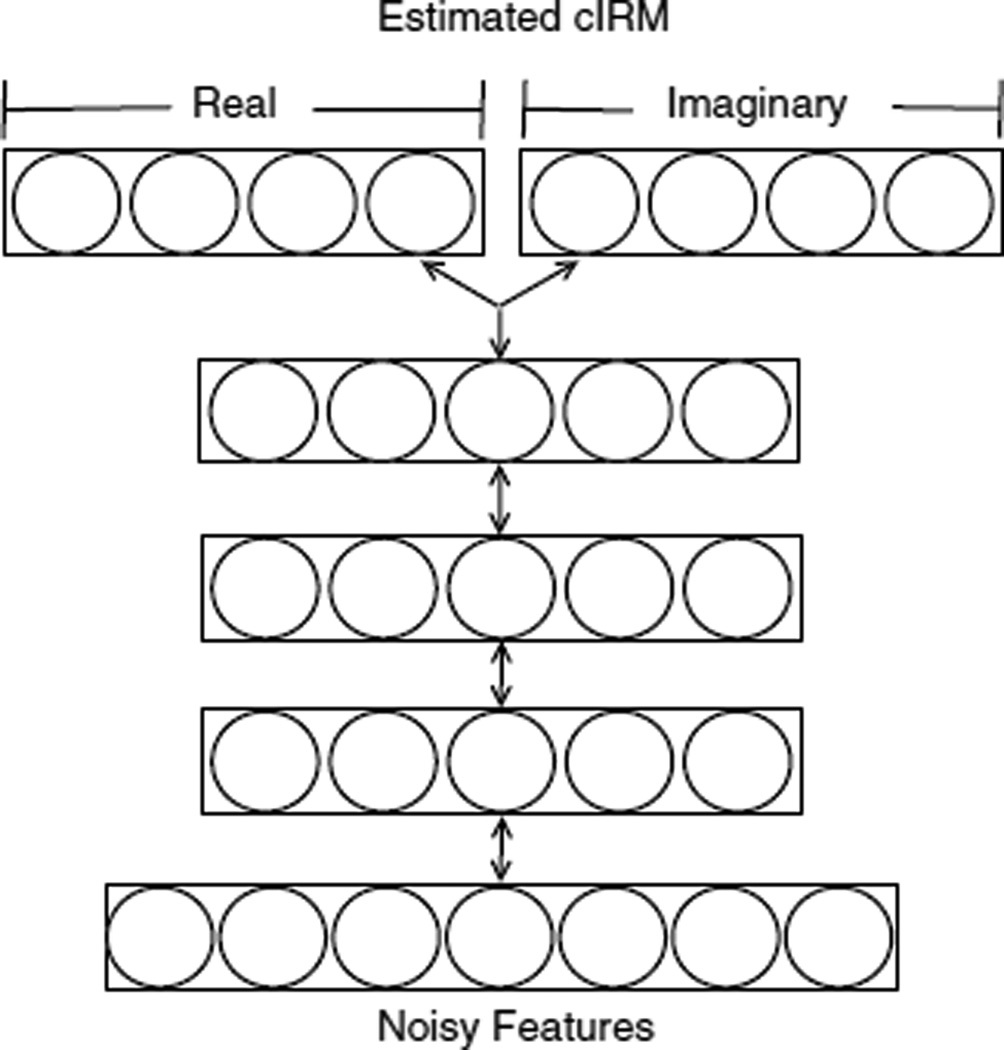
The DNN that is used to estimate the cIRM is depicted in Fig. 3. As done in previous studies [11], [15], the DNN has three hidden layers where each of the hidden layers has the same number of units. The input layer is given the following set of complementary features that is extracted from a 64-channel gammatone filterbank: amplitude modulation spectrogram (AMS), relative spectral transform and perceptual linear prediction (RASTA-PLP), mel-frequency cepstral coefficients (MFCC), and cochleagram response, as well as their deltas. The features used are the same as in [11]. A combination of these features has been shown to be effective for speech segregation [16]. We also evaluated other features, including noisy magnitude, noisy magnitude and phase, and the real and imaginary components of the noisy STFT, but they were not as good as the complementary set. Useful information is carried across time frames, so a sliding context window is used to splice adjacent frames into a single feature vector for each time frame [11], [17]. This is employed for the input and output of the DNN. In other words, the DNN maps a window of frames of the complementary features to a window of frames of the cIRM for each time frame. Notice that the output layer is separated into two sub-layers, one for the real components of the cIRM and the other for the imaginary components of the cIRM. This Y-shaped network structure in the output layer is commonly used to jointly estimate related targets [18], and in this case it helps ensure that the real and imaginary components are jointly estimated from the same input features.
Fig. 3.
DNN architecture used to estimate the complex ideal ratio mask.
For this network structure, the mean-square error (MSE) function for complex data is used in the backpropagation algorithm to update the DNN weights. This cost function is the summation of the MSE from the real data and the MSE from the imaginary data, as shown below:
| (19) |
where N represents the number of time frames for the input, Or(t, f) and Oi(t, f) denote the real and imaginary outputs from the DNN at a T-F unit, and Mr(t, f) and Mi(t, f) correspond to the real and imaginary components of the cIRM, respectively.
Specifically, each DNN hidden layer has 1024 units [11]. The rectified linear (ReLU) [19] activation function is used for the hidden units, while linear units are used for the output layer since the cIRM is not bounded between 0 and 1. Adaptive gradient descent [20] with a momentum term is used for optimization. The momentum rate is set to 0.5 for the first 5 epochs, after which the rate changes to 0.9 for the remaining 75 epochs (80 total epochs).
IV. Results
A. Dataset and System Setup
The proposed system is evaluated on the IEEE database [21], which consists of 720 utterances spoken by a single male speaker. The testing set consists of 60 clean utterances that are downsampled to 16 kHz. Each testing utterance is mixed with speech-shaped noise (SSN), cafeteria (Cafe), speech babble (Babble), and factory floor noise (Factory) at SNRs of −6, −3, 0, 3, and 6 dB, resulting in 1200 (60 signals × 4 noises × 5 SNRs) mixtures. SSN is a stationary noise, while the other noises are non-stationary and each signal is around 4 minutes long. Random cuts from the last 2 minutes of each noise are mixed with each testing utterance to create the testing mixtures. The DNN for estimating the cIRM is trained with 500 utterances from the IEEE corpus, which are different from the testing utterances. Ten random cuts from the first 2 minutes of each noise are mixed with each training utterance to generate the training set. The mixtures for the DNN are generated at −3, 0, and 3 dB SNRs, resulting in 60000 (500 signals × 4 noises × 10 random cuts × 3 SNRs) mixtures in the training set. Note that the −6 and 6 dB SNRs of the testing mixtures are unseen by the DNN during training. Dividing the noises into two halves ensures that the testing noise segments are unseen during training. In addition, a development set determines parameter values for the DNN and STFT. This development set is generated from 50 distinct clean IEEE utterances that are mixed with random cuts from the first 2 minutes of the above four noises at SNRs of −3, 0, and 3 dB.
Furthermore, we use the TIMIT corpus [22] which consists of utterances from many male and female speakers. A DNN is trained by mixing 500 utterances (10 utterances from 50 speakers) with the above noises at SNRs of −3, 0, and 3 dB. The training utterances come from 35 male and 15 female speakers. Sixty different utterances (10 utterances from 6 new speakers) are used for testing. The testing utterances come from 4 male and 2 female speakers.
As described in Sec. III-B, a complementary set of four features is provided as the input to the DNN. Once the complementary features are computed from the noisy speech, the features are normalized to have zero mean and unit variance across each frequency channel. It has been shown in [23] that applying auto-regressive moving average (ARMA) filtering to input features improves automatic speech recognition performance, since ARMA filtering smooths each feature dimension across time to reduce the interference from the background noise. In addition, an ARMA filter improves speech separation results [24]. Therefore, we apply ARMA filtering to the complementary set of features after mean and variance normalization. The ARMA-filtered feature vector at the current time frame is computed by averaging the two filtered feature vectors before the current frame with the current frame and the two unfiltered frames after the current frame. A context window that spans five frames (two before and two after) splices the ARMA-filtered features into an input feature vector.
The DNN is trained to estimate the cIRM for each training mixture where the cIRM is generated from the STFTs of noisy and clean speech as described in (16) and (17). The STFTs are generated by dividing the time-domain signal into 40 ms (640 sample) overlapping frames, using 50% overlap between adjacent frames. A Hann window is used, along with a 640 length FFT. A three-frame context window augments each frame of the cIRM for the output layer, meaning that the DNN estimates three frames for each input feature vector.
B. Comparison Methods
We compare cIRM estimation to IRM estimation [11], phase-sensitive masking (PSM) [12], time-domain signal reconstruction (TDR) [13], and complex-domain nonnegative matrix factorization (CMF) [25], [26], [27]. Comparing against IRM estimation helps determine if processing in the complex domain provides improvements over processing in the magnitude domain, while the other comparisons determine how complex ratio masking performs relative to these recent supervised methods that incorporate a degree of phase.
The IRM is generated by taking the square root of the ratio of the speech energy to the sum of the speech and noise energy at each T-F unit [11]. A separate DNN is used to estimate the IRM. The input features and the DNN parameters match those for cIRM estimation with the only exception that the output layer corresponds to the magnitude, not the real and imaginary components. Once the IRM is estimated, it is applied to the noisy magnitude response which, with the noisy phase, produces a speech estimate. The PSM is similar to the IRM, except that the ratio between the clean speech and noisy speech magnitude spectra is multiplied by the cosine of the phase difference between the clean speech and noisy speech. Theoretically this amounts to using just the real component of the cIRM. TDR directly reconstructs the clean time-domain signal by adding a subnet to perform the IFFT. The input to this IFFT subnet consists of the activity of the last hidden layer of a T-F masking subnet (resembling a ratio mask) that is applied to the mixture magnitude, and the noisy phase. The input features and DNN structures for PSM and TDR estimation match that of IRM estimation.
CMF is an extension of non-negative matrix factorization (NMF) with the phase response included in the process. More specifically, NMF factors a signal into a basis and activation matrix, where the basis matrix provides spectral structure and the activation matrix linearly combines the basis elements to approximate the given signal. It is required that both matrices be nonnegative. With CMF, the basis and weights are still nonnegative, but a phase matrix is created that multiplies each T-F unit, allowing each spectral basis to determine the phase that best fits the mixture [26]. We perform speech separation using supervised CMF as implemented in [27], where the matrices for the two sources (speech and noise) are separately trained from the same training data used by the DNNs. The speech and noise basis are each modeled with 100 basis vectors, which are augmented with a context window that spans 5 frames.
For a final comparison, we combine different magnitude spectra with phase spectra to evaluate approaches that enhance either magnitude or phase responses. For phase estimation, we use a recent system that enhances the phase response of noisy speech [7] by reconstructing the spectral phase of voiced speech using the estimated fundamental frequency. It analyzes the phase spectrum to enhance the phase along time and in-between harmonics along the frequency axis. Additionally, we use a standard phase enhancing method by Griffin and Lim [28], which repeatedly computes the STFT and the inverse STFT by fixing the magnitude response and only allowing the phase response to update. Since these approaches only enhance the phase responses, we combine them with the magnitude responses of speech separated by an estimated IRM (denoted as RM-K&G and RM-G&L) and of noisy speech (denoted as NS-K&G and NS-G&L), as done in [7]. These magnitude spectra are also combined with the phase response of speech separated by an estimated cIRM, and they are denoted as RM-cRM and NS-cRM, respectively.
C. Objective Results
The separated speech signals from each approach are evaluated with three objective metrics, namely the perceptual evaluation of speech quality (PESQ) [29], the short-time objective intelligibility (STOI) score [30], and the frequency-weighted segmental SNR (SNRfw) [31]. PESQ is computed by comparing the separated speech with the corresponding clean speech, producing scores in the range [−0.5, 4.5] where a higher score indicates better quality. STOI measures objective intelligibility by computing the correlation of short-time temporal envelopes between clean and separated speech, resulting in scores in the range of [0, 1] where a higher score indicates better intelligibility. SNRfw computes a weighted signal-to-noise ratio aggregated across each time frame and critical band. PESQ and SNRfw have been shown to be highly correlated to human speech quality scores [31], while STOI has high correlation with human speech intelligibility scores.
The objective results of the different methods using the IEEE utterances are given in Tables I, II, and III, which show the results at mixture SNRs of −3, 0, and 3 dB, respectively. Boldface indicates the system that performed best within a noise type. Starting with Table I, in terms of PESQ, each approach offers quality improvements over noisy speech mixtures, for each noise. CMF performs consistently for each noise, but it offers the smallest PESQ improvement over the noisy speech. The estimated IRM (i.e. RM), estimated cIRM (i.e. cRM), PSM and TDR each produce considerable improvements over the noisy speech and CMF, with cRM performing best for SSN, Cafe, and Factory noise. Going from ratio masking in the magnitude domain to ratio masking in the complex domain improves PESQ scores for each noise. In terms of STOI, each algorithm produces improved scores over the noisy speech, where again CMF offers the smallest improvement. The STOI scores for the estimated IRM, cIRM, and PSM are approximately identical. In terms of SNRfw, the estimated cIRM performs best for each noise except for Babble noise where PSM produces the highest score.
TABLE I.
Average performance scores for different systems on −3 dB IEEE mixtures. Bold indicates best result.
| PESQ | STOI | SNRfw | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SSN | Cafe | Babble | Factory | SSN | Cafe | Babble | Factory | SSN | Cafe | Babble | Factory | |
| Mixture | 1.85 | 1.72 | 1.79 | 1.68 | 0.62 | 0.57 | 0.58 | 0.58 | 1.83 | 2.86 | 2.73 | 2.19 |
| RM | 2.23 | 2.09 | 2.32 | 2.17 | 0.77 | 0.69 | 0.80 | 0.71 | 5.82 | 5.45 | 7.36 | 5.49 |
| cRM | 2.51 | 2.27 | 2.44 | 2.37 | 0.78 | 0.71 | 0.79 | 0.73 | 7.50 | 6.59 | 7.68 | 6.69 |
| PSM | 2.34 | 2.16 | 2.46 | 2.25 | 0.78 | 0.70 | 0.81 | 0.72 | 7.24 | 6.53 | 8.85 | 6.57 |
| TDR | 2.29 | 2.15 | 2.23 | 2.24 | 0.73 | 0.67 | 0.73 | 0.69 | 5.29 | 4.75 | 5.81 | 4.72 |
| CMF | 1.98 | 1.96 | 1.90 | 1.98 | 0.69 | 0.63 | 0.64 | 0.65 | 3.54 | 3.60 | 4.02 | 3.24 |
TABLE II.
Average performance scores for different systems on 0 dB IEEE mixtures. Bold indicates best result.
| PESQ | STOI | SNRfw | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SSN | Cafe | Babble | Factory | SSN | Cafe | Babble | Factory | SSN | Cafe | Babble | Factory | |
| Mixture | 1.97 | 1.89 | 1.96 | 1.82 | 0.70 | 0.64 | 0.66 | 0.65 | 2.59 | 3.96 | 3.68 | 2.89 |
| RM | 2.47 | 2.34 | 2.54 | 2.39 | 0.84 | 0.78 | 0.85 | 0.79 | 7.54 | 7.06 | 8.68 | 7.06 |
| cRM | 2.74 | 2.55 | 2.67 | 2.60 | 0.85 | 0.79 | 0.84 | 0.80 | 8.51 | 7.91 | 8.90 | 7.77 |
| PSM | 2.61 | 2.44 | 2.69 | 2.47 | 0.84 | 0.78 | 0.86 | 0.79 | 8.83 | 7.99 | 10.00 | 7.95 |
| TDR | 2.52 | 2.40 | 2.44 | 2.45 | 0.81 | 0.77 | 0.80 | 0.77 | 6.65 | 6.16 | 7.11 | 5.95 |
| CMF | 2.16 | 2.17 | 2.09 | 2.16 | 0.77 | 0.71 | 0.72 | 0.73 | 4.71 | 4.89 | 5.14 | 4.36 |
TABLE III.
Average performance scores for different systems on 3 dB IEEE mixtures. Bold indicates best result.
| PESQ | STOI | SNRfw | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SSN | Cafe | Babble | Factory | SSN | Cafe | Babble | Factory | SSN | Cafe | Babble | Factory | |
| Mixture | 2.10 | 2.07 | 2.14 | 1.99 | 0.77 | 0.71 | 0.73 | 0.72 | 3.59 | 4.48 | 4.98 | 3.76 |
| RM | 2.70 | 2.59 | 2.77 | 2.65 | 0.88 | 0.84 | 0.89 | 0.85 | 9.24 | 8.45 | 9.97 | 8.67 |
| cRM | 2.94 | 2.79 | 2.87 | 2.81 | 0.89 | 0.84 | 0.88 | 0.85 | 9.21 | 8.87 | 9.84 | 8.71 |
| PSM | 2.85 | 2.69 | 2.92 | 2.71 | 0.89 | 0.84 | 0.89 | 0.85 | 10.10 | 9.12 | 10.89 | 9.23 |
| TDR | 2.70 | 2.60 | 2.64 | 2.64 | 0.87 | 0.83 | 0.85 | 0.83 | 7.85 | 7.42 | 8.42 | 7.29 |
| CMF | 2.34 | 2.35 | 2.30 | 2.36 | 0.83 | 0.77 | 0.78 | 0.79 | 6.01 | 5.82 | 6.46 | 5.59 |
The performance trend at 0 dB SNR is similar to that at −3 dB, as shown in Table II, with each method improving objective scores over unprocessed noisy speech. CMF at 0 dB offers approximately the same amounts of PESQ and STOI improvements over the mixtures as at −3 dB. The STOI scores for CMF are also lowest, which is consistent with the common understanding that NMF-based approaches tend to not improve speech intelligibility. CMF improves SNRfw on average by 1.5 dB over the noisy speech. Predicting the cIRM instead of the IRM significantly improves objective quality. The PESQ scores for cRM are better than PSM and TDR for each noise except for Babble. The objective intelligibility scores are approximately identical for RM, cRM, and PSM across all noise types. In terms of the SNRfw performance, PSM performs slightly better across each noise type.
Table III shows the separation performance at 3 dB, which is relatively easier than the −3 and 0 dB cases. In general, the estimated cIRM performs best in terms of PESQ, while the STOI scores between RM, cRM, and PSM are approximately equal. PSM produces the highest SNRfw scores. CMF offers consistent improvements over the noisy speech, but it performs worse than the other methods.
The above results for the masking-based methods are generated when the DNNs are trained and tested on unseen noises, but with seen SNRs (i.e. −3, 0, and 3 dB). To determine if knowing the SNR affects performance, we also evaluated these systems using SNRs that are not seen during training (i.e. −6 and 6 dB). Table IV shows the average performance at −6 and 6 dB. The PESQ results at −6 dB and 6 dB are highest for the estimated cIRM for SSN, Cafe, and Factory noise, while PSM is highest for Babble. The STOI results are approximately the same for the estimated cIRM, IRM, and PSM. PSM performs best in terms of SNRfw.
TABLE IV.
Average scores for different systems on −6 and 6 dB IEEE mixtures. Bold indicates best result.
| PESQ | STOI | SNRfw | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SSN | Cafe | Babble | Factory | SSN | Cafe | Babble | Factory | SSN | Cafe | Babble | Factory | |
| Mixture | 1.99 | 1.91 | 1.96 | 1.86 | 0.70 | 0.65 | 0.66 | 0.66 | 3.10 | 4.14 | 4.28 | 3.38 |
| RM | 2.47 | 2.34 | 2.53 | 2.41 | 0.81 | 0.75 | 0.82 | 0.76 | 7.46 | 7.00 | 8.43 | 7.13 |
| cRM | 2.65 | 2.48 | 2.60 | 2.56 | 0.82 | 0.75 | 0.82 | 0.77 | 7.90 | 7.35 | 8.41 | 7.44 |
| PSM | 2.58 | 2.39 | 2.65 | 2.47 | 0.81 | 0.75 | 0.83 | 0.77 | 8.24 | 7.50 | 9.29 | 7.63 |
| TDR | 2.47 | 2.34 | 2.39 | 2.41 | 0.78 | 0.73 | 0.77 | 0.74 | 6.66 | 6.19 | 7.22 | 6.18 |
| CMF | 2.16 | 2.15 | 2.11 | 2.18 | 0.74 | 0.70 | 0.71 | 0.72 | 5.01 | 5.01 | 5.47 | 4.67 |
To further analyze our approach, we evaluate the PESQ performance of each system (except CMF) using the TIMIT corpus as described in Sec. IV-A. The average results across each noise are shown in Table V. Similar to the single speaker case above, cRM outperforms each approach for SSN, Cafe, and Factory noise, while PSM is the best for Babble noise.
TABLE V.
Average PESQ scores for different systems on −3, 0, and 3 dB TIMIT mixtures. Bold indicates best result.
| SSN | Cafe | Babble | Factory | |
|---|---|---|---|---|
| Mixture | 1.86 | 1.78 | 1.88 | 1.73 |
| RM | 2.31 | 2.16 | 2.34 | 2.23 |
| cRM | 2.52 | 2.32 | 2.35 | 2.41 |
| PSM | 2.44 | 2.23 | 2.41 | 2.33 |
| TDR | 2.38 | 2.27 | 2.32 | 2.33 |
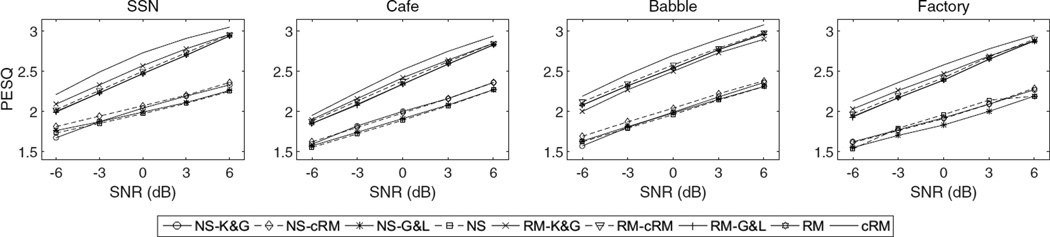
Fig. 4 shows the PESQ results when separately-enhanced magnitude and phase responses are combined to reconstruct speech. The figure shows the results for each system at all SNRs and noise types. Recall that the magnitude response is computed from the noisy speech or speech separated by an estimated IRM, while the phase response is computed from the speech separated by an estimated cIRM or from the methods in [7], [28]. The results for the unprocessed noisy speech, an estimated cIRM, and an estimated IRM are copied from Tables I through IV and are shown for each case. When the noisy magnitude response is used (lower portion of each plot), the objective quality results between the different phase estimators are close across different noise types and SNRs. More specifically, for Cafe and Factory noise the results for NS-K&G and NS-cRM are equal, with NS-G&L performing slightly worse. This trend is also seen with SSN at SNRs above 0 dB. Similar results are obtained when the magnitude response is masked by an estimated IRM, with each phase estimator producing similar PESQ scores. These results also reveal that small objective speech quality improvement is sometimes obtained when these phase estimators are applied to unprocessed and IRM-enhanced magnitude responses, as seen by comparing the phase enhanced signals to unprocessed noisy speech and speech separated by an estimated IRM. This comparison indicates that separately enhancing the magnitude and phase responses would not be optimal. On the other hand, it is clear from the results that jointly estimating the real and imaginary components of the cIRM leads to PESQ improvements over the other methods across noise types and SNR conditions.
Fig. 4.
PESQ results for different methods of combining separately estimated phase and magnitude responses. Enhancement results for each noise type and SNR are plotted.
D. Listening Results
In addition to the objective results, we conducted a listening study to let human subjects compare pairs of signals. IEEE utterances are used for this task. The first part of the listening study compares complex ratio masking to ratio masking, CMF, and methods that separately enhance the magnitude and phase. The second part of the listening study compares cIRM estimation to PSM and TDR which are sensitive to phase. During the study, subjects select the signal that they prefer in terms of quality, using the preference rating approach for quality comparisons [32], [33]. For each pair of signals, the participant is instructed to select one of three options: signal A is preferred, signal B is preferred, or the qualities of the signals are approximately identical. The listeners are instructed to play each signal at least once. The preferred method is given a score of +1 and the other is given a score of −1. If the third option is selected, each method is awarded the score of 0. If the subject selects one of the first two options, then they provide an improvement score, ranging from 0 to 4 for the higher quality signal. Improvement scores of 1, 2, 3 and 4 indicate that the quality of the preferred signal is slightly better, better, largely better, and hugely better than the other signal, respectively (see [33]). In addition, if one of the signals is preferred the participant indicates the reasoning behind their selection, where they can indicate that the speech quality, noise suppression, or both helped lead them to their decision.
For the first part of the listening study, the signals and approaches are generated as described in Secs. III through IV-B, including the estimated cIRM, estimated IRM, CMF, NS-K&G, and unprocessed noisy speech. Signals processed with combinations of SSN, Factory, and Babble noise at 0 and 3 dB SNRs are assessed. The other SNR and noise combinations are not used to ensure that the processed signals are fully intelligible to listeners, since our goal is a perceptual quality assessment and not intelligibility. Each subject test consists of three phases: practice, training, and formal evaluation phase, where the practice phase familiarizes the subject with the types of signals and the training session familiarizes the subject with the evaluation process. The signals in each phase are distinct. In the formal evaluation phase, the participant performs 120 comparisons, where 30 comparisons of each of the following pairs are performed: (1) noisy speech to estimated cIRM, (2) NS-K&G to estimated cIRM, (3) estimated IRM to estimated cIRM, and (4) CMF to estimated cIRM. The 30 comparisons equate to five sets of each combination of SNR (0 and 3 dB) and noise (SSN, Factory, and Babble). The utterances used in the study are randomly selected from the test signals, and the order of presentation of pairs is randomly generated for each subject, and the listener has no prior knowledge on the algorithm used to produce a signal. The signals are presented diotically over Sennheiser HD 265 headphones using a personal computer, and each signal is normalized to have the same sound level. The subjects are seated in a sound proof room. Ten subjects (six males and four females), between the ages of 23 and 38, each with self-reported normal hearing, participated in the study. All the subjects are native English speakers and they were recruited from The Ohio State University. Each participant received a monetary incentive for participating.
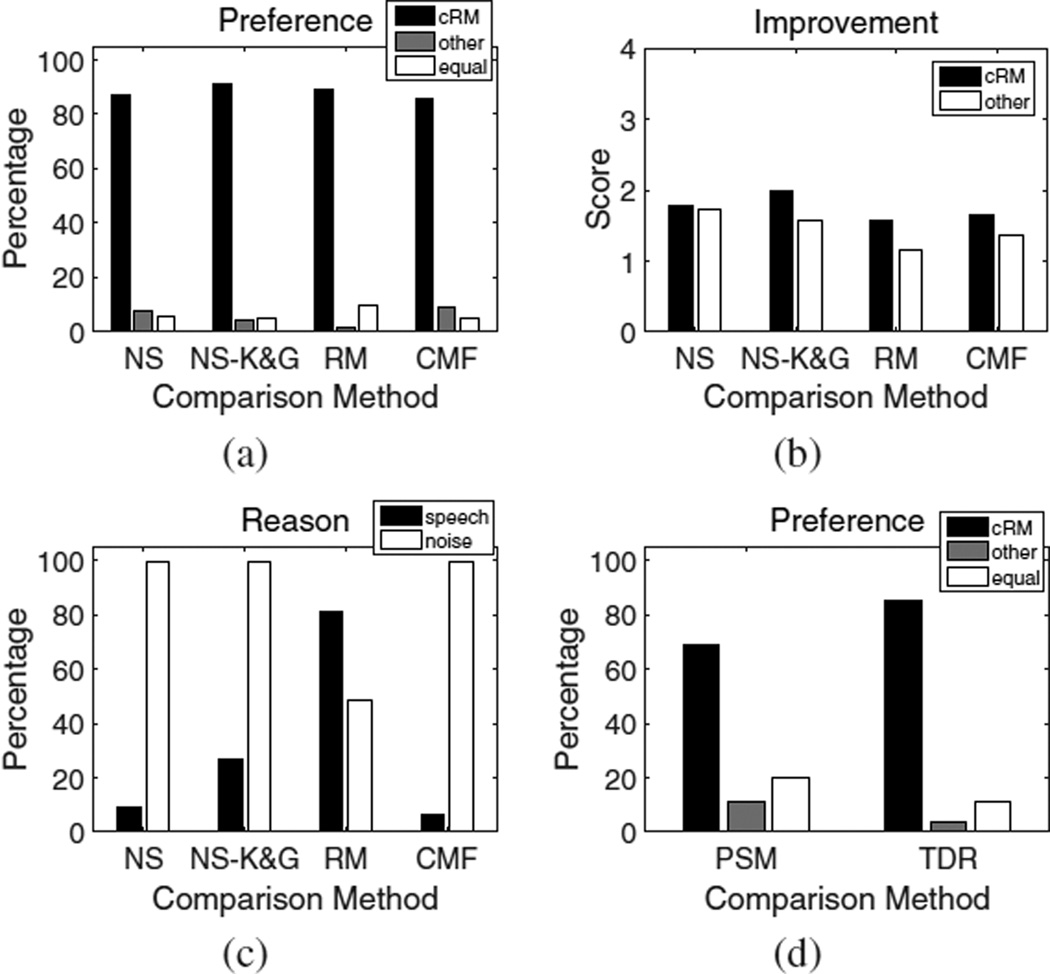
The listening study results for the first part of the listening study are displayed in Fig. 5(a)–(c). The preference scores are shown in Fig 5(a), which shows the average preference results for each pairwise comparison. When comparing the estimated cIRM to noisy speech (i.e. NS), users prefer the estimated cIRM at a rate of 87%, while the noisy speech is preferred at a rate of 7.67%. The quality of the two signals is equal at 5.33% of the time. The comparison with NS-K&G gives similar results where the cRM, NS-K&G, and equality preference rates are 91%, 4.33%, and 4.67%, respectively. The most important comparison is between the estimated cIRM and IRM, since this indicates whether complex-domain estimation is useful. For this comparison, participants prefer the estimated cIRM over the IRM at a rate of 89%, where 1.67% and 9.33% preference rates are selected for the estimated IRM and equality, respectively. The comparison between the estimated cIRM and CMF produces similar results, and the estimated cIRM, CMF, and equality have selection rates of 86%, 9%, and 5%, respectively. The improvement scores for each comparison is depicted in Fig. 5(b). This plot shows that on average, users indicate that the estimated cIRM is approximately 1.75 points better than the comparison approach, meaning that the estimated cIRM is considered better according to our improvement score scale. The reasoning results for the different comparisons are indicated in Fig. 5(c). Participants indicate that noise suppression is the main reason for their selection when the estimated cIRM is compared against NS, NS-K&G, and CMF. When the estimated cIRM is compared with the estimated IRM, users indicate that speech quality is the reason for their selection with a 81% rate and noise suppression with a 49% rate.
Fig. 5.
Listening results from the pairwise comparisons. Plots (a), (b), and (c) show the preference ratings, improvement scores, and reasoning results for the first part of the listening study, respectively. Preference results from the second part of pairwise comparisons are shown in (d).
Separate subjects were recruited for the second part of the listening study. In total, 5 native English subjects (3 females and 2 males) between the ages of 32 and 69, each with self-reported normal hearing, participated. One subject also participated in the first part of the study. cRM, TDR, and PSM signals processed with combinations of SSN, Factory, Babble, and Cafe noise at 0 dB SNRs are used during the assessment. Each participant performs 40 comparisons, where 20 comparisons are between cRM and TDR signals and 20 comparisons are between cRM and PSM signals. For each of the 20 comparisons in each of the two cases, 5 signals from each of the 4 noise types are used. The utterances were randomly selected from the test signals and the listener has no prior knowledge on the algorithm used to produce a signal. Subjects provide only signal preferences when comparing cIRM estimation to PSM and TDR estimation.
The results for the second part of the listening study are shown in Fig. 5(d). On average, cRM signals are preferred over PSM signals with a 69% preference rate, while PSM signals are preferred at a rate of 11%. Listeners feel the quality of cRM and PSM signals is identical at a rate of 20%. The preference rate and equality rates between cRM and TDR signals are 85% and 4%, respectively, and subjects prefer TDR signals over cRM signals at a 11% rate.
V. Discussion and Conclusion
An interesting question is what the appropriate training target should be when operating in the complex domain. While we have shown results with the cIRM as the training target, we have performed additional experiments with two other training targets, i.e. a direct estimation of the real and imaginary components of clean speech STFT (denoted as STFT) and an alternative definition of a complex ideal ratio mask. With the alternative definition of the cIRM, denoted as cIRMalt, the real portion of the complex mask is applied to the real portion of noisy speech STFT, and likewise for the imaginary portion. The mask and separation approach are defined below:
| (20) |
where separation is performed at each T-F unit. The data, features, target compression, and DNN structure defined in Sections III and IV are also used for the DNNs of these two targets, except for STFT where we find that compressing with the hyperbolic tangent improves PESQ scores, but it severely hurts STOI and SNRfw. The STFT training target is thus uncompressed. We also find that the noisy real and imaginary components of the complex spectra work better as features for STFT estimation. The average performance results, using IEEE utterances, over all SNRs (−6 to 6 dB, with 3 dB increment) and noise types for these targets and the estimated cIRM are shown in Table VI. The results show that there is little difference in performance between the estimated cIRM and the estimated cIRMalt, but directly estimating the real and imaginary portions of the STFT is not effective.
TABLE VI.
Comparison between different complex-domain training targets across all SNRs and noise types.
| PESQ | STOI | SNRfw | |
|---|---|---|---|
| cRM | 2.62 | 0.81 | 8.08 |
| cRMalt | 2.61 | 0.81 | 7.99 |
| STFT | 1.92 | 0.68 | 3.68 |
In this study, we have defined the complex ideal ratio mask and shown that it can be effectively estimated using a deep neural network. Both objective metrics and human subjects indicate that the estimated cIRM outperforms the estimated IRM, PSM, TDR, CMF, unprocessed noisy speech, and noisy speech processed with a recent phase enhancement approach. The improvement over the IRM and PSM is largely attributed to simultaneously enhancing the magnitude and phase response of noisy speech, by operating in the complex domain. The importance of phase has been demonstrated in [4], and our results provide further support. The results also reveal that CMF, which is an extension of NMF, suffers from the same drawbacks as NMF, which assumes that a speech model can be linearly combined to approximate the speech within noisy speech, while a noise model can be scaled to estimate the noise portion. As indicated by these results and previous studies [34], [15], this assumption does not hold well at low SNRs and with non-stationary noises. The use of phase information in CMF for performing separation is not enough to overcome this drawback. The listening study reveals that the estimated cIRM can maintain the naturalness of human speech that is present in noisy speech, while removing much of the noise.
An interesting point is when a noisy speech signal is enhanced from separately estimated magnitude and phase responses (i.e. RM-K&G, RM-G&L, and RM-cRM), the performance is not as good as joint estimation in the complex domain. Sec. IV also shows that the DNN structure for cIRM estimation generalizes to unseen SNRs and speakers.
The results also reveal somewhat of a disparity between the objective metrics and listening evaluations. While the listening evaluations indicate a clear preference for the estimated cIRM, such a preference is not as clear-cut in the quality metrics of PESQ and SNRfw (particularly the latter). This may be attributed to the nature of the objective metrics that ignores phase when computing scores [35].
To our knowledge, this is the first study employing deep learning to address speech separation in the complex domain. There will likely be room for future improvement. For example, effective features for such a task should be systematically examined and new features may need to be developed. Additionally, new activation functions in deep neural networks may need to be introduced that are more effective in the complex domain.
Acknowledgments
We would like to thank Brian King and Les Atlas for providing their CMF implementation, and Martin Krawczyk and Timo Gerkmann for providing their phase reconstruction implementation. We also thank the anonymous reviewers for their helpful suggestions. This research was supported in part by an AFOSR grant (FA9550-12-1-0130), an NIH grant (R01 DC012048), and the Ohio Supercomputer Center.
Biographies

Donald S. Williamson received the B.E.E degree in electrical engineering from the University of Delaware, Newark, in 2005 and the M.S. degree in electrical engineering from Drexel University, Philadelphia, PA, in 2007. He is currently pursuing the Ph.D. degree in computer science and engineering at The Ohio State University, Columbus. His research interests include speech separation, robust automatic speech recognition, and music processing.
Yuxuan Wang photograph and biography not available at the time of publication.
DeLiang Wang photograph and biography not available at the time of publication.
Contributor Information
Donald S. Williamson, Department of Computer Science and Engineering, The Ohio State University, Columbus, OH 43210 USA (williado@cse.ohio-state.edu).
Yuxuan Wang, Department of Computer Science and Engineering, The Ohio State University, Columbus, OH 43210 USA. He is now with Google, Inc., Mountain View, CA 94043 USA (wangyuxu@cse.ohio-state.edu).
DeLiang Wang, Department of Computer Science and Engineering and the Center for Cognitive and Brain Sciences, The Ohio State University, Columbus, OH 43210 USA (dwang@cse.ohio-state.edu).
References
- 1.Wang DL, Lim JS. The unimportance of phase in speech enhancement. IEEE Trans. Acoust. Speech Signal Process. 1982;30:679–681. [Google Scholar]
- 2.Ephraim Y, Malah D. Speech enhancement using a minimum mean-square error short-time spectral amplitude estimator. IEEE Trans. Acoust. Speech Signal Process. 1984;32:1109–1121. [Google Scholar]
- 3.Oppenheim AV, Lim JS. The importance of phase in signals. Proc. IEEE. 1981;69:529–541. [Google Scholar]
- 4.Paliwal K, Wójcicki K, Shannon B. The importance of phase in speech enhancement. Speech Commun. 2010;53:465–494. [Google Scholar]
- 5.Gunawan D, Sen D. Iterative phase estimation for the synthesis of separated sources from single-channel mixtures. IEEE Signal Process. Lett. 2010;17:421–424. [Google Scholar]
- 6.Mowlaee P, Saeidi R, Martin R. Phase estimation for signal reconstruction in single-channel speech separation. Proc. INTER-SPEECH. 2012:1–4. [Google Scholar]
- 7.Krawczyk M, Gerkmann T. STFT phase reconstruction in voiced speech for an improved single-channel speech enhancement. IEEE/ACM Trans. Audio Speech Lang Process. 2014;22:1931–1940. [Google Scholar]
- 8.Kim G, Lu Y, Hu Y, Loizou P. An algorithm that improves speech intelligibility in noise for normal-hearing listeners. J. Acoust. Soc. Am. 2009;126:1486–1494. doi: 10.1121/1.3184603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Healy EW, Yoho SE, Wang Y, Wang DL. An algorithm to improve speech recognition in noise for hearing-impaired listeners. J. Acoust. Soc. Am. 2013;134:3029–3038. doi: 10.1121/1.4820893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sugiyama K, Miyahara R. Phase randomization – a new paradigm for single-channel signal enhancement. Proc. ICASSP. 2013:7487–7491. [Google Scholar]
- 11.Wang Y, Narayanan A, Wang DL. On training targets for supervised speech separation. IEEE/ACM Trans. Audio Speech and Lang. Process. 2014;22:1849–1858. doi: 10.1109/TASLP.2014.2352935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Erdogan H, Hershey JR, Watanabe S, Roux JL. Phase-sensitive and recognition-boosted speech separation using deep recurrent neural networks. Proc. ICASSP. 2015:708–712. [Google Scholar]
- 13.Wang Y, Wang DL. A deep neural network for time-domain signal reconstruction. Proc. ICASSP. 2015:4390–4394. [Google Scholar]
- 14.Loizou PC. Speech Enhancement: Theory and Practice. Boca Raton, FL, USA: CRC; 2007. [Google Scholar]
- 15.Williamson DS, Wang Y, Wang DL. Estimating nonnegative matrix model activations with deep neural networks to increase perceptual speech quality. J. Acoust. Soc. Am. 2015;138:1399–1407. doi: 10.1121/1.4928612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang Y, Han K, Wang DL. Exploring monaural features for classification-based speech segregation. IEEE Trans. Audio Speech and Lang. Process. 2013;21:270–279. [Google Scholar]
- 17.Zhang X-L, Wang DL. Boosted deep neural networks and multi-resolution cochleagram features for voice activity detection. Proc. INTERSPEECH. 2014:1534–1538. [Google Scholar]
- 18.Caruana R. Multitask learning. Mach. Learn. 1997;28:41–75. [Google Scholar]
- 19.Glorot X, Bordes A, Bengio Y. Deep sparse rectifier neural networks. Proc. AISTATS. 2011;15:315–323. [Google Scholar]
- 20.Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2010;12:2121–2159. [Google Scholar]
- 21.IEEE. IEEE recommended practice for speech quality measurements. IEEE Trans. Audio Electroacoust. 1969;17:225–246. [Google Scholar]
- 22.Garofolo JS, Lamel LF, Fisher WM, Fiscus JG, Pallett DS, Dahlgren NL. DARPA TIMIT acoustic phonetic continuous speech corpus. 1993 Available: http://www.ldc.upenn.edu/Catalog/LDC93S1.html. [Google Scholar]
- 23.Chen C, Bilmes JA. MVA processing of speech features. IEEE Trans. Audio Speech Lang. Process. 2007;15:257–270. [Google Scholar]
- 24.Chen J, Wang Y, Wang D. A feature study for classification-based speech separation at low signal-to-noise ratios. IEEE/ACM Trans. Audio Speech Lang Process. 2014;22:2112–2121. [Google Scholar]
- 25.Parry RM, Essa I. Incorporating phase information for source separation via spectrogram factorization. Proc. ICASSP. 2007:661–664. [Google Scholar]
- 26.Kameoka H, Ono N, Kashino K, Sagayama S. Complex NMF: A new sparse representation for acoustic signals. Proc. ICASSP. 2009:3437–3440. [Google Scholar]
- 27.King B, Atlas L. Single-channel source separation using complex matrix factorization. IEEE Trans. Audio Speech Lang. Process. 2011;19:2591–2597. [Google Scholar]
- 28.Griffin DW, Lim JS. Signal estimation from modified short-time Fourier transform. IEEE Trans. Acoust. Speech Signal Process. 1984:236–243. ASSP-32. [Google Scholar]
- 29.ITU-R. Perceptual evaluation of speech quality (PESQ), an objective method for end-to-end speech quality assessment of narrowband telephone networks and speech codecs. 2001:862. [Google Scholar]
- 30.Taal CH, Hendriks RC, Heusdens R, Jensen J. An algorithm for intelligibility prediction of time frequency weighted noisy speech. IEEE Trans. Audio Speech and Lang. Process. 2011;19:2125–2136. doi: 10.1121/1.3641373. [DOI] [PubMed] [Google Scholar]
- 31.Hu Y, Loizou PC. Evaluation of objective quality measures for speech enhancement. IEEE Trans. Audio Speech Lang. Process. 2008;16:229–238. [Google Scholar]
- 32.Arehart KH, Kates JM, Anderson MC, Harvey LO. Effects of noise and distortion on speech quality judgments in normal-hearing and hearing-impaired listeners. J. Acoust. Soc. Am. 2007;122:1150–1164. doi: 10.1121/1.2754061. [DOI] [PubMed] [Google Scholar]
- 33.Koning R, Madhu N, Wouters J. Ideal time-frequency masking algorithms lead to different speech intelligibility and quality in normal-hearing and cochlear implant listeners. IEEE Trans. Biomed. Eng. 2015;62:331–341. doi: 10.1109/TBME.2014.2351854. [DOI] [PubMed] [Google Scholar]
- 34.Williamson DS, Wang Y, Wang DL. Reconstruction techniques for improving the perceptual quality of binary masked speech. J. Acoust. Soc. Am. 2014;136:892–902. doi: 10.1121/1.4884759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gaich A, Mowlaee P. On speech quality estimation of phase-aware single-channel speech enhancement. Proc. ICASSP. 2015:216–220. [Google Scholar]