Abstract
The existing missing data literature does not provide a clear prescription for estimating interaction effects with missing data, particularly when the interaction involves a pair of continuous variables. In this article, we describe maximum likelihood and multiple imputation procedures for this common analysis problem. We outline 3 latent variable model specifications for interaction analyses with missing data. These models apply procedures from the latent variable interaction literature to analyses with a single indicator per construct (e.g., a regression analysis with scale scores). We also discuss multiple imputation for interaction effects, emphasizing an approach that applies standard imputation procedures to the product of 2 raw score predictors. We thoroughly describe the process of probing interaction effects with maximum likelihood and multiple imputation. For both missing data handling techniques, we outline centering and transformation strategies that researchers can implement in popular software packages, and we use a series of real data analyses to illustrate these methods. Finally, we use computer simulations to evaluate the performance of the proposed techniques.
Keywords: missing data, maximum likelihood estimation, multiple imputation, centering, interaction effects
The last decade has seen increasing interest in “modern” missing data handling approaches that assume a missing at random (MAR) mechanism, whereby the probability of missing data on a variable y is related to other variables in the analysis model but not to the would-be values of y itself. Maximum likelihood estimation and multiple imputation are the principle MAR-based procedures in behavioral science applications, and both procedures are widely available in software packages. Although the missing data literature has grown rapidly in recent years, many practical issues remain unresolved. For example, the literature does not provide a clear prescription for estimating interaction effects with missing data. Methodologists have outlined multiple group procedures for situations where one of the interacting variables is categorical and complete (Enders, 2010; Enders & Gottschall, 2011; Graham, 2009), but missing data handling becomes more complicated when the interaction involves a pair of continuous variables. The purpose of this article is to describe maximum likelihood and multiple imputation procedures for this common analysis problem.
The structural equation model (SEM) framework is ideally suited for maximum likelihood estimation because it can accommodate incomplete predictors and outcomes. To take advantage of this flexibility, we describe three latent variable model specifications for interaction analyses with missing data. These models apply procedures from the latent variable interaction literature (e.g., Jöreskog & Yang, 1996; Kenny & Judd, 1984; Marsh, Wen, & Hau, 2004, 2006) to regression models with measured variables. We also discuss multiple imputation for interaction effects, focusing on an approach that applies standard imputation procedures (e.g., data augmentation; Schafer, 1997) to the product of two raw score predictors.
To probe interaction effects, researchers can center predictor variables prior to analysis (Aiken & West, 1991) or transform estimates to the desired simple slopes (Bauer & Curran, 2005; Hayes & Matthes, 2009; Preacher, Curran, & Bauer, 2006). Missing data can complicate the application of these familiar techniques, and popular software programs may accommodate one approach but not the other. For both missing data handling techniques, we describe the process of probing interaction effects, and we outline centering and transformation strategies that researchers can implement in popular software packages. We use a series of real data analyses to illustrate these methods.
Finally, we use computer simulations to study the performance of the missing data handling methods for interaction effects. Maximum likelihood estimation and multiple imputation invoke assumptions that are necessarily violated when the analysis model includes a product variable (e.g., multivariate normality). Previous research suggests that MAR-based methods can yield consistent estimates when normality is violated (e.g., Demirtas, Freels, & Yucel, 2008; Enders, 2001; Savalei & Bentler, 2005; Yuan, 2009; Yuan & Bentler, 2010; Yuan & Zhang, 2012), but it is unclear whether this finding extends to interaction effects.
Motivating Example
Throughout the article, we use data from Montague, Enders, and Castro's (2005) study that examined whether primary school academic achievement and teacher ratings of academic competence are predictive of middle school reading achievement. Our analyses are based on a sample of N = 74 adolescents who were identified as being at risk for developing emotional and behavioral disorders when they were in kindergarten and first grade. Table 1 gives maximum likelihood estimates of the descriptive statistics and correlations. Notice that all variables are incomplete, and the primary school reading assessment has substantial missingness.
Table 1.
Descriptive Statistics From the Reading Achievement Data (N = 74)
| Variable | 1 | 2 | 3 |
|---|---|---|---|
| 1. Primary school reading (x) | 1.00 | ||
| 2. Primary school learning problems (z) | –0.22 | 1.00 | |
| 3. Middle school reading (y) | 0.77 | –0.47 | 1.00 |
| M | 8.95 | 5.38 | 8.42 |
| SD | 1.78 | 1.16 | 1.64 |
| % missing | 67.57 | 1.35 | 16.22 |
To illustrate interaction analyses with missing data, we consider a regression model where middle school reading achievement is predicted by teacher ratings of learning problems in primary school, primary school reading achievement, and their interaction, as follows:
To make the ensuing discussion as general as possible, we henceforth define primary school reading achievement (the focal predictor) as x and primary school learning problems (the moderator) as z. Using this generic notation, the regression model is
| (1) |
where α is the intercept, γ1 and γ2 are lower order (i.e., conditional) effects, γ3 is the interaction effect, and ζ is the usual regression residual.
More than a decade ago, the American Psychological Association's Task Force on Statistical Inference warned that complete-case analyses are “among the worst methods available for practical applications” (Wilkinson and the Task Force on Statistical Inference, American Psychological Association, Science Directorate, 1999, p. 598). Because this approach is still very common in published research articles, we began by analyzing the subsample of n = 20 complete cases. The estimates were as follows: , , , . Two aspects of the complete-case analysis are worth highlighting. First, the interaction increased R2 by .065 but was not statistically significant (p = .087). Given the strong reliance on null hypothesis significance tests in the behavioral sciences (Cumming et al., 2007), we suspect that most researchers would not attempt to probe the interaction. Second, excluding incomplete cases requires the missing completely at random (MCAR) assumption, whereby the probability of missing data is unrelated to the analysis variables. However, the data provide strong evidence against the MCAR assumption; a comparison of the incomplete and complete cases revealed that students with missing primary school reading scores have significantly lower test grades in middle school, t(60) = 2.737, p = .008, d = 0.761. A large body of literature suggests that complete-case estimates are prone to substantial bias when MCAR does not hold (for a review, see Enders, 2010), so there is good reason to view these estimates with caution.
Latent Variable Formulation for a Manifest Variable Regression
A brief review of the SEM specification for manifest variable regression provides the background for understanding a latent variable interaction model for missing data. To simplify the presentation, we consider a manifest variable regression model with two predictors, x and z (i.e., Equation 1 without the interaction term). To begin, a measurement model links each manifest variable to a corresponding latent variable, as follows:
| (2) |
where τ denotes a measurement intercept, λ is a factor loading, ξx and ξz are latent exogenous variables, ηy is the latent endogenous variable, and δ and ε are residuals. Software packages typically impose three identification constraints: (a) measurement intercepts set to zero, (b) factor loadings fixed to one, and (c) residuals held equal to zero. Collectively, these constraints define latent variables as exact duplicates of their manifest variable counterparts, such that the measurement models reduce to ξx = x, ξz = z, and ηy = y. Consequently, ξ and η are not latent variables in the conventional sense but are surrogates for the manifest variables.
A latent variable regression describes the associations among the manifest variables
| (3) |
where α is a regression intercept, γ1 and γ2 are regression coefficients for ξx and ξz, respectively, and ζ is a residual. In matrix form, ξ is an N by 2 matrix of latent variable scores, ξx and ξz, and Γ is a column vector containing the two regression slopes. The one-to-one linkage between the latent and manifest variables implies that the coefficients have the same interpretation as those from a standard regression model (e.g., γ1 is the expected change in y for a one-unit increase in x, holding z constant). Consistent with standard regression models, the SEM that we consider in this article assumes that ζ follows a normal distribution with a zero mean and a residual variance ψ. The model also assumes that ξx and ξz (and thus x and z) are normally distributed with means κx and κz and a covariance matrix Φ. As we describe in the next section, this assumption is important for missing data handling.
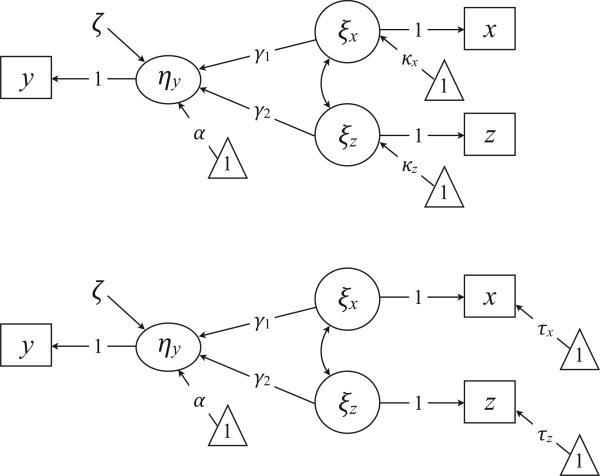
The SEM mean structure provides a mechanism for “centering” latent exogenous variables without transforming the raw data. In the default parameterization, fixing the measurement intercept to zero defines ξx as a raw score, such that κx estimates the mean of x. Alternatively, constraining the latent mean to zero and estimating the measurement intercept shifts the mean estimate to τ and defines ξx as a deviation score. Figure 1 shows the path diagrams of the two models. Notice that the models use different parameters to represent the means of x and z, but they are otherwise identical. Centering latent variables is a convenient strategy that we revisit with interaction models.
Figure 1.
Two latent variable specifications for a manifest regression model. The triangles denote a unit vector, and the directional arrows originating from the triangles represent mean structure parameters (e.g., structural regression intercept, latent mean, or measurement intercept). Parameters constrained to zero (e.g., the δ and ε residuals) are omitted from the diagrams. The top diagram represents a model with the measurement intercepts constrained to zero, and the bottom diagram is a model with the latent means constrained to zero.
Maximum Likelihood Estimation With Missing Data
The maximum likelihood estimator in SEM programs uses a log likelihood function to quantify the discrepancy between the data and the model. Assuming a multivariate normal population distribution for the manifest variables, the sample log likelihood is
| (4) |
where ki is a scaling factor that depends on the number of complete data points for case i, vi is the data vector for case i, and μi(θ) and Σi(θ) are the model-implied mean vector and covariance matrix, respectively. The key component of the log likelihood is a squared z-score (Mahalanobis distance) that quantifies the standardized difference between a participant's score vector and the corresponding model-implied means.
| (5) |
The goal of estimation is to identify the parameter values that minimize the sum of the squared z-scores (and thus maximize the sample log likelihood). The i subscript allows the size and contents of the matrices to adjust across missing data patterns, such that depends only on the parameters that correspond to the observed data for a particular case.
To illustrate the missing data log likelihood function, reconsider the latent variable regression model from the top panel of Figure 1. The relevant matrices are as follows:
where ΓΦΓ′ + ψ is the model-implied variance of y, and Φ is the covariance matrix of x and z. The standardized distance measure for cases with missing y values depends only on the x and z parameters, as follows:
Similarly, the values for cases with missing data on x and z depend only on the y parameters.
Although it is not necessarily obvious from the previous equations, basing estimation on the observed data (as opposed to excluding incomplete data records) can improve the accuracy and precision of estimates and requires the more lenient MAR assumption.
An important feature of the SEM log likelihood is that all manifest variables function as outcomes, regardless of their role in the analysis. Returning to Figure 1, notice that ξx and ξz are the predictors, and x and z are dependent variables. As a consequence, the SEM estimator assumes that the manifest variables are multivariate normal. This is in contrast to ordinary least squares regression, where predictor variables are treated as fixed (i.e., no distributional assumptions). Although the SEM requires stricter distributional assumptions, multivariate normality is important for missing data handling because it is the mechanism by which the estimator “imputes” missing values during optimization. As a practical matter, assuming multivariate normality allows for incomplete predictors and outcomes.1
A Latent Variable Interaction Model for Missing Data
The normality assumption is problematic for an interaction effect because the product of two random variables is nonnormal in shape (Craig, 1936; Lomnicki, 1967; Springer & Thompson, 1966) and because the parameters of the x and z distributions determine the parameters of xz product (Aiken & West, 1991; Bohrnstedt & Goldberger, 1969). Methodologists have developed approaches that use mixture distributions to model nonnormality from an interaction effect (e.g., latent moderated structural [LMS] equations; Kelava et al., 2011; Klein & Moosbrugger, 2000), but these models require at least two indicators per construct for identification. Consequently, we focus on three interaction models that use an incomplete product term as the sole indicator of a latent variable. These models are closely related to other product indicator models in the literature (e.g., Jöreskog & Yang, 1996; Kenny & Judd, 1984; Marsh et al., 2004, 2006), particularly that of Marsh et al. (2004).
To begin, a measurement model links each manifest variable to a corresponding latent variable. Equation 2 gives the measurement models for x, z, and y. We establish a measurement model for the xz product by multiplying the x and z equations, as follows:
Replacing the ξxξz product with a single latent variable and adding a residual term gives the measurement model for xz:
| (6) |
Consistent with the lower order predictors, xz has a loading of one on its corresponding latent variable ξxz, and the residual is fixed at zero. The product variable requires three additional constraints: (a) the intercept is held equal to the product of the x and z intercepts, (b) the cross-loading of xz on ξx is set equal to τz, and (c) the cross-loading of xz on ξz is fixed at τx.
The structural regression is the same as Equation 1 but replaces manifest variables with latent variables, as follows:
| (7) |
As before, the SEM assumes that ζ follows a normal distribution with a zero mean and a residual variance ψ. The model further assumes that the latent exogenous variables (and thus the manifest predictors) are normally distributed with a mean vector κ = [κx κz κxz] and a covariance matrix Φ. Again, the multivariate normality assumption is important for missing data handling.
The variance of a product variable is a complex function of the x and z parameters (Aiken & West, 1991; Bohrnstedt & Goldberger, 1969). Rather than imposing complicated constraints on the elements in Φ, we follow Marsh et al.'s (2004) unconstrained approach by freely estimating the covariance matrix of the predictors. This approach has four important advantages. First, the resulting model is consistent with ordinary least squares regression in the sense that the partial regression coefficients condition on the sample estimates of the variances and covariances. Second, parameter estimates should be more robust to normality violations because the necessary constraints on Φ assume that x and z have symmetric distributions (Aiken & West, 1991; Bohrnstedt & Goldberger, 1969). Third, freely estimating the latent variable covariance matrix greatly simplifies model specification and computer syntax. Finally, freeing the parameters yields a saturated model that more closely aligns with the corresponding complete-data analysis. A disadvantage of the unconstrained approach is the potential loss of power that occurs when x and z are normally distributed (Marsh et al., 2004). However, we feel that this disadvantage is trivial because manifest variables are often nonnormal.
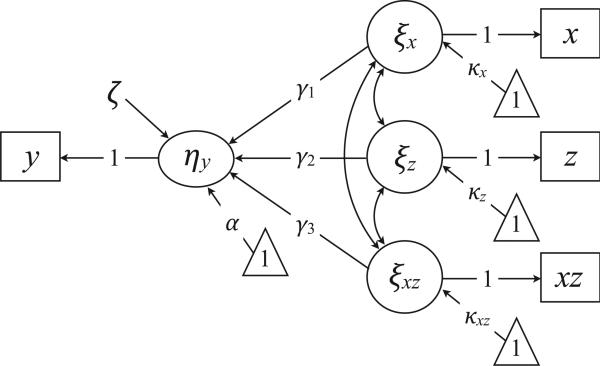
Figure 2 shows a path diagram of the latent variable interaction model. As depicted, the model is not identified because it includes a measurement intercept and a latent mean for each predictor. We subsequently describe three parameterizations of the model that impose different identification constraints on the mean structure. These constraints determine the substantive interpretation of the lower order coefficients and provide a mechanism for estimating various conditional effects (i.e., simple slopes).
Figure 2.
A latent variable interaction model. The triangles denote a unit vector, and the directional arrows originating from the triangles represent mean structure parameters (e.g., structural regression intercept, latent mean, or measurement intercept). Measurement model residuals are omitted from the diagram because these parameters are constrained to zero. As depicted, the model is not identified because it includes a measurement intercept and a latent mean for each predictor. The models that we describe in this article impose different mean structure constraints.
The Default Model
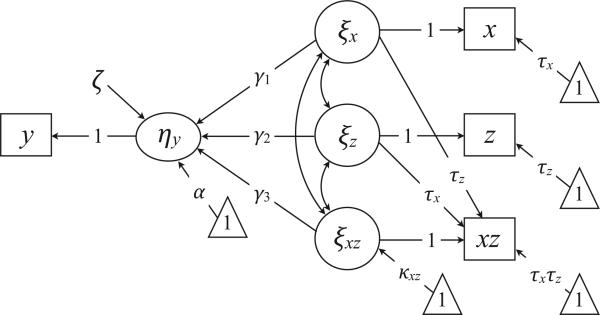
Recall from a previous section that the default specification for manifest variable regression constrains the measurement intercepts to zero and estimates the latent variable means. Fixing τx and τz to zero eliminates cross-loadings from the xz measurement model (see Equation 6), leading to the simplified path diagram in Figure 3. To highlight the free parameters, we omit parameters that are fixed at zero during estimation (i.e., cross-loadings, measurement intercepts, residuals). We henceforth refer to Figure 3 as the “default model” because SEM programs allow researchers to specify this analysis without explicitly defining latent variables or imposing parameter constraints.2
Figure 3.
The default interaction model. The triangles denote a unit vector, and the directional arrows originating from the triangles represent mean structure parameters (e.g., regression intercept or latent means). The diagram omits all parameters that are fixed at zero during estimation (i.e., cross-loadings, measurement intercepts, residuals). Constraining the measurement intercepts eliminates cross-loadings, leading to a simplified model specification.
Latent Variable Analysis 1
To illustrate an interaction analysis with missing data, we fit the default model in Figure 3 to the reading achievement data. Appendix A of the online supplemental materials gives the Mplus syntax for the analysis, and the input file is available for download at www.appliedmissingdata.com/papers. It is important to emphasize the analysis includes all 74 cases and invokes the more lenient MAR assumption whereby observed scores in the analysis model determine missingness.
The left panel of Table 2 gives selected parameter estimates and standard errors from the analysis. Because the latent variables are exact duplicates of their manifest variable counterparts, the structural regression coefficients have the same meaning as those from an ordinary least squares regression with raw score predictors. For example, the regression intercept is the expected value of y (middle school reading achievement) when both predictors equal zero. Because the model includes an interaction, the lower order regression slopes are also conditional effects. For example, is the conditional effect of x on y when z equals zero (i.e., the influence of primary school reading achievement for students with a zero score on the learning problems index), and is the conditional effect of z on y when x equals zero. The interaction effect () suggests that the association between x and y (primary and middle school reading scores, respectively) becomes more positive as z (learning problems) increases. Unlike the earlier complete-case analysis, the interaction was statistically significant (p = .037). This difference can be due to sampling variation, an increase in power, or a decrease in nonresponse bias (or a combination of the three). Although not shown in the table, the elements in κ are MAR-based estimates of the predictor variable means, and Φ contains the variances and covariances of the predictors. These parameters are not part of a standard regression model and result from assuming a normal distribution for the predictors.
Table 2.
Parameter Estimates From the Latent Variable Analyses
| Default model |
Free mean |
Constrained mean |
||||
|---|---|---|---|---|---|---|
| Effect | Estimate | SE | Estimate | SE | Estimate | SE |
| Intercept (α) | 15.858 | 5.425 | 8.483 | 0.229 | 8.517 | 0.219 |
| Primary school reading (γ1) | –0.466 | 0.549 | 0.671 | 0.092 | 0.671 | 0.092 |
| Primary school learning problems (γ2) | –2.490 | 0.996 | –0.596 | 0.158 | –0.596 | 0.158 |
| Interaction (γ3) | 0.212 | 0.101 | 0.212 | 0.101 | 0.212 | 0.101 |
Following a significant interaction, researchers typically examine the influence of the focal predictor and different values of the moderator. In this example, the lower order conditional effects are nonsensical because x and z cannot take on values of zero. Centering predictors prior to analysis (Aiken & West, 1991) or transforming estimates following the analysis (Bauer & Curran, 2005; Hayes & Matthes, 2009; Preacher et al., 2006) produce conditional effects that are interpretable within the range of the data. Because the default model does not provide a mechanism for centering latent variables, researchers would need to center the incomplete predictors (e.g., at MAR-based mean estimates) prior to estimating the model.
Transforming estimates is convenient with the default model because specialized software tools for probing complete-data interactions effects (e.g., Preacher et al., 2006) can perform the necessary computations. The simple slope for the regression of y on x (the focal predictor), conditional on a particular value of z (the moderator) is
| (8) |
and the corresponding standard error is
| (9) |
where zc is the target value of the moderator, and var( from •) and cov(•) are elements the parameter covariance matrix. Referencing the ratio of the simple slope to its standard error (i.e., a z statistic) to a standard normal distribution gives a significance test for the conditional effect.
To illustrate the transformation procedure, consider the conditional effect of x on y at the mean of z (i.e., the influence of primary school reading for a student with average learning problems). Substituting the appropriate coefficients and the mean of z into Equation 8 gives the simple slope:
As a second example, consider the conditional effect of x on y at one standard deviation above the mean of z (i.e., the influence of primary school reading for a student with substantial learning problems). The simple slope is
where the terms in parentheses define a score value at one standard deviation above the mean (the square root of is an MAR-based estimate of the z standard deviation). As a final example, the simple slope of x on y at one standard deviation below the mean of z is
The Mplus program in the online supplemental materials uses the MODEL CONSTRAINT command to compute the conditional effects and their standard errors, and specialized software tools for probing complete-data interactions effects can also perform these computations (see Preacher et al., 2006).
Interaction Models With Centered Latent Variables
Recall from an earlier section that constraining the latent means to zero and estimating the measurement intercepts defines latent variables as deviation scores, effectively “centering” the exogenous variables. Centering latent variables is convenient because it requires little effort and yields lower order effects that are interpretable within the range of the data. Moreover, the centered model provides a mechanism for estimating and testing conditional effects without the need for transformations.
For the lower order latent variables, constraining κx and κz to zero shifts the predictor means to the intercepts and defines ξx and ξz as deviation scores. Estimating τx and τz activates two cross-loadings in the xz measurement model (see Equation 6) and requires three additional constraints: (a) the influence of ξx on xz is set equal to τz, (b) the influence of ξz on xz is set equal to τx, and (c) the xz measurement intercept is fixed at the product of τx and τz. Centering ξxz is inappropriate because the mean of a product variable does not equal zero, even when the x and z means are zero. Bohrnstedt and Goldberger (1969) have shown that the expected value (i.e., mean) of a product variable equals the covariance between x and z plus the product of the x and z means, as follows:
| (10) |
Because the xz measurement intercept absorbs the product of the x and z means, Equation 10 implies that κxz should equal the covariance between x and z. Although constraining the latent mean would simplify the model, estimating κxz maintains consistency with a complete-data regression analysis in the sense that the latent variable model perfectly reproduces the sample moments. Note that κxz will not necessarily equal the covariance between ξx and ξz because the model treats κxz and φξx ξz as a unique parameters.
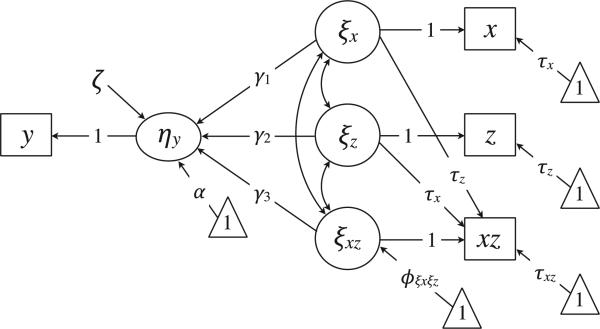
Figure 4 shows a path diagram of the interaction model with ξx and ξz in deviation score format. To highlight the free parameters, we omit parameters that are fixed at zero during estimation. We henceforth refer to Figure 4 as the “free mean model” because it treats κxz as a free parameter during estimation. Note that default and free mean models are equivalent parameterizations of the general model from Figure 2. The following algebraic transformations relate the parameters from the two models:
where the (D) and (FM) superscripts denote the default and free mean models, respectively.
Figure 4.
The free mean interaction model. The triangles denote a unit vector, and the directional arrows originating from the triangles represent mean structure parameters (e.g., regression intercept or latent means). The diagram omits all parameters that are fixed at zero during estimation (i.e., cross-loadings, measurement intercepts, residuals). The model estimates the κxz latent mean and constrains the xz measurement intercept equal to the product of τx and τz.
Latent Variable Analysis 2
To illustrate an analysis with centered latent variables, we fit the free mean model in Figure 4 to the reading achievement data. Appendix B of the online supplemental materials gives the Mplus syntax for the analysis, and the input file is available for download at www.appliedmissingdata.com/papers. The middle panel of Table 2 gives selected parameter estimates and standard errors from the analysis. Because ξx and ξz are deviation scores, the structural regression coefficients have the same meaning as those from an ordinary least squares regression with centered predictors. For example, is the conditional effect of x on y when z is at the mean (i.e., the influence of primary school reading for a student with average learning problems). Similarly, is the conditional effect of z on y when x is at its mean. Finally, the interaction effect suggests that the association between x and y (primary and middle school reading scores, respectively) becomes more positive as z (learning problems) increases. Again, note that the interaction effect is statistically significant (p = .037).
The free mean model yields lower order coefficients that are interpretable within the range of the data, and the transformations in Equations 8 and 9 can generate additional conditional effects. For example, the simple slope of x on y at one standard deviation above the mean of z (i.e., the influence of primary school reading for a student with substantial learning problems) is as follows:
Similarly, the conditional effect of x on y at one standard deviation below the mean of z is
Notice that these estimates are identical to the transformed estimates from the default model. This result is expected because the two models are equivalent (i.e., an algebraic transformation relates the two sets of parameters).
The literature recommends using meaningful values of zc (e.g., a diagnostic cutoff, the mean of a normative group) to probe interaction effects whenever possible (Cohen, Cohen, West, & Aiken, 2003, p. 269; West, Aiken, Wu, & Taylor, 2007). Because the free mean model expresses the latent predictors in deviation score format, the target value of zc should be a deviation score. A slight modification to Equation 8 gives the appropriate transformation
| (11) |
where is an MAR-based estimate of the z mean.
The Constrained Mean Model
The final latent variable model reverses the constraint on the xz mean structure by freely estimating the measurement intercept and constraining the latent mean equal to the covariance between ξx and ξz. (i.e., κxz =φξx ξz). Under this setup, the xz measurement model becomes
| (12) |
where τxz is a free intercept parameter. We henceforth refer to this as the constrained mean model because κxz is now a fixed parameter. Figure 5 shows a path diagram of the model. The free mean and constrained mean models are identical in the sense that they (a) generate the same model-implied mean vector and covariance matrix, (b) perfectly reproduce the sample moments, and (c) produce estimates with the same substantive interpretation. However, the two models do not necessarily produce the same parameter estimates.
Figure 5.
The constrained mean model. The triangles denote a unit vector, and the directional arrows originating from the triangles represent mean structure parameters (e.g., regression intercept or latent means). The diagram omits all parameters that are fixed at zero during estimation (i.e., cross-loadings, measurement intercepts, residuals). The model estimates the xz measurement intercept and constrains the κxz latent mean to the covariance between x and z (i.e., κxz =ϕξxξz).
Latent Variable Analysis 3
We fit the constrained mean model in Figure 5 to the reading achievement data. Appendix C of the online supplemental materials gives the Mplus syntax for the analysis, and the input file is available for download at www.appliedmissingdata.com/papers. The right panel of Table 2 gives selected parameter estimates and standard errors from the analysis. As seen in the table, the free mean and constrained mean models produced identical regression slopes but slightly different intercept coefficients ( vs. ). This disparity owes to differences in the latent mean estimates; the free mean model produced , whereas the constrained mean model produced . Despite the numeric differences, the two models produce identical substantive interpretations, and the process of estimating simple slopes is the same. The syntax in Appendix C of the online supplemental materials includes code to estimate the simple effect of x at one standard deviation above and below the z mean.
An Alternate Approach to Probing Interaction Effects
Throughout the analysis examples we used the transformation in Equations 8 and 9 to estimate and test simple slopes. This option is convenient with Mplus because the MODEL CONSTRAINT command can define simple slopes as additional parameters, the values of which are determined by the interaction model parameters. However, not all SEM software packages offer this functionality. Although specialized web-based software tools (Preacher et al., 2006) can also perform these computations, culling the necessary information from the computer output can be time-consuming and error-prone.
Following the centering-based approach to estimating simple slopes (Aiken & West, 1991), constraining κz (and possibly κx) to values other than zero provides a mechanism for estimating and testing conditional effects. For example, constraining κz to negative one times the square root of φξz centers ξz at a value one standard deviation above the z mean, giving a γ1 coefficient that estimates the conditional effect of x on y at a high value of z. Similarly, constraining κz to the square root of φξz centers ξz at one standard deviation below the z mean, such that γ1 estimates the simple slope of x for a low value of z. This method is flexible and can be implementing in any commercial SEM program. Appendix D of the online supplemental materials provides additional details on this approach.
Multiple Imputation
Multiple imputation is a second MAR-based procedure for treating incomplete interaction effects. Multiple imputation consists of three steps: an imputation phase, an analysis phase, and a pooling phase. The imputation phase generates multiple copies of the data set, each of which contains unique estimates of the missing values. This phase typically employs an iterative algorithm (e.g., data augmentation; Schafer, 1997) that repeatedly cycles between an imputation step (I-step) and a posterior step (P-step). The I-step uses a regression model to draw imputations from a multivariate normal distribution, and the subsequent P-step draws a new covariance matrix and mean vector from a distribution of plausible parameter values (i.e., a posterior distribution). These parameter values carry forward to the next I-step where they are the building blocks for a new regression model and new imputations. In the analysis phase, researchers use standard software to analyze each imputed data set, and the subsequent pooling phase combines the estimates and standard errors into a single set of results. Many popular software programs now provide facilities that automate this process.
Imputing Product Terms
Product terms add complexity to imputation-based missing data handling. For one, the imputation phase must incorporate the interaction effect or its subsequent estimate will be biased toward zero (Enders, 2010; Enders & Gottschall, 2011; Graham, 2009; Schafer, 1997). von Hippel (2009) investigated three possible approaches to imputing an incomplete interaction term. The impute-then-transform method fills in x, z, and y and subsequently computes the xz product from the imputed x and z values. Executing the imputation phase without the interaction attenuates the resulting point estimate because the imputations are consistent with an additive model that includes only lower order effects. The so-called passive imputation method includes xz in the imputation process but subsequently replaces it with the product of the imputed x and z values prior to analysis. Passive imputation is a variation of impute-then-transform and produces similar biases. Finally, the transform-then-impute method includes xz in the imputation process and uses the filled-in product term in the subsequent analysis phase. Because the xz imputations are drawn from a normal distribution with a unique mean and variance, the imputed values do not equal the product of the x and z imputations. Nevertheless, von Hippel showed that transform-then-impute is the only method capable of reproducing the population parameters. Consequently, we focus on this approach for the remainder of the article, and we extend von Hippel's work by outlining centering procedures and methods for probing interactive effects with multiply imputed data.
Consistent with maximum likelihood estimation, multiple imputation requires distributional assumptions for the incomplete variables, typically multivariate normality. As noted previously, product variables are at odds with this assumption. To illustrate the issue, consider the I-step for a case with missing values on x and xz. Using the covariance matrix and mean vector from the preceding P-step, the imputation algorithm estimates a regression model where z and y (the complete variables) predict x and xz (the incomplete variables). The regression parameters define a bivariate normal distribution of plausible replacement scores that is centered at a pair of predicted values and has a covariance matrix equal to the residual covariance matrix from the regression analysis. More formally, the imputations at I-step (t + 1) are drawn from the following probability distribution:
| (13) |
where and represent the imputations, θ(t) denotes the parameters from the preceding P-step, ~ N is the bivariate normal distribution, X contains the complete predictors (z, y, and a unit vector for the intercept), β(t) is a matrix of regression coefficients, and is the residual covariance matrix. Drawing imputations from Equation 13 is potentially problematic because a product variable is nonnormal in shape and because the regression parameters do not explicitly model the deterministic features of the xz distribution. Whether these issues pose a problem for the resulting parameter estimates is an open question that we investigate later in the article.
Multiple Imputation Analysis 1
To illustrate a multiple imputation analysis, we applied Schafer's (1997) data augmentation algorithm to the reading achievement data. To begin, we used the MI procedure in SAS to generate 50 imputed data sets. Following the transform-then-impute approach (von Hippel, 2009), the imputation phase included the product of primary school reading scores and learning problems ratings. Although researchers often center predictors prior to computing the product term, we used raw score variables for the analysis. After generating the imputations, we used the REG procedure to fit the model from Equation 1 to each data set, and we subsequently used the MIANALYZE procedure to pool the estimates and standard errors. Appendix E of the online supplemental materials gives the SAS syntax for the analysis, and the input file is available for download at www.appliedmissingdata.com/papers.
The left panel of Table 3 gives selected parameter estimates and standard errors from the analysis. Because imputation is on the raw score metric, the regression coefficients have the same meaning as those from an ordinary least squares regression with raw score predictors. For example, is the conditional effect of x on y when z equals zero (i.e., the influence of primary school reading scores for students with a zero score on the learning problems index), and is the conditional effect of z on y when x equals zero. The interaction effect () suggests that the association between x and y (primary and middle school reading scores, respectively) becomes more positive as z (learning problems) increases. Unlike the earlier complete-case analysis, the interaction was statistically significant (p = .025). This difference owes to an increase in power, a decrease in nonresponse bias, or both.
Table 3.
Parameter Estimates From the Multiple Imputation Analyses
| Raw score |
Free mean |
Constrained mean |
||||
|---|---|---|---|---|---|---|
| Effect | Estimate | SE | Estimate | SE | Estimate | SE |
| Intercept (α) | 16.942 | 5.069 | 8.498 | 0.158 | 8.519 | 0.135 |
| Primary school reading (γ1) | –0.569 | 0.503 | 0.630 | 0.105 | 0.630 | 0.105 |
| Primary school learning problems (γ2) | –2.615 | 0.922 | –0.623 | 0.163 | –0.623 | 0.163 |
| Interaction (γ3) | 0.223 | 0.092 | 0.223 | 0.092 | 0.223 | 0.092 |
Consistent with the latent variable model, researchers can use centering or transformations to probe the interaction effect. We describe the transformation procedure here and take up centering in the next section. Following Rubin's (1987) pooling rules, the multiple imputation estimate of a simple slope is the arithmetic average of the conditional effects from the m data sets, as follows:
| (14) |
We omit the pooling equations for the standard error because we anticipate that most researchers will not perform the computations by hand.
To illustrate the transformation procedure, we computed the conditional effect of x on y at the mean of z (i.e., the influence of primary school reading for a student with average learning problems). Substituting the appropriate coefficients and the mean of z into Equation 14 gives the simple slope:
As a second example, consider the conditional effect of x on y at one standard deviation above the mean of z (i.e., the influence of primary school reading for a student with substantial learning problems). The simple slope is
Finally, the simple slope at one standard deviation below the mean is
Note that these estimates are quite similar to those from the latent variable analyses.
Post-Imputation Centering
The transformation approach to probing an interaction effect is difficult to implement without flexible pooling software (e.g., the SPSS pooling facility does not accommodate the procedure). In a complete-data analysis, centering provides an alternate mechanism for implementing the pick-a-point approach to estimating simple slopes (Aiken & West, 1991). For example, if a researcher wants to compute the simple slope of y on x at zc, the steps are as follows: (a) center z at zc, (b) compute the xz product term, and (c) estimate the regression model. This process defines γ1 as the conditional influence of x on y at zc. Because the imputation phase must include the product variable, performing steps (a) and (b) prior to imputation is a natural choice. This sequence works well when zc does not depend on the data (e.g., zc is a clinically meaningful score value).
In the absence of meaningful cutoffs, researchers often examine conditional effects at different points in the z distribution. In this situation, centering prior to imputation is unwieldy because it requires new imputations for each simple slope. To avoid this problem, we developed a post-imputation centering approach that consists of the following steps: (a) compute the xz product by multiplying the raw x and z variables, (b) perform imputation, (c) rescale the predictor variables and the product term to deviation score format, (d) estimate the regression model, and (e) pool the estimates and standard errors. This procedure can generate any number of conditional effects from a single collection of imputed data sets. Further, the procedure is easy to implement in general-use software packages such as SPSS and SAS. The reminder of this section describes the rescaling procedure for step (c).
The centering expressions for lower order predictors are
| (15) |
where and are the centered variables from data set i, x(i) and z(i) are the corresponding raw scores, and and are the centering constants that correspond to the desired conditional effects. The centering expression for the interaction is based on the algebraic expansion of the product of two deviation scores
where subtracting the collection of terms in brackets converts the raw score product to a metric that is consistent the lower order predictors. Applying this idea to multiple imputation gives the following centering expression the product variable:
| (16) |
It is important to emphasize that xz(i) is the imputed product term rather than the product of the imputed x and z variables.
Multiple Imputation Analysis 2
To illustrate post-imputation centering, we reanalyzed the imputed data sets from the previous analysis example. To provide a comparison to the centered latent variable models, we began by using Equations 15 and 16 to rescale the imputations to a centered solution where x and z are deviations from the mean (i.e., and ). Appendix F of the online supplemental materials gives the SAS and SPSS syntax for the analysis, and the input files are available at www.appliedmissingdata.com/papers.
The middle panel of Table 3 gives selected parameter estimates and standard errors from the analysis. The regression coefficients have the same meaning as those from an ordinary least squares regression with centered predictors. For example, is the conditional effect of x on y when z is at the mean (i.e., the influence of primary school reading for a student with average learning problems), and is the conditional effect of z on y when x is at its mean. Finally, the interaction effect () suggests that the association between x and y (elementary and high school reading scores, respectively) becomes more positive as z (learning problems) increases.
Next, we rescaled the predictors to obtain the conditional effect of x on y at one standard deviation above mean of z (i.e., the influence of primary school reading for a student with substantial learning problems). To estimate this simple slope, we used to rescale z and xz and reanalyzed the data. The resulting estimate was . Finally, repeating this process using gives the simple slope at one standard deviation below the mean of z, the estimate of which was . Notice that post-imputation centering and transformation (Equation 14) produced identical estimates of the conditional effects (standard errors were also the same). At an intuitive level, the two procedures should be equivalent because the use the same imputations and the same values of and . Recall that, in the latent variable framework, the default and free mean models were similarly equivalent.
Constrained Mean Centering
In the SEM framework, we described two centered models that use a latent variable (ξxz) to represent the deviation score version of xz. In the context of multiple imputation, each is essentially a different realization of ξxz, and the mean of is analogous to the κxz latent mean from the centered models. These linkages suggest a modification to post-imputation centering that parallels the difference between the free mean and constrained mean latent variable models.
Returning to Equation 10, notice that the expected value (i.e., mean) of a deviation score product equals the covariance between x and z. In the latent variable framework, the κxz latent mean can be freely estimated (the free mean model) or held equal to this covariance (the constrained mean model). The centering expression from Equation 16 is consistent with free mean model in the sense that is not constrained to a particular value and captures the portion of the xz mean that remains after subtracting out the product of the x and z means. For this reason, we henceforth refer to Equation 16 as free mean centering. We modified post-imputation centering by subtracting the estimate of the product variable mean and replacing it with the components of the expected value expression in Equation 10, as follows:
| (17) |
Although not obvious from the equation, the bracketed terms implement a “constraint” that forces equal to the covariance between x and z in data set i. In line with our previous terminology, we henceforth refer to Equation 17 as constrained mean centering.
Multiple Imputation Analysis 3
To illustrate constrained mean centering, we reanalyzed the imputed data sets from the previous analysis examples. To provide a comparison to the previous analyses, we used Equations 15 and 17 to rescale the imputations to a centered solution where x and z are deviations from the mean (i.e., and ). Appendix G of the online supplemental materials gives the SAS and SPSS syntax for the analysis, and the input files are available at www.appliedmissingdata.com/papers. As seen in right panel of Table 3, free mean and constrained mean centering produced identical regression slopes but slightly different intercept coefficients ( vs. ). This disparity owes to the fact that the analyses produced different estimates of the product term mean; free mean centering produced , whereas the constrained mean estimate was . Despite these numeric differences, the choice of centering approach does not affect the substantive interpretation of the estimates, and it does not alter the process of probing simple slopes. Appendix G of the online supplemental materials includes code to estimate the simple effect of x at one standard deviation above and below the z mean.
Simulation Studies
We used Monte Carlo computer simulations to evaluate the performance of the maximum likelihood estimation and multiple imputation. Although there is no reason to expect differences between the two approaches, we know of no published simulations that have investigated the issue of incomplete interactive effects. Previous research suggests that MAR-based methods can yield consistent estimates when normality is violated (e.g., Demirtas et al., 2008; Enders, 2001; Savalei & Bentler, 2005; Yuan, 2009; Yuan & Bentler, 2010; Yuan & Zhang, 2012), but it is unclear whether this finding extends to interactions. Further, von Hippel's (2009) analytic work has limited generalizability because it examined imputation from a known (rather than estimated) population covariance matrix. The simulation syntax is available upon request.
The regression model from Equation 1 served as the data-generating population model for the simulations. Because we did not expect the manipulated factors to exert complicated non-linear effects, we chose to minimize the complexity of the design while still examining a range of conditions that encompasses the variety of substantive research applications. Specifically, we introduced three distribution shapes for x and z (normal, kurtotic, skewed and kurtotic), three interaction effect size values (zero, small, and large increment in R2), four sample size conditions (Ns between 50 and 5,000), two missing data mechanisms (MCAR and MAR), and four missing data handling methods (the free and constrained mean latent variable models, and multiple imputation with free and constrained mean centering). Note that we chose not to manipulate the missing data rate because this factor tends to produce predictable and uninteresting findings (e.g., as the missing data rate increases, so do the negative consequences of missing data). Rather, we imposed a constant 20% missing data rate on one of the predictors (and thus the interaction). We chose this rather extreme value because we felt that it would clearly expose any problems with the missing data handling approaches. The remainder of this section describes the simulation conditions in more detail.
Sample Size
We implemented four sample size conditions, N = 50, 200, 400, and 5,000. In Jaccard and Wan's (1995) review of published multiple regression applications, the 75th percentile of the sample size distribution was approximately 400, and the median value was roughly 175. Consequently, we believe that our sample size conditions are fairly representative of published research studies, particularly in the field of psychology. We implemented the N = 5,000 condition to study the large-sample properties of the missing data methods.
Distribution Shape
Because behavioral science data rarely satisfy multivariate normality (Micceri, 1989), we varied the distribution of the lower order predictors. We opted to investigate three distributional conditions (normal, kurtotic-only, skewed and kurtotic). In the normal distribution condition, both x and z had skewness and excess kurtosis values of zero. The kurtosis-only condition had skewness and kurtosis values equal to 0 and 4, respectively, and the skewed condition had skewness and kurtosis values of 2 and 6, respectively. Previous simulation studies have characterized the latter values as relatively extreme (Curran, West, & Finch, 1996). We used Fleishman's power method (Fleishman, 1978; Vale & Maurelli, 1983) to impose the desired distribution shapes for x and z. The power method tends to produce skewness and kurtosis estimates that are less extreme than the target values, particularly at smaller sample sizes. Our simulation checks indicated that skewness and kurtosis estimates were substantially lower than the target values in the N = 50 condition and improved as sample size increased. This trend is consistent with our previous experiences with this approach (e.g., Enders, 2001).
Population Parameters and Data Generation
Table 4 summarizes the data generation parameters. For all simulations, we arbitrarily set the predictor means to μx = 12 and μz = 25, respectively, and we fixed the predictor variances to . For simplicity, we fixed the correlation between x and z at ρx·z = .30, corresponding with Cohen's definition of a medium effect size (Cohen, 1988). Again, we did not manipulate the mean and the variance of the product term because x and z determine these parameters.
Table 4.
Population Parameters for the Simulation Studies
| Symmetric x and z |
Skewed x and z |
|||
|---|---|---|---|---|
| Parameter | ||||
| α | 5.000 | 5.000 | 5.000 | 5.000 |
| γ1 = γ2 | 5.000 | 5.000 | 5.000 | 5.000 |
| γ 3 | 0.705 | 1.576 | 0.642 | 1.628 |
| 598.000 | 563.333 | 714.000 | 859.000 | |
Note. The symmetric columns include the normal and kurtosis-only conditions.
Because the interaction effect was our primary focus, we implemented three effect size increments for this variable (, and .05). To begin, we arbitrarily chose to have the lower order terms explain 30% of the variance when the interaction term was omitted from the model. For simplicity, we imposed equality constraints on the lower order regression slopes, such that γ1 = γ2 = 5. We arbitrarily set the intercept coefficient to the same value. For the non-zero effect size conditions, we specified a γ3 coefficient and a residual variance that incremented the total R2 by either .01 or .05. Chaplin (1991) reviewed the literature and found that interactions in field studies typically account for one to three percent of the variance in the outcome. Thus, , represents a relatively small interaction effect, and , represents a large effect. Methodological reviews also suggest that the total R2 values from our simulations are representative of interaction effects from published research studies (Jaccard & Wan, 1995).
Our method for deriving the population value for the interaction coefficient warrants a brief discussion. As explained previously, the x and z distributions determine the distribution of the product. When x and z are symmetrically distributed (as in the normal and the kurtosis-only conditions), well-known expressions define the covariance between x (or z) and the xz product (Aiken & West, 1991, pp. 180–181; Bohrnstedt & Goldberger, 1969). Consequently, the value of γ3 is fully determined after specifying the effect size and the other regression model parameters. However, when one or both of the component distributions is asymmetric (e.g., the nonnormal condition with non-zero skewness), it is no longer possible to analytically derive γ3 because the covariances between the lower order terms and the product term are a complex function of skewness. Consequently, we implemented a simulation that iteratively auditioned values for the interaction coefficient in the skewed condition (N = 1,000,000 in each artificial data set). We saved the coefficients and the R2 values from this simulation and subsequently chose the γ3 value that produced the desired increment in R2.
After specifying the population parameters, we used the IML procedure in SAS 9.2 (SAS Institute, 2008) to generate 2,000 artificial data sets within each between-subjects design cell. The data generation procedure utilized the following steps. First, we generated the predictor variable scores from a standard normal distribution with a mean of zero and a variance of one. Second, we imposed the desired variances and covariance on x and z. Third, we used the Fleishman's (1978) power method to introduce skewness and kurtosis. Fourth, we generated the interaction term by multiplying x and z. Fifth, we generated a vector of residual terms from a normal distribution with a mean of zero and a variance equal to the residual variance from the population regression model. Sixth, we generated the y values by substituting the variables from previous steps into the population regression model. The preceding steps produced artificial data sets with predictors in deviation score format. In the final step, we imposed a mean structure by adding the desired means to x and z and recomputing the interaction term.
Missing Data Mechanisms
We implemented two missing data mechanisms: MCAR and MAR. In the MCAR condition, we generated a vector of uniform random numbers and subsequently deleted x (and thus xz) scores for cases in the lower quintile of the random number distribution. In the MAR condition, the probability of missing data was related to the values of z. We first divided the z distribution into quintiles and then used a uniform random number to randomly delete 75% of the x values from within the first (i.e., lowest) z quintile, 15% of the x values from within the second z quintile, and 10% of the x values from within the third z quintile (i.e., the probability of missingness is highest for low values of z). To explore the impact of missingness in the long tail of the skewed distribution, we used a similar procedure to delete x for high values of z. Because there was no reason to believe that the pattern of missingness would matter in the symmetric distribution conditions, we reversed the missingness probabilities only in skewed design cells with an MAR mechanism. The MCAR and MAR deletion mechanisms produced a 20% missing data rate on x and xz. Although there is no way to speak to the generalizability of our deletion mechanism, the lack of previous research provides a rationale for studying an ideal situation where the cause of missingness is part of the analysis model. Further, a mechanism where missingness is a function of an observed predictor variable is optimal for complete-case analysis, a method that we use to benchmark the performance of maximum likelihood and multiple imputation. Finally, as noted previously, we chose not to manipulate the missing data rate because this factor tends to produce predictable results. Instead, we chose a single missing data rate and a selection mechanism that we felt was extreme enough to expose potential problems.
Missing Data Handling
For each replication, we used Mplus to estimate the free mean and constrained mean interaction models (we did not include the default model because it is equivalent to the free mean model). Note that we used normal-theory (as opposed to robust) standard errors for all analyses because we believed that most substantive researchers would choose this option when implementing multiple imputation in SAS or SPSS. This ensured that the maximum likelihood and multiple imputation analyses invoked comparable assumptions.
We used the MI procedure in SAS to generate 20 imputed data sets for each replication. The imputation phase included the four analysis variables, all of which were in raw score format. After exploring the convergence behavior of data augmentation in a number of test data sets, we implemented a single data augmentation chain with 300 burn-in iterations and 300 between-imputation iterations (i.e., the first imputed data file was saved after 300 computational cycles and subsequent data sets were saved every 300 iterations thereafter). Prior to analyzing the filled-in data sets, we centered the lower order predictors at their means and rescaled the interaction using free mean and constrained mean centering (Equations 16 and 17, respectively). Finally, we used the REG to estimate the regression model and used the MIANALYZE procedure to combine the resulting estimates and their standard errors.
A large body of methodological literature has discounted complete-case analyses and other ad hoc missing data handling approaches (for a review, see Enders, 2010). Although deletion is generally a bad idea, complete-case analysis is known to produce valid estimates in regression models where missingness on a predictor depends on the observed values of another predictor (Little, 1992). Consequently, we included this approach in our simulations because it provides a useful benchmark for evaluating maximum likelihood and multiple imputation, and because it approach is still very common in published research articles.
Outcome Variables
For the zero effect size conditions, we examined the Type I error rates for the interaction coefficient. For the non-zero effect size conditions, we examined standardized bias, mean squared error, and confidence interval coverage. We computed standardized bias by dividing raw bias (the difference between an average estimate and the population parameter) by the standard deviation (i.e., empirical standard error) of the complete-data estimates within a particular design cell. This metric expresses bias in standard error units (Collins, Schafer, & Kam, 2001). We augmented standardized bias with the mean squared error (i.e., the average squared difference between an estimate and the population parameter). Because the mean squared error is the sum of sampling variance and squared bias, it quantifies the overall accuracy of an estimate.
Finally, we assessed confidence interval coverage by computing the proportion of replications where the 95% confidence interval contained the true population parameter. If parameter estimates and standard errors are accurate, confidence interval coverage for a .05 alpha level should equal 95%. In contrast, if the standard errors are too small, confidence intervals will not capture the population parameter as frequently as they should, and coverage rates will drop below 95%. From a practical standpoint, coverage provides a benchmark for assessing the accuracy of the standard error estimates because it directly related to Type I error inflation (e.g., a 90% coverage value suggests a twofold increase in Type I errors, an 85% coverage value reflects a threefold increase, and so on).
Results
To begin, we examined the design cells where the population interaction equaled zero (i.e., the analysis model included an interaction effect when the population model did not). The primary concern was whether γ3 exhibited excessive Type I errors. In the N = 50 condition, maximum likelihood estimation produced slightly elevated Type I error rates (e.g., values close to .07 were typical), but values were otherwise quite close to the nominal .05 rate. This was true for MCAR and MAR mechanisms. Turning to confidence interval coverage, all methods produced accurate coverage values for γ1 and γ2. Complete-case analysis and multiple imputation produced somewhat lower coverage rates for the intercept coefficient, with most values ranging between .90 and .92. In the MAR simulation, complete-case analysis produced coverage values as low as .50 in the large sample condition. Maximum likelihood produced error rates close to the nominal level.
Parameter Recovery
Next, we examined parameter recovery in the design cells where the population interaction was non-zero. To examine the quality of the data generation, we examined raw and standard bias of the complete-data estimates. As expected, these estimates exhibited no systematic biases.
Estimates were uniformly accurate in the MCAR conditions; across all design cells and all missing data handling methods, the largest standardized bias value was approximately .06 (6% of a complete-data standard error unit), and the average standardized bias value was .002. This result is consistent with previous research and statistical theory (Rubin, 1976). Mean squared error (MSE) values from the MCAR simulations generally favored the MAR-based analyses, particularly when the interaction effect was small in magnitude. For the α and γ2 coefficients (the regression intercept and the slope of the complete predictor, respectively), the complete-case MSE values were typically 15%–20% larger than those of the maximum likelihood and multiple imputation. Because MSE is inversely related to sample size, these differences indicate that a 15%–20% increase in the complete-case sample size is needed to achieve the same precision as an MAR-based approach. The complete-case MSE values for γ1 (the incomplete predictor) were typically 5% larger, and MSE values for the interaction effect were virtually identical across methods. In the nonnormal conditions with a large interaction effect, MSE differences were less pronounced but still favored MAR-based estimation (e.g., the complete-case MSE values for the γ2 coefficient was typically 5% larger than maximum likelihood and multiple imputation). Table 5 uses MSE ratios from the N = 200 condition to illustrate these trends. The MSE ratio is the fraction of the missing data MSE to the complete-data MSE, such that values closer to unity denote better overall accuracy (e.g., a ratio of 1.20 indicates that the MSE for a missing data handling approach is 20% larger than that of the complete-data estimator). As seen in the table, the MSE ratios for the MAR-based approaches were virtually always lower than those of complete-case analysis, which owes to the fact that maximum likelihood and multiple imputation have less sampling variation.
Table 5.
Mean Squared Error (MSE) Ratios: MCAR Mechanism and N = 200
| Small interaction effect |
Large interaction effect |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Distribution | Parameter | CCA | FMLV | CMLV | FMC | CMC | CCA | FMLV | CMLV | FMC | CMC |
| Normal | α | 1.21 | 1.02 | 1.01 | 1.01 | 1.01 | 1.20 | 1.01 | 1.00 | 1.01 | 1.01 |
| γ 1 | 1.27 | 1.21 | 1.21 | 1.21 | 1.21 | 1.24 | 1.19 | 1.19 | 1.19 | 1.19 | |
| γ 2 | 1.29 | 1.08 | 1.08 | 1.08 | 1.08 | 1.30 | 1.11 | 1.11 | 1.12 | 1.12 | |
| γ 3 | 1.26 | 1.27 | 1.27 | 1.27 | 1.27 | 1.23 | 1.23 | 1.23 | 1.23 | 1.23 | |
| Skewed | α | 1.27 | 1.02 | 1.02 | 1.02 | 1.02 | 1.26 | 1.03 | 1.04 | 1.03 | 1.04 |
| γ 1 | 1.32 | 1.29 | 1.29 | 1.30 | 1.30 | 1.29 | 1.29 | 1.29 | 1.28 | 1.28 | |
| γ 2 | 1.29 | 1.13 | 1.13 | 1.14 | 1.14 | 1.33 | 1.22 | 1.22 | 1.22 | 1.22 | |
| γ 3 | 1.34 | 1.35 | 1.35 | 1.36 | 1.36 | 1.29 | 1.32 | 1.32 | 1.31 | 1.31 | |
| Kurtotic | α | 1.25 | 1.02 | 1.02 | 1.01 | 1.02 | 1.22 | 1.01 | 1.01 | 1.01 | 1.01 |
| γ 1 | 1.27 | 1.24 | 1.24 | 1.23 | 1.23 | 1.24 | 1.21 | 1.21 | 1.21 | 1.21 | |
| γ 2 | 1.30 | 1.09 | 1.09 | 1.09 | 1.09 | 1.27 | 1.17 | 1.17 | 1.17 | 1.17 | |
| γ 3 | 1.33 | 1.34 | 1.34 | 1.33 | 1.33 | 1.26 | 1.27 | 1.27 | 1.27 | 1.27 | |
Note. Ratio of missing data MSE to complete-data MSE. The x and xz variables (γ1 and γ3, respectively) have 20% missing data. MCAR = missing completely at random; CCA = complete-case analysis; FMLV = free mean latent variable model; CMLV = constrained mean latent variable model; FMC = free mean centering; CMC = constrained mean centering.
Turning to the MAR mechanism, the combination of effect size and distribution shape had a complex influence on parameter recovery. Table 6 uses standardized bias values from the N = 200 condition to illustrate these results. Following Collins et al. (2001), we highlight bias values that exceed .40 (i.e., 40% of a complete-data standard error unit) in absolute value. As seen in the table, complete-case analysis produced severely biased estimates of the intercept coefficient. In the large effect size conditions, the γ1 coefficient (the slope of the incomplete predictor) also exhibited substantial biases. The MAR-based approaches also produced estimates with bias values exceeding .40, but the nature of this bias was somewhat idiosyncratic and dependent on distribution shape (e.g., symmetric distributions produced bias in the γ2 coefficient, whereas the positively skewed distribution with missingness in the upper tail produced bias in γ1).
Table 6.
Standardized Bias: MAR Mechanism and N = 200
| Small interaction effect |
Large interaction effect |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Distribution | Parameter | CCA | FMLV | CMLV | FMC | CMC | CCA | FMLV | CMLV | FMC | CMC |
| Normal | α | 1.72 | 0.16 | 0.04 | 0.16 | 0.04 | 1.82 | 0.29 | 0.05 | 0.29 | 0.04 |
| γ 1 | 0.40 | –0.06 | –0.06 | –0.08 | –0.08 | 0.94 | –0.12 | –0.12 | –0.14 | –0.14 | |
| γ 2 | 0.15 | –0.20 | –0.20 | –0.19 | –0.19 | 0.30 | –0.44 | –0.44 | –0.43 | –0.43 | |
| γ 3 | –0.05 | –0.07 | –0.07 | –0.08 | –0.08 | 0.02 | –0.06 | –0.06 | –0.07 | –0.07 | |
| Skewed (lower tail missing) | α | 1.19 | 0.11 | 0.03 | 0.11 | 0.03 | 1.14 | 0.25 | 0.08 | 0.25 | 0.08 |
| γ 1 | 0.29 | –0.02 | –0.02 | –0.05 | –0.05 | 0.52 | –0.10 | –0.10 | –0.12 | –0.12 | |
| γ 2 | 0.10 | 0.06 | 0.06 | 0.07 | 0.07 | 0.17 | 0.00 | 0.00 | 0.01 | 0.01 | |
| γ 3 | –0.03 | –0.06 | –0.06 | –0.06 | –0.06 | –0.02 | –0.11 | –0.11 | –0.12 | –0.12 | |
| Skewed (upper tail missing) | α | –1.70 | 0.03 | –0.07 | 0.04 | –0.07 | –1.54 | 0.05 | –0.23 | 0.05 | –0.23 |
| γ 1 | –0.31 | 0.26 | 0.26 | 0.23 | 0.23 | –0.81 | 0.42 | 0.42 | 0.38 | 0.38 | |
| γ 2 | –0.13 | –0.02 | –0.02 | 0.00 | 0.00 | –0.26 | 0.21 | 0.21 | 0.22 | 0.22 | |
| γ 3 | 0.01 | 0.07 | 0.07 | 0.06 | 0.06 | –0.03 | 0.30 | 0.30 | 0.27 | 0.27 | |
| Kurtotic | α | 1.66 | 0.18 | 0.03 | 0.18 | 0.03 | 1.69 | 0.36 | 0.10 | 0.36 | 0.10 |
| γ 1 | 0.39 | –0.07 | –0.07 | –0.09 | –0.09 | 0.87 | –0.07 | –0.07 | –0.09 | –0.09 | |
| γ 2 | 0.10 | –0.34 | –0.34 | –0.33 | –0.33 | 0.25 | –0.59 | – 0.59 | –0.57 | –0.57 | |
| γ 3 | 0.01 | –0.01 | –0.01 | –0.02 | –0.02 | –0.04 | –0.10 | –0.10 | –0.11 | –0.11 | |
Note. Bold typeface denotes bias that exceeds .40 of a complete-data standard error unit. The x and xz variables (γ1 and γ3, respectively) have 20% missing data. MAR = missing at random; CCA = complete-case analysis; FMLV = free mean latent variable model; CMLV = constrained mean latent variable model; FMC = free mean centering; CMC = constrained mean centering.
Table 7 presents the corresponding MSE ratios from the N = 200 condition. Recall that MSE ratios reflect the fraction of the missing data MSE to the complete-data MSE, such that values closer to unity reflect greater overall accuracy. As seen in the table, the MSE ratios generally favored MAR-based estimation (i.e., MSE ratios were lower for these approaches), even for coefficients with larger bias values in Table 6 (e.g., the γ2 estimate from the kurtotic condition). It is interesting that the complete-case estimates of γ3 were somewhat more accurate in the positively skewed condition with missingness in the upper tail. Because this parameter exhibited minimal bias (see Table 6), the accuracy advantage is largely due to a smaller sampling variance. The same finding holds for γ1 coefficient, but only in the small effect size condition. The table uses bold typeface to highlight MSE ratios that favor complete-case analysis.
Table 7.
Mean Squared Error (MSE) Ratios: MAR Mechanism and N = 200
| Small interaction effect |
Large interaction effect |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Distribution | Parameter | CCA | FMLV | CMLV | FMC | CMC | CCA | FMLV | CMLV | FMC | CMC |
| Normal | α | 4.23 | 1.01 | 1.04 | 1.01 | 1.04 | 4.65 | 1.12 | 1.07 | 1.12 | 1.07 |
| γ 1 | 1.39 | 1.22 | 1.22 | 1.22 | 1.22 | 2.11 | 1.25 | 1.25 | 1.26 | 1.26 | |
| γ 2 | 1.66 | 1.17 | 1.17 | 1.18 | 1.18 | 1.72 | 1.36 | 1.36 | 1.36 | 1.36 | |
| γ 3 | 1.73 | 1.69 | 1.69 | 1.68 | 1.68 | 1.76 | 1.67 | 1.67 | 1.68 | 1.68 | |
| Skewed (lower tail missing) | α | 2.74 | 1.02 | 1.01 | 1.02 | 1.01 | 2.63 | 1.08 | 1.02 | 1.08 | 1.02 |
| γ 1 | 1.23 | 1.19 | 1.19 | 1.20 | 1.20 | 1.41 | 1.18 | 1.18 | 1.18 | 1.18 | |
| γ 2 | 1.18 | 1.05 | 1.05 | 1.06 | 1.06 | 1.21 | 1.05 | 1.05 | 1.05 | 1.05 | |
| γ 3 | 1.21 | 1.18 | 1.18 | 1.18 | 1.18 | 1.21 | 1.16 | 1.16 | 1.15 | 1.15 | |
| Skewed (upper tail missing) | γ | 4.07 | 1.11 | 1.25 | 1.11 | 1.26 | 3.48 | 1.24 | 1.39 | 1.24 | 1.40 |
| γ 1 | 1.52 | 1.70 | 1.70 | 1.69 | 1.69 | 2.02 | 1.93 | 1.93 | 1.90 | 1.90 | |
| γ 2 | 2.63 | 1.73 | 1.73 | 1.73 | 1.73 | 2.76 | 2.60 | 2.60 | 2.58 | 2.58 | |
| γ 3 | 3.66 | 3.99 | 3.99 | 3.95 | 3.95 | 3.89 | 4.86 | 4.86 | 4.82 | 4.82 | |
| Kurtotic | α | 4.00 | 1.03 | 1.05 | 1.03 | 1.05 | 4.15 | 1.19 | 1.09 | 1.19 | 1.09 |
| γ 1 | 1.43 | 1.34 | 1.34 | 1.34 | 1.34 | 2.01 | 1.28 | 1.28 | 1.29 | 1.29 | |
| γ 2 | 1.63 | 1.31 | 1.31 | 1.31 | 1.31 | 1.68 | 1.65 | 1.65 | 1.64 | 1.64 | |
| γ 3 | 1.89 | 1.85 | 1.85 | 1.85 | 1.85 | 1.92 | 1.86 | 1.86 | 1.86 | 1.86 | |
Note. Ratio of missing data MSE to complete-data MSE. Bold typeface denotes cases where the complete-case MSE is lower than a missing at random (MAR)-based MSE. The x and xz variables (γ1 and γ3, respectively) have 20% missing data. CCA = complete-case analysis; FMLV = free mean latent variable model; CMLV = constrained mean latent variable model; FMC = free mean centering; CMC = constrained mean centering.
Coverage
Finally, we examined confidence interval coverage. In the MCAR simulation, the vast majority of coverage values were quite close to the nominal 95% level. Coverage values for the regression slopes typically ranged between 93% and 95% and did not vary across conditions. Complete-case analysis and multiple imputation produced somewhat lower coverage values for the intercept coefficient (e.g., values close to 90% were typical), whereas maximum likelihood values for γ0 were again close to the 95% level. We suspect that this discrepancy occurred because the maximum likelihood analyses treat the predictors as random variables with a distribution, whereas the ordinary least squares analyses treat predictors as fixed. The MAR coverage rates followed a similar pattern, except that the complete-case coverage values were quite low in some cases. Table 8 uses coverage values from the N = 200 condition to illustrate these results. For comparison purposes, we also include coverage values from the complete-data estimates.
Table 8.
Confidence Interval Coverage: MAR Mechanism and N = 200
| Small interaction effect |
Large interaction effect |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Distribution | Parameter | COMP | CCA | FMLV | CMLV | FMC | CMC | COMP | CCA | FMLV | CMLV | FMC | CMC |
| Normal | α | 0.904 | 0.539 | 0.938 | 0.953 | 0.892 | 0.897 | 0.913 | 0.521 | 0.940 | 0.967 | 0.887 | 0.908 |
| γ 1 | 0.945 | 0.930 | 0.952 | 0.952 | 0.953 | 0.953 | 0.945 | 0.855 | 0.940 | 0.940 | 0.938 | 0.938 | |
| γ 2 | 0.943 | 0.945 | 0.948 | 0.948 | 0.949 | 0.949 | 0.951 | 0.940 | 0.943 | 0.943 | 0.939 | 0.939 | |
| γ 3 | 0.949 | 0.943 | 0.941 | 0.941 | 0.944 | 0.944 | 0.960 | 0.959 | 0.950 | 0.950 | 0.958 | 0.958 | |
| Skewed (lower tail missing) | α | 0.911 | 0.734 | 0.941 | 0.953 | 0.902 | 0.908 | 0.922 | 0.759 | 0.939 | 0.962 | 0.905 | 0.910 |
| γ 1 | 0.952 | 0.934 | 0.940 | 0.940 | 0.945 | 0.945 | 0.938 | 0.913 | 0.945 | 0.945 | 0.943 | 0.943 | |
| γ 2 | 0.944 | 0.946 | 0.944 | 0.944 | 0.945 | 0.945 | 0.943 | 0.936 | 0.944 | 0.944 | 0.942 | 0.942 | |
| γ 3 | 0.948 | 0.944 | 0.939 | 0.939 | 0.940 | 0.940 | 0.954 | 0.951 | 0.946 | 0.946 | 0.950 | 0.950 | |
| Skewed (upper tail missing) | α | 0.911 | 0.575 | 0.912 | 0.923 | 0.950 | 0.960 | 0.922 | 0.646 | 0.920 | 0.943 | 0.949 | 0.967 |
| γ 1 | 0.952 | 0.939 | 0.942 | 0.942 | 0.935 | 0.935 | 0.938 | 0.890 | 0.919 | 0.919 | 0.919 | 0.919 | |
| γ 2 | 0.944 | 0.952 | 0.914 | 0.914 | 0.912 | 0.912 | 0.943 | 0.942 | 0.850 | 0.850 | 0.846 | 0.846 | |
| γ 3 | 0.948 | 0.943 | 0.940 | 0.940 | 0.938 | 0.938 | 0.954 | 0.948 | 0.941 | 0.941 | 0.941 | 0.941 | |
| Kurtotic | α | 0.903 | 0.568 | 0.934 | 0.952 | 0.887 | 0.899 | 0.893 | 0.536 | 0.909 | 0.948 | 0.852 | 0.885 |
| γ 1 | 0.953 | 0.937 | 0.942 | 0.942 | 0.947 | 0.947 | 0.939 | 0.853 | 0.939 | 0.939 | 0.939 | 0.939 | |
| γ 2 | 0.946 | 0.953 | 0.934 | 0.934 | 0.935 | 0.935 | 0.941 | 0.932 | 0.911 | 0.911 | 0.909 | 0.909 | |
| γ 3 | 0.957 | 0.950 | 0.942 | 0.942 | 0.948 | 0.948 | 0.948 | 0.945 | 0.941 | 0.941 | 0.946 | 0.946 | |
Note. Bold typeface denotes coverage values below 90%. With 2,000 replications, the standard error of the nominal .95 proportion is .005. The x and xz variables (γ1 and γ3, respectively) have 20% missing data. MAR = missing at random; COMP = complete data analysis; CCA = complete-case analysis; FMLV = free mean latent variable model; CMLV = constrained mean latent variable model; FMC = free mean centering; CMC = constrained mean centering.
Discussion
The existing missing data literature does not provide a clear prescription for estimating interaction effects with missing data, particularly when the interaction involves a pair of continuous variables. This article describes maximum likelihood and multiple imputation procedures for this common analysis problem. To this end, we outlined three latent variable model specifications for interaction analyses with missing data. These models apply procedures from the latent variable interaction literature—in particular, Marsh et al. (2004)—to analyses with a single indicator per construct (e.g., a regression analysis with scale scores). We also discussed multiple imputation for interaction effects, emphasizing an approach that applies standard imputation procedures (e.g., data augmentation; Schafer, 1997) to the product of two raw score predictors. A real data analysis and Monte Carlo simulations showed that maximum likelihood and multiple imputation produced remarkably similar estimates, even with relatively small samples. This result agrees with existing literature that demonstrates the equivalency of these two approaches (Collins et al., 2001; Schafer, 2003) and suggests that the choice of analytic method is largely one of personal preference (although maximum likelihood is arguably easier to implement for researchers who are facile with SEM software).
The methods that we outline in this article allow the researcher to freely estimate the product term mean (the free mean latent variable model and free mean centering) or partially constrain its value (the constrained mean latent variable model and constrained mean centering). Our results show that these two approaches produce different estimates of the intercept coefficient when the mechanism is MAR. It is difficult to recommend one method over the other based on their mean squared errors. Considered as a whole, the constrained mean approaches produced smaller MSE values in a majority of design cells, but the exact pattern of results was a complex function sample size, distribution shape, and effect size. We tentatively recommend a constrained mean approach (latent variable model or post-imputation centering), acknowledging that there are situations where the free mean approaches will provide a lower MSE (e.g., positively skewed predictors with missingness in the upper tail). Note that the choice of centering method matters only when estimating effects that involve the intercept.
Because the methodological literature has largely discounted complete-case analyses, it may come as a surprise that maximum likelihood and multiple imputation generally provided only a modest improvement over deletion. It is important to note that complete-case analyses are known to produce valid estimates of regression slopes when (a) missingness on a predictor depends the observed values of another predictor, and (b) the incomplete predictor is linearly related to the observed predictor (Little, 1992). Our simulation design was optimal for complete-case analysis because both conditions were met. Based on the extant literature, we do not expect deletion to perform as well under different MAR configurations (e.g., missingness due to auxiliary variables not in the regression model).
Our study raises a number of avenues for future research. First, our simulation results underscore the need for additional analytic work. In models with linearly related variables, Yuan (2009) and Yuan and Bentler (2010) showed that normal-theory missing data handling methods yield consistent estimates under an MAR mechanism when normality is violated. However, the standardized bias values from our simulations suggest that this property may not extend to non-linear models. Second, Yuan and Zhang (2012) recently outlined a two-stage missing data handling approach that first obtains robust M-estimates of the mean vector and the covariance matrix and subsequently uses the moments as input data for a structural equation model. Because the two-step approach down-weights outliers in the initial step, it may reduce bias when the mechanism is MAR. Finally, we did not investigate the performance of other common nonlinear effects (e.g., polynomials). For example, it is straightforward to extend the approaches in this article to quadratic effects because a quadratic term is simply the interaction between a variable and itself. Appendix H of the online supplemental materials describes the latent variable specification and post-imputation centering expression for quadratic regression models. Future simulation or analytic work could evaluate these approaches.
As with any Monte Carlo study, characteristics of our computer simulations may limit their generalizability. Although we attempted to choose conditions that would expose potential problems with the methods (e.g., a large proportion of missing data, relatively extreme distribution shapes, a strong selection mechanism), a number of limitations are worth considering. For example, we investigated an MAR mechanism where the propensity for missing data on one predictor was monotonically related to the values of the other predictor. Future studies could examine more complicated dropout mechanisms, perhaps with non-linear associations (e.g., “convex” or “sinister” processes; Collins et al., 2001). Non-ignorable (i.e., not missing not at random [NMAR]) mechanisms are another possibility that we did not consider. Future studies could also explore different distributional conditions. The lower order distributions exert a complex influence on the product term's distribution (Aroian, 1947; Aroian, Taneja, & Cornwell, 1978; MacKinnon, 2008), and thoroughly manipulating these distributions could produce a number of interesting product term distributions. Our simulations suggest that the type of MAR mechanism and distribution shape (e.g., missingness in the upper vs. lower tail of a skewed distribution) may exert a complicated influence on parameter recovery. Future studies should attempt to clarify this issue.
Supplementary Material
Acknowledgments
This article was supported in part by National Institute on Drug Abuse Grant DA09757.
Footnotes
Supplemental materials: http://dx.doi.org/10.1037/a0035314.supp
Note that the default parameterization in Mplus (Muthén & Muthén, 1998–2012) treats predictors as fixed. Specifying the variances and covariances among the predictors in the MODEL command invokes a normal distribution for the predictors.
Specifying the default model in Mplus requires only three lines of syntax: x z xz; x z xz with x z xz; y on x z xz;
Contributor Information
Craig K. Enders, Department of Psychology, Arizona State University.
Amanda N. Baraldi, Department of Psychology, Arizona State University.
Heining Cham, Department of Psychology, Arizona State University.; Department of Psychology, Fordham University.
References
- Aiken LS, West SG. Multiple regression: Testing and interpreting interactions. Sage; Newbury Park, CA: 1991. [Google Scholar]
- Aroian LA. The probability function of a product of two normally distributed variables. Annals of Mathematical Statistics. 1947;18:265–271. doi:10.1214/aoms/1177730442. [Google Scholar]
- Aroian LA, Taneja VS, Cornwell LW. Mathematical forms of the distribution of the product of two normal variables. Communications in Statistics: Theory and Methods. 1978;7:165–172. doi:10.1080/03610927808827610. [Google Scholar]
- Bauer DJ, Curran PJ. Probing interactions in fixed and multilevel regression: Inferential and graphical techniques. Multivariate Behavioral Research. 2005;40:373–400. doi: 10.1207/s15327906mbr4003_5. doi:10.1207/s15327906mbr4003_5. [DOI] [PubMed] [Google Scholar]
- Bohrnstedt GW, Goldberger AS. On the exact covariance of products of random variables. Journal of the American Statistical Association. 1969;64:1439–1442. doi:10.1080/01621459.1969.10501069. [Google Scholar]
- Chaplin WF. The next generation in moderation research in personality psychology. Journal of Personality. 1991;59:143–178. doi: 10.1111/j.1467-6494.1991.tb00772.x. doi: 10.1111/j.1467-6494.1991.tb00772.x. [DOI] [PubMed] [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. 2nd ed. Erlbaum; Hillsdale, NJ: 1988. [Google Scholar]
- Cohen J, Cohen P, West SG, Aiken LS. Applied multiple regression/correlation analysis for the behavioral sciences. 3rd ed. Erlbaum; Mahwah, NJ: 2003. [Google Scholar]
- Collins LM, Schafer JL, Kam C-M. A comparison of inclusive and restrictive strategies in modern missing data procedures. Psychological Methods. 2001;6:330–351. doi:10.1037/1082-989X.6.4.330. [PubMed] [Google Scholar]
- Craig CC. On the frequency function of xy. Annals of Mathematical Statistics. 1936;7:1–15. doi:10.1214/aoms/1177732541. [Google Scholar]
- Cumming G, Fidler F, Leonard M, Kalinowski P, Christiansen A, Kleinig A, Wilson S. Statistical reform in psychology: Is anything changing? Psychological Science. 2007;18:230–232. doi: 10.1111/j.1467-9280.2007.01881.x. doi:10.1111/j.1467-9280.2007.01881.x. [DOI] [PubMed] [Google Scholar]
- Curran PJ, West SG, Finch JF. The robustness of test statistics to nonnormality and specification error in confirmatory factor analysis. Psychological Methods. 1996;1:16–29. doi:10.1037/1082-989X.1.1.16. [Google Scholar]
- Demirtas H, Freels SA, Yucel RM. Plausibility of multivariate normality assumption when multiple imputing non-Gaussian continuous outcomes: A simulation assessment. Journal of Statistical Computation and Simulation. 2008;78:69–84. doi:10.1080/10629360600903866. [Google Scholar]
- Enders CK. The impact of nonnormality on full information maximum likelihood estimation for structural equation models with missing data. Psychological Methods. 2001;6:352–370. doi:10.1037/1082-989X.6.4.352. [PubMed] [Google Scholar]
- Enders CK. Guilford Press; New York, NY: 2010. Applied missing data analysis. [Google Scholar]
- Enders CK, Gottschall AC. On the use of multiple imputation with multiple group latent variable models. Structural Equation Modeling. 2011;18:35–54. doi:10.1080/10705511.2011.532695. [Google Scholar]
- Fleishman AI. A method for simulating non-normal distributions. Psychometrika. 1978;43:521–532. doi:10.1007/BF02293811. [Google Scholar]
- Graham JW. Missing data analysis: Making it work in the real world. Annual Review of Psychology. 2009;60:549–576. doi: 10.1146/annurev.psych.58.110405.085530. doi:10.1146/annurev.psych.58.110405.085530. [DOI] [PubMed] [Google Scholar]
- Hayes AF, Matthes J. Computational procedures for probing interactions in OLS and logistic regression: SPSS and SAS implementations. Behavior Research Methods. 2009;41:924–936. doi: 10.3758/BRM.41.3.924. doi:10.3758/BRM.41.3.924. [DOI] [PubMed] [Google Scholar]
- Jaccard J, Wan CK. Measurement error in the analysis of interaction effects between continuous predictors using multiple regression: Multiple indicator and structural equation approaches. Psychological Bulletin. 1995;117:348–357. doi:10.1037/0033-2909.117.2.348. [Google Scholar]
- Jöreskog KG, Yang F. Nonlinear structural equation models: The Kenny–Judd model with interaction effects. In: Marcoulides GA, Schumacker RE, editors. Advanced structural equation modeling techniques. Erlbaum; Hillsdale, NJ: 1996. pp. 57–88. [Google Scholar]
- Kelava A, Werner CS, Schermelleh-Engel K, Moosbrugger H, Zapf D, Ma Y, West SG. Advanced nonlinear latent variable modeling: Distribution analytic LMS and QML estimators of interaction and quadratic effects. Structural Equation Modeling. 2011;18:465–491. doi: 10.1080/10705511.2011.582408. [Google Scholar]
- Kenny DA, Judd CM. Estimating the nonlinear and interactive effects of latent variables. Psychological Bulletin. 1984;96:201–210. doi:10.1037/0033-2909.96.1.201. [Google Scholar]
- Klein AG, Moosbrugger H. Maximum likelihood estimation of latent interaction effects with the LMS method. Psychometrika. 2000;65:457–474. doi:10.1007/BF02296338. [Google Scholar]
- Little RJA. Regression with missing X's: A review. Journal of the American Statistical Association. 1992;87:1227–1237. [Google Scholar]
- Lomnicki ZA. On the distribution of products of random variables. Journal of the Royal Statistical Society. 1967;29:513–524. [Google Scholar]
- MacKinnon DP. Introduction to statistical mediation analysis. Erlbaum; Mahwah, NJ: 2008. [Google Scholar]
- Marsh HW, Wen Z, Hau KT. Structural equation models of latent interactions: Evaluation of alternative estimation strategies and indicator construction. Psychological Methods. 2004;9:275–300. doi: 10.1037/1082-989X.9.3.275. doi:10.1037/1082-989X.9.3.275. [DOI] [PubMed] [Google Scholar]
- Marsh HW, Wen Z, Hau KT. Structural equation models of latent interaction and quadratic effects. In: Hancock G, Mueller RO, editors. Structural equation modeling: A second course. Information Age.; Greenwich, CT: 2006. pp. 225–265. [Google Scholar]
- Micceri T. The unicorn, the normal curve, and other improbable creatures. Psychological Bulletin. 1989;105:156–166. doi:10.1037/0033-2909.105.1.156. [Google Scholar]
- Montague M, Enders C, Castro M. Academic and behavioral outcomes for students at risk for emotional and behavioral disorders. Behavioral Disorders. 2005;31:84–94. [Google Scholar]
- Muthén LK, Muthén BO. Mplus user's guide. 7th ed. Muthén & Muthén; Los Angeles, CA: 1998–2012. [Google Scholar]
- Preacher KJ, Curran PJ, Bauer DJ. Computational tools for probing interactions in multiple linear regression, multilevel modeling, and latent curve analysis. Journal of Educational and Behavioral Statistics. 2006;31:437–448. doi:10.3102/10769986031004437. [Google Scholar]
- Rubin DB. Inference and missing data. Biometrika. 1976;63:581–592. doi:10.1093/biomet/63.3.581. [Google Scholar]
- Rubin DB. Multiple imputation for nonresponse in surveys. 1987 doi:10.1002/9780470316696. [Google Scholar]
- SAS Institute . SAS (Version 9.2) [Computer software] Author; Cary, NC: 2008. [Google Scholar]
- Savalei V, Bentler PM. A statistically justified pairwise ML method for incomplete nonnormal data: A comparison with direct ML and pairwise ADF. Structural Equation Modeling. 2005;12:183–214. doi: 10.1207/s15328007sem1202_1. [Google Scholar]
- Schafer JL. Analysis of incomplete multivariate data. 1997 doi: 10.1201/9781439821862. [Google Scholar]
- Schafer JL. Multiple imputation in multivariate problems when the imputation and analysis models differ. Statistica Neerlandica. 2003;57:19–35. doi:10.1111/1467-9574.00218. [Google Scholar]
- Springer MD, Thompson WE. The distribution of independent random variables. SIAM Journal on Applied Mathematics. 1966;14:511–526. doi:10.1137/0114046. [Google Scholar]
- Vale DC, Maurelli VA. Simulating multivariate nonnormal distributions. Psychometrika. 1983;48:465–471. doi:10.1007/BF02293687. [Google Scholar]
- von Hippel PT. How to impute squares, interactions, and other transformed variables. Sociological Methodology. 2009;39:265–291. doi: 10.1111/j.1467-9531.2009.01215.x. [Google Scholar]
- West SG, Aiken LS, Wu W, Taylor AB. Multiple regression: Applications of the basics and beyond in personality research. In: Robins RW, Fraley RC, Krueger R, editors. Handbook of research methods in personality psychology. Guilford Press; New York, NY: 2007. pp. 573–601. [Google Scholar]
- Wilkinson L, the Task Force on Statistical Inference, American Psychological Association, Science Directorate Statistical methods in psychology journals: Guidelines and explanations. American Psychologist. 1999;54:594–604. doi:10.1037/0003-066X.54.8.594. [Google Scholar]
- Yuan K-H. Normal distribution based pseudo ML for missing data: With applications to mean and covariance structure analysis. Journal of Multivariate Analysis. 2009;100:1900–1918. doi:10.1016/j.jmva.2009.05.001. [Google Scholar]
- Yuan K-H, Benter PM. Consistency of normal distribution based pseudomaximum likelihood estimates when data are missing at random. The American Statistician. 2010;64:263–267. doi: 10.1198/tast.2010.09203. doi:10.1198/tast.2010.09203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan K-H, Zhang Z. Robust structural equation modeling with missing data and auxiliary variables. Psychometrika. 2012;77:803–826. doi:10.1007/s11336-012-9282-4. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.