Abstract
The kinetics and nonequilibrium thermodynamics of open state and inactive state drug binding mechanisms have been studied here using different voltage protocols in sodium ion channel. We have found that for constant voltage protocol, open state block is more efficient in blocking ionic current than inactive state block. Kinetic effect comes through peak current for mexiletine as an open state blocker and in the tail part for lidocaine as an inactive state blocker. Although the inactivation of sodium channel is a free energy driven process, however, the two different kinds of drug affect the inactivation process in a different way as seen from thermodynamic analysis. In presence of open state drug block, the process initially for a long time remains entropy driven and then becomes free energy driven. However in presence of inactive state block, the process remains entirely entropy driven until the equilibrium is attained. For oscillating voltage protocol, the inactive state blocking is more efficient in damping the oscillation of ionic current. From the pulse train analysis it is found that inactive state blocking is less effective in restoring normal repolarisation and blocks peak ionic current. Pulse train protocol also shows that all the inactive states behave differently as one inactive state responds instantly to the test pulse in an opposite manner from the other two states.
Keywords: damping of ionic current, drug binding kinetics, nonequilibrium thermodynamics, Sodium ion channel
Introduction
The sodium ion channel1,2,3,4 is an optimal drug target for therapeutic action as inactivation plays an important role by temporarily preventing the channel from reopening even though the cell is still depolarized. If the inactivation process is hampered, various physiological problems appear, like cardiac arrest, hyper excitability, hysteria etc, due to the persistent current.5,6,7,8 In particular, sodium channels are targeted for anesthesia and treatments for genetic diseases in the brain, skeletal muscles, and heart.9 The physiological importance of the voltage gated sodium channel is associated with numerous pathologies namely cardiovascular, neuronal, neuromuscular, musculoskeletal, metabolic, and respiratory systems10,11 due to the inherited ion channel diseases due to mutations.12,13 Discovery of drug to cure these diseases are difficult owing to the fact that thorough molecular approaches are ineffective and most ion channel drugs are discovered using lab cultured tissues and animal based pharmacological methods14,15,16 which cannot be tested on human beforehand. The complete understanding of the mechanism of blocking of drugs and how the intrinsic properties of channel gating affect drug access, binding affinity and unblocking are still not clearly understood. Many existing drugs thus failed to reduce mortality17,18 due to incomplete knowledge of drug binding mechanism in ion channels and little knowledge of the molecular and physiochemical basis of drug receptor interaction. Thus the understanding of the drug binding kinetics and its energetics in presence of various membrane depolarisations is one of our goals in this paper.
For the previous few decades the study of inactivation had been a major investigation for many elctrophysiologists studying the cell under voltage clamp and patch clamp techniques. Many drugs or blocks like TTX,19 conotoxins,20 pronase,21 mexiletine,22 lidocaine22 have been evolved which specifically target binding with the open state or the inactive states of the sodium channel, leading to ceased sodium current influx. Most of the studies involve the discovery of various blockers, their region of binding to the channel protein and the structural change of the channel protein caused in presence of drugs. As drug binding kinetics are very much affected by the various types of channel mutations, biological environment and also similar drugs show different binding kinetics23,24 in different systems, it is difficult to comprehend drug binding interactions in a general framework. To generalize drug binding kinetics from single channel realization, we present here simple probabilistic approach using the 9 state model of Bezanilla25 for cardiac sodium channel. In spite of a great deal of effort to understand the drug binding kinetics the nonequilibrium thermodynamic characterization of binding have been still overlooked. Thus in our study we investigate the following questions: (1) What are the basic kinetic difference between a drug blocking open state and a drug accessing directly the inactive state of the channel with the variation of drug concentration and voltage? (2) For constant depolarisation which type of drug binding is more effective in blocking the ionic current? (3) What is the thermodynamic difference between a normal inactivation process and a drug induced inactivation? (4) Are these drugs binding processes entropy driven or free energy driven? (5) How these 2 types of drug binding kinetics differ from constant voltage case in presence of oscillating voltage protocol, emerging as nonequilibrium response spectroscopic technique26,27,28 which also mimic the neuronal oscillations29,30 in membrane potential? (6) How the channel and its drug binding mechanism responds to the pulse train voltage protocol and its varying pulse width. In this context we have taken a standard single sodium ion channel model which we have extended with drug bound states corresponding to the open state and inactive state blocking, considering local anesthetics such as mexiletine and lidocaine as open state and the inactive state blockers, respectively.
Layout of the paper is as follows. First the kinetic scheme of drug binding has been discussed. Then considering the effect of open state blocker and inactive state blocker we have presented the kinetic and nonequilibrium thermodynamic characterisation of two types of drug binding in presence of three types of voltage protocols. In different subsections we have studied the effect of drug in presence of constant voltage, oscillating voltage and pulse train protocols.
Kinetics of Drug Binding
The study of local anesthetics (LA) and their binding kinetics to the binding site of sodium ion channel has been important since past few decades.4,31,32,33 Hille,34 in his modulated receptor hypothesis explains the shift of inactivation in presence of use-dependent block of sodium currents during repetitive pulses.35,36,37 The hypothesis predicted that the open and inactivated states of voltage gated Na channels have higher affinities toward LA drugs than that of the resting state. The guarded-receptor model emphasizes the dependence of hydrophilic or hydrophobic path of the drug in binding and unbinding kinetics.38 There have been a lot of drugs3,39,40 invented which binds with sodium channel, can be broadly divided into 2 classes,41,42 as open state blocker and inactive state stabilizing blocker. From clinical stand point, drugs that have strong open channel blocking potency are called class 1a antiarrhythmics, such as quinidine, mexilitine and disopyramide whereas class 1b antiarrhythmics like lidocaine preferentially block peak over late current.43 Unlike most positively charged local anesthetics the neutral tricyclic anticonvulsant drugs, namely phenytoin, carbamazepine, and lamotrigine etc have similar blocking affinities for both open or inactivated-state.44
Till now the clear distinction between activities of open state blocker and inactive state blocker is yet not clear and well established. Various experimental protocols such as constant voltage clamp, oscillating voltage as nonequilibrium response spectroscopic technique and pulse train protocol have been used enormously but how these protocols affect the drug binding is not yet clear. We consider the drug binding model based on the single sodium ion channel model presented by Vandenberg and Bezanilla.25 In this model the ion conducting state or open state is represented by P5, whereas the states P1 to P4 are closed states and P6 to P8 are the inactivated states. At the resting potential (−70 mV), the most preferred state is P0. However, when depolarization occurs the channel goes to the open state and produces the macroscopic ionic current, I(t) with influx of Na+ ions into the cell. Then the channel goes to the inactivated states and the inward ionic current is terminated. The voltage-dependent forward and backward transition probabilities, αi(V(t)) and βi(V(t)), respectively can be represented by
| (1) |
Here q1± are the gating charges involved with each forward and backward transitions, respectively; αi(0) and βi(0) are the forward and backward transitions at zero voltage, respectively, with . Here δi is dimensionless fractional electrical distance (0 < δi < 1) with u = 1.2 as in Millonas.26 The time evolution of the probabilities of these 9 states can be written in terms of 2 general master equations. For convenience, we have considered 2 indices, A and I, which represent the active states (P0 to P5) and inactive states (P6 to P8), respectively. Thus master equation can be written in terms of 2 states. The corresponding active state master equation can be written as:
| (2) |
where PA(n,t) represents the probability of remaining in the n-th active state at time t. Similar sort of expression holds for inactive state master equation as:
| (3) |
For active states the value of n varies from 0 to 5 whereas for inactive states we have n = 6, 7 and 8 with αn(V(t)) and βn(V(t)) are designated as the forward and backward transition probabilities of n-th state. Here we consider and . The parameters associated with these 9 coupled differential equations are given in the following Table 1.26 At any instant of time t, the ionic current, I(t) is calculated by the following equation:
| (4) |
Here g0 and gV are experimentally fitted parameters describing the voltage dependence of the sodium ion conductance as described in the caption of the Table 1.
Table 1.
Model parameters. The forward and backward transition rates at zero voltage is given in this table with the data of gating charges and fractional electrical distances as used by Millonas et al.26 The instantaneous conductance gV expressed as , where unit of gV is μS and g1 = −8.21 × 10−4, g2 = −4.72 ×10−6, g3 = 1.49 × 10−8 with g0 = 0.0169 is the overall scaling factor representing the cell expression rate. Vr is the reversal potential for the sodium ion channel under study, usually 67.0 mV
| Rate index | i (0)(s−1) | i(0) (s−1) | qi | i |
|---|---|---|---|---|
| 1 | 4779 | 10.3 | 2.83 | 0.053 |
| 2 | 5045 | 12.1 | 3.16 | 0.5 |
| 3 | 1684 | 2360 | 0.077 | 0.78 |
| 4 | 19.8 | 5.573 | 0.12 | |
| 5 | 800 | 59.8 | 0.16 | 0.33 |
We take the example of an open state drug blocker as mexiletine and inactive state blocker as lidocaine.22 Thus here we add an extra drug bound state P5M with P5 for the study of mexiletine drug binding kinetics and we add 3 drug bound states such as P6L, P7L, P8L with P6, P7 and P8, respectively to study the kinetics in presence of lidocaine. The models are given in Figure 1. For simplicity we consider a drug binds to an open state and inactive state with similar binding affinity. We have taken the forward rate constant for binding kon = [D] × 105s−1, where [D] is the molar drug concentration [M] and koff = 10−2s−1.31 For simplicity we keep the rate constants same for mexiletine and lidocaine. For system under constant, oscillating and pulse train voltage protocols we use these drug binding rates which are not voltage dependent in any case.
Figure 1.
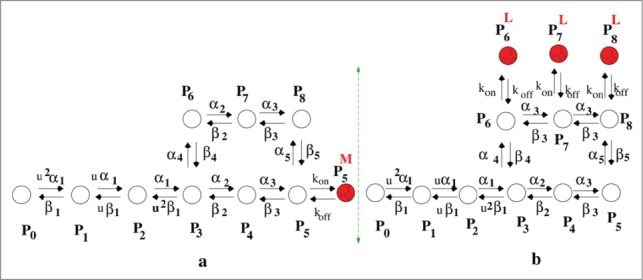
Kinetic model of drug binding. (A) model of open state drug blocking is a 10 state model and (B) model for inactive state drug blocker is a 12 state model.
Kinetic and Thermodynamic Effects of Different Voltage Protocols on Drug Binding
Here we study the effect of 3 types of voltage protocols for these drug blockers. First we have kept the voltage constant as used in constant voltage clamp dynamics. Secondly we use oscillating voltage protocol, a protocol which helps us to study the system in nonequilibrium environment. Next we have studied the system under pulse train protocol. Here we vary the pulse durations of the base pulse and test pulse and their effect is studied in presence of open state blocker and inactive state blocker with various concentrations. How the alteration of pulse duration affects or facilitates the drug binding is one of the goals of this part. In each protocol we are comparing whether inactive state blockers or the open state blockers are more effective in blocking the ionic current.
Constant voltage clamp dynamics
Constant voltage clamp dynamics has been widely used protocol to study ion channels since the work of Hodgkin-Huxley.1,2 The voltage clamp technique is used by electro-physiologists to measure the ionic current through the membrane of excitable cells while holding the membrane voltage at a set level. A series of voltage ramp can be used which allows the membrane voltage to be altered independently of the ionic currents allowing to study the current-voltage relationships of the voltage gated sodium channel.
Here we have plotted the ionic current at different concentrations of mexiletine and lidocaine keeping the voltage constant i.e, −20 mV. From Figure 2A it is seen that the ionic current is suppressed with the increase in the drug concentration. It is also observed that the peak of the ionic current is also decreased but from the Figure 2B it is seen that lidocaine block has no effect on the peak current which affects the current after the peak is reached that is at tail part only. The effect of the mexiletine is clearly visible for a wide range of drug concentration but the effective range of visible change for lidocaine is very small, i.e., in the very low concentration range, 0.005–0.01 M, after that or the concentration greater than that does not change the kinetics appreciably and the graphs overlap, as for example [D] = 10 M, overlaps on [D] = 0.1 M.
Figure 2.
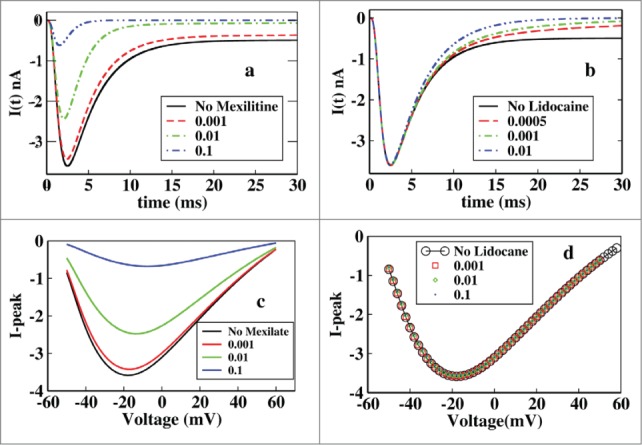
Effect of mexilitine and lidocaine on ionic current and its peak in presence of constant voltage protocol. (A) Effect of mexiletine of different concentrations on ionic current are shown here, with mexiletine concentrations 0.001 M, 0.01 M, 0.1 M. (B) Effect of lidocaine is shown with concentrations 0.0005 M, 0.001 M, 0.01 M. (C) Peak current has been plotted at various constant depolarisations and varied for different concentrations of mexiletine. (D) Similar graph has been plotted for lidocaine like in (C).
Next we have investigated the relation between peak-current and various constant depolarising voltages for different drug concentrations. Here we first put the system in −70 mV depolarisation (a resting potential for the cell), and send it to a steady state until all the parameters become time independent. Then we switch on the drug block sites along with the depolarising voltage and let the system settle down to steady-state and then estimate the peak current.
From Figure 2C it is seen that for a particular mexiletine concentration the peak of ionic current gradually increases with depolarisation and then after passing through a maximum it decreases again. With increase in mexiletine concentration there is a relative reduction of peak current clearly visible. But in the case of lidocaine a different nature is observed. For a particular lidocaine concentration the peak current shows similar nature as mexiletine but for increasing lidocaine concentration there is no effect on peak current as seen from Figure 2D.
It is worth mentioning that although there is no effect on peak current due to increasing concentration of lidocaine but there is a clear change in the peak over late current. The late current sharply decreases with the increase in the lidocaine concentration as seen from Figure 2B. This behavior of lidocaine is also consistent with the experiments done earlier as was previously reported that lidocaine was more effective in late component of Na+ current than peak current in ΔKPQ channels expressed in mamalian cells.45,46,47,48,49 Lidocaine preferentially blocked late over peak current and the blockade was equally effective in all 3 channels having mutations N1325S, R1644H and ΔKPQ expressed in Xenopus oocytes.50 Lidocaine inhibits dispersed reopening in single channels without affecting mean open times. Clinical studies showed that the late current is more sensitive than peak current to block by class Ib51 antiarrhythmic drugs like lidocaine.45,47,52
Next we have studied the nonequilibrium thermodynamics of the system in presence of drug. Here we assume that the system is in contact with an isothermal bath at temperature T. The total internal energy U(t), the free energy, F(t) and the system entropy, S(t) is given as follows:53
| (5) |
| (6) |
| (7) |
Now we have calculated and which gives the information about how far the system is from the equilibrium in terms of these thermodynamic parameters namely,
| (8) |
where is the internal energy of the system at equilibrium and Pie is the probability of the ith state at equilibrium. Similarly we can write
| (9) |
and
| (10) |
From the Figure 3A it is seen that without the presence of drug the process is initially entropy driven and soon after the inactivation process starts it becomes free energy driven as seen from the Figure 2A. It remains free energy driven upto the equilibrium until all of the 3 quantities become zero at equilibrium. It may be concluded that the normal inactivation process in sodium channel is free energy driven without the presence of any drug. From Figure 3B it is seen that in presence of 0.001 M mexilitine the process is also initially entropy driven and then after a long time it becomes free energy driven. In Figure 3C it is seen that in presence of lidocaine the process entirely remains entropy driven till the equilibrium reaches. The ionic current graphs are plotted below for each case which shows the similar time scales for reaching the equilibrium. It is observed here from both the graphs of ionic current and thermodynamic potentials that lidocaine blocks faster than that of mexilitine.54,55
Figure 3.
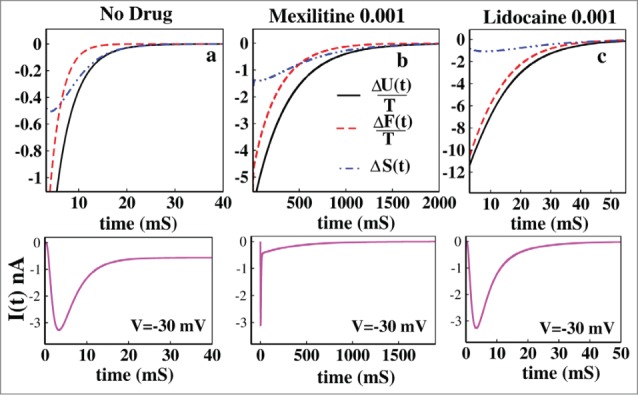
Thermodynamic properties of drug binding. (A) ΔU(t)/T, ΔF(t)/T and ΔS(t) have been shown without the presence of drug. In (B) the same thermodynamic parameters have been studied in presence of 0.001 M mexilitine and in (C) with 0.001 M lidocaine. The black solid curve stands for the ΔU(t)/T, the red dashed curve stands for ΔF(t)/T and the blue dot-dashed curve stands for ΔS(t). For all the cases voltage has been kept fixed to −30 mV. The ionic current graphs are shown below for each case which shows the similar kinetic and thermodynamic time scales for reaching the equilibrium.
Oscillating voltage protocol
Oscillating voltage protocol is an emerging technique27,28 to study the ion channels in nonequilibrium environment. In individual neurons the oscillations may appear due to oscillating nature of action potential and membrane depolarisation.29,30 To realize the effect of drug in ionic current in presence of inherent gating kinetics of channel the oscillating voltage protocol may give the nearly similar cell situation in terms of neuronal oscillation. The functional form of the voltage, V(t) used is V (t) = V0 + A sin(wt), where V0 is the mean voltage taken as zero and ω = 2πν with amplitude, A = 30 mV and frequency, ν = 30 Hz consistant with biological range. From the nonequilibrium thermodynamics we know that the total dissipation function or the total entropy production rate(epr) is expressed as,53
| (11) |
taking entropy in units of Boltzmann constant, kB. Here, qij is the transition rate which converts the state from i to j and similar definition holds for reverse transition rate qji. Here we have considered that system remains in the contact with the environment with a constant temperature.
Left panel of Figure 4 is the ionic current and in the right panel the corresponding total epr are shown. From Figure 4A it is seen that without the presence of drug the ionic current oscillates and ultimately attains a time periodic steady value. From the Figure B it is seen that the total entropy production rate is always positive and the system shows a time periodic steady nature of dissipation. Thus it goes to a driven nonequilibrium steady state in presence of oscillating voltage. But in presence of drugs of both kinds the system ultimately relaxes to equilibrium as seen from the Figure 4D and F. Thus the thermodynamics of the system entirely changes in presence of drug for oscillating external perturbation. In presence of drug the external oscillation cannot hold the system to nonequilibrium steady-state any more but relaxes to the equilibrium due to the fact that these drugs have very very high binding affinities to the channel sites. The rate of relaxing to equilibrium in presence of lidocaine is much faster than the mexiletine for a particular drug concentration.
Figure 4.
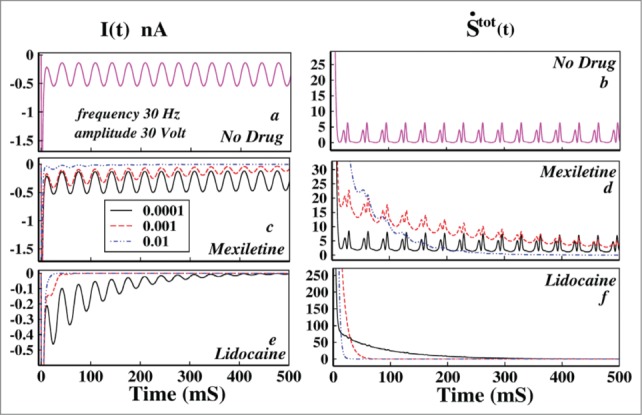
Effect of oscillating voltage protocol in ionic current and total entropy production rate leading to damping. In the left panel the ionic current and in right panel the total epr has been plotted. In (A) ionic current without the presence of any drug has been plotted and in (B) the corresponding total epr is given. In (C) the ionic current in presence of mexiletine, in (D) the corresponding total epr has been shown. In (E AND F) ionic current and total epr in presence of lidocaine are plotted, respectively. In (C–F) the black solid line indicates drug concentration of 0.0001 M, the red dashed line indicates drug concentration of 0.001 M and the blue dot-dashed line indicates 0.01 M drug concentration.
However, one important observation is that the ionic current in presence of drug gradually damps down as seen from Figure 4C and E. The total epr also gradually damps down to equilibrium. Damping of these kinetic and thermodynamic quantities in presence of drug is directly related to the fact that the action potential also damps down.4 It is seen that even with a minute concentration, lidocaine damps down both the ionic current and total epr in a much faster rate to equilibrium than mexilitine which is evident from the comparative study of the graphs in presence of drug.
Pulse train analysis
The pulse train protocol is also being widely used to understand the channel gating and inactivation procedure.56,57 These studies mainly involve characterization of time course for inactivation or more precisely the time course of recovery from inactivation.58,59,60 Here we want to investigate how the inactivation of sodium channel plays a role in ionic current when subjected to various depolarising pulse train separated by recovery intervals. First we keep the voltage at −20 mV for few seconds and then bring back the system to base voltage which is −80 mV and then after few milliseconds we start the test pulse train of −20 mV. Each pulse in the pulse train is brought back to base voltage for few milliseconds and then again fired to test voltage again. Here we are changing the base pulse and test pulse duration and studying how the system reacts to it. This study is important as it replicates the biological situation where a pulse comes and sodium channel responds to it and within few milliseconds system goes to inactivation followed by termination of ionic current influx until the potassium channel brings the system back to the resting potential which is more or less −80 mV. Thus here the test pulse (−20 mV) perturbs the system and the base pulse causes refractory changes to get the system ready for the next incoming pulse. Another interesting fact of using such protocol is that one can actually control the population of a state as desired. For example the test pulse will populate the open state and inactive states while the base pulse will again depopulate them. Here we have studied the system with and without presence of open state binding drug, mexiletine and inactive state binding drug, lidocaine with changing duration of the test pulse and base pulse.
First of all we would like to see how the system reacts to pulse train in presence of 2 kinds of drug already mentioned in different concentrations. We have considered the drug concentrations 0.01, 0.001, 0.0005 and 0.0001 M for both the 2 types of drugs. We kept the test pulse duration at 0.03 seconds and the base pulse duration at 0.01 seconds. The Figure 5A shows how the pulse train is applied.
Figure 5.
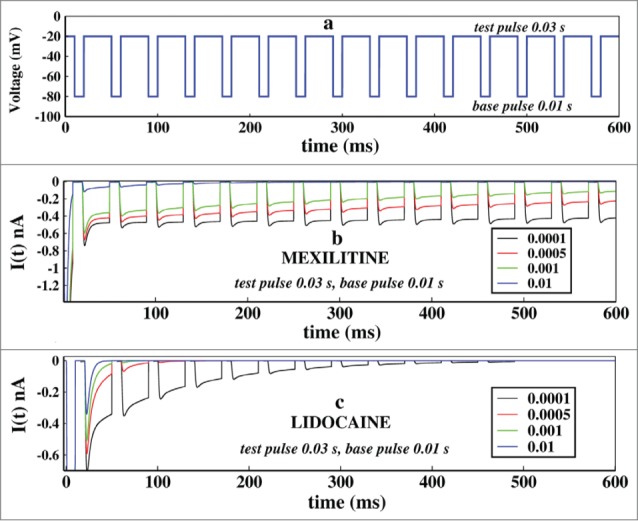
Effect of concentration of drugs in ionic current, in presence of pulse train protocol. In (A), first the voltage is kept at −20 mV and after few milliseconds it is brought back to base −80 mV after that the pulse train begins. Here the base pulse duration is 0.01s and test pulse duration is 0.03 s. In (B), the effect of Mexiletine in ionic current is shown for increasing concentrations such as 0.0001, 0.0005, 0.001 and 0.01 M respectively. In (c), similar plot is shown for lidocaine. For both the cases the test pulse is kept for 0.03 s and the base pulse is kept for 0.01 s.
In Figure 5B we have plotted the ionic current in presence of mexiletine drug. It shows that with gradual increase in the drug concentration the peak of the ionic current gradually decreases down. With increasing drug concentration the open state blocking occurs with faster rate leading to a gradual decrease in ionic current. In Figure 5B the effect of lidocaine is shown. Lidocaine being an inactive state stabilizing drug stabilises the inactive states at much faster rate and almost have no impact on refractory period or base pulse in it, leading to the faster termination of ionic current. With a concentration more than 0.01 M, lidocaine permanently prohibits the channel from reopening.22 Comparing the above 2 pictures of drug binding it is seen that lidocaine is more effective and faster ionic current blocker than mexiletine, as also observed from oscillating and constant voltage protocol in previous subsections.
Next we focused on the effects of change of base and test pulse durations in ionic currents keeping the drug concentrations same at 0.001 M. For that purpose we have chosen 2 pulse regions. We start with the very short pulse regions where we keep the test pulse at 0.0008 seconds and base pulse at 0.0002 seconds and also see the effect just altering the pulse durations of each other. In Figure 6A we have plotted the ionic currents at a test pulse duration of 0.0008 seconds and in Figure 6B the test pulse durations are kept at 0.0002 seconds. Comparing the 2 figures it is seen that the system actually responds to the larger test pulse than the smaller one. As the test pulses are very short in Figure 6B, system fails to understand the fast depolarisation and the channel almost remains closed all the time. The inset graphs of Figure 6A and Figure 6B are the asymptotic values of ionic currents in presence of drugs.
Figure 6.

Effect of very short test pulse and base pulse durations on ionic current: In (A), the ionic current is plotted with time for no drug, in presence of mexilitine and in presence of lidocain. The test pulses are kept for 0.0008s and the base pulse is kept foe 0.0002 s. In (B), similar plot is done but with test pulses duration of 0.0002s and the base pulse duration of 0.0002s. All the drug concentrations are kept at 0.001 M.
In Figure 7A we have plotted similar curves as in Figure 6, but with pulse durations of larger time scales, such as test pulses of 0.03 s and base pulse durations of 0.01 seconds. In Figure 7B the alternate duration of pulses are plotted. Comparing the Figures 7A and B it is important to note that the lidocaine almost immediately blocks the ionic current after the first two or three pulses in larger time scales, than in very short pulses. This is because due to the longer exposure to the depolarisation the lidocaine stabilises the inactive states more effectively. The plot for shorter test pulse of 0.01 seconds have been shown in Figure 7B, which shows that system partially responds to the voltage change and the peak currents are higher than in Figure 6B. In addition one can observe from the asymptotic values of ionic current that mexilitine more effectively blocks the ionic current in presence of longer test pulses. For both the cases lidocaine shows less sensitivity toward pulse durations as it almost immediately inhibits the ionic current.
Figure 7.
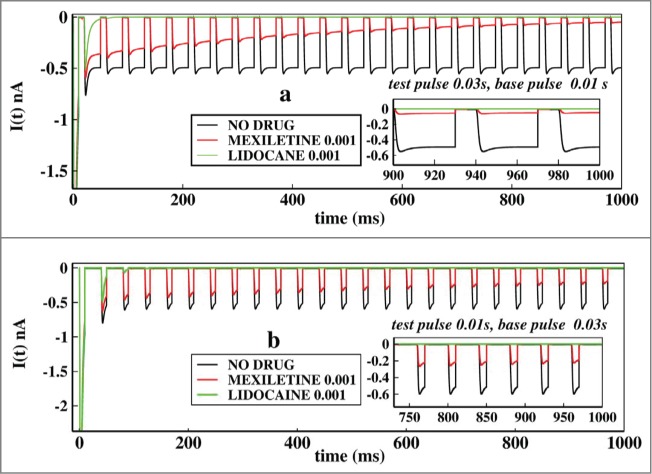
Effect of longer test pulse and base pulse durations on ionic current. In (A), the ionic current is plotted with time for no drug, in presence of mexilitine and in presence of lidocaine. The test pulses are kept for 0.03 s and the base pulse is kept foe 0.01 s. In (B), similar plot is shown but with test pulses duration of 0.01s and the base pulse duration of 0.03s. All the drug concentrations are kept at 0.001 M.
Next we have focused on the probabilities of the states which actually have the detailed information of the system responding to the pulse train protocol in presence of the drug. Thus we have studied the probabilities in presence of mexilitine and lidocaine with pulse durations as mentioned in Figure 8. Here we have particularly seen the system dynamics for consecutive 4 pulses. The probabilities of the original 9 states of the system responds almost similarly but with different magnitudes in presence of mexilitine and lidocaine but their time dependences are almost the same. For convenience we have plotted only the mexilitine in presence of 0.001 M concentration.
Figure 8.
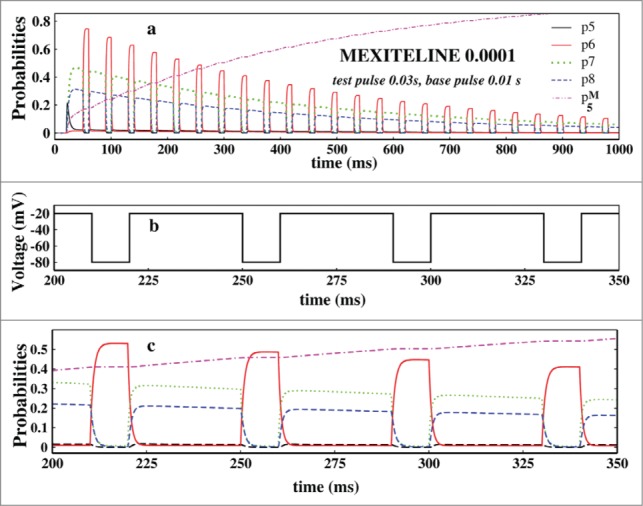
Study of probabilities. In (A), the open state probability and the 3 inactive state probabilities and the drug binding state probabilities have been plotted in presence of 0.0001 M mexilitine concentration and in presence of pulses mentioned. In (B), the 4 test pulses of (A) which have been studied is shown here. In (C), the aforesaid probabilities are plotted for the above 4 pulses.
In Figure 8A we have plotted the probabilities of open state, P5 and the inactive states, P6, P7 and P8 and the drug binding state, P5M for mexilitine. Figure 8B shows the 4 pulses of which probabilities have been studied in Figure 8C. From the Figure 8C it is seen that P6 increases at the test pulse peaks, whereas the P7 and P8 increases in the base pulses and vice versa. There is a clear phase lag in the activities of P6 and P7, P8. P7 and P8 responds almost similarly but with a slight difference in amplitudes. P6 responds instantly at the test pulse, whereas the other 2 states are responding in a opposite manner and the magnitudes of the P7 and P8 depend on the details of the inactivation path61 and rate constants.
Conclusion
In general we have studied the drug binding kinetics of voltage gated sodium ion channel in presence of two types of drug binding mechanisms, one which binds to the open state of the channel such as mexilitine and other binding to the inactive states of the channel such as lidocaine. We have studied kinetics in presence of voltage protocols using constant, oscillating and pulse train where the first one is used by the electrophysiologist in voltage clamp and patch clamp techniques while the oscillating voltage basically mimics the neuronal oscillation which can be caused by the periodic change of membrane voltage. The pulse train protocol is useful which gives the sodium channel a refractory period in which the channel reactivates from the inactivation. Here we have shown the interesting dependence of drug binding mechanism on voltage variation which helps us to understand the toxic activity of drugs in living biological cell.
In constant voltage case the open state blocker acts more slowly than the inactive state blocker in blocking the ionic current. Open state blocker has drastic effect on peak ionic current in presence of constant voltage case but inactive state blocker does not show any observable effect on peak ionic current and only affects the tail part of it. The system in absence of any drug relaxes to equilibrium initially driven by entropy and then driven by free energy. The inactivation of sodium ion channel may be inferred as a free energy driven process. In presence of open state drug blocker the process initially for a long time remains entropy driven and then becomes free energy driven. But in presence of inactive state blocker the process entirely remains entropy driven till the equilibrium reaches. Thus these two types of drug binding are thermodynamically distinguishable which can be compared through calorimetric measurement.
For oscillating voltage protocol, inactive state blocker blocks the current in a faster rate than the open state blocker and also more sensitive to change in concentration than that of the constant voltage case. For equal concentrations inactive state blocker damps the ionic current and the total epr with higher extent than the open state blocker. From the pulse train analysis it is again established that inactive state blocker is a better ionic current blocker than open state blocker thereby inactive state blocking is less effective in restoring normal repolarisation and blocks the peak current. The longer test pulse is actually sensed by the system for both small and large time scales but it is not effectively sensed by the system when it is subjected to shorter test pulse. Open state blocker shows considerable blocking ability toward longer test pulse duration than shorter test pulse duration. From pulse train protocol it is revealed that not all inactive states respond to the external voltage in a similar manner. The one which is directly attached to closed states responds instantly at the test pulse, whereas the other two inactive states are responding in a delayed manner depending on the inactivation paths and rate constants.
Disclosure of Potential Conflicts of Interest
No potential conflicts of interest were disclosed.
References
- 1.Hodgkin AL. Evidence for electrical transmission in nerve Part I. J Physiol 1937; 90:183-210; PMID:16994885; http://dx.doi.org/ 10.1113/jphysiol.1937.sp003507 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hodgkin AL. Evidence for electrical transmission in nerve Part II. J. Physiol 1937; 90:211-32; PMID:16994886; http://dx.doi.org/ 10.1113/jphysiol.1937.sp003508 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Catterall WA. Sodium channels, inherited epilepsy, and antiepileptic drugs. Annu Rev Pharmacol Toxicol 2014; 54:317-38 PMID:24392695; http://dx.doi.org/ 10.1146/annurev-pharmtox-011112-140232 [DOI] [PubMed] [Google Scholar]
- 4.Scholz A. Mechanisms of (local) anaesthetics on voltage-gated sodium and other ion channels. Br J Anaesth 2002; 89:52-61; PMID:12173241; http://dx.doi.org/ 10.1093/bja/aef163 [DOI] [PubMed] [Google Scholar]
- 5.Kiss T. Persistent Na-channels: origin and function. A review. Acta Biol Hung 2008; 59:1-12; PMID:18652365; http://dx.doi.org/ 10.1556/ABiol.59.2008.Suppl.1 [DOI] [PubMed] [Google Scholar]
- 6.Mustafa BA. Djamgoz and rustem onkal . Persistent current blockers of voltage-gated sodium channels: a clinical opportunity for controlling metastatic disease. Recent Pat Anticancer Drug Discov 2013; 8:66-84; PMID:23116083 [DOI] [PubMed] [Google Scholar]
- 7.Lin WH, Wright DE, Muraro NI, Baines RA, Alternative splicing in the voltage-gated sodium channel DmNav regulates activation, inactivation, and persistent current. J Neurophysiol 2009; 102:1994-2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wayne E Crill. Persistent sodium current in mammalian central neurons. Annu Rev Physiol 1996; 58:349-62 [DOI] [PubMed] [Google Scholar]
- 9.Catterall WA, Goldin AL, Waxman SG. International Union of Pharmacology. XLVII. Nomenclature and Structure-Function Relationships of Voltage-Gated Sodium Channels. Pharmacol Rev 2005; 57:397-409; PMID:16382098; http://dx.doi.org/ 10.1124/pr.57.4.4 [DOI] [PubMed] [Google Scholar]
- 10.Catterall WA. . From Ionic Currents to Molecular Mechanisms: The Structure and Function of Voltage-Gated Sodium Channels. Neuron 2000; 26:13-25; PMID:10798388; http://dx.doi.org/ 10.1016/S0896-6273(00)81133-2 [DOI] [PubMed] [Google Scholar]
- 11.Ashcroft FM. From molecule to malady. Nature 2006; 440:440-7; PMID:16554803; http://dx.doi.org/ 10.1038/nature04707 [DOI] [PubMed] [Google Scholar]
- 12.Dichgans M, Freilinger T, Eckstein G, Babini E, Lorenz-Depiereux B, Biskup S, Ferrari MD, Herzog J, van den Maagdenberg AM, Pusch M, et.al, Mutation in the neuronal voltage-gated sodium channel SCN1A in familial hemiplegic migraine. Lancet 2005; 366:371-7; PMID:16054936; http://dx.doi.org/ 10.1016/S0140-6736(05)66786-4 [DOI] [PubMed] [Google Scholar]
- 13.George AL, Jr. Inherited disorders of voltage-gated sodium channels. J Clin Invest 2005; 115:1990-9; PMID:16075039; http://dx.doi.org/ 10.1172/JCI25505 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wickenden A1, Priest B, Erdemli G. Ion channel drug discovery: challenges and future directions. Future Med Chem 2012; 4:661-79; PMID:22458684; http://dx.doi.org/ 10.4155/fmc.12.4 [DOI] [PubMed] [Google Scholar]
- 15.Clare JJ. Targeting ion channels for drug discovery. Discov Med 2010; 9:253-60; PMID:20350493 [PubMed] [Google Scholar]
- 16.Perrior T. Overcoming Bottlenecks in drug discovery; Drug Discovery World 2010; Fall: 29-33; fall-10-bottlenecks-p29.pdf [Google Scholar]
- 17.Echt DS, Liebson PR, Mitchell LB, Peters RW, Obias-Manno D, Barker AH, Arensberg D, Baker A, Friedman L, Greene HL. Mortality and morbidity in patients receiving encainide, flecainide, or placebo. The Cardiac Arrhythmia Suppression Trial. N Engl J Med 1991; 324:781-8; PMID:1900101; http://dx.doi.org/ 10.1056/NEJM199103213241201 [DOI] [PubMed] [Google Scholar]
- 18.Task Force of the Working Group on Arrhythmias of the European Society of Cardiology . The Sicilian gambit. A new approach to the classification of antiarrhythmic drugs based on their actions on arrhythmogenic mechanisms. Circulation 1991; 84:1831-51; PMID:1717173; http://dx.doi.org/ 10.1161/01.CIR.84.4.1831 [DOI] [PubMed] [Google Scholar]
- 19.Carmeliet E. Voltage-dependent block by tetrodotoxin of the sodium channel in rabbit cardiac Purkinje fibers. Biophys J 1987; 51:109-14; PMID:2432950; http://dx.doi.org/ 10.1016/S0006-3495(87)83315-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sarma SP, Kumar GS, Sudarslal S, Iengar P, Ramasamy P, Sikdar SK, Krishnan KS, Balaram P. Solution structure of delta-Am2766: a highly hydrophobic delta−conotoxin from conus amadis that inhibits inactivation of neuronal voltage-gated sodium channels. Chem Biodivers 2005; 2:535-56; PMID:17192003; http://dx.doi.org/ 10.1002/cbdv.200590035 [DOI] [PubMed] [Google Scholar]
- 21.Armstrong CM, Bezanilla F, Rojas E. Destruction of sodium conductance inactivation in squid axons perfused with pronase. J Gen Physiol 1973; 62:375-91; PMID:4755846; http://dx.doi.org/ 10.1085/jgp.62.4.375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Clancy CE, Zhu ZI, Rudy Y. Pharmacogenetics and anti arrhythmic drug therapy: a theoretical investigation. Am J Physiol Heart Circ Physiol 2007; 292:H66-75; PMID:16997895 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zamponi GW, Doyle DD, French RJ. State-dependent block underlies the tissue specificity of lidocaine action on batrachotoxin-activated cardiac sodium channels. Biophysical J 1993; 65:91-100; http://dx.doi.org/ 10.1016/S0006-3495(93)81043-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zamponi GW, French RJ. Dissecting lidocaine action: die diethylamide and phenol mimic separate modes of lidocaine block of sodium channels from heart and skeletal muscle. Biophysical J 1993; 65:2335-47; http://dx.doi.org/ 10.1016/S0006-3495(93)81292-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Vandenberg CA, Bezanilla F. A sodium channel gating model based on single channel, macroscopic ionic, and gating currents in the squid giant axon. Biophysics J 1991; 60:1511-33; http://dx.doi.org/ 10.1016/S0006-3495(91)82186-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Millonas MM, Hanck DA. Nonequilibrium response spectroscopy of voltage-sensitive ion channel gating. Biophys J 1998; 74:210-29; PMID:9449324; http://dx.doi.org/ 10.1016/S0006-3495(98)77781-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hosein-Sooklal A, Kargol A. Wavelet analysis of nonequilibrium ionic currents in human heart sodium channel (hH1a). J Membr Biol 2002; 188:199-212; PMID:12181611; http://dx.doi.org/ 10.1007/s00232-001-0188-9 [DOI] [PubMed] [Google Scholar]
- 28.Kargol A, Hosein-Sooklal A, Constantin L, Przestalski M. Application of oscillating potentials to Shaker potassium channel. Gen Physiol Biophys 2004; 23:53-75; PMID:15270129 [PubMed] [Google Scholar]
- 29.Llinas R, Yarom Y. Oscillatory properties of guinea-pig inferior olivary Neurones and their pharmacological modulation: An in vitro study. J Physiol 1986; 376:163-82; PMID:3795074; http://dx.doi.org/ 10.1113/jphysiol.1986.sp016147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Llinas RR, Grace AA, Yarom Y. In vitro neurons in mammalian cortical layer 4 exhibit intrinsic oscillatory activity in the 10- to 50-Hz frequency range. Proc Nati Acad Sci USA 1991; 88:897-901; http://dx.doi.org/ 10.1073/pnas.88.3.897 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Fozzard HA, Lipkind GM. The tetrodotoxin binding site is within the outer vestibule of the sodium channel. Marine Drugs 2010; 8:219-34; PMID:20390102; http://dx.doi.org/ 10.3390/md8020219 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Starmer CF, Lastra AA, Nesterenko VV, Grant AO. Proarrhythmic response to sodium channel blockade. Theoretical model and numerical experiments. Circulation 1991; 84:1364-77; PMID:1653123; http://dx.doi.org/ 10.1161/01.CIR.84.3.1364 [DOI] [PubMed] [Google Scholar]
- 33.Stramer CF. How antiarrhytmic drugs increase the rate of sudden cardiac death. Int J Bifurcation Chaos 2002; 12:1953; http://dx.doi.org/ 10.1142/S0218127402005625 [DOI] [Google Scholar]
- 34.Hille B. Local anesthetics: Hydrophilic and hydrophobic pathways for the drug receptor reaction. J Gen Physiol 1977; 69:497-515; PMID:300786; http://dx.doi.org/ 10.1085/jgp.69.4.497 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wang GK, Strichartz GR. State-Dependent Inhibition of Sodium Channels by Local Anesthetics: A 40-Year Evolution. Biochem (Mosc) Suppl Ser A Membr Cell Biol 2012; 6:120-7; PMID:23710324; http://dx.doi.org/ 10.1134/S1990747812010151 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Khodorov BI, Shishkova L, Peganov E, Revenko S. Inhibition of sodium currents in frog Ranvier node treated with local anesthetics. Role of slow sodium inactivation. Biochim Biophys Acta 1976; 433:409; http://dx.doi.org/ 10.1016/0005-2736(76)90105-X [DOI] [Google Scholar]
- 37.Courtney KR. Mechanism of frequency-dependent inhibition of sodium currents in frog myelinated nerve by the lidocaine derivative GEA. J Pharm Exp Therop 1975; 195:225-36 [PubMed] [Google Scholar]
- 38.Lee PJ, Sunami A, Fozzard HA. Cardiac specific external paths for lidocaine, defined by isoform-specific residues, accelerate recovery from use-dependent block. Circ Res 2001; 89:1014-21; PMID:11717158; http://dx.doi.org/ 10.1161/hh2301.100002 [DOI] [PubMed] [Google Scholar]
- 39.Crumb WJ Jr, Clarkson CW. Characterization of cocaine-induced block of cardiac sodium channels. Biophys J 1990; 57:589-99; PMID:2155033; http://dx.doi.org/ 10.1016/S0006-3495(90)82574-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lee CH, Ruben PC. Interaction between voltage-gated sodium channels and the neurotoxin, tetrodotoxin. Channels 2008; 2:407-12; PMID:19098433; http://dx.doi.org/ 10.4161/chan.2.6.7429 [DOI] [PubMed] [Google Scholar]
- 41.Lipkind GM, Fozzard HA. Molecular modeling of local anesthetic drug binding by voltage-gated sodium channels. Mol Pharmacol 2005; 68:1611-22; PMID:16174788 [DOI] [PubMed] [Google Scholar]
- 42.Gilliam FR 3rd, Starmer CF, Grant AO. Blockade of rabbit atrial sodium channels by lidocaine characterization of continuous and frequency-dependent blocking. Circ Res 1989; 65:723-39; PMID:2548763; http://dx.doi.org/ 10.1161/01.RES.65.3.723 [DOI] [PubMed] [Google Scholar]
- 43.Campbell TJ, Wyse KR, Pallandi R. Di_erential e_ects on action potential of class IA, B and C antiarrhythmic drugs: modulation by stimulation rate and extracellular K+ concentration. Clinc Exp Pharmacol Physiol 1991; 18:533-41; http://dx.doi.org/ 10.1111/j.1440-1681.1991.tb01488.x [DOI] [PubMed] [Google Scholar]
- 44.Lipkind GM, Fozzard HA. Molecular model of anticonvulsant drug binding to the voltage-gated sodium channel inner pore. Mol Pharmacol 2010; 78:631-8; PMID:20643904; http://dx.doi.org/ 10.1124/mol.110.064683 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.An RH, Bangalore R, Rosero SZ, Kass RS. Lidocaine block of LQT-3 mutant human Na channels. Circ Res 1996; 79:103-8; PMID:8925557; http://dx.doi.org/ 10.1161/01.RES.79.1.103 [DOI] [PubMed] [Google Scholar]
- 46.Bennett PB, Yazawa K, Makita N, George AL Jr. Molecular mechanism of an inherited cardiac arrhythmia. Nature 1995; 376:683-5; PMID:7651517; http://dx.doi.org/ 10.1038/376683a0 [DOI] [PubMed] [Google Scholar]
- 47.Dumaine R, Wang Q, Keating MT, Hartmann HA, Schwartz PJ, Brown AM, Kirsch GE. Multiple mecha nisms of Na+ channel linked long-QT syndrome. Circ Res 1996; 78:916-24; PMID:8620612; http://dx.doi.org/ 10.1161/01.RES.78.5.916 [DOI] [PubMed] [Google Scholar]
- 48.Bean BP, Cohen CJ, Tsien RW. Lidocaine block of cardiac sodium channels. J Gen Physiol 1983; 81:613-42; PMID:6306139; http://dx.doi.org/ 10.1085/jgp.81.5.613 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bennett PB, Valenzuela C, Chen LQ, Kallen RG. On the molecular nature of the lidocaine receptor of cardiac Na+ channels. Circ Res 1995; 77:584-92; PMID: 7641328; http://dx.doi.org/ 10.1161/01.RES.77.3.584 [DOI] [PubMed] [Google Scholar]
- 50.Dumaine R, Kirsch GE. Mechanism of lidocaine block of late current in long Q-T mutant Na+ channels. Am Physiol Soc 1998; 274:H477-87 [DOI] [PubMed] [Google Scholar]
- 51.Hondeghem LM. Interaction of class I drugs with the cardiac sodium channel In: Antiarrhythmic Drugs. edited by Vaughan Williams E. M. Berlin: Springer-Verlag, 1989, p. 157174 [Google Scholar]
- 52.Wang DW, Yazawa K, Makita N, George AL Jr, Bennett PB. Pharmacological targeting of long QT mutant sodium channels. J Clin Invest 1997; 99:1714-20; PMID:9120016; http://dx.doi.org/ 10.1172/JCI119335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ge H, Qian H. Physical origins of entropy production, free energy dissipation, and their mathematical representations. Phys Rev 2010; E 81:051133. [DOI] [PubMed] [Google Scholar]
- 54.Ono M, Sunami A, Sawanobori T, Hiraoka M. External pH modi_es sodium channel block by mexiletine in guinea pig ventricular myocytes. Cardiovasc Res 1994; 28:973-9; PMID:7954609; http://dx.doi.org/ 10.1093/cvr/28.7.973 [DOI] [PubMed] [Google Scholar]
- 55.Ono M, Sunami A, Hiraoka M. Interaction between external Na+ channel in guinea-pig ventricular Myocytes. Pugers Arch 1995; 431:101-9; http://dx.doi.org/ 10.1007/BF00374382 [DOI] [PubMed] [Google Scholar]
- 56.Stramer CF, Agustus O Grant. Phasic ion channel blockade, kinetic model and parameter estimation procedure. Mol Pharmacol 1985; 28:348-56; PMID:2414642 [PubMed] [Google Scholar]
- 57.Vilin YY, Ruben PC. Slow inactivation in voltage-gated sodium channels, molecular substrates and contributions to channelopathies. Cell Biochem Biophys 2001; 35:171-90; PMID:11892790; http://dx.doi.org/ 10.1385/CBB:35:2:171 [DOI] [PubMed] [Google Scholar]
- 58.Luo CH, Rudy Y. A dynamic model of the cardiac ventricular action potential. I. Simulations of ionic currents and concentration changes. Circ Res 1994; 74:1071-96; PMID:7514509; http://dx.doi.org/ 10.1161/01.RES.74.6.1071 [DOI] [PubMed] [Google Scholar]
- 59.Clancy CE, Rudy Y. Na(+) channel mutation that causes both brugada and long-QT syndrome phenotypes a simulation study of mechanism. Circulation 2002; 105:1208-13; PMID:11889015; http://dx.doi.org/ 10.1161/hc1002.105183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Groome JR, Lehmann-Horn F, Holzherr BD. Open- and closed-state fast inactivation in sodium channels Differential effects of a site-3 anemone toxin. Channels 2011; 5:65-78; PMID:21099342; http://dx.doi.org/ 10.4161/chan.5.1.14031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Armstrong CM. Na channel inactivation from open and closed states. Proc Nat Aacad Sci 2006; 103:17991-6; http://dx.doi.org/ 10.1073/pnas.0607603103 [DOI] [PMC free article] [PubMed] [Google Scholar]


