Scaling Reward Value with Demand Curves versus Preference Tests

Abstract

In Experiment 1, six capuchins lifted a weight during a 10-minute session to receive a food piece. Across conditions, the weight was increased across six different amounts for three different food types. The number of food pieces obtained as a function of the weight lifted was fitted by a demand equation that is hypothesized to quantify food value. For most subjects, this analysis showed that the three food types differed little in value. In Experiment 2, these monkeys were given pairwise choices among these food types. In 13 of 18 comparisons, preferences at least equaled a 3-to-1 ratio; in seven comparisons, preference was absolute. There was no relation between values based on degree of preference versus values based on the demand equation. When choices in the present report were compared to similar data with these subjects from another study, between-study lability in preference emerged. This outcome contrasts with the finding in demand analysis that test-retest reliability is high. We attribute the unreliability and extreme assignment of value based on preference tests to high substitutability between foods. We suggest use of demand analysis instead of preference tests for studies that compare the values of different foods. A better strategy might be to avoid manipulating value by using different foods. Where possible, value should be manipulated by varying amounts of a single food type because, over an appropriate range, more food is consistently more valuable than less. Such an approach would be immune to problems in between-food substitutability.

The goal of the present report is to introduce a behavioral-economic technique for scaling reward value. We review the relevant history below and consider the well-known inequity-aversion test of Brosnan and de Waal (2003) as one experimental context to illustrate why a behavioral-economic approach may have utility for comparative psychologists. We underscore that this work does not test inequity aversion. Instead, this topic frames the discussion of the measure of value.

A Selective History of Measuring Reinforcer Value

The question of how to scale the value of a reward has been of enduring interest to animal learning theorists. Skinner (1932a, 1932b) noted that the form of the curve created by graphing amount of food consumed as a function of time was unchanged whether the food was consumed directly, or delivered as a consequence of a lever press. Based on this outcome, he argued that the rate of lever pressing could serve as a surrogate for the strength of the eating reflex.

In many contexts, response rate serves as a good measure of reinforcer value. For example, Clark (1958) found response rates correlated with both the rate of reinforcement a schedule provides and with manipulations of hours of food deprivation. These successes notwithstanding, response-rate measures often encounter a problem with ceiling effects: If an animal is responding at its highest rate for a reinforcer, subsequent increases in reinforcer value cannot result in still higher response rates. In consequence, response rate is often insensitive to value changes that occur when reinforcer values are already high.

An alternative scheme is to measure value not in terms of changes in response rate, but in terms of changes in preference. Herrnstein (1970) found that with two variable-interval (VI) schedules that provide the same food reinforcer, the relative response rate (response to one VI divided by all responses) often equaled the relative reinforcement rate (reinforcers from that VI divided by all reinforcers). If one assumes that the value of an alternative that provides twice as much reinforcement as another is two-to-one, the finding of twice as much responding to the alternative providing twice as much value raises the possibility that relative response rate offers a linear scale of the relative value of two identical reinforcers.

Preference models such as Herrnstein’s (1970) assume what Krantz (1964) has called “simple scalability”—the existence of a single monotonic dimension of, say, “likeability” in which preference maps subjective relative value or utility. Unfortunately, this assumption is likely wrong. Microeconomic studies in the human economy have shown that preference varies not just as a function of value, but also as a function of other factors such as substitutability.

The substitutability of two goods is defined by the degree to which increases in the price of one good leads to greater consumption (demand) of the other good. For example, raising the price of white eggs leads to increases in demand for brown eggs, an outcome indicating these goods are substitutable. Alternatively, there are complementary goods where increasing the price of one decreases demand for both. For example, if the price of tennis racquets increased, you might expect demand for both racquets and tennis balls to decrease.

Hursh (1978) demonstrated that such observations translate directly into monkey behavior. In his study, preferences for two foods indicated they were highly substitutable. When the price of one food increased—a circumstance arranged by requiring more responding to produce food—the demand for the other food increased. However, when the choice was between food and water and the price of water increased, the demand for both food and water decreased, indicating the two were complements.

This history shows that scaling the value of two goods depends on how the goods interact in terms of substitutability. Yet these dependencies seldom seem of concern to specialists in areas cognate to learning theory. Typically, when two qualitatively different goods are to be compared in choice or some other arrangement, some investigators define the value of two goods based on a pretest in which the foods are compared solely by a trials-based preference test (e.g., delay discounting: Beran, Savage-Rumbaugh, Pate, & Rumbaugh 1999; Evans & Beran 2007; inequity aversion: Brosnan & de Waal 2003; food variety and food preference: Addessi, Mancini, Crescimbene, Ariely & Visalberghi 2010).

An Illustration of the Utility of a Behavioral-Economic Approach

The use of preference tests to assign relative value may be consequential. For example, consider inequity aversion—a phenomenon based on the idea that when one of a pair of adjacent monkeys or apes gets a higher-value good, the other of the pair is upset when it is offered a lower-value good. This inequity is reflected in that animal’s increased likelihood to reject the lower-value good even though in other contexts this good was acceptable for consumption (e.g., see female capuchin data in Brosnan & de Waal 2003).

Community acceptance of this phenomenon has been burdened by questions of its definition (Henrich 2004), and possible procedural confounds (Roma, Silberberg, Ruggiero & Suomi 2006); however, its greatest burden may well be the difficulty some investigators have had in reproducing its effects (e.g., male capuchins in Brosnan & de Waal 2003; McAuliffe, Chang, Leimgruber, Spaulding, Blake, & Santos 2015; Sheskin, Ashayeri, Skerry, & Santos 2014; Silberberg, Crescimbene, Addessi, Anderson, & Visalberghi 2009).

The typical procedure for assigning value to different foods used in inequity tests is based on a pretest to determine which food is preferred and which food is not. The relative value of the two foods presented in choice is scaled by the percentage of choices of the preferred food. While the question we ask likely holds for all studies that use a preference test to assign values, current research interest in the inequity effect makes it a useful context in which to present subsequent discussion.

To illustrate the relative-value research problem, Silberberg et al. (2009) claimed in their failed inequity test that their preferred and unpreferred foods were comparable to those used in Brosnan and de Waal’s (2003) demonstration of inequity because in both cases the preferred food garnered approximately 90% of the choices in a preference pretest. However, as argued above, economic substitutability affects preference interactions between goods. Perhaps this equation of preference was due not to comparable relative values, but to degree of substitutability. If these goods were highly substitutable, a small difference in value could translate into a large difference in preference.

To make this point clear, we borrow a human-economy example from Casey, Silberberg, Paukner, & Suomi (2014). Imagine a consumer is given a choice between identically priced cars that differ in only one regard—one has leather seats and the other has vinyl seats. We would expect consumers to show a large preference for the car with leather seats, an outcome suggesting a large value difference if judged solely by the standard that size of preference defines relative value. However, what would happen if you used not the metric of the primatologist studying the inequity effect, but rather that of the microeconomist? Entertaining that these goods are highly substitutable, the microeconomist might test the possibility that the value difference is small even though the preference is large. To make this test, all that need be done is raise the price of the car with leather seats a small fraction of its total cost—say, $200. If there were now a large change in preference toward the car with vinyl seats, it would be clear that the value difference between these cars was small (it took only a small price increase to change preference), despite what a prior preference test based on equally priced cars suggests. The microeconomist would find these outcomes unsurprising: Given that these goods share virtually all characteristics (seat covering is the sole difference), small price changes should produce large shifts in preference, just like they do when consumers evaluate price changes in deciding whether to buy white or brown eggs.

In some of the studies where inequity aversion has failed (e.g., McAuliffe et al., 2015; Silberberg et al. 2009) the foods offered in the pre-experimental preference test were categorically the same (two cereals in McAuliffe et al.; two seeds in Silberberg et al.). In contrast, in the original demonstration of inequity aversion (Brosnan & de Waal 2003), a fruit and a vegetable were compared. Based on an economic analysis, finding a large preference between categorically substitutable goods (seed versus seed and fruit versus fruit) may represent a smaller value difference than that when a fruit is compared with a vegetable as in Brosnan and de Waal even if the preferences for one good over another were comparable in all studies. Given that inequity aversion presumes a monkey analog of human inequity aversion, demonstration of the effect may require a large value difference between goods. In the absence of a large difference, a monkey or a human may not feel inequitably treated simply because they prefer one to the other. Based on this analysis from economics, the possibility exists that Silberberg et al. (2009) and McAuliffe et al. (2015) failed to show inequity aversion because the value differences between the two goods were not large, despite large preference differences.

Exponential Model of Demand

These points call for a new approach, one based on economic analysis. Casey et al. (2014) engaged in such an approach, termed cross-modal scaling. In their report, they scaled preferences of two putatively highly substitutable goods (fruits) to a third, putatively less substitutable good (cereal). They found that when two fruits were compared, monkey preferences for one over the other were very high. However, when fruit was scaled against a cereal, the preferences for that same fruit were much lower. They argued that the value of the fruits should be scaled in terms of the number of pieces of cereal necessary to produce indifference in choice between a fruit type and cereal.

The Casey et al. (2014) scaling technique holds promise as an alternative to a simple preference test because it could be easily conducted before using qualitatively different foods in an experiment. However, a more time-tested method is available, based on work with economic demand curves.

As used with nonhumans, a demand curve is a graphical representation of consumption plotted against price where price is defined as the amount of work (e.g., number of lever presses) required to “buy” a reward. The results mirror those of the human economy: as prices increase, consumption decreases, resulting in a positively accelerated, monotone-decreasing function in consumption (Y axis), price (X axis) space. When microeconomists find that price increases lead to disproportionately large decreases in consumption, demand for that good is termed “elastic.” Conversely, if consumption decreases are disproportionately small, they are “inelastic.” Demand for necessities (e.g., food) tends to be inelastic while demand for luxuries (e.g., going to the movies) tends to be elastic. Hursh (1980) argued that the degree of inelasticity could serve as a plausible scale of a good’s value—the more inelastic the demand, the greater the value of the good.

Hursh and Silberberg (2008) created the following equation to model demand curves:

$$logQ=log{Q}_{\mathit{0}}+k(e^{-\alpha Q_{\mathit{0}}C}-1)$$ (1)

The independent variable, C, is the cost of the good based on the effort required to produce it. Q₀ and α are free parameters estimated from the best-fit function. The span of the exponential-decay function, k, equals the estimated range of the dependent variable, Q. The function ranges between Q₀ at a price of zero to Q₀–k at infinite price. The exponential term, Q₀C, represents the true cost of the reinforcer adjusted for the level of responding required to defend a Q₀ level of demand. The parameters Q₀ and α signify, respectively, the maximum level of consumption at minimal price, and the rate constant of the exponential, which sets the sensitivity of demand to increases in price.

Hursh and Silberberg (2008) argue that when their equation is applied to a demand curve, it creates a single parameter, α, the size of which is inversely related to value. Thus, using the equation with a demand curve created by a particular reward, the essential value of that reward can be scaled by 1/α and compared to the 1/α scores of other rewards.

The present report uses their technique in a new setting. Traditionally, price is manipulated by changing the number of responses that an animal must emit in order to receive a reward. As is typically the case in demand-curve generation in nonhumans, labor is directly exchanged for goods, without the intermediary of money (i.e., a barter system). In this study, unlike others, price is defined not by the number of responses emitted per reinforcer, but by the amount of weight an animal worker will lift for a given good. In Experiment 1, a demand curve was constructed by recording consumption of a food as function of the weight lifted to produce it. By modeling the demand curve with Equation 1, it should be possible to assign an essential value to different foods. In Experiment 2, we use the same foods in Experiment 1 in a preference test in order to determine how essential value and preference relate to one another as metrics for scaling value. In both experiments, two foods were different fruits and a third was a cereal—a good presumably less substitutable for a fruit than one fruit is for another (Casey et al. 2014).

The behavioral economist has four expectations from these experiments. First, as price for the reward increases, demand for it should decrease. Second, in terms of a demand analysis, fruits will differ less in value from one another than they will from cereal. Third, in choice between two fruits versus choice between a fruit and a cereal, the preference differences will be larger for the more substitutable goods, the fruits, than for the fruit-versus-cereal choice. Finally, the size of the preference for a good will not be highly correlated with demand. Instead, preference size may be better predicted by the substitutability of the goods offered in choice rather than the value predictions of an analysis based on demand curves.

Experiment 1

The purpose of Experiment 1 was to generate demand curves for three different foods, two fruits and one cereal. By applying the exponential model of demand to the data obtained, it was possible to define each good’s value to the animal consumer.

Method

Subjects

Six adult male tufted capuchin monkeys (Cebus apella) housed in indoor cages (1.78-m high by 9-m wide by 1.85-m deep) at the NICHD Laboratory of Comparative Ethology in Poolesville, MD served as subjects. They were pair housed in two cage arrays, each occupying different sides of the animal-colony room. They were fed biscuit and treat rations in the morning and the afternoon, and had unrestricted access to water. Daily enrichment was available in the form of toys placed in the home cages, which were removed during testing. Subjects were divided into two groups based on which cage array they occupied. One group was composed of two pair-housed subjects (four subjects in total). The other was composed of one monkey from each of two pairs of monkeys (two monkeys in total). The two groups were tested on alternating days, five days per week. All applicable international, national, and/or institutional guidelines for the care and use of animals were followed and approved by IACUC.

Apparatus

All monkeys were tested in a steel and Plexiglas chamber (45-cm high by 40-cm wide by 48-cm deep) that was attached to the home cage. A Lee’s Kritter Krawler Small Animal Ball (a toy made for rodents) was attached to one end of a 43-cm long blue plastic chain, the other end of which was attached to the lower of two bars in front of the chamber. The weight of the ball was adjusted by unscrewing a cap on the bottom of the ball, and inserting either 14- or 28-g steel fishing sinkers inside. Each monkey was separated from its cage mate at the time of testing by closing the back door of the chamber. A white board was put up to block the subject’s sight of other monkeys in the room.

Procedure

Subjects were given one session every other day during the interval between their morning and afternoon rations. Each trial began with the experimenter seated approximately 0.5 m in front of the chamber with her open hand showing a food reward, and the weighted ball-and-chain apparatus hanging downward from the subject’s chamber. If a response occurred—defined as pulling the chain until the ball at the other end could go no farther, or until the subject held the ball in its hands—the experimenter immediately delivered the reinforcer in her hand. Typically, the subject released the chain to grasp the food reinforcer. On those occasions when the monkey did not release the raised chain, it was immediately taken from the monkey’s grasp and extended toward the floor. The next trial began immediately after the food item was taken by the subject. Each session ended after 10 min, regardless of subject behavior.

Each of the six phases of this experiment consisted of two sessions in which the subject responded by lifting a specified weight to receive a particular food reinforcer. Each of the weights defining a phase (64, 191, 319, 574, 1084 and 2015 g) was presented in ascending order. By virtue of this arrangement it took 12 sessions (2 sessions X 6 different weights) to complete a single determination of the response frequency of each subject to the three different rewards (two different fruits and one cereal) used in this study. The types of rewards used and their sizes and order of presentation were the same as in Casey et al. (2014; see Table 1 for a list of each subject’s reward types and the order of food types across phases in the present study). Each food reward was cut to the size of a piece of cereal. All monkeys were familiar with pulling the plastic chains, but not with the attached ball. Therefore, they were given one 10-min pretest session in order to give them experience with the task. Each was reinforced with the first fruit type identified in Table 1. All monkeys mastered the task in this pretest session.

Table 1.

Food type, essential values (1/α), and r² values for each subject in Figure 2

Subject	Food	1/α	r2
Jr. Mint	Grape	1.43E+06	0.95
	Apple	1.67E+06	0.89
	Honey Nut Cheerios	2.00E+06	0.95
Hotrod	Banana	8.33E+05	0.84
	Apple	9.09E+05	0.81
	Apple Jacks	1.39E+06	0.89
Shane	Grape	1.02E+06	0.83
	Apple	1.01E+06	0.99
	Honey Nut Cheerios	1.22E+06	0.79
Lenny	Grape	2.78E+06	0.85
	Apple	2.94E+06	0.87
	Fruit Loops	2.56E+06	0.95
Icarus	Banana	2.04E+05	0.94
	Apple	3.85E+05	0.94
	Honey Nut Cheerios	8.33E+05	0.87
Jaws	Blueberry	4.55E+05	0.88
	Banana	3.45E+04	0.91
	Cheerios	5.00E+05	0.74

Results and Discussion

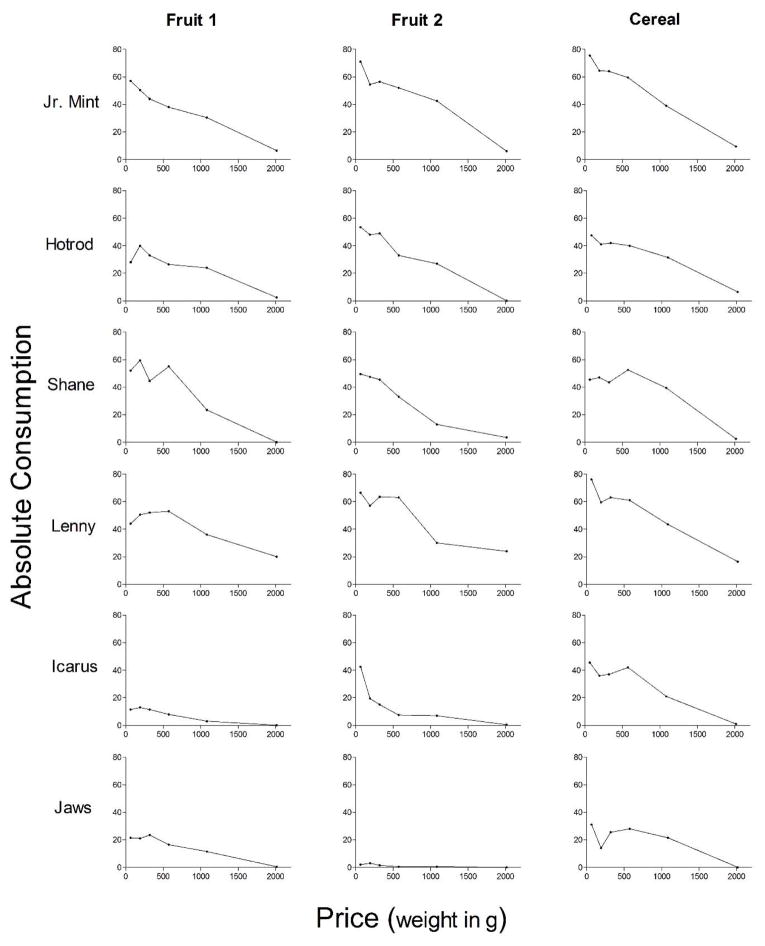
Figure 1 presents the number of reinforcers each subject obtained as a function of weight in grams averaged over the two sessions defining each weight, food-type condition for each subject (rows of figure) and each food type (columns of figure). As expected, each of these demand curves shows that as the effort required to complete a response increased, the number of responses (and, hence, food consumption) tended to decrease.

Figure 1.

Number of pieces of food consumed as a function of the weight lifting in g required to produce each piece. Columns present food type and rows present performances for each subject.

It should be noted that in this test, increasing price through an increase in weight likely affected several variables including the rate of reinforcement and the topography of the monkey’s response. For example, lifting a heavier weight would be expected to reduce the rate of reward if, say, the monkey rested after lifting a heavier weight. As regards response typography, perhaps heavier weights required monkeys to “put their back into it” while lighter weights did not. The general approach of demand analysis has been to ignore such factors, and only look for orderly functional relations between price and demand. That order is evident in Figure 1. Whatever the impact of weight on reward rate and response topography might be, it is well described by the exponential model of demand.

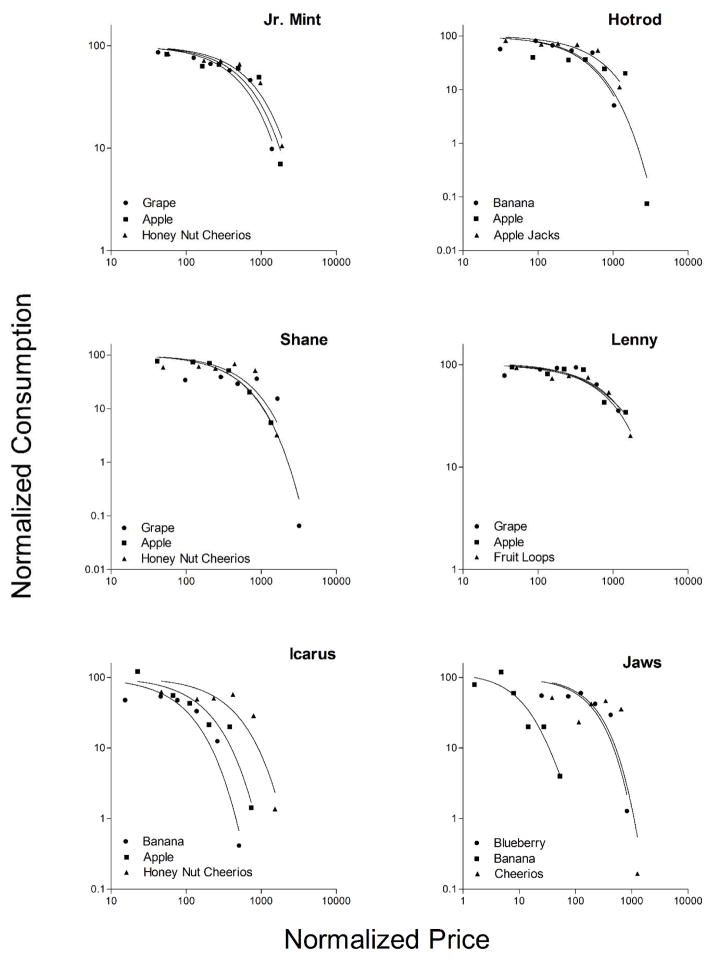
In Figure 2, the data from Figure 1 were normalized using the procedure outlined in Hursh and Winger (1995). The purpose of normalization is to accommodate differences in consumptions of different food types by different subjects. The normalization procedure sets maximal consumption at the theoretically lowest price of zero weight for each subject and food type. Each value is divided by that subject’s Q₀ for that particular food and multiplied by 100. To normalize price, each weight was multiplied by Q₀ and then divided by 100. The exponential demand equation was then fitted to the logarithm of normalized consumption as a function of the logarithm of normalized price. The parameter k was set at 10, which was held constant across all data sets.

Figure 2.

Normalized number of food pieces consumed by each subject as a function of the normalized weight in g that had to be lifted to produce a piece of food. See text for explanation of the normalization method. Equation 1 is fitted to the data in each panel. All food types are presented in each panel so that the different demand curves for each food type may be compared visually. Both axes are logarithmically scaled

Figure 2 combines all three demand curves and sorts them by subject. In consequence, it is easy to compare how a given subject values each of the three foods offered in the experiment simply by comparison of the curves. Notice that Lenny’s demand curves essentially superimpose, an outcome showing that he values all of these foods nearly identically. Jaws mimics this result in terms of blueberry and Cheerios (these curves superimpose), but demand for banana is discernibly weaker for this subject. Except for Jaws’ demand for banana and the entire data set of Icarus, subjects in this experiment show little difference in demand among the food types they were offered. Table 1 presents the essential value (1/α—that is, the degree to which a subject defends consumption of a particular food as the price of that food increases) and r² data for each curve in Figure 2.

Figure 3 presents the essential value data for all of the foods used in this report as a function of their order of presentation. As is apparent, the two fruits have nearly identical essential values, while the values for cereal appear somewhat higher. A one-way ANOVA was used to determine there was no significant difference among the average α values, indicating no differences in essential-value determinations or, for that matter, among the food types [F (2, 15) = .19, p = .83; 95% CI (8.00E+5, 1.66E+6].

Figure 3.

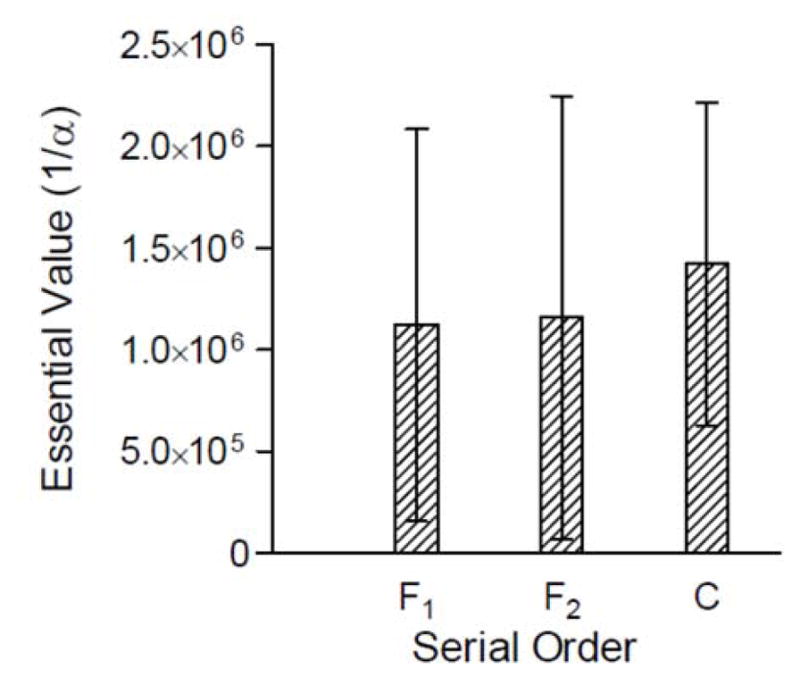
The across-subject mean essential values of each of three food types. F1 refers to the first fruit used, F2 refers to the second fruit used, and C refers to the cereal used. The error bars define the 95% confidence intervals

Experiment 2

Experiment 1 provided data on the essential value of foods based on the exponential model of demand. The purpose of Experiment 2 was to assess relative value between pairs of goods based on a preference test, and to compare the outcomes obtained with the essential-value data from Experiment 1.

Subjects

The subjects used in Experiment 1 were used in Experiment 2.

Apparatus

Subjects were tested in the steel and Plexiglas testing box used in Experiment 1; however, the chain-pull apparatus was not present.

Procedure

The rewards used in Experiment 1 were used in Experiment 2. Each trial began by presenting the monkey with two reward options, 38 cm apart on a 33- by 40.5-cm plastic board, and advancing the board to within the subject’s reach. A choice consisted of reaching with one hand for one of the two rewards. Each subject was tested twice in a 30- trial session for a total of 60 trials. Twenty of these trials were assigned to each of the three reward pairs (fruit 1 versus fruit 2, fruit 1 versus cereal, and fruit 2 versus cereal). Trials were randomized within each session, and the rewards counterbalanced on each side of the plastic board. In other regards, the procedure was unchanged from Experiment 1.

Results and Discussion

Figure 4 plots essential value in Experiment 1 as a function of preference rank in Experiment 2 (see Table 2 for preference data). This figure shows that value as measured by preference shows no agreement with value as defined by a demand analysis. This outcome forces a critical question: Given the absence of empirical compatibility, which of these two measures should one use to index value?

Figure 4.

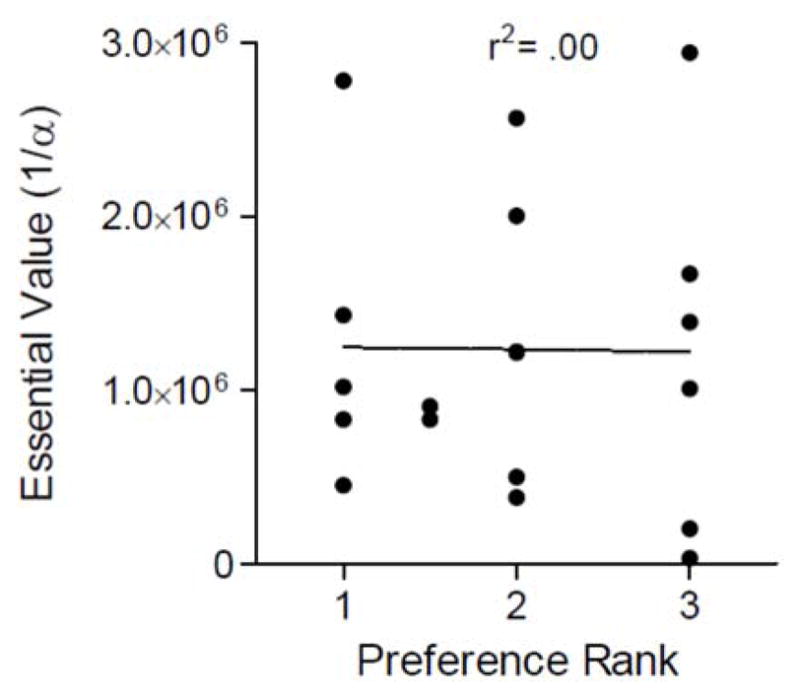
The essential value of each food type for each subject as a function of the ordinal rank of preference from a preference test. The proportion of data variance accommodated by the best-fit function drawn through the data is also presented

Table 2.

Subjects, food alternatives, and choice ratios over 20 trials

Subjects	Food Alternatives	Choices
Jr. Mint	Grape/Apple	20:0
	Grape/Honey Nut Cheerios	18:2
	Apple/Honey Nut Cheerios	4:16
Hotrod	Banana/Apple	10:10
	Banana/Apple Jacks	11:9
	Apple/Apple Jacks	14:6
Shane	Grape/Apple	19:1
	Grape/Honey Nut Cheerios	20:0
	Apple/Honey Nut Cheerios	9:11
Lenny	Grape/Apple	20:0
	Grape/Fruit Loops	20:0
	Apple/Fruit Loops	0:20
Icarus	Banana/Apple	3:17
	Banana/Honey Nut Cheerios	1:19
	Apple/Honey Nut Cheerios	7:13
Jaws	Blueberry/Banana	20:0
	Blueberry/Cheerios	15:5
	Banana/Cheerios	0:20

In the Introduction, we noted that measures of preference between qualitatively different goods are inherently flawed because the value of a good changes as a function of its substitutability with the alternative good present in choice. Thus, we questioned test validity. By obviating choice, the demand analysis presented in this report is immune to this criticism. While this fact supports favoring a demand analysis, this is support by argument, not by demonstration. To add evidence to argument, we now offer data that illustrate the superiority of a demand analysis not in terms of validity, but of reliability.

The preference test used in Experiment 2 was designed to replicate the preference test from Casey et al. (2014), using not only the same foods in the same amounts, but also the same subjects, albeit with a three-year delay. Figure 5 plots these data as the relative fruit-1 choice frequency (choice of fruit 1 divided by all choices) in the present study as a function of the relative fruit-1 choice frequency in Casey et al. (2014). The diagonal line drawn from the origin defines perfect stability of preference between these successive preference tests. These data show preference is labile and the line of perfect stability accommodates a minority of the data variance (r²=.31). This result echoes similar findings in other studies where lability in test-retest reliability assessments has been seen (e.g., Addessi et al. 2010).

Although we have no test-retest reliability data for the demand curves in the present report, prior work shows that demand analyses are not similarly troubled. The food-reinforcer data from Raslear, Bauman, Hursh, Shurtleff and Simmons (1988; see Figure 2A) and Cassidy and Dallery (2012; see Figure 10) show that demand curves change little across redeterminations. Hence, in terms of reliability, demand analysis seems superior to a preference test in determining the value of a reinforcer.

It is easy to rationalize the lability of preference in test-retest comparisons in Figure 5. With highly substitutable goods (fruit versus fruit), small differences between their characteristics can result to exclusive choice of one alternative over another. As argued in the Introduction, a small price change could dramatically shift preference between highly similar cars. If these goods differed more in substitutability (e.g., a car versus a motorcycle), preference would be less labile, a fact that would be reflected by requiring larger price changes to alter preferences. Taking this point farther, consider what would happen if the goods were not substitutable at all (e.g., tires and cars needing tire replacement). You would find preference to be largely invariant (e.g., purchase of four tires for every car) across large changes in price for one or the other good. For this reason, we find it unsurprising that many of the fruit-versus-fruit preferences were absolute, an outcome consistent with the idea that these goods do not differ widely in value even though preference differences were large. Indeed, only when these goods are compared in a demand analysis can the small value differences between them be discerned (e.g., see Lenny in Figure 2).

This argument supports two predictions for Experiment 2. Regarding the first prediction, when value is measured in terms of preference (relative choice frequencies), the differences between highly substitutable goods should often be greater and more labile than between goods that are less substitutable. In other words, the size of this preference should be less for fruit versus cereal than for fruit versus fruit, just as should be the case for the preference between a car without tires and new tires, compared to the preference between two tire brands.

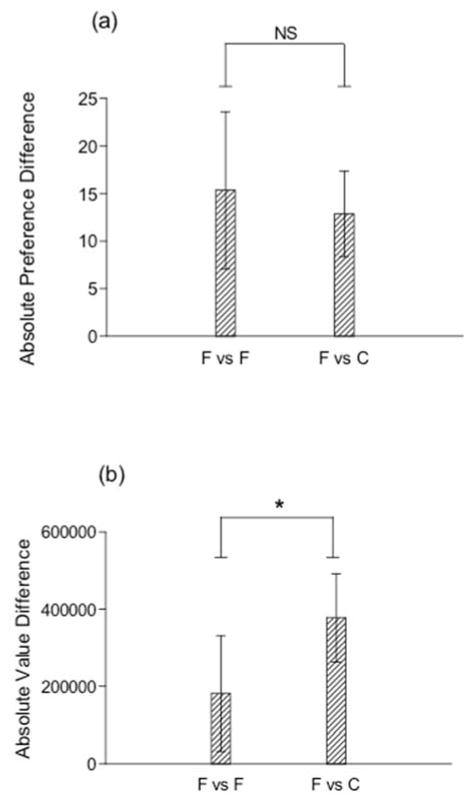
This prediction was evaluated in Figure 6a. It presents the absolute differences between choices for fruit 1 versus fruit 2, and between either fruit versus cereal. While the data are ordinally consistent with the prediction—they show a greater preference difference between the putatively more substitutable pair of goods (fruit versus fruit rather than fruit versus cereal)— this difference is not statistically significant [t (16) = .68, p = .51, 95% CI (−5.29, 10.29)].

Figure 6.

Panel a presents the mean and the 95% confidence intervals of the mean for the absolute difference in the number of choices of food items when both foods were fruits (left bar) and when one was a fruit and the other a cereal (right bar). Panel b presents the mean and 95% confidence intervals of the mean for the absolute essential-value difference between two fruits (left bar) and a fruit and a cereal (right bar). These measures are based on Equation 1 from Experiment 1. F refers to fruit and C refers to cereal

The second prediction was evaluated in Figure 6b—that when value is assessed by a demand analysis, the smaller preference seen for the less substitutable goods (fruits versus cereals) nevertheless differ more in value from each other than the pairs of fruits. As seen in this panel, this prediction is apparent and statistically significant [t (16) = −2.322, p = .03, 95% CI (−3.75E+5, −1.71E+4), d= −1.16].

It is also possible to test the significance of the conjoint prediction that the fruit-versus-cereal preference difference should be lower than the fruit-versus-fruit comparison in the top panel even though a value determination from a demand analysis in the lower panel supports the opposite conclusion. We tested this conjoint prediction with concatenated chi-square tests (see Winer, 1971), and it is statistically significant [χ² (2, N = 2) = 10.90, p < .03, V=1.16].

General Discussion

In Experiment 1, we recorded the frequency with which a monkey would lift a particular weight for each of three foods in a 10-min session. All performances followed the Law of Demand: As “price” increased across sessions, an outcome arranged by increasing the amount of effort the monkey expended to lift a weight for a food item, the number of food items “purchased” decreased. Regardless of the food type, the demand curves generated by this price manipulation were well-described by Equation 1. If this equation is given credence, a single parameter, α, is inversely related to the value of each food. When scaled in terms of essential value (1/α) the three food types did not differ much from one another for four of the six monkeys (see Figure 2), and there were no significant differences in their values (see Figure 3).

Experiment 2 measured value another way, by looking at preferences among the three foods when they were offered in pairwise choice. This measure assumes that if one good is of more value than another, it would be preferred, and the greater the difference in preference, the greater the difference in value. One might anticipate that these measures would be closely related to one another. However, Figure 4 shows that there is no relation between the value scores based on a preference test and those based on the exponential model of demand (Equation 1). This outcome leads to an important question: which of these two measures is to be preferred as a value measure?

We argued that Equation 1 is the superior measure of value because it is less labile in its value designations than is a preference test. We demonstrated the lability of preference tests by comparing between-fruit preference data in this study against those from a prior study in which the same fruits and monkeys were used. We found little relation between these successive preference tests (see Figure 5). Given these data are not consistent in redetermination, it seems difficult to assign relative value to goods offered in choice based on historical preference data. As noted above (although not demonstrated in this study), reliability across redeterminations is a consistent characteristic of essential value as measured by demand analysis because α scores from Equation 1 are largely unchanged across redeterminations.

Figure 5.

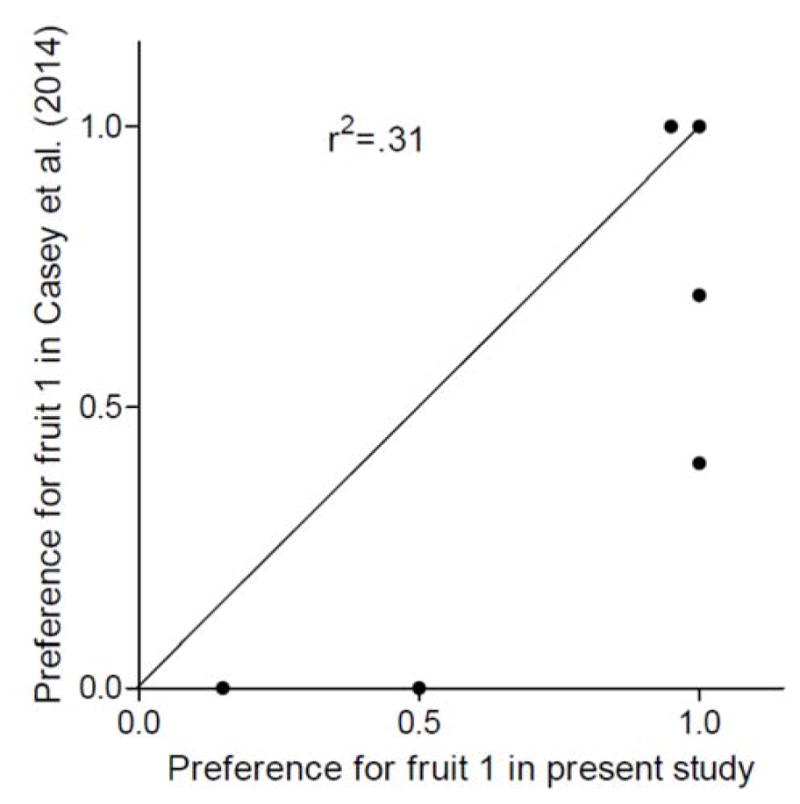
Relative response rate for fruit 1 (choices of fruit 1 divided by all fruit choices) from Casey et al. (2014) as a function of relative response rate for fruit 1 from the present report. The diagonal through the plot defines the locus of perfect invariance in outcome between these two determinations

The greater stability of α favors its use over degree of preference as a measure of value. Indeed, at least for the data shown in Experiment 2, to argue otherwise is to endorse a measure of value that is in flux. Nevertheless, the greater stability of α matters little if α is not a plausible correlate of what could sensibly be called “value.” Microeconomists view it as sensible, and often use the so-called “diamond-water paradox” to illustrate to students its superiority over preference measures. In many circumstances, a diamond is preferred to a glass of water. If, however, each good is scarce, this preference would reverse—that is, consumers would defend their water consumption over a diamond. As is apparent, this reversal in choice is only paradoxical if one insists value is measured by preference. Measured by demand analysis, there is no paradox because consumers will quit defending diamond consumption before they will quit defending water consumption. Water is the higher-value good.

We believe researchers would be better served by valuing foods by demand analysis. Given the stability that is evident in demand-determined essential values, these determinations might only need to be done once for a given animal, and then could be generally applied without being repeated in subsequent studies. Alternatively, researchers might abjure use of qualitatively different foods, using instead different food amounts. Indeed, in terms of the variability of outcome in inequity aversion tests, one can be confident that more food of the same kind is of greater value than less food, at least for modest amounts. This expected result has nothing to do with substitutability. Rather it is due to a large income difference between identical foods in different amounts offered in choice.

Ironically, the notion of nonhuman inequity aversion is derived from a literature where all tests of the effect are based on payoff differences where a single good (i.e., money) is used (Fehr & Schmidt 1999). Given this fact, it is curious that tests of nonhuman inequity aversion are typically based on goods that vary not in amount, but in kind. Perhaps if nonhuman inequity aversion in monkeys was tested using, say, one versus four raisins, a robust inequity effect would emerge that endures incidental variation in procedure and species. Indeed, there is a large literature in choice that supports the view not only that more is preferred to less, but that such effects are consistently reproducible both within subjects and between species.

From the perspective of a microeconomist, presenting different amounts of a unitary good in choice should result in preferences for larger-over-smaller amounts. However, even with such an arrangement, preference levels are sensitive to income levels. For example, Hastjarjo and Silberberg (1992) found in a delay-discounting design that impulsivity grew with food income level when rats earned their daily food ration within the experiment. Thus, the degree of rat impulsivity was not simply a consequence of a species’ patience; it was also a consequence of its session-wide income. If a daily ration could be earned by behaving impulsively, rats do so; if not, they become patient. Related income effects have also been noted when the goods offered in choice differ in kind (e.g., Elsmore, Fletcher, Conrad, & Sodetz 1980). Data such as these join those presented in this report in pointing to the importance of understanding the economy in which psychological processes are evaluated. Once this is understood, studies in which foods of contrasting value are to be presented might have the differences expressed in terms of food amounts, and not food qualities.