Jacobian-Based Iterative Method for Magnetic Localization in Robotic Capsule Endoscopy

Abstract

The purpose of this study is to validate a Jacobian-based iterative method for real-time localization of magnetically controlled endoscopic capsules. The proposed approach applies finite-element solutions to the magnetic field problem and least-squares interpolations to obtain closed-form and fast estimates of the magnetic field. By defining a closed-form expression for the Jacobian of the magnetic field relative to changes in the capsule pose, we are able to obtain an iterative localization at a faster computational time when compared with prior works, without suffering from the inaccuracies stemming from dipole assumptions. This new algorithm can be used in conjunction with an absolute localization technique that provides initialization values at a slower refresh rate. The proposed approach was assessed via simulation and experimental trials, adopting a wireless capsule equipped with a permanent magnet, six magnetic field sensors, and an inertial measurement unit. The overall refresh rate, including sensor data acquisition and wireless communication was 7 ms, thus enabling closed-loop control strategies for magnetic manipulation running faster than 100 Hz. The average localization error, expressed in cylindrical coordinates was below 7 mm in both the radial and axial components and 5° in the azimuthal component. The average error for the capsule orientation angles, obtained by fusing gyroscope and inclinometer measurements, was below 5°.

I. Introduction

Wireless capsule endoscopy (WCE) allows physicians to visualize internal organs for diagnosis and potentially for intervention. This paper focuses on creating a modeling and algorithmic framework for localization of magnetically actuated WCEs. All the existing platforms for remote magnetic manipulation of a WCE inside the patient’s body operate in open loop [1], i.e., the capsule pose (i.e., position and orientation) is not tracked and used for control feedback purposes. Position control of WCEs is typically based on the assumption that the permanent magnet inside the capsule aligns with the external magnetic field. Pose tracking of the WCE would allow the capsule to automatically optimize magnetic coupling to maintain effective magnetic actuation, enabling the user to detect if the capsule is not following the expected trajectory (i.e., the capsule is trapped within a tissue fold), and to take appropriate countermeasures for reestablishing an effective motion. An example of position closed-loop control for a magnetically manipulated WCE is presented in [2], where optical tracking with external cameras is adopted to localize the capsule. To apply these results in a clinical setting and move toward the closed-loop manipulation of magnetic WCE position and orientation, online pose tracking without line-of-sight is crucial [3], [4].

Known methods for WCE pose tracking were designed largely for diagnostic purposes (i.e., to associate a lesion visualized by the capsule to its position inside the patient’s body) [5]–[8] and are not compatible with magnetic manipulation due to electromagnetic interference with the external source of the driving field. Recently, a number of groups working on robotic magnetic manipulation of WCE began studying localization strategies that are compatible with magnetic manipulation. These works implement localization based on measuring the magnetic field at the WCE via magnetic field sensors (MFSs). Generally, these works rely on absolute localization using simple dipole models (e.g., [9] and [10]) or lookup tables based on finite-element solutions to the exact magnetic field (e.g., [3] and [11]). The simple dipole models provide limited localization performance when the WCE is close to the magnetic field source. They work best when the WCE workspace is far away from the driving magnet. However, to maximize the magnetic coupling, the WCE should ideally operate as close as possible to the driving magnet. The drawbacks of lookup-table-based localization are the slow refresh rate and large memory requirements.

The performance of current WCE localization algorithms provide modest localization accuracy within limited workspace. In [10], multiple measurements taken of the capsule moving along its main axis toward the external magnet allows the user to obtain the position in three degrees of freedom (DOF) with an error below 4 mm when the capsule is within 6 cm of an external magnet. Continuous rotation of the capsule by an external revolving magnetic field combined with on-board magnetic field sensing [9] allows detection of the capsule position and orientation with an average error of 11 mm and 11° within the operative workspace. Real-time systems, such as in [3], [4], and [11], leverage sensor fusion (i.e., inertial and magnetic field sensing) and search within precompiled finite-element magnetic maps. In particular, the method proposed in [11] achieves a refresh rate of 50 ms and a position error of 10 mm within a 12-cm workspace. Better performances are obtained in [4], where the refresh rate goes down to 30 ms and the error drops below 6 mm within a 15-cm workspace. Finally, in our previous work [4], the sensor data acquisition and the localization algorithm required 6.5 and 16 ms per loop, respectively. One of the aims of our proposed new localization method is to decrease computational time, thus achieving both sensor acquisition and localization within 10 ms, allowing the implementation of a 100-Hz WCE manipulation closed-loop control.

In this paper, we validate our proposed algorithm on a WCE localization setup that includes an extracorporeal magnetic field source that manipulates an intracorporeal WCE. The localization strategy proposed herein aims to provide the change in pose of a WCE with respect to an external magnetic field source having known position and orientation. Using an approach similar to that used in [3], [4], and [11], the capsule is henceforth assumed to be equipped with an inertial measurement unit (IMU) and six orthogonal MFSs. When inertial data from IMU are integrated, as we propose in our method, drift becomes an issue over time. For this reason, our approach is best used in synergy with an absolute localization technique [3], [4] working at a slower refresh rate. In such a scheme, the absolute localization can repeatedly provide initialization values to our algorithm, thus preventing the integration error from exceeding a desired value.

The contribution of this paper stems from putting forward a new approach for WCE localization by using an iterative Jacobian-based method. To the best of our knowledge, iterative methods for WCE pose tracking that are compatible with magnetic manipulation have not been presented in prior works, partly because a complete analytical solution for the magnetic field is not available. To overcome this challenge, we apply finite-element solutions to the magnetic field problem and least-squares interpolations to obtain closed-form and fast estimates of the magnetic field. By defining a closed-form expression for the Jacobian of the magnetic field relative to changes in the WCE pose, we are able to obtain an iterative WCE localization method without the inaccuracies stemming from dipole assumptions and without the downside of a slow refresh rate.

II. Method

A. Iterative Method for Magnetic Localization

Our localization approach is inspired by Jacobian-based methods (also known as resolved rates methods stemming from [12]). These methods are commonly used in robotics to solve systems of nonlinear equations subject to the limitations of firstorder linearization. In this paper, we assume that the refresh rate for pose tracking is fast enough that only small movements of the WCE may occur between subsequent pose measurements. We also assume that the orientation of the capsule is known through the algorithm described in Section III running on IMU data.

In order to apply an iterative method to magnetic localization, we need to consider the magnetic field, generated by a known source, as the following time-invariant nonlinear mathematical expression:

$${\mathbf{B}}_i=f\left({\mathbf{p}}_i\right),f\left({\mathbf{p}}_i\right):{\mathbb{R}}^3\to {\mathbb{R}}^3.$$ (1)

This equation will be denoted as magnetic direct relationship (MDR). Referring to Fig. 1, the MDR associates the coordinates of a point outside the magnetic field source p_i = [x_i, y_i, z_i]^T to a corresponding vector function of magnetic field values B_i = [B_ix, B_iy, B_iz]^T.

Fig. 1.

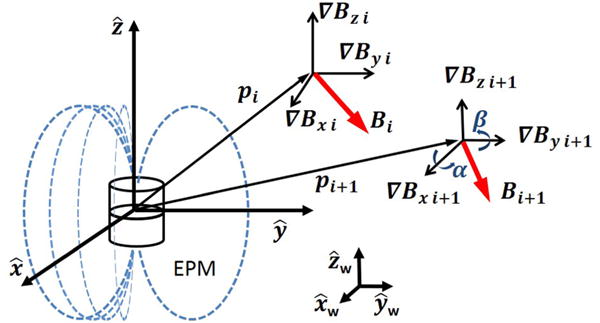
Schematic representation of the source of magnetic field (EPM in the figure) and two sequential positions (i.e., p_i and p_i+1) of the capsule to be localized. The capsule orientational angles yaw and pitch are referred to as α and β, respectively.

If the capsule position changes from p_i to p_i+1 during a time increment Δt, the displacement Δp produces a change in the magnetic field measurements from B_i to B_i+1 according to (1). The partial derivative of the magnetic field vector, i.e., $\frac{\partial }{\partial p}{\mathbf{B}}_i$ is given by

$$\frac{\partial {\mathbf{B}}_i}{\partial \mathbf{p}}={\nabla }_{p}f\left({\mathbf{p}}_i\right)=\left[\begin{array}{ccc}\frac{\partial {\mathbf{B}}_x}{\partial p_x}& \frac{\partial {\mathbf{B}}_x}{\partial p_y}& \frac{\partial {\mathbf{B}}_x}{\partial p_z}\\ \frac{\partial {\mathbf{B}}_y}{\partial p_x}& \frac{\partial {\mathbf{B}}_y}{\partial p_y}& \frac{\partial {\mathbf{B}}_y}{\partial p_z}\\ \frac{\partial {\mathbf{B}}_z}{\partial p_x}& \frac{\partial {\mathbf{B}}_z}{\partial p_y}& \frac{\partial {\mathbf{B}}_z}{\partial p_z}\end{array}\right]$$ (2)

where ∇_pf(p_i) designates the gradient of f with respect to p. Using (2) in a first-order Taylor series approximation, we obtain

$${\mathbf{B}}_{i+1}={\mathbf{B}}_i+\frac{\partial {\mathbf{B}}_i}{\partial \mathbf{p}}\mathrm{\Delta }\mathbf{p}={\mathbf{B}}_i+{\nabla }_{p}f\left({\mathbf{p}}_i\right)\mathrm{\Delta }\mathbf{p}.$$ (3)

The magnetic inverse relationship (MIR), providing the current capsule position p_i+1, can be derived by inverting (3) as

$${\mathbf{p}}_{i+1}={\mathbf{p}}_i+{\nabla }_p{f}^{-1}\left({\mathbf{p}}_i\right)\mathrm{\Delta }{\mathbf{B}}_i.$$ (4)

Moving from differential to the finite-difference iterative method, $\frac{\partial \mathbf{B}}{\partial p}\mathrm{\Delta }\mathbf{p}$ replaced by ΔB_i, where ΔB_i is defined as ΔB_i = (B_i+1 − B_i). In addition, according to [13], the gradient of a generic vectorial function, which is defined as f(x): ℝⁿ → ℝ, is the transpose of the Jacobian as: ∇_xf(x) = (J_xf(x))^t. Then, (4) becomes

$${\mathbf{p}}_{i+1}={\mathbf{p}}_i+{\mathbf{J}}_p^{-1}\mathrm{\Delta }{\mathbf{B}}_i$$ (5)

where ${\mathbf{J}}_p^{-1}$ is the inverse of the Jacobian.

An explicit formulation of the MDR (1) can be obtained by finite-element integration of magnetic field models, as suggested in [14], while a numerical estimate can be provided by a standard finite-element method software package, such as Comsol Multiphysics or ANSYS Maxwell. In the next subsections, we introduce a nonlinear interpolation method for a dataset of magnetic field values related to the position p_i. Then, the interpolation is used to provide an analytical expression of the MDR through modal representation, numerical algebra theory, and the Kronecker product. Finally, a first-order resolved rates method using the Jacobian expression for the MIR is derived.

Fig. 2 represents the proposed magnetic localization algorithm exploiting sensor fusion of magnetic field and inertial measurements. The magnetic field interpolation (also called magnetic field calibration) is achieved offline, which leads to obtain the characteristic matrices A_r and A_z. Once the interpolation is obtained, the online algorithm takes as input the magnetic field, the inertial measurements, and the external permanent magnet (EPM) orientation, returning the capsule pose. The capsule position is referred to the EPM frame, whereas the orientation expressed in Euler angles is relative to the world frame. The blocks DMR-IMR—which stand for direct and inverse magnetic relationship—and the iterative Jacobian method are presented in Section II-B, while the 3-D reconstruction is presented in Section II-C.

Fig. 2.

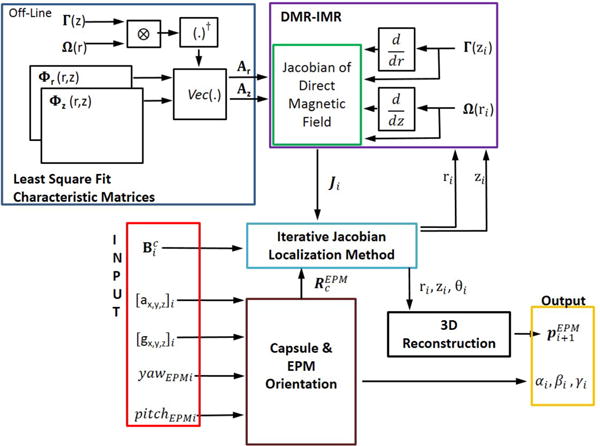
Block diagram of the proposed iterative algorithm for WCE pose detection. The diagram displays system input, output, Jacobian of the MDR, 3-D reconstruction, and the offline least-squares fit calibration, which leads to the characteristic matrices A_r and A_z.

B. Direct and Inverse Magnetic Relationship

The magnetic field of a cylindrical axially magnetized permanent magnet exhibits cylindrical symmetry around its main axis $\left(\widehat{\mathbf{z}}\right)$ [15], [16]. If such a magnet is used as the external source of a magnetic field for capsule manipulation, as suggested in our previous work [3], [4], the localization can take advantage of the symmetry to reduce the computational burden. In particular, the 3-D position-tracking problem can be reduced to two dimensions. Then, once the position in 2-D is obtained, the third coordinate can be derived by sensor fusion as explained in Section II-C.

As represented in Fig. 3, the magnetic field is distributed around the main axis of symmetry of the EPM, $\widehat{\mathbf{z}}$, while B_θ—angular component of the magnetic field along θ—is null. The vector ${\stackrel{\sim }{\mathbf{p}}}_c={\left[r,\theta ,z\right]}^t$ represents a generic point on the loci of points, whose location satisfies the condition of having the same magnetic field B_c. This set of points of the locus generates a circumference ϒ (represented in Fig. 3) that can be analytically described as ϒ = [r, θ, z] |r, z = const ∈ ℝ, and θ ∈ 0 → 2π. We refer to ${\stackrel{\sim }{\mathbf{p}}}_c={\left[r,\theta ,z\right]}^t$ as the generic point on the loci, which is expressed in the three cylindrical coordinates, whereas p_c lies on the plane ℋ and is obtained by applying a rotation about $\widehat{\mathbf{z}}$ to ${\stackrel{\sim }{\mathbf{p}}}_c$. The plane ℋ is defined as: ℋ = ℝ²: {(r, z)|r, z ∈ ℝ and θ = 0}.

Fig. 3.

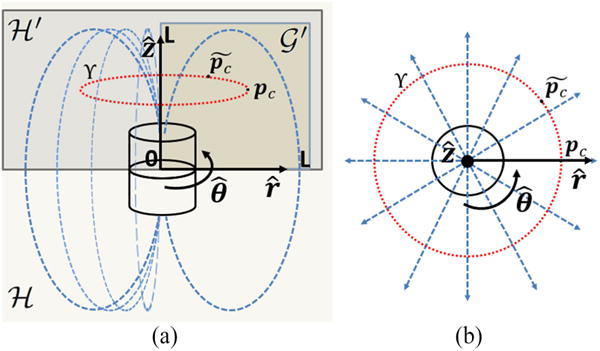
Schematic view of the magnetic field distribution for a cylindrical axially magnetized permanent magnet. (a) View of the ℋ planes, its subset ℋ′, and the domain $\mathcal{G}\prime$. (b) Radial distribution of the magnetic field on the plane $\left[\widehat{r},\widehat{\theta }\right]$.

Considering the magnetic field applied on a generic point ${\stackrel{\sim }{\mathbf{p}}}_c$, its components are expressed as B_c = [B_r(r,z),B_θ(r,z),B_z(r,z)], where B_θ (r, z) = 0. Therefore, (1) could be furthermore simplified by defining the mathematical representation Ψ for the magnetic field B_c. The magnetic field B_c is given by the 2-D transformation Ψ for any given point ${\stackrel{\sim }{\mathbf{p}}}_c$ around the magnetic field source, such as Ψ: ${\stackrel{\sim }{\mathbf{p}}}_c$ → B_c. B_r(r,z) and B_z(r,z) are two scalar values representing the radial and the axial component of the magnetic field vector, which are functions of axial and radial spatial coordinates with respect to the center of the EPM.

The solution to the system of equations expressed by the transformation Ψ—in terms of both radial B_r(r,z) and axial B_z(r,z) magnetic field—is unique in the semidomain ℋ′ defined as in Fig. 3 (note that the semidomain ℋ′ can be either related to the south or the north pole of the cylindrical axially magnetized EPM). Then, we define a finite domain $\mathcal{G}\prime$, where the magnetic field radial component B_r is always positive. On the other hand, if considering the domain ℋ, the transformation Ψ leads to two solutions in diagonally opposite quadrants in Fig. 3. Since the patient cannot be simultaneously above and below the magnet, we exclude one quadrant for practical implementation reasons. The region is a square plane having size L along $\widehat{r}$ and $\widehat{\mathbf{z}}$, where the spatial transformation f(p_c) in (1) is simplified and solvable as

$$\begin{array}{l}\mathrm{\Psi }\left({\mathrm{p}}_c\right):{\mathbb{R}}^2\to {\mathbb{R}}^2\\ \text{where}{\mathrm{p}}_c\in \mathcal{G}\prime :\mathcal{G}\prime =\left\{\left(r,z\right)\in \left[0,L\right]\right\}.\end{array}$$ (6)

The transformation Ψ(p_c) can be expressed by two scalar mathematical functions, each with two inputs. The two functions provide the magnetic field radial component as

$$B_r={\psi }_r\left(r,z\right):{\mathbb{R}}^2\to \mathbb{R}.$$ (7)

and the magnetic field axial component as

$$B_z={\psi }_z\left(r,z\right):{\mathbb{R}}^2\to \mathbb{R}.$$ (8)

The numerical solution of (7) and (8) can be obtained by either applying the current density magnetic model or the charge density magnetic model, as demonstrated in [15] and [16]. Then, the magnetic field values can be casted in two data matrices Φ_r ∈ ℝ^m×p and Φ_z ∈ ℝ^m×p. These matrices represent the m × p magnetic field numerical solutions for any given position p_c within $\mathcal{G}\prime$, where m is the number of magnetic field measurements taken along the $\widehat{\mathrm{r}}$ direction and p is the number of magnetic field measurements taken along $\widehat{\mathbf{z}}$. The collection of numerical solutions [Φ_r, Φ _z]^T of (7) and (8), are expressed as

$$\begin{array}{l}{\mathbf{\Phi }}_r=\left[{\mathbf{\Phi }}_{\mathit{rij}}\left(r_i,z_j\right)\right]\\ i\in \mathbb{N}:\left[1\le i\ge m\right];j\in \mathbb{N}:\left[1\le j\ge p\right]\end{array}$$ (9)

$$\begin{array}{l}{\mathbf{\Phi }}_z=\left[{\mathbf{\Phi }}_{zij}\left(r_i,z_j\right)\right]\\ i\in \mathbb{N}:\left[1\le i\ge m\right];j\in \mathbb{N}:\left[1\le j\ge p\right]\end{array}$$ (10)

where Φ_rij and Φ_zij are the magnetic field values at position (i,j), which could be generally expressed as Φ_ij. The single matrix element Φ_ij can be approximated by applying the modal representation defined in [17]–[19] as

$$\begin{array}{l}{\mathbf{\Phi }}_{ij}={\mathrm{B}}_i\left(r,z\right)=\mathit{\omega }{\left(r\right)}^T\mathbf{a}\left(z\right),\\ \text{where}\left(\mathbf{a},\mathit{\omega }\right)\in {\mathbb{R}}^n.\end{array}$$ (11)

The vector of the modal factors, i.e., a(z), can be expressed as

$$\begin{array}{l}\mathbf{a}\left(z\right)=\mathbf{A}\mathit{\gamma }\left(z\right),\\ \text{where}\left(\mathbf{A},\mathit{\gamma }\right)\in {\mathbb{R}}^n.\end{array}$$ (12)

In this equation, A is the characteristic matrix of coefficients for the particular magnetic field shape that, together with the two orthogonal bases ω = {ω₀, ω₁, …, ω_n} and γ = {γ₀, γ₁, …, γ_q}, represents the interpolation functions that best numerically approximate the transformation Φ_ij over the domain of interest [20]. Once the interpolation functions ω and γ are chosen (see Section IV-A), and the characteristic matrices of coefficients A_r and A_z for radial and axial magnetic field, respectively, are derived, the interpolation problem can be easily solved. The best dataset interpolation is chosen by adopting the orthogonal function that minimizes the least-squares error between the reference measure f(x) and the approximated value y*, such as ||f(x) − y*|| < δ. Examples of orthogonal functions investigated in this study include standard polynomial functions, Chebyshev polynomials [18], [19], Fourier harmonic basis [20], [21], and composition of these.

In the following paragraph, we describe how to derive the characteristic matrices of coefficients A_r and A_z for the algebraic equations system in (11) and (12) by using the following matrix representation, as suggested in [18] and [19]:

$$\mathbf{\Phi }={\mathbf{\Omega }}_{m\times n}{\mathbf{A}}_{n\times q}{\mathbf{\Gamma }}_{q\times p}$$ (13)

where Φ is either the MDR solutions of Φ_r or Φ_z within r, z ∈ [0 → L], while Ω and Γ are the modal basis matrices and constitute the collection of n orthogonal basis for Ω and q orthogonal basis for Γ. Finally, m and p are the number of values estimated in the domain r ∈ [0, L] and z ∈ [0, L], respectively.

The solutions for A_r and A_z can be obtained by applying the Kronecker product theory as in [18], [19], and [22], where the symbol ⊗ represents the Kronecker product of two matrices as

$$\mathit{Vec}\left(\mathbf{\Phi }\right)=\left[{\mathbf{\Gamma }}^T\otimes \mathbf{\Omega }\right]\mathit{Vec}\left(\mathbf{A}\right).$$ (14)

The result provided by the algebraic interpolation is the generic matrix of coefficients A, which is given by

$$\begin{array}{l}\mathit{Vec}\left(\mathbf{A}\right)={\left[{\mathbf{\Gamma }}^T\otimes \mathbf{\Omega }\right]}^{†}\mathit{Vec}\left(\mathbf{\Phi }\right),\\ \text{where}\mathit{Vec}\left(\mathbf{A}\right)={\left[a_{11}\dots a_{n1}\dots a_{n2}\dots a_{np}\right]}^T.\end{array}$$ (15)

Once the matrices A_r and A_z are known, the MDR, such as ψ(z, y) : (z, y) → (Φ_ij), is solved for any point within the domain $\mathcal{G}\prime =\left\{\left(r,z\right)\in \left[0,L\right]\right\}$.

Given the calibration matrices A_r and A_z, and the orthogonal basis ω(r) and γ(z), the system of equation expressed in (11) and (12) is completely determined. By differentiating ω(r) and γ(z) in ∂r and ∂z, respectively, we can obtain the complete formulation of the MIR in (2). The following system of equations—expressed for the single solution [Φ_r, Φ_z]^T— provides the ground to derive the Jacobian:

$$\{\begin{array}{c}{\mathbf{\Phi }}_r=\mathit{\omega }\left(r\right){\mathbf{A}}_r\mathit{\gamma }\left(z\right)\\ {\mathbf{\Phi }}_z=\mathit{\omega }\left(r\right){\mathbf{A}}_z\mathit{\gamma }\left(z\right).\end{array}$$ (16)

Applying (2) to this system of equations, and deriving the partial derivatives of Φ = [Φ_r, Φ_z]^T such as $\frac{\partial {\mathbf{\Phi }}_r}{\partial r},\frac{\partial {\mathbf{\Phi }}_r}{\partial z},\frac{\partial {\mathbf{\Phi }}_z}{\partial r},\frac{\partial {\mathbf{\Phi }}_z}{\partial z}$ the gradient of Φ becomes

$$\nabla \mathbf{\Phi }=\{\begin{array}{c}\nabla {\mathbf{\Phi }}_r=\frac{\partial \left(\mathit{\omega }\left(r\right){\mathbf{A}}_r\mathit{\gamma }\left(z\right)\right)}{\partial r}+\frac{\partial \left(\mathit{\omega }\left(r\right){\mathbf{A}}_r\mathit{\gamma }\left(z\right)\right)}{\partial \mathrm{z}}\\ \nabla {\mathbf{\Phi }}_z=\frac{\partial \left(\mathit{\omega }\left(r\right){\mathbf{A}}_z\mathit{\gamma }\left(z\right)\right)}{\partial r}+\frac{\left(\partial \mathit{\omega }\left(r\right){\mathbf{A}}_z\mathit{\gamma }\left(z\right)\right)}{\partial z}.\end{array}$$ (17)

Considering that the derivatives of the constant coefficient matrices A_r and A_z are null, as well as $\frac{\partial \mathit{\omega }\left(r\right)}{\partial z}$ and $\frac{\partial \mathit{\gamma }\left(z\right)}{\partial r}$, (17) simplifies to

$$\begin{array}{l}\frac{\partial {\mathbf{\Phi }}_r}{\partial r}=\frac{\partial \mathit{\omega }\left(r\right)}{\partial r}{\mathbf{A}}_r\mathit{\gamma }\left(z\right)\\ \frac{\partial {\mathbf{\Phi }}_r}{\partial z}=\mathit{\omega }\left(r\right){\mathbf{A}}_r\frac{\partial \mathit{\gamma }\left(z\right)}{\partial z}\\ \frac{\partial {\mathbf{\Phi }}_z}{\partial r}=\frac{\partial \mathit{\omega }\left(r\right)}{\partial r}{\mathbf{A}}_z\mathit{\gamma }\left(z\right)\\ \frac{\partial {\mathbf{\Phi }}_z}{\partial z}=\mathit{\omega }\left(r\right){\mathbf{A}}_z\frac{\partial \mathit{\gamma }\left(z\right)}{\partial z}.\end{array}$$ (18)

In order to obtain the expression of $\frac{\partial \mathrm{\omega }\left(r\right)}{\partial r}$ and $\frac{\partial \mathit{\gamma }\left(z\right)}{\partial z}$, a derivation is applied to the vectors constituting the orthogonal basis ω(r), γ(z). This leads to the following expression for the Jacobian J_Φ:

$${\mathbf{J}}_{\mathbf{\Phi }}={\nabla }_{\stackrel{\sim }{p}c}\mathbf{\Phi }\left(r,z\right)=\left[\begin{array}{cc}\frac{\partial {\mathbf{\Phi }}_r}{\partial r}& \frac{\partial {\mathbf{\Phi }}_r}{\partial z}\\ \frac{\partial {\mathbf{\Phi }}_z}{\partial r}& \frac{\partial {\mathbf{\Phi }}_z}{\partial z}\end{array}\right].$$ (19)

Therefore, the magnetic field vector incremental difference $\mathrm{\Delta }{\mathbf{B}}_i={\left[\mathrm{\Delta }{B}_r,\mathrm{\Delta }{B}_z\right]}_i^T$ is given by

$$\mathrm{\Delta }{\mathbf{B}}_i={\left[\begin{array}{c}\mathrm{\Delta }{B}_r\\ \mathrm{\Delta }{B}_z\end{array}\right]}_i={\mathbf{J}}_{\mathbf{\Phi }}\mathrm{\Delta }{\mathbf{p}}_{ci}.$$ (20)

This result can be used in (3) to estimate the magnetic field B_i+1 by continuously updating ΔB_i to the current magnetic

$${\mathbf{B}}_{i+1}={\mathbf{B}}_i+\mathrm{\Delta }{\mathbf{B}}_i={\mathbf{B}}_i+{\mathbf{J}}_{\mathbf{\Phi }}\mathrm{\Delta }{\mathbf{p}}_{ci}.$$ (21)

In conclusion, the following equation shows the iterative method to localize the WCE, estimating the current position p_ci+1 = [r_i+1, z_i+1]^T of the capsule as

$${\mathbf{p}}_{ci+1}={\mathbf{p}}_{ci}+\mathrm{\Delta }{\mathbf{p}}_{ci}={\mathbf{p}}_{ci}+{\mathrm{J}}_{\mathbf{\Phi }}^{-1}\mathrm{\Delta }{\mathbf{B}}_i$$ (22)

where J⁻¹ is the pseudoinverse of the Jacobian, which applies the least-squares method of optimization to the solution [23]. The term ΔB_i is the difference in magnetic field recorded from the previous measurement.

C. Three-Dimensional Reconstruction

In order to track the WCE by applying the iterative algorithm, both the spatial orientation of the capsule and the external magnetic source pose must be known with respect to a common reference frame. The magnetic field vector B_c at the capsule position ${\stackrel{\sim }{\mathrm{p}}}_c$—expressed in the capsule frame $\left[{\widehat{\mathrm{x}}}_c,{\widehat{\mathrm{y}}}_c,{\widehat{\mathrm{z}}}_c\right]$—is measured by the onboard sensors. This vector can be expressed in the EPM frame $\left[\widehat{\mathbf{x}},\widehat{\mathbf{y}},\widehat{\mathbf{z}}\right]$ by applying the geometrical transformation ${\mathbf{R}}_c^{\mathrm{EPM}}$, thus obtaining B.

Then, considering Figs. 1 and 3, the magnetic field vector B is expressed in cylindrical coordinates from its Cartesian coordinates, such as B = [B_x,B_y,B_z]^T → [B_r, B_z]^T and θ, where θ corresponds to the azimuthal coordinate of the capsule position ${\stackrel{\sim }{\mathrm{p}}}_c$. The relationships that transform the magnetic field vector ${\mathbf{B}}_c=\left[B_x\widehat{\mathbf{x}},B_y\widehat{\mathbf{y}},B_z\widehat{\mathbf{z}}\right]$ from Cartesian to cylindrical coordinates are

$$\begin{array}{l}{\mathbf{B}}_r=\sqrt{\left(B_x\widehat{\mathbf{x}}\right)+{\left(B_y\widehat{\mathbf{y}}\right)}^2}\widehat{\mathbf{r}}\\ {\mathbf{B}}_z=B_z\widehat{\mathbf{z}}\\ \mathbf{\theta }=\mathrm{atan}2\left(B_y,B_x\right)\widehat{\mathbf{\theta }}\end{array}$$ (23)

where B_x, B_y, B_z are the Cartesian components of the magnetic field vector B with respect to the EPM frame $\left[\widehat{\mathbf{x}},\widehat{\mathbf{y}},\widehat{\mathbf{z}}\right]$. The axial and radial magnetic field components can be fed into the iterative algorithm, which derives the radial and axial coordinates of the capsule p_c = [p_r, p_z]. These can be used in combination with θ to derive the three Cartesian coordinates as

$$\begin{array}{l}{\mathbf{p}}_x=p_r\cos \left(\theta \right)\widehat{\mathbf{x}}\\ {\mathbf{p}}_y=p_y\sin \left(\mathrm{\theta }\right)\widehat{\mathbf{y}}\\ {\mathbf{p}}_z=p_z\widehat{\mathbf{z}}.\end{array}$$ (24)

III. Capsule Orientation Algorithm

This section presents the algorithm used to detect the change in capsule orientation and to generate the rotational matrix R_c with respect to the global frame. This algorithm based on the fusion of inclinometer and gyroscope outputs is widely adopted in the literature and is provided here for the sake of completeness. The capsule orientation knowledge is required in our magnetic localization approach in order to express the magnetic field vector B_c in the EPM frame.

Referring to Fig. 1, the accelerometer can be used as an inclinometer to obtain the absolute values of the two orientational angles α and β [24]. The rotations about x_c and y_c are derived directly from the gravitational vector g projection mapped on the three orthogonal axes of the onboard accelerometer as

$$\begin{array}{l}\mathit{\alpha }=\mathrm{atan}2(a_y,\sqrt{a_x^2+a_z^2})\\ \mathit{\beta }=\mathrm{atan}2(a_x,\sqrt{a_y^2+a_z^2})\end{array}$$ (25)

where a_x, a_y, a_z are the three accelerometer outputs.

A number of methods for inertial navigation can be adopted to estimate the third orientation angle γ, which is the rotational angle along the gravitational vector g. Examples span from fusing gyroscope and inclinometer measurements [25], [26] to applying a quaternion-based algorithm to inertial data [27]. The approach we have adopted involves applying the axis-angle method for rotational matrices to the gyroscope outputs [28]. Briefly, it is possible to extract the rotation γ about the global axis z_w by building the rotational matrix ###ΔR_c with respect to the moving frame attached to the capsule $\left[{\widehat{\mathbf{x}}}_c,{\widehat{\mathbf{y}}}_c,{\widehat{\mathbf{z}}}_c\right]$. The instantaneous variations in capsule orientation can be derived from the gyroscope outputs as

$$\mathrm{\Delta }{\alpha }_c=g_x\mathrm{\Delta }t,\mathrm{\Delta }{\beta }_c=g_y\mathrm{\Delta }t,\mathrm{\Delta }{\mathit{\gamma }}_c=g_z\mathrm{\Delta }t$$ (26)

where Δ[α_c,β_c,γ_c] are the instantaneous angle variations at the capsule moving frame within a measurement loop that lasts Δt. The instantaneous capsule rotational matrix ΔR_c is then defined as

$$\mathrm{\Delta }{\mathbf{R}}_c={\mathbf{R}}_x\left(\mathrm{\Delta }{\alpha }_c\right){\mathbf{R}}_y\left(\mathrm{\Delta }{\beta }_c\right){\mathbf{R}}_z\left(\mathrm{\Delta }{\mathit{\gamma }}_c\right)$$ (27)

where R_x, R_y, and R_z are the rotational matrixes with respect to the x_c-, y_c-, and z_c-axis, respectively. Then, the axial-angle representation of the rotational matrix ΔR_c is derived, thus achieving the angle of rotation θ and the axis of rotation ω as

$$\begin{array}{l}\theta =\arccos (\frac{\text{trace}(\mathrm{\Delta }{\mathbf{R}}_c)-1}{2})\\ \omega =\frac{1}{2\sin (\theta )}{\displaystyle \sum _{j=1}^3({\widehat{\mathbf{e}}}_{c_j,i}\times {\widehat{\mathbf{e}}}_{c_{j}i+1})}\end{array}$$ (28)

where ê_{cj, i} and ê_{cj, i+1} are the unit vectors of the capsule frame at the ith and (i+1)th iterations, respectively. Finally, the axis-angle representation θ, ω must be reoriented according to the capsule orientation with respect to the global frame at the previous time step, ${\mathbf{R}}_c^{t-1}$. The third coordinate of the axial-angle representation corresponds to the capsule angle variation Δγ about ${\widehat{\mathrm{z}}}_w$. The capsule absolute orientation γ about the global axis ${\widehat{\mathrm{z}}}_w$ is achieved by summation of Δγ at each loop.

IV. Simulation-Based Validation

The proposed approach was validated using an NdFeB cylindrical EPM with an axial N52-grade magnetization, a diameter of 5 cm, and a length of 5 cm. The size L of the squared domain $\mathcal{G}\prime$ was fixed at 15 cm. The reference values for the magnetic field in $\mathcal{G}\prime$ were obtained using Comsol Multiphysics, using a pitch of 0.2 mm for the mesh. The mathematical analysis and simulations were performed by using MATLAB (MathWorks Inc).

A. Magnetic Direct Relationship

COMSOL Multiphysics (COMSOL, Stockholm, Sweden) was also used to create the 15 × 15 matrix Φ_r and the 18 × 18 matrix Φ_z relative to the radial and axial components of the magnetic field, respectively. These two matrices were interpolated using two vectors of modal basis functions ω and γ. The vector ω captures variations of the magnetic field as a function of radial distance r, which is given by

$$\begin{array}{l}\mathit{\omega }\left(r\right)=[1/2,\cos \left(\frac{\pi r}{L}\right),\sin \left(\frac{\pi r}{L}\right),\dots \\ \dots ,\cos \left(\frac{\pi 12r}{L}\right),\sin \left(\frac{\pi 12r}{L}\right),r,r^2,\dots r^5].\end{array}$$ (29)

Similarly, the dependence of the magnetic field on variations of the axial component z is captured by γ(z)

$$\begin{array}{c}\mathit{\gamma }\left(z\right)=[1/2,\cos \left(\frac{\pi z}{L}\right),\sin \left(\frac{\pi z}{L}\right),\dots \\ \dots ,\cos \left(\frac{\pi 12z}{L}\right),\sin \left(\frac{\pi 12z}{L}\right),z,z^2,\dots ,z^5].\end{array}$$ (30)

The modal basis functions were chosen based on simulation of the approximation residue with the minimum number of terms that provide a relative error of less than 10% within a portion of at least 70% of the domain $\mathcal{G}\prime$.

Both A_r and A_z were derived applying (15), thus obtaining 31 × 31 matrices. The interpolation was obtained by applying (11) and (12) to any radial and axial coordinates of the domain $\mathcal{G}\prime$. The interpolation error was evaluated by comparing the interpolated magnetic field with the reference values derived by COMSOL Multiphysics. Given the position vector ${\mathbf{p}}_{ci}={\left[r,z\right]}_i^T$ within $\mathcal{G}\prime$, Fig. 4(a) shows the module of the relative error for the radial magnetic field component, while Fig. 4(b) shows the module of the relative error for the axial component. Table I reports the portions of $\mathcal{G}\prime$ where the interpolation error is below 1%, 5%, 10%, and 20% for both the axial and the radial component of the magnetic field. The radial component estimation presents a relative error below 10% for the 86% of the radial magnetic field map. The axial component estimation shows that the 70% of the axial magnetic field map presents a relative error below 10%. Whenever the value of magnetic field intensity is very small, or null, a small approximation noise leads to a high relative error, as shown in Fig. 4. These results show an efficient estimation of both B_r and B_z, thus allowing the MDR to be analytically derived via (16).

Fig. 4.

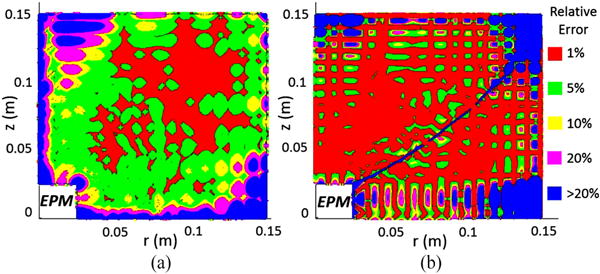
Relative error for the (a) radial and (b) axial magnetic field estimated by the MDR within $\mathcal{G}\prime$.

TABLE I.

Portions of $\mathcal{G}\prime$ Showing Different Levels of Relative Error in the Interpolated Magnetic Field From the Proposed Method and the Single Magnetic Dipole Model

Level of relative error	Radial Component	Axial Component
Below 1%	42%	30%
Below 5%	78%	61%
Below 10%	86%	70%
Below 20%	92%	79%
Magnetic dipole model	Radial Component	Axial Component
Below 1%	12%	0.4%
Below 5%	63%	2%
Below 10%	81%	5%
Below 20%	90%	10%

Fig. 5 shows the ratio of the relative error of the single-dipole model [29] to the relative error of our interpolation method, where the relative error is calculated with respect to the reference values derived by COMSOL Multiphysics. The blue regions—ratio between 0 and 1—of the maps correspond to a similar or better performance of interpolation for the dipole model compared with the proposed method. The dark red regions correspond to a ratio greater than 8. Table I reports the portions of $\mathcal{G}\prime$, where the interpolation error of the dipole model is below 1%, 5%, 10%, and 20% for both the axial and the radial component of the magnetic field. From these results, we can conclude that the proposed approach provides a more accurate approximation for the magnetic field in both components.

Fig. 5.

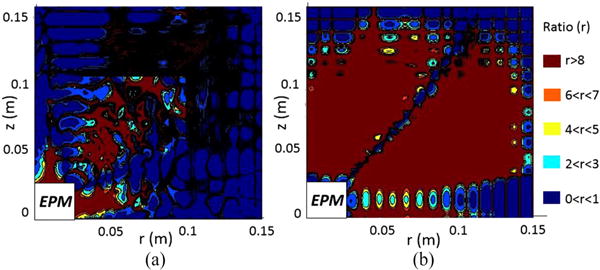
Ratio of relative errors of the single-dipole model to the interpolation model for the (a) radial and (b) axial magnetic field components. Black regions stem from visualization artifacts due to oscillations in the ratio from three to eight times.

B. Magnetic Inverse Relationship

The pose detection iterative method based on (22) was assessed by simulating the capsule motion along a spiral path, starting from a central position in the map p_c ≈ [0.09,0.055] m, reaching a final diameter of 1 cm, and assuming the orientation given. Fig. 6 shows the reference trajectory and its pose estimation. The color map represents the relative error of the radial coordinate. The estimation of the simulated capsule pose results in an axial coordinate relative error below 1%, with respect to its current position, for almost the entire simulation. The radial coordinate relative error is below 1% for the upper-right, lower-left, and lower-right quadrants of the spiral path represented in Fig. 6. The upper-left quadrant presents a relative error below 5%. This increased error is related to the radial localization error map of Fig. 4(a). Since the center of the spiral is at the upper-left quadrant of Fig. 4(a), where the radial error increases with proximity to the top-left corner, the error of localization along the spiral exhibits a similar trend. In addition, considering the noise of MFS readings, the outcome of the localization algorithm for each capsule position is represented by an ellipsoid of uncertainty (in cyan in Fig. 6). In this simulation, we used the noise levels of ±0.08 and ±0.05 mT in measuring B_r and B_z based on experimental characterization from the platform described in Section V-A. This simulation demonstrates an average sub-millimeter localization accuracy for both the radial and axial component.

Fig. 6.

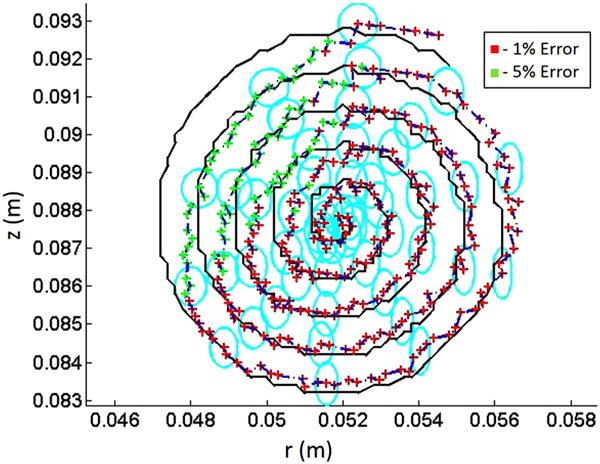
Simulated motion of a capsule along a spiral trajectory in the center of $\mathcal{G}\prime$. The black line represents the reference trajectory, while the crossed line shows the capsule position estimated by applying the Jacobian-based iterative method. The cyan ellipses represent the ellipsoid of localization uncertainty due to MFS noise. Colors in the crossed line express the relative error in position detection for the radial component.

V. Experimental Assessment

A. Experimental Platform

1) Hardware

The experimental platform, represented in Fig. 7(a), is composed of the WCE, the EPM, a robotic manipulator (RM), and a personal computer (PC) connected to a wireless transceiver via the universal serial bus (USB) port. The real-time algorithm runs on the PC and communicates with the capsule through a USB transceiver. The EPM is an NdFeB (magnetization N52, magnetic remanence 1.48 T) cylindrical permanent magnet with axial magnetization. The EPM diameter and length are both equal to 50 mm, while the mass is 772 g. A six-DOF robot (RV6SDL, Mitsubishi Corp., Japan) mounts at its end-effector the EPM. The robot is controlled in real time through a multithread C++ software application, which is described in Section V-A3. The manipulator is used to control and track the EPM position and orientation with respect to the global reference frame $\left[{\widehat{\mathrm{x}}}_w,{\widehat{\mathrm{y}}}_w,{\widehat{\mathrm{z}}}_w\right]$, which is assumed to be superimposed on the manipulator ground frame $\left[{\widehat{\mathbf{x}}}_0,{\widehat{\mathbf{y}}}_0,{\widehat{\mathbf{z}}}_0\right]$. The current EPM pose for the localization algorithm is derived from the robot end-effector pose, which is available at the application interface level with a resolution of 2 × 10⁻² mm in position and 1 × 10⁻³ degree in orientation. The EPM orientation frame $\left[\widehat{\mathbf{x}},\widehat{\mathbf{y}},\widehat{\mathbf{z}}\right]$ is an input for the localization algorithm (as described in Section II-C), while the EPM pose, as acquired by the robot encoders, is used as a reference position for the experimental assessment. A load cell (MINI 45, ATI Industrial Automation, USA), mounted in between the EPM and the RM, allows the EPM to be moved via admittance control for the general assessment described in Section V-B5.

Fig. 7.

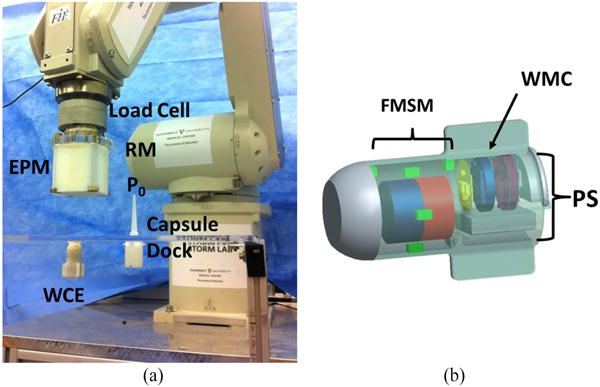
Experimental platform. (a) RM and EPM. (b) Visual rendering of the wireless capsule endoscope (WCE) and its internal components, where FMSM is the force and motion sensing module, WMC is the wireless microcontroller, and PS is the power supply.

2) Wireless Capsule

The WCE, schematically represented in Fig. 7(b), hosts the force and motion sensing module (FMSM), which was presented in [4], wireless microcontroller (WMC), and power supply (PS). The outer shell is fabricated in VeroWhite 3-D printer material (OBJET 30, Stratasys, USA). The current prototype is 36 mm in length, 17.5 mm in diameter, and 15 g in mass. The capsule shell has four lateral wings that are used as a reference to achieve a precise alignment for the capsule frame $\left[{\widehat{\mathbf{x}}}_c,{\widehat{\mathbf{y}}}_c,{\widehat{\mathbf{z}}}_c\right]$ during the calibration.

The FMSM is composed of six MFSs (MFS, A1391, Allegro MicroSystems, USA), an IMU embedding both an accelerometer and a gyroscope (LSM 330, STMicroelectronics, Switzerland), and an off-the-shelf NdFeB (N52) cylindrical magnet, which was axially magnetized with 1.48 T of magnetic remanence, 11 mm in diameter, and 11 mm in height. The readings of the magnetic sensors integrated in the FMSM are acquired by the onboard 16-bit analog-to-digital converter (ADC, AD7689, Analog Devices, Inc., USA). An acquisition cycle starts from sampling six analog inputs connected to the MFS outputs. Then, the six digitized values of acceleration and angular speed are received from the IMU. This dataset is acquired every 4.4 ms by the WMC (CC2530, Texas Instruments, USA) and used to build a 36-byte package together with the capsule status indicators (i.e., battery level, start/stop bytes). This package is then transmitted by the WMC to the external transceiver over a 2.4-GHz carrier frequency, with a refresh time of 6 ms (wireless data throughput 42.4 kbit/s), resulting in a sampling rate of 166 Hz. The external transceiver is based on an identical WMC that communicates with the PC through a USB-serial converter (UM232R, FTDI, U.K.).

The power supply module embeds a low-dropout voltage regulator (LDO) (TPS73xx, Texas Instruments, USA) to provide a stable supply to both the FMSM and the communication module. In order to limit the current consumption when the device is not acquiring measurements, a digital output of the microcontroller can drive the SLEEP pin of all the MFS. This results in a current consumption, which varies between 400 mA, when the microcontroller is in low power mode, and 20 mA when it is in IDLE mode with the radioactive. Average current consumption rises to 48 mA during a single cycle of sensor data acquisition and wireless transmission. The power source used is a 50-mAh, 3.7-V rechargeable LiPo battery (Shenzhen Hondark Electronics Co., Ltd., China).

3) Software Architecture

A multithread C++ WIN32 application running on the PC unbundles the data and shares them with three other parallel threads. The first thread controls the RM through a UDP/IP communication with a refresh rate of 140 Hz. It sends the desired pose to the robot controller and then receives the robot pose feedback. The second thread implements a digital Kalman filter for each of the six MFS and the six IMU outputs before running the iterative localization algorithm. The algorithm outputs the 6-DOF capsule pose estimation p = [x, y, z, α, β, γ] with respect to the EPM frame $\left[\widehat{\mathbf{x}},\widehat{\mathbf{y}},\widehat{\mathbf{z}}\right]$. The third thread manages a TCP/IP communication with a MATLAB application (Mathworks, USA), which displays the localization algorithm estimation. The data transfer rate for the robot controller applications is 83 Hz. The refresh time for the capsule pose estimation p and the capsule wireless data transfer is 6.8 ms (refresh rate 150 Hz). Referring to Fig. 8, the MATLAB application displays the capsule position and orientation p = [x, y, z, α, β, γ] with respect to the EPM reference frame $\left[\widehat{\mathbf{x}},\widehat{\mathbf{y}},\widehat{\mathbf{z}}\right]$ in real time (refresh every 30 ms) on a 3-D plot. Current pose numerical values are also displayed.

Fig. 8.

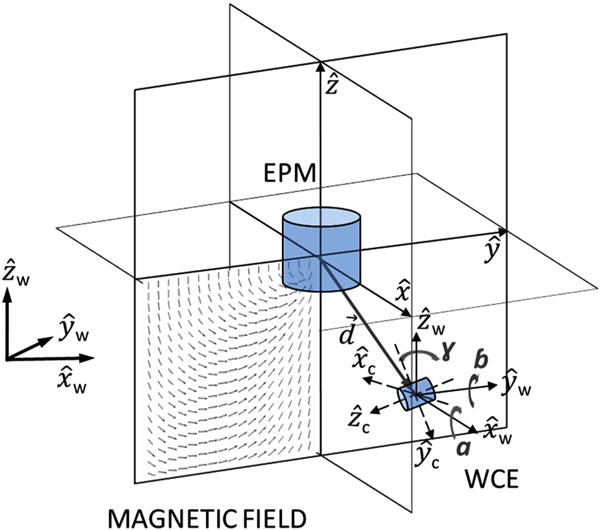
Schematic representation of the global frame, EPM frame, and capsule frame. The capsule orientation angles [α, β, γ] are shown with respect the global frame.

B. Experiments and Results

1) Capsule Orientation Algorithm Assessment

Because the localization method we propose also relies on real-time capsule orientation data, the first step in the experimental assessment consisted in validating the algorithm described in Section III. In order to quantify the absolute error in capsule orientation, the WCE was rigidly attached to the end-effector of the RM. The orientation of the WCE was varied within a range of ±90° about each of the three axes [x_EPM, y_EPM, z_EPM] by adopting combined motions for a total of one minute. Inertial data acquired by the WCE were sent over the wireless link, while the orientation of the end-effector, as measured by the RM built-in encoders, was adopted as a reference. The average orientation error was 3.4° ± 3.2° for α, 3.7° ± 3.5° for β, and 3.6° ± 2.6° for γ.

A second experiment aimed to quantify the steady-state drift for the capsule orientation algorithm. This is particularly relevant for the estimation of γ, which is obtained by iterative integration unlike α and β. For this test, the WCE was locked into the capsule dock (see Fig. 7 or Multimedia Attachment 1) for 7.5 min while acquiring data and running the capsule orientation algorithm. The average error and its standard deviation over the entire period was 0.34° ± 0.18° for α, 0.27° ±0.17° for β, and 1.8° ± 1.1° for γ, while the absolute error at the end of the 7.5 min was 0.5° for α, 0.2° for β, and 5.2° for γ.

2) Steady-State Positional Drift Evaluation

This set of experiments, referred to as T01, was aimed at evaluating the localization algorithm behavior in steady conditions. Before the trials began, the iterative localization algorithm was initialized as shown in Multimedia Attachment 1. The calibration consisted of three steps. First, the capsule was placed into the capsule dock, with a known position and orientation with respect to the global frame [x_w,y_w, z_w]. Then, the MFSs in the WCE were biased while maintaining the EPM outside the workspace. Finally, the EPM was moved to a reference position with respect to the WCE, and the relative distance between the EPM and the WCE, as derived by design, was used to initialize p(t = 0) (digitization phase in Multimedia Attachment 1).

After the initial calibration, the EPM was moved to eight different positions within the workspace, while the WCE was maintained in the capsule dock. Each position was chosen to be at about 10 cm from the center of the workspace along both the radial and axial coordinates. The radial and axial coordinates of the EPM were fixed to 80 and 130 mm, respectively. The azimuth coordinate θ_EPM was changed from zero to 2π in π/4 steps. Each EPM position was maintained for 1 min, while recording the localization data. The results were compared with the reference EPM pose as derived by the RM encoders. Table II reports the azimuth coordinate, the average radial error, and the average axial error for each of the eight EPM positions.

TABLE II.

Results of the Steady-State Positional Drift Experiment (T01)

θEPM(°)	T01-RE (mm)	T01-AR (mm)
0	0.3 ± 0.3	1.5 ± 0.5
45	1.5 ± 0.9	0.3 ± 0.3
90	7.2 ± 2.8	6.4 ± 3.3
135	4.4 ± 2.1	3.4 ± 1.6
180	0.5 ± 0.5	1.8 ± 0.8
225	5.1 ± 2.8	2.5 ± 1.2
270	3.7 ± 1.5	0.6 ± 0.2
315	0.5 ± 0.4	0.4 ± 0.3

For each trial, the relative error, the drift, and the residual measurement noise were statistically analyzed, while the system was not subjected to relative motion between the WCE and the EPM. The proposed localization method presented an average absolute and relative error for the radial component of 2.9 ± 1.4 mm and 1.85 ± 2.1%, respectively. The average absolute and relative errors for the axial component were 2.1 ± 1.0 mm and 1.9 ± 0.9%, respectively.

Typical trends for radial and axial component estimation are shown in Fig. 9. During the trials, the pose estimation presented a drift due to the system noise and the iterative integration. However, the relative error was always below 5%. The residual measurement noise [see Fig. 9(d)] had a Gaussian distribution (Jarque-Bera normality test with h equal to 1 and p-value 0.1) with null average and a bandwidth below 0.5%, which remained constant for the entire duration of each trial. The magnetic field measurement noise fused with the IMU measurements did not affect the localization algorithm, thus resulting in stable long-term behavior.

Fig. 9.

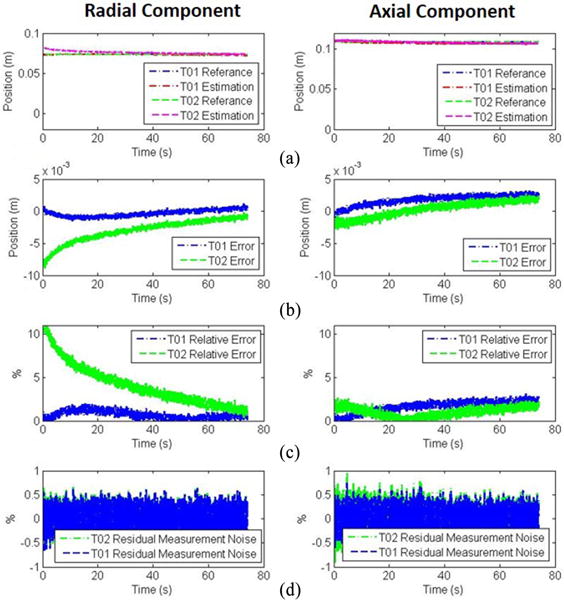
Results for the steady-state positional drift experiment (T01) and for the initialization error evaluation (T02) with an initialization error of 10 mm. Both T01 and T02 results are evaluated for the radial (left column) and the axial (right column) component. (a) Reference position versus estimation. (b) Absolute positional errors. (c) Relative positional errors. (d) Residual measurement noise. The azimuth error is presented in Fig. 12.

3) Robustness to Initialization Errors

This set of experiments, referred to as T02, was aimed at assessing the algorithm sensitivity to errors in position initialization. These trials were performed by moving the EPM to the same eight positions used for T01, while maintaining the WCE fixed into the capsule dock. For each EPM position, four different tests were performed by adding an increasing error e to the initialization distance p(t = 0) as measured during calibration. In particular, the error e had a random direction in $\widehat{\mathbf{r}}$ and $\widehat{\mathbf{z}}$ and an increasing module (i.e., 1, 5, 10, and 20 mm). As in T01, each test was 1 min long.

Considering all 32 tests performed, the average absolute and relative error for the radial component were 15.5 ± 4.2 mm and 19.5 ± 6.0%, respectively. The axial component had an average absolute error of 13.6 ± 3.9 mm and an average relative error of 12.1 ± 3.5%.

Typical trends for radial and axial component estimation affected by a 10-mm error in position initialization are shown in Fig. 9. In this case, the absolute and the relative error [see Fig. 9(b) and (c), respectively] decreased within the duration of the trial, never exceeding 10% of the reference value. Interestingly, the localization algorithm was able to correct the initialization error with time. The residual measurement noise for both the radial and the axial component [see Fig. 9(d)] presented the same behavior observed in T01 trials.

4) Robustness to Positional Lag

This set of trials aimed at evaluating the effect that a lag between the EPM and the WCE may have on the localization algorithm. In particular, our goal was to quantify the minimum value for the relative speed between the EPM and the WCE that would prevent the localization algorithm to converge. For reference, the typical endoscope absolute speed during a colonoscopy is in the order of 0.8–1.6 mm/s [30]. However, for magnetic capsule endoscopy, the relative EPM-WCE speed is ideally null, as the WCE should be following the EPM motion under the effect of magnetic coupling. This is true as long as the WCE is able to freely move inside the lumen.

After the initial calibration as described for T01, five trials were performed by moving the EPM at increasing speeds while collecting localization data. Like the previous experiments, the WCE was locked into the capsule dock. The EPM was initially positioned at 110 mm along the radial component and 110 mm along the axial component, and then moved by 200 mm along y_w at a constant acceleration. For the five trials, acceleration was set to 0.396, 0.793, 1.190, 1.587, and 1.984 m/s², respectively. Multimedia Extension 1 shows one of these trials, while the results for the experiment with 1.984 m/s² acceleration are reported in Fig. 10. As expected, the EPM motion along y_w affected only the radial component of the localization algorithm, leaving the axial component almost unperturbed.

Fig. 10.

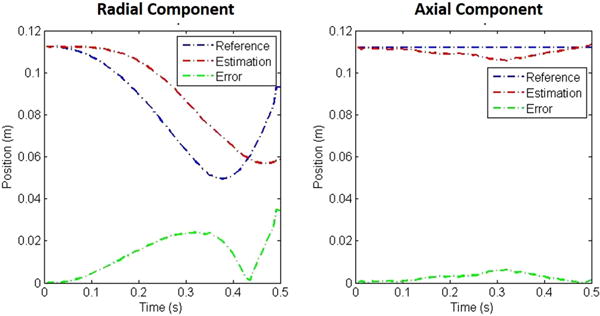
Position estimation results during the positional lag trial with uniform acceleration of 1.984 m/s.

For this set of trials, the localization algorithm presented a relative error in the radial component of 10% for a relative speed of 0.221 ± 0.046 m/s. This increased up to 20% for a relative speed of 0.335 ± 0.050 m/s. The average absolute error in the radial component was 11.86 ± 8.36 mm, with an average relative error of 16.3 ± 10.2%. For the axial component, the average absolute error was 2.66 ± 1.8 mm, with an average relative error of 2.3 ± 1.6%.

Given these results, we can conclude that the algorithm is sensitive to the relative speed between the WCE and the EPM and the relative error exceeds 10% if the relative speed is greater than 0.2 m/s. As previously discussed, this speed is well above the values that we expect to experience during magnetic manipulation of a WCE.

5) General Assessment

The final experiment aimed at validating the localization algorithm for a generic trajectory of the EPM, with the WCE fixed into the capsule dock. After calibration, the EPM was moved via admittance control to form a 3-D loop within the workspace, starting from the initialization position p(t = 0). During this trial, the EPM coordinates spanned from about −10 to 10 cm along both ${\widehat{x}}_w$ - and ${\widehat{y}}_w$ -axes, and from 6 to 12 cm away from the WCE position along the ${\widehat{\mathbf{z}}}_w$-axis.

For the entire trajectory, the proposed method of localization presented an average absolute error in the radial component of 6.2 ± 4.4 mm and an average relative error of 5.7 ± 7.6%. The average absolute error for the axial component was 6.9 ± 3.9 mm, with an average relative error of 7.0 4.9%. The average absolute error for the azimuth component (θ) was 5.4° ± 7.9°.

The trajectory (as reconstructed from the RM encoders) and its estimation are represented in Fig. 11. Typical trends for the radial (r), the axial (z), and the azimuthal (θ) component estimations are shown in Fig. 12(a), (c), and (e), while the absolute and relative errors are reported in Fig. 12(b), (d), and (f). The azimuthal component presents a large absolute error when the radial component of the capsule position is approaching zero. This is due to minor misalignments between the capsule and the EPM. This error is significantly attenuated in the conversion of the pose from cylindrical to Cartesian coordinates by applying (24), as the radial component p_r is very small or equal to zero.

Fig. 11.

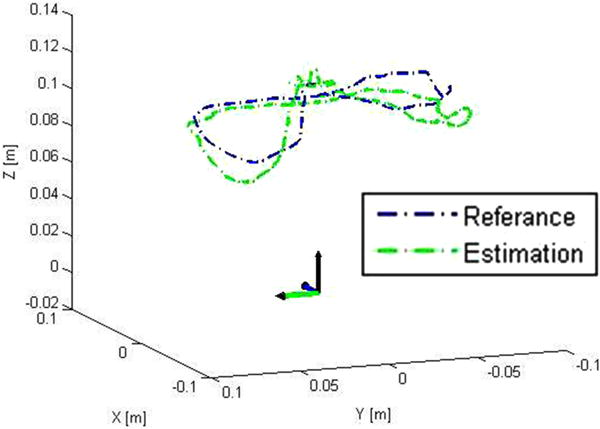
Three-dimensional representation of the EPM trajectory and its estimation by the localization algorithm.

Fig. 12.

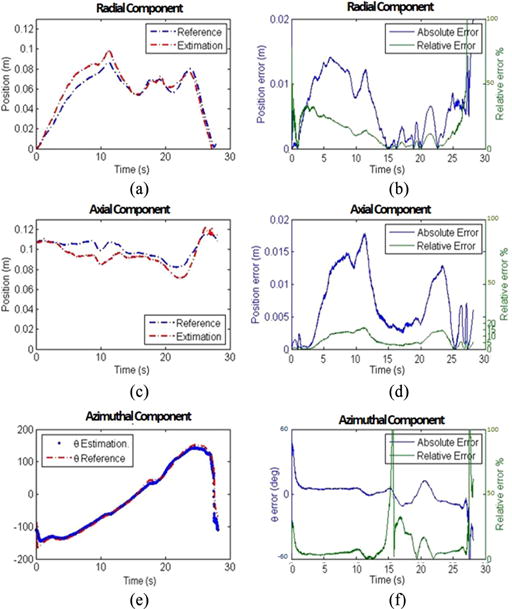
Typical trends for the (a) radial, (c) axial, and (e) azimuth components during the final experiment, and related absolute and relative errors (b, d, and f, respectively).

It is worth noting that the experimental assessment showed an error that is about one order of magnitude larger than what was observed by simulation. This is probably due to the noise introduced by the sensors and by the digitization process.

Real-time operation of the localization algorithm for random motion of the WCE is shown in Multimedia Extension 2. On the left side of the screen, the localization output is plotted in real time showing the WCE and the EPM reference frames.

In Multimedia Extension 3, the localization is performed while moving the EPM parallel to a plexiglass pipe placed at an angle with respect to the global frame. In this case, the WCE is free to move in the pipe under the effect of magnetic coupling. The distance between the EPM and the WCE is about 10 cm. The localization real-time output p = [x, y, z, α, β, γ] and the EPM position are both superimposed to the video stream. This demonstrates the ability of the proposed localization algorithm to track the WCE in real time during magnetic manipulation.

VI. Conclusion

This paper was motivated by the limitations of existing magnetic localization algorithms in terms of computational time, precision, and compatibility with magnetic manipulation of endoscopic capsules. To overcome these limitations, we put forward a new method for real-time localization using fusion of inertial data with information from MFSs, combined with an iterative Jacobian-based approach. Our strategy uniquely applies a parameterization of the magnetic field by using least-squares interpolation over an exact finite-element solution, thus overcoming the limitations of the simplistic dipole model. To achieve this parameterization, we used Kronecker products and a modal fitting to describe the magnetic field. To assist with real-time localization (which is paramount for solving a nonlinear inverse problem), we used the Jacobian of the magnetic field intensity relative to pose perturbations of the endoscopic capsule. This allowed the use of a local linearization approach that is similar to the resolved rates method for inverse kinematics of serial robots.

Our algorithm was evaluated by simulation and experiments. We investigated the robustness of our pose estimates of the wireless capsule to initialization errors. We also characterized the residual measurement noise and the effect of positional lag when the magnet driving the capsule was moving. Our results showed that, even though the proposed algorithm exhibits limitations of convergence for fast relative motions, the pose estimation of the magnetic capsule for clinically realistic speeds was effective and reliable. In particular, experimental results showed an average error (expressed in cylindrical coordinates) below 7 mm in both the radial and axial components, and 5° in the azimuthal component. The average errors for the capsule orientation angles, obtained by fusing gyroscope and inclinometer measurements, were 0.3° for α and β, and 5° for γ. Overall, the relative error always remained below 10%. The proposed localization algorithm was able to run at a 1-ms refresh rate, an order of magnitude below what was reported in previous works. The overall refresh rate, including sensor data acquisition and wireless communication, was 7 ms, thus enabling closed-loop control strategies for WCE magnetic manipulation running faster than 100 Hz. Since the least-squares interpolation presents some regions of the magnetic field domain $\mathcal{G}\prime$ where the relative error is greater than 20%, in future applications the robot path planner can be instructed to follow the capsule and to enclose it in an optimal localization area to avoid these regions.

Drift—a common problem in integrative methods—may become an issue over time and affect the precision of localization. A possible solution is to integrate the proposed approach with absolute localization strategies [3], [4] or with techniques fusing multiple sensor data having different resolutions and refresh rates, as proposed in [31]–[33] for SLAM applications. Since the final goal is to localize the capsule during magnetic manipulation, the behavior of the algorithm must be quantitatively assessed with the capsule in motion against a reference localization method (i.e., vision-based localization, as in [2]), exploiting also inertial navigation system theory by applying the extended Kalman filter [34], [35].

In summary, the proposed localization strategy is compatible with magnetic manipulation of WCE, does not require clear line-of-sight, and has a resolution that is finer than the capsule size, and a refresh rate that is adequate for real-time closed-loop robotic control. This represents an enabling technology that can move us toward intelligent control of a WCE during an endoscopic procedure.

Biographies

Christian Di Natali (S’10) received the B.S. and M.S. degrees (Hons.) in biomedical engineering from University of Pisa, Pisa, Italy, in 2008 and 2010, respectively.

In 2011, he joined Institute of BioRobotics of Scuola Superiore Sant’Anna, Pisa, as Research Assistant. In 2015, he received the Ph.D. degree in mechanical engineering from Vanderbilt University, Nashville, TN, USA, where he was actively involved in the design of advanced magnetic coupling for surgery and endoscopy, controlled mechatronic platforms, and magnetic localization.

Marco Beccani (S’11) received the Master’s degree in electronic engineering from University of Pisa, Pisa, Italy, in 2010 and the Ph.D. degree in mechanical engineering from Vanderbilt University, Nashville, TN, USA, in 2015.

He is a Postdoctoral Fellow with University of Pennsylvania, Philadelphia, PA, USA.

Nabil Simaan (SM’04) received the Ph.D. degree in mechanical engineering from Technion: Israel Institute of Technology, Haifa, Israel, in 2002.

In 2005, he joined Columbia University, New York, NY, NY, as an Assistant Professor. He was promoted to Associate Professor in 2010, and subsequently joined Vanderbilt University, Nashville, TN, USA, in the fall of 2010.

Dr. Simaan received the National Science Foundation Career Award to design new algorithms and robots for safe interaction with the anatomy in 2009.

Pietro Valdastri (M’05–SM’13) received the Master’s (Hons.) degree in electronic engineering from University of Pisa, Pisa, Italy, in 2002 and the Ph.D. degree in biomedical engineering from Scuola Superiore Sant’Anna, Pisa.

He is currently an Assistant Professor with the Department of Mechanical Engineering, Vanderbilt University, Nashville, TN, USA, and the Director of STORM Laboratory.

Dr. Valdastri received the National Science Foundation Career Award to study and design capsule robots for medical applications in 2015.